当前位置：文档之家 › 函数的连续性课件

函数的连续性课件

  • 格式：ppt
  • 大小：660.50 KB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

7-函数的连续性省公开课一等奖全国示范课微课金奖PPT课件

7-函数的连续性省公开课一等奖全国示范课微课金奖PPT课件

单调递增 (递减). (证实略)
比如,

y
sin
x
在
[
2
,
2
] 上连续单调递增，
其反函数 y arcsin x 在 [－1 , 1] 上也连续单调递增.
第16页
又如, y ex 在 ( , ) 上连续单调 递增, 其反函数 y ln x 在 ( 0, ) 上也连续单调递增.
定理3. （连续函数复合函数是连续）
x0
x) x
loga
e
例2. 求 lim a x 1. x0 x
解: 令 t a x 1, 则 x loga (1 t) ,
原式 lim t ln a t0 loga (1 t)
说明: 当 a e, x 0 时, 有 ln(1 x) ~ x, ex 1 ~ x
第22页
3
例3. 求 lim(1 2x)sin x .
x , 1 x
f (x) 0
当 x 1 时, x , f (x) 1 1 x
故 x 1 为跳跃间断点.
在 x 0, 1处, f (x) 连续.
第13页
内容小结
1. f (x) 在点 x0 连续等价形式
lim
x x0
f
(x)
f (x0 )
lim [
x0
f
( x0
x)
f
(x0 )]
0
f (x0 ) f (x0 ) f (x0 )
左连续 右连续
2. f (x) 在点 x0 间断类型
可去间断点 第一类间断点 跳跃间断点 左右极限都存在
第二类间断点
无穷间断点 振荡间断点
左右极限最少有一 个不存在
第14页

函数的连续性

函数的连续性
§1.6 连续函数的概念与性质
一、函数的连续性 二、函数的间断点
三、闭区间上连续函数的性质
首页
上页
返回
下页
结束
铃
一、函数的连续性
变量的增量
设函数y=f(x)在点x0的某一个邻域U(x0)内有定义 在邻域U(x0)内 若自变量x从初值x0变到终值x1 则称Dx=x1-x0为自变量x的增量 称Dy=f(x0+Dx)-f(x0)为函数y的增量
二、函数的间断点
y
y
f (x)在 x0 处无定义
O
x
0
x0
x
0
x0
y
f (x)在 x0 处无极限
O
x
0
x0
y
lim
xx0
f (x)

f
(x0 )
O

x
0
x0
二、函数的间断点
•间断点的定义
设函数 f(x)在点x0的某去心邻域内有定义 在此前提 下 如果函数 f(x)有下列三种情形之一
(1)在x0没有定义
这是因为 函数P(x)在(- +)内任意一点 x0处有定 义 并且
lim
x x0
P(
x)
=
P(x0
)

注: 如果区间包括端点 那么函数在右端点连续是指左连续
在左端点连续是指右连续
下页
连续函数
在区间上每一点都连续的函数 叫做在该区间上的 连续函数 或者说函数在该区间上连续
并且
f(0)=1>0 f(1)=-2<0
根据零点定理 在(0 1)内至少有一点x 使得 f(x)=0
即
x 3-4x 2+1=0

第二章7函数的连续性

第二章7函数的连续性
例4 求
x 2 2
e
解 考虑函数在 x =0 点的左右极限 4 3 1 x x 2 e x sin x 2e e sin x lim lim 4 4 x 0 x 0 1 e x x x e x 1
o
y
1
1
x
o
1
x
x 0为其跳跃间断点 .
练习题 1. 讨论函数 间断点的类型.
答案: x = 1 是第一类可去间断点 , x = 2 是第二类无穷间断点 .
x =0连续函数. 提示: f (0 0) 0 ,
1 x sin , x 0 , a ____ 0 时 f ( x) 在 2. 设 f ( x) x 2 a x , x0
e x cos x 例11 求 lim x 0 arcsin( 1 x )
x2
x 2
x 2
x 2
x 2
2
x 2
0 e cos x e cos 0 2 lim 解 x 0 arcsin( 1 x) arcsin( 1 0)
2
课本94页---习题28 ( 1 2 x 1) arcsin x （2） 求 lim x 0 tan x 2 2x x ( 1 2 x 1) arcsin x 2 解 lim lim 1 2 2 x 0 x 0 tan x x tan x sin x （3） 求 lim x 0 2 x 2 (e x 1) tan x sin x tan x sin x 解 lim lim x 0 2 x 2 (e x 1) x0 2 x 2 x 3 1 1 tan x(1 cos x) tan x sin x lim lim lim x 0 2 3 x 0 2 x3 2 x x x 0

函数的连续性

函数的连续性

f
2(x)
lim
x x0
f
(
x
)
lim
证明
由已知lim uu0
f (u)
f
(u0
),
lim
xx0
(
x
)
(
x0
)
lim xx0
f [(x)] lim uu0
f (u)
f (u0 )
f [(x0 )]
y
f
[
(
x
)]在x
处连续
0
lim f [ ( x)] f [ lim ( x)]
x x0
x x0
定理3 若函数y=f(x)在某区间上单值，单
调且连续，则它的反函数在对应的区间上也单 值，单调且连续且它们的单调性相同.
借助于该定理知,反三角函数,对数函数 在其定义域内也是连续的.
结论:基本初等函数在其定义域内是连续的.
定理4:初等函数在其定义区间内是连续的.
故初等函数的定义区间即为其连续区间
定理4:初等函数在其定义区间内是连续的.
注意：1.该定理很重要,应熟记.
f
(x)
1 x
,
x
0
0, x 0
x 0处无极限
函数 f ( x)在点 x0处连续必须满足的三个条件 :
(1)
f ( x)在点x0处有定义;
(2) lim x x0
f ( x)存在;
(3) lim x x0
f (x)
f ( x0 ).
一 1. .
函数在点x
处连续
0
定义 12 设函数 f ( x) 在U ( x0 )内有定义,如果
如果函数在开区间(a,b)内连续, 并且在左端点

数学分析 函数的连续性(课堂PPT)

数学分析 函数的连续性(课堂PPT)
例如, 函数y sin x在区间 (,)内是连续的.
如果函数在开区间(a,b)内连续, 并且在左端点
x a处右连续, 在右端点x b处左连续, 则称
函数 f ( x)在闭区间 [a,b]上连续. 记为：
f ( x) C[a,b].
2
10
例3 证明函数 y sin x在区间(,)内连续.
证 任取 x (,),
2
27
但反之不成立.
例
f
(
x)
1, 1,
x0 x0
在 x0 0不连续
但 | f ( x) |、 f 2 ( x) 在x0 0 连续
2
28
练习题
一、 填空题：
1、 指出 y x 2 1 在 x 1 是第_______类间 x2 3x 2
断点；在 x 2 是第_____类间断点 .
lim y 0，那末就称函数 f ( x)在点 x 连续, x 称为
x 0
0
0
f ( x)的连续点.
即
lim [
x 0
f
(
x0
x)
f ( x0 )] 0
2
5
例1
试证函数
f
(x)
x
sin
1 x
,
x 0, 在x 0
0, x 0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
当 x 0时, sin 1 上下震荡. x
这种情况称x=0为震荡间断点.
2
14
例5 符号函数
1 当x 0
y
sgn
x
0
当x 0

《连续性与间断点》课件

《连续性与间断点》课件

连续函数与无穷间断点
定义
无穷间断点是指函数在该点的极 限为无穷大。
举例
$f(x) = frac{1}{x}$在x=0处存在无 穷间断点，因为lim(x->0)f(x)=∞ 。
性质
无穷间断点会破坏函数的连续性， 因为该点的极限为无穷大。
PART 04
连续性与间断点的应用
利用连续性判断函数性质
总结词
连续函数与跳跃间断点
定义
性质
跳跃间断点是指函数在该点的左右极 限不相等，即函数在该点处发生“跳 跃”。
跳跃间断点会破坏函数的连续性，因 为该点的左右极限不相等。
举例
$f(x) = begin{cases} x, & x leq 0 2x, & x > 0 end{cases}$在x=0处存 在跳跃间断点，因为lim(x>0+)f(x)=0!=lim(x->0-)f(x)=0。
在某一点左侧和右侧的函数值相 等，即$f(x_{0} - 0) = f(x_{0} + 0)$，则称$x_{0}$为函数$f(x)$的 可去间断点。
描述
可去间断点是间断点中最容易处 理的一种，可以通过补充定义使 得函数在该点连续。
第二类间断点（跳跃间断点、无穷间断点）
定义
在某一点左侧和右侧的函数值不相等，即$f(x_{0} - 0) neq f(x_{0} + 0)$，则称 $x_{0}$为函数$f(x)$的跳跃间断点。如果函数值在某一点趋于无穷，则称该点为 无穷间断点。
详细描述
在物理学、工程学、经济学等领域中，许多实际问题 需要用到连续性与间断点的概念。例如，在物理学中 的速度、加速度、力的变化规律分析中，可以利用连 续性来描述平滑的变化过程；在经济学中的供需关系 、价格形成机制中，可以利用间断点来描述市场价格 的突变和调整。此外，在信号处理、图像处理等领域 中，连续性与间断点的概念也具有重要应用价值。

函数的连续性.pptx

函数的连续性.pptx

f (x)
0
x
在 点
连 续 的
0充
概念描述
概念引入 概念描述 举例分析 教学总结
3 函数在一点处连续的等价定义
lim
xx0
f
(x)
f
( x0 )
自变量的增量 x x x0
x x0 x x x0 0
因变量的增量
y f (x) f (x0)
lim y 0 x0
y
f (x0 )
f (x)
应用举例
概念引入 概念描述 应用举例 教学总结
例3 用连续性的增量定义证明函数 y x2在 x 2处连续.
证 设自变量在2处的增量为x,则相应的函数增量为
y (2 x)2 22 4x (x)2
因为
lim y
x0
lim
x0
4x
(x)2
0
所以根据连续性的增量定义可得
函数 y x2在 x 2处连续.
故函数 f ( x)在点x 0处不连续.
应用举例
概念引入 概念描述 应用举例 教学总结
例2
试证函数
f
(
x
)
x
sin
1 x
,
x 0, 在x 0
0, x 0,
处连续.
证 f (0) 0,
1
lim x sin 0,
x0
x
lim f (x) f (0), x0 由定义知，函数 f ( x)在 x 0处连续.
x0
x0
故推出a 2时，该函数在x 0处连续.
总结反思
函数 f (x)在 x0 处满足左连续
且右连续
概念引入 概念描述 举例分析 总结反思
设函数 f (x) 在U ( x0 )内有定义,若

函数的连续性(课件)

函数的连续性(课件)
四、函数的连续性
(一)、连续的定义 1.函数的增量
设函数f ( x)在O ( x0 )内有定义, x O ( x0 ), x x x0 , 称为自变量在点x0的增量.
y f ( x ) f ( x0 ), 称为函数 f ( x )相应于x的增量.
y
y f ( x)
x0
要使 f (0 0) f (0 0) f (0), a 1, 故当且仅当a 1时, 函数 f ( x )在 x 0处连续.
(三)、连续函数的性质
若函数f ( x ), g( x )在点x0处连续, 则 f ( x ) g( x ), f ( x) f ( x ) g( x ), (g( x0 ) 0)在点x0处也连续. g( x )
2)可去间断点 lim f ( x) A , 但(1)A f ( x0 ),
x x 0
或( 2) f ( x)在点x0处无定义 则称点x0为函数f ( x)的可去间断点.
注意 可去间断点只要改变或者补充间断处函 数的定义, 则可使其变为连续点.
例5
讨论函数 2 x , 0 x 1, f ( x ) 1, x1 x 1, 1 x, 在x 1的连续性
y
y
x
y f ( x)
y
x
0
0
x0
x 0 x x
x0
x 0 x
x
2.连续的定义
定义2.9 设函数y f(x)的定义域为D, x0 D, 若 lim f ( x) f ( x0 ), 则称f ( x)在x0连续.
x x 0
x0称为f ( x)的连续点.
与 lim f ( x) A定义的区别在于:

函数的连续性

函数的连续性

y y f x
a o

x b
17
例1.证明方程 x3 3x2 1 在(0,1)内至少有一个根. 证. 设 f (x) x3 3x2 1, f (x) C[0,1],
f (0) 1, f (1) 1, f (0) f (1) 0,
由零点定理知,在(0,1)内至少有一点 ,使得 f ( ) 0.
间断点的分类:
第一类间断点 ( 特点:左、右极限都存在 )

f f
( (
x0 x0
0) 0)
f ( x0 f ( x0
0 ), 0 ),
可去间断点； 跳跃间断点；
第二类间断点 (特点：左、右极限至少有一个不存在）
7
例4. 函数 f (x) 1 在x 0处无定义, 从而间断.
所以 f (x)在 x 0 处连续.
6
二、函数的间断点及其分类
f
(x) 在点x0
处连续.
12))..fli(mx0
) f
; (x)
;
3)
.
x x0
lim
x x0
f (x)
f ( x0 ).
以上三个条件只要有一条不满足,函数f (x) 在点 x0 处不连续. 即 f (x) 在点 x0 处间断, 并称 x0为函数f (x)的间断点.
10
定理1.9.2 (复合函数的连续性)
设函数 u g( x ) 在点 x x0 处连续, 函数 y f (u)在点u u0处连续, 则 函数 y f ( g( x )) 在点 x x0 处连续
g( x0 ) u0
lim f ( g( x )) f ( lim g( x ))

函数的连续性

函数的连续性
x y sin u 在(, )内连续, y sin 1 在(, 0) (0, )内连续.
x
定理6 一切初等函数在其定义区间内都是连续的.
定义区间是指包含在定义域内的区间.
注意 1. 初等函数仅在其定义区间内连续, 在 其定义域内不一定连续;
例如, y cos x 1, D {x | x 2k , k Z}
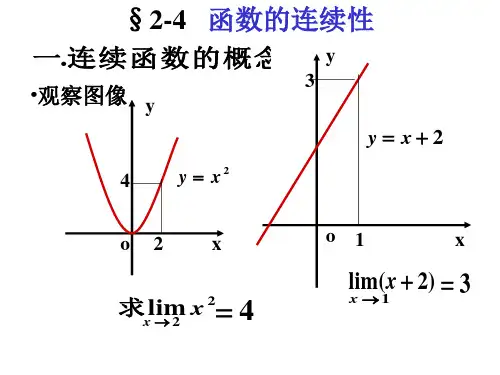
函数的连续性
一、函数的连续性 二、连续性原理 三、函数的间断点 四、闭区间上连续函数的性质
一、函数的连续性
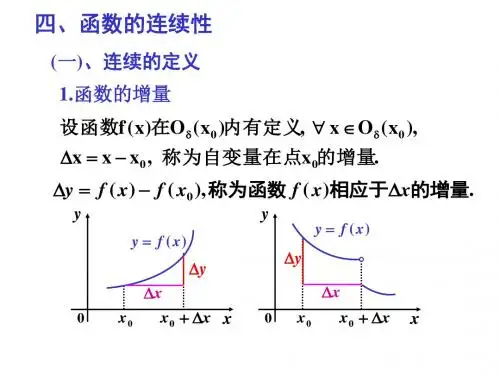
1.函数的增量
设函数 f ( x)在U ( x0 )内有定义, x U ( x0 ), x x x0 , 称为自变量在点 x0的增量.
y f ( x) f ( x0 ),称为函数 f ( x)相应于x的增量.
又 f (0) 1 0, f (1) 2 0, 由零点定理,
3.第二类间断点
如果 f ( x) 在点 x0 处的左、右极限至 少有一个不存在, 则称点 x0 为函数 f ( x)的 第二类间断点.
例6
讨论函数
f
(x)
1 x
,
x 0,在x 0处的连续性.
x, x 0,
y
解 f (0 0) 0, f (0 0) ,
x 0为函数的第二类间断点.
上连续，且 f (a)与 f (b) 异号(即 f (a) f (b) 0 ),
那末在开区间a, b内至少有函数f ( x) 的一个零
点,即至少有一点 (a b)，使 f () 0 .
即方程 f ( x) 0在(a, b)内至少存在一个实根 .
几何解释:
y
连续曲线弧 y f ( x)的两个 端点位于x轴的不同侧,则曲 a o
求 lim
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

f
(x)


x 2

2
x 1 x 1
2.5 2
o1
x
例如函数
f
( x)

1( x 1( x
0), 0),
y
如图，在点x=0附近，
1
o
x lim f (x) 1 f (0),
-1
x0
lim f (x) 1 f (0),
x0
因而函数 f (x) 在x=0处是右连续，而非左连续。
2、闭区间上连续：如果函数 f (x)
在开区间 (a, b) 内连续，在左端点x a
处右连续，在右端点x b 处左连续，就
说函数 f (x) 在闭区间[a, b] 上连
续。
例如，函数 y 1 x2 在闭区间[-1，1]上 连 内续 连， 续而，函在数闭间y [01，x 在1]上开不区连间续（，0，因1为） 它在左端点x=0处不是右连续。
x 1 4、 f (x) 0.5
x 1 x 1
y 2
o1
x=1处的极限存在，且 x 等于2，但不等于f（1）
lim f (x) 2 0.5 f (1)
x1
导致函数图象断开的原因：
y
y
y
2
2.5 2
2
o1 x
o1
x
o1
x
1、函数在 x 1 处没有定义
2、函数在 x 1时极限不存在
3、函数在 x 1处的极限值和
函数值不等
一般地，函数f（x）在点x0处连续 必须同时具备三个条件：
1、f (x0 ) 存在，即函数 f (x)
在点x0处有定义。
y 2
2、 lim f (x) 存在。 o 1 x
处连续
2、
f(x)在点x0处右连续。
lim
x x0
f (x)
f ( x0 )
f(x)在 x0 处左连续。
lim
x x0
f (x)
f (x0 )
3、 开区间内连续， 闭区间上连续
4、 结论：函数在一点处连续的充要 条件是即左连续又右连续
lim
x x0
f (x) lim x x0
练习：
1、连续函数的图象有什么特点？观察下列 函数的图象，说出函数在x=a处是否连续：
y
y
y
Oa x 连续
（1） y
Oa x 不连续
（2）
y
Oa x 连续
（3）
y
不连续 O a （4）
x
Oa x
不连续
（5）
O 不连续
a
x
（6）
y
y
oa
x
o
a
x
（7） 不连续
（8） 连续
2、利用下列函数的图象，说明函数在 给定点或开区间内是否连续。
2、 f (x) x2 1 x 1
x 1(x 1)
y 2
o1
x
在x 1处没有定义.
x 1
3、
f
(x)


x 2

2
x 1 x 1
y
（1）在x=1处有定义
2.5
2
（2） lim f (x) 2.5
x1
o1
x lim f (x) 2 x1
（3）函数f（x）的极限不存在。
(1) f (x) 1 ,点x 0; x
(2)h(x) sin x,点x 0.
解：如图
（1）函数
f (x) 1 x
在点x=0处
没有定义，因而它在点x=0
处不连续。
（2）因为 lim sin x 0 sin 0 x0
h(x) sin x在点x 0处连续.
二、单侧连续性：
x2
不连续
y
连续
o
x
(3) f (x) ax2 bx c,开区间(,); 连续
(4) f (x) x2 4 ,开区间(0,2). x2
连续
本节小结：
1、设函数f(x)在x x0 处及其附近有定义，
。 而且 lim f
则称函数f(x)x在x0点
(
x)
x0
f (x0 )
(1) f
( x)

1 x2
,点x
0;
(2) f (x) | x |, 点x 0；
(3) f (x) ax2 bx c,开区间(,);
(4) f (x) x2 4 ,开区间(0,2). x2
(1) f (x) 1 ,点x 0; (2) f (x) | x |,点x 0；
结论：函数在一点处连续的充要 条件是即左连续又右连续
lim
x x0
f
( x)
lim x x0
f (x)
f (x0 )

lim
xx0
f (x)
f (x0 )
y
o
x0
x
三、函数的连续性：
1、开区间内连续：如果f (x) 在某一开
区间 (a,b) 内每一点处都连续，就说函
数f（x）在开区间（a，b）内连续，或 说f（x）是开区间（a，b）内的连续函数。
f (x)
f (x0 )
5、 会用数形结合思想解某些数学问题 作业：P103习题1、2、3
如果函数 f (x) 在点 x0 处及其右侧
附近有定义 并且
y
lim
x x0
f (x)
f (x0 )
Oa x
则称f(x)在点 x0处右连续。
类似地：
如果函数 f (x) 在点x0处及其
左侧附近有定义，并且
lim
x x0
f (x)
f
(x0 )
则称f(x)在x0处是左连续。 如
y
x 1
一种是连续变化的情况 温度计
另一种是间断的或跳跃的
例如邮寄信件时的邮费随邮件质量的增加 而作阶梯式的增加等，这些例子启发我们去研 究函数连续与不连续的问题。
y分
80 60 40 20
40 80 120 160 x分
§2.6 函数的连续性(1)
一、函数在某一点处的连续性
y
1.y f (x)
o
(1)在x0处有定义.
(2) lim xx0
f
(x)

lim
xx0
f
(x)

f
( x0 )
x0
(3) lim
xxx0
f
(x)

f
( x0 )
如图：从直观上看，我们说一个函数在一点x=x0处 连续是指这个函数的图象在x=x0处没有中断，所以 以上图象就是连续函数的图象。也就是说，这个函
数在点x0处是连续的。
x x0
lim f (x) f (1)
x1
3、
lim
xx0
f
(x)

f
( x0 )
y
o
x0
定义：设函数f(x)在x x0处及其
附近有定义，而且
lim
xx0
f (x)
f (x0 )
则称函数f(x)在点 x0 处连续，
x0称为函数f(x)的连续点。
例1 讨论下列函数在给定点处的连续性：