空间直角坐标系

空间直角坐标系课件空间直角坐标系课件空间直角坐标系是数学中的一个重要概念，它在几何学、物理学等领域都有广泛的应用。

本文将通过介绍空间直角坐标系的定义、特点以及应用等方面，来探讨这一主题。

一、定义与特点空间直角坐标系是由三个相互垂直的坐标轴构成的，分别是x轴、y轴和z轴。

这三个轴构成了一个三维的坐标系，用来描述空间中的点的位置。

在空间直角坐标系中，每个点都可以用一个有序的三元组(x, y, z)来表示，其中x表示点在x 轴上的坐标，y表示点在y轴上的坐标，z表示点在z轴上的坐标。

空间直角坐标系具有以下特点：1. 三个坐标轴相互垂直：x轴与y轴、x轴与z轴、y轴与z轴两两垂直。

2. 坐标轴上的单位长度相等：在空间直角坐标系中，每个坐标轴上的单位长度相等，通常表示为1。

3. 坐标轴上的正方向：x轴正方向为从左向右，y轴正方向为从下向上，z轴正方向为从里向外。

二、应用领域空间直角坐标系在几何学、物理学等领域都有广泛的应用。

1. 几何学中的应用空间直角坐标系在几何学中被用来描述点、直线、平面等几何图形。

通过坐标系中的点的位置关系，可以计算两点之间的距离、直线的斜率、平面的方程等。

同时，空间直角坐标系还可以用来表示和计算向量的坐标。

2. 物理学中的应用在物理学中，空间直角坐标系常被用来描述物体的运动、力的作用等。

通过坐标系中的点的位置变化，可以计算物体的位移、速度、加速度等物理量。

同时，空间直角坐标系还可以用来表示和计算力的分解、合成等问题。

3. 工程学中的应用在工程学中，空间直角坐标系被广泛应用于建筑、机械、电子等领域。

通过坐标系中的点的位置关系，可以计算建筑物的结构、机械零件的尺寸、电子元器件的布局等。

同时，空间直角坐标系还可以用来表示和计算工程中的力、力矩等问题。

三、坐标系的转换在实际应用中，有时需要将一个空间直角坐标系转换为另一个空间直角坐标系。

坐标系的转换可以通过旋转、平移等方式进行。

通过坐标系的转换，可以方便地进行坐标的变换和计算。

空间直角坐标系在数学和物理学中，空间直角坐标系是一种常用的坐标系统，用于描述三维空间中的点、向量和物体的位置。

它由三个互相垂直的坐标轴（x轴、y轴和z轴）组成，构成了一个三维的直角坐标系。

一、空间直角坐标系的定义空间直角坐标系以原点为起点，通过选定的单位长度建立了三个相互垂直的坐标轴。

x轴代表水平方向，y轴代表垂直于x轴的水平方向，z轴代表竖直方向垂直于x、y轴。

这样，每一个点都可以用三个数字（x，y，z）表示其在空间直角坐标系中的位置。

二、坐标轴的性质和方向在空间直角坐标系中，每个坐标轴都具有以下性质：1. x轴：位于水平方向，从负无穷到正无穷延伸。

正方向为从左往右。

2. y轴：位于垂直于x轴的水平方向，从负无穷到正无穷延伸。

正方向为从前往后。

3. z轴：位于竖直方向，从负无穷到正无穷延伸。

正方向为从下往上。

空间直角坐标系中，x轴和y轴的交点称为原点（O），z轴的正方向与x轴和y轴的正方向形成右手螺旋规则关系。

三、点的表示和距离计算在空间直角坐标系中，任意一点P的坐标为（x，y，z）。

这意味着点P在x轴上的坐标为x，在y轴上的坐标为y，在z轴上的坐标为z。

点P到原点的距离可以由勾股定理计算：距离= √(x² + y² + z²)四、向量和运算在空间直角坐标系中，向量可以用其起点和终点的坐标差来表示。

例如，向量V可以表示为V = (x2 - x1, y2 - y1, z2 - z1)，其中(x1, y1, z1)为起点坐标，(x2, y2, z2)为终点坐标。

向量的加法和减法可以分别通过坐标的相加和相减进行计算。

例如，向量A = (x1, y1, z1)和向量B = (x2, y2, z2)的加法结果为A + B = (x1 +x2, y1 + y2, z1 + z2)。

五、空间坐标系的应用空间直角坐标系在几何学、物理学、工程学等领域中都有广泛的应用。

它可以用来描述点、线、面和三维物体的位置关系和运动状态。

空间直角坐标系概念空间直角坐标系是描述三维空间中点位置的一种数学工具。

它由三条相互垂直的轴组成，分别称为x轴、y轴和z轴，并且它们的交点被定义为原点O。

坐标轴及取向空间直角坐标系的坐标轴分别沿着三个方向延伸，形成一个三维的直角坐标网格。

其中，x轴水平向右延伸，y轴垂直向上延伸，z轴从原点O垂直向外延伸。

三个坐标轴的正向取向约定如下：•x轴正向：由原点O指向右侧•y轴正向：由原点O指向上方•z轴正向：由原点O指向观察者坐标表示在空间直角坐标系中，点的位置可以通过坐标进行表示。

每个点的坐标由三个实数(x, y, z)表示，其中x代表点在x轴上的投影长度，y代表点在y轴上的投影长度，z代表点在z轴上的投影长度。

点的坐标表示可以用元组表示法：(x, y, z)，例如点P的坐标为(3, 4, 5)，表示P 在x轴上的投影长度为3，y轴上的投影长度为4，z轴上的投影长度为5。

坐标系与空间图形的关系空间直角坐标系为我们描述和研究三维空间中的几何和物理问题提供了方便。

通过坐标系，我们可以精确地描述和定位空间中的点、直线、平面以及各种立体图形。

对于在坐标系中给定的点P(x, y, z)，我们可以通过确定其在每个坐标轴上的投影长度来准确地找到这个点。

同时，我们可以绘制平行于坐标轴的直线、平面和正多面体等图形，并通过坐标轴的刻度对它们进行测量。

坐标系转换在空间直角坐标系中，我们可以使用坐标系转换来完成不同坐标系之间的转换。

常见的坐标系转换包括：1.直角坐标系到柱坐标系的转换：给定点的直角坐标(x, y, z)，可以通过计算极径r和极角θ来表示它在柱坐标系中的位置。

2.直角坐标系到球坐标系的转换：给定点的直角坐标(x, y, z)，可以通过计算球心到该点的距离ρ，极角θ和方位角φ来表示它在球坐标系中的位置。

坐标系转换可以方便地在不同的坐标系中描述和研究问题，使问题的处理更加灵活和高效。

总结空间直角坐标系是描述三维空间中点位置的数学工具。

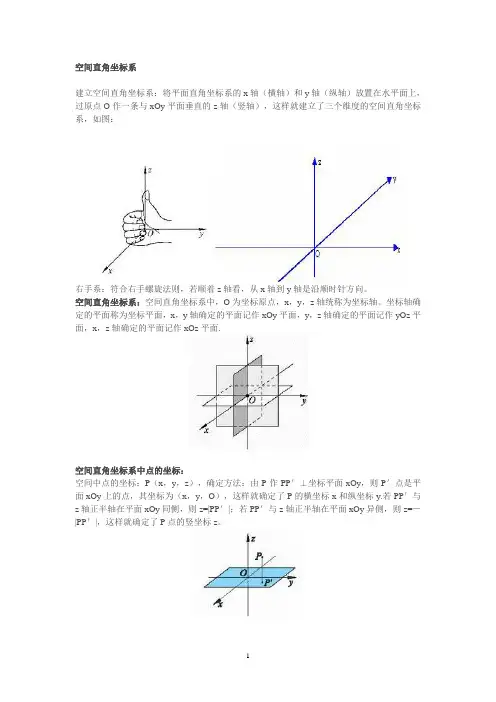
空间直角坐标系建立空间直角坐标系：将平面直角坐标系的x轴（横轴）和y轴（纵轴）放置在水平面上，过原点O作一条与xOy平面垂直的z轴（竖轴），这样就建立了三个维度的空间直角坐标系，如图：右手系：符合右手螺旋法则，若顺着z轴看，从x轴到y轴是沿顺时针方向。

空间直角坐标系：空间直角坐标系中，O为坐标原点，x，y，z轴统称为坐标轴。

坐标轴确定的平面称为坐标平面，x，y轴确定的平面记作xOy平面，y，z轴确定的平面记作yOz平面，x，z轴确定的平面记作xOz平面.空间直角坐标系中点的坐标：空间中点的坐标：P（x，y，z），确定方法：由P作PP＇⊥坐标平面xOy，则P＇点是平面xOy上的点，其坐标为（x，y，O），这样就确定了P的横坐标x和纵坐标y.若PP＇与z轴正半轴在平面xOy同侧，则z=|PP＇|；若PP＇与z轴正半轴在平面xOy异侧，则z=－|PP＇|，这样就确定了P点的竖坐标z。

坐标平面上点的坐标：①xOy 平面上点的坐标：（x ，y ，0）；xOz 平面上点的坐标：（x ，O ，z ）；yOz 平面上点的坐标：（0，y ，z ）；②x 轴上点的坐标：（x ，0，0）；y 轴上点的坐标：（0，y ，0）；z 轴上点的坐标：（0，0，z ）点的对称坐标点),,(c b a P 关于x 轴的对称点的坐标为),,(c b a --点),,(c b a P 关于y 轴的对称点的坐标为),,(c b a --；点),,(c b a P 关于z 轴的对称点的坐标为),,(c b a --；点),,(c b a P 关于坐标平面xOy 的对称点为),,(c b a -；点),,(c b a P 关于坐标平面xOz 的对称点为),,(c b a -；点),,(c b a P 关于坐标平面yOz 的对称点为),,(c b a -；点),,(c b a P 关于原点的对称点),,(c b a ---。

中点坐标公式：已知空间两点),,(),,(222111z y x Q z y x P ，则线段PQ 的中点坐标)2,2,2(212121z z y y x x +++空间直角坐标系中长方体各顶点的坐标：设长方体ABCD －A ＇B ＇C ＇D ＇的长、宽、高分别为，将A 点放在坐标原点，AB 放在x 轴正半轴上，AD 放在y 轴正半轴上，如图：则A （0，0，0），B （a ，0，0），C （a ，b ，0），D （0，b ，0），A ＇（0，0，c ），B ＇（a ，0，c ），C ＇（a ，b ，c ），D ＇（0，b ，c ）.空间两点间的距离公式空间任意两点A （x 1，y 1，z 1），B （x 2，y 2，z 2），则|AB|=例1：如图，正三棱柱ABC－A1B1C1各棱长均为2，试建立适当坐标系，确定各顶点的坐标。

空间直角坐标系公式引言：空间直角坐标系是描述空间中点位置的常用工具，它通过三个相互垂直的坐标轴来确定一个点的位置。

本文将介绍空间直角坐标系的公式及其应用。

一、空间直角坐标系的定义空间直角坐标系是由三个相互垂直的坐标轴组成，分别是x轴、y 轴和z轴。

这三个轴的交点被定义为原点O，它们的方向和长度可以任意确定。

二、空间直角坐标系的公式在空间直角坐标系中，每个点的位置可以通过三个坐标值来表示，分别是x坐标、y坐标和z坐标。

假设某点的坐标为(x, y, z)，那么它与坐标轴的关系可以通过以下公式来表示：1. x轴上的投影：P(x, 0, 0)2. y轴上的投影：P(0, y, 0)3. z轴上的投影：P(0, 0, z)4. 坐标原点O：P(0, 0, 0)三、空间直角坐标系的应用空间直角坐标系广泛应用于物理学、几何学和工程学等领域。

下面将介绍一些常见的应用。

1. 点的距离计算在空间直角坐标系中，两点之间的距离可以通过勾股定理来计算。

假设两点分别为A(x1, y1, z1)和B(x2, y2, z2)，它们之间的距离d 可以通过以下公式计算：d = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)2. 点的中点计算在空间直角坐标系中，两点之间的中点坐标可以通过以下公式计算：中点坐标 = ((x1 + x2) / 2, (y1 + y2) / 2, (z1 + z2) / 2)3. 点的划分比例计算在空间直角坐标系中，可以通过给定两点和一个比例来计算划分点的坐标。

假设两点为A(x1, y1, z1)和B(x2, y2, z2)，要求划分比例为m:n，划分点的坐标为P(x, y, z)。

可以通过以下公式计算：x = (mx2 + nx1) / (m + n)y = (my2 + ny1) / (m + n)z = (mz2 + nz1) / (m + n)4. 直线的方程计算在空间直角坐标系中，可以通过给定一点和一个方向向量来计算直线的方程。

空间直角坐标系与大地坐标系的区别一、介绍在地理和测绘学领域，空间直角坐标系和大地坐标系都是常用的坐标系统。

它们在表示和定位地球表面和地下空间位置时起着重要作用。

两者在概念、原理和应用上有着明显的区别，本文将从深度和广度两个方面对空间直角坐标系和大地坐标系进行全面评估，以便更好地理解它们的特点和适用范围。

二、概念和原理解析1. 空间直角坐标系空间直角坐标系是以直角坐标系为基础的三维坐标系统，其中的位置点由三个相互垂直的轴表示，分别为X轴、Y轴和Z轴。

在空间直角坐标系中，一个点的位置可由其在三个轴上的投影相对于坐标原点的距离来确定。

这种坐标系统适用于描述和定位地球表面之上的点位，并被广泛应用于工程测量、地理信息系统等领域。

2. 大地坐标系大地坐标系是以地球椭球体表面的地理坐标系为基础的三维坐标系统，其中的位置点由经度、纬度和高程三个参数来表示。

在大地坐标系中，经度和纬度确定了地球表面上的一个点的位置，高程则表示该点相对于平均海平面的垂直高度。

这种坐标系统适用于描述和定位地球表面和地下空间的点位，其精度和稳定性比空间直角坐标系更高。

三、深度分析1. 空间直角坐标系的特点在空间直角坐标系中，点的位置由X、Y、Z三个参数表示，可直观地描述位置之间的相对关系，适用于大规模工程测量和地理信息系统建设。

它的数学表达简单明了，易于计算和处理。

2. 大地坐标系的特点大地坐标系以地球椭球体表面的地理坐标为基础，能够准确描述地球表面的位置，具有较高的精度和稳定性。

其坐标参数经度和纬度可以准确地表示地理位置，高程参数则可用来描述地形和地势特征。

四、广度探讨1. 空间直角坐标系的应用空间直角坐标系广泛应用于工程测量、地图制图、城市规划等领域，能够准确表示建筑物、道路、地形等物体的位置和形状，支持复杂空间信息的处理和分析。

2. 大地坐标系的应用大地坐标系主要用于地理信息系统、卫星定位、导航等领域，能够精确表示地球表面上点位的地理位置和高程信息，支持地球科学研究和定位导航技术的发展。

空间直角坐标系的平面方程空间直角坐标系是一种常用的坐标系，由三个相互垂直的坐标轴组成，分别为x轴、y轴和z轴。

在空间直角坐标系中，平面可以用方程来表示，常见的平面方程有点法式、一般式和交点式。

1. 点法式：平面上的任意一点P(x, y, z)到平面上一点Q(x0, y0, z0)的距离与平面法向量n的内积等于0。

即：n·PQ = n·(P-Q) = 0，其中，n = (A, B, C)是平面的法向量，(x0, y0, z0)是平面上的已知点，(x, y, z)是平面上的任意一点。

点法式也可写为一般式：A(x-x0) + B(y-y0) + C(z-z0) = 0。

点法式是直观的表示平面的方程，容易从平面方程中读取出平面的法向量以及过平面上一点的坐标。

2. 一般式：平面的一般式方程形式为：Ax + By + Cz + D = 0，其中，A, B, C, D为实数，且A、B、C不同时为0。

一般式方程中的(A, B, C)为平面的法向量，而常数D则决定了平面的位置。

一般式方程比点法式更加简洁，更容易直接得到平面的法向量以及平面与坐标轴的交点坐标。

3. 交点式：平面与坐标轴的交点坐标可以用交点式方程表示。

当平面与x轴的交点坐标为(x, 0, 0)时，平面与x轴的交点式方程为：Ax + D = 0。

同样地，可以得到平面与y轴和z轴的交点式方程。

平面方程的相关参考内容包括如下内容：- 平面几何相关的教材和教辅资料，如《高中数学平面几何》、《高等代数几何学》等。

这些资料通常会详细介绍平面方程的相关理论和推导过程，帮助读者理解和掌握平面方程的概念和使用方法。

- 线上教学资源，如MOOC平台（慕课网、网易云课堂等）上的相关公开课程。

这些课程通常有专门的章节或视频讲解平面方程的知识点，配有例题和习题，方便学生对平面方程进行练习和巩固。

- 数学论坛和博客中有关于平面方程的讨论和解答。

在这些论坛和博客中，读者可以找到其他人提问和讨论的平面方程问题，以及其他人给出的解答和解释。

空间直角坐标系的平面方程空间直角坐标系是三维空间中最常用的坐标系之一，它由三个相互垂直的坐标轴组成，分别为x轴、y轴和z轴。

通过这三个坐标轴，我们可以在三维空间中精准地描述一个点的位置。

而平面方程则是通过坐标系中的点来描述平面的方程。

在空间直角坐标系中，平面方程的一般形式可表示为Ax + By + Cz + D = 0，其中A、B、C和D为实数常数。

这个方程描述了空间中所有满足该方程的点所构成的平面。

要确定一个平面的方程，我们需要知道平面上的一点以及平面的法向量。

法向量是垂直于平面的向量，它的方向决定了平面的朝向。

根据平面上的一点和法向量，我们可以使用向量的点积来得到平面的方程。

假设平面上有一点P(x0, y0, z0)，而平面的法向量为n(A, B, C)。

则从平面上任意一点Q(x, y, z)到点P的向量可以表示为向量PQ = <x-x0, y-y0, z-z0>。

根据向量PQ和法向量n的点积关系，有：<n, PQ> = 0展开得到：A(x - x0) + B(y - y0) + C(z - z0) = 0整理上式可得平面的方程：Ax + By + Cz - (Ax0 + By0 + Cz0) = 0这就是空间直角坐标系中平面的方程。

在该方程中，A、B、C分别对应平面的法向量的分量，而Ax0 + By0 + Cz0则是平面上任意一点的坐标乘以法向量的分量之和。

需要注意的是，如果A、B、C不全为0，则平面可以看作是一个无限大的平面。

如果A、B、C中有一个为0，那么平面将退化为一个平行于其他两个坐标轴的平面。

除了一般形式的平面方程，我们还可以根据不同的信息形式推导出不同的平面方程。

例如，如果已知平面上的三个点P1(x1, y1, z1)、P2(x2, y2, z2)和P3(x3, y3,z3)，我们可以通过求解这些点确定的向量所构成的矩阵的行列式来得到平面的方程。

另外，如果已知平面的法向量n以及平面上的一点P0，则可以使用法向量和点的坐标来得到平面的方程。