最新高考-高考数学定积分 精品
- 格式:doc
- 大小:416.14 KB
- 文档页数:6
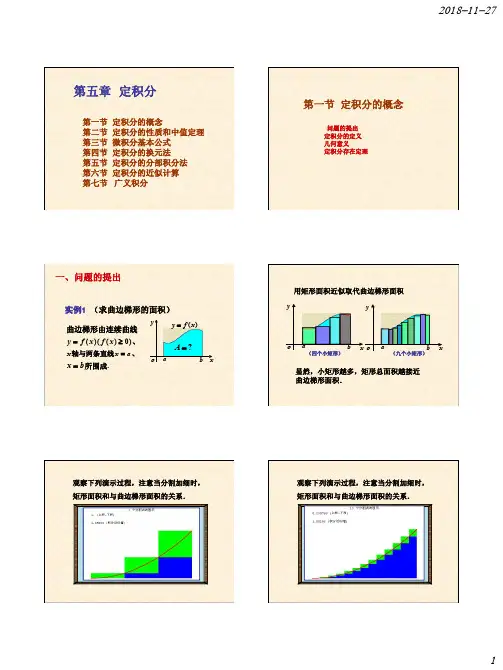
第五章 定积分第一节 定积分的概念第二节 定积分的性质和中值定理第三节 微积分基本公式第四节 定积分的换元法第五节 定积分的分部积分法第六节 定积分的近似计算第七节 广义积分问题的提出定积分的定义 几何意义定积分存在定理第一节 定积分的概念abxyo?=A 曲边梯形由连续曲线实例1 (求曲边梯形的面积))(x f y =)0)((≥x f 、x 轴与两条直线a x =、b x =所围成.一、问题的提出)(x f y =ab xyoab x yo用矩形面积近似取代曲边梯形面积显然,小矩形越多,矩形总面积越接近曲边梯形面积.(四个小矩形)(九个小矩形)观察下列演示过程,注意当分割加细时,矩形面积和与曲边梯形面积的关系.观察下列演示过程,注意当分割加细时,矩形面积和与曲边梯形面积的关系.观察下列演示过程,注意当分割加细时,矩形面积和与曲边梯形面积的关系.观察下列演示过程,注意当分割加细时,矩形面积和与曲边梯形面积的关系.观察下列演示过程,注意当分割加细时,矩形面积和与曲边梯形面积的关系.曲边梯形如图所示,,],[1210b x x x x x a b a n n =<<<<<=- 个分点,内插入若干在区间a bxyoi ξi x 1x 1-i x 1-n x ;],[],[11---=∆i i i i i x x x x x n b a 长度为,个小区间分成把区间形面积,曲边梯形面积用小矩上任取一点在每个小区间i i i x x ξ-],[1ii i x f A ∆ξ≈)(:))(],[(1近似为高为底,以i i i f x x ξ-(1)分割(2)近似ini i x f A ∆≈∑=)(1ξ曲边梯形面积的近似值为ini i x f A ∆=∑=→)(lim 10ξλ时,趋近于零即小区间的最大长度当分割无限加细)0(},,max{,21→∆∆∆=λλn x x x 曲边梯形面积为(3)求和(4)取极限实例2 (求变速直线运动的路程)设某物体作直线运动,已知速度)(t v v =是时间间隔],[21T T 上t 的一个连续函数,且0)(≥t v ,求物体在这段时间内所经过的路程.思路:把整段时间分割成若干小段,每小段上速度看作不变,求出各小段的路程再相加,便得到路程的近似值,最后通过对时间的无限细分过程求得路程的精确值.(1)分割212101T t t t t t T n n =<<<<<=- 1--=∆i i i t t t ii i t v s ∆≈∆)(τ部分路程值某时刻的速度(3)求和ii ni t v s ∆≈∑=)(1τ(4)取极限},,,max{21n t t t ∆∆∆= λini i t v s ∆=∑=→)(lim 10τλ路程的精确值(2)近似设函数)(x f 在],[b a 上有界,记},,,max{21n x x x ∆∆∆= λ,如果不论对],[b a 在],[b a 中任意插入若干个分点bx xx x x a nn =<<<<<=-121把区间],[b a 分成n 个小区间,各小区间的长度依次为1--=∆i i i x x x ,),2,1( =i ,在各小区间上任取一点i ξ(i i x ∆∈ξ),作乘积i i x f ∆)(ξ ),2,1( =i 并作和i i ni x f S∆=∑=)(1ξ,二、定积分的定义定义怎样的分法,⎰==ba I dx x f )(ii ni x f ∆∑=→)(lim 10ξλ被积函数被积表达式积分变量积分区间],[b a 也不论在小区间],[1i i x x -上点i ξ怎样的取法,只要当0→λ时,和S 总趋于确定的极限I ,我们称这个极限I 为函数)(x f 在区间],[b a 上的定积分,记为积分上限积分下限积分和几点说明:(1) 定积分是一个数值,它仅与被积函数及积分区间有关,⎰b a dx x f )(⎰=b a dt t f )(⎰=ba duu f )(而与积分变量的字母无关.)( ,)()( 2⎰⎰⎰=-=aaabbadx x f dx x f dx x f 规定:)(.],[)(],[)( 3的取法无关的分法及的和式的极限与所表示上可积,则在区间若)(i bab a dx x f b a x f ξ⎰,0)(≥x f ⎰=ba Adx x f )(曲边梯形的面积,0)(≤x f ⎰-=ba Adx x f )(曲边梯形的面积的负值a b xyo)(x f y =AxyoabA -)(x f y =三、定积分的几何意义1A 2A 3A 4A 4321)(A A A A dx x f ba ⎰=-+-,],[)(变号时在区间b a x f 三、定积分的几何意义.)(是面积的代数和⎰badx x f几何意义:积取负号.轴下方的面在轴上方的面积取正号;在数和.之间的各部分面积的代直线的图形及两条轴、函数它是介于x x b x a x x f x ==,)(++--当函数)(x f 在区间],[b a 上连续时,定理1定理2 设函数)(x f 在区间],[b a 上有界,且只有有限个间断点,则)(x f 在四、定积分的存在定理区间],[b a 上可积.例1 利用定义计算定积分.12dx x ⎰解将]1,0[n 等分,分点为nix i =,(n i ,,2,1 =)小区间],[1i i x x -的长度nx i 1=∆,(n i ,,2,1 =)取i i x =ξ,(n i ,,2,1 =)i i n i x f ∆∑=)(1ξi i ni x ∆=∑=21ξ,12i ni ix x ∆=∑=.,102的选取无关及法故和式极限与区间的分可积因为i dx x ξ⎰n n i ni 121⋅⎪⎭⎫ ⎝⎛=∑=∑==n i i n 12316)12)(1(13++⋅=n n n n ,121161⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=n n ∞→⇒→n 0λdx x ⎰102i i ni x ∆=∑=→210lim ξλ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=∞→n n n 121161lim .31= 几何上是曲线y=x 2,直线x=1及x 轴围成的曲边三角形面积.例2 利用定义计算定积分.121dx x⎰解在]2,1[中插入分点 12,,,-n q q q ,典型小区间为],[1ii q q -,(n i ,,2,1 =)小区间的长度)1(11-=-=∆--q qq q x i i i i ,取1-=i i qξ,(n i ,,2,1 =)i i ni x f ∆∑=)(1ξi ni ix ∆=∑=11ξ)1(1111-=-=-∑q q q i ni i ∑=-=ni q 1)1()1(-=q n 取2=nq即nq 12=),12(1-=n n )12(lim 1-+∞→xx x x xx 112lim1-=+∞→,2ln =)12(lim 1-∴∞→nn n ,2ln =dx x ⎰211i ni ix ∆=∑=→101lim ξλ)12(lim 1-=∞→n n n .2ln =i i ni x f ∆∑=)(1ξ原式⎥⎦⎤⎢⎣⎡π+π-++π+π=∞→n n n n n n n nsin )1(sin 2sin sin 1lim π=∑=∞→n i n n i n 1sin 1lim n n i ni n π⋅⎪⎭⎫ ⎝⎛ππ=∑=∞→1sin lim 1.sin 10⎰ππ=xdx ix ∆i ξ例3:将下列和式极限表示成定积分.⎥⎦⎤⎢⎣⎡-+++∞→n n n n n n πππ)(sin sin sin lim121 :五、小结1.定积分的实质:特殊和式的极限.2.定积分的思想和方法:分割化整为零求和积零为整取极限精确值——定积分求近似以直(不变)代曲(变)取极限Z .思考n n n n f n f n f ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim 试证.1)(ln ⎰=dxx f e 2:将和式极限,表示成定积分.⎥⎦⎤⎢⎣⎡-++-+-∞→2222241241141lim n n n n n 证明n n n n f n f n f ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫⎝⎛∞→ 21lim ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→=n n n n f n f n f e21lim ln n n n n f n f n f ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim 试证.1)(ln ⎰=dx x f e 利用对数的性质得⎪⎭⎫⎝⎛∑==∞→n i f n ni n e1ln 1lim n n i f ni n e1ln lim 1⋅⎪⎭⎫ ⎝⎛∑==∞→ 指数上可理解为:)(ln x f 在]1,0[区间上的一个积分和.分割是将]1,0[n 等分分点为nix i =,(n i ,,2,1 =)⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→=n n n n f n f n f e21ln lim 极限运算与对数运算换序得nn i f n i n 1ln lim 1⋅⎪⎭⎫ ⎝⎛∑=∞→⎰=10)(ln dx x f 故nn n n f n f n f ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim.10)(ln ⎰=dxx f e 因为)(x f 在区间]1,0[上连续,且0)(>x f 所以)(ln x f 在]1,0[上有意义且可积 ,2:将和式极限,表示成定积分.⎥⎦⎤⎢⎣⎡-++-+-∞→2222241241141lim n n n n n ⎰∑-=-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-++-+-=⎥⎦⎤⎢⎣⎡-++-+-=∞→∞→∞→1021222222222411)(41lim )(41)2(41)1(411lim 41241141lim dxx n ni n n n n n n n n n n i n n n 解第二节 定积分的性质、中值定理1.定积分性质2.中值定理对定积分的补充规定:(1)当b a =时,0)(=⎰ba dx x f ;(2)当b a >时,⎰⎰-=abb adx x f dx x f )()(.说明 在下面的性质中,假定定积分都存在,且不考虑积分上下限的大小.一、定积分性质和中值定理证⎰±ba dxx g x f )]()([i i i ni x g f ∆±=∑=→)]()([lim 10ξξλi i ni x f ∆=∑=→)(lim 10ξλii ni x g ∆±∑=→)(lim 10ξλ⎰=ba dx x f )(.)(⎰±ba dx x g ⎰±b a dx x g x f )]()([⎰=b a dx x f )(⎰±ba dx x g )(.(此性质可以推广到有限多个函数作和的情况)性质1⎰⎰=ba b a dx x f k dx x kf )()( (k 为常数).证⎰ba dx x kf )(ii ni x kf ∆=∑=→)(lim 10ξλi i n i x f k ∆=∑=→)(lim 1ξλii ni x f k ∆=∑=→)(lim 10ξλ.)(⎰=ba dx x f k 性质2⎰ba dx x f )(⎰⎰+=bcca dx x f dx x f )()(.补充:不论 的相对位置如何, 上式总成立.c b a ,,例 若,c b a <<⎰c a dx x f )(⎰⎰+=cb b a dx x f dx x f )()(⎰b a dx x f )(⎰⎰-=cb c a dxx f dx x f )()(.)()(⎰⎰+=bc ca dx x f dx x f (定积分对于积分区间具有可加性)假设bc a <<性质3dx b a ⋅⎰1dx ba⎰=a b -=.则0)(≥⎰dx x f ba. )(b a <证,0)(≥x f ,0)(≥ξ∴i f ),,2,1(n i =,0≥∆i x ,0)(1≥∆ξ∴∑=i i ni x f },,,max{21n x x x ∆∆∆= λi i ni x f ∆∴∑=→)(lim 1ξλ.0)(⎰≥=ba dx x f 性质4性质5如果在区间],[b a 上0)(≥x f ,例1 比较积分值dx e x⎰-20和dx x ⎰-20的大小.解令,)(x e x f x -=]0,2[-∈x ,0)(>x f ,0)(02>-∴⎰-dx x exdx ex⎰-∴2,02dx x ⎰->于是dx e x ⎰-2.20dx x ⎰-<性质5的推论:证),()(x g x f ≤ ,0)()(≥-∴x f x g ,0)]()([≥-∴⎰dx x f x g ba ,0)()(≥-⎰⎰ba ba dx x f dx x g 于是 dx x f ba ⎰)( dx x g ba ⎰≤)(.则dx x f ba ⎰)( dx x g ba ⎰≤)(. )(b a <如果在区间],[b a 上)()(x g x f ≤,(1)dx x f b a ⎰)(dx x f ba⎰≤)(.)(b a <证,)()()(x f x f x f ≤≤- ,)()()(dx x f dx x f dx x f ba ba ba ⎰⎰⎰≤≤-∴即dx x f ba ⎰)(dx x f ba⎰≤)(.说明: 可积性是显然的.|)(x f |在区间],[b a 上的性质5的推论:(2)设M 及m 分别是函数证,)(M x f m ≤≤ ,)(⎰⎰⎰≤≤∴ba ba b a Mdx dx x f dx m ).()()(a b M dx x f a b m ba -≤≤-⎰(此性质可用于估计积分值的大致范围)则 )()()(a b M dx x f a b m ba -≤≤-⎰.)(x f 在区间],[b a 上的最大值及最小值,性质6例2 估计积分dx x⎰π+03sin 31值的范围.解,sin 31)(3xx f +=],,0[π∈∀x ,1sin 03≤≤x ,31sin 31413≤+≤x ,31sin 31410030dx dx x dx ⎰⎰⎰πππ≤+≤.3sin 31403π≤+≤π∴⎰πdx x例3 估计积分dx xx⎰ππ24sin 值的范围.解,sin )(xx x f =2sin cos )(x x x x x f -='2)tan (cos x x x x -=⎥⎦⎤⎢⎣⎡∈2,4ππx ,0<)(x f 在]2,4[ππ上单调下降,,22)4(π=π=f M ,2)2(π=π=f m ,442π=π-π=-a b ,422sin 4224π⋅π≤≤π⋅π∴⎰ππdx x x .22sin 2124≤≤∴⎰ππdx x x 如果函数)(x f 在闭区间],[b a 上连续,上的平均值在],[)()(1b a x f dxx f a b ba⎰-则在积分区间],[b a 上至少存在一个点 ξ,使dx x f b a ⎰)())((a b f -=ξ. )(b a ≤≤ξ性质7(定积分中值定理)积分中值公式证Mdx x f a b m ba≤-≤∴⎰)(1)()()(a b M dx x f a b m ba -≤≤-⎰ 由闭区间上连续函数的介值定理知在区间],[b a 上至少存在一个点 ξ,)(1)(⎰-=ξbadx x f a b f dx x f ba ⎰)())((ab f -=ξ.)(b a ≤≤ξ即在区间],[b a 上至少存在一个点ξ,1. 积分中值公式的几何解释:xyoa b ξ)(ξf 使得以区间],[b a 为以曲线)(x f y =底边,为曲边的曲边梯形的面积等于同一底边而高为)(ξf 的一个矩形的面积。




高考数学定积分与微积分基本定理选择题1. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值2. 下列关于定积分与微积分基本定理的说法错误的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值3. 下列关于定积分与微积分基本定理的说法错误的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值4. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值5. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值6. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值7. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值8. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值9. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值10. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值11. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值12. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值13. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值14. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值15. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值16. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值17. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值18. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值19. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值20. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值21. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值22. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值23. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值24. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值25. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值26. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值27. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值28. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值29. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值30. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值31. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值32. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值33. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值34. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值35. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值36. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值37. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值38. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值39. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值40. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值41. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值42. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值43. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值44. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值45. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值46. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值47. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值48. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值49. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值50. 下列关于定积分与微积分基本定理的说法正确的是()A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值。



福建省各地高三最新模拟数学理试题分类汇编1、(福建省安溪八中高三12月月考)=-⎰-dx x 2224 ▲▲▲ .答案:π22、(福建省四地六校高三12月第三次月考)若函数f(a)=⎠⎛0a (2+sin x)dx ,则f ⎝⎛⎭⎫π2等于答案:π+13、(福建省长乐二中等五校高三上学期期中)如图,已知幂函数ay x =的图象过点(2,4)P ,则图中阴影部分的面积等于答案:384、(福建省东山第二中学高三上学期期中)计算:21x dx -=ò答案:525、(福建省龙岩一中高三上学期第三次月考)已知函数()⎪⎩⎪⎨⎧>≤≤--=,1,,11,12x e x x x f x 则⎰-21d )(x x f =__________.答案:22e e π+-6、(福建省南安一中)由曲线2,x y x y ==所围成图形的面积是_______答案:137、(福建省莆田一中)已知a 为常数,则使得⎰>e1d 1x xa 成立的一个充分而不必要条件是()A .0>aB .0<aC .e >aD .e <a答案:C8、(福建省清流一中)若8)cos (62=+⎰dx bx x a ,则=+⎰-dx bx x a )cos (662__________答案:16定积分9、(福建省泉州一中)如图,已知幂函数ay x =的图象过点(2,4)P ,则图中阴影部分的面积等于 . 答案:8310、(福建省福州八中高三毕业班第一次质检)设m =⎠⎛0π(sin t +cos t)dt ,求二项式(m x -1x)6展开式中含x 2项的系数及各项系数之和解析 ∵m =⎠⎛0π(sin t +cos t)dt =(sin t -cos t)| π0=2.…………4分∴(m x -1x )6=(2x -1x)6, 又T r +1=C r 626-r(-1)r x 3-r ,……………………………………………8分 令3-r =2,∴r =1,∴x 2项的系数为-192. ………………………………………………10分 令x =1知各项系数之和为1.……………………………………13分。

高考专题--定积分与微积分的基本定理高考考点:1、定积分的计算2、定积分的应用高考中对定积分的考查主要是考查定积分的概念和几何性质,以及利用微积分定理计算定积分、使用定积分求曲边梯形的面积,并能解决一些简单的物理问题等.在解题时要熟练运用微积分定理及定积分的相关运算性质求解,必要时运用数形结合的思想求解. 考点1 定积分的计算题组一 用牛顿—莱布尼茨公式求定积分调研1 已知函数1(10)()πcos (0)2x x f x x x +-≤≤⎧⎪=⎨<≤⎪⎩,则π21()d f x x -=⎰A .12 B .1 C .2 D .32【答案】D 【解析】πππ200222101113()d (1)d cos d ()|sin |1222x f x x x x x x x x ---=++=++=+=⎰⎰⎰,故选D.☆技巧点拨☆1.用牛顿—莱布尼茨公式求定积分的步骤(1)把被积函数变形为幂函数、正弦函数、余弦函数、指数函数与常数的积的和或差; (2)把定积分用定积分性质变形为求被积函数为上述函数的定积分; (3)分别用求导公式找到一个相应的原函数; (4)利用牛顿—莱布尼茨公式求出各个定积分的值; (5)计算原始定积分的值. 2.分段函数的定积分分段函数求定积分,可先把每一段函数的定积分求出后再相加. 题组二 用定积分的几何意义求定积分 调研2 计算333(cos )d x x x -=⎰.【答案】0【解析】∵3cos y x x =为奇函数,∴333(cos )d 0x x x -=⎰.调研3 若222d 2mx x x -π--=⎰,则m 等于 A .−1 B .0 C .1D .2【答案】B【解析】由已知可得: 22y x x =--的图象为圆:22(1)1x y ++=对应的上半部分,由定积分的几何意义可得0m =,故选B. ☆技巧点拨☆1.求定积分的三种方法(1)利用定义求定积分(定义法),可操作性不强; (2)利用微积分基本定理求定积分;(3)利用定积分的几何意义求定积分.当曲边梯形面积易求时,可通过求曲边梯形的面积求定积分.例如,定积分121d x x -⎰的几何意义是求单位圆面积的14,所以120π1d =4x x -⎰.2.奇偶函数的定积分(1)若奇函数y =f (x )的图象在[−a ,a ]上连续,则()d 0aa f x x -=⎰; (2)若偶函数y =g (x )的图象在[−a ,a ]上连续,则0()d 2()d aaag x x g x x -=⎰⎰.考点2 定积分的应用题组一 利用定积分求平面图形的面积 调研1 已知a >0,若曲线y x =、x a =与0y =所围成的封闭区域的面积为2a ,则a =________.【答案】49【解析】由题意322002d |3aa a x x x ==⎰,所以a =49. 调研2 已知{()|,01}1,0x y x y Ω≤≤≤≤=,A 是由直线x =1,y =0和曲线y =x 4所围成的曲边三角形的平面区域,若向平面区域Ω内随机投一点M ,则点M 落在区域A 内的概率为________. 【答案】15【解析】区域Ω对应的是边长为1的正方形,其面积为S =1.区域A 是由直线x =1,y =0和曲线y =x 4围成的曲边三角形,如图中阴影部分,故区域A 的面积为S A =14510011d |55x x x ==⎰.所以点M 落在区域A 内的概率为15. ☆技巧点拨☆利用定积分求平面图形的面积是近几年高考考查定积分的一个重要考查方向,多以选择题、填空题的形式考查.难度一般不大,属中低档题型.常见的题型及其解法如下: 1.利用定积分求平面图形面积的步骤 ①根据题意画出图形;②借助图形确定出被积函数,求出交点坐标,确定积分的上、下限; ③把曲边梯形的面积表示成若干个定积分的和; ④计算定积分,写出答案.注意:当曲边梯形位于x 轴上方时,定积分的值为正;当曲边梯形位于x 轴下方时,定积分的值为负;当位于x 轴上方的曲边梯形与位于x 轴下方的曲边梯形面积相等时,定积分的值为零. 2.知图形的面积求参数求解此类题的突破口:画图,一般是先画出它的草图;然后确定积分的上、下限,确定被积函数,由定积分求出其面积,再由已知条件可找到关于参数的方程,从而可求出参数的值. 3.与概率相交汇问题解决此类问题应先利用定积分求出相应平面图形的面积,再用相应概率公式进行计算. 题组二 定积分的物理意义调研3 一列火车在平直的铁轨上行驶,由于遇到紧急情况,火车以速度55()51V t t t=-++(t 的单位:s ,v 的单位:m/s)紧急刹车至停止.在此期间火车继续行驶的距离是 A .55ln 10 mB .55ln 11 mC .(12+55ln 7) mD .(12+55ln 6) m【解析】令55501t t -+=+,注意到t >0,得t =10,即行驶的时间为10 s. 行驶的距离s =1021000551(5)d [555ln(1)]|55ln1112t t t t t t -+=-++=+⎰,即紧急刹车后火车继续行驶的距离为55ln 11 m. ☆技巧点拨☆利用定积分解决变速直线运动问题和变力做功问题时,关键是求出物体做变速直线运动的速度函数和变力与位移之间的函数关系,确定好积分区间,得到积分表达式,再利用微积分基本定理计算即得所求. 强化训练:1.由曲线1xy =与直线y x =,3y =所围成的封闭图形的面积为 A .2ln3-B .ln3C .2D .4ln3-【答案】D2.设()[](]cos ,0,π1,π,2πx x f x x ⎧∈⎪=⎨∈⎪⎩,则()2π0d f x x =⎰A .0B .πC .π-D .π2【答案】B 【解析】由已知得()2πd f x x =⎰π2ππ2π0π0πcos d 1d sin ||πx x x x x +=+=⎰⎰,故选B.3.若π20π22sin d 4n x x ⎛⎫=+ ⎪⎝⎭⎰,则2ny y ⎛⎫+ ⎪⎝⎭的展开式中常数项为A .8B .16C .24D .604.已知平面区域(){,|0π,01}x y x y Ω=≤≤≤≤,现向该区域内任意掷点,则该点落在曲线2sin y x =下方的概率是 A .12B .1π C .2πD .π4【答案】A5.已知函数()f x 的部分图象如图所示,向图中的矩形区域随机投出200粒豆子,记下落入阴影区域的豆子数,通过100次这样的试验,算得落入阴影区域的豆子的平均数为66,由此可估计()2d f x x ⎰的值约为A .9925B .9950 C .310D .35【解析】由定积分的几何意义知()2d f x x ⎰的值即为阴影部分面积S ,再由几何概型可知6620023S=⨯,解得9950S =.故本题选B . 6.()22214d x x -+-=⎰___________.【答案】42π+ 【解析】由题意得()2222222214d 1d 4d x x x x x ---+-=+-⎰⎰⎰,令24y x =-,则()2240x y y +=≥,其图象为半圆,且面积为2π,又22221d |4x x --==⎰,所以填42π+. 7.如图所示,在平面直角坐标系内,四边形ABCD 为正方形且点C 坐标为11,2⎛⎫⎪⎝⎭.抛物线Γ的顶点在原点,关于x 轴对称,且过点C .在正方形ABCD 内随机取一点M ,则点M 在阴影区域内的概率为_________.【答案】238.设曲线cos y x =与x 轴、y 轴、直线π6x =围成的封闭图形的面积为b ,若()22ln 2g x x bx kx =--在[)1,+∞上单调递减,则实数k 的取值范围是__________.【答案】[0,)+∞【解析】由题意可知,ππ660π11cos d sin |sinsin 00622b x x x ===-=-=⎰,则()222ln 22ln g x x bx kx x x kx =--=--,()22g x x k x-'=-, 由()22ln 2g x x bx kx =--在[)1,+∞上单调递减,9.2(1)d x x -=⎰.【答案】0 【解析】2220011(1)d ()|42022x x x x -=-=⨯-=⎰.10.曲线2y x =与直线y x =所围成的封闭图形的面积为 . 【答案】16【解析】由题意可得封闭图形的面积为122310011111()d ()|23236x x x x x -=-=-=⎰. 11.执行如图所示的程序框图,输出的T 的值为 .【答案】错误!未找到引用源。

高考数学定积分应用选择题1. 定积分可以用来求解函数在区间上的最大值和最小值,已知函数f(x)在区间[a, b]上的最大值为M,最小值为m,则定积分∫[a,b]f(x)dx等于什么?2. 已知函数f(x)在区间[a, b]上的定积分∫[a,b]f(x)dx为10,且f(x)在[a, b]上是单调递增的,那么在区间[a, b]上f(x)的值域为[____,____]。
3. 已知函数f(x)在区间[a, b]上是单调递减的,那么在区间[a,b]上f(x)的定积分∫[a,b]f(x)dx等于什么?4. 已知函数f(x)在区间[a, b]上的定积分∫[a,b]f(x)dx为10,且f(x)在[a, b]上是单调递减的,那么在区间[a, b]上f(x)的值域为[____,____]。
5. 函数f(x)在区间[a, b]上的定积分∫[a,b]f(x)dx等于什么?6. 已知函数f(x)在区间[a, b]上的定积分∫[a,b]f(x)dx为10,那么在区间[a, b]上f(x)的值域为[____,____]。
7. 已知函数f(x)在区间[a, b]上是单调递增的,那么在区间[a,b]上f(x)的定积分∫[a,b]f(x)dx等于什么?8. 已知函数f(x)在区间[a, b]上的定积分∫[a,b]f(x)dx为10,且f(x)在[a, b]上是单调递减的,那么在区间[a, b]上f(x)的值域为[____,____]。
9. 已知函数f(x)在区间[a, b]上的定积分∫[a,b]f(x)dx等于什么?10. 已知函数f(x)在区间[a, b]上的定积分∫[a,b]f(x)dx为10,那么在区间[a, b]上f(x)的值域为[____,____]。
11. 已知函数f(x)在区间[a, b]上是单调递增的,那么在区间[a,b]上f(x)的定积分∫[a,b]f(x)dx等于什么?12. 已知函数f(x)在区间[a, b]上的定积分∫[a,b]f(x)dx为10,且f(x)在[a, b]上是单调递减的,那么在区间[a, b]上f(x)的值域为[____,____]。
定积分一、基础知识1、相关术语:对于定积分()baf x dx ⎰(1),:a b 称为积分上下限,其中a b ≥ (2)()f x :称为被积函数(3)dx :称为微分符号,当被积函数含参数时,微分符号可以体现函数的自变量是哪个,例如:()2bax t x d x+⎰中的被积函数为()2f x x tx =+,而()2baxt x d t +⎰的被积函数为()2f t xt x =+2、定积分()baf x dx ⎰的几何意义:表示函数()f x 与x 轴,,x a x b ==围成的面积(x 轴上方部分为正,x 轴下方部分为负)和,所以只有当()f x 图像在[],a b 完全位于x 轴上方时,()baf x dx ⎰才表示面积。
()baf x dx ⎰可表示数()f x 与x 轴,,x a x b ==围成的面积的总和,但是在求定积分时,需要拆掉绝对值分段求解3、定积分的求法:高中阶段求定积分的方法通常有2种:(1)微积分基本定理:如果()f x 是区间[],a b 上的连续函数,并且()()'F x f x =,那么()()()()|bb a af x dx F x F b F a ==-⎰使用微积分基本定理,关键是能够找到以()f x 为导函数的原函数()F x 。
所以常见的初等函数的导函数公式要熟记于心:()f x C = ()'0f x = ()f x x α= ()'1f x x αα-=()sin f x x = ()'c o s f x x = ()c o s f x x = ()'s i n f x x =- ()x f x a = ()'ln x f x a a = ()x f x e = ()'xf x e= ()log a f x x = ()'1ln f x x a =()ln f x x = ()'1f x x= ① 寻找原函数通常可以“先猜再调”,先根据导函数的形式猜出原函数的类型,再调整系数,例如:()3f x x =,则判断属于幂函数类型,原函数应含4x ,但()'434xx =,而()3f x x=,所以原函数为()414F x x C =+(C 为常数) ② 如果只是求原函数,则要在表达式后面加上常数C ,例如()2f x x =,则()2F x xC =+,但在使用微积分基本定理时,会发现()()F b F a -计算时会消去C ,所以求定积分时,()F x 不需加上常数。
图3定积分应用1、直角坐标系下平面图形面积的计算①连续曲线()(()0),y f x f x x a x b =≥==及及x 轴所围成的平面图形面积为()baA f x dx =⎰②设平面图形由上下两条曲线y =f 上(x )与y =f 下(x )及左右两条直线x =a 与x =b 所围成, 则面积元素为[f 上(x )- f 下(x )]dx , 于是平面图形的面积为: dx x f x f S ba ⎰-=)]()([下上. ③连续曲线()(()0),x y y c y d φφ=≥==及y 及y轴所围成的平面图形面积为()dcA y dy φ=⎰④由方程1()x y φ=与2()x y φ=以及,y c y d ==所围成的平面图形面积为12[()()]dcA y y dy φφ=-⎰ 12()φφ>例1 计算两条抛物线2x y =与2y x =所围成的面积.解 求解面积问题,一般需要先画一草图(图3),我们要求的是阴影部分的面积.需要先找出交点坐标以便确定积分限,为此解方程组:⎩⎨⎧==22y x x y得交点(0,0)和(1,1).选取x 为积分变量,则积分区间为]1,0[,根据公式(1) ,所求的面积为31)3132()(103102=-=-=⎰x x x dx x x S .一般地,求解面积问题的步骤为:(1) 作草图,求曲线的交点,确定积分变量和积分限. (2) 写出积分公式. (3) 计算定积分.例2 计算抛物线y 2=2x 与直线y =x -4所围成的图形的面积. 解 (1)画图.(2)确定在y 轴上的投影区间: [-2, 4]. (3)确定左右曲线: 4)( ,21)(2+==y y y y 右左ϕϕ.(4)计算积分⎰--+=422)214(dy y y S 18]61421[4232=-+=-y y y .例3 求在区间[21,2 ]上连续曲线 y=ln x ,x 轴及二直线 x =21,与x = 2所围成平面区域(如图2)的面积 。
高考中的定积分定积分是微积分根本概念之一,应掌握其概念、几何意义、微积分根本定理以及简单应用.下面例析在高考中的考查方式.一、计算型是指给出定积分表达式,求其值,通常解法有:定义法,几何意义法,根本定理法及性质法等.例1计算以下定积分: ⑴2211(2)x dx x -⎰;⑵30(sin sin 2)x x dx π-⎰. 分析:直接运用定义,找到一个原函数.解:⑴函数y =212x x -的一个原函数是y =32ln 3x x -. 所以2211(2)x dx x -⎰=3212(ln )|3x x -=162ln 233--=14ln 23-. ⑵函数y =sin x -sin2x 的一个原函数为y =-cos x +12cos2x . 所以30(sin sin 2)x x dx π-⎰=(-cos x +12cos2x )30|π=(-12-14)-(-1+12)=-14. 评注:利用微积分根本定理求定积分,其关键是求出被积函数的原函数.对于被积函数是绝对值或分段函数时,应充分利用性质()()()bc ba a c f x dx f x dx f x dx =+⎰⎰⎰,根据定义域,将积分区间分成假设干局部,分别求出积分值,再相加.练习:计算以下定积分:⑴322dx ⎰;⑵21|32|x dx -⎰. (答案:⑴39ln22+;⑵12). 二、逆向型 主要定积分的值,求定积分中参数.例2设函数2()(0)f x ax c a =+≠,假设100()()f x dx f x =⎰,001x ≤≤,那么0x 的值为 . 分析:此题是逆向思维题,可用求积分的一般方法来解决.解:112310001()()()3f x dx ax c dx ax cx =+=+⎰⎰ 203a c ax c =+=+. 033x =∴. 评注:常用方程思想加以解决.练习:a >0,且2aa x dx -•⎰=18,求a 的值.(答案:3)三、应用型主要指求围成的平面图形的面积及旋转体的体积.例3由直线12x =,x =2,曲线1y x =及x 轴所围图形的面积为〔 〕A .154B .174C .1ln 22D .2ln 2分析:可先画出图象,找出范围,用积分表示,再求积分即.解:如图,面积22112211ln |ln 2ln 2ln 22S x x ===-=⎰,应选(D).评注:用积分求围成面积,常常分四步:①画草图;②解方程组求出交点;③确定积分的上下限;④计算.练习:求由曲线y 2=x , y =x 2所转成的面积.(答案:13).。
定积分【知识梳理】(1)概念设函数f (x )在区间[a ,b ]上连续,用分点a =x 0<x 1<…<x i -1<x i <…x n =b 把区间[a ,b ]等分成n 个小区间,在每个小区间[x i -1,x i ]上取任一点ξi (i =1,2,…n )作和式I n =∑ni f1=(ξi )△x (其中△x 为小区间长度),把n →∞即△x →0时,和式I n 的极限叫做函数f (x )在区间[a ,b ]上的定积分,记作:⎰badx x f )(。
这里,a 与b 分别叫做积分下限与积分上限,区间[a ,b ]叫做积分区间,函数f (x )叫做被积函数,x 叫做积分变量,f (x )dx 叫做被积式。
基本的积分公式:⎰dx 0= ;⎰dx x m = (m ∈Q , m ≠-1);⎰x 1dx = ;⎰dx e x = ;⎰dx a x=a a x ln +C ;⎰xdx cos = ;⎰xdx sin = (表中C 均为常数)。
(2)定积分的性质 ①()ba kf x dx =⎰(k 为常数); ②()()baf xg x dx ±=⎰;③⎰⎰⎰+=bacabcdx x f dx x f dx x f )()()((其中a <c <b )。
(3)定积分求曲边梯形面积由三条直线x =a ,x =b (a <b ),x 轴及一条曲线y =f (x )(f (x )≥0)围成的曲边梯的面积⎰=ba dx x f S )(。
如果图形由曲线y 1=f 1(x ),y 2=f 2(x )(不妨设f 1(x )≥f 2(x )≥0), 及直线x =a ,x =b (a<b )围成,那么所求图形的面积 S =S 曲边梯形AMNB -S 曲边梯形DMNC = 。
【课前预习】 1.求下列定积分. (1)02dx π-⎰= ; (2)312x dx ⎰= ;(3)1831x dx -⎰= ; (4)122()x x dx ---⎰= ;2.求下列定积分.(1)24cos xdx ππ-⎰= ; (2)36sin xdx ππ-⎰= ;(3)22xdx ⎰= ; (4)21e edx x⎰= ; 【典型例题】题型一:利用积分公式求定积分值例1.计算下列定积分的值(1)⎰--312)4(dx x x ;(2)⎰-215)1(dx x ;(3)dx x x ⎰+20)sin (π;(4)dx x ⎰-222cos ππ;题型二:利用定积分求平面图形的面积例2 已知直线y ax =与曲线xy e b =+相交于点(0,0),(1,)y ,求直线y ax =与xy e b =+所围成的图形的面积。
§6.3定积分【复习目标】(1)通过实例(如求曲边梯形的面积、变力做功等),从问题情境中了解定积分的实际背景;借助几何直观体会定积分的基本思想,了解定积分的概念;会求简单的定积分。
(2)通过实例(如变速运动物体在某段时间内的速度与路程的关系),直观了解微积分基本定理的含义。
【重点难点】定积分的几何意义;利用定积分性质化简被积函数;求定积分值。
【知识梳理】(1)概念设函数f (x )在区间[a ,b ]上连续,用分点a =x 0<x 1<…<x i -1<x i <…x n =b 把区间[a ,b ]等分成n 个小区间,在每个小区间[x i -1,x i ]上取任一点ξi (i =1,2,…n )作和式I n =∑ni f 1=(ξi )△x (其中△x 为小区间长度),把n →∞即△x →0时,和式I n 的极限叫做函数f (x )在区间[a ,b ]上的定积分,记作:⎰badx x f )(。
这里,a 与b 分别叫做积分下限与积分上限,区间[a ,b ]叫做积分区间,函数f (x )叫做被积函数,x 叫做积分变量,f (x )dx 叫做被积式。
基本的积分公式:⎰dx 0= ;⎰dx x m= (m ∈Q , m ≠-1);⎰x 1dx = ;⎰dx e x = ;⎰dx a x=a a x ln +C ;⎰xdx cos = ;⎰xdx sin =(表中C 均为常数)。
(2)定积分的性质 ①()ba kf x dx =⎰(k 为常数); ②()()baf xg x dx ±=⎰;③⎰⎰⎰+=bacabcdx x f dx x f dx x f )()()((其中a <c <b )。
(3)定积分求曲边梯形面积由三条直线x =a ,x =b (a <b ),x 轴及一条曲线y =f (x )(f (x )≥0)围成的曲边梯的面积⎰=badx x f S )(。
如果图形由曲线y 1=f 1(x ),y 2=f 2(x )(不妨设f 1(x )≥f 2(x )≥0), 及直线x =a ,x =b (a<b )围成,那么所求图形的面积 S =S 曲边梯形AMNB -S 曲边梯形DMNC = 。
【课前预习】 1.已知2()f x x =,则与1()f x dx ⎰的值最接近的是( )A .10111()1010i i f =-⋅∑ B .100111()100100i i f =-⋅∑ C .1000111()10001000i i f =-⋅∑D .10000111()1000010000i i f =-⋅∑ 2.1||x dx ⎰= ( )A .0B .12C .1D .323.1-⎰= ( )A .πB .2πC .3D .324.求下列定积分. (1)02dx π-⎰= ; (2)3120x dx ⎰= ;(3)1831x dx -⎰= ; (4)122()x x dx ---⎰= ;5.求下列定积分.(1)24cos xdx ππ-⎰= ; (2)36sin xdx ππ-⎰= ;(3)22xdx ⎰= ; (4)21e edx x⎰= ; 【典型例题】题型一:利用定义求定积分例1.利用定积分定义,求1⎰题型二:利用积分公式求定积分值例2.计算下列定积分的值(1)⎰--312)4(dx x x ;(2)⎰-215)1(dx x ;(3)dx x x ⎰+2)sin (π;(4)dx x ⎰-222cos ππ;题型三:利用定积分求平面图形的面积例3 已知直线y ax =与曲线x y e b =+相交于点(0,0),(1,)y ,求直线y ax =与x y e b =+所围成的图形的面积。
题型四:已知定积分的值,求积分限或待定系数的值 ★例4 设函数sin()(0)3y x πωωω=->的周期为T ,若32T ππ<<,且66sin()32x dx πππωω--=⎰,求ω的值.题型五:求变速直线运动的路程及变力所做的功★例5 A ,B 两点在正东方向且相距100m ,质点M 从A 出发,沿东偏北30︒方向,以速度1(/)v m s =做直线运动,同时质点N 从B 出发,沿西偏北60︒方向以速度210(/)v at m s =+做直线运动.若质点M 与N 在C 点处相遇,求N 的速度★例6 在地面垂直向上发射火箭,设火箭质量为m ,火箭距地面高为h .求证:h →+∞时,克服重力所做的功为mRg .【巩固练习】1.曲线4y x =与曲线2y x =所围成图形的面积是 ( ) A .1240()x x dx -⎰B .1420()x x dx -⎰ C .02412()x x dx --⎰ D .04212()x x dx --⎰2.曲线dx = ( )A .2π-B .π-C .2πD .π 3.(sin cos )x x dx ππ--⎰= ( )A .1-B .0C .1D .2 4.1(1ln )ex dx +⎰= ( )A .2e B .2e C .e D .1e -5.2211x e dx --⎰= .6.已知函数112(1),01()2),(23)x x x f x x x --⎧+≤≤=≤≤≤≤⎪⎩,求30()f x dx ⎰★7.求曲线213:(10)2C y x x x =---≤≤与曲线2:(10)3x C y x x =-≤≤+所围成的图形的面积S .【本课小结】【课后作业】1.一物体做变速直线运动, v t -曲线如图所示, 则物体在0~6s s 间的运动路程为 ( )BA .254B .252C .25D .502.222(cos sin )22x x dx ππ--=⎰( )B A .2π B .π C .32π D .2π3.设2112log M xdx =⎰,2113log N xdx =⎰,则 ( )BA .M N >B .M N <C .||||M N <D .||||M N = 4.22|1|x e dx --=⎰5. 已知122011,()(2)a f a ax a x dx -≤≤=-⎰,求()f a 的值域★6.设()y f x =是二次函数,方程()0f x =有两个相等的实根,且()22f x x '=+. (1) 求()y f x =的表达式;(2)求()y f x =的图象与两坐标轴所围成图形的面积;(3)若直线(01)x t t =-<<把()y f x =的图象与两坐标轴所围成图形的面积二等分,求t 的值.§6.3定积分(简答)【课前预习】1.D2.C3.B4. (1)2π (2)25 (3) 92 (4)236- 5.(1)12+(2)122- (3)23log e (4)1 【典型例题】例1 (1)分割 (2)近似代替 (3)作和 (4)逼近12=⎰例2 (1(2)因为56)1(])1(61[-='-x x ,所以61|)1(61)1(216215=-=-⎰x dx x ;(3)(4)例3 13[(1)(1)]22x eS e x e dx =---=-⎰. ★例46666sin()cos()336x x dx x ππππππωωωω---=--==⎰15sin,22(),562666xx k k k Z ωωππππω∴==++∈∴=或.★例5 设质点M 与N 在0t t =时相遇.∵100,30,60,50AB A B AC BC =∠=︒∠=︒∴==∵(10)50t t at dt =+=⎰⎰,220003,(10)50,10,1,10(/)2t tN a t t t a v t m s =+=∴==-∴=-.★例62()()Mmf x GR x =+ 设克服重力所做的功为W ,则20011()()()hhMm Mm W G dx G GMm R x R x R R h==-=-+++⎰ 当0x =时,()f x mg =,∴2211,()R g G W mR g M R R h=∴=-+ 当h →+∞时,克服重力所做的功为W mRg =. 【巩固练习】1.C2.B3.B4.C5. 3322e e --6.(222ln 2ln 233-++- ★7.00002321111311()()[3ln(3)]2322x S x x dx dx x x dx x x dx x ----''=---=----++⎰⎰⎰⎰ln 27ln 81=--【课后作业】1.B2.B3.B4.222e e -+-5. 12212232002272()(2)(),()[,]322369a a a a f a ax a x dx x x f a =-=-=-+∴∈-⎰. ★6.(1)2()21f x x x =++ (2)13(3)由题意有0221(21)(21)ttx x dx x x dx ---++=++⎰⎰,得1t =.。