张家港市第一中学2020-2021第一学期初一数学第一次阶段性学情调研

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）试题1:的相反数是（）A．－2 B．2 C． D．试题2:某种面粉包装袋上的质量标识为“25±0.5kg”，则下列四袋面粉中不合格的是（）A. 26.1kgB. 25.5kgC. 24.8kgD. 24.5kg试题3:下列各数中，负数有（） A．2个 B．3个C．4个D．5个试题4:据统计，截止2010年10月31日上海世博会累计入园人数为 7308万, 这个数字用科学记数法表示为 ( )A．7×107 B．7.308×106 C．7.308×107 D．7308×104试题5:下列说法中，正确的是( )A．在数轴上表示－a的点一定在原点的左边B．有理数a的倒数是C．一个数的相反数一定小于或等于这个数D．如果一个数的绝对值等于这个数的相反数，那么这个数是负数或零试题6:下列各组式子中为同类项的是( )A．5x2y与－2xy2 B．－3x2y与yx2C．4x与4x2 D．6x3y4与－6x3z4试题7:如下图是一数值转换机的示意图，若输入的值为32，，则输出的结果为（）．是A． B．否 C． D．试题8:已知x、y互为相反数，a、b互为倒数，m的绝对值是3，则（） A．12 B．10 C．9 D．11试题9:已知：，则代数式的值为（）．A．5 B．14 C．13 D．7试题10:－3的倒数是，试题11:|－5|＝．试题12:比较大小，用“<”“>”或“＝”连接：(1)－ ______－； (2)－3.14 －︱－π︱试题13:单项式－的系数是多项式－a3b＋3a2－9是次三项式试题14:某日中午，北方某地气温由早晨的零下2℃上升了9℃，傍晚又下降了3℃，这天傍晚北方某地的气温是______℃．试题15:若4x2m y m+n与－3x6y2是同类项,则mn= ．试题16:一个三角形的第一条边为（x+2)cm,第二条边比第一条边长小3cm,第三条边长是第二边长的2倍，用含x的代数式表示这个三角形的周长试题17:手工拉面是我国的传统面食．制作时，拉面师傅将一根很粗的面条，把两头捏合在一起拉伸，再捏合，再拉伸，反复几次，就把这根很粗的面条截成了许多细细的面条，请问这样第次捏合后可拉出128根面条．试题18:定义：是不为1的有理数，我们把称为的差倒数，如：2的差倒数是，的差倒数是．已知，是的差倒数，是的差倒数，是的差倒数，……，依此类推，则．试题19:把下列各数填入表示它所在的数集的大括号内：（本小题4分）－2.4，3，2.008，－，1，－，0，－(－2.28)，，－|－4|正数集合：｛…｝负有理数集合：｛…｝整数集合：｛…｝负分数集合：｛…｝试题20:－9＋12－（－3）＋8试题21:试题22:试题23:试题24:4x－(x－3y)试题25:5a2－[3a－(2a－3)+4a2]试题26:已知t =,求代数式的值.试题27:如果代数式(2x2+ax－y+6)－(2bx2－3x+5y－1)的值与字母x所取的值无关，试求代数式的值. 试题28:试题29:试题30:若新规定这样一种运算法则：a※b=a2+2ab，（本小题5分）例如3※(－2)=32+2×3×(－2)=－3（1）试求（－2）※3的值（2）若（－2）※x= －2+ x , 求x的值试题31:23.有理数、、在数轴上的位置如图, （本小题6分）(1)判断正负，用“>”或“<”填空: c－b 0, a－b 0, a＋c 0.(2)化简: |c－b|＋|a－b|－|a＋c|试题32:国庆前夕，我国首个空间实验室“天宫一号”顺利升空，同学们倍受鼓舞，开展了火箭模型制作比赛，如图为火箭模型的截面图，下面是梯形，中间是长方形，上面是三角形．(1)用a、b的代数式表示该截面的面积S；(2)当a＝2cm，b＝3cm时，求这个截面的面积．试题33:某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入.下表是某周的生产情况（超产记为正、减产记为负）:星期一二三四五六日增减+5 －2 －4 ＋12 －10 ＋16 －9(1）根据记录的数据可知该厂星期六生产自行车___________ __辆；(2）根据记录的数据可知该厂本周实际生产自行车_____________辆；(3）产量最多的一天比产量最少的一天多生产自行车____________辆；(4）该厂实行每周计件工资制，每生产一辆车可得50元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？试题34:张家港市出租车收费标准如下：乘车里程3公里以内的收起步价10元，超过3公里的部分，每公里2元，超过15公里的部分，每公里3元．(1)如果有人乘出租车行驶了10公里，那么他应付车费_______元；(2)如果有人乘出租车行驶了x公里（x为大于15的整数），那么他应付多少车费？(3)某乘客乘出租车从张家港到江阴，共付车费43元，试估算从张家港到江阴大约多少公里？（结果取整数）试题35:观察下列有规律的数：，，，，，……根据规律可知（1）第7个数_____________,第n个数是______________(n是正整数) （2）是第__________个数（3）计算试题1答案:D试题2答案:A试题3答案:C试题4答案:C试题5答案:D试题6答案:B试题7答案:D试题8答案:D试题9答案:B试题10答案:，试题11答案:5试题12答案:＞，＞试题13答案:，四，试题14答案:4试题15答案:－3试题16答案:（4x－1）cm试题17答案:7试题18答案:4试题19答案:正数集合：｛ 3,2.008， ,－(－2.28) …｝负有理数集合：｛－2.4, , －,－|－4| …｝整数集合：｛ 3，0，－|－4| …｝负分数集合：｛－2.4，－，－…｝试题20答案:14试题21答案:－6试题22答案:－38试题23答案:试题24答案:3x+3y试题25答案:a2－a－3试题26答案:－1试题27答案:a=－3,b=1,试题28答案:－4试题29答案:－17试题30答案:(1) －8 (2)试题31答案:(1) ＞,＜,＞ (2) －2a试题32答案:(1) S=2ab+2a2(2) S=20cm2试题33答案:(1) 216 (2) 1408 (3) 26 (4) 70520 元试题34答案:（1）24元（2）（3x－11）元（3）18公里试题35答案:（1），（2） 11 （3）。

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）试题1:－2的倒数是 ( )A．－2 B．2 C．D．－试题2:下列四个数中，在－2与0之间的数是 ( )A．－1 B．1 C．－3 D．3试题3:某种零件规格是mm，下列尺寸的该种零件，不合格的是（）A．19.7 mm B．19.8 mm C．20 mm D．20.05 mm试题4:下列各式正确的是( . )A．= B．＞C．－3.14＞－ D．0＜－(+100)试题5:五个有理数的积为负数，其中负因数的个数一定不可能是（）A、1个B、3个C、4个D、5个试题6:下列运算正确的是 ( )A. B.C.3÷D.试题7:已知，两数在数轴上对应的点如图所示，下列结论正确的是（）A． B． C ． D．试题8:下列说法正确的是（）A.一定是负数B. 绝对值等于本身的数一定是正数C.若||=2，则=D. 若，则==0试题9:若＝1，＝4，且ab<0，则a＋b的值为（）A、B、C、D、试题10:在日历纵列上（如图）圈出了三个数，算出它们的和，其中不可能的一个是（）A．28 B．33 C．45 D．57试题11:规定向东为正，那么向西走5千米记为_______千米．试题12:某日最高温度是8℃，最低温度是－3℃，则这一天的日温差是_______℃．试题13:在数轴上将表示－2的点沿数轴移动3个单位长度，得到的点所表示的数是_______试题14:若，则试题15:绝对值不大于的所有整数的和是试题16:如图，从长为6、宽为4的长方形一角剪去一个小长方形，剩下图形的周长为试题17:某班5名学生在一次数学测验中的成绩以90分为标准，超过的分数记为正数，不足的分数记为负数，记录如下：－4，＋9，0，－1，＋6，则他们的平均成绩是分试题18:观察：，，，……猜想：（为正整数）试题19:试题20:试题21:试题22:试题23:试题24:试题25:－4、－5、＋7三个数的和比这三个数绝对值的和小多少？试题26:从－l中减去、－，结果是多少？试题27:若互为相反数，互为倒数，的绝对值是5，求的值试题28:给出下列各数：，－（+6），－1.5，0，，4．在这些数中，(1)整数是，非正数是(2)互为相反数的是，绝对值最小的数是______(3)画出数轴，将这些数表示在数轴上，并把这些数用“<”号连接起来。

江苏省张家港市2021-2021学年七年级数学上学期第一次课堂调研试题一、选择题〔每题3分，共24分〕60m 表示“向北走60m 〞，那么“向南走40m 〞可以表示为 〔 〕 A.m 20-B. m 40-C. m 20D. m 4023-的结果是 〔 〕A ．9B ．9-C ．6D ．6-…，0，－π，(－4)2，13，0．1010010001…〔相邻两个1之间依次多一个0〕中，无理数的个数是 〔 〕 A ．1B ．2C ．3D ．44．世界文化遗产长城总长约为6700000m ，假设将6700000用科×10n〔n 是正整数〕，那么n 的值为 ( ) A ．5B ．6C ．7D ．85．假设a ＝－a ，那么实数a 在数轴上的对应点一定在 〔 〕 A ．原点左侧 B ．原点或原点左侧 C ．原点右侧 D ．原点或原点右侧 6．实数a ，b 在数轴上的位置如下图，以下各式成立的是 〔 〕A ．a b<0 B ．a －b >0 C ．ab >0 D ．a ＋b >07.以下说法正确的选项是 〔 〕 ①0是绝对值最小的有理数 ②相反数大于本身的数是负数 ③数轴上原点两侧的数互为相反数 ④两个数比拟，绝对值大的反而小 A ．①② B ．①③ C ．①②③ D ． ①②③④ 8．为求1+2+22+23+…+22021的值，可令S=1+2+22+23+…+22021，那么2S=2+22+23+…+22021，因此2S －S=22021－1．仿照以上推理，计算出1+5+52+53+…+52021的值为 ( )A ．52021－1 B ．52021－1 C ．2016514- D ．2017514-二、填空题〔每题3分，共24分〕9．32-的倒数是 ． 10．不小于－3的负整数是 .11．数轴上距离3的点5个单位长度所表示的数是 ． 12. x =3，y =2，且0xy <，那么y x -等于 .13．假设2123x y ⎛⎫-++ ⎪⎝⎭＝0，那么y x的值是 ．14.计算(－0.25)2007×(－4)2021=____________.15.观察1+3=22，1+3+5=32，1+3+5+7=42，1+3+5+7+9=52……，那么猜测：1+3+5+…+(2n+1)= ．〔n 为正整数〕16．按右图程序计算，假设开场输入的值为9，那么输出的结果为 ．三、解答题〔共52分〕17．〔此题4分〕先把以下各数在数轴上表示出来，再按从小到大的顺序排列起来. 3.5，－(－2)，－1，122-．18．〔此题18分〕计算：(1) 24+(14)+(16)+8； (2) 157()(36)2912-+⨯-；〔3〕()()16944981-÷⨯÷-；(4)2129312323⎛⎫-÷+-⨯+ ⎪⎝⎭；(5) ()()32123332--÷⨯-- ； (6) 411110.563⎡⎤⎛⎫----⨯⨯ ⎪⎢⎥⎝⎭⎣⎦.19. 〔此题6分〕我们定义一种新运算：ab b a b a +-=*2.〔1〕求)3(2-*的值. 〔2〕求[])3(2)2(-**-的值．20. 〔此题8分〕一辆货车从货场A 出发，向东走了2千米到达批发部B ，继续向东走1.5千米到达商场C ，又向西走了5.5千米到达超市D ，最后回到货场．〔1〕用一个单位长度表示1千米，以东为正方向，以货场为原点，画出数轴并在数轴上标明货场A ，批发部B ，商场C ，超市D 的位置． 〔2〕超市D 距货场A 多远？ 〔3〕货车一共行驶了多少千米？21. 〔此题8分〕某灯具厂方案一天生产300盏景观灯，但由于各种原因，实际每天生产景观灯数与方案每天生产景观灯数相比有出入.下表是某周的生产情况(增产记为正、减产记为负):星期 一 二 三 四 五 六 日增减3+ 5- 2- 9+ 7- 12+ 3-〔1〕求该厂本周实际生产景观灯的盏数;〔2〕求产量最多的一天比产量最少的一天多生产景观灯的盏数;〔3〕该厂实行每周计件工资制，每生产一盏景观灯可得60元，假设超额完成任务，那么超过局部每盏另奖20元，假设未能完成任务，那么少生产一盏扣25元，那么该厂工人这一周的工资总额是多少元?22、〔此题8分〕观察以下等式111122=-⨯，1112323=-⨯，1113434=-⨯， 将以上三个等式两边分别相加得：1111111113111223342233444++=-+-+-=-=⨯⨯⨯． 〔1〕猜测并写出：1(1)n n =+ ．〔2〕直接写出以下各式的计算结果： ①111112233420062007++++=⨯⨯⨯⨯ ；②1111122334(1)n n ++++=⨯⨯⨯+ ．〔3〕探究并计算：124⨯+146⨯+168⨯+…+120122014⨯= ．参考答案一、选择题 BBBBB AAD 二、填空题9. 32-10. -3、-2、-1 11. 8或-2 12. 5或-5 13.91 14. -4 15. ()21+n 16. 112 三、解答题17. 图略；()5.321212<--<-<- 18 〔1〕、2 〔2〕、-19 〔3〕、1 〔4〕、4 〔5〕、-9 〔6〕、-2 19.〔1〕、1 〔2〕、1 20. 解：〔1〕数轴“略〞；〔2〕2千米； 〔3〕11千米。

张家港市第一中学2020－2021第一学期第一次阶段性学情调研初一数学一、选择题（本题每题2分，共30分） 1. 有理数31的相反数是( ) A. 31 B.－31 C. 3 D. －3 2. 有理数－2的倒数是( ) A. －2 B.－21 C. 2 D. 31 3. 在－(－5)，－(－5)2，－5-，(－5)3中负数有( )A. 0个B. 1个C. 2个D. 3个4. 跳远测验合格标准是4.00m ，夏雪跳出4.12m ，记为+0.12m ，小芬跳出3.95m ，记作( )A .+0.05m B. －0.05m C. +3.95m D. －3.95m5. 大于－3.5且小于2.5的整数共有( )个．A. 6 B. 5 C. 4 D. 36. 已知数a 、b 在数轴上对应的点在原点两侧，并且到原点的位距离相等；数x 、y 是互为倒数， 那么2xy b a 2-+的值等于( )A. 2 B.－2 C. 1 D. －17. 十一黄金周期间，孙大圣的家乡花果山接待游客约277000人，将277000用科学记数法表 示为( ) A. 27.7410⨯ B.2.77410⨯ C.2.77510⨯ D. 2.77610⨯ 8. 在数722,1010010001.0,2π,0,32 -中，无理数有( )A. 1个B. 2个C. 3个D. 4个9.有理数a ，b 所对应的点在如图所示位置，则下列表示正确的是( )A. a+b>0B.0>⨯b aC.0<b a D.b a > 10.若a a -=，则a 为( ) A. 负数 B. 正数 C. 非负数 D. 非正数1l. 如果m ⨯n >0，且m+n<0，则下列选项正确的是( )A. m<0，n<0B. m>0，n <0C.m ，n 异号，且负数的绝对值大D. m, n 异号，且正数的绝对值大12. 下列几种说法中，正确的是 ( )A. 最大的负有理数是－1B. 任何有理数的绝对值都是正数C. 0是最小的数D. 绝对值相等的两个数互为相反数或相等13. 已知a 、b 为有理数，且ab>0，则abab b b a a ++的值是( ) A. 3 B. －1 C. －3 D. 3或－l14. 填在下面各正方形中的四个数之间都有相同的规律，根据此规律，m 的值是( )15. 规定以下两种变换：①f(m ，n)=(m ，－n)，如f(2，1)=(2，－1)；②g(m ，n)=(－m ，－n)，如g(2，1)=(－2，－1)，按照以上变换有：f[g(3，4)]=f(－3，－4)=(－3，4)，那么g[f(－2，3)]等于( )A. （－2 ，－3）B. （2，－3）C. （－2，3）D. 3（2，3）二. 填空题（本题每空2分，共38分） 16. 比较大小 －722 －3（填=，>，<号） 17. 在数轴 上，若点A 与表示－l 的点相距3个单位，则点A 表示的数是18. 倒数等于本身的数是19. 的平方等于1620. 绝对值不大于3的所有负整数的和是21. 冬天某日上午的温度中5℃，中午上升了2℃达到最高温度，到夜间最冷时又下降了9℃， 则这天的是冷是 ℃22. 一个数是8，另一个数比它的相反数小1，另一个数是23. 已知2，－3，－4，6四个数，取其中的任意两个数求积，积最小是24. 某公交车原有20人，经过3个站台时上下车情况如下（上车为正，下车为负）：(+3，－5)、（+2，－5）、(6，－3)．则车上还有 人．25. 已知0)3(22=++-b a ，则b a 的值是26. 计算：=-+-++-+-+-+-100110004321)1()1()1()1()1()1(27. 若a<0，b>0，则a －b 一定是 (填负数，0或正数)28. 已知计算规则为bc ad d c ba -=，则45.042--= （填计算结果）29. 如图所示是计算机某计算程序，若开始输入x= －2，则最后输出的结果是 ．30. 规定符号（a ，b ）表示a 、b 两个数中小的一个，符号[a ，b]表示a 、b 两个数中大的一个， 则[－8，(－2, －6) ]= ．31. 已知6,8==b a ，若b a b a +=+，求a －b= ．32.已知,88,15441544,833833,3223222222b a b a ⨯=+⨯=+⨯=+⨯=+则 a+b =________．33.观察下列算式，...1176497,168077,24017,3437,497,77654321======通过观察， 用你发现的规律，写出7204的末位数字是 ．34.有一张纸片，第一次把它撕成4片，第二次把其中一片又撕成4片......如此下去，第10次 撕后共得小纸片 片．三、解答题：（共62分）35.（6分）①请你在数轴上表示下列有理数；)4(,0,5.2,21----②将上列各数用“<”号连接起来： ．36.计算下列各题（每题4分，共24分）（1） －20－（－14）－（－18）－13 （2）－21－12+33+12－67（2）)6(328747-⨯-÷ （4）)36()1279543(-⨯+--（5） 3243213)32(18⨯-⨯+-⨯ （6）[]24)3(5212--⨯--37.（5分）已知a 、b 为有理数，现规定一种新运算，满足a*b=a ⨯b －a+b(1) 求2*4的值； （2）求（1*3）*（－2）的值.38.（7分）阅读与计算：出租车司机小李某天上午营运时是A 广场门口出发，沿东西走向的 大街上进行的，如果规定向东为正，向西为负，他这天上午所接送八位乘客的行车里程(单位： km)如下：－3，+6，－2，+1，－5，－2，+9，－6.(1) 将最后一位乘客送到目的地时，小李在A 广场门口 （填东或西）面， km 处.(2) 若汽车消耗天然气量为0.2m 3/km ，这天上午小李接送乘客，出租车共消耗天然气多少立方米？39.（7分）探索规律：观察下面※由组成的图案和算式，解答问题：22431==+ 1+3+5=9=3224167531==+++252597531==++++（1）请猜想1+3+5+7+...+19=____________；（2）请猜想1+3+5+7+...+（2n －1）= _________；（3）请用上述规律计算：61+63+65+...+199的值.40.（6分）在计算 100993233...3331++++++的值时， 可设 S=100993233...3331++++++① ① 3⨯得31011003233...333+++++=S ② ②－①得 ,132101-=S 所以213101-=S （1）试利用上述方法求 2333218888++++⋅⋅⋅+的值， （2）猜一猜，下面哪个答案是231n x x x x ++++⋅⋅⋅+（x ≠1）的值.（把正确的题号写在横线上）.A.211-+n xB.111--+x x nC. 11-+x x n D.11--x x n41.（7分）如图，已知A ，B 分别为数轴上的两点，点A 表示的数是－30，点B 表示的数是50，直接写出下列各题答案．(1) 请写出到点A 和点B 距离都相等的点M 表示的数是 .(2) 现有一只蚂蚁P 从点B 出发，以每秒3个单位长度的速度沿数轴向左移动，同时另一只蚂蚁Q 恰好从点A 出发，以每秒2个单位长度的速度沿数轴向右移动，设两只蚂蚁在数轴上的点C 相遇，此时两只蚂蚁运动的时间为 秒，点C 对应的数是 .。

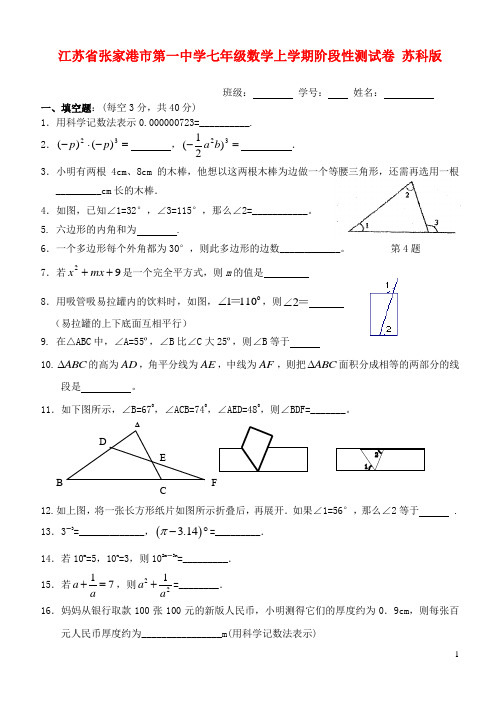
21A BCDEF 江苏省张家港市第一中学七年级数学上学期阶段性测试卷 苏科版班级： 学号： 姓名：一、填空题：(每空3分，共40分)1．用科学记数法表示0.000000723=__________. 2．=-⋅-32)()(p p ，=-32)21(b a ． 3．小明有两根4cm 、8cm 的木棒，他想以这两根木棒为边做一个等腰三角形，还需再选用一根_________cm 长的木棒．4．如图，已知∠1=32°，∠3=115°，那么∠2=___________。

5. 六边形的内角和为 .6．一个多边形每个外角都为30°，则此多边形的边数____________。

第4题 7．若92++mx x 是一个完全平方式，则m 的值是8．用吸管吸易拉罐内的饮料时，如图，ο1101＝∠，则＝2∠ （易拉罐的上下底面互相平行）9. 在△ABC 中，∠A=55º，∠B 比∠C 大25º，则∠B 等于10.ABC ∆的高为AD ，角平分线为AE ，中线为AF ，则把ABC ∆面积分成相等的两部分的线段是 。

11．如下图所示，∠B=670，∠ACB=740，∠AED=480，则∠BDF=_______。

12.如上图，将一张长方形纸片如图所示折叠后，再展开．如果∠1=56°，那么∠2等于 . 13．3－3=_____________，()3.14π-︒=_________．14．若10m =5，10n =3，则102m －3n=_________．15．若17a a+=，则221a a +=________．16．妈妈从银行取款100张100元的新版人民币，小明测得它们的厚度约为0．9cm ，则每张百元人民币厚度约为________________m(用科学记数法表示)（A ）（C ）（D ）（B ）（A ）D C BA （B ）D C B A （C ）D C B A （D ）D CB A17．计算：20022－2001×2003=__________．18．x 2+x+b 乘以x 2－ax －2的结果不含x 3项，则a=_________． 二、选择题：(每题3分，共24分)19.下列图形中，不能通过其中一个四边形平移得到的是 （ ）20．在下列各图的△ABC 中，正确画出AC 边上的高的图形是 （ ）21．下面计算正确的是 （ ）A 、a 4- a 4=a 0B. a 2÷a -2=a 4 C. a 2÷a -2=a 0D.a 4×a 6=a 2422．下列各式能用平方差公式计算的是（ ）A ．))(3(b a b a -+B ．)3)(3(b a b a +---C ．)3)(3(b a b a --+D ．)3)(3(b a b a -+- 23. 多项式36a 2bc －48ab 2c ＋24abc 2的公因式是（ ）A ．12a 2b 2c 2B ．6abcC ．12abcD ．36a 2b 2c24. 一个多边形的边数每增加一条，这个多边形的 （ ）A ．内角和增加3600B ．外角和增加3600C ．外角和增加1800D ．内角和增加180025．如图，△ABC 中，∠ABC 和∠ACB 平分线交于点O ， ∠BOC=120°，则∠A= ( )A 、30°B 、40°C 、55°D 、60°第18题26．如图，ABCDE 是封闭折线，则∠A+∠B+∠C+∠D+∠E 度数 为 ( ) A 、180 B 、270 C 、360 D 、540三、解答题：(共24+24+4+6+4+4分) 第19题 27.计算：（每题4分，共24分）（1）()()()12323223π--⎛⎫+-︒--+- ⎪⎝⎭(2) 98×272÷(－3) 1823)3()()2().3(a a a •-- （4）)21(3y x y -（5）)32)(23(b a a b -+ (6)(2a+b) 2－(2a －b)(a+b)28. 因式分解：（每题4分，共24分）(1)3ax －3ay 2(2)(a ＋b)2－a 2（3）()()x y y x a -+-93 （4）811824+-x x（5）652+-x x （6）2212b a a -++29． 如图AE ∥BD ，∠CBD=57°，∠AEF=125°，BC=4，CD=5．(1)求∠C 的度数；(2)求BD 的取值范围．(本题4分)30. 如图，E 为△ABC 的边BC 上一点，D 在BA 的延长线上，DE 交AC于点F ，∠B=45°，∠C=30°，∠EFC=70°，求∠D 的度数。

张家港市2022～2022学年度第一学期期末调研测试卷初一数学考前须知：本试卷共8页，全卷共三大题29小题，总分值130分，考试时间120分钟． 一、选择题：(本大题共10小题，每题3分，共30分，在每题给出的四个选项中，只有一项为哪一项符号题目要求的)1．－2的相反数是 ( ) A ．12 B ．－12C ．2D ．－2 2．有理数a 、b 在数轴上的位置如下图，那么a+b 的值 ( ) A ．大于0 B ．小于0 C ．小于a D ．大于b3．以下四个图中，是三棱锥的外表展开图的是 ( )4．用代数式表示“a 的3倍与b 的平方的差"，正确的选项是 ( ) A ．(3a －b)2 B ．3(a －b)2 C ．3a －b 2 D ．(a －3b)2 5．以下说法中正确的个数是。

( ) (1)以a 和8都是单项式．(2)多项式－3a 2 b+7a 2 b 2－2ab+1的次数是3．(3)单项式229xy -的系数为－2。

(4)x 2+2xy —y 2可读作x 2、2xy 、－y 2的和．A ．1个B ．2个C ．3个D ．4个 6．方程2(x －1)=13(4x －3)的解是 ( ) A ．32 B ．－32 C ．92 D ．－927．下面四个整式中，不学表示图中阴影局部面积的是 ( ) A ．(x+3)(x+2)一2x B ．25x x + C ．3(x +2)+x 2 D ．x(x+3)+68．如图，∠AOB=130°，射线OC 是么AOB 内部任意一条射线，OD 、OE 分别是么AOC 、∠BOC 的平分线，以下表达正确的选项是 ( ) A ．∠DOE 的度数不能确定 B ．∠AOD=12EOC C ．∠BOE=2∠COD D ．∠AOD+∠BOE=65° 9．代数式x +2y+1的值是3，那么代数式132x y --的值是 ( ) A ．1 B ．2 C ．3 D ．4 10．如图是由几个相同的小正方体搭成的几何体的三视图，那么搭成这个几何体的小主方体的个数是A ．9B ．8C ．7D ．6二、填空题：(本大题共8小题，每题3分，共24分，把答案填在题中横线上) 11．(1)3-________，(2)31()2-=________，(3)113的倒数是________．12．(1)0．4°=_____分，(2)58°5 4’=______度，(3)52°45’+30°32’=_____度____分． 13．用科学记数法表示：696000000=6．96×10n ，那么n=_________． 14．如图，A 、O 、B 在同一条直线上，如果OA 的方向是北偏西24°28’，那么OB 的方向是东偏南________(即∠BOC 的大小)．15．如图，∠AOC=90°，∠BOC 与∠COD 互补，∠COD=115°那么 ∠AOB 的度数为________．16．关于x 、y 的单项式A=3nx 3y m 、B=2mx n y 2，假设A+B=kx 3y 2， 那么A －B=___________．17．3243x y kx y k +=⎧⎨-=+⎩，如果x 与y 互为相反数，那么2421k k ++=________18．x ，y 为有理数，现规定一种新的运算*，满足x*y=xy+1，那么(1*4)*(－2)=________三、解答题：(本大题共11小题，共76分，解容许写出必要的计算过程、推演步骤或文字说明)(本大题共3小题，每题8分，总分值24分) 19．计算：(1)111(4)()99618-⨯--⨯， (2)324350.2(2)5⎡⎤---÷⨯-⎢⎥⎣⎦20．(1)计算：5(x+y)－4(3x －2y)+3(2x －3y)．(2)先化简，再求值：221(1)2(2)2x x x --+--，其中x=－2．21．解以下方程(组)： (1)2151136x x +--= (2)32539x y x y -=⎧⎨+=⎩(本大题共2小题，每题5分，总分值10分) 22．以下图是数值转换机的示意图．(1)假设输入的x 是7，那么输出结果y 的值是_______________；(2)假设输出结果y 的值是7，求输入的x 的值．23．如图，线段AB=8cm ，C 是线段AB 上一点，AC=3．2cm ，M 是AB 的中点，N 是AC 的中点．(1)求线段CM 的长；(2)求线段MN 的长．(本大题共2小题，每题6分，总分值12分) 24．xy ＜0，x ＜y 且2x =，4y =． (1)求x 和y 的值；(2)求241()()2x x y +++的值．25．如图，点D 、E 在BC 上，∠BDF=∠AEG 都是直角，且∠1=∠2．(1) ∠2=3∠4，求∠1的度数；(2)探究∠3与∠4的关系，并说明理由．(本大题共2小题，每题7分，总分值1 4分)26．某电器销售商为促销产品，将进价为a 元／件，标价为b 元／件的某种电器打折销售，如果按标价的六折出售，每件将亏本36元；如果按标价的八折出售，每件将盈利52元． (1)求这种电器每件的进价和标价各是多少元?(2)为保证盈利不低于10％，这种电器最多能打几折?27．阅读材料：我们知道：点A 、B 在数轴上分别表示有理数a 、b ，A 、B 两点之间的距离表示为AB ，在数轴上A 、B 两点之间的距离AB a b =-．所以式子3x -的几何意义是数轴上表示有理数3的点与表示有理数x 的点之间的距离． 根据上述材料，解答以下问题：(1)假设31x x -=+，那么x=____________； (2)式子31x x -++的最小值为_______________； (3)假设317x x -++=，求x 的值．28．(本大题总分值8分)某商场方案从厂家购进50台电视机，厂家生产三种不同型号的电视机，出厂价分别为：甲种每台1500元，乙种每台2100元，丙种每台2500元．(1)假设甲、乙、丙三种型号的电视机的数量比为3：2：5，那么该商场共需投资多少元? (2)假设该商场同时购进两种不同型号的电视机共50台，恰好用去9万元，请你设计一下商场的进货方案．29．(本大题总分值8分)(1)图1是由假设干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈， 以下各层均比上一层多一个圆圈，一共堆了n 层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为：1+2+3+…+n=___________；(2)运用第(1)题的结论，试求1+2+3+…+99的值； (3)在一次数学活动中，为了求2345111111222222n +++++⋅⋅⋅+的值，小明设计了如图3所示的边长为1的正方形图形．请你利用这个几何图形求2345111111222222n +++++⋅⋅⋅+的值为______________；(4) 运用第(3)题的结论，试求511234795191612244896192+++++的值；。

初一数学第十五周双休日家作班级 姓名 学号1.下列说法中正确的是( )A.直线有无数个端点B.线段有2个端点C.射线没有端点D.以上都不対 2.如图，下列说法中错误的是( )A. 点A ，B 都在直线a 上B. A ，B 两点确定一条直线ABC.直线a 经过点A ，BD.点A 是直线a 的一个端点 3.如图，点M 是线段AB 的中点，下列表达中错误的是( ) A. AM=BM B. AM=12AB C. BM=12D. AB=2BM 4.下面图形不能围成一个长方体的是( )A B C D 5.下列各组的两个代数式中，是同类项的是( ) A.m 与1π B.0与12C.2a 与3bD.x 与x 2 6.多项式232x x +-中，下列说法错误的是( )A.这是一个二次三项式B.二次项系数是1C.一次项系数是3D.常数项是2 7.下列说法不正确的是( )A.倒数是它本身的数是±1B.相反数是它本身的数是0C.绝对值是它本身的数是0D.平方是它本身的数是0和18.将一等腰直角三角形纸片对折后再对折，得到如图所示的图形，然后将阴影部分剪掉，把余部分展开后的平面图形是( ) AA B C D 9.下图是一数值转换机的示意图，若输入的x 值为20，则输出的结果为( ) AA.150B.120C.60D.3010.如图，数轴上的A 、B 、C 、D 四点所表示的数分别为a 、b 、c 、d ，且O 为原点.根据图中各点位置，判断a c -之值与下列选项中哪个不同 ( ) DA.a d c d +--B.a b c b -+-C.a d d c ---D.a b c ++11.右图中以点A 为端点的线段有 条，分别是 .12.数字3270000000用科学记数法表示为 . 13.比较大小:0 －0.01;23-34-. 14已知3x y -+=，则722x y -+的值为 .15.如图，经过创平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是 .16.如图，从A 到B 有多条道路，人们往往走中间的直路，而不会走其他弯曲的路，能解释这一实际应用的数学知识是 .17.一个正方体的表面展开图如图所示，每个面内都标注了字母.如果从正方体的右面看是面D ，面C 在后面，则正方体的上面是 面. E18.从棱长为2的正方体毛坯的一角，挖去一个棱长为a(a ＜2)的小正方体，得到了一个如图所示的零件，则这个零件的表面积(所有面的面积)是 . 24第15题 第16题 第17题 第18题19.计算:(1)13116448⎛⎫⎛⎫-+÷- ⎪ ⎪⎝⎭⎝⎭ (2)()322524-⨯--÷ (3)()241123522-+⨯--÷⨯20.先化简，再求值:()()()2214121422x x x x --++-，其中x ＝－3.21.解方程:(1)()()2345x x -=-+ (2)3157146y y ---=22. 如图，线段AB ＝14cm ，C 是AB 上的一点，AC ＝9cm ，O 为AB 的中点.求线段OC 的长.23如图，线段AB ＝80.C 是AB 上一点，AC ＝50，M 是AC 的中点，N 为BC 的中点求MN 的长.24.如图，已知线段AB＝6，延长线段AB到C，使BC＝2AB;点D是AC的中点. 求:(1)AC的长;(2)BD的长.25.如图，已知∠AOB是直角，∠BOC＝30°，OM平分∠AOC，ON平分∠BOC，(1)求∠MON的度数;(2)如果将“∠AOB是直角”改为“∠AOB＝m”，其他条件不变，则∠MON的度数为.(3)你从(1)、(2)的结果及解法中，发现了什么规律?26.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图.(1)请你画出这个几何体的三种左视图;(2)若组成这个几何体的小正方体的块数为n，请你写出n的所有可能值.27.将长为2，宽为a(1＜a＜2)的长方形纸片如图那样折一下，剪下一个边长等于长方形宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下，剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如此反复操作下去，若在第n次操作后剩下的长方形为正方形，则操作终止.(1)第一次操作后，剩下的长方形两边长分别为;(用含a的代数式表示)(2)若第二次操作后，剩下的长方形恰好是正方形，则a＝;(3)若第三次操作后，剩下的长方形恰好是正方形，试求a的值.28.已知数轴上两点A、B对应的数分别为－1、3，点P为数上一动点，其对应的数为x.(1)若点P到点A、点B的距离相等，求点P对应的数;(2)数轴上是否存在点P，使点P到点A、点B的距离之和为8?若存在，请求x值;若不存在说理由;(3)现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动，点P 以6个单位长度/秒的速度同时从O点向左运动.当点A与点B之间的距离为3个单位长度时，求点P所对应的多少?29.(1)图中共有几条线段?请分别写出来.(2)图中共有几条射线?能用字母表示的有哪几条?请写出来.(3)图中以A为顶点的角有几个?请分别写出来.(平角除外，可以自己添上数字或字母)30.如图，已知点O在直线AB上，作射线OC，点D为平面内点，∠AOC+∠BOD=90°;(1)若∠AOC:∠BOD＝4:5则∠BOD等于度;(2)若∠AOC＝α(0°＜α≤45)，ON平分∠COD;①当点D在∠BOC内，补全图形，直接写出∠AON的值(用含α的式子表示);②若∠AON+∠COD＝180°求出α的值.。

七年级数学（上）期末复习专题测试《平面图形的认识（一）》考试时间:90分钟 满分:100分一、选择题(每题3分，共30分)1.若2945'α∠=︒，则α∠的余角等于( )A. 60°55'B. 60°15'C. 150°55'D. 150°15' 2.给出下列说法:①如果123180∠+∠+∠=︒，那么1,2,3∠∠∠互为补角;②如果90A B ∠+∠=︒，那么A ∠是余角; ③互为补角的两个角的平分线互相垂直; ④有公共顶点且相等的角是对顶角;⑤如果两个角相等，那么它们的余角也相等. 其中正确的个数是( )A. 1B. 2C. 3 D .4 3.如图，,AB CD 相交于点O ，EO AB ⊥，则1∠与2∠的关系是( ) A.相等 B.互余 C.互补D.对顶角4. 如图，一副直角三角尺按不同的位置摆放，其中满足αβ∠=∠的图形的个数是( ) A. 1 B. 2 C. 3 D. 45.如图，直线,AB CD 相交于点O ，75AOC ∠=︒，OE 把BOD ∠分成两部分，且:1:2BOE EOD ∠∠=，则AOE ∠的度数为( )A. 160°B. 155°C. 150°D. 130°6. 已知D 为线段AC 的中点，B 为直线AC 上的一点，且12BC AB =.若1BD =cm ，则线段AC 的长为 ( )A.23cm B. 32cm C. 6 cm 或23cm D.6 cm 或32cm 7.如图，将长方形ABCD 沿线段OG 折叠到''OB C G 的位置.若'100OGC ∠=︒，则'DGC ∠ 的度数为( )A. 20°B. 30°C. 40°D. 50° 8.如图，,,A O B 三点在同一条直线上.若1∠是锐角，则1∠的余角是( ) A.1212∠-∠ B.132122∠-∠ C. 1(21)2∠-∠ D. 1(12)3∠+∠ 9.已知30AOB ∠=︒，自AOB ∠的顶点O 引射线OC .若:4:3AOC AOB ∠∠=，则BOC ∠的度数是( )A. 100°B. 40°或30°C. 70°D. 10°或70° 10.如图，在长方形ABCD 中，:1:2AB BC =，12AB =cm ，点P 从点A 出发，沿边AB 以2 cm/s 的速度向点B 移动，点Q 从点D 出发，沿边DA 以1 cm/s 的速度向点A 移动.假设,P Q 两点同时出发，用t s 表示移动时间(06t <<).在整个运动过程中，给出下列结论：①图中共有11条线段；②图中共有19个小于平角的角；③当2t =时，:4:3PB BC =；④四边形QAPC 的面积为36 cm 2其中正确的有( )A. 1个B. 2个C. 3个D. 4个二、填空题(每题3分，共24分)11.若35α∠=︒，则α∠的补角为 度.12.已知两个角的和是67°56'，差是12°40'，则这两个角的度数分别是 . 13.如图，已知OA OB ⊥，12AOD COD ∠=∠，3BOC AOD ∠=∠，则COD ∠的度数是 .14.若一个角的补角是这个角余角的4倍，则这个角的度数是 .15.已知线段8AB =，C 是AB 的中点，点D 在直线CB 上，且 1.5DB =，则线段CD 的长为 . 16.如图，已知A 是射线BE 上一点，过点A 画AC BF ⊥，垂足为C ，过点C 画CD BE ⊥，垂足为D .给出下列结论: ①1∠是ACD ∠的余角; ②图中互余的角共有3对;③图中1∠的补角只有DCF ∠;④图中与ADC ∠互补的角共有3个， 其中正确的是 .(填序号)17.一副直角三角尺如图放置，将三角尺ADE 绕点A 逆时针旋转α∠(090α︒<∠<︒)，使得三角尺ADE 的一边所在的直线与BC 垂直，则α∠的度数为 .18.若直线上有5个点，我们进行第一次操作：在每相邻两点间插如1个点，则直线上有9个点;第二次操作：在这9个点中的每相邻两点间继续插入1个点，则直线上有 个点.现在直线上有n 个点，经过3次这样的操作后，直线上共有 个点. 三、解答题(共46分)19. ( 6分)如图，所有小正方形的边长都为1，,,A B C 三点都在格点上.(1)过点B 画直线AC 的垂线，垂足为G ;(2)比较BC 与BG 的大小：BC (填“>”“<”或“=”)BG ，理由是 ; (3)已知5AC =，求BG 的长.20. (6分)如图所示的方格纸中，C 是AOB ∠的边OB 上的一点，按下列要求画图并回答问题.(1)过点C 画OB 的垂线，交OA 于点D .该垂线经过的格点有哪些?请在图中标出该垂线所经过的格点;(网格线的交点称为格点) (2)过点C 画OA 的垂线，垂足为E .①线段CE 的长度是点C 到直线 的距离，线段 的长度是点D 到直线OB 的距离.②因为直线外一点与直线上各点连接的所有线段中，垂线段最短，所以CD ，CE ，OD ，OC 这四条线段的大小关系是 ;(用“<”号连接)(3)过点D 画直线//DF OB .若AOB x ∠=︒，则ADC ∠= (用含x 的代数式表示)21. (5分)如图，已知,B C 两点把线段AD 分成2:5:3三部分，M 为AD 的中点，6BM = cm ，求CM 和AD 的长.22. (6分)如图，O 为直线AB 上一点，OC 为射线，,OD OE 分别为AOC ∠，BOC ∠的平 分线.(1)判断射线,OD OE 的位置关系，并说明理由; (2)若30AOD ∠=︒，试说明：OC 为AOE ∠的平分线; (3)若:2:11AOD AOE ∠∠=，求BOE ∠的度数.23.(6分) (1)如图，点C 在线段AB 上，,M N 分别是,AC BC 的中点。

2021-2021学年七年级数学上学期第一次学情调研试题〔答卷时间是：120分钟 满分是：150分〕根底卷Ⅰ〔120分〕 一、选择题〔每一小题3分，一共30分〕1．恒大“海上威尼斯〞正在圆陀角风景区全力打造一个完美的“威尼斯〞，建成后将媲美九大世界著名海湾景区。

据福布斯2021年9月19的最新数据显示，恒大集团董事局主席许家印以391亿美元的身价成中国新首富，略高于马化腾和马云。

391亿用科学记数法表示为 〔 〕 A ．×108B ．3.91×109C ．3.91×1010D ．3.91×10112．假如a 与1互为相反数，那么a 等于( )A ．1B ．－2C ． 2D ．－13．如图1，数轴上一动点A 向左挪动2个单位长度到达点B ，再向右挪动5个单位长度到达点C ．假设点C 表示的数为1，那么点A 表示的数为〔 〕Ａ．7Ｂ．3Ｃ．3- Ｄ．2-4．计算：()()=+----⨯-1233113〔 〕A ．1-B ．1C ．D ．3 5. a 是有理数,那么112000a +的值不能是10 图1( )A ． 1B ．0C ． -1D ．-20006．不改变原式的值，将6－〔＋3〕－〔－7〕＋〔－2〕中的减法改成加法并写成略加号和．．．．的形式是( )A ．－6－3＋7－2B ． 6－3－7－2Ｃ． 6－3＋7－2 Ｄ． 6＋3－7－2 7．以下说法正确的个数是( )①一个有理数不是整数就是分数；②一个有理数不是正数就是负数； ③一个整数不是正的，就是负的；④一个分数不是正的，就是负的.B. 2C. 3D. 4 8．m 、n 均为非零有理数，以下结论正确的选项是〔 〕 A ．假设m ≠n ，那么m 2≠n 2B ．假设m 2＝n 2，那么m ＝nC ．假设m ＞n ＞0，那么m 1＞n1 D ．假设m ＞n ＞0，那么m 2＞n 29．假设四个有理数a,b,c,d 满足11111997199819992000a b c d ===-+-+,那么a,b,c,d 的大小关系是( )A ．a>c>b>dB ．b>d>a>c ；C ．c>a>b>dD ．d>b>a>c 10．〔－2〕100比〔－2〕99大 〔 〕A ．2B ．－2C ．299D ．3×299二、填空题〔每一小题3分，一共24分〕11．The average number of p,q,r is 4,and average number of p,q,r,x is ﹣2，then x = ．(英文词典：average number 平均数)12． 的绝对值是它本身．13．702班有a 人，702班的人数是701人数的2倍少b 人，那么701班的人数为_______人．14．假设规定一种特殊运算※为：a ※b=ab ﹣，那么〔﹣1〕※〔﹣2〕= ． 15．假设|a-3|=3，那么a= ．16．小明编了一个程序：输入任何一个有理数时，显示屏上的结果总等于输入的有理数的平方减去2得到的差。

江苏省张家港市 学年七年级数学上学期期末调研试题注意事项：1．本试卷共6页，全卷共三大题28小题，总分值130分，考试时刻120分钟；2．答题前，考生先将自己的学校、班级、姓名、考试号填写在答题卷密封线内相应的位置上； 3．选择题、填空题、解答题必需用黑色签字笔答题，答案填在答题卷相应的位置上；4．在草稿纸、试卷上答题无效；5．各题必需答在黑色答题框内，不得超出答题框．一、选择题：（本大题共10小题，每题3分，共30分，在每题给出的四个选项中，只有一项为哪一项符合题目要求的，把你以为正确的答案填在答题卷相应的空格内）1．23的相反数是 A ．23 B ． －23 C ．32 D ．－322．在－二、0、二、－4这四个数中，最小的数是A ．－4B ．0C ．2D ．－23．国家运动场“鸟巢”的建筑面积达258000m2，用科学记数法表示为A ．×105B ．×105C ．×106D ．×1064．以下方程中，解为2的是A ．3x ＋6＝0B ．11042x -+= C ．12x -= D ．3－2x ＝1 5．如图，数轴上的点A 、B 别离表示数－3、＋2，假设点C 是AB 的中点，那么点C 所表示的数是A ．0B ．－23C ．－12D ．－16．如图，甲从A 点动身向北偏东70°方向走到点B ，乙从点A 动身向南偏西15°方向走到点C ，那么∠BAC 的度数是A ．85°B ．160°C ．125°D ．105°7．食堂的存煤打算用假设干天，假设天天用130kg ，那么缺少60kg ；假设天天用120kg ，那么还剩余60kg ．设食堂的存煤共有xkg ，打算用y 天，那么下面所列方程组正确的选项是A ．6013060120x y x y +=⎧⎨-=⎩B ．6013060120x y x y -=⎧⎨+=⎩C ．6013060120y x y x +=⎧⎨-=⎩D ．6013060120y x y x -=⎧⎨+=⎩8．给出如下结论：①单项式－232x y的系数为－32，次数为2；②当x＝5，y＝4时，代数式x2－y2的值为1；③化简(x＋14)－2（x－14）的结果是－x＋34；④假设单项式57ax2y n＋1与－75ax m y4的差仍是单项式，那么m＋n＝5.其中正确的结论有A．1个B．2个C．3个D．4个9．有理数a、b在数轴上的对应点的位置如下图，那么化简a b b-+的结果是A．a B．－a C．2b－a D．a－2b10.如图，假设∠1＝40°，∠2＝40°，∠3＝110°36'，那么24的度数为A．° B．°C．°D．°二、填空题：（本大题共8小题，每题3分，共24分，把你的答案填在答题卷相应的横线上)11．计算：213⎛⎫-- ⎪⎝⎭＝▲．12.归并同类项：7x2－3x2＝▲．13.假设有理数a、b知足2a-＋(b＋1)2＝0，那么a＋b的值为▲．O14.假设方程2(2x－1)＝3x＋1与方程＝x－1的解相同，那么m的值为▲．15.如图是一个数值转换机，假设输入的a值为－3，那么输出的结果应为▲．16.如图，AD＝12DB，E是BC的中点，BE＝15AC＝2cm，那么线段DE＝▲ cm.17.如图，AB、CD相交于点O，OE是∠AOC的平分线，∠BOD＝70°，∠EOF＝65°，那么∠AOF的度数为▲°．18.如图，ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点别离与A'、D'对应．假设∠1＝65°，那么∠2＝▲°．三、解答题：（本大题共10小题，共76分，把解答进程写在答题卷相应的位置上，解答时应写出必要的计算进程、推演步骤或文字说明）19．（此题总分值10分）计算：(1)128355315⎛⎫⨯-+⨯⎪⎝⎭(2)()()234120.5458⎛⎫-÷⨯+-⨯-⎪⎝⎭20．（此题总分值10分）解以下方程（组）(1)3321x yx y+=⎧⎨-=-⎩(2)123123x x+--=21．（此题总分值5分）如图，小华用假设干个正方形和长方形预备拼成一个长方体的展开图，拼完后，小华看来看去总感觉所拼图形似乎存在问题．(1)请你帮小华分析一下拼图是不是存在问题：假设有多余块，那么把图中多余部份涂黑；假设还缺少，那么直接在原图中补全；(2)假设图中的正方形边长为2cm，长方形的长为3cm，宽为2cm，请直接写出修正后所折叠而成的长方体的体积：▲ cm3．22．（此题总分值5分）如图，A、B、C是网格图中的三点．(1)作直线AB、射线AC、线段BC．(2)过B作AC的平行线BD．(3)作出表示B到AC的距离的线段B E.(4)判定BD与BE的位置关系是▲．(5)线段BE与BC的大小关系是：BE ▲ BC(填“>”、“<”、“＝”)．23．（此题总分值6分）若是代数式5a＋3b的值为－4，那么代数式2(a＋b－1)＋4（2a＋b＋2）的值是多少？24．（此题总分值6分）如图，BD平分∠ABC，ED∥BC，∠1＝25°，∠4＝130°．(1)求∠2，∠3的度数；(2)证明：DF∥AB．25．（此题总分值8分）已知A＝32x＋14y＋2，B＝15124x y+-．(1)求A＋B；2A－B；(2)求知足A＋B＝5，2A－B＝194的x、y的值．26．（此题总分值8分）如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝120°．将一直角三角板的直角极点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，另一边ON仍在直线AB的下方．(1)假设OM恰好平分∠BOC，求∠BON的度数；(2)假设∠BOM等于∠COM余角的3倍，求∠BOM的度数；(3)假设设∠BON＝α(0°<α<90°)，试用含α的代数式表示∠COM.27．（此题总分值8分）某校为了做好大课间活动，打算用400元购买10件体育用品，备选体育用品及单价如下表（单位：元）(1)假设400元全数用来购买篮球和羽毛球拍共10件，问篮球和羽毛球拍各购买多少件？(2)假设400元全数用来购买篮球、排球和羽毛球拍三种共10件，能实现吗？假设能，求出篮球、排球、羽毛球拍各购买多少件；假设不能，请说明理由．28．（此题总分值10分）如图，直线l上有A、B两点，AB＝12cm，点O是线段AB上的一点，OA＝2OB．(1)OA＝▲ cm，OB＝▲ cm；(2)假设点C是线段AB上一点，且知足AC＝CO＋CB，求CO的长；(3)假设动点P、Q分别从A、B同时动身，向右运动，点P的速度为2cm／s，点Q的速度为1cm/s，设运动时刻为ts．当点P与点Q重合时，P、Q两点停止运动．①当t为何值时，2OP－OQ＝4；②当点P通过点O时，动点M从点0动身，以3cm/s的速度也向右运动．当点M追上点Q后当即返回，以3cm/s的速度向点P运动，碰到点P后再当即返回，以3cm/s的速度向点Q运动，如此来回，直到点P、Q停止时，点M也停止运动．在此进程中，点M行驶的总路程是多少？。