离散数学( 第10讲习题课2)
- 格式:ppt
- 大小:653.00 KB
- 文档页数:31


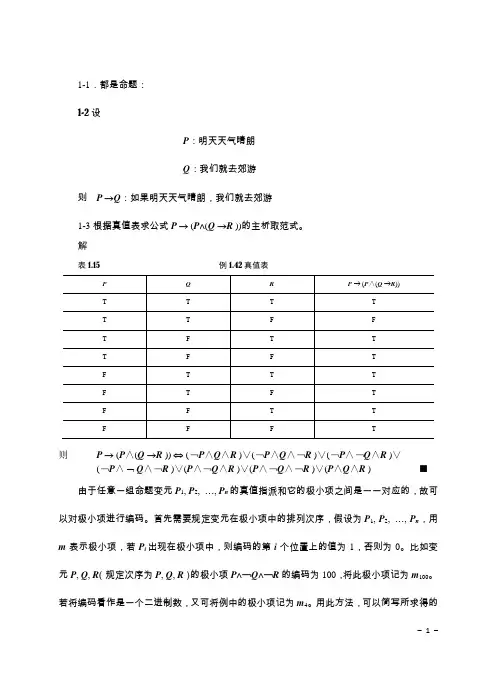
1-1.都是命题:1-2设P:明天天气晴朗Q:我们就去郊游则P →Q:如果明天天气晴朗,我们就去郊游1-3根据真值表求公式P → (P∧(Q →R ))的主析取范式。
解表1.15 例1.42真值表则P → (P∧(Q →R )) ⇔ (﹁P∧Q∧R )∨(﹁P∧Q∧﹁R )∨(﹁P∧﹁Q∧R )∨⌝(﹁P∧Q∧﹁R )∨(P∧﹁Q∧R )∨(P∧﹁Q∧﹁R )∨(P∧Q∧R ) ■由于任意一组命题变元P1, P2, …, P n的真值指派和它的极小项之间是一一对应的,故可以对极小项进行编码。
首先需要规定变元在极小项中的排列次序,假设为P1, P2, …, P n,用m表示极小项,若P i出现在极小项中,则编码的第i个位置上的值为1,否则为0。
比如变元P, Q, R(规定次序为P, Q, R)的极小项P∧﹁Q∧﹁R的编码为100,将此极小项记为m100。
若将编码看作是一个二进制数,又可将例中的极小项记为m4。
用此方法,可以简写所求得的给定公式的主析取范式。
P → (P∧(Q →R )) ⇔m0∨m1∨m2∨m3∨m4∨m5∨m7(规定P, Q, R的次序为P, Q, R)公式P → (P∧(Q →R ))的主析取范式。
解P → (P∧(Q →R ))⇔﹁P∨(P∧(﹁Q∨R ))⇔ (﹁P∨P)∧(﹁P∨﹁Q∨R)⇔ (﹁P∨﹁Q∨R )⇔ (﹁P∨﹁Q∨R )1-4试证明(﹁P →Q )∧(P →R )∧(﹁Q∨S ) ⇒S∨R。
证明(1)﹁P →Q P(2)﹁Q∨S P(3)Q →S T, (2), E16(4)﹁P →S T, (1), (3), I13(5)﹁S →P T, (4), E18(6)P →R P(7)﹁S →R T, (5),(6), I13(8)﹁﹁S∨R T, (7),E16(9)S∨R T, (8), E11-5如果迈克有电冰箱,则或者他卖了洗衣机,或者他向别人借了钱。
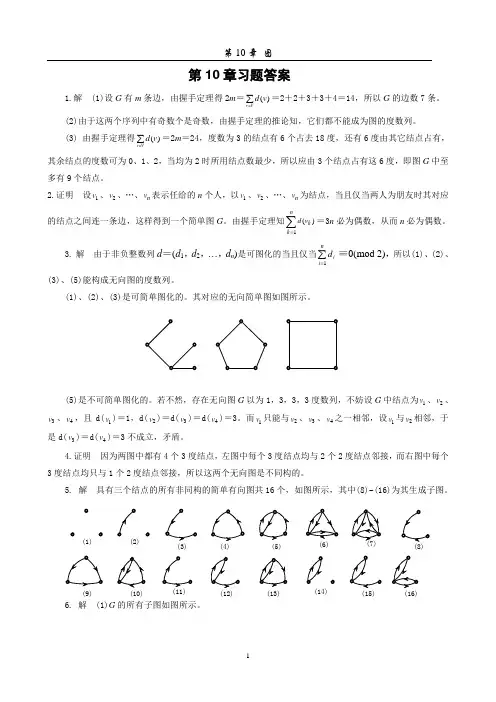
第10章习题答案1.解 (1)设G 有m 条边,由握手定理得2m =∑∈Vv v d )(=2+2+3+3+4=14,所以G 的边数7条。
(2)由于这两个序列中有奇数个是奇数,由握手定理的推论知,它们都不能成为图的度数列。
(3) 由握手定理得∑∈Vv v d )(=2m =24,度数为3的结点有6个占去18度,还有6度由其它结点占有,其余结点的度数可为0、1、2,当均为2时所用结点数最少,所以应由3个结点占有这6度,即图G 中至多有9个结点。
2.证明 设1v 、2v 、…、n v 表示任给的n 个人,以1v 、2v 、…、n v 为结点,当且仅当两人为朋友时其对应的结点之间连一条边,这样得到一个简单图G 。
由握手定理知∑=nk kv d 1)(=3n 必为偶数,从而n 必为偶数。
3. 解 由于非负整数列d =(d 1,d 2,…,d n )是可图化的当且仅当∑=ni i d 1≡0(mod 2),所以(1)、(2)、(3)、(5)能构成无向图的度数列。
(1)、(2)、(3)是可简单图化的。
其对应的无向简单图如图所示。
(5)是不可简单图化的。
若不然,存在无向图G 以为1,3,3,3度数列,不妨设G 中结点为1v 、2v 、3v 、4v ,且d(1v )=1,d(2v )=d(3v )=d(4v )=3。
而1v 只能与2v 、3v 、4v 之一相邻,设1v 与2v 相邻,于是d(3v )=d(4v )=3不成立,矛盾。
4.证明 因为两图中都有4个3度结点,左图中每个3度结点均与2个2度结点邻接,而右图中每个3度结点均只与1个2度结点邻接,所以这两个无向图是不同构的。
5. 解 具有三个结点的所有非同构的简单有向图共16个,如图所示,其中(8)~(16)为其生成子图。
6. 解 (1)G 的所有子图如图所示。
(1)(3)(5)(6)(9)(10)(13)(14)(2)图(8)~(18)是G 的所有生成子图。
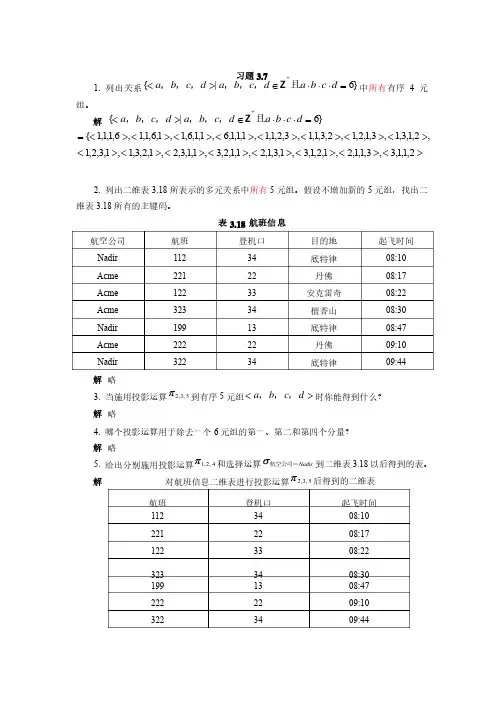
习题3.71. 列出关系}6|{=×××Î><+d c b a d c b a d c b a 且,,,,,,Z 中所有有序4元组。
组。
解}6|{=×××Î><+d c b a d c b a d c b a 且,,,,,,Z ,2,1,3,1,3,1,2,1,2,3,1,1,3,2,1,1,1,1,1,6,1,1,6,1,1,6,1,1,6,1,1,1{><><><><><><><><=><><><><><><><><2,1,1,3,3,1,1,2,1,2,1,3,1,3,1,2,1,1,2,3,1,1,3,2,1,2,3,1,1,3,2,12. 列出二维表3.18所表示的多元关系中所表示的多元关系中所有所有5元组。
假设不增加新的5元组,找出二维表3.18所有的主键码。
所有的主键码。
表3.18 航班信息航空公司航空公司 航班航班 登机口登机口 目的地目的地 起飞时间起飞时间 Nadir 112 34 底特律底特律 08:10 Acme 221 22 丹佛丹佛 08:17 Acme 122 33 安克雷奇安克雷奇 08:22 Acme 323 34 檀香山檀香山 08:30 Nadir 199 13 底特律底特律 08:47 Acme 222 22 丹佛丹佛 09:10 Nadir 32234底特律底特律09:44解 略3. 当施用投影运算5,3,2p 到有序5元组><d c b a ,,,时你能得到什么?时你能得到什么? 解 略4. 哪个投影运算用于除去一个6元组的第一、第二和第四个分量?元组的第一、第二和第四个分量? 解 略5. 给出分别施用投影运算4,2,1p 和选择运算Nadir 航空公司=s 到二维表3.18以后得到的表。



第二章谓词逻辑
1、在一元谓词逻辑中,分别在(a)(b)(c)时将下面命题符号化并讨论命题的真值:
1)凡是整数都能被2整除
2)有的整数能被2整除
其中(a):个体域为整数集合;(b):个体域为偶数集合;(c)个体域为实数集合2、在一元谓词逻辑中将下面命题符号化
1)所有的整数,不是负整数,就是正整数,或者是0
2)有的实数是有理数,有的实数是无理数
3)发明家都是聪明的并且勤劳的。
王进是发明家。
所以王进是聪明的并且是勤劳的。
4)实数不都是有理数
5)】
6)不存在能表示成分数的有理数
7)不存在最大的自然数
3、求下列公式的前束范式
1)()()()(,) x F x y G x y ∀→∀
2)()()()(,) x F x x G x y ∀→∀
3)()()()(,) x F x x G x y ∀→∃
4)()(()(,))(()()()(,)) x F x G x y y H y z L y z ∀→→∃→∃
4、人都喜欢吃蔬菜,但不是所有的人都喜欢吃鱼。
所以,存在喜欢吃蔬菜而不喜欢吃鱼
的人。
F(x):x为人;G(x):x喜欢吃蔬菜;H(x):x喜欢吃鱼
5、没有白色的乌鸦。
北京鸭是白色的。
因此,北京鸭不是乌鸦。
F(x):x是乌鸦;H(x):
x是北京鸭;G(x):x是白色的。

第十章 树10.1画出所有不同构的,有5个顶点的树。
解图10.1 习题1图10.2 证明:一棵树的顶点度数之和为)1 |(|2-V ,其中V 是顶点集。
证明一棵树的所有顶点的度数之和∑==ni iE v 1||2)deg(,因为树的1||||-=V E ,所以)1|(|2||2)deg(1-==∑=V E v ni i。
故一棵树的顶点度数之和为)1 |(|2-V 。
10.3 一棵树有3个2度顶点,5个3度顶点,8个4度顶点,问有几个一度顶点?解设树T 有n 个一度顶点,则∑)deg(v =)1853(21483523-+++=⨯+⨯+⨯+⨯n n ,从而有23=n 。
即该棵树有23个一度顶点。
10.4 一棵树2n 个顶点的度数为2,3n 个顶点的度数为3,…,k n 个顶点度数为k ,问有几个顶点度数为1个顶点。
解设有1n 个度数为1的顶点。
顶点数k n n n v +++=...21,边数1)...(121-+++=-=k n n n v e 。
由握手定理知:∑==-=ni i v v e 1)deg()1(22,故k n n n n n n k k ⨯++⨯+⨯=-+++...212) (22121)因此,2)2(...2431+-+++=k n k n n n10.5 证明:一棵树若有三片树叶,则至少有一个顶点度数大于等于3。
证明反证法。
设),(E V T =且没有一个顶点度数大于等于3,则对于V v ∈∀,有2)de g (≤v ,从而有:∑-+≤)3|(|23)deg(V v||21)1|(|2E V <--=与握手定理矛盾。
故至少有一个顶点度数大于等于3。
10.6 ),(E V T =是一棵树,证明:若T 仅有两个1度顶点,则T 是一条直线。
证明假设T 不是一条直线,因为T 仅有两个1度顶点,所以树中至少存在一个顶点,其度数3≥。
从而有:∑-++⨯≥)3|(|2312)deg(V v1)1|(|2+-=V 1||2+=E ||2E > 与握手定理矛盾。


第二章习题 1. 填空(1))(x A ,)(y B (2)))()((x A x C x →∀ (3)))()((y B x A x →∀(4))),()()((y x H y F x F y x ⌝→∧∀∀ (5)))()((x G x F x ⌝∧∃ (6)T(7))),(),((z y Q y x P y ∧∀,),(),(z y Q y x P ∧,),(y x P (8)))()((!x P x Q x ∧∃ ))()((!!x P x Q x ∧∃ (9)x y ,和z(10)))()((y R x Q x →∀,))(Z )(Q (x x x ∧∃,))()(R )(Q (x Z x x x ⌝∧∧∃ 2.选择题(1)B (2)B (3)A (4)B (5)C (6)C (7)B (8)B (9)B (10)D (11)C (12)A 3.下列哪些是谓词公式解:公式(1)—(8)均为谓词公式。
4.在谓词逻辑中将下列命题符号化 (1)有些汽车比所有火车都跑得慢;解:令)(x A :x 是汽车,)(x B :x 是火车,),(y x C :x 比y 跑得慢。
符号化为)))),()((()((y x C y B y x A x →∀∧∃ (2)会叫的狗未必会咬人;解:令)(x A :x 会叫,)(x B :x 是狗,)(x C :x 会咬人符号化为))()()((x C x B x A x ⌝∧∧∃ (3)存在最小自然数解:令A (x ):x 是自然数,B (x,y ):x 小于y 符号化为),()(()((x y B y A y x A x ⌝→∀⋂∃(4)对于每个实数都存在比它大的有理数解:令A (x ):x 是实数,B (x ):x 是有理数,R (x,y ):x 比y 大 符号化为),()(()((x y R y B y x A x ⋂∃→∀(5)每个自然数都有唯一的后继 解:令A (x ):x 是自然数,B (x,y ):x 是y 的后继 符号化为),()((!)((x y B y A y x A x ⋂∃→∀) (6)没有以0为后继的自然树解:令A (x ):x 是自然数,B (x,y ):x 是y 的后继 符号化为),0()((x B x A x ⋂⌝∃(7)存在唯一的偶实数解:令A (x ):x 是偶数,令B (x ):x 是素数 符号化为)()((!x B x A x ⋂∃(8)没有即是奇数也是偶数的数解:令A (x ):x 是奇数,令B (x ):x 是偶数 符号化为)()((x B x A x ⋂⌝∃(9)天下乌鸦一般黑解:令A (x ):x 是乌鸦,令B (x ):x 是黑的 符号化为)()((x B x A x →∀(10)一个数是素数当且仅当它只能被1和它自身整除解:;:)(;:),(;.:),(B ;.:)(是实数相等与整除被是素数x x D y x y x C y x y x x x A 符号化为:)))),()1,(()),()((()((x y C y C y x B y D y x A x ∨→∧∃↔∀ 5、利用所给定命题和谓词,将下列诸命题符号化。
离散数学课后习题答案(左孝凌版左孝凌版))1-1,1-2(1)解:a)是命题,真值为T。
b)不是命题。
c)是命题,真值要根据具体情况确定。
d)不是命题。
e)是命题,真值为T。
f)是命题,真值为T。
g)是命题,真值为F。
h)不是命题。
i)不是命题。
(2)解:原子命题:我爱北京天安门。
复合命题:如果不是练健美操,我就出外旅游拉。
(3)解:a)(┓P∧R)→Qb)Q→Rc)┓Pd)P→┓Q(4)解:a)设Q:我将去参加舞会。
R:我有时间。
P:天下雨。
Q↔(R∧┓P):我将去参加舞会当且仅当我有时间和天不下雨。
b)设R:我在看电视。
Q:我在吃苹果。
R∧Q:我在看电视边吃苹果。
c)设Q:一个数是奇数。
R:一个数不能被2除。
(Q→R)∧(R→Q):一个数是奇数,则它不能被2整除并且一个数不能被2整除,则它是奇数。
(5)解:a)设P:王强身体很好。
Q:王强成绩很好。
P∧Qb)设P:小李看书。
Q:小李听音乐。
P∧Qc)设P:气候很好。
Q:气候很热。
P∨Qd)设P:a和b是偶数。
Q:a+b是偶数。
P→Qe)设P:四边形ABCD是平行四边形。
Q:四边形ABCD的对边平行。
P↔Qf)设P:语法错误。
Q:程序错误。
R:停机。
(P∨Q)→R(6)解:a)P:天气炎热。
Q:正在下雨。
P∧Qb)P:天气炎热。
R:湿度较低。
P∧Rc)R:天正在下雨。
S:湿度很高。
R∨Sd)A:刘英上山。
B:李进上山。
A∧Be)M:老王是革新者。
N:小李是革新者。
M∨Nf)L:你看电影。
M:我看电影。
┓L→┓Mg)P:我不看电视。
Q:我不外出。
R:我在睡觉。
P∧Q∧Rh)P:控制台打字机作输入设备。
Q:控制台打字机作输出设备。
P∧Q1-3(1)解:a)不是合式公式,没有规定运算符次序(若规定运算符次序后亦可作为合式公式)b)是合式公式c)不是合式公式(括弧不配对)d)不是合式公式(R和S之间缺少联结词)e)是合式公式。
(2)解:a)A是合式公式,(A∨B)是合式公式,(A→(A∨B))是合式公式。
离散数学答案屈婉玲版第二版高等教育出版社课后答案第一章部分课后习题参考答案16设p、q的真值为0;r、s的真值为1,求下列各命题公式的真值。
(1)p∨(q∧r)⇔0∨(0∧1)⇔0(2)(p?r)∧(﹁q∨s)⇔(0?1)∧(1∨1)⇔0∧1⇔0.(3)(⌝(4)(176能被2q:3r:2s:619(4)(p(5)(p(6)((p答:(pqp→q⌝0011111011011110010011110011所以公式类型为永真式(5)公式类型为可满足式(方法如上例)(6)公式类型为永真式(方法如上例)第二章部分课后习题参考答案3.用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出成真赋值.(1)⌝(p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)答:(2)(p→(p∨q))∨(p→r)⇔(⌝p∨(p∨q))∨(⌝p∨r)⇔⌝p∨p∨q∨r⇔1所以公式类型为永真式(3)P qrp∨qp∧r(p∨q)→(p∧r)0000010010014.(2)(p→(4)(p∧证明(2(45.(1)(⌝p→q)→(⌝q∨p)(2)⌝(p→q)∧q∧r(3)(p∨(q∧r))→(p∨q∨r)解:(1)主析取范式(⌝p→q)→(⌝q∨p)⇔⌝(p∨q)∨(⌝q∨p)⇔(⌝p∧⌝q)∨(⌝q∨p)⇔(⌝p∧⌝q)∨(⌝q∧p)∨(⌝q∧⌝p)∨(p∧q)∨(p∧⌝q)⇔(⌝p∧⌝q)∨(p∧⌝q)∨(p∧q)⇔∑(0,2,3)主合取范式:(⌝p→q)→(⌝q∨p)⇔⌝(p∨q)∨(⌝q∨p)⇔(⌝p∧⌝q)∨(⌝q∨p)⇔(⌝p⇔1∧(p⇔(p∨⇔∏(2)⌝(p→q)⇔(p∧(3)⇔⌝⇔1∧1⇔1所以该式为永真式.永真式的主合取范式为1主析取范式为∑(0,1,2,3,4,5,6,7)第三章部分课后习题参考答案14.在自然推理系统P中构造下面推理的证明:(2)前提:p→q,⌝(q∧r),r结论:⌝p(4)前提:q→p,q↔s,s↔t,t∧r结论:p∧q证明:(2)①⌝(q∧r)前提引入②⌝q∨⌝r①置换③q→⌝r②蕴含等值式④r⑤⌝q⑥p→q⑦¬p(3证明(4①t②t③q④s⑤q⑥(⑦(⑧q⑨q⑩p15在自然推理系统P中用附加前提法证明下面各推理:(1)前提:p→(q→r),s→p,q结论:s→r证明①s附加前提引入②s→p前提引入③p①②假言推理④p→(q→r)前提引入⑤q→r③④假言推理⑥q前提引入⑦r⑤⑥假言推理16在自然推理系统P中用归谬法证明下面各推理:(1)前提:p→⌝q,⌝r∨q,r∧⌝s结论:⌝p证明:①p②p③﹁④¬⑤¬⑥r⑦r⑧r3.:(1)均有2=(x+)(x).(2)其中(a)(b)解:F(x):2=(x+)(x).G(x):x+5=9.(1)在两个个体域中都解释为)(x∀,在(a)中为假命题,在(b)中为真命题。
离散数学习题解 第二部分 代数系统习题四 第四章代数系统1.设I 为整数集合。
判断下面的二元关系是否是I 上的二元运算a )+={(x ,y ),z|x ,y ,zI 且z=x+y}b )-={((x ,y ),z )|x ,y ,zI 且z=x -y}c )×={((x ,y ),z )|x ,y ,zI 且z=x ×y}d )/={((x ,y ),z )|x ,y ,zI 且z=x/y}e )R={((x ,y ),z )|x ,y ,zI 且z=x y }f )={((x ,y ),z )|x ,y ,zI 且z=yx }g )min = {((x ,y ),z )|x ,y ,zI 且z=max (x ,y )} h )min = {((x ,y ),z )|x ,y ,zI 且z=min (x ,y )} i )GCD = {((x ,y ),z )|x ,y ,zI 且z= GCD (x ,y )} j )LCM={((x ,y ),z )|x ,y ,z ∈I 且z= LCM (x ,y )}[解] a )是。
由于两个整数之和仍为整数,且结果唯一,故知+:I 2→I 是I 上的一个二元运算。
b )是。
由于两个整数之差仍为整数,且结果唯一,故知一:I 2→I 是I 上的一个二元运算。
c )是。
由于两个整数这积仍为整数,且结果唯一,故知x :I 2→I 是I 上的一个二元运算。
d )不是:例如若x=5,y=6,则z=x/y=5/6∉I ;当y=0时z=x|y=x/0无定义。
e )不是。
例如若x=2,y= -2,则z=x y =2 –2=221=I 41∉;若x=y=0,则z=x y =0,则z=I 2x ∉=χ;g )是。
由于两个整数中最大者仍为整数,且结果唯一。
故知max :I 2→I 是I 上的一个二元运算。
h )是。
由于两个整数中最小者仍为整数,且结果唯一。
离散数学(第⼆版)课后习题答案详解(完整版)习题⼀1.下列句⼦中,哪些是命题?在是命题的句⼦中,哪些是简单命题?哪些是真命题?哪些命题的真值现在还不知道?(1)中国有四⼤发明.答:此命题是简单命题,其真值为 1.(2)5 是⽆理数.答:此命题是简单命题,其真值为 1.(3)3 是素数或 4 是素数.答:是命题,但不是简单命题,其真值为1.(4)2x+ <3 5 答:不是命题.(5)你去图书馆吗?答:不是命题.(6)2 与3 是偶数.答:是命题,但不是简单命题,其真值为0.(7)刘红与魏新是同学.答:此命题是简单命题,其真值还不知道.(8)这朵玫瑰花多美丽呀!答:不是命题.(9)吸烟请到吸烟室去!答:不是命题.(10)圆的⾯积等于半径的平⽅乘以π.答:此命题是简单命题,其真值为 1.(11)只有6 是偶数,3 才能是2 的倍数.答:是命题,但不是简单命题,其真值为0.(12)8 是偶数的充分必要条件是8 能被3 整除.答:是命题,但不是简单命题,其真值为0.(13)2008 年元旦下⼤雪.答:此命题是简单命题,其真值还不知道.2.将上题中是简单命题的命题符号化.解:(1)p:中国有四⼤发明.(2)p: 是⽆理数.(7)p:刘红与魏新是同学.(10)p:圆的⾯积等于半径的平⽅乘以π.(13)p:2008 年元旦下⼤雪.3.写出下列各命题的否定式,并将原命题及其否定式都符号化,最后指出各否定式的真值.(1)5 是有理数.答:否定式:5 是⽆理数. p:5 是有理数.q:5 是⽆理数.其否定式q 的真值为1.(2)25 不是⽆理数.答:否定式:25 是有理数. p:25 不是⽆理数. q:25 是有理数. 其否定式q 的真值为1.(3)2.5 是⾃然数.答:否定式:2.5 不是⾃然数. p:2.5 是⾃然数. q:2.5 不是⾃然数. 其否定式q 的真值为1.(4)ln1 是整数.答:否定式:ln1 不是整数. p:ln1 是整数. q:ln1 不是整数. 其否定式q 的真值为1.4.将下列命题符号化,并指出真值.(1)2 与5 都是素数答:p:2 是素数,q:5 是素数,符号化为p q∧,其真值为 1.(2)不但π是⽆理数,⽽且⾃然对数的底e 也是⽆理数.答:p:π是⽆理数,q:⾃然对数的底e 是⽆理数,符号化为p q∧,其真值为1.(3)虽然2 是最⼩的素数,但2 不是最⼩的⾃然数.答:p:2 是最⼩的素数,q:2 是最⼩的⾃然数,符号化为p q∧? ,其真值为1.(4)3 是偶素数.答:p:3 是素数,q:3 是偶数,符号化为p q∧,其真值为0.(5)4 既不是素数,也不是偶数.答:p:4 是素数,q:4 是偶数,符号化为? ∧?p q,其真值为0.5.将下列命题符号化,并指出真值.(1)2 或3 是偶数.(2)2 或4 是偶数.(3)3 或5 是偶数.(4)3 不是偶数或4 不是偶数.(5)3 不是素数或4 不是偶数.答: p:2 是偶数,q:3 是偶数,r:3 是素数,s:4 是偶数, t:5 是偶数(1)符号化: p q∨,其真值为1.(2)符号化:p r∨,其真值为1.(3)符号化:r t∨,其真值为0.(4)符号化:? ∨?q s,其真值为1.(5)符号化:? ∨?r s,其真值为0.6.将下列命题符号化.(1)⼩丽只能从筐⾥拿⼀个苹果或⼀个梨.答:p:⼩丽从筐⾥拿⼀个苹果,q:⼩丽从筐⾥拿⼀个梨,符号化为: p q∨ .(2)这学期,刘晓⽉只能选学英语或⽇语中的⼀门外语课.答:p:刘晓⽉选学英语,q:刘晓⽉选学⽇语,符号化为: (? ∧∨∧?p q)(p q) .7.设p:王冬⽣于1971 年,q:王冬⽣于1972 年,说明命题“王冬⽣于1971 年或1972年”既可以化答:列出两种符号化的真值表:合命题可以发现,p 与q 不可能同时为真,故上述命题有两种符号化⽅式.8.将下列命题符号化,并指出真值., 就有;(1)只要, 则;, 才有;(3)只有, 才有;(4)除⾮, 否则;(5)除⾮(6)仅当.答:设p: , 则: ; 设q: , 则: .(1);(2);;(3);(4);(5);(6);(7).答:根据题意,p 为假命题,q 为真命题.(1);(2);(3);(4).答:根据题意,p 为真命题,q 为假命题.(1)若2+2=4,则地球是静⽌不动的;(2)若2+2=4,则地球是运动不⽌的;(3)若地球上没有树⽊,则⼈类不能⽣存;(4)若地球上没有⽔,则是⽆理数.12.将下列命题符号化,并给出各命题的真值:(1)2+2=4 当且仅当3+3=6;(2)2+2=4 的充要条件是3+3 6;(3)2+2 4 与3+3=6 互为充要条件;(4)若2+2 4,则3+3 6,反之亦然.答:设p:2+2=4,q:3+3=6.(1)若今天是星期⼀,则明天是星期⼆;(2)只有今天是星期⼀,明天才是星期⼆;(3)今天是星期⼀当且仅当明天是星期⼆;(4)若今天是星期⼀,则明天是星期三.答:设p:今天是星期⼀,q:明天是星期⼆,r:明天是星期三.(1)刘晓⽉跑得快,跳得⾼;(2)⽼王是⼭东⼈或者河北⼈;(3)因为天⽓冷,所以我穿了⽻绒服;(4)王欢与李乐组成⼀个⼩组;(5)李欣与李末是兄弟;(6)王强与刘威都学过法语;(7)他⼀⾯吃饭,⼀⾯听⾳乐;(8)如果天下⼤⾬,他就乘班车上班;(9)只有天下⼤⾬,他才乘班车上班;(10)除⾮天下⼤⾬,否则他不乘班车上班;(11)下雪路滑,他迟到了;(12)2 与4 都是素数,这是不对的;(13)“2 或 4 是素数,这是不对的”是不对的.答:q:⼤熊猫产在中国.r:太阳从西⽅升起. 求下列符合命题的真值:(1)(2)(3)(4)解:p真值为1,q 真值为1,r 真值为0.(1)0,(2)0,(3)0,(4)116.当p,q 的真值为0,r,s 的真值为1 时,求下列各命题公式的真值:(1)(2)(3)(4)解:(1)0,(2)0,(3)0,(4)117.判断下⾯⼀段论述是否为真:“ 是⽆理数.并且,如果3 是⽆理数,则也是⽆理数.另外,只有6 能被2 整除,6 才能被4 整除.”解:p: 是⽆理数q: 3 是⽆理数r:是⽆理数s: 6 能被2 整除t:6 能被 4 整除符号化为: ,该式为重⾔式,所以论述为真。
第十章部分课后习题参考答案4.判断下列集合对所给的二元运算是否封闭: (1) 整数集合Z 和普通的减法运算。
封闭,不满足交换律和结合律,无零元和单位元(2) 非零整数集合错误!未找到引用源。
普通的除法运算。
不封闭(3) 全体n n ⨯实矩阵集合错误!未找到引用源。
(R )和矩阵加法及乘法运算,其中n错误!未找到引用源。
2。
封闭 均满足交换律,结合律,乘法对加法满足分配律; 加法单位元是零矩阵,无零元;乘法单位元是单位矩阵,零元是零矩阵;(4)全体n n ⨯实可逆矩阵集合关于矩阵加法及乘法运算,其中n 错误!未找到引用源。
2。
不封闭(5)正实数集合错误!未找到引用源。
和错误!未找到引用源。
运算,其中错误!未找到引用源。
运算定义为:错误!未找到引用源。
不封闭 因为 +∉-=--⨯=R 1111111ο(6)n 错误!未找到引用源。
关于普通的加法和乘法运算。
封闭,均满足交换律,结合律,乘法对加法满足分配律 加法单位元是0,无零元;乘法无单位元(1>n ),零元是0;1=n 单位元是1(7)A = {},,,21n a a a Λ 错误!未找到引用源。
n 错误!未找到引用源。
运算定义如下:错误!未找到引用源。
封闭 不满足交换律,满足结合律,(8)S = 错误!未找到引用源。
关于普通的加法和乘法运算。
封闭 均满足交换律,结合律,乘法对加法满足分配律 (9)S = {0,1},S 是关于普通的加法和乘法运算。
加法不封闭,乘法封闭;乘法满足交换律,结合律(10)S = 错误!未找到引用源。
,S 关于普通的加法和乘法运算。
加法不封闭,乘法封闭,乘法满足交换律,结合律5.对于上题中封闭的二元运算判断是否适合交换律,结合律,分配律。
见上题7.设* 为+Z错误!未找到引用源。
上的二元运算+yx,,∀Z∈X * Y = min ( x,y ),即x和y之中较小的数.(1)求4 * 6,7 * 3。
4, 3Z上是否适合交换律,结合律,和幂等律?(2)* 在+满足交换律,结合律,和幂等律(3)求*运算的单位元,零元及+Z中所有可逆元素的逆元。