成都七中高2009级期末考试.doc

成都市二o0九年高中阶段教育学校统一招生考试试卷（含成都市初三毕业会考）全卷分A 卷和B 卷，A 卷满分90分，B 卷满分20分，全卷共110分；考试时间90分钟。

A 卷（共90分）第1卷（选择题，共28分） 注意事项：1.第1卷共2页。

答第1卷前，考生务必将自己的姓名、准考证号、考试科目涂写在 试卷和答题卡上。

考试结束，监考员将试卷和答题卡一并收回。

2 •第1卷全是选择题，各题均有四个选项，只有一项符合题目要求。

每小题选出答案 后，用2B 铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其 他答案，不能答在试卷上。

请注意机读答题卡的横竖格式。

一、单项选择题（每小题 2分，共28分）1. 图1所示现象中，应该用光的折射规律来解释的是2 . 下列数据最符合实际的是A •拿起一颗葡萄的力约为 5NB •甲型HINI 流感病毒的长度约为I cmC .人的正常体温约为 39CD .无线电波在空气中的传播速度约为 3X I08 m/s3. 下列物体中，用到了半导体材料的是A •智能机器狗B •白炽灯泡C •普通干电池D •滑动变阻器4.图2所示的运动情景中，最明显的反映出力使物体发生形变的是5.下列用电器在工作过程中，电能几乎全部转化为内能的是A .电脑B .电风扇C .洗衣机D .电炉踢出的足球能堆煤飞幷C瑜车在公路上息驰D拦网改总扌孝球运动青向6. 下列过程中，将内能转化为机械能的是A .汽油机的压缩冲程B .水蒸气顶起水壶盖的过程C •小孩沿滑梯下滑的过程D •流星在大气层中穿行的过程7.当喇叭里响起“我和你，心连心，共住地球村……”的男声演唱时，小明和小亮齐声说： “是刘欢在演唱！”他们作出判断的依据是：不同演员声音的A .音调不同B .响度不同C .音色不同D .声速不同&去年春节前后，我国南方部分地区遭遇了低温雨雪天气， 某些地区的树枝上甚至出现了图 3所示的“雾淞”。

四川省成都七中高2009级阶段测试题数学 (理科)班次_____姓名____________学号_____一．选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．设全集U ={1，3，5，7}，集合M ={1，a －5}，,U M U C M ⊆={5，7}，则a 的值为（ ） A. 2 B. 8 C. －2 D. －82. 1 + tan 1501－tan 150 =( )A ．－ 3B ． －3 3C ．3 3D ． 33.已知p ：342x ->，q ：2102x x >--，则﹁p 是﹁q 的（ ）A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分又不必要条件4．在等差数列{}n a 中，已知,23=a 则前5项之和等于（ ） A. 10 B. 16 C. 20 D. 525.αβ，是两个不重合的平面，a 、b 是两条不同直线，在下列条件下，可判定α∥β的是( )A. αβ，都平行于直线a 、bB. α内有三个不共线点到β的距离相等C.a 、b 是α内两条直线，且a ∥β，b ∥βD.a 、b 是两条异面直线且a ∥α，b ∥α，a ∥β，b ∥β6．设平面上有四个互异的点A ，B ，C ，D ，已知(2-+)²(-)=0，则 △ABC 的形状一定是 ( )Ａ．直角三角形 Ｂ．等腰三角形 Ｃ．锐角三角形 Ｄ．正三角形7.函数()2x xe ef x --=(x ∈ R )的反函数是1()f x -，则1(2)f - 的值为( )A ．ln(2B ．1ln(22C ．1ln(22+ D ．ln(28．已知]2,2[)(62)(23-+-=，在为常数m m x x x f 上有最大值3，那么此函数在[－2，2]上的最小值为（ ） A ．－37B ．－29C ．－5D ．－119.若()m x x f ++=)cos(2ϕω，对任意实数t 都有)()4(t f t f -=+π，且1)8(-=πf ，则实数m 的值等于( )A.±1B.±3C.－3或1D.－1或3 10.如图，正五边形ABCDE 中，若把顶点A 、B 、C 、D 、E 染上 红、黄、绿、三种颜色中的一种，使得相邻顶点所染颜色不相同，则不同的染色方法共有 （ ） A ．30种 B ．27种 C ．24种 D ．21种ECBA DED CB A11. 如图，在矩形ABCD 中，4,3,AB BC E ==是CD 的 中点，沿AE 将ADE ∆折起，使二面角D AE B --为60︒，则四棱锥D ABCE -的体积是（ ）.939 2739 913 271312. 已知函数),2[)(+∞-的定义域为x f ，且)2()4(-=f f ，)()(x f x f 为')(x f y '=的图象如图所示.则平面区域⎪⎩⎪⎨⎧<+≥≥1)2(00y x f y x 所围成的面积是( )A ．2B ．4C ．5D ．8二．填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上） 13．当6)1(x x x -的展开式的第5项的值等于215，x = ，此时=+++∞→)111(lim 2n n xx x .14．已知yx y x R y x 1114*,+=+∈，则，且的最小值为_______. 15.已知过球面上A 、B 、C 三点的截面和球心的距离是球半径是14，且5,0AB AC BC =⋅= ，那么球的表面积为_______________.16．关于函数21()lg (0),x f x x x+=≠有下列命题：①其图像关于y 轴对称；②当x ＞0时，()f x 是增函数；当x ＜0时，()f x 是减函数；③()f x 的最小值是lg 2；④当10,2x x -<<>时，()f x 是增函数；⑤()f x 无最大值，也无最小值.其中所有正确结论的序号是 .高2009级数学阶段测试题(理科)班次_____姓名____________学号_____1314 15 1617．（本小题满分12分）已知5||5||8011AC AB AD DB CD AD ===⋅= ，，，，(1)求||AB AC - ；(2)设BAC θ∠=，且已知4cos()54πθx πx +=-<<-，，求sin x . 18．（本小题满分12分） 如图，直四棱柱ABCD —A 1B 1C 1D 1的高为3，底面是边长为4且∠DAB=60°的菱形，AC ∩BD=0，A 1C 1∩B 1D 1=O 1，E 是O 1A 的中点. （1）求二面角O 1－BC －D 的大小； （2）求点E 到平面O 1BC 的距离.19．（本小题满分12分）已知{a n }为等比数列，{b n }为等差数列，其中a 2=b 4,a 3=b 2,a 4=b 1，且a 1=64,公比q ≠1（Ⅰ）求a n ,b n ；（Ⅱ）设c n =log 2a n ，求数列{c n a n }的前n 项和T n 20. （本小题满分12分）已知函数f （x ）的图象与函数h （x ）=x +x1+2的图象关于点A （0，1）对称. （1）求f （x ）的解析式； （2）若g （x ）=f （x ）+xa,且g （x ）在区间（0，2］上为减函数，求实数a 的取值范围. 21.（本小题满分13分）已知函数241)x (f x +=)R x (∈.(1) 求()(1)f x f x +-的值(2) 若数列}a {n 的通项公式为)m ,,2,1n ,N m ()mn(f a n =∈=+, 求数列}a {n 的前m 项和;S m(3) 设数列}b {n 满足: 31b 1=, n 2n 1n b b b +=+. 设1b 11b 11b 1T n 21n ++++++= . 若(2)中的n S 满足对任意不小于2的正整数n, n n T S <恒成立, 试求m 的最大值.22．(本小题满分13分) 已知函数21f(x)=lnx,g(x)=ax +bx (a 0).2≠（I ）若a= 2 , h(x)=f(x)g(x)－时函数－ 在其定义域是增函数，求b 的取值范围；（II ）在（I ）的结论下，设函数2x x (x)=e +be ,x ∈[0,ln2],求函数(x)ϕϕ的最小值；（III ）设函数)(x f 的图象C 1与函数)(x g 的图象C 2交于点P 、Q ，过线段PQ 的中点R 作x 轴的垂线分别交C 1、C 2于点M 、N ，问是否存在点R ，使C 1在M 处的切线与C 2在N 处的切线平行？若存在，求出R 的横坐标；若不存在，请说明理由. 参考解答：1.B.因为U ={1，3，5，7}，,U M U C M ⊆={5，7}，{}1,3,53,8M a a ∴=∴-==2.D.00000001tan15tan 45tan15tan 601tan151tan 45tan15++===-- 3.A.2:2;:12,3p x q x p q ⌝≤≤⌝-≤≤∴⌝⊂⌝4.A.5123453510S a a a a a a =++++== .5.D. A 错，若a ∥b ，则不能断定α∥β；B 错，若A 、B 、C 三点不在β的同一侧，则不能断定α∥β；C错，若a ∥b ，则不能断定α∥β；D 正确.226..2()()()()0,B DB DC DA DB DA DB DA AB AC AB AC AB AC AB AC AB AC+-=-+-=+∴+-=-=∴=7.D.22ln(22x xx e e e x --=⇒== 由. 8．A 解析：，可得，令2,00)(126)(212==='-='x x x f x x x f 故在[－2，2]上最大值为3)0(==m f ，所以最小值为37)2(-=-f .()(),48()12,()12,1-388f t f t x f m f m m ππππ+=-==-=-+=-=+∴= 9.由可知图象的一条对称轴为或，应选C.10..10310=30A A ⨯列举法：点染红色有种方法，所以共有种方法011.A.,,60,9,.13ABCE D ABCE D DO ABCE DF AE F DOF DFO DF S V A -⊥⊥∠∆∠=∴=== 过点作面作于连结FO,则DFO 为平面角，易求在中，又应选[])()-2002x y 0y f x =+∞+≥ 12.B.由图像可知在，减函数是，在，上是增函数，又 B.4,,4200,42),4(1)2(应选面积为可行域为直角三角形其画出可行域，⎪⎩⎪⎨⎧≤+≥≥∴≤+∴=≤+∴y x y x y x f y x f 二．填空题42456111513.(()15,22T C x x x =-=⨯=∴= 22111111111(1)122222lim n n n nn x x x →+∞+++=+++=--= ， 14. 9.∵9454411*,,≥++=+++=+∴∈yxx y y y x x y x y x R y x 当且仅当61,31==y x 取等号 112222115.,,0,45152080,()()24233O O R AC BC AB R R R S π=⋅=∴∴-=⇒=⇒=设球心为O 截面圆O ，则为截面圆的直径r=由min min 116.()lg(),()(),(1)01,(),1,()212,()lg 2,(3)(1,0),(2,),1()()4)(3)(5).134f x x f x f x xx f x x f x x f x xg x x f x x=+∴-=∴<<≥∴+=∴=∴-+∞=+∴∴∴ 正确；当时为减函数时为增函数，（）不正确；（）正确；在上单增，为增函数，（正确；正确,不正确因此正确的为（）（）（）三．解答题：17.解：(1)由已知，5|||016AD AB CD AD =⋅=5|=，且，2即CD AD ⊥， 所以1cos 2BAC ∠== ，… 3 分由余弦定理||||7AB AC BC -=== ；… 6 分(2)由(1)，14cos cos()cos()2335ππθθθx x ==+=+=，，，所以3sin()35πx +=±，243312πππππx x -<<--<+<而，，… 8 分如果0312ππx <+<，则13sin()sin sin 312625πππx +<<=<，所以3sin()35πx +=-，… 10 分此时3sin sin[()]3310ππx x +=+-==- .… 12 分18．解法一（1）过O 作O F ⊥BC 于F ，连接O 1F ，∵OO 1⊥面AC ，∴BC ⊥O 1F ，… 2分 ∴∠O 1F O 是二面角O 1－BC －D 的平面角，∵OB=2，∠OB F =60°，∴O F… 4分 在Rt △O 1O F 在，tan ∠O 1FO=1OO OF ==∴∠O 1F O=60° 即二面角O 1—BC —D 为60°… 6分（2）在△O 1AC 中，OE 是△O 1AC 的中位线，∴OE ∥O 1C ，∴OE ∥O 1BC ，… 2分∵BC ⊥面O 1OF ，∴面O 1BC ⊥面O 1O F ，交线O 1F .过O 作OH ⊥O 1F 于H ，则OH 是点O 到面O 1BC 的距离，∴OH=3.2∴点E 到面O 1BC 的距离等于3.2… 6分解法二：（1）∵OO 1⊥平面AC ， ∴OO 1⊥OA ，OO 1⊥OB ，又OA ⊥OB ， 建立如图所示的空间直角坐标系（如图） ∵底面ABCD 是边长为4，∠DAB=60°的菱形， ∴OB=2，则A （23，0，0），B （0，2，0），C （－0，0），O 1（0，0，3）… 2分设平面O 1BC 的法向量为1n=（x ，y ，z ）， 则1n ⊥1O B ，1n ⊥1OC，∴23030y z z -=⎧⎪⎨--=⎪⎩，则z=2，则x =y=3， ∴1n =3，2），而平面AC 的法向量2n =（0，0，3）… 4分 ∴cos<1n ，2n21436||||2121=⨯=⋅n n ， 设O 1－BC －D 的平面角为α， ∴cos α=1,2∴α=60°.故二面角O 1－BC －D 为60°.… 6分 （2）设点E 到平面O 1BC 的距离为d ，… 1分∵E 是O 1A 的中点，∴1EO =0，32），… 3分则d=2323)3(|)2,3,3()23,0,3(|||||22211=++--⋅-=⋅n n EO ∴点E 到面O 1BC 的距离等于32.… 6分 19.解：（I ）依题意032),(32244342=+--+=a a a a a a a 即 03213131=+-∴q a q a q a …2分，21101322==⇒=+-∴q q q q 或211=∴≠q q …4分1)21(64-⨯=n n a 故 ，bn=8+8³(n-1)=8n 5分 （II ）n c nn n -==⨯=--72log ])21(64[log 7212 …………6分()()()()()()()⎪⎪⎭⎫ ⎝⎛⨯--⎪⎭⎫ ⎝⎛+++-=-----⎪⎭⎫ ⎝⎛⨯-+⨯+⨯+⨯=----⎪⎭⎫ ⎝⎛⨯-++⨯+⨯+⨯=-----1n 2n 0n2101121021n 72121211264T 122217214215216642121721421521664 得n n n n n T n T()7215-n 640-⎪⎭⎫⎝⎛+=∴n n T …………12分20.解:（1）设f （x ）图象上任一点坐标为（x ,y ），点（x ,y ）关于点A （0，1）的对称点（－x ,2－y ）在h （x ）图象上.∴2－y =－x +x -1+2.∴y =x +x 1, 即f （x ）=x +x1.… 4分 （2）g （x ）=x + xa 1+,∵g ′（x ）=1－21x a +,… 8分，g （x ）在（0，2］上递减，∴1－21xa +≤0在x ∈（0,2］时恒成立,，a ≥x 2－1在x ∈（0,2）时恒成立.… 10分∵x ∈（0,2]时，（x 2－1） max =3,∴a ≥3.… 12分 21．（本小题满分13分）解: 001111411()(1)4242422(42)2x x x x x f x f x -+-=+=+=++++ （）…4分 (2)由(1)可知, 21)x 1(f )x (f =-+, 所以)1m k 1(21)m k 1(f )m k (f -≤≤=-+ ,即,21a a , 21)m k m (f )m k (f k m k =+∴=-+- ………………6分 由m 1m 321m a a a a a S +++++=- , ……………… ① 得,a a a a a S m 13m 2m 1m m +++++=--- ………………②由①＋②, 得,612m 61221m a 221)1m (S 2m m -=⨯+-=+⨯-= ∴).1m 3(121S m -=……8分 (3) ∵,31b 1=)1b (b b b b n n n 2n 1n +=+=+,……③，对任意的0b ,N n n >∈+ .……④由③、④, 得,1b 1b 1)1b (b 1b 1n n n n 1n +-=+=+即1n n n b 1b 11b 1+-=+. ∴1n 1n 11n n 3221n b 13b 1b 1)b 1b 1()b 1b 1()b 1b 1(T +++-=-=-++-+-= . ∵,b b ,0b b b n 1n 2n n 1n >∴>=-++ ∴数列}b {n 是单调递增数列. ∴n T 关于n 递增. 当2n ≥, 且+∈N n 时, 2n T T ≥.……10分∵,8152)194(94b ,94)131(31b ,31b 321=+==+==∴.5275b 13T T 12n =-=≥…12分 ∴,5275S m <即,5275)1m 3(121<-∴,394639238m =< ∴m 的最大值为6. ………13分 22．解：（I ）依题意：.ln )(2bx x x x h -+=()h x 在（0,+∞）上是增函数，1()20h x x b x'∴=+-≥对x ∈（0,+∞）恒成立， …………2分∴≤+>+≥ 112.0,则2b x x x x x(].22,∞-∴的取值范围为b …………4分（II ）设].2,1[,,2∈+==t bt t y e t x则函数化为22().1,2[1,2],242b b by t b y =+-∴-≤-≤≤ 当即在上为增函数当t=1时，y m I n =b+1；…………6分,]2,1[4,22;42,24,2212min 上是减函数在函数时即当时当时即当y ，b bb ，y b t b b -≤≥--=-=-<<-<-< 当t=2时，y m I n =4+2b…………8分.4)(,24.1)(,222,2b x b b x b --<<-+≤≤-的最小值为时当的最小值为时当综上所述ϕϕ当)(,4x b ϕ时-≤的最小值为.24b +…………9分（III ）设点P 、Q 的坐标是.0),,(),,(212211x x y x y x <<且则点M 、N 的横坐标为.221x x x +=C 1在点M 处的切线斜率为.2|1212121x x x k x x x +==+=C 2在点N 处的切线斜率为.2)(|212221b x x a b ax k x x x ++=+=+=…………10分假设C 1在点M 处的切线与C 2在点N 处的切线平行，则.21k k =22122121211212222221121211()2()()2.()22()()ln ln ln ,22a x x x x a x x b b x x x x x x x a a x bx x bx y y x x x +--=+=+-++=+-+=-=-=即则……………11分.1)1(2)(2ln 1212211212x x x x x x x x x x +-=+-=∴设,1,1)1(2ln ,112>+-=>=u uu u x x u 则 ……………… ①[)2222(1)14(1)()ln , 1.().1(1)(1)1,()0.()1,,2(1)()(1)0,ln .1u u r u u u r u u u u u u u r u r u u r u r u u --'=->=-=+++'>∴>+∞->=>+ 令则所以在上单调递增故则这与①矛盾，假设不成立.故C 1在点M 处的切线与C 2在点N 处的切线不平行.…13分。

成都市高2009级成都七中模拟考试英语试卷考试时间：120分钟试题满分：150分本试卷分第一卷（选择题）和第二卷（非选择题）两部分。

第一卷第1至9页，第二卷第10至11页，全卷共11页。

注意事项：1. 请同学们务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上并在第二卷规定的位置上填写自己的班次、姓名和考号。

2. 第一卷的答案用铅笔填涂在机读卡上, 第二卷的答案用钢笔或圆珠笔写在规定的位置上。

3. 考试结束时，将机读卡和第二卷一并交回。

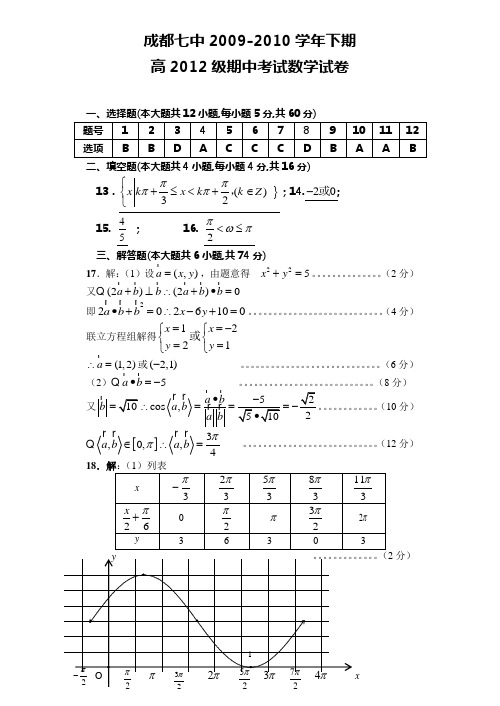
第一卷（三部分，共115分）第一部分：听力（共两节，20小题；每小题1.5分，满分30分）第二部分：英语知识运用（共两节，满分45分）第一节单项填空（共15小题；每小题1分，满分15分）从A, B, C, D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。

21. —I put him down for a well-educated man.—________?—I mean that he's a well-educated man.A. I beg your pardonB. Speak louder, will youC. What's thatD. Will you repeat word for word22. —What do you think of the manager of your company?—Oh, he is _______ manager who's pleasant to work with. It's ______ pleasure to work with him.A. the; aB. a; aC. a; theD. 不填; a23. What _______! Where did you get them?A. big fishB. a big fishC. a piece of big fishD. big a fish24. I know nothing about the match ________ I read in the newspaper.A. besidesB. exceptC. except thatD. except what25. The step you have taken is ________ much risk.A. one ofB. the one ofC. the oneD. that one26. This book is said to be a special one, which ______ many events not found in other history books.A. writesB. coversC. printsD. reads27. Last summer holiday, I went back to my hometown, ________ the neighbours and the house________ I used to be familiar with were gone.A. only finding; whichB. only to find; thatC. to find; whomD. found; that28. You can hardly imagine the difficulty the woman had ________ her children.A. brought upB. to bring upC. bringing upD. to have brought up29. Having decided to rent a flat, we ________ contacting all the accommodation agencies in the city .A. set aboutB. set downC. set outD. set up30. So many directors ________, the board meeting had to be put off.A. were absentB. been absentC. had been absentD. being absent31. — We want someone to design the new art museum for us.—________ the young fellow have a try?A. MayB. ShallC. WillD. Need32. The building of the stadium lasted three years ________ it was completed.A. whenB. beforeC. untilD. after33. —Will you attend the meeting this afternoon?—But I ________ told anything about it.A. wasn'tB. am notC. haven't beenD. won't be34. Some women ________ a good salary in a job instead of staying home, but they decided not towork for the sake of the family.A. must makeB. should have madeC. would makeD. could have made35. In this university a medal with ten thousand dollars ________ gains success in science andtechnology every two years .A. is given to whoeverB. are given to anyone whoC. gives to whomeverD. give to everyone第二节完形填空(共20小题；每小题1.5分，满分30分)阅读下面短文，掌握其大意，然后从36～55各题所给的四个选项(A、B、C和D)中，选出最佳选项，并在答题卡上将该项涂黑。

成都七中高2009级期末考试考试时间120分钟 满分150分一、选择题：本大题共12小题，每题5分，共60分1．若0cos >θ，且02sin <θ，则角θ的终边所在象限是（ ）（A ）一象限 （B ）二象限 （C ）三象限 （D ）四象限 2．下列命题中正确的是（ ）（A ）d b c a d c b a ->-⇒>>, （B ）cbc a b a >⇒> （C ）b a bc ac <⇒< （D ）b a bc ac >⇒>223．点M 分有向线段21M M 的比为λ，已知点)5,1(1M ，)3,2(2M ，2-=λ，则点M 的坐标为（ ）（A ）（3，8） （B ）（1，3） （C ）（3，1） （D ）3(-，)1-4．已知b a ,为任意非零向量，有下列命题： ①||||b a =；②22)()(b a =；③2()a a b =⋅，其中可以作为b a =的必要不充分条件的命题是（ ）（A ）① （B ）①② （C ）②③ （D ）①②③5．=⨯+αααα2cos cos 2cos 12sin 22（ ） （A ）αtan （B ）α2tan （C ）1 （D ）21 6．若函数)sin()(θω+=x x f 的图象（部分）如图所示，则ω和θ的取值是（ ）（A ）3,1πθω== （B ）3,1πθω-==（C ）6,21πθω==（D ）6,21πθω-== 7．设)5,4(),,2(),1,(C b B a A 为坐标平面上三点，O 为坐标原点，若与在方向上的投影相同，则b a 与满足的关系式是（ ）（A ）354=-b a （B ）345=-b a （C ）4514a b += （D ）1445=+b a 8．设π20<≤x ，且x x x cos sin 2sin 1-=-，则（ ） （A ）π≤≤x 0 （B ）474ππ≤≤x （C ）454ππ≤≤x （D ）232ππ≤≤x 9．已知b a ,都是正数，下列命题正确的是（ ）l 1l 2l 3（A ）2211222b a b a ab b a +≤+≤≤+ （B ）b a b a ab b a 1122222+≤+≤≤+（C ）2211222b a b a ba ab +≤+≤+≤ （D ）2211222b a b a ab b a +≤+≤≤+10．已知向量)2,1(=，)4,2(--=，5||=，若25)(=⋅+，则与的夹角为（ ）（A ） 30 （B ） 60 （C ）120 （D ）15011．设)(t f y =是某港口水的深度y （米）关于时间t （时）的函数，其中240≤≤t ，下表是该港口某一天从0时至24时记录的时间t 与水深y 的关系:经观察，)(t f y =可以近似看成)sin(ϕω++=x A K y 的图象，下面的函数中最能近似地表示表中数据对应关系的函数是（ ） （A ）t y 6sin 312π+=，]24,0[∈t （B ）)6sin(312ππ++=t y ，]24,0[∈t（C ）t y 12sin312π+=，]24,0[∈t （D ）)212sin(312ππ++=t y ，]24,0[∈t 12．如图123,,l l l 是同一平面内的三条平行线，12l l 与间的距离为1，23l l 与间的距离为2，正三角形ABC 的三顶点分别在123,,l l l 上，则△ABC 的边长是（ ） （A ） （B （C （D 二、填空题：本大题共4小题，每题4分，共16分。

成都七中2009级高三年级理科综合试卷2009.03.05 本卷分Ⅰ卷和Ⅱ卷。

第Ⅰ卷第1至5页，第Ⅱ卷6至13页。

共300分，时间150分钟。

第Ⅰ卷(选择题共126分)注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、学号、考试科目涂写在答题卡上。

考试结束，将答题卡交回。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，不能答在试题卷上。

可能用到的原子量：H-1，C-12，O-16，S-32，Br-80，Ag-108一、本题共13题，每题6分，共78分。

下列各题的选项中，只有一个是符合题目要求的。

1.下列有关水对动、植物生命活动影响的叙述，不正确的有（）项①在休眠的植物体内自由水与结合水的比值降低，有利于降低植物的新陈代谢，有利于度过不利的环境条件②衰老的细胞内自由水含量降低③癌细胞是一种分裂失控的细胞，其自由水含量较正常的细胞低④参与营养物质、代谢废物的运输,也能够贮藏能量和为生命活动供能A.0B.1C.2D.32.下图表示光合作用与呼吸作用过程中物质变化的关系，下列说法中，不正确．．．的是①能为各种生命活动提供能量最多的是过程5②C4植物维管束鞘细胞中2过程只有一种途径③过程1、3和4产生的[H]都能与氧结合生成水④过程2需多种酶参与，且需ATP提供能量A．③B．②③ C．①②D．③④3．下列关于生物新陈代谢的叙述中正确的是（）①在夏季晴朗的天气，金鱼藻的光合作用没有“午休”现象②食物中脂肪在人体内经过消化后，以甘油和脂肪酸的形式吸收并运输到组织器官③弱光下适当提高二氧化碳的浓度不能提高光合作用的速率④人体内非必需氨基酸的来源有三个途径，必需氨基酸的来源有两个途径A．①②B．③④C．②③D．①④4．下列关于细胞融合及培养等过程的叙述正确的是（）A．若a、b分别代表被子植物的一个精子和一个极核，则d细胞为受精极核B．若a、b是两种植物的原生质体，则培育N植株的原理是细胞增殖C．若N植株比M植株光合作用效率高，原因之一可能是前者具有双亲的叶绿体D．理论上，不能用类似单克隆抗体的制备方法在体外大量生产干扰素5．右图表示使人体获得免疫力的两种方法。

成都市高2009级成都七中模拟考试英语试题及参考答案七彩教育网成都市高2009级成都七中模拟考试英语试卷考试时间：120分钟试题满分：150分本试卷分第一卷和第二卷两部分。

第一卷第1至9页，第二卷第10至11页，全卷共11页。

注意事项： 1. 请同学们务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上并在第二卷规定的位置上填写自己的班次、姓名和考号。

2. 第一卷的答案用铅笔填涂在机读卡上, 第二卷的答案用钢笔或圆珠笔写在规定的位置上。

3. 考试结束时，将机读卡和第二卷一并交回。

第一卷第一部分：听力第二部分：英语知识运用第一节单项填空从A, B, C, D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。

21.—I put him down for a well-educated man. —________? —I mean that he’s a well-educated man. A. I beg your pardon B. Speak louder, will you C. What’s that D. Will you repeat word for word 22. —What do you think of the manager of your company? —Oh, he is _______ manager who’s pleasant to work with. It’s ______ pleasure to work with him. A. the;a B. a; a C. a; the D. 不填; a23. What _______! Where did you get them? A. big fish B. a big fish C. a piece of big fish D. big a fish 24. I know nothing about the match ________ I read in the newspaper.A. besidesB. exceptC. except thatD. except what 25. The step you have taken is ________ much risk. A. one of B. the one of C. the one D. that one 26. This book is said to be a special one, which ______ many events not found in other history books.A. writesB. coversC. printsD. reads 27. Last summer holiday, I went back to my hometown, ________ the neighbours and the house 七彩教育网全国最新初中、高中试卷、课件、教案下载七彩教育网________ I used to be familiar with were gone. A. only finding; which B. only to find; that C. to find; whom D. found; that 28. You can hardly imagine the difficulty the woman had ________ her children. A. brought up B. to bring up C. bringing up D. to have brought up 29. Having decided to rent a flat, we ________ contacting all the accommodation agencies in the city .A. set aboutB. set downC. set outD. set up 30. So many directors ________, the board meeting had to be put off. A. were absent B. been absent C. had been absent D. being absent 31. —We want someone todesign the new art museum for us. —________ the young fellow have a try?A. MayB. ShallC. WillD. Need 32. The building of the stadium lasted three years ________ it was completed. A. when B. before C. until D. after 33. —Will you attend the meeting this afternoon? —But I ________ told anyt hing about it. A. wasn’t B. am not C. haven’t been D. won’t be 34. Some women ________ a good salary in a job instead of staying home, but they decided not to work for the sake of the family. A. must make B. should have made C. would make D. could have made 35. In this university a medal with ten thousand dollars ________ gains success in science and technology every two years . A. is given to whoever B. are given to anyone who C. gives to whomever D. give to everyone 第二节完形填空(共20小题；每小题分，满分30分) 阅读下面短文，掌握其大意，然后从36～55各题所给的四个选项(A、B、C和D)中，选出最佳选项，并在答题卡上将该项涂黑。

成都七中2009年外地生招生考试 数学模拟试题参考答案及评分标准第Ⅰ卷一、单项选择（共12小题，每小题5分，满分60分）第Ⅱ卷二、填空题 （共4小题，每小题4分，满分16分）13．2 14． 3520 15． 211≤<-m 16．4n+2三、计算题 （共6小题，满分74分）17．（本小题满分12分）（1）解：原式=xy y xy x y xy x 25)23(4422222--+-++=x y y xy x y xy x 25234422222-+--++·······················2分=xxy x 2222+-=y x +-······················································2分当2-=x ，21=y 时原式=2521)2(=+--··························2分 （2）解： 联立21y x =+和2331y x x =+- 可得133122-+=+x x x ········2分化简可得0232=-+x x 解方程，得11-=x 322=x ········································2分 当11-=x 时，11-=y 则一交点为)1,1(-- 当322=x 时，372=x 则一交点为)37,32( 综上所述，直线21y x =+与抛物线2331y x x =+-的交点坐标为)1,1(--，)37,32(·················································2分18．（本小题满分12分） 解： （1）··························4分（2）·································1分·············2分······················································2分 （3）································1分·········································2分222211tan tan 232342AB PC BPC ABE ADEPFE DFP PFE DFPPF DF PF EF FD EF PFAEAB AE BP AE AE APB ABE PE BE AE a PE a BE a AP a AE PE BE PC PC PE PB PC FC FE FD PF PF FC ∴∠=∠=∠∠=∠∴∴=∴=⋅∴⊥∠==∠=======∴====∴=⋅=∴==⋅=∴==∥又△∽△连接为直径令，，为切线12190PCPF ADB AB ADB PE PB PA PDPD BD AD ADBRt =∴=∴∠=︒⋅=⋅∴===∴△为等腰直角三角形为直径△为等腰△19．（本小题满分13分）（1）连结。

成都七中2009—2010学年下期半期考试 高2011级物理试题注意事项：1．本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．共120分．考试时间90分钟 2．答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目用铅笔填写在答题卡上．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上．3．答第Ⅱ卷前，先将密封线内的项目填写清楚．用钢笔或圆珠笔直接在试卷上答题．第Ⅰ卷(选择题共48分)一、本题共12小题，每小题4分，共48分。

在每小题给出的四个选项中，有的不止一个选项符合题意，全选对得4分，选对不全得2分，不选或有错得0分。

1、下列关于电磁波的叙述中，正确的是 ( ) A ．变化的磁场周围一定会产生电磁波B ．电磁波在任何介质中的传播速度均为3.00×108 m ／sC ．电磁波由真空进入介质传播时，波长将变短D ．电磁波在某介质中的波速v 、频率f 、波长λ的关系不满足v =λf 2、关于磁感线和电场线的下列说法中，正确的是( )A ．电场线越密的地方电场越强；同样，磁感线越密的地方磁场也越强B ．在电场中任意两条电场线不会相交；同样，在磁场中任意两条磁感线也不会相交C ．静电场中的电场线不是闭合的，同样，磁感线也是不闭合的D ．沿电场线的方向电势越来越低，而沿磁感线的方向则磁场越来越弱 3、如图1所示的电路中，L 1和L 2是完全相同的灯泡，线圈L 的自感系数很大，它的电阻可以忽略不计。

则下列说法中正确的是( ) A ．闭合S 后，灯L 2先亮，灯L 1后亮，最后两灯一样亮 B ．闭合S 后，灯L 1的电流方向向右，L 2的电流方向向左 C ．断开S 后，灯L 2立刻熄灭、则L 1过一会儿熄灭D ．断开S 瞬间，灯L 1的电流方向向右，L 2的电流方向向左4、如图2所示，一只阴极射线管，左侧不断有电子射出，若在管的正下方放一通电直导线AB 时，发现射线的径迹往下偏，则( ) A ．导线中的电流从A 流向B B ．导线中的电流从B 流向AC ．若要使电子束的径迹向上偏，可以通过改变AB 中的电流方向来实现D ．电子束径迹的偏向与AB 中的电流方向无关5、如图3所示，直线ab 上方有垂直于纸面的匀强磁场。

成都七中2009-2010学年下期高2012级期中考试数学试卷考试时间:120分钟;试卷总分:150分第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的)1．cos 480=A ．12B ．12- C ．2 D ．2- 2．在平面直角坐标系中,若角α的顶点在坐标原点,始边在x 轴的非负半轴上,终边经过点),(a a P ,(其中0a <),则αsin 的值是A ．22 B ．－22 C ．22± D ．1 3．已知向量a 、b 不共线，,),(b a d R k b a k c -=∈+=如果d c //， 那么A ．1k =且与同向B ．1k =且与反向C ．1k =-且与同向D ．1k =-且与反向4．若过两点)6,5(),2,1(21P P -的直线与x 轴相交于点P ,则点P 分有向线段12P P 所成的比λ的值为A ．－13B ．－15C ．15D ．135．若4A B π+=,则(1tan )(1tan )A B ++的值是A ．1BC ．2D ．2-6．函数)sin(ϕω+=x A y 在一个周期内的图象如下，此函数的解析式为A ．)32sin(2π-=xy B ．)32sin(2π+=x y C ．)322sin(2π+=x yD ．)32sin(2π-=x y7．若sin 2sin(),(0,2)x x x θθπ=+∈，则θ等于A ．611πB ．67πC ．53πD ．23π 8．已知函数R x x x x f ∈+=,sin )2cos 1()(2，则)(x f 是A ．最小正周期为π的奇函数B ．最小正周期为π的偶函数C. 最小正周期为2π的奇函数 D ．最小正周期为2π的偶函数 9．设向量a 、b 、c 为三个非零向量，若a b c m a b c =++ ，则m 的取值范围是A ．[]0,2B ．[]0,3 C.{}0,1,2,3 D ．{}0,310． 条件“tan tan αβ=”是“tan()0αβ-=”成立的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件11．已知非零向量AB 与AC 满足0=∙+且21=∙，则ABC ∆为A ．等边三角形B ．直角三角形C ．等腰非等边三角形D ．三边均不相等的三角形12．在∆ABC 中，已知tan sin 2A B C +=，给出以下四个论断： ①tan .cot 1A B =②0sin sin A B <+≤③22sin cos 1A B += ④222c o s c o s s i nA B C += 其中正确的是 A ．①③ B ．②④ C ．①④ D ．②③二、填空题(本大题共4小题,每小题4分,共16分.把答案填在横线上)13．使不等式tan 0x ≥成立的x 的取值集合是 ． 14．在平面直角坐标系中，,i j 分别是与,x y 轴正方向同向的单位向量，平面内三点A 、B 、C 满足AB i j =+ ，2AC i m j =+ ．若A 、B 、C三点构成直角三角形，则实数m 的值为 ． 15．已知⎪⎭⎫ ⎝⎛3∈=⎪⎭⎫ ⎝⎛-4,2,1024cos πππx x ，则x sin = ． 16．已知ω是正实数，设[]{()cos ()S f x x ωθωθ==+是奇函数}，若对每个实数a ，(,2)S a a ω+ 的元素不超过2个，且存在a 使(,2)S a a ω+ 含有2个元素，则ω的取值范围是 ．成都七中2009-2010学年下期高2012级期中考试数学试卷命题人:杜利超 审题人:张世永座位号:□□ 第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题4分,共16分.把答案填在横线上)13．___________________ . 14．____________________ .15．___________________ . 16．____________________ .三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)已知向量→→b a ,满足()3,1,5||-==→→b a ，且→→→⊥⎪⎭⎫ ⎝⎛+b b a 2．（1）求向量→a 的坐标； （2）求向量→a 与→b 的夹角.18.(本小题满分12分)已知函数()3sin()326x f x π=++． （1）用五点法画出它在一个周期内的闭区间上的图象；（2（318.19.(本小题满分12分)已知,,A B C 的坐标分别为3003A B （，），（，）, 3(cos ,sin ),(,)22C ππααα∈.（1）若||||AC BC = ，求角α的值； （2）若1AC BC ⋅=- ，求22sin sin 21tan ααα++．20.(本小题满分12分)已知函数()2sin()2cos 6f x x x π=+-．（1）求函数()f x 的单调递增区间； （2）当,2x ππ⎡⎤∈⎢⎥⎣⎦时，求函数()f x 的最小值及相应x 的取值； （3）把函数()y f x =的图象按向量m 平移得到函数()g x 的图象，若函数()g x 是偶函数，写出 m 最小的向量m 的坐标．O P D CB A21.(本小题满分12分)如图，某地有三家工厂，分别位于矩形ABCD 的两个顶点A ，B 及CD 的中点P 处．AB ＝20km ，BC ＝10km ．为了处理这三家工厂的污水，现要在该矩形区域上（含边界）且与A ，B 等距的一点O 处，建造一个污水处理厂，并铺设三条排污管道AO ，BO ，PO ．记铺设管道的总长度为ykm ．（1）按下列要求建立函数关系式：（i ）设BAO θ∠=（rad ），将y 表示成θ的函数；（ii ）设OP x =（km ），将y 表示成x 的函数；（2）请你选用（1）中的一个函数关系确定污水处理厂的位置，使铺设的污水管道的总长度最短．22.(本小题满分14分)设(0,)απ∈，函数)(x f 的定义域为]1,0[，且,0)0(=f 1)1(=f ，对定义域内任意的,x y ，满足)()sin 1(sin )()2(y f x f y x f αα-+=+． （1）试用α表示)21(f ，并在11()22f =时求出α的值； （2）试用α表示13(),()44f f ，并求出α的值；（3）N n ∈时，12n na =，求)(n a f ,并猜测∈x ]1,0[时，)(x f 的表达式.。

成都七中2009-2010学年下期高2012级期中考试数学试卷13．}()32x k x k k Zππππ⎧+≤<+∈⎨⎩，；14.20-或;15.45； 16.2πωπ<≤三、解答题(本大题共6小题,共74分)17．解：（1）设(,)a x y=，由题意得225x y+=。

（2分）又(2)(2)0a b b a b b+⊥∴+∙=即22026100a b b x y∙+=∴-+=。

（4分）联立方程组解得1221x xy y==-⎧⎧⎨⎨==⎩⎩或(1,2)a∴=或(2,1)-。

（6分）（2）5a b∙=-。

（8分）又b=cos,2a ba ba b∙===-。

（10分）[]3,0,,4a b a bππ∈∴=。

（12分）2分）4分）(2)周期T ＝π4，振幅A ＝3，初相6πϕ=，由262πππ+=+k x ，得)(322Z k k x ∈+=ππ即为对称轴；。

（8分） （3）①由x y sin =的图象上各点向左平移6πϕ=个长度单位，得)6sin(π+=x y 的图象；②由)6sin(π+=x y 的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），得)62sin(π+=x y 的图象；③由)62sin(π+=x y 的图象上各点的纵坐标伸长为原来的3倍（横坐标不变），得)62sin(3π+=x y 的图象；④由)62sin(3π+=x y 的图象上各点向上平移3个长度单位，得)62sin(3π+=x y ＋3的图象。

（12分）19．解：（1）(cos 3,sin ),(cos ,sin 3),AC BC αααα=-=-。

（2分）||AC ∴=||BC =。

（4分） 35||||sin cos .(,),.224AC BC πππαααα==∈∴= 得又。

（6分） （2）由1,(cos 3)cos sin (sin 3) 1.AC BC αααα⋅=--+-=-得2sin cos .3αα∴+= ① 。

成都七中2008-2009学年下期 高2011级期末考试数学试卷考试时间:120分钟;试卷总分:150分 命题人:邱 旭 审题人:魏 华第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的)1.已知a<b<0,则下列不等式正确的是A.a 2<b 2B.a 3<b 3C.ab<b 2D.ba 11< 2.下列函数中,在(0,2π)上递增的偶函数是 A.y=sinx B.y=cosx C.y=tanx D.y=|sinx| 3.设x 为第三象限角,则函数f(x)=tanx+cotx 有A.最大值2B.最大值-2C.最小值2D.最小值-2 4.sin 12π+cos 12π的值为A.26B.23C.22D.215.不等式(x-1)•|x|<0的解集是A.{x|x<1}B.{x|x>1}C.{x|0<x<1}D.{x|x<1且x ≠0}6.已知P 是ΔABC 所在平面内的一动点,且)21(λ+=(λ≥0),则点P 的轨迹一定通过ΔABC 的A.外心B.内心C.重心D.垂心 7.已知a,b,c 均为正实数,若不等式m ≤(a+b+c)•(cb a 11++)恒成立,则实数m 的最大值是 A.9 B.4 C.3 D.28.已知点P(cos θ,sin θ)在直线y=2x 上,则cos2θ的值为A.53-B.54- C.54 D.539.将函数y=sin(2x-3π)-1的图象按向量a 平移后,得到函数y=sin2x 的图象,则使|a |最小的a 的坐标为A.(3π,-1) B.(3π-,1) C.(6π-,1) D.(6π,-1)10.已知点P 分有向线段A B 所成的比为-2,设OP =x OA +y OB (O 为直线AB 外一点),则实数对(x,y)的取值是A.(-1,2)B.(1,-2)C.(2,-1)D.(-2,1) 11.设函数f(x)=sin(6π+x)sin(3π-x),若不等式f(x)≥f(x 0)对x ∈R 恒成立,则x 0的最小正值为A.65πB.67πC.125πD.127π12.设a,b 都是正实数,若向量x =(a,b)与y =(1-b,a-1)满足关系式y =x λ(其中λ∈R),则称为“和谐向量”.那么这些“和谐向量”的模的最大值为A.2B.2C.1D.22二、填空题(本大题共4小题,每小题4分,共16分.把答案填在Ⅱ卷横线上)13.求值:=--1022032cos cos _________. 14.已知集合A={x|x 2+2x-3>0},B={x|log 2x ≤1},则A ∩B=_________. 15.如图所示为函数y=sin(ωx+φ)(其中ω>0,且-π≤φ<π)的部分图象,则φ=_________.16.设△ABC 的内角A,B,C 的对边分别为a,b,c,若a=(b+c)cosC,则△ABC 的形状是_________.座位号:□□成都七中2008-2009学年下期高2011级期末考试数学试卷命题人:邱旭审题人:魏华第Ⅱ卷(非选择题,共90分)一填空题二、填空题(本大题共4小题,每小题4分,共16分)13.__________; 14.__________;15.__________; 16.__________.三、解答题(本大题共6小题,74分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)设a=(sinx,cosx),b=(3cosx,-cosx),函数f(x)=a·b.(1)求f(x)的最小正周期;(2)当x∈[0,2π]时,求f(x)的值域.18.(本小题满分12分)已知tan2α-cot 2α=2,且α∈)2,2(ππ .(1)求α的值; (2)若cos(α+β)=54,求sin2β的值.19.(本小题满分12分)已知平面内三个向量,,,它们每两个之间的夹角均为120º,且•=-2. (1)若||=2,求证:(-)⊥; (2)若++=,求||的最小值.20.(本小题满分12分)已知△ABC 的面积为3,内角A,B,C 的对边a,b,c 满足a 2+b 2=c 2+4.(1)求角C 的大小;(2)求sin 2A+sin 2B-sinAsinB 的值.21.(本小题满分12分)已知函数f(x)=xx 12+(x ≠0). (1)求不等式f(x)≤f(x 1)的解集; (2)求证:f(1)+f(21)+f(31)+…+f(n 1)<242++n n (n ∈N *).22.(本小题满分14分)已知a,b 都是正实数. (1)若a+b=1,且x,y ∈R,求证:ax 2+by 2≥(ax+by)2;(2)若a+b=m,且m ≥1,求证:bb a a 21)1(-⋅-≤2)22(m m -.。

1成都七中高2009级阶段性考试2月月考数学试题（文科）（总分150分，时间120分钟） 第I 卷（选择题共60分）一、选择题（每小题只有一个正确答案，每小题5分，共60分） 1、全集{}{}{}0,1,3,5,7,9,0,5,9,3,5,7()S S C A B AB ====则A 、{}5,3B 、{}7,3C 、{}7,5,3D 、∅ 2、条件甲“50<<x ”是条件乙“3|2|<-x 的（ ） A 、充分不必要条件 B 、必要不充分条件 C 、充要条件 D 、既不充分也不必要条件 3、已知两个不同平面βα,和两条不重合的直线m ，n 。

有下列四个命题： ① 若αα⊥⊥n m n m 则,,//；②若βαβα//,,则⊥⊥m m ；③若βαβα⊥⊂⊥则,,//,n n m m ；④若n m n m //,,//则=⋂βαα其中正确命题个数是（ ） A 、0个 B 、1个 C 、2个 D 、3个 4、{}n a 为等差数列，若{}n n a s a a 是,1264=+的前n 项和，则9s =（ ） A 、48 B 、54 C 、60 D 、665、在矩形ABCD 中，AB=4，BC=3，沿AC 将矩形ABCD 折成直二面角D AC B --，则四面体ABCD 的外接球的体积为（ ） A 、π12125 B 、π9125 C 、π6125 D 6、过抛物线)0(22>=p px y 的焦点F 的直线l 交抛物线于点A 、B,交其准线于点C ，若===P AF BF BC 则且,3||||2||（ ） A 、43 B 、29 C 、49 D 、237、如图：在底面边长为1的正四棱柱1111D C B A ABCD -中， P 为底面ABCD 所在平面内一动点，点P 到直线BC 的距离等于它到直线1AA 的距离，则P 点的轨迹方程以是（ ）A 、x y =2B 、x y 42-= C 、y x =2D 、y x 22-= 8、已知ABC ∆的三个内角A 、B 、C 成等差数列，且AB=2，AC=3，则C cos =（ ）A 、36 B 、33 C 、32 D 、36- 9、设)0)(()(2≠++=a c bx ax x x f 在11-==x x 和处有极值，则下列点中一定在x 轴上的是（ ）A 、),(b aB 、),(c aC 、),(c bD 、),(c b a +10、函数)1(log 2+-=ax x y a 有最小值，则实数a 的取值范围是（ ）A 、10<<aB 、120≠<<a a 且C 、21<<aD 、2≥a11、以双曲线1422=-my x 的离心率为半径，以右焦点为圆心的圆与双曲线的渐近线相切，则m=（ ） A 、23 B 、34 C 、45 D 、56 12、某旅馆有三人间，两人间，单人单三种房间各一间，有3位成人带2个小孩来此投宿，小孩不宜单住一间（必须有成人陪同），则不同的住宿方式有（ ）种。

成都七中2019-2009学年度高三年级模拟考试理科综合试卷2009.2.19本试卷分第Ⅰ卷和第Ⅱ卷两部分。

第Ⅰ卷第1至6页，第Ⅱ卷7至16页。

共300分，考试时间150分钟。

第Ⅰ卷(选择题共126分)注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、学号、考试科目涂写在答题卡上。

考试结束，将答题卡交回。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，不能答在试题卷上。

可能用到的原子量：H-1，C-12，O-16，Na-23，K-23，S-32，Cu-64 ，Ba-137 一、本大题共13题，每题6分，共78分。

在下列各题的四个选项中，只有一个选项是符合题目要求的。

1．右图表示某雄性高等动物细胞分裂过程中，每条染色体上DNA数量的变化曲线，下列叙述不正确的是A．若是人体细胞，则DE段细胞中的染色体数目只有46条B．CD段的变化是由于着丝点的分裂C．BC段细胞内染色体数：核DNA分子数=1：2D．D点后的细胞中不一定含有Y染色体2．如右图所示，为了鉴定男孩8与本家族的亲子关系，需采用特殊的鉴定方案。

下列方案可行的是A.比较8与2的线粒体DNA 序列B.比较8与3的线粒体DNA 序列C.比较8与5的Y 染色体DNA 序列D.比较8与2的X 染色体DNA 序列 3. 下列关于微生物生长叙述中，正确的是A ．调整期合成的酶都是诱导酶B ．稳定期有害产物积累最多，细胞死亡率最大C ．无机氮源不能为微生物的生命活动提供能源D ．生长期各阶段的细胞内都会发生酶活性的调节4．下列关于免疫的叙述，不正确的是A ．吞噬细胞既可以参与特异性免疫，又可参与非特异性免疫B ．当细菌外毒素再次侵入机体后，效应B 细胞和记忆细胞都能产生抗毒素中和外毒素C ．已免疫的B 淋巴细胞在体外也能分泌抗体D ．人体感染酿脓链球菌后会引起风湿性心脏病，属于自身免疫病5．下图为某生态系统能量流动示意图(单位：J ／cm 2·a)，以下分析不正确的是A ．甲通过光合作用固定在有机物中的总能量为1250 J ／cm 2·aB ．乙到丙的能量传递效率为15％C ．每一营养级的能量大部分用于呼吸作用和被丁利用D ．在此生态系统中，一只狼捕食一只野兔，获得的能量只能在l0％-20％之间6．生活中的某些问题，常常涉及到化学知识，下列分析正确的是A ．氯气和二氧化硫均可作为漂白剂，若同时使用它们去漂白某一润湿的有色物质，漂白效果会明显加强B ．为了消除碘缺乏病，卫生部规定食盐必须加碘，其中碘以单质的形式存在C ．苯酚有杀菌和止痛作用，药皂中也掺有少量苯酚，所以我们可以用苯酚对环境消毒或直接涂抹于皮肤上进行捎毒D ．工业酒精不能加水当饮料酒品尝，其原因是它含有甲醇，它虽具有酒香味，但饮后会导致中毒，甚至死亡、7．设N A 为阿伏加德罗常数。

成都七中2008—2009学年度下期高一年级期末考试化学试卷考试时间：100分钟总分：110分命题人：廖志诚审题人：徐军程嘉可能用到的原子量：H—1 O—16 N—14 P—31 Fe—56 Cu—64 Mg—24 S—32 C—12 K—39 Na—23第Ⅰ卷选择题(共50分)一、选择题。

（每小题一个答案，将答案转涂在答题卡上，每小题2分，共50分）1．下列关于硅单质及其化合物的说法不正确．．．的是A．硅是构成一些岩石和矿物的基本元素B．水泥、玻璃、水晶饰物都是硅酸盐制品C．二氧化硅广泛用于制作光导纤维D．陶瓷是人类应用很早的硅酸盐材料2．下列有关化学用语表达不正确．．．的是A．115号元素X的一种核素中子数174，表示为289115X B．次氯酸结构式：H—O—Cl C．S2－的离子结构示意图：D．NH4Cl的电子式：3．下列关于环境问题的说法不正确．．．的是A．SO2在空气中的含量是城市空气日报的内容之一B．臭氧层被破坏是导致皮肤发生癌变的重要原因之一C．pH小于7.0的降水通常称为酸雨D．化石燃料的燃烧是引起温室效应的主要原因之一4．下列说法不正确．．．的是A．金刚石与C60互为同素异形体，且其中的化学键类型相同B．SiO2既能与HF溶液反应，又能与NaOH溶液反应，所以SiO2为两性氧化物C．向Na2SiO3溶液中通入CO2，有白色胶状沉淀生成D．NaOH溶液贮存在带橡胶塞的试剂瓶中5．下列结论正确．．的是①微粒半径：Ca>S2－>Cl－>F ②氢化物的稳定性：HF>HCl>H2S>PH3③离子的还原性：S2－> O2－>Br－> I－④氧化性：Cl2>S>P>Si⑤酸性：H2SO4>HClO4>H2SeO4 ⑥非金属性：F>O>S>SiA．①②④⑥B．①③④C．①③D．⑤⑥6．氮化硅是新型无机非金属材料，其中Si与N原子最外层均达到8电子结构。

成都七中2009级高三年级热身考试理科综合试卷2009.6.3生物参考答案和评分意见1、B【分析】由图可知：a-b段，随着营养液中氧含量升高，植物对K+吸收速率升高；说明营养液中O2含量影响吸收速率；而植物吸收O2是进行有氧呼吸为K+吸收提供能量。

b-c段，随着营养液中氧含量升高，植物对K+吸收速率相对稳定，说明除了O2含量，还有其他因素制约K+吸收速率。

但仅从图中无法判断该植物吸收K+是否要需要载体。

【考点】：1、植物吸收矿质元素的方式；2、识图，分析能力【易错点】：1、不能严格据图分析，混淆所学相关内容与实际图表的含义。

【复习提示】：1、正确分析相关图表所给数据，不要随意添加，修改其中的内容。

2．B【分析】A:淋巴T细胞分泌物能够激活靶细胞的溶酶体酶，促进靶细胞的自溶裂解，膜蛋白无关；B:机体的免疫反应首先需要膜蛋白对抗原的识别，塞米松能钝化免疫反应，因此有可能使免疫细胞的膜蛋白活性下降，不能识别抗原，导致机体免疫能力下降。

C: 生物导弹”能有效杀伤癌细胞属于直接使细胞死亡，与膜蛋白无关。

D: 胰岛素作用于肝脏使血糖降低，也与膜蛋白无关。

【考点】：1、膜蛋白的作用以及具体事例【易错点】：1、在具体分析中，混淆某物质对膜蛋白和对细胞的作用。

【复习提示】：正确认识膜蛋白的作用，并归纳常与之相关的实例。

3、D【分析】A:由甲图可知：由甲图可知，限制AB段光合作用速度的因素主要是光照强度，三种温度对植物的影响一定光照强度下保持一致的，说明温度不是一直限制AB段光合作用速度。

B: 强光照下，光反应阶段并未受到限制；光合作用速度不再增加的原因是由于受到其他因素的限制，如CO2的供应不足导致暗反应受阻。

C:由乙图可知，CD段光合作用速度下降的原因是温度过高，导致光合作用的酶活下降。

D：由乙图可知，光合作用的最适温度为37.5℃。

因此，在光照强度为B、温度为30℃时，再适当提高温度，光合作用速度仍会提高。

【考点】：1、识图，分析能力；2、光合作用的影响因素【易错点】：1、光照未饱和与饱和时，影响光合作用的主要因素分别是什么。

成都七中2008-2009学年度高三年级模拟考试理科综合试卷2009.5.25本试卷分第Ⅰ卷和第Ⅱ卷两部分。

第Ⅰ卷第1至6页，第Ⅱ卷7至16页。

共300分，考试时间150分钟。

第Ⅰ卷(选择题 共126分)注意事项： 1．答第Ⅰ卷前，考生务必将自己的姓名、学号、考试科目涂写在答题卡上。

考试结束，将答题卡交回。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，不能答在试题卷上。

可能用到的原子量：H-1， C-12， O-16， Na-23， K-23， Si-28， S-32 ，Ag-108 一、本大题共13题，每题6分，共78分。

在下列各题的四个选项中，只有一个选项是符合题目要求的。

1、下列关于绿色植物新陈代谢相关知识的叙述，正确的是 A. C 3植物CO 2的固定和还原都需要ATP 提供能量B.将一植株的叶子去掉一半，将直接影响对矿质养料的吸收C.叶子变黄后主要依靠类胡萝卜素实现光能转换为电能D.C 3植物叶片内进行光合作用的细胞是叶肉细胞，C 4植物叶片内进行光合作用的细胞是叶肉细胞、维管束鞘细胞 2、“光改变生长素的分布”这一现象可能的解释有：①光使向光—侧的生长素分解；②光使生长素向背光—侧运输。

某生物兴趣小组设计实验进行探究，实验步骤如下：将生 长状况相同的胚芽鞘尖端切下来，放在琼脂切块上，分别 放在单侧光下(如右图所示，云母片不透光也不能透过生长素，但不影响生长素向下运输和琼脂块中收集的生长素的量)。

一段时间后，比较四个琼脂块中收集到的生长素(IAA)的量a 、b 、c 、d 。

相关实验预期正确的是A ．若a=b ，且b d >，说明在单侧光照射下，向光侧的生长素被分解，而不是向光侧的生长素向背光侧转移B ．若a b d >=，说明在单侧光照射下，向光侧的生长素向背光侧转移，而不是向光侧的生长素被分解C ．若a b >，且b d >，说明在单侧光照射下，既有向光侧的生长素向背光侧转移，又有向光侧的生长素被分解D ．若a=b ，且c d >，说明在单侧光照射下，既有向光侧的生长素向背光侧转移，又有向光侧的生长素被分解3、免疫是机体的一种保护性生理功能，机体通过免疫调节维持内环境的平衡和稳态，以下叙述的现象与正常免疫调节相符的是A.不经吞噬细胞加工、处理，抗原无法对B 淋巴细胞起到刺激作用B.淋巴细胞只有在受到抗原刺激后，才能形成效应细胞和记忆细胞C.非特异性免疫过程中，吞噬细胞的吞噬作用不具有识别作用D.淋巴因子的释放发生在细胞免疫的反应阶段 4、下列关于生物工程技术的叙述中，正确的是A.从遗传学上讲，番茄-马铃薯这种变异的来源是染色体变异B.将人的干扰素基因与大肠杆菌含抗四环素基因的质粒结合，导入大肠杆菌，在培养基中加入四环素，结果大肠杆菌正常生长繁重，说明大肠杆菌中一定含有目的基因C.动物细胞融合可以克服远源杂交不亲和障碍，扩大了用于杂交的亲本组合范围 D ．在用酵母菌生产酒的过程中，以酒精浓度测定酵母菌的生长状况5、科学家对生活在某生态系统的一个蜘蛛种群的能量进行定量分析，得出了能量流经这种肉食动物的有关数据如下（能量以种群的质量表示）：下列叙述正确的是A ．根据图中的数据不能算出猎物种群和蜘蛛间的能量传递效率B ．蜘蛛的最低营养级是第二营养级C ．图中Ⅹ代表从食物种群中流入到蜘蛛体内的能量D ．如果蜘蛛全部死亡，对该生态系统其他物种不会有影响6、下列变化中涉及化学变化的是⑴ 爆竹燃放 ⑵ 碘的升华 ⑶ 金属钝化 ⑷铝热反应 ⑸干冰汽化⑹加热氯化铵 ⑺ 甘油加水作护肤剂 ⑻ 明矾净水 ⑼ 蜂蚁螫咬后涂稀氨水可以减痛 ⑽ 医用酒精可用于皮肤消毒 ⑾ 烹鱼时加入少量的料酒和食醋可减少腥味 ⑿ 橡胶老化 ⒀ 用四氯化碳可擦去圆珠笔油渍 ⒁ 蛋白质的盐析A ．⑴⑶⑷⑸⑺⑿⒀ B. ⑵⑷⑸⑺⑿⒀⒁ C. ⑵⑸⑺⒀⒁ D. 以上选项均不正确 7、设阿伏加德罗常数为N A ，下列说法正确的是A ．用100ml 4mol/L 盐酸与8.7gMnO 2共热能制取氯气0.2N AB ．一定温度下0.1L 0.1mol/L 的HA 和1L0.01mol/L 的HA 所含A －微粒数均为0.01N AC ．4.5 gSiO 2晶体中含有的硅氧键数目为0.3 N AD ．用Pt 做电极电解硝酸铜溶液,当阳极产生的气体在标况下为22.4L,转移电子数目为N A末被蜘蛛捕获的（876.1g ）同化的（X ）（7.30g ）未被同化的（0.63g ）被吃下的（7.93g ）未被吃下的（2.37g ）被蜘蛛捕获的（10.3g ） = 储存在猎物种群 有机物中的能量 （886.4g ）=8、下列离方程式书写正确的是（ ） A ．乙醛和银氨溶液的反应：CH 3CHO + 2Ag(NH 3)2OH △ CH 3COO － + NH 4+ + 2Ag ↓ + 3NH 3 + 2H 2O B ．将1mol 过氧化钠投入含有1molAlCl 3的溶液中：6Na 2O 2 ＋ 6H 2O ＋ 4Al 3+ ＝ 4Al(OH )3↓ ＋ 3O 2↑ ＋ 12Na + C ．酸性条件下KIO 3溶液与KI 溶液发生反应生成I 2：IO 3－ ＋ 5I － ＋ 3H 2O ＝ 3I 2 ＋ 6OH －D ．溴乙烷中滴入AgNO 3溶液： Br - + Ag += AgBr ↓9、A 、B 、C 、D 、E 五种元素原子序数逐渐增大，且均不超过18，其中A 与C 、B 与E 分别为同族元素。