矢量和标量

标量与矢量知识点1. 引言在物理学和数学中，标量和矢量是两个非常重要的概念。

它们用于描述物体的性质和运动，并在各个学科中都有广泛的应用。

本文将介绍标量和矢量的基本概念、区别以及一些常见的应用场景。

2. 标量的定义与特点标量是一个只有大小（大小可以是实数或复数）而没有方向的量。

在物理学中，温度、质量、时间和体积等都属于标量。

标量可以用一个实数或复数来表示，例如：T=30℃，m=5kg。

标量具有以下特点：- 大小：标量具有具体的数值，表示量的大小；- 无方向：标量没有方向，只有大小的概念； - 可以进行数值运算：标量之间可以进行加、减、乘、除等运算。

3. 矢量的定义与特点矢量是一个既有大小又有方向的量。

在物理学中，速度、力、位移和加速度等都属于矢量。

矢量通常用带有箭头的字母表示，例如：v⃗表示速度矢量。

矢量具有以下特点： - 大小：矢量具有具体的数值，表示量的大小； - 方向：矢量具有方向，可以用箭头表示； - 可以进行矢量运算：矢量之间可以进行加、减、乘、除等运算，并且结果仍然是一个矢量。

4. 标量与矢量的区别标量和矢量之间的主要区别在于是否具有方向。

标量只有大小，而矢量既有大小又有方向。

举个例子来说明：假设有一个车辆在直线上行驶，速度为30 km/h。

这个速度是一个标量，因为它只有大小，没有方向。

但是，如果我们知道车辆的速度是30 km/h，并且向东方行驶，那么速度就是一个矢量，因为它既有大小又有方向。

另一个例子是力的概念。

如果我们只知道一个物体受到了5 N的力，那么这个力是一个标量，因为它只有大小。

但是，如果我们知道这个力是向上的，那么力就是一个矢量，因为它既有大小又有方向。

5. 标量与矢量的应用场景标量和矢量在物理学、工程学、计算机图形学等领域中有广泛的应用。

以下是一些常见的应用场景：5.1 物理学在物理学中，标量和矢量被用于描述物体的性质和运动。

例如，速度、加速度和力都是矢量，而温度、质量和体积都是标量。

物理中常见的矢量和标量1.引言1.1 概述矢量和标量是物理学中常见的概念。

在物理学中，我们经常需要描述和测量物体的某些特性或属性，而这些特性或属性可以被分为两类：矢量和标量。

矢量是有大小和方向的量。

它们可以用箭头表示，箭头的长度表示量的大小，箭头的方向表示量的方向。

例如，速度、力、位移和加速度等都是矢量量，它们除了有大小之外还有方向。

与此相反，标量是只有大小而没有方向的量。

标量只有数值大小，没有箭头来表示方向。

例如，时间、质量、温度和能量等都是标量量，它们只有一个数值大小而没有具体的方向。

矢量和标量在物理学中有着广泛的应用。

在运动学中，我们可以使用矢量来描述物体的运动状态，例如速度矢量可以告诉我们物体的速度和方向。

在力学中，矢量可以用来描述物体所受的力和力的作用方向。

在电磁学中，电场和磁场都可以用矢量来描述。

总结起来，物理学中常见的矢量和标量分别指的是有大小和方向的量以及只有大小而没有方向的量。

它们在描述和测量物理现象中起着关键的作用。

在接下来的文章中，我们将详细讨论矢量和标量的定义、特点以及它们在物理学中的应用。

文章结构部分的内容可以如下编写：1.2 文章结构本文将按照以下结构来介绍物理中常见的矢量和标量：第二部分将详细介绍矢量的定义和特点。

我们将从矢量的基本概念开始，解释什么是矢量以及它们的特点。

我们将探讨矢量的大小和方向，以及如何表示和运算矢量。

接着，第二部分将转向标量的定义和特点。

我们将解释什么是标量以及它们与矢量的区别。

我们将讨论标量的大小但没有方向的特点，并介绍一些常见的标量物理量。

第三部分将探讨矢量和标量在物理中的应用。

我们将以实际的例子来说明矢量和标量在物理学中的重要性和用途。

我们将讨论矢量和标量在运动学、力学和其他物理学领域中的应用，并解释它们如何帮助我们理解和描述物理现象。

最后，我们将在第三部分总结本文的主要内容和观点。

我们将强调矢量和标量在物理学中的作用，以及它们在解决物理问题时的重要性。

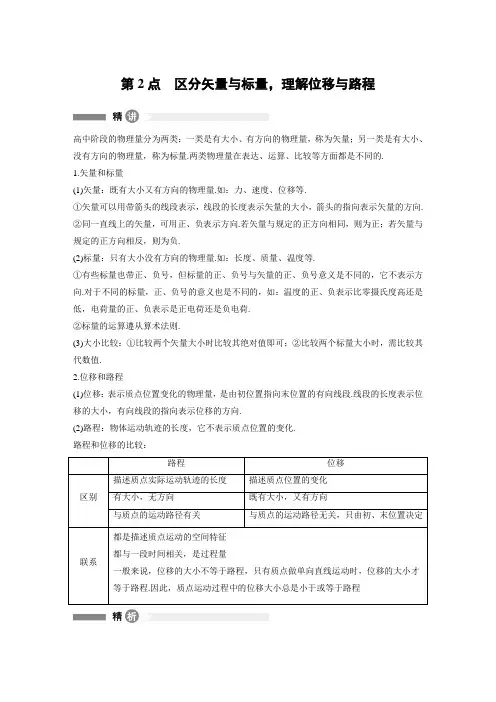
第2点区分矢量与标量，理解位移与路程高中阶段的物理量分为两类：一类是有大小、有方向的物理量，称为矢量；另一类是有大小、没有方向的物理量，称为标量.两类物理量在表达、运算、比较等方面都是不同的.1.矢量和标量(1)矢量：既有大小又有方向的物理量.如：力、速度、位移等.①矢量可以用带箭头的线段表示，线段的长度表示矢量的大小，箭头的指向表示矢量的方向.②同一直线上的矢量，可用正、负表示方向.若矢量与规定的正方向相同，则为正；若矢量与规定的正方向相反，则为负.(2)标量：只有大小没有方向的物理量.如：长度、质量、温度等.①有些标量也带正、负号，但标量的正、负号与矢量的正、负号意义是不同的，它不表示方向.对于不同的标量，正、负号的意义也是不同的，如：温度的正、负表示比零摄氏度高还是低，电荷量的正、负表示是正电荷还是负电荷.②标量的运算遵从算术法则.(3)大小比较：①比较两个矢量大小时比较其绝对值即可；②比较两个标量大小时，需比较其代数值.2.位移和路程(1)位移：表示质点位置变化的物理量，是由初位置指向末位置的有向线段.线段的长度表示位移的大小，有向线段的指向表示位移的方向.(2)路程：物体运动轨迹的长度，它不表示质点位置的变化.路程和位移的比较：路程位移区别描述质点实际运动轨迹的长度描述质点位置的变化有大小，无方向既有大小，又有方向与质点的运动路径有关与质点的运动路径无关，只由初、末位置决定联系都是描述质点运动的空间特征都与一段时间相关，是过程量一般来说，位移的大小不等于路程，只有质点做单向直线运动时，位移的大小才等于路程.因此，质点运动过程中的位移大小总是小于或等于路程对点例题 某学生参加课外体育活动，他在一个半径为R 的圆形跑道上跑步，从O 点沿圆形跑道逆时针方向跑了4.75圈到达A 点，求它通过的位移和路程.思路点拨 位移是矢量，求某一过程的位移，既要求出大小，还要标明方向.描述物体在平面内的曲线运动时，需要建立平面直角坐标系.当物体做曲线运动时，其位移的大小与路程是不相等的，且路程大于位移的大小.解题指导 如图所示，有向线段OA 即为该学生通过的位移x ＝R 2＋R 2＝2R ，位移方向与x 轴的夹角为φ＝45°.通过的路程为s ＝4×2πR ＋34×2πR ＝192πR . 答案 见解题指导如图1所示为中国古代的太极图，图中大圆的半径为R ，圆心在O 点，AC 是直径，中央“S ”型部分是两个半径均为R 2的半圆.某人晨练时按此图自A 点出发，沿图中箭头所示路径ABCOA 前进，第一次返回A 点的过程中，他的路程和位移大小分别是( )图1A.0,0B.0,2πRC.2πR,0D.2πR,2πR 答案 C解析 位移由初位置指向末位置，质点沿半径为R 的半圆运动，当质点由A 点运动到C 点再返回A 点，位移大小等于0，路程等于ABC 的半个圆弧长加上中央两个小半圆弧长之和，等于2πR ，故C 正确.A 、B 、D 错误.。

矢量和标量运算
矢量和标量是线性代数中的两个重要概念，它们在数学和物理学中都有广泛的应用。

在这里，我将简要介绍矢量和标量以及它们的运算。

1. 标量：标量是一个只有大小，没有方向的量。

在数学上，标量通常用一个实数或复数表示。

标量可以表示物理量的大小，比如质量、时间、温度等。

标量之间可以进行常规的算术运算，比如加减乘除等。

2. 矢量：矢量是一个既有大小又有方向的量。

在数学上，矢量通常用一个有序的数组或坐标来表示。

在物理学中，矢量可以表示力、速度、位移等具有方向的物理量。

矢量之间的运算包括矢量加法、数量乘法（标量与矢量相乘）、点积（内积）和叉积（外积）等。

矢量和标量的运算：
-矢量加法：两个矢量相加的结果是一个新的矢量，其大小由两个矢量的大小和夹角决定，方向由两个矢量的方向决定。

-数量乘法：一个标量与一个矢量相乘，结果是一个新的矢量，其大小等于标量与矢量的大小相乘，方向不变。

-点积（内积）：两个矢量的点积是一个标量，它等于两个矢量的大小乘积再乘以它们夹角的余弦值。

-叉积（外积）：两个矢量的叉积是一个新的矢量，其大小等于两个矢量的大小乘积再乘以它们夹角的正弦值，方向垂直于这两个矢量所在的平面。

矢量和标量的运算在物理学、工程学、计算机图形学等领域都有广泛的应用，它们是理解和描述自然现象以及进行科学计算和工程设计的重要工具。

高中物理量矢量标量
在物理学中，物理量可分为矢量和标量。

矢量（Vector）：
1.定义：矢量是有大小和方向的量。

它们可以用箭头或向量来表示，箭头的
长度表示量的大小，箭头的方向表示量的方向。

2.例子：位移、速度、加速度、力等都是矢量量。

3.表示方法：通常用粗体字母表示，如位移用r、速度用v表示。

标量（Scalar）：
1.定义：标量是只有大小而没有方向的量。

它们可以通过一个数值来描述。

2.例子：质量、时间、温度、电荷等都是标量量。

3.表示方法：通常用普通字母表示，例如质量用m、时间用t表示。

区别：
1.方向性：矢量有方向，标量没有方向。

2.表示方法：矢量通常用箭头或向量表示，标量用单个数值表示。

3.运算：矢量在运算中需要考虑方向性，例如矢量的相加需考虑方向，而标
量的运算仅仅涉及数值的加减乘除。

在物理学中，矢量和标量的概念是非常重要的。

例如，当描述运动时，速度是一个矢量，因为它不仅有大小（即速度的大小），还有方向（即速度的方向）。

而时间则是一个标量，因为它只有数值上的大小而没有方向。

理解这些概念对于物理学、工程学和许多其他科学领域的问题建模和解决非常重要，因为矢量和标量有不同的数学性质和行为。

高一物理标量和矢量
物理学中的标量和矢量是两个重要的概念，它们有着根本的不同点。

标量是一种物理量，只有大小，而不受方向或位置的影响。

它们可以表示力，速度，压力，温度，能量等等。

比如，力可以用大小来表示，而无需考虑其方向。

另外，标量可以以一个数量来表示，或者用象征性的符号来表达。

而矢量是一种物理量，具有大小和方向的特点。

它表示的是一种力的方向，比如光方向，风方向或者一种物理效应的传播方向等等。

矢量的大小可以用向量的长度来表示，同时可以用指示箭头或向量符号来表示其方向。

两者之间最明显的不同在于，标量只有大小这一个特性，矢量及其大小还有方向两个特性。

在进行物理物体运动和物理效应传播等研究时，它们都扮演着重要的角色，标量表示物理量的变化情况，而矢量表示物理效应或力的传播方向。

总之，标量和矢量是物理学中重要的概念，他们有着根本的不同。

标量只有大小，而矢量具有大小和方向的特点，都在不同的研究中扮演着重要的角色，了解它们有助于我们更好地理解物理学中的现象及事件。

矢量和标量的区别有3点：
1、概念的区别
一种是在选定测量单位以后，仅需用数字表示大小的量叫标量；另一种是在选定测量单位后，除用数字表示其大小外，还需用一定的方向才能说明性质，叫矢量。

2、运算法则区别
在中学物理中，长度、质量、时间、密度、功、能量、温度、电流强度等都是标量，标量运算服从代数运算法则。

力、位移、速度、加速度、动量、冲量、电场强度、磁感应强度等都是矢量，矢量的运算要遵循平行四边形法则或三角形法则。

矢量常用带有箭头的直线段表示。

线段的长度代表矢量大小，箭头代表矢量的方向。

3、正负号区别
在中学物理中，无论是矢量，还是标量，都存在正负号问题。

但矢量正负号跟标量正负号有本质区别。

⑴矢量正负号：在选定一个正方向的前提下，矢量的正负号实质上表示矢量的方向。

若矢量为正，表示该矢量跟选定正方向相同；矢量为负表示跟选定正方向相反。

⑵标量正负号：虽然标量无方向，但有的标量也存在正、负号问题。

矢量[1]（vector quantity）和标量（scalar quantity）的定义简单的理解：“矢量和标量的定义如下：（到大学物理中会详细研究）（1）定义或解释：有些物理量，既要有数值大小(包括有关的单位)，又要有方向才能完全确定。

这些量之间的运算并不遵循一般的代数法则，而遵循特殊的运算法则。

比如说位移这样的物理量，这样的量叫做物理矢量。

有些物理量，只具有数值大小(包括有关的单位)，而不具有方向性。

这些量之间的运算遵循一般的代数法则。

例如温度、质量这些物理量，这样的量叫做物理标量。

（2）说明：①矢量之间的运算要遵循特殊的法则。

矢量加法一般可用平行四边形法则。

由平行四边形法则可推广至三角形法则、多边形法则或正交分解法等。

矢量减法是矢量加法的逆运算，一个矢量减去另一个矢量，等于加上那个矢量的负矢量。

A-B=A+(-B)。

矢量的乘法。

矢量和标量的乘积仍为矢量。

矢量和矢量的乘积，可以构成新的标量，矢量间这样的乘积叫标积；也可构成新的矢量，矢量间这样的乘积叫矢积。

例如，物理学中，功、功率等的计算是采用两个矢量的标积。

W=F·S，P=F·v，物理学中，力矩、洛伦兹力等的计算是采用两个矢量的矢积。

M=r×F，F=qv×B。

②物理定律的矢量表达跟坐标的选择无关，矢量符号为表述物理定律提供了简单明了的形式，且使这些定律的推导简单化，因此矢量是学习物理学的有用工具。

”（3）矢量有两种，一种为只有大小与方向的物理量，譬如速度，我们称之为“奇矢量”；另外一种不但有大小与方向的物理量，而且还在矢量间作用产生效果所需时间的一个量，譬如力，我们称之为“偶矢量”或“极限矢量（即时、有上限）”，因为它们在矢量间作用产生效果所需的时间是即时与光速的。

矢量的大小比较一般来说，矢量只有在同方向上才可比较大小，不同方向上的矢量一般不能比较大小。

个人的理解：矢量规律的总结，基于人们对空间广义的对称性的理解。

高中物理矢量和标量
高中物理矢量和标量
一、什么是矢量
1、矢量是指有大小和方向的物理量，大小可以通过它的模量反映出来，而方向可以通过它的有向性来确定。

2、矢量有很多种形式，其中常见的包括力，速度，加速度，磁场强度，电场强度等物理量。

二、什么是标量
1、标量是指没有方向性的物理量，它只有大小，而没有方向，诸如时间，温度，长度，能量，功率等都是标量。

2、在力学中，动能，位能，势能也属于标量。

因为它们实际上也只是
一个表示物体的潜在能量的值，而没有任何方向性。

三、矢量和标量的区别
1、矢量具有方向和大小，而标量只具有大小。

2、矢量可以相互加减，而标量只能进行加减，乘除运算。

3、矢量可以使用一般化坐标来表示，而标量只能用一个实数来表示。

4、矢量可以用虚矢量和实矢量来区分，而标量只能用实数来表示。

四、高中物理中矢量和标量的用途
1、矢量在表示物理量方面具有很大的优势，物理量的大小不仅可以表示为实数，而且还可以表示为方向，基于此可以绘制出各种物理量的分布和变化。

2、标量通常用于表示物理量的大小，诸如静电势，重力势等都是没有任何方向性的物理量，只能通过它们的实数值来表示。

3、矢量和标量在高中物理学中可以用于分析物理问题，帮助学生理解物理现象，归纳总结物理规律。

在物理学中，矢量是带有方向和大小的量。

它们在数学上表示为带有方向的线段，并且它们的运算遵循特定的规则。

矢量的运算包括加法、减法、数乘和点积。

例
如，在二维平面中，一个矢量可以表示为(x, y) 的形式，其中x 和y 分别是横纵坐标。

在三维空间中，一个矢量可以表示为(x, y, z) 的形式，其中x、y 和z
分别是横、纵和竖坐标。

标量是不带方向的量，它们在数学上表示为单独的数字。

标量的运算包括加法、减法、乘法和除法。

在物理学中，常见的标量包括质量、长度、时间、温度和能量。

例如，在力学中，力是一个矢量，因为它具有方向和大小。

而质量是一个标量，因为它只是一个数字，没有方向。