统计公差分析方法概述

统计公差分析方法概述公差分析是设计和制造过程中的重要环节，用于评估产品的尺寸和形状的变化并确定其质量要求。

它帮助确定制造过程中允许的变化范围，以确保产品的功能和性能满足设计要求。

下面是公差分析方法的概述：1.公差概念和术语：公差是表示产品尺寸和形状变异的一种度量，是设计要求和制造能力之间的差异。

了解公差的基本概念和术语对于进行有效的公差分析非常重要。

例如，公差带、公差上限、公差下限、公差等级等。

2.公差链：公差链是将不同部件的公差延伸到整个产品装配中的一种方法。

通过分析公差链，可以确定整个装配的总体公差，并评估其对产品性能的影响。

公差链分析通常采用功能环或冗余环的方法。

3.公差配合：公差配合是指零件之间在装配时的相互作用。

公差配合分析可以确定零件之间的配合方式，并对其作用进行评估。

常见的公差配合包括配合间隙、过盈配合和间隙配合等。

4. 公差分析工具：公差分析通常使用一些专门的工具来辅助。

例如，一维公差分析工具（如Matlab、Excel等）用于分析单个尺寸的公差，根据统计数据计算出尺寸的上下限。

使用二维和三维CAD软件进行公差堆叠分析，可以在装配设计阶段模拟零件堆叠时产生的误差变化。

5.公差分配：公差分配是将总体公差分配给不同的零件以实现装配要求的过程。

公差分配通常基于设计要求、制造能力和装配要求等考虑因素。

公差分配需要根据装配关系和功能要求来确定每个零件的公差。

6.公差检验：公差分析的最后一步是进行公差检验，以确保产品的尺寸和形状在规定的公差范围内。

公差检验可以通过测量和检测工具来进行，例如卡尺、测量仪器、投影仪等。

公差检验是确保产品质量和性能的关键步骤。

7.公差优化：公差优化是指通过优化公差的分配和设计来最小化产品的尺寸和形状变化，以提高产品的质量和性能。

公差优化可以通过使用计算机辅助设计（CAD）软件和专业的公差优化工具来实现。

总之，公差分析是设计和制造中的关键环节，有助于确保产品质量和性能满足要求。

统计公差分析方法概述(2012-10-23 19:45:32)分类：公差设计统计六标准差统计公差分析方法概述一.引言公差设计问题可以分为两类：一类是公差分析(Tolerance Analysis ,又称正计算) ,即已知组成环的尺寸和公差,确定装配后需要保证的封闭环公差；另一类是公差分配(Tolerance Allocation ,又称反计算) ,即已知装配尺寸和公差,求解组成环的经济合理公差。

公差分析的方法有极值法和统计公差方法两类,根据分布特性进行封闭环和组成环公差的分析方法称为统计公差法.本文主要探讨统计公差法在单轴向(One Dimension)尺寸堆叠中的应用。

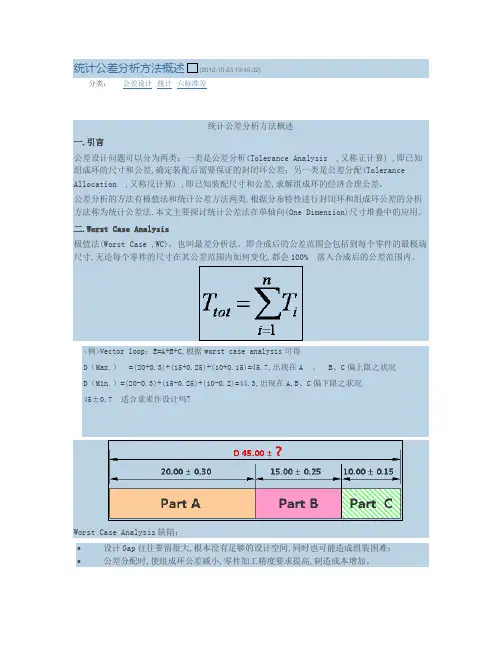
二.Worst Case Analysis极值法(Worst Case ,WC)，也叫最差分析法，即合成后的公差范围会包括到每个零件的最极端尺寸,无论每个零件的尺寸在其公差范围内如何变化,都会100% 落入合成后的公差范围内。

<例>Vector loop：E=A+B+C,根据worst case analysis可得D（Max.）=(20+0.3)+(15+0.25)+(10+0.15)=45.7,出现在A、B、C偏上限之状况D（Min.）=(20-0.3)+(15-0.25)+(10-0.2)=44.3,出现在A,B、C偏下限之状况45±0.7适合拿来作设计吗?Worst Case Analysis缺陷：•设计Gap往往要留很大,根本没有足够的设计空间,同时也可能造成组装困难；•公差分配时,使组成环公差减小,零件加工精度要求提高,制造成本增加。

以上例Part A +Part B+ Part C，假设A、B、C三个部材,相对于公差规格都有3σ的制程能力水平，则每个部材的不良机率为1-0.9973=0.0027；在组装完毕后所有零件都有缺陷的机率为：0.0027^3=0.000000019683。

这表明几个或者多个零件在装配时,同一部件的各组成环,恰好都是接近极限尺寸的情况非常罕见。

统计公差分析方法概述一、引言公差设计问题可以分为两类:一类就是公差分析(Tolerance Analysis ,又称正计算) ,即已知组成环的尺寸与公差,确定装配后需要保证的封闭环公差;另一类就是公差分配(Tolerance Allocation ,又称反计算) ,即已知装配尺寸与公差,求解组成环的经济合理公差。

公差分析的方法有极值法与统计公差方法两类,根据分布特性进行封闭环与组成环公差的分析方法称为统计公差法、本文主要探讨统计公差法在单轴向(One Dimension)尺寸堆叠中的应用。

二、Worst Case Analysis极值法(Worst Case ,WC),也叫最差分析法,即合成后的公差范围会包括到每个零件的最极端尺寸,无论每个零件的尺寸在其公差范围内如何变化,都会100% 落入合成后的公差范围内。

<例>Vector loop:E=A+B+C,根据worst case analysis可得D(Max、)=(20+0、3)+(15+0、25)+(10+0、15)=45、7,出现在A、B、C偏上限之状况D(Min、)=(20-0、3)+(15-0、25)+(10-0、2)=44、3,出现在A,B、C偏下限之状况45±0、7适合拿来作设计不?Worst Case Analysis缺陷:•设计Gap往往要留很大,根本没有足够的设计空间,同时也可能造成组装困难;•公差分配时,使组成环公差减小,零件加工精度要求提高,制造成本增加。

以上例Part A +Part B+ Part C,假设A、B、C三个部材,相对于公差规格都有3σ的制程能力水平,则每个部材的不良机率为1-0、9973=0、0027;在组装完毕后所有零件都有缺陷的机率为:0、0027^3=0、3。

这表明几个或者多个零件在装配时,同一部件的各组成环,恰好都就是接近极限尺寸的情况非常罕见。

三、统计公差分析法•由制造观点来瞧,零件尺寸之误差来自于制程之变异,此变异往往呈现统计分布的型态,因此设计的公差规格常被视为统计型态。

公差分析报告基本知识公差分析是工程设计中非常重要的一项技术，它主要用于确定产品制造过程中所允许的尺寸变差范围，以保证产品在使用过程中的正常功能。

本篇文章将介绍公差分析的基本知识，包括公差的定义、公差的类型、公差的表示方法、公差链和公差分析方法等内容。

一、公差的定义公差是指将产品实际尺寸与设计尺寸之间的差值，它是制约产品功能和性能的重要因素。

公差是在设计阶段就需要考虑和确定的，通过公差的控制可以保证产品在制造和使用过程中的稳定性和可靠性。

二、公差的类型1.一般公差：是指对于产品的一般尺寸，根据所处的尺寸量级和表面质量要求而规定的公差。

2.几何公差：是指控制产品几何形状和位置关系的公差，包括平面度、圆度、圆柱度、直线度、平行度、垂直度等。

3.形位公差：是指产品形状和位置关系的公差，包括位置公差、姿态公差、形位公差、轴向公差等。

4.配合公差：是指对于产品的配合尺寸，根据配合要求而规定的公差，包括间隙、过盈和配合紧度等。

三、公差的表示方法公差的表示方法主要有四种：1.加减公差法：即在设计尺寸基础上，通过加减法确定上下限公差。

2.限界公差法：即在设计尺寸基础上，通过上限和下限值确定公差范围。

3.基础尺寸法：即以一个基础尺寸作为基准，通过加减公差法确定其他尺寸的上下限公差。

4. 数值公差法：即通过数值来表示公差的大小，如0.01mm、0.1mm 等。

四、公差链公差链是指产品由多个零件组成时，各个零件公差相加所形成的总公差。

在进行公差分析时，需要考虑到各种公差之间的相互关系和叠加效应，以保证整体装配的精度和可靠性。

五、公差分析方法公差分析有多种方法，主要包括：1.构造法：根据零件的功能要求，通过构造关系和尺寸链的分析，确定零件的公差。

2.统计法：通过对产品和工艺数据的统计分析，确定公差的适用范围和控制要求。

3.模拟法：通过建立数学模型，模拟产品在设计和制造过程中的变化和误差，分析公差对产品性能的影响。

4.比较法：通过对已有样品或标准件的测量和分析，确定公差的适用范围和控制要求。

公差数据处理与分析技巧公差数据处理与分析技巧公差是指在制造过程中，由于各种原因造成的产品尺寸、形状、位置等方面的偏差。

准确地处理和分析公差数据对于确保产品质量和满足设计要求至关重要。

下面将介绍一些公差数据处理与分析的技巧。

首先，对于公差数据的处理，我们需要进行数据的收集和整理。

在制造过程中，我们需要收集每个产品的测量数据，包括尺寸、形状、位置等方面的数据。

这些数据需要按照一定的规范进行整理和记录，以便后续的分析和处理。

其次，我们需要对公差数据进行统计和分析。

统计分析能够帮助我们了解产品的制造过程中存在的问题，并找到解决问题的方法。

常用的统计分析方法包括均值、标准差、概率分布等。

通过对公差数据的统计分析，我们可以了解产品的尺寸偏差的分布情况，以及存在的异常情况。

此外，我们还需要进行公差数据的可视化处理。

可视化处理可以帮助我们更直观地了解公差数据的分布情况和变化趋势。

常用的可视化处理方法包括绘制直方图、散点图、箱线图等。

通过对公差数据的可视化处理，我们可以更加清楚地了解产品的尺寸偏差的分布情况，以及存在的异常情况。

最后，我们需要对公差数据进行合理的解释和应用。

在处理和分析公差数据的过程中，我们需要根据产品的设计要求和使用环境，对公差数据进行合理的解释。

通过合理解释公差数据，我们可以为产品的制造过程提供合理的指导和改进措施。

综上所述，公差数据处理与分析技巧对于确保产品质量和满足设计要求至关重要。

通过对公差数据的收集、整理、统计、分析和可视化处理，我们可以更好地了解产品的尺寸偏差情况，为产品的制造过程提供合理的指导和改进措施。

公差数据处理与分析技巧不仅可以提高产品的质量，还可以提高制造效率，降低成本，提升企业的竞争力。

公差计算方法在工程设计和制造过程中，公差是一个非常重要的概念。

公差是指零件尺寸和形状的允许偏差范围，它能够确保零件在装配时能够正常工作。

因此，正确的公差设计和计算对于产品质量和性能至关重要。

本文将介绍公差的基本概念以及常见的公差计算方法。

一、公差的基本概念。

1. 公差的定义。

公差是指零件尺寸和形状允许的最大偏差范围，通常用上下偏差表示。

上偏差是指零件尺寸允许的最大偏大值，下偏差是指零件尺寸允许的最大偏小值。

公差一般由基本尺寸、上偏差和下偏差三部分组成。

2. 公差的作用。

公差的作用是确保零件在装配时能够正常工作。

合理的公差设计能够保证零件的互换性和装配性，避免因尺寸偏差过大而导致的装配困难或功能失效。

二、公差计算方法。

1. 最大材料条件法。

最大材料条件法是一种常用的公差计算方法。

它是根据零件的最大材料条件来确定公差的上下偏差。

最大材料条件是指零件尺寸取最大值时的状态，通常用最大实体尺寸表示。

2. 最小材料条件法。

最小材料条件法是另一种常用的公差计算方法。

它是根据零件的最小材料条件来确定公差的上下偏差。

最小材料条件是指零件尺寸取最小值时的状态，通常用最小实体尺寸表示。

3. 统计公差法。

统计公差法是一种基于统计学原理的公差计算方法。

它通过对零件尺寸的统计分析，确定公差的上下偏差，以确保在一定的概率范围内零件能够正常工作。

4. 累积公差法。

累积公差法是一种考虑多个零件装配后公差叠加影响的公差计算方法。

它通过对多个零件公差的叠加影响进行分析，确定装配后零件的总公差范围。

三、公差计算的注意事项。

1. 根据零件的功能和装配要求确定合理的公差范围。

2. 考虑材料和加工工艺的影响，选择合适的公差计算方法。

3. 在公差设计和计算中，应充分考虑装配误差和使用环境的影响。

4. 对于关键零件和高精度零件，应进行严格的公差控制和检验。

结语。

公差的正确设计和计算对于产品质量和性能具有重要影响。

合理的公差范围能够确保零件在装配和使用过程中能够正常工作，提高产品的可靠性和稳定性。

22
DFMA
谢 谢 ！
23
3.当公差分析的结果不满足要求时：

DFMA
减少尺寸链的长度； A为54.00±0.20，C为25.00±0.15，D为28.50±0.15
优化的设计
18
四. 公差分析指南
3.当公差分析的结果不满足要求时：

DFMA
使用定位特征； 好处：
定位特征可以提供较精密的尺寸公差 定位特征的尺寸可以放置于比较容易进行尺寸管控的区域 使用定位特征时可以减少和避免对其他尺寸的公差要求，只需严格管控定 位特征的相关尺寸，就可以满足产品设计要求 因为定位特征精度高，使用定位特征有利于减少零件之间的尺寸公差累积
DFMA
制造工艺能力决定了公差分析中公差的设定； 二维图纸中公差标注与公差分析中的公差一致； 对公差分析中的尺寸需要进行制程管控；
制造工艺 能力
公差分析中 公差的设定
二维图样零 件公差标注
零件尺寸 制程管控
15
四. 公差分析指南
3.当公差分析的结果不满足要求时： 不推荐的做法：

DFMA
调整尺寸链中的尺寸公差大小； 降低目标尺寸判断标准；
100±0.20
3
一. 公差分析的介绍
2.公差的本质：

DFMA
公差是产品设计和产品制造的桥梁和纽带，是保证产品以优异的质量、 优良的性能和较低的成本进行制造的关键。
设计 功能 性能 外观 可装配性 设计限制 稳健性设计 设计意图 产品质量 客户满意
公差
制造 制造费用 装配费用 制造方法选择 机器 夹具 检验 不良率 返工率
推荐的做法：

减少尺寸链的长度； 使用定位特征；

三.统计公差分析法 由制造观点来看,零件尺寸之误差来自于制程之变异,此变异往往呈现统计分布的型态,因此设计的公差规格常被视为统计型态。 统计公差方法的思想是考虑零件在机械加工过程中尺寸误差的实际分布,运用概率统计理论进行公差分析和计算,不要求装配过程中 100 %的成功率(零件的100 %互换) ,要求在保证一定装配成功率的前提下,适当放大组成环的公差,降低零件(组成环) 加工精度,从而 减小制造和生产成本。 在多群数据的线性叠加运算中,可以进行叠加的是『变异』值。
Worst Case Analysis缺陷： 设计Gap往往要留很大,根本没有足够的设计空间,同时也可能造成组装困难； 公差分配时,使组成环公差减小,零件加工精度要求提高,制造成本增加。 以上例Part A +Part B+ Part C，假设A、B、C三个部材,相对于公差规格都有3σ的制程能力水平，则每个部材的不 良机率为1-0.9973=0.0027；在组装完毕后所有零件都有缺陷的机率为：0.0027^3=0.000000019683。这表明几个 或者多个零件在装配时,同一部件的各组成环,恰好都是接近极限尺寸的情况非常罕见。
四.方和根法 计算公式（平方相加开根号）
假设每个尺寸的 Ppk 指标是1.33并且制程 是在中心
比较Worst case与统计公差法 公差合成后所得的公差范围缩小了,对设计者而言,较小的公差范围意味着较准确的组装与配合,累积 下来的误差也会减少。 在公差分配的情况时,每个零件所得到的公差范围变大了,对制造者而言,较大的公差范围意味着较容 易制作及控制生产质量,有利于制造者。
<例>Vector loop：E=A+B+C,根据worst case analysis可得 D（Max.） =(20+0.3)+(15+0.25)+(10+0.15)=45.7,出现在A 、 B、C偏上限之状况 D（Min.）=(20-0.3)+(15-0.25)+(10-0.2)=44.3,出现在A,B、C偏下限之状况 45±0.7 适合拿来作设计吗?

产品装配不良率改善了46%! ! !
总结
采用传统的公差尺寸计算方法，只是考虑到了理论上最差或者最好的情况， 与现实是脱离的。
当以磁盘的厚度及公差为依据，来设计盒子的宽度时，由于传统尺寸链公差 计算方法考虑了理论上的最差情况，导致盒子的宽度过宽，磁盘装入后间隙 太松，表现为设计不足问题。（Under Design）
统计公差设计概要
·什么是统计公差设计？ - 利用统计学的知识。基于产品的变差分布，和多重分布组合对产品设计结果的影响，来确定产品的
名义尺寸和定义合理的公差。 · 为什么使用统计公差？
- 强调系统性的理解设计要求。 - 减低设计不足或设计过剩的风险。 - 合理定义零件的公差要求。 - 减少设计的重复计算和后续设计更改次数。 - 面向变差的设计，有别于常规设计。 · 使用统计公差至少有以下好处： - 可以尽可能的避免设计过剩，降低产品的制造成本。 - 通过理解变差的概念，减少设计的重复计算和后续设计更改次数。 · 统计公差有哪些输入？ - 理解客户要求。 - 理解系统或产品的设计理论值（名义值）。 - 过程能力数据。 - 过程公差。 · 前提，风险和需要考虑的方面: - 前提1，知道客户的要求。 - 前提2，知道输入与输出的关系。 - 前提3，制造过程受控并能保持要求的过程能力，或满足公差要求。 - 要求工艺和技术协同设计工作。
公差下限
99.73% 的磁 盘
公差上限
有0.135% 的磁盘厚度
< 3.048mm
有0.135% 的磁盘厚度
> 3.302mm
传统公差
让我们从不同的角度看这个问题：
− 尺寸链关系如下图所示
盒子
统计公差
磁盘 #1 磁盘 #2 磁盘 #3 磁盘 #4 磁盘 #5 磁盘 #6 磁盘 #7 磁盘 #8 磁盘 #8 磁盘 #9 磁盘 #10

统计公差分析方法概述公差分析方法是一种用于确定产品或系统中各种因素之间的相互关系和限制的工程方法。

它被广泛应用于各种制造和设计领域，包括机械、电子、航空航天、汽车等。

公差分析的目标是确保产品或系统在正常运行条件下能够满足设计要求。

本文将概述几种常见的公差分析方法。

一、基本术语和概念在介绍具体的公差分析方法之前，有必要先了解一些基本术语和概念。

1. 公差（Tolerance）：公差是指在设计和制造过程中所允许的误差或偏差范围。

公差可以是线性的，也可以是角度的。

2. 上限（Upper Limit）和下限（Lower Limit）：上限是指公差范围的最大值，下限是指公差范围的最小值。

3. 偏差（Deviation）：偏差是指产品或系统与其设计要求之间的差异。

4. 平均值（Mean）：平均值是指一系列测量值的算术平均数。

5. 标准偏差（Standard Deviation）：标准偏差是指一系列测量值与其平均值之间的平均差异。

6. Cp和Cpk指数：Cp指数是指一个过程的上下限规格范围与标准差之比。

Cpk指数是指一个过程的上限或下限与该过程能够达到的最大或最小值之间的差异与三倍的标准差之比。

二、公差分析方法1. 极差法（Range Method）极差法是一种简单直观的公差分析方法。

它通过测量一系列零件或产品的最大值和最小值来确定公差范围。

极差（Range）= 最大值 - 最小值优点：简单易懂，容易理解。

缺点：只考虑了最大值和最小值，没有考虑其他测量值的变化情况。

2. 平均偏差法（Average Deviation Method）平均偏差法是一种计算平均偏差和标准偏差的公差分析方法。

它可以提供关于产品或系统的整体偏差情况的信息。

平均偏差（Average Deviation）= 所有测量值的总和 / 测量值的个数标准偏差（Standard Deviation）= 各个偏差值与平均偏差之差的平方和的平均数的平方根优点：考虑了所有测量值的变化情况，能够提供更准确的分析结果。

零件 4
10.00 ± 0.15
零件 3
零件 2 零件 1
堆叠公差分析过程
1. 确定组装要求 2. 建立封闭尺寸链图 3. 转换名义尺寸，将公差 转成对称公差 4. 按要求计算名义尺寸 5. 确定公差分析的方法 6. 按要求计算变异
• 在堆叠公差时，有以下几种方法:
– 手工. – 用电子数据表，比如Nokia Excel 模板. 这在
WC
• 在堆叠中，如果少于4个尺寸的 • 如果对这个制造工艺了解不足够的
RSS
• 在堆叠中，如果有4个或多于4个尺寸的 • 只要有可能就尝试用它 • 当对制造工艺非常了解（旧的类似零件）
Nokia 专案的公差分析
这部分主要介绍在Nokia专案设计应用的公差分析表格，它可以给参与专案设计的 设计者一些基本能力。
变异
下偏差
上偏差
目标 规格范围
两种主要的变异类型
1. 加工制程的变异
– 材料特性的不同 – 设备或模具的错误 – 工序错误 / 操作员的错误 – 模具磨损 – 标准错误
2. 组装制程的变异
– 工装夹具错误 – 组装设备的精度
变异的控制
变异的控制
从加工制造
解决方案
制成的选择 制程的控制 (SPC)
6. 按要求计算变异
n
Ttot Ti i 1
Ttot
= 最大的预期间隙变量(对称公差) .
n
= 独立尺寸的堆叠数量.
Ti
= 第i个尺寸对称公差.
Ttot = 0.15 + 0.25 + 0.30 + 0.40 = 1.10
最小间隙 最大间隙
Xmin Xmax
= =
dGap dGap

603?005其合成之后的squrt0033320052006其組裝仍然滿足6的制程條件所以我們可以算出組裝之后的6036同樣進行公差分解的時候6asm0250256squrt1222?1200295?60177所以對于分解之后的兩個零件其尺寸變為50177mm60177mmmodifiedrootsumsquaresmrss由此可見rss與mrss在6的前提下是完全相同的
公差的分配說明如下:
Worst case
從公差的合成與分解來看, 我們使用worst case法進行公差的分析和定義 可以保證零件100%滿足裝配關系. 但是此方法同樣帶來一些隱患: 1. 公差帶過大, 容易造成較大的間隙或者過盈.
如上例中 A, B, C三個零件相互配合.如果要將 Part A+B 放入 Part C 時,會發生過緊 干涉的情況, 因為 Part C 最窄只有 10.75 mm,但是 Part A+B 卻可能有 11.50 mm 的情況則 有 0.75 mm 的干涉;另一方面,當 Part C 最寬11.25 mm,而 Part A+B 為10.5 mm 的最小值時, 又有 0.75 mm 的間隙產生.由此可知公差範圍過大所造成的難以控制的缺點.
公差分析方法
Chaos
分析方法分類
一般來講, 我們常用的公差定義與分析方法可 以分為以下幾種:
1. Worst case 2. RSS 3. MRSS 4. 6 σ
Worst case
此為最傳統的公差分析法. 其中涉及到兩個概念, 公差的合成與公差的分配. 公差的合成說明如下:
Worst case
Root Sum Squares (RSS)
我們前面所說的Part A and Part B, 從統計上來講, 其主要的分布如下. (暫時不涉及具體的制程能力水平)

Weibull
c b
田口试验法的精度只能达到 3 阶 。为了提高计 算精度 ,一些学者提出了改进的田口试验法[4 ] ,它是 一种乘积高斯积分方法 , 并要求各组成环设计变量 为正态分布 ,可用于高于 3 阶的公差分析中 。
3. 5 卷积法
概率密度函数 f ( x)
f ( x) =
随机抽样公式 ( R 为计 算机产生的随机数)
ei )
(5)
式中 ,Δ0 , Δ 为封闭环和第 i 个组成环的中间偏差 ; ei 为第 i 个组成环的相对不对称系数 。 对于正态分布 , K0 = 1 , ei = 0 ; 对于三角分布 , K0 = 1122 , ei = 0 ; 对 于 瑞 利 分 布 , K0 = 1144 , ei = 0128 ; 其它各种常见分布的相对分布系数 K0 和相对 不对称系数 ei 可查表得到 [1 ,2 ] 。 3. 2 修正的方和根法 修 正 方 和 根 法 ( MRSS , Modified Root Sum Squared) 的基本公式为 [3 ]
X = ( b - a) R + a X0 =
1/ ( b - a) , a Φ x Φ b 0 , 其它 x2
若一个线性尺寸链由两个组成环构成 , 这两个 组成环分别用随机变量 x 和 y 来描述 。这两个相互 独立的随机变量 x 和 y 分别具有概率密度函数 f x ( x ) , x ∈[ a , b ] 和 f y ( y ) , y ∈[ c , d ] ; 其封闭环 z = g
3. 3 蒙特卡洛模拟法 用蒙特卡洛模拟法 (Monte Carlo Simulation) 进行
1
K0
i =1
2 2 2 ζ ∑ i Ki T i

公差计算方法
公差计算方法是算数统计中重要的计算概念。

它是用来描述一个等差数列的连续的差值的一种计算方法。

一般而言，公差的计算可以是：令t1, t2, t3... tn（n≥2）为一个等差数列中的n个项，则t2-t1，t3-t2，…,tn-tn-1所表示的n-1个差值都相等，这n-1个相等的差值即为该等差数列的公差。

若要根据一个等差数列中的任意两项计算出公差，可以首先把等差数列表示为：t1，t1+d，t1+2d，t1+3d，...，t1+nd，其中d即为公差，然后根据实际已知的数据，把其中的两项替换为所给的任意两项，将其根据等式的形式表示出，最后以d的形式解出，即可求出该数列的公差。

例如，有等差数列3,5,7,9,11，要求其公差，可以把上述数列表示为t1，t1+d，t1+2d，t1+3d，t1+4d，则把t1=3，t1+4d=11替换为给定数列中的两项，即3+4d=11，以d的形式解出，得到d=2，即该数列的公差为2。

由此可见，计算公差的方法有多种，但最重要的是要根据实际情况确定计算方式，并用公式正确表示，将求出的公差应用到实际生活当中，为精确地计算出数据服务。

但是使用RSS仍然沒有辦法擺脫每個廠商不同的制程能力的影響, 可能會 存在某些廠商可以達到要求, 某些廠商無法做到.
Modified Root Sum Squares (MRSS)
普通的RSS仍然忽略了一個條件, 即廠商的制程能力可以達到的水準. 單方 面的從設計的角度來定義公差, 脫離了實際制程方面的限定. 所以為了解決這個問題, 我們引入 MRSS的概念. 我們假設廠商可以達到6sigma的制程能力.
公差分析方法
Chaos
分析方法分類
一般來講, 我們常用的公差定義與分析方法可 以分為以下幾種:
1. Worst case 2. RSS 3. MRSS 4. 6 σ
Worst case
此為最傳統的公差分析法. 其中涉及到兩個概念, 公差的合成與公差的分配. 公差的合成說明如下:
Worst case
我们假设组装的制程为6 σ, Part A的廠商只能達到4 σ, Part B的廠商可以達 到6 σ; 亦即 σ1 = 1.5σ2 那么分解之后 對于Part A來講, T=4 σ1=0.208, 對于Part B來講, T=6 σ2=0.204, 由此可見, 制程能力較低的廠商需要更加嚴格的管制其尺寸.
Root Sum Squares (RSS)
通過兩種方法的介紹, 我們可以看出來兩種方法的優缺點:
1.對于公差帶合成, 我們使用RSS方法合成時候的公差要比WC的時候要小. 這樣就意味著有較準確的組裝與配合.
2.對于公差的分解, 我們使用RSS方法, 分解出來的零件公差要比WC法要大. 這樣既意味著, 對于制造者來說, 零件可以變動的范圍大, 更有利于生產.
2. 公差定義過于理論化, 缺乏客觀實際的程序.
以此類方式決定的公差範圍尺寸,必須仰賴設計者的經驗,且必須經過多次的試作 才可真正決定;若生產條件改變:如更換生產廠商,模具修改…等,皆有可能使原訂之公差範 圍無法達成,而被迫放寬或產生大量不良品的損失.

计算： 计算X的名义值：（方法与极值法相同） DX = 0.50 毫米 计算X的公差
2 TX = TA2 + TB2 + TC2 + TD + TE2
= 0.20 2 + 0.10 2 + 0.10 2 + 0.15 2 + 0.10 2 = 0.04 + 0.01 + 0.01 + 0.0225 + 0.01 = 0.0925 = 0.30
X=0.5±0.30
13
四. 公差分析指南
1.公差分析应当从哪里开始？
定义产品规格 概念设计 材料和工艺选择 成本分析 DFMA设计 DFMA讨论 样品制作 产品制造 DFMA
DFMA
公差分析应当 从概念设计阶段开始
产品装配 测试 小批量试产 量产
14
四. 公差分析指南
2.公差的一致性

推荐的做法：

减少尺寸链的长度； 使用定位特征；
16
四. 公差分析指南
3.当公差分析的结果不满足要求时：

DFMA
减少尺寸链的长度； A为54.00±0.20，B为12.00±0.10，C为13.00±0.10，D为 16.00±0.15，E为12.50±0.10
原始的设计
17
四. 公差分析指南
DFMA
极值法：极值法是考虑零件尺寸最不利的情况，通过尺寸链中尺寸的最大值 或最小值来计算目标尺寸的值 均方根法：均方根法是统计分析法的一种，是把尺寸链中的各个尺寸公差的 平方之和再开根即得到目标尺寸的公差
10
三. 公差分析的计算方法
1.计算方法：
计算方法 计算公式 1. 不可能性；

统计公差分析方法概述(2012-10-23 19:45:32)分类：公差设计统计六标准差统计公差分析方法概述一.引言公差设计问题可以分为两类：一类是公差分析(Tolerance Analysis ,又称正计算) ,即已知组成环的尺寸和公差,确定装配后需要保证的封闭环公差；另一类是公差分配(Tolerance Allocation ,又称反计算) ,即已知装配尺寸和公差,求解组成环的经济合理公差。

公差分析的方法有极值法和统计公差方法两类,根据分布特性进行封闭环和组成环公差的分析方法称为统计公差法.本文主要探讨统计公差法在单轴向(One Dimension)尺寸堆叠中的应用。

二.Worst Case Analysis极值法(Worst Case ,WC)，也叫最差分析法，即合成后的公差范围会包括到每个零件的最极端尺寸,无论每个零件的尺寸在其公差范围内如何变化,都会100% 落入合成后的公差范围内。

<例>Vector loop：E=A+B+C,根据worst case analysis可得D（Max.）=(20+0.3)+(15+0.25)+(10+0.15)=45.7,出现在A、B、C偏上限之状况D（Min.）=(20-0.3)+(15-0.25)+(10-0.2)=44.3,出现在A,B、C偏下限之状况45±0.7适合拿来作设计吗?Worst Case Analysis缺陷：•设计Gap往往要留很大,根本没有足够的设计空间,同时也可能造成组装困难；•公差分配时,使组成环公差减小,零件加工精度要求提高,制造成本增加。

以上例Part A +Part B+ Part C，假设A、B、C三个部材,相对于公差规格都有3σ的制程能力水平，则每个部材的不良机率为1-0.9973=0.0027；在组装完毕后所有零件都有缺陷的机率为：0.0027^3=0.000000019683。

这表明几个或者多个零件在装配时,同一部件的各组成环,恰好都是接近极限尺寸的情况非常罕见。