2.3高斯列主元消去法(可编辑修改word版)

Gauss列主元消去法、QR(MATLAB)Gauss列主元消去法是一种线性方程组的求解方法，也称Gauss消去法。

其基本思想是将方程组转化为上三角矩阵，然后通过反向代入求解。

该方法的优点在于计算精度高，求解速度快，但缺点是需要大量的计算，尤其是在矩阵阶数较高时。

具体来讲，Gauss列主元消去法的步骤如下：步骤一：将系数矩阵A进行LU分解，其中L是下三角矩阵、U是上三角矩阵。

设$A=LU$，则原方程组可以写成$LUx=b$。

步骤二：通过初等矩阵左乘系数矩阵A，将每一列的主元变为该列所有元素中绝对值最大的那个元素。

这个过程称为选主元，可以避免计算中的数值不稳定问题。

步骤三：将选主元后的系数矩阵A进行LU分解，得到$L^{'}$、$U^{'}$。

步骤五：通过反向代入求解$U^{'}x=y$，得到$x$的解。

Gauss列主元消去法的实现通常通过矩阵的变换来实现。

对于$n$阶矩阵$A=[a_{ij}]$，通过一系列的行变换，可以将其变为上三角矩阵。

其中的变换可以表示为：$$ R_{i} \leftrightarrow R_{j} $$其中，$R_{i}$和$R_{j}$分别表示矩阵$A$中的第$i$行和第$j$行，$k$是一个非零常数。

这些变换被称为初等行变换。

在MATLAB中，可以使用已经实现好的{\color{blue}\texttt{gauss}}函数来求解线性方程组。

该函数实现的算法是Gauss列主元消去法。

其调用格式为：x = gauss(A,b)其中，$A$是系数矩阵，$b$是结果向量。

函数返回结果向量$x$。

如果$A$或$b$不合法，则函数会返回一个空向量。

除了Gauss列主元消去法，还有一种常用的求解线性方程组的方法是QR分解法。

步骤二：通过正交矩阵左乘系数矩阵$A$，使其变为一个上三角矩阵。

这个过程称为正交相似变换。

步骤三：将$b$进行正交相似变换，得到$Q^{T}b$。

Guass列选主元消去法和三⾓分解法 最近数值计算学了Guass列主消元法和三⾓分解法解线性⽅程组，具体原理如下：1、Guass列选主元消去法对于AX =B1）、消元过程：将（A|B）进⾏变换为，其中是上三⾓矩阵。

即：k从1到n-1a、列选主元选取第k列中绝对值最⼤元素作为主元。

b、换⾏c、归⼀化d、消元2）、回代过程：由解出。

2、三⾓分解法（Doolittle分解）将A分解为如下形式由矩阵乘法原理a、计算U的第⼀⾏，再计算L的第⼀列b、设已求出U的1⾄r-1⾏，L的1⾄r-1列。

先计算U的第r⾏，再计算L的第r列。

a）计算U的r⾏b）计算L的r列C#代码： 代码说明：Guass列主消元法部分将计算出来的根仍然储存在增⼴矩阵的最后⼀列，⽽Doolittle分解，将分解后的结果也储存⾄原来的数组中，这样可以节约空间。

using System;using System.Windows.Forms;namespace Test{public partial class Form1 : Form{public Form1(){InitializeComponent();}private void Cannel_Button_Click(object sender, EventArgs e){this.textBox1.Clear();this.textBox2.Clear();this.textBox3.Clear();boBox1.SelectedIndex = -1;}public double[,] GetNum(string str, int n){string[] strnum = str.Split(' ');double[,] a = new double[n, n + 1];int k = 0;for (int i = 0; i < n; i++){for (int j = 0; j < strnum.Length / n; j++){a[i, j] = double.Parse((strnum[k]).ToString());k++;}}return a;}public void Gauss(double[,] a, int n){int i, j;SelectColE(a, n);for (i = n - 1; i >= 0; i--){for (j = i + 1; j < n; j++)a[i, n] -= a[i, j] * a[j, n];a[i, n] /= a[i, i];}}//选择列主元并进⾏消元public void SelectColE(double[,] a, int n){int i, j, k, maxRowE;double temp; //⽤于记录消元时的因数for (j = 0; j < n; j++){maxRowE = j;for (i = j; i < n; i++)if (System.Math.Abs(a[i, j]) > System.Math.Abs(a[maxRowE, j]))maxRowE = i;if (maxRowE != j)swapRow(a, j, maxRowE, n); //与最⼤主元所在⾏交换//消元for (i = j + 1; i < n; i++){temp = a[i, j] / a[j, j];for (k = j; k < n + 1; k++)a[i, k] -= a[j, k] * temp;}}return;}public void swapRow(double[,] a, int m, int maxRowE, int n){int k;double temp;for (k = m; k < n + 1; k++){temp = a[m, k];a[m, k] = a[maxRowE, k];a[maxRowE, k] = temp;}}public void Doolittle(double[,] a, int n){for (int i = 0; i < n; i++){if (i == 0){for (int j = i + 1; j < n; j++)a[j, 0] = a[j, 0] / a[0, 0];}else{double temp = 0, s = 0;for (int j = i; j < n; j++){for (int k = 0; k < i; k++){temp = temp + a[i, k] * a[k, j];}a[i, j] = a[i, j] - temp;}for (int j = i + 1; j < n; j++){for (int k = 0; k < i; k++){s = s + a[j, k] * a[k, i];}a[j, i] = (a[j, i] - s) / a[i, i];}}}}private void Exit_Button_Click(object sender, EventArgs e){this.Close();}private void Confirm_Button_Click(object sender, EventArgs e){if (this.textBox2.Text.Trim().ToString().Length == 0){this.textBox2.Text = this.textBox1.Text.Trim();}else{this.textBox2.Text = this.textBox2.Text + "\r\n" + this.textBox1.Text.Trim();}this.textBox1.Clear();}private void Calculate_Button_Click(object sender, EventArgs e){string str = this.textBox2.Text.Trim().ToString();string myString = str.Replace("\n", " ").Replace("\r", string.Empty);double[,] a = new double[this.textBox2.Lines.GetUpperBound(0) + 1, this.textBox2.Lines.GetUpperBound(0) + 2];a = GetNum(myString, this.textBox2.Lines.GetUpperBound(0) + 1);if (boBox1.Text == "Guass列主消元法"){Gauss(a, this.textBox2.Lines.GetUpperBound(0) + 1);for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++){this.textBox3.Text = this.textBox3.Text + "\r\nX" + (i + 1) + "=" + a[i, this.textBox2.Lines.GetUpperBound(0) + 1]; }}else if (boBox1.Text == "Doolittle三⾓分解法"){this.textBox3.Enabled = true;Doolittle(a, this.textBox2.Lines.GetUpperBound(0) + 1);bel3.Text = "分解后的结果：";this.textBox3.Clear();this.textBox3.Text += "L矩阵：\r\n";for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++) {for (int j = 0; j < this.textBox2.Lines.GetUpperBound(0) + 1; j++) {if (j < i){this.textBox3.Text += a[i, j].ToString() + "\t";}else if (i == j){this.textBox3.Text += "1\t";}else{this.textBox3.Text += "0\t";}}this.textBox3.Text += "\r\n";}this.textBox3.Text += "\r\nU矩阵：\r\n";for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++) {for (int j = 0; j < this.textBox2.Lines.GetUpperBound(0) + 1; j++) {if (j >= i){this.textBox3.Text += a[i, j].ToString() + "\t";}else{this.textBox3.Text += "0\t";}}this.textBox3.Text += "\r\n";}}}private void textBox1_KeyDown(object sender, KeyEventArgs e){if (e.KeyCode == Keys.Enter){if (this.textBox1.Text.Trim().ToString().Length == 0){Calculate_Button_Click(sender, e);}else{Confirm_Button_Click(sender, e);}}}private void button1_Click(object sender, EventArgs e){this.textBox2.Enabled = true;}}} 运⾏截图： ⾄此完毕。

列主元高斯消去法例题
高斯列主元消去法是一种常用的线性方程组求解方法，它通过利用矩阵的列主元部分进行消元，从而得到线性方程组的解向量。

下面是一个例题:
给定以下线性方程组:
```
2x + 3y + z = 7
4x - 5y - 2z = 3
x + 3y - 2z = 2
```
使用高斯列主元消去法求解，首先我们需要将系数矩阵 A 表示为列主元矩阵的形式:
```
2 3 1 | 7
4 -
5 2 | 3
1 3 -
2 | 2
```
然后，我们可以使用消元法逐步将系数矩阵 A 化为上三角矩阵: ```
2 3 1 | 7
0 0 1 | -1
0 0 0 | 0
1 3 -
2 | 2
```
最后，我们利用得到的上三角矩阵求解线性方程组的解向量: ```
x = (-3*7 + 4*2 - 1*2) * 1/2 = -1
y = (2*7 - 3*2 + 1*2) * 1/2 = 1
z = (2*7 - 4*2 - 1*2) * 1/2 = -3
```
因此，线性方程组的解向量为:x = -1, y = 1, z = -3。

高斯列主元消去法的优点在于其稳定可靠，能够快速求解线性方程组的解向量，尤其是对于大型线性方程组，其计算效率更高。

同时，它也能够很好地处理线性方程组中的符号问题，使得求解过程更加稳定。

1. 用高斯列主元消去法解线性方程组Ax=b 。

⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--⨯=11212592.1121130.6291.51314.59103.015A ，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=2178.4617.59b 。

编程思路：在消元之前，在剩余的元素中选取绝对值最大的为主元，并将其换到主元的位置，以防止出现小数被大数吃掉的现象。

然后再将矩阵化为三角矩阵，按照高斯消去法进行计算，最后进行回代求解。

程序代码：#include <stdio.h>#include <math.h>void main(){//定义变量//float Ab[4][5],x;int i,j,m,k;//输入增广矩阵Ab//printf("please input coefficient matrix Ab by line\n");for(i=0;i<4;i++){for(j=0;j<5;j++){scanf("%f",&Ab[i][j]);}}//输出已输入矩阵，验证是否有误//for(i=0;i<4;i++){for(j=0;j<5;j++){printf("%8.4f ",Ab[i][j]);}printf("\n");}printf("\n\n\n\n\n\n");//消元过程//for(k=0;k<=3;k++){//寻找列主元行号//m=k;for(i=k+1;i<=3;i++){x=fabs(Ab[m][k]);if(fabs(Ab[i][k])>x)m=i;}printf("%d\n\n\n\n",m);if(Ab[m][k]==0){printf("error");return;}else{//交换两行//for(j=k;j<=4;j++){x=Ab[k][j];Ab[k][j]=Ab[m][j];Ab[m][j]=x;}for(i=0;i<4;i++){for(j=0;j<5;j++){printf("%8.4f ",Ab[i][j]);}printf("\n");}printf("\n\n\n\n\n\n");for(i=k+1;i<=3;i++){Ab[i][k]=Ab[i][k]/Ab[k][k];for(j=k+1;j<=4;j++){Ab[i][j]=Ab[i][j]-Ab[i][k]*Ab[k][j];}}}}//输出变换后的矩阵//for(i=0;i<4;i++){for(j=0;j<5;j++){printf("%8.4f ",Ab[i][j]);}printf("\n");}//回代过程//Ab[3][4]=Ab[3][4]/Ab[3][3];for(i=2;i>=0;i--){x=0;for(j=i+1;j<4;j++){x=x+Ab[i][j]*Ab[j][4];}Ab[i][4]=(Ab[i][4]-x)/Ab[i][i];}//输出结果//for(k=0;k<=3;k++){printf("%f ",Ab[k][4]);}}数据输入运行结果2．用追赶法解正定矩阵Ax=b 。

高斯列主消元法法和L U分解法高斯列主消元法：#include<stdio.h>#include<math.h>#define N 10int main(){int i=0,j=0,r=0,n=0,k=1;float a[N][N],x[N],max=-1,sum1=0,sum2=0; //输入矩阵维数printf("Please enter n 0<n<11:\n");scanf("%d",&n);//输入矩阵元素，最后一列为b[]for(i=1;i<=n;i++){for(j=1;j<=n+1;j++){printf("Please enter a[%d][%d]:\n",i,j); scanf("%f",&a[i][j]);}}do{for(i=k;i<=n;i++){if(fabs(a[i][k])>max){max=a[i][k];r=i;}if(a[r][k]==0){printf("Cannot solve!\n");return 0;}}//换行for(j=1;j<=n+1;j++){sum1=a[k][j];a[k][j]=a[r][j];a[r][j]=sum1;}//将矩阵化为上三角矩阵for(i=k+1;i<=n;i++){for(j=k+1;j<=n+1;j++){a[i][j]=a[i][j]-(a[i][k])*(a[k][j])/(a[k][k]); }}k=k+1;max=-1;}while(k<(n-1));//求x[]x[n]=(a[n][n+1])/(a[n][n]);for(k=n-1;k>=1;k--){for(j=k+1;j<=n;j++)sum2=sum2+(a[k][j])*(x[j]);x[k]=(a[k][n+1]-sum2)/(a[k][k]);sum2=0;}//输出结果for(i=1;i<=n;i++){printf("x[%d]=%f\n",i,x[i]);}while(1);return 0;}LU分解法：#include <stdio.h>#include <stdlib.h>#define N 10 //矩阵大小范围/** 使用已经求出的x，向前计算x（供getx()调用）* float a[][] 矩阵U* float x[] 方程组解* int i 解的序号（数组X元素序号）* int n 矩阵大小* return 公式中需要的和*/float getmx(float a[N][N], float x[N], int i, int n) {float mx = 0;int r;for(r=i+1; r<n; r++){mx += a[i][r] * x[r];}return mx;}/** 使用已经求出的y，向前计算y（供gety()调用）* float a[][] 矩阵L* float y[] 数组Y* int i 数组Y元素序号* int n 矩阵大小* return 公式中需要的和*/float getmy(float a[N][N], float y[N], int i, int n){float my = 0;int r;for(r=0; r<n; r++){if(i != r) my += a[i][r] * y[r];}return my;}/** 解方程组，计算某x* float a[][] 矩阵U* float x[] 方程组解* int i 解的序号* int n 矩阵大小* return 方程组的第i个解（数组X的第i个元素值）*/float getx(float a[N][N], float b[N], float x[N], int i, int n){float result;if(i==n-1) //计算最后一个x的值result = (float)(b[i]/a[n-1][n-1]);else //计算其他x值（对于公式中的求和部分，需要调用getmx()函数） result = (float)((b[i]-getmx(a,x,i,n))/a[i][i]);return result;}/** 解数组Y，计算其中一元素值* float a[][] 矩阵L* float y[] 数组Y* int i 数组Y元素序号* int n 矩阵大小* return 数组Y的第i个元素值*/float gety(float a[N][N], float b[N], float y[N], int i, int n){float result;if(i==0) //计算第一个y的值result = float(b[i]/a[i][i]);else //计算其他y值（对于公式中的求和部分，需要调用getmy()函数） result = float((b[i]-getmy(a,y,i,n))/a[i][i]);return result;}int main(){ float l[N][N]={0}; //定义L矩阵float u[N][N]={0}; //定义U矩阵float y[N]={0}; //定义数组Yfloat x[N]={0}; //定义数组Xfloat a[N][N]; //定义系数矩阵float b[N]; //定义右端项float sum=0;int i,j,k;int n;int flag=1;while(flag){printf("请输入系数矩阵的大小："); scanf("%d", &n);if(n>N){printf("矩阵过大！\n");continue;}flag=0;}printf("请输入系数矩阵值：\n");for(i=0; i<n; i++){for(j=0; j<n; j++){printf("a[%d][%d]: ", i, j);scanf("%f", &a[i][j]);}}printf("请输入右端项数组：\n");for(i=0; i<n; i++){printf("b[%d]: ", i);scanf("%f", &b[i]);}/*显示原始矩阵*/printf("\n原始矩阵：\n");for(i=0; i<n; i++){for(j=0; j<n; j++)printf("%0.3f ",a[i][j]);printf("\n");printf("\n\n");/*初始化矩阵l*/for(i=0; i<n; i++){for(j=0; j<n; j++){if(i==j) l[i][j] = 1;}}/*开始LU分解*//*第一步：对矩阵U的首行进行计算*/for(i=0; i<n; i++){u[0][i] = (float)(a[0][i]/l[0][0]);}/*第二步：逐步进行LU分解*/for(i=0; i<n-1; i++){/*对“L列”进行计算*/for(j=i+1; j<n; j++){for(k=0,sum=0; k<n; k++){if(k != i) sum += l[j][k]*u[k][i];}l[j][i] = (float)((a[j][i]-sum)/u[i][i]);}/*对“U行”进行计算*/for(j=i+1; j<n; j++){for(k=0,sum=0; k<n; k++){if(k != i+1) sum += l[i+1][k]*u[k][j]; }u[i+1][j] = (float)((a[i+1][j]-sum));}/*输出矩阵l*/printf("矩阵L：\n");for(i=0; i<n; i++){for(j=0; j<n; j++){printf("%0.3f ", l[i][j]);}printf("\n");}/*输出矩阵u*/printf("\n矩阵U：\n");for(i=0; i<n; i++){for(j=0; j<n; j++){printf("%0.3f ", u[i][j]);}printf("\n");}/*回代方式计算数组Y*/for(i=0; i<n; i++){y[i] = gety(l,b,y,i,n);}/*显示数组Y*/printf("\n\n数组Y：\n");for(i=0; i<n; i++){printf("y%d = %0.3f\n", i+1,y[i]); }/*回代方式计算数组X*/for(i=n-1; i>=0; i--){x[i] = getx(u,y,x,i,n);}/*显示数组X*/printf("\n\n数组X：\n");for(i=0; i<n; i++){printf("x%d = %0.3f\n", i+1,x[i]); }return 0;}。

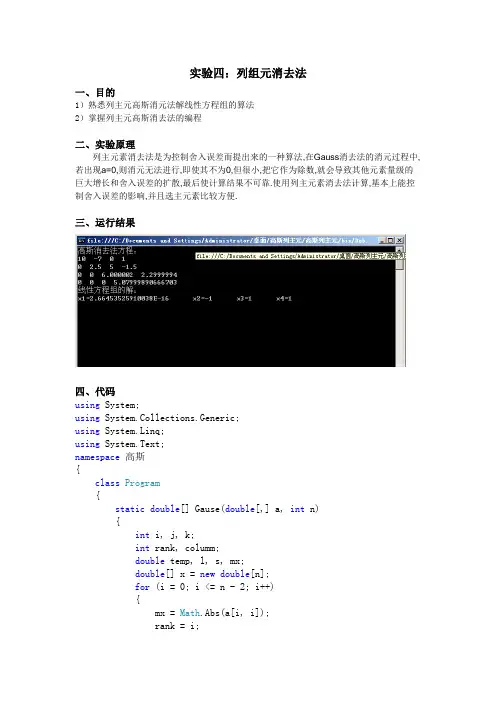
实验四：列组元消去法一、目的1）熟悉列主元高斯消元法解线性方程组的算法2）掌握列主元高斯消去法的编程二、实验原理列主元素消去法是为控制舍入误差而提出来的一种算法,在Gauss消去法的消元过程中,若出现a=0,则消元无法进行,即使其不为0,但很小,把它作为除数,就会导致其他元素量级的巨大增长和舍入误差的扩散,最后使计算结果不可靠.使用列主元素消去法计算,基本上能控制舍入误差的影响,并且选主元素比较方便.三、运行结果四、代码using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace高斯{class Program{static double[] Gause(double[,] a, int n){int i, j, k;int rank, columm;double temp, l, s, mx;double[] x = new double[n];for (i = 0; i <= n - 2; i++){mx = Math.Abs(a[i, i]);rank = i;columm = i;for (j = i + 1; j <= n - 1; j++) //选主元if (Math.Abs(a[j, i]) > mx){mx = Math.Abs(a[j, i]);rank = j;columm = i;}for (k = 0; k <= n; k++) //主元行变换{temp = a[i, k];a[i, k] = a[rank, k];a[rank, k] = temp;} //消元for (j = i + 1; j <= n - 1; j++){l = a[j, i] / a[i, i];for (k = i; k <= n; k++)a[j, k] = a[j, k] - l * a[i, k];}}x[n - 1] = a[n - 1, n] / a[n - 1, n - 1]; //回代方程求解x for (i = n - 2; i >= 0; i--){s = 0;for (j = i + 1; j <= n - 1; j++)s = s + a[i, j] * x[j];x[i] = (a[i, n] - s) / a[i, i];}return x;}static void Main(string[] args){double[,] a = new double[4, 5] { { 10, -7, 0, 1, 8 }, { -3, 2.099999, 6, 2, 5.900001 }, { 5, -1, 5, -1, 5 }, { 2, 1, 0, 2, 1 } };int n = 4;double[] x = new double[n];x = Gause(a, n);Console.WriteLine("高斯消去法方程：");for (int i = 0; i < n; i++){for (int j = 0; j < n; j++)Console.Write(a[i, j].ToString() + " ");Console.WriteLine();}Console.WriteLine("线性方程组的解：");for (int i = 0; i <= n - 1; i++)Console.Write("x" + (i + 1).ToString() + "=" +x[i].ToString() + " ");Console.WriteLine();Console.ReadLine();}}}四、分析通过本次实验的学习，学会根据算法编写基本的相关程序，虽然此次程序模板由老师给予，但认真阅读理解程序有助于今后的学习，再利用计算机中的C语言对高斯列主元消去法可以快速得到线性方程组的解，由简单的线性方程组可以推广到一般n阶线性方程组，这对如何利用高斯列主元消去法解决实际问题有了一定的经验。

高斯消去法高斯消去法，又称高斯消元法，实际上就是我们俗称的加减消元法。

数学上，高斯消去法或称高斯－约当消去法，由高斯和约当得名（很多人将高斯消去作为完整的高斯－约当消去的前半部分），它是线性代数中的一个算法，用于决定线性方程组的解，决定矩阵的秩，以及决定可逆方矩阵的逆。

当用于一个矩阵时，高斯消去产生“行消去梯形形式”。

目录例如信息学方面的应用下面介绍一下矩阵的初等行变换:对于增广矩阵A求解线性方程组的步骤：历史编辑本段例如一个二元一次方程组，设法对每个等式进行变形，使两个等式中的同一个未知数的系数相等，这两个等式相减，得到一个新的等式，在这个新的等式中，系数相等的未知数就被除去了（系数为0）。

同样的也适合多元多次方程组。

编辑本段信息学方面的应用高斯消元是求解线性方程组的重要方法，在OI中有广泛的应用。

本文就来讨论这个方法。

什么是线性方程组？含m个方程和n个未知量的方程组定义为a(11)x(1)+a(12)x(2)+...+a(1n)x(n)=b(1)a(21)x(1)+a(22)x(2)+...+a(2n)x(n)=b(2)...a(m1)x(1)+a(m2)x(2)+...+a(mn)x(n)=b(m)这个方程组称为m*n线性方程组，其中a(ij)和b(i)为实数，括号中为下标。

这个方程组有多种表示方法。

例如，我们知道m*n矩阵（用大写字母表示）是一个m行n列的数阵，n维向量（用加粗的小写字母表示）是n个数的数组，也就是一个n*1矩阵（列向量。

我们不考虑行向量）。

另外，大家也都知道矩阵乘法。

因此一个m*n线性方程组可以表示为Ax=b，其中A是由系数aij组成的m*n矩阵即系数矩阵，x是n维的未知数向量，b是m维的结果向量。

如果把向量b写到A的右边得到m*(n+1)的矩阵，得到的新矩阵称为这个方程组的增广矩阵。

每一个方程组均对应于一个增广矩阵。

编辑本段下面介绍一下矩阵的初等行变换:1 交换两行2 用非零实数乘以任一行3 把某一行的倍数加到另一行上同理可以定义初等列变换。

3.高斯列主元消去法,求解其次线性方程组C/C++ codeprintf("Now input b(i),i,j=0...%d:\n",n-1); for(i=0;i<n;i++)scanf("%f",&b[i]);for(i=0;i<n-2;i++){ for(j=i+1,mi=i,mx=fabs(a[i][j]);j<n-1;j++) if(fabs(a[j][i])>mx){ mi=j;mx=fabs(a[j][i]);if(i<mi){ tmp=b[i];b[i]=b[mi];b[mi]=tmp;for(j=i;j<n;j++){ tmp=a[i][j];a[i][j]=a[mi][j];a[mi][j]=tmp;for(j=i+1;j<n;j++){ tmp=-a[j][i]/a[i][i];b[j]+=b[i]*tmp;for(k=i;k<n;k++)a[j][k]+=a[i][k]*tmp;x[n-1]=b[n-1]/a[n-1][n-1];for(i=n-2;i>=0;i--){ x[i]=b[i];for(j=i+1;j<n;j++)x[i]-=a[i][j]*x[j];x[i]/=a[i][i];for(i=0;i<n;i++)printf("Answer:\n x[%d]=%f\n",i,x[i]); getch();return0;#include<math.h>#include<stdio.h>#define NUMBER 20#define Esc 0x1b#define Enter 0x0dfloat A[NUMBER][NUMBER+1] ,ark;int flag,n;exchange(int r,int k);float max(int k);message();main()float x[NUMBER];int r,k,i,j;char celect;clrscr();printf("\n\nUse Gauss.");printf("\n\n1.Jie please press Enter.");printf("\n\n2.Exit press Esc.");celect=getch();if(celect==Esc)exit(0);printf("\n\n input n=");scanf("%d",&n);printf(" \n\nInput matrix A and B:");for(i=1;i<=n;i++)printf("\n\nInput a%d1--a%d%d and b%d:",i,i,n,i);for(j=1;j<=n+1;j++) scanf("%f",&A[i][j]);for(k=1;k<=n-1;k++)ark=max(k);if(ark==0)printf("\n\nIt's wrong!");message();else if(flag!=k)exchange(flag,k);for(i=k+1;i<=n;i++)for(j=k+1;j<=n+1;j++)A[i][j]=A[i][j]-A[k][j]*A[i][k]/A[k][k];x[n]=A[n][n+1]/A[n][n];for( k=n-1;k>=1;k--)float me=0;for(j=k+1;j<=n;j++)me=me+A[k][j]*x[j];x[k]=(A[k][n+1]-me)/A[k][k];for(i=1;i<=n;i++)printf(" \n\nx%d=%f",i,x[i]); message();exchange(int r,int k)int i;for(i=1;i<=n+1;i++)A[0][i]=A[r][i];for(i=1;i<=n+1;i++)A[r][i]=A[k][i];for(i=1;i<=n+1;i++)A[k][i]=A[0][i];float max(int k)int i;float temp=0;for(i=k;i<=n;i++)if(fabs(A[i][k])>temp)temp=fabs(A[i][k]);4.龙贝格求积公式，求解定积分C/C++ codesum+=(f(p)+f(q))/2;return(h*sum);void main(){ int i;int n=N,m=0;float T[MAX+1][2];T[0][1]=LBG(a,b,n);n*=2;for(m=1;m<MAX;m++){ for(i=0;i<m;i++)T[i][0]=T[i][1];T[0][1]=LBG(a,b,n);n*=2;for(i=1;i<=m;i++)T[i][1]=T[i-1][1]+(T[i-1][1]-T[i-1][0])/(pow(2,2*m)-1);if((T[m-1][1]<T[m][1]+e)&&(T[m-1][1]>T[m][1]-e)) { printf("Answer=%f\n",T[m][1]); getch();return ;希望以上资料对你有所帮助，附励志名言3条：1、宁可辛苦一阵子，不要苦一辈子。

实验二：Gauss列主元消去法程序1：Gauss列主元消去法A=input('请输入线性方程组的增广矩阵A=');n=length(A)-1;x=zeros(n,1);aa=zeros(n,1);for j=1:nfor i=1:(n+1)AA(j,i)=abs(A(j,i));endendfor k=1:(n-1)for i=k:naa(i-(k-1))=AA(i,k);endfor i=k:nif AA(i,k)==max(aa)breakendendif AA(i,k)==0breakfprintf('方程组系数矩阵奇异\n');elsefor j=k:(n+1)jh=A(i,j);A(i,j)=A(k,j);A(k,j)=jh;endendfenzi=A(k,k);for j=k:(n+1)A(k,j)=A(k,j)/fenzi;endfor p=(k+1):njj=A(p,k);for j=k:(n+1)A(p,j)=A(p,j)-jj*A(k,j);endendendif k==(n-1)x(n)=A(n,(n+1))/A(n,n);for i=(n-1):(-1):1he=0;for j=(i+1):nhe=he+A(i,j)*x(j);endx(i)=A(i,(n+1))-he;endendx用Gauss列主元消去法解方程组：1．请输入线性方程组的增广矩阵A=[1e-008,2,3,1;-1,3.172,4.623,2;-2,1.072,5. 643,3]x =-0.4653-0.07000.38002．请输入线性方程组的增广矩阵A=[4,-2,4,10;-2,17,10,3;-4,10,9,-7];x =2.94640.6071-0.14293．请输入线性方程组的增广矩阵A=[0.3e-020,1,0.7;1,1,0.9]x =0.20000.7000程序2：不选主元的高斯消去法A=input('请输入线性方程组的增广矩阵A=');n=length(A)-1;x=zeros(n,1);for k=1:(n-1)if A(k,k)==0breakfprintf('方程组不能用普通的高斯消去法解\n');elsefenzi=A(k,k);for j=k:(n+1)A(k,j)=A(k,j)/fenzi;endfor p=(k+1):njj=A(p,k);for j=k:(n+1)A(p,j)=A(p,j)-jj*A(k,j);endendx(n)=A(n,(n+1))/A(n,n);for i=(n-1):(-1):1he=0;for j=(i+1):nhe=he+A(i,j)*x(j);endx(i)=A(i,(n+1))-he;endendendx用不选主元的Gauss消去法解方程组：1．请输入线性方程组的增广矩阵A=[4,-2,4,10;-2,17,10,3;-4,10,9,-7];x =2.94640.6071-0.14292．请输入线性方程组的增广矩阵A=[1e-008,2,3,1;-1,3.172,4.623,2;-2,1.072,5. 643,3];x =-0.4653-0.07000.38003．请输入线性方程组的增广矩阵A=[0.3e-020,1,0.7;1,1,0.9]x =0.7000。