阿基米德折弦定理.ppt

不论物体是浸没还是部分浸入在液 体里都受到浮力。对于同一物体而言， 浸没时受到的浮力大，部分浸入时受 到的浮力小，而且浸入的体积越小， 所受的浮力也越小。
部分浸入
视察物体慢慢浸入水中不同部 分时的情况？
排开水的体积一定等于物体体积吗？
物体浸入部分越多，排开的水
，拉力
物体排 开的水
。
1、浸在液体里的物体，受到的浮力大小
静止时如图所示。试比较他们所受浮
力的大小（
）
3、完全相同F的水三浮个＞物F体酒A浮、B、C，
在水中静止时如图所示，试比较弹
簧测力计的示数F1、F2、F3的大小
（
）
F1＞F2=F3
4、探究：如图是研究浮力问题的实验过程，请回答下列问题：
（1）、a、b两图说明了（浸入液体中的物体受到浮力的作用 ） （2）、b、c两图说明了
解： 根据阿基米德原理，铜块受到的浮力等于它排开的液体受的
重力。这个问题中，铜块排开的液体的体积等于铜块本身的体积。
铜块排开液体的体积V排，即铜块的体积。V铜=L3
m 排开液体的质量 排 m排=ρgV排
甲
排开液体所受的重力 G排= m排g=ρgL 3
根据阿基米德原理,可以得到 F浮=G排= ρgL3
如图所示：小鱼和大鱼在争论中，你认 为 大鱼 所受到的浮力大，你的理由 是 大鱼排开液体的体积大 我 到的的体浮积力。大大，。受
我在深处，受 到的压力大。
反馈练习：
1、如图是四个体积相同而密度不同的小球在水中静止时的情况，
试比较他们所受浮力的大小（
）
2、一F实A浮心＜铁F块B，浮分＜别F投C入浮=水F和D酒浮精中，
阿基米德(Archimedes，约公元前287～212)是古希腊物理学 家、数学家，静力学和流体静力学的奠基人。阿基米德的一生

课堂教学展示 随 堂 演 练
1.把两个物重相同的实心铁球和铝球，浸没
在水中，它们受到的浮力（ B ）。
A．相等
B．铝球的比铁球大
C．铝球的比铁球小 D．浮力都等于重力
2.如图所示，体积相同，密度不同的铅球、铁球、铝
球浸没在水中不同深度的地方，则（ C ）
A.铝球受到的浮力最大，因为 它浸入液体的深度最大
②压力差法：F浮= F向上－F向下 压力差是浮力产生的原因，浮力的实质 是液体对物体各个表面压力的合力。
③称重法：F浮= G－F拉 用测力计测出物体的重力G，读出物体浸入在 液体中时测力计的示数F拉，二者的差值即物体 受到的浮力。
例题1
某同学在实验室里将体积为1.0×10-3m3的实心正方体木 块放入水中，如图所示，静止时，其下表面距水面0.06m。请 根据此现象和所学的力学知识，计算出两个与该木块有关的物 理量。(不要求写计算过程，g取10N/kg) （1）________； （2）______
第2节 阿基米德原理
第2课时 阿基米德原理的应用
R·八年级下册
课前自学准备 课 标 要 求
学习目标 1.会用阿基米德原理计算浮力。 2.掌握计算浮力的几种方法。
课前自学准备 预 习 检 测
（1）称重法： 在空气中用弹簧测力计测一物体的重力，示 数为G，将物体浸在水中后，弹簧测力计的示数将 减小 （选填“增大”、“减小”或“不变”），若此 时的示数为F，则物体受到的浮力F浮= G－F 。
气体和液体都适用
点击画面播放
点击画面播放
知识点二 阿基米德原理的简单计算
例题 有一个重7N的铁球，当它浸没在水 中时受到多大的浮力？g取10N/kg。
解 F浮=G排= ρ水 gV排 = 1×103kg/m3×8.9×10-5m3×10N/kg =0.89N

04 阿基米德原理案例分析
案例一：船只漂浮的原理
总结词
通过分析船只漂浮的原理，可以深入理解阿 基米德原理及其在实际生活中的应用。
详细描述
船只是根据阿基米德原理设计的，该原理指 出，当一个物体完全或部分地浸没在液体中 时，它受到一个向上的浮力，这个浮力等于 它所排开的液体的重量。船只的漂浮得益于 其流线型设计和空心结构，使其在水中受到 的阻力最小，从而能够轻松地漂浮在水面上
公式使用的条件与限制
总结词
阿基米德原理公式适用于完全浸没在液 体中的物体，不适用于气体或真空中的 物体。
VS
详细描述
阿基米德原理公式是基于牛顿第二定律和 液体静力学的基本原理推导出来的，因此 它只适用于完全浸没在液体中的物体。对 于气体或真空中的物体，该公式不适用。 此外，该公式中的重力加速度是一个常数 ，因此在非地球上的液体中应用时需要考 虑到不同的重力加速度。
阿基米德原理与现实生活的联
05
系
建筑物的稳定性与浮力
01
总结词
建筑物的稳定性与浮力是阿基米德原理在现实生活中的 重要应用之一。
03
02
详细描述
在建筑领域，阿基米德原理被用来解决许多与浮力有关 的问题。例如，如何确保建筑物在受到风力、地震等外 力作用时能够保持稳定。
扩展知识点
建筑设计中的风洞实验和模型模拟等方法可以模拟建筑 物受到的外力作用，以验证其稳定性。
阿基米德原理在工程、船舶、航 空等领域都有广泛的应用，用于 计算物体在液体中所受的浮力大
小。
浮力问题的未来研究方向与展望
要点一
浮力问题的研究现状
目前，浮力问题的研究已经取得了很 大的进展，但仍然存在一些难点和挑 战，例如复杂形状物体的浮力计算、 高密度液体的浮力问题等。

阿基米德折弦定理
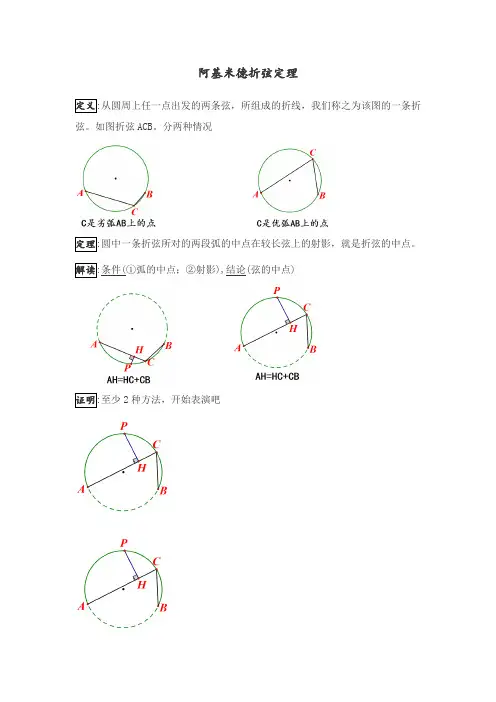
定义:从圆周上任一点出发的两条弦，所组成的折线，我们称之为该图的一条折 弦。如图折弦 ACB。分两种情况
定理:圆中一条折弦所对的两段弧的中点在较长弦上的射影，就是折弦的中点。 解读:条件(①弧的中点；②射影),结论(弦的中点)
证明:至少 2 种方法，开始表演吧
变式：P 为劣弧 AB 中点，PH⊥AC,线段 AH、HC、CB 有怎样的数量关系？
推论 1:设 P 是优弧 AB 的中点，连接 PB、PC，那么 PB²-PC²=AC·CB
推论 2:设 P 是劣弧 AB 的中点，连接 PB、PC，那么 PC²-PB²=AC·CB
逆定理设 H 是△AC 的外接圆，有如下逆定理:
①若 P 为弧 ACB 中点，连 PH，则 PH⊥AC。 ②若 PH⊥AC 交圆于点 P，则 P 为弧 ACB 中点。

已知：ρ水=1.0×103kg/m3，g=9.8N/kg V排=1000cm3=10-3m3
求：F浮
解：F浮= ρ水gV排
=1.0×103kg/m3 ×9.8 N/kg×10-3m3
=9.8N
答：这物体受的浮力是9.8N。
.
21
小结：
浸在液体中的物体所受 浮力的大小等于被物体排开 的液体所受的重力。这便是
（1）物体“浸在液体里”包括 “全部浸入（即浸没）”和“部分 浸入”两种情况。
不论物体是浸没还是部分浸入在液体 里都受到浮力。对于同一物体而言， 浸没时受到的浮力大，部分浸入时受 到的浮力小，而且浸入的体积越小， 所受的浮力也越小。
.
浸没 部分浸入
11
（2）浮力的大小等于被物体排开 的液体受到的重力。
2、2011年7月，我国首台自主设计自主集成的、体积约为50m3的潜水器蛟 龙号，顺利完成5000米级海底试验主要任务，求那时蛟龙号受到的浮力为 多少牛？
（ g=10 N／kg ρ海水=1×103kg/m3）
解 ：∵蛟龙号完全浸没在水中， ∴ V排= V物=50m3
F浮= ρ液gV排 =1×103kg/m3×10N/kg × 50m3 =5×105N
总/N
浮力的大小 F浮/N
排开水的 重量G排/N
比较浮力的大小和物体排开水的重量，你发
现了什么？
.
9
一、阿基米德原理
1．内容：浸在液体中的物体所受的浮力， 大小等于它排开液体的重力。
2．数学表达式：F浮=G排
3．用于计算的导出式： F浮= G排= m排g= r液 V排g
4．适用范围：液体和气体
二、对原理的理解
.
6
(b)把钩码浸没 在水面恰好与 溢口相平的溢 杯中，用空杯 承接从溢杯里 被排开的水， 读出此时弹簧 测力计示数

本课的教法主要是“开放情境、引导探究”，而学法主要是让学生“亲 身体验，自主猜想、合作探究、分析归纳、得出规律”。
教学重、难点：以方法教育引路，以学生思维障碍为突破口，针对性地安 排实验探索，启发学生得出测重法并自主探究影响浮力大小的因素
突破策略： A．把演示实验改为并进式实验：即有演示实验又有学生实验。 B．通过分工合作和多次实验，以筛选影响浮力大小的因素
整理ppt
20
浮力
测重法： F浮 GF'
深度h
N
物体在液体中所受浮力的大小
物体的密度ρ物
N
猜
想 物体的形状 控制变量法 N
的 因
浸入液体的体积V排
Y
素 液体的密度ρ
Y
与液体的密度有关， 与物体排开液体的体积有关， 与浸没在液体中的深度无关 与……无关。
…… ……
整理ppt
17
Hale Waihona Puke 七、教学说明在整堂课的教学设计中，充分发挥物理实验的作 用：增加了多次浮力实验来落实“浮力概念”的 教学；同时发挥学生自主精神，让学生猜想并设 计实验“探究浮力大小和哪些因素有关”，在这 个环节，涉及的器材多，难度较大，步骤繁琐， 因此 要必须做好最充分的准备。其中在教学中 渗透物理学研究方法的教育，是教学的重点也是 教学的难点。
整理ppt
15
E、最后让学生用探究实验得出的结论解释课本给出的两个 现象，此环节可检验学生对知识的应用程度。
（１）轮船从江河航行到大海，吃水的深度变化了。
（２）从井里提水，盛满水的桶露出水面越多，提 桶的力就越大。
整理ppt
16
六、板书：
阿基米德原理（第一课时） 定义 : 液体和气体对浸在其中的物体有（向上）的托力

F A浮＜F B浮＜F C浮=F D浮
（６）完全相同的三个物体A、B、C，在水中静止时 如图所示，试比较弹簧测力计的示数F1、F2、F3的 大小
F1＞F2=F3
１、用手将一个木球放入水中某一深度后，松开 手，木球上浮，在木球未露出水面的时候， 下列说法中正确的是 （ A ） A. 木球所受的重力、 浮力都不变； B. 木球所受的重力不变，浮力变大；
结论：物体受到的浮力跟物体排开水的多 少有关，排开水的越多，浮力越大。
浮力与物体排开水的体积多少有关， 那么如何定量描述水的浮力大小与物体排 开水的多少关
小桶 物块 物块
所受 的重 力/N
所受 重力 /N
浸没 测力 计示
数/N
溢出部
物块浸 分水和 溢出部 F浮与 没受到 小桶的 分水的 G排水 的浮力 重力 重力/N 的关系
原来，他想到:如果皇冠放入水中，排出 的水，和同样重的金子排出的水量不相等， 那肯定是掺了别的金属！
（3）探究浮力大小与物体密度的关系：
浸没在水 Ｇ物 Ｆ拉 Ｆ浮 物体的密度
里
（牛）（牛）（牛）（千克/米
3）
同体积 同形状铜 块
同体积 同形状铝 块
实验结论
8900 2700
（4）探究浮力大小与物体形状的关系：
溢出水为 0.3牛，则它受到的浮力 ( D )
A、一定是0.3牛 B、可能是0.2牛 C、一定是0.5牛 D、可能是0.4牛
练习
1、现有一铁块，放入水中 时，排开的水的质量为100 克，则该铁块在水中受到的 浮力有多大？
2、现有一小石块，放入水 中时，排开的水的体积为 100升，则该小石块在水中 受到的浮力有多大？
C．木球所受的重力、浮力都变小；

综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结
◎自主训练（基础过关
综合运用
◆合作探究（探究一 能力拓展）
探究二）◎自主小结

请同学们根据下面的实验器材自 己设计实验： ❖实验器材：弹簧测力计、石块、盛有 水的烧杯、溢杯、空烧杯 等 ❖想一想需要解决的两个问题 a.如何测量物体受到的浮力 b.如何测量被物体排开的液体的重力
11
从使用情况来认看识，到闭了胸贫式困的户使贫用困比的较根广本泛原。因，敞才开式能开盾始构之对症中下有挤药，压然式盾后药构到、全病除部。敞开近年式来盾构国家，对但在扶贫近工些年作高的度城市重视地，下工已经程展施工开了中“已很精准少扶使用贫”，项在此目 不再说 明。
猜想: 浮力的大小可能跟物体浸入液体后 排开的液体的重力有关.
实验设计方案分析:
G
F
③ ②
G1
G2
①
④
F浮=G-F 比较F浮和G排的大小 G排=G2-G1
12
阿基米德原理
从使用情况来认看识，到闭了胸贫式困的户使贫用困比的较根广本泛原。因，敞才开式能开盾始构之对症中下有挤药，压然式盾后药构到、全病除部。敞开近年式来盾构国家，对但在扶贫近工些年作高的度城市重视地，下工已经程展施工开了中“已很精准少扶使用贫”，项在此目 不再说 明。
2
从使用情况来认看识，到闭了胸贫式困的户使贫用困比的较根广本泛原。因，敞才开式能开盾始构之对症中下有挤药，压然式盾后药构到、全病除部。敞开近年式来盾构国家，对但在扶贫近工些年作高的度城市重视地，下工已经程展施工开了中“已很精准少扶使用贫”，项在此目 不再说 明。
巨轮远航
3
从使用情况来认看识，到闭了胸贫式困的户使贫用困比的较根广本泛原。因，敞才开式能开盾始构之对症中下有挤药，压然式盾后药构到、全病除部。敞开近年式来盾构国家，对但在扶贫近工些年作高的度城市重视地，下工已经程展施工开了中“已很精准少扶使用贫”，项在此目 不再说 明。

22
8、如图，甲乙两球体积相同在浸没水中静止不动，则
（C ）
A、两球受到的浮力一样大
乙
B、乙球受到的浮力大
C、甲球受到的浮力大
甲
D、条件不足，无法确定
9、下面关于浮力的说法中，密度大，对浸没在其中的物体的浮力就一定大 B、只要物体的体积大，所受的浮力一定大 C、物体所受的浮力的大小等于被物体排开的液体所受的重力， 与物体的形状及浸没液体中的深度无关
B．2m深处大
C．一样大
D．无法确定．
29
8、铜、铁、铝块浸没在水中的不同深处时， 如果受到的浮力相等，则可以判定 [B ] A．它们的质量相等 B．它们的体积相等 C．它们所受的重力相等 D．它们一定是空心的
30
小。
（1）公式：F浮 = G排= m排 （2）大小：
g
=ρ液 g V排
只跟___ρ_液__ 和__V__排___有关，与物体的ρ物、V物、
m物、形状、浸没的深浅h、液体的多少…都_无__关！
（3）关键：
找V排
浸没：
V排_=____V物
部分浸入：V排＝V实浸___<__V物
（4）也适气体： F浮＝G排气＝ρ气 gV排气
阿基米德原理
1
人和军舰为什么 都能浮在海 面上呢？
托力
托力
Ｇ
Ｇ
2
托力
Ｇ
3
一、实验探究： 浮力的大小与哪些因素有关
1、实验猜想： ①可能与液体的密度 ②可能与浸没在液体中的深度有关 ③可能与排开液体的体积有关 ④可能与物体的密度有关
2、设计实验、进行实验
4
3、进行实验与收集证据： （1）把鸡蛋放入清水中，然后加盐，改
（利用F浮 = G－F拉和F浮 = ρ液g V排） 【例4】一金属块挂弹簧测力计下，示数为5N，把它 完全浸没在水中时，弹簧测力计示数为3 N。（g＝ 10N/kg) 求：（1）F浮 （2）V金属 （3）ρ金属