高考物理电磁学大题习题20题Word版含答案及解析

高考物理电磁学大题练习20题Word版含答案及解析方向与图示一致。

金属棒的质量为m，棒的左端与导轨相接，右端自由。

设金属棒在磁场中的电势能为0.1)当磁场的磁感应强度为B1时，金属棒在匀强磁场区域内做匀速直线运动，求金属棒的速度和通过电阻的电流强度。

2)当磁场的磁感应强度随时间变化时，金属棒受到感生电动势的作用，求金属棒的最大速度和通过电阻的最大电流强度。

答案】(1) v=B1d/2m。

I=B1d2rR/(rL+dR) (2) vmaxBmaxd/2m。

ImaxBmaxd2rR/(rL+dR)解析】详解】(1)由洛伦兹力可知，金属棒在匀强磁场区域内受到向左的洛伦兹力，大小为F=B1IL，方向向左，又因为金属棒在匀强磁场区域内做匀速直线运动，所以受到的阻力大小为F1Fr，方向向右，所以有：B1IL=Fr解得：v=B1d/2m通过电阻的电流强度为：I=B1d2rR/(rL+dR)2)当磁场的磁感应强度随时间变化时，金属棒受到感生电动势的作用，其大小为：e=BLv所以金属棒所受的合力为：F=BLv-Fr当合力最大时，金属棒的速度最大，即：BLvmaxFr=0解得：vmaxBmaxd/2m通过电阻的电流强度为：ImaxBmaxd2rR/(rL+dR)题目一：金属棒在电动机作用下的运动一根金属棒在电动机的水平恒定牵引力作用下，从静止开始向右运动，经过一段时间后以匀速向右运动。

金属棒始终与导轨相互垂直并接触良好。

问题如下：1) 在运动开始到匀速运动之间的时间内，电阻R产生的焦耳热；2) 在匀速运动时刻，流过电阻R的电流方向、大小和电动机的输出功率。

解析：1) 运动开始到匀速运动之间的时间内，金属棒受到电动机的牵引力向右运动，电阻R中会产生电流。

根据欧姆定律和焦耳定律，可以得到电阻R产生的焦耳热为：$Q=I^2Rt$，其中I为电流强度，t为时间。

因此，我们需要求出这段时间内的电流强度。

根据电动机的牵引力和电阻R的阻值，可以得到电路中的总电动势为$E=FL$，其中F为电动机的牵引力，L为金属棒的长度。

高三物理电磁学练习题及答案一、选择题1. 带电粒子在磁场中受力的大小与以下哪个因素无关？A. 粒子的电荷量B. 粒子的速度C. 粒子所受磁场的大小D. 粒子所受磁场的方向2. 一个导线以匀速矩形轨道绕一个垂直于轨道面的固定轴旋转。

导线的两端接有电源，通过导线的电流大小和方向在转过一个周期后是：A. 大小不变，方向也不变B. 大小不变，方向相反C. 大小相反，方向不变D. 大小相反，方向相反3. 两个平行的长直导线之间通过电流会发生什么现象？A. 两导线之间会产生吸引力B. 两导线之间会产生斥力C. 两导线之间会发生磁场D. 两导线之间电流大小会发生变化4. 一根导线形状为正方形，两边的两段导线与均匀磁场垂直并相等。

通过导线的总电流为I，导线所在的平面与磁场之间夹角为θ。

则导线所受力的大小为：A. IθB. Iθ/2C. Iθ^2D. Iθ^2/25. 在变化磁场中一个回路内的感应电动势的大小与以下哪个因素无关？A. 磁场的变化速率B. 回路面积的大小C. 回路的形状D. 磁场的方向二、填空题1. 两根平行导线之间的距离为0.2 m，通过第一根导线的电流为2 A，第二根导线与第一根导线的角度为30°，则在第二根导线上的磁感应强度为_____ T。

2. 一根长直导线通过电流3 A，产生的磁场的磁感应强度为____ T。

3. 一个圆形回路的半径为0.2 m，它所在的平面与一个磁场垂直，磁感应强度为0.5 T，磁场持续变化，则回路内感应电动势的大小为_____ V。

4. 一根导线形状为正方形，两边的两段导线与均匀磁场垂直并相等。

通过导线的总电流为4 A，导线所在的平面与磁场之间夹角为60°。

则导线所受力的大小为_____ N。

三、计算题1. 一条长直导线通过电流I，产生的磁场与另一根平行导线距离为d，并在两导线之间产生一个力作用。

当其中一根导线的电流大小为2I时，两导线之间的力变为原来的几倍？2. 一个包围面积为0.2 m^2的圆形回路，其平面与磁场成60°角，磁感应强度为0.4 T，磁场变化的速率为5 T/s，计算回路中感应电动势的大小。

高考物理电磁学多选题考前必做20题1．如图所示，等量正电荷形成的电场，MN 是两个正电荷连线的中垂线，O 为垂足，a 、b 是距离O 很近的两点，一个带负电的粒子（重力不计）只在电场力的作用下以一定速度沿MN 直线进入电场顺次经过a 、O 、b 点，在粒子从a 到b 的过程中，下列说法正确的是（ ）A ．粒子在O 点的电势能为零B ．粒子在O 点的动量最小C ．粒子的电势能先减小后增大D ．粒子的加速度先减小后增大2．如图所示，带电量为Q 的正点电荷固定在倾角为30°的光滑绝缘斜面底端C 点，斜面上有A 、B 、D 三点，A 和C 相距为L ，B 为AC 中点，D 为A 、B 的中点。

现将一带电小球从A 点由静止释放，当带电小球运动到B 点时速度恰好为零。

已知重力加速度为g ，带电小球在A 点处的加速度大小为4g ，静电力常量为k 。

则（ ）A ．小球从A 到B 的过程中，速度最大的位置在D 点B ．小球运动到B 点时的加速度大小为2g C ．BD 之间的电势差U BD 大于DA 之间的电势差U DAD ．AB 之间的电势差U AB =kQ L3．如图所示，两个等量异种点电荷分别位于P 、Q 两点，P 、Q 两点在同一竖直线上，水平面内有一正三角形ABC ，且PQ 连线的中点O 为三角形ABC 的中心，M 、N 为PQ 连线上关于O 点对称的两点，则下列说法中正确的是（ ）A ．A 、B 、C 三点的电势相等B．电子在O点具有的电势能大于在B点具有的电势能C．M点场强等于N点场强D．将一正点电荷从A点移到O点，电场力做正功4．如图甲所示，一绝缘的圆环上均匀分布着正电荷，一光滑细杆过圆心且垂直于圆环平面，杆上套有带正电的小球。

t=0时刻把小球从a点由静止释放后，小球沿细杆运动经过b、c两点，小球运动的v—t图像如图乙所示。

下列判断正确的是（）A．小球从a点运动到点的过程中电势能增大B．圆环在圆心处产生的电场强度为0C．a点的电场强度大于b点的电场强度D．a、b两点电势差U ab小于b、c两点电势差U bc5．如图所示。

高三物理电磁学练习题及答案2023一、选择题1. 下列哪个选项最准确地描述了电磁感应的现象？A. 通过一个闭合线圈中的直流电流，可以产生磁场。

B. 一个导体在磁场中运动，会产生感应电动势。

C. 交流电经过变压器后，可以改变电压的大小。

D. 静止的导体不会受到磁场的作用力。

2. 两个相邻的导线，电流方向相同时，它们之间的相互作用力是：A. 引力B. 排斥力C. 无相互作用力D. 无法确定3. 一根导线在垂直于磁场方向以速度v匀速运动，切割磁感线的长度为L，则感应电动势的大小为：A. v/LB. v*LC. v+LD. v-L4. 在电路中，若磁感应强度减小，则感应电动势的方向是：A. 不变B. 没有感应电动势C. 与原来相反D. 无法确定5. 一台发电机将机械能转化为电能的过程属于：A. 电磁感应B. 电阻发热C. 机械运动D. 热传导二、填空题1. 在电磁感应现象中，当磁感应强度发生变化时，产生的电动势的方向满足________法则。

答案：楞次定律2. 单位时间内磁通量的变化率称为________。

答案：感应电动势3. 一台发电机的转子中有1000个磁针，转速为1800转/分，每个磁针的磁连量为0.002Wb。

该发电机输出的交流电频率为________Hz。

答案：60Hz4. 一根导线以速度v绕半径为r的圆周做匀速运动，如果磁感应强度的大小为B，则感应电动势的大小为________。

答案：B*v*r5. 电磁铁的磁感应强度为0.8T，长度为20cm，它在磁场中运动，切割磁感线的速度为10m/s，则感应电动势的大小为________。

答案：1.6V三、解答题1. 一根长直导线$AB$位于均匀磁场中，垂直于纸面向里，如图所示。

当导线以速度$v$向左运动时，求：(1) 导线$AB$之间的感应电动势大小。

(2) 感应电动势的方向。

(3) 当$v=10\ m/s$时，导线$AB$之间的感应电动势大小为0.02 V，请计算磁场的强度。

高三物理电磁大题练习题电磁学是物理学的重要分支，也是高中物理教学的重点内容之一。

在高三物理学习阶段，电磁学大题练习题的实施对于学生的知识掌握和能力提升具有重要意义。

本次练习题旨在帮助高三学生巩固和应用电磁学的知识，培养解决实际问题的能力，提高解题的思维灵活性。

1.电流与磁场1.1 一根直导线形成的长度为L的圆圈电路，电流为I，求该电路中心处的磁感应强度B。

1.2 在与磁场垂直的平面内，有一导线AB，长度为L，电阻为R，电流为I。

导线与磁场的夹角为θ，AB和磁场的夹角为90°。

求通过该导线的电流所受到的磁场力F。

2.电磁感应2.1 一个长直导线产生磁场B1，该导线的长度为L，求距离导线x 处的磁感应强度B2。

2.2 有一个互感器，其初级线圈匝数为N1，输入交流信号的频率为f，初级电压为U1。

当次级线圈的匝数为N2时，求次级电压U2。

3.电磁波3.1 某无线电台的工作频率为f，求电磁波的波长λ。

3.2 向前传播的电磁波在单位时间内穿过单位面积的能量为E，求该电磁波的能流密度S。

4.电磁波的反射和折射4.1 当光线从真空射向折射率为n的介质时，入射光线、反射光线和折射光线之间有何关系？4.2 一束光线从空气射入折射率为n1的介质，然后折射到折射率为n2的介质，接着从这个介质射入折射率为n3的介质。

求光线在这三个介质中的传播速度之比。

以上是高三物理电磁大题的练习题，希望同学们认真思考、仔细分析，并运用所学的电磁学知识进行解答。

通过练习，相信大家能够更好地理解和掌握电磁学的基本原理和应用，为应对高考物理提供有力的支持。

祝愿同学们取得优异的成绩！。

1
B.
2
如图所示，两根平行金属导轨置于水平面内，导轨之间接有电阻
中的感应电流逐渐减小
3
时，线圈中的电流改变方向
一个周期内，线圈产生的热量为
4
、总电阻为的正
边与磁场边界平行，如图（a）所示，已知导线框一直向右做匀速
时刻进入磁场．线框中感应电动势随时间变化的图线如图（b）所示（感
左转轴上侧绝缘漆挂掉，右转轴下侧的绝缘漆刮掉左转轴上下两侧绝缘漆都挂掉，右转轴下侧的绝缘漆刮掉
5
D.
和．圆形匀强磁场的边缘恰好与线圈重合，则穿6
7
磁场的方向；
答案B.
1
A 2
中的感应电流逐渐减小3
时，线圈中的电流改变方向
一个周期内，线圈产生的热量为
，所以线圈平面平行于磁感线，故A正确；
和，故B错误；
C．在交变电流产生的过程当中，磁通量最大时，感应电动势以及感应电流最小，故C 4
5
左转轴上侧绝缘漆挂掉，右转轴下侧的绝缘漆刮掉
左转轴上下两侧绝缘漆都挂掉，右转轴下侧的绝缘漆刮掉
6
D.
7
磁场的方向；第6页(共7页)
第7页(共7页)。

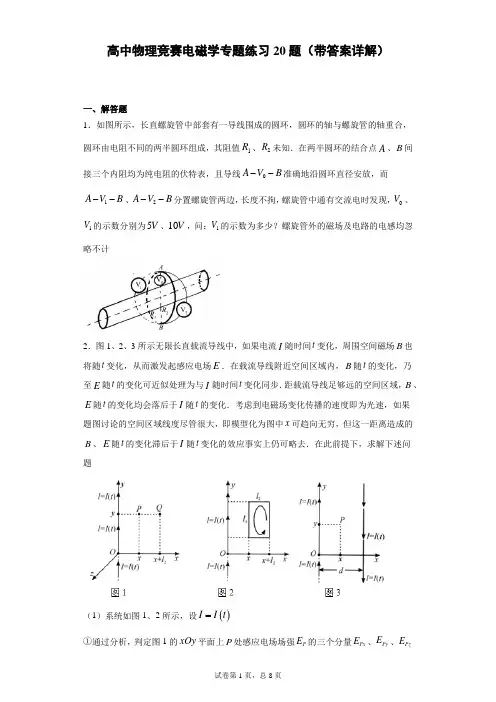
高中物理竞赛电磁学专题练习20题（带答案详解）一、解答题1．如图所示，长直螺旋管中部套有一导线围成的圆环，圆环的轴与螺旋管的轴重合，圆环由电阻不同的两半圆环组成，其阻值1R 、2R 未知．在两半圆环的结合点A 、B 间接三个内阻均为纯电阻的伏特表，且导线0A V B --准确地沿圆环直径安放，而1A V B --、2A V B --分置螺旋管两边，长度不拘，螺旋管中通有交流电时发现，0V 、1V 的示数分别为5V 、10V ，问：1V 的示数为多少？螺旋管外的磁场及电路的电感均忽略不计2．图1、2、3所示无限长直载流导线中，如果电流I 随时间t 变化，周围空间磁场B 也将随t 变化，从而激发起感应电场E ．在载流导线附近空间区域内，B 随t 的变化，乃至E 随t 的变化可近似处理为与I 随时间t 变化同步．距载流导线足够远的空间区域，B 、E 随t 的变化均会落后于I 随t 的变化．考虑到电磁场变化传播的速度即为光速，如果题图讨论的空间区域线度尽管很大，即模型化为图中x 可趋向无穷，但这一距离造成的B 、E 随t 的变化滞后于I 随t 变化的效应事实上仍可略去．在此前提下，求解下述问题（1）系统如图1、2所示，设()I I t =①通过分析，判定图1的xOy 平面上P 处感应电场场强P E 的三个分量Px E 、Py E 、PzE中为零的分量②图2中12l l ⨯长方形框架的回路方向已经设定，试求回路电动势ε③将图1中的P 、Q 两处感应电场场强的大小分别记为P E 、Q E ，试求P Q -E E 值 （2）由两条无限长反向电流导线构成的系统如图3所示，仍设()I I t =，试求P 处感应电场场强P E 的方向和大小3．现构造如图1所示网络，该网络为无穷正方形网络，以A 为原点，B 的坐标为()1985,930．现在两个这样的网络C C A B 和L L A B ，其单位长度上所配置的电学元件分别为电容为C 的电容器及电感为L 的线圈，且网络中的电阻均忽略不计，并连接成如图2所示的电路S 为调频信号发生器，可发出频率()0,f Hz ∈+∞的电学正弦交流信号．即()0sin 2πS U U ft =，0U 为一已知定值，R 为一已知保护电阻试求干路电流达到最大时，S 的频率m f 以及此时干路的峰值电流max I4．在空间中几个点依次放置几个点电荷1q ，2q ，3q ，4q ，…，n q ，对于点i ，其余1n -个点电荷在这一点上的电势和为i U ，若在这n 个点上换上另n 个点电荷1q '，2q '，3q '，…，n q '，同理定义()1,2,,i U i n '=（1）证明：()112nni i i i i i qU q U n ==''=≥∑∑（2）利用（1）中结论，证明真空中一对导体电容器的电容值与这两个导体的带电量无关．（这对导体带等量异号电荷）（3）利用（1）中的结论，求解如下问题：如图所示，正四面体ABCD 各面均为导体，但又彼此绝缘．已知带电后四个面的静电势分别为1ϕ、2ϕ、3ϕ和4ϕ，求四面体中心O点的电势O ϕ5．有七片完全相同的金属片，面积为S ，放置在真空中，除4和5两板间的间距为2d 外，其他相邻两板间距均为d ，且1和5、3和7用导线相连，试求：（1）4与6两板构成的电极的电容（2）若在4和6间加上电压U ，求各板的受力．6．如图所示，一电容器由一圆形平行金属板构成，金属板的半径为R ，间距为d ，现有一点P ，在两金属板的中位面（即平行于两板，且平分两极板所夹区域的平面）上，P 到两中心O 的距离为()0R r r +>R ，已知极板所带的面电荷密度为σ±，且R r d ，试求P 点的场强大小P E7．在一环形铁芯上绕有N 匝外表绝缘的导线，导线两端接到电动势为ε的交流电源上，一电阻为R 、自感可略去不计的均匀细圆环套在这环形铁芯上，细圆环上a 、b 两点间的环长（劣弧）为细圆环长度的1n．将电阻为r 的交流电流计G 接在a 、b 两点，有两种接法，分别如图1、图2所示，试分别求这两种接法时通过G 的电流8．有一个平面正方形无限带电网络，每个格子边长均为r ，线电荷密度为()0λλ>，有一带电电量为()0Q Q >、质量为m 的粒子恰好处于一个格子的中心，若给它某个方向的微扰，使其位移d ，dr ．试求它受到电场力的大小，并描述它以后的运动．（提示：可能用到的公式2222π11116234=++++）9．（1）一维电磁驻波()()sin x E x A k x =在x 方向限制在0x =和x a =之间．在两个端点处驻波消失，求x k 的可能值．（2）弦理论认为物理空间多于三维，多出的隐藏维空间像细圆柱的表面一样卷了起来，如图中y 坐标所示，设圆柱的半径为()b a ，在圆柱面上电磁波的形式为()()(),sin cos x y E x y A k x k y =，其中y 是绕圆柱的折叠空间的坐标．求y k 的可能值．（3）光子能量W =()1239hc eV nm =⨯，eV 表示1电子伏特，1nm 等于910m -．目前人类能产生的最高能量的光子大约为121.010eV ⨯．如果该能量能够产生一个折叠空间的光子，b 的值满足什么条件？10．在图1所示的二极管电路中，从A 端输入图2所示波形的电压，若各电容器最初都没有充电，试画出B 、D 两点在三个周期内的电压变化．将三极管当作理想开关，B 点电压的极限是多少？11．理想的非门可以视为一个受控电压源：当输入端电压小于6C U V =时，输出端相当于和地线之间有一个理想电压源，电源电压012U V =；当输入端电压大于C U 时，输出端相当于和地线之间短路．等效电路图如图1所示．不同非门中接地点可以视为是同一个点，我们利用非门、电容和电阻能够做成一个输出方波信号的多谐振荡器．给出图2电路中02U 随着时间的变换关系．提示：如图3的RC 电路，从刚接通电路开始，电容上的电压随时间变化规律为()()01t RC U t U e -=-12．如图所示，在圆形区域中（足够大），有垂直于纸面向内随时间均匀增加的磁场Bk t∆=∆．在与圆心O 距离为d 的位置P 处有一个钉子，钉住了一根长度为l ，质量为m 的均匀绝缘棒的中心，绝缘棒能在平面内自由无摩擦地自由转动．绝缘棒上半截均匀带正电，电量为Q ，下半截均匀带负电，电量为Q -．初始时刻绝缘棒垂直于OP（1）计算在P 点处钉子受到的压力（2）若绝缘棒受到微小扰动，在平面内来回转动起来（速度很小，洛仑兹力可以忽略），求证此运动是简谐振动，并计算周期．（绝缘棒绕质心的转动惯量为2112I ml =） 13．如图1所示的电阻网络中，图中各段电阻的阻值均为r（1）试求AB R 、AC R（2）现将该网络接入电路中，如图2所示．AC 间接电感L ，A 、B 间接一交流电源，其角频率为ω，现为提高系统的动率因数，在A 、B 间接一电容C ，试求使功率因数为1的电容C ，已知rL αω=14．两个分别绕有1N 和2N 匝的圆线圈，半径分别为1r ，2r 且21r r ，设大圆的电阻为R ，试求：（1）两线圈在同轴共面位置的互惑系数（2）在小线圈中通以稳恒电流I ，并使之沿轴线以速度v 匀速运动．始终保持二者共轴，求两线圈中心相距为x 时，大线圈中的感生电动势（3）若把小线圈从共面移到很远处，求大线圈中通过的感生电量．（忽略所有自感） 15．如图所示为一两端无限延伸的电阻网络，设每小段电阻丝电阻均为1Ω，试问：A 、B 间等效电阻AB R 为多少？（结果保留三位有效数字）16．如图a 所示，电阻101k R R ==Ω，电动势6V E =，两个相同的二极管D 串联在电路中，二极管D 的D D I U -特性曲线如图b 所示．试求： (1)通过二极管D 的电流； (2)电阻1R 消耗的功率．17．如图甲所示，两台发电机并联运行，共同供电给负载，负载电阻24R =Ω．由于某种原因，两台发电机的电动势发生差异，1130V ε=、11r =Ω、2117V ε=、20.6r =Ω．求每台发电机中的电流和它们各自发出的功率．18．如图1所示的无限旋转内接正方形金属丝网络由一种粗细一致、材料相同的金属丝构成，其中每一个内接正方形的顶点都在外侧正方形四边中点上．已知与最外侧正方形边长相同的同种金属丝A B ''的电阻为0R ，求网络中 (1)A 、C 两端间等效电阻AC R ； (2)E 、G 两端间等效电阻EC R ．19．正四面体框架形电阻网络如图所示，其中每一小段的电阻均为R，试求：(1)AB两点间的电阻；(2)CD两点间的电阻．20．在如图所示的网络中，仅知道部分支路上的电流值及其方向、某些元件参数和支路交点的电势值（有关数值及参数已标在图甲上），请你利用所给的有关数值及参数求出含有电阻x R的支路上的电流值x I及其方向．参考答案1．220V U V =或0． 【解析】 【详解】因螺旋管中通有交流电，故回路中产生的电动势也是交变的，但可以仅限于某确定时刻的感生电动势、电压和电流的瞬时值，这是因为在无电感、电容的情况下，各量有效值的关系与瞬时值的关系相同．（1）当12R R <，取A B U U >时，回路中的电流如图所示，则0001102V I R I R ε+-=，0100102V V I R I R ε'+-=， 0002202V I R I R ε-+=，0200202V V I R I R ε'-+=． 整理可得0120001202V V V V I R I R I R I R ε''=+=-．所以，2201201220V V V V U I R I R I R V ''==+= （2）当12R R >，取A B U U <时，0I 反向，其他不变，则1020010202V V V V I R I R I R I R ε''=-=+所以，221021020V V V V U I R I R I R ''==-=（此时20R =，即2R 段为超导体，10R ≠） 综上所述，220V U V =或0 2．（1）①0Pz E =②012d ln2πd l x l l t x με+⎛⎫=⎪⎝⎭③02d ln 2πd P Q x l I E E t x μ+⎛⎫-=⎪⎝⎭（2）()0d ln2πd P I d xE x t xμ-⎛⎫=⎪⎝⎭，基准方向取为与y 轴反向 【解析】 【详解】（1）①若0Pz E ≠，则在过P 点且与xOy 坐标面平行的平面上，取一个以x 为半径，以y 轴为中央轴的圆，设定回路方向如题解图所示．由系统的轴对称性，回路各处感应电场E 的角向分量与图中Pz E 方向一致地沿回路方向，且大小相同，由E 的回路积分所得的感应电动势0ε≠．另一方面，电流I 的磁场B 在该回路所包围面上磁通量恒为零，磁通量变化也为零，据法拉第电磁感应定律应有0ε=．两者矛盾，故必定是0Pz E =．若0Py E ≠，由系统的轴对称性，在题解图1的圆柱面上各处场强E 的y 方向分量方向、大小与图中Py E 方向、大小相同．若取一系列不同半径x 的同轴圆柱面，每个圆柱面上场强E 的y 方向分量方向相同、大小也相同，但大小应随x 增大而减小．这将使得题文图2中的矩形回路感生感应电动势0ε≠，与法拉第电磁感应定律相符，因此允许0Py E ≠若0Px E ≠，由轴对称性，题解图1的圆柱面上各处场强E E 的径向分量方向与Px E 对应的径向方向一致，两者大小也相同．将题解图1中的圆柱面上、下封顶，成为一个圆筒形高斯面，上、下两个端面d ⋅E S 通量积分之和为零，侧面d ⋅E S 通量积分不为零，这与麦克斯韦假设所得1d d 0se sV V ρε⋅==⎰⎰⎰⎰⎰E S 矛盾，故必定是0Px E =②据法拉第定律，参考题文图2，有()21d d d x l x B x l x t ε+=--⎰，其中()02πI B x xμ= 所以，001221d d ln ln d 2π2πd Il x l x l l l t x t xμμε++⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭ ③据麦克斯韦感应电场假设，结合（1.1）问解答，有()()121=d LE l E x lE x l l ε⋅=-+⎰结合①②问所得结果，有()()012121d ln 2πd l x l I E x l E x l l t xμ+⎛⎫-+=⎪⎝⎭()()022d ln 2πd x l I E x E x l t xμ+⎛⎫-+=⎪⎝⎭即得()()022d ln 2πd P Q x l I E E E x E x l t xμ+⎛⎫-=-+=⎪⎝⎭（2）从物理上考虑，远场应()220l E x l →∞+→代入上式，得()202d ln 2πd P l x l I E E x t xμ→∞+⎛⎫==→∞ ⎪⎝⎭为行文方便，将P E 改述为()02d ln 2πd z P P l x l I E E x t xμ→∞+⎛⎫→=→∞ ⎪⎝⎭()P E x 为发散量，系因模型造成，并非真实如图所示，由左侧变化电流贡献的()P x 左E 和右侧变化电流贡献的()P x 右E 合成的()P E x ，基准方向取为与y 轴反向．即有()()()P P P E x E x E x =-左右()()00d d ln ln 2πd 2πd P x d x l x l I I E x t x t xμμ∞+-++⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭左右 ()()()00d d ln ln 2πd 2πd P d x l d x x l I I E x t d xt d xμμ∞-+-++⎛⎫⎛⎫== ⎪ ⎪--⎝⎭⎝⎭右左使得()()0d ln 2πd P I d xE x E x t xμ-⎛⎫==⎪⎝⎭3．0maxU I R=，2πmf ω== 【解析】 【详解】不妨设电感网络等效电感AB L L α=，则其阻抗L αω=Z j （j 为单位虚根） 又由于C C A B 与L L A B 的结构相同，故在阻抗上形式具有相似性，有1C Cαω=⋅Z j ，从而总阻抗11L C R R L R L C C αωααωωω⎛⎫⎛⎫=++=+-=+- ⎪ ⎪⎝⎭⎝⎭Z Z Z Z j j j又峰值00U I =Z，所以，100I U -=⋅ 所以，当10L Cωω-=，即ω=0I 最大 此时，0max U I R=，而2πmf ω== 4．（1）证明见解析（2）证明见解析（3）12344O ϕϕϕϕϕ+++=【解析】 【详解】（1）设i 点对j 点所产生的电势为ij i a q ，同理易知j 点对i 点产生电势为ji j a q ，而对于此二点系统，我们有ij j ji i U q U q =，即ij i j ji j i a q q a q q = 所以，ij ji a a =，易知ij a 为只与位置有关的参量． 又1231231n ni i i i i n ij j j U a q a q a q a q a q ==++++=∑（令0ii a =）则1231231n ni i i i i n ij j j U a q a q a q a q a q =''''''=++++=∑（ij a 只与位置有关）所以，111,1111nn n n n n ni i i ij j ij i j i ij j i i i i j i j i j i qU q a q a q q q a q q U =======⎛⎫⎛⎫'''''==== ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∑∑∑所以原式（格林互易定理）成立（2）分别设两导体前后所带静电分别为1Q ±，2Q ±，其对应的电容分别为1C 、2C 则由（1）知，()121122121221niii qU QUQU Q U U ='=-=-∑（其中21U ，22U 为带2Q ±时两导体电势） 同样()211212211121ni ii q UQ U Q U Q U U ='=-=-∑（其中11U ，12U 为带1Q ±时两导体电势）由（1）知二者相等，则()()1212221112Q U U Q U U -=- 所以，121211122122Q Q C C U U U U ===--即与导体带电量多少无关．（3）由题意，设四个面与中心O 的电荷量分别为1q 、2q 、3q 、4q 、0 同时，四个面与中心的电势分别为1ϕ、2ϕ、3ϕ、4ϕ、O ϕ．现将外面四个面接地，中心放一个电量为Q 的点电荷，中心电势为U ，而四个面产生的感应电荷都相等，为4Q-，则此时四个面与中心O 的电荷和电势分别为 4Q -、4Q -、4Q -、4Q-、Q ；0、0、0、0、U 由格林互易定理可得123404444O Q Q Q Q U ϕϕϕϕϕ⎛⎫⎛⎫⎛⎫⎛⎫⋅-+⋅-+⋅-+⋅-+⋅= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭即可得12344O ϕϕϕϕϕ+++=5．（1）04616161919S C C d ε==（2）204232361U S F d ε=，方向向上；205213722U S F dε=，方向向下；206216722U S F d ε=，方向向上；207281722U S F dε=，方向向上 【解析】 【详解】（1）由4与6两板构成的电极的电容结构可等效为图所示的电容网络，其中图101223345667SC C C C C C dε======，04522SC C dε==． 由图可知，各电容器所带的电量满足342356Q Q Q =+，451267Q Q Q +=，2312Q Q =． 各支路的电压满足如下关系：3456Q Q U C C +=，45672Q Q U C C +=，23566712Q Q Q Q C C C C+=-． 由上述各式解得1223119Q Q CU ==，341019Q CU =，45619Q CU =，56919Q CU =，67719Q CU =， 则344504616161919Q Q SC C U d ε+===． 为求4、6端的电容，我们也可通过先求如图左所示的电阻网络的阻值，进而求得电容．将图中O ABC -的Y 形接法部分转化为△接法，得到图2右所示电路，其阻值如图所示，进而易得到461916R R =． 直流电路的电阻、电压、电流之间有U I R=． 由电容组成的电路的电容、电压、电量之间有Q CU =． 类比有1C R~． 且上述的电阻电路与电容电路匹配，所以，46461C R ~，即有04616161919S C C dε==．（2）由于各板的受力为系统中其他板上的电荷在该板处产生的电场对其板上电荷的作用力，故而通过高斯定理易求得各板处的场强，进而求得各板的受力为20121111202722U S Q F E Q Q d εε==⋅=，方向向下，在原系统中．（1E 求法：1板上侧面不带电，下侧面带电12Q ，正电，即011219USQ Q dε==，由电荷守恒知，27~板带电总量为1Q ，为负电，将27~视为整体，由高斯定理易得到1102Q E ε=） 下面符号i Q 表示第i 块板所带的总电量．2220F E Q ==．（该板显然有20Q =）2456701233332009922722Q Q Q Q U S Q Q F E Q Q d εεε⎛⎫++++==-⋅= ⎪⎝⎭，方向向下．式中00033423109191919US US USQ Q Q d d dεεε=-+=-+=-， 0434451619US Q Q Q d ε=+=， 054556319USQ Q Q d ε=-+=，0656671619USQ Q Q d ε=--=-，0767719USQ Q dε=-=-．同理可得：204232361U SF d ε=，方向向上； 205213722U SF d ε=，方向向下； 206216722U SF d ε=，方向向上； 207281722U SF dε=，方向向上．6．02πP dE rσε=【解析】 【详解】我们用磁场来类比，引入假想的磁荷1m q 、2m q ，且定义123014πm m q q r μ==F r ，且1213014πm m q q r μ==F H r ． 下面我们通过磁偶极子与环电流找到联系：对于一1m ±q 的磁偶极子，磁矩m m q =p l ，而对于一个电流为I 的线圈，磁矩0m I μ'=p S ，当m m '=p p 时，有0m q I μ=l S ．对于此题，我们认为上、下两极板带磁荷面密度为m σ±，则对于S ∆面积中的上、下磁荷，我们看作磁偶极子，则若用环电流代替，有0m Sd I S σμ∆=∆， 所以，0m dI σμ=． 于是，该两带电磁荷板可等效为许多小电流元的叠加，而这样的电流源会在内部抵消，最后只剩下最外层一大圆，且0m dI σμ=． 在P 点处的磁场强度，由于R r ，故可认为由一距P 距离为r 的无限长通电导线所产生，且其中的电流为I ，则002π2πm P d BIH r rσμμ===． 由于电、磁场在引入磁荷后，在形式上完全一样，则02πP dE rσε=7．()21n N n R n r ε⎡⎤-+⎣⎦【解析】 【详解】解法（1）：细圆环中的电动势为R Nεε=．细圆环上ab 段的电阻为劣弧ab R R n=． 优弧()1ab n R R n-'=．如题图1中接上G 后，G 的电阻r 与ab R 并联，然后再与ab R '串联，这时总电阻便为()11ab ab ab n R rR rRR R r R nr R n-'=+=+++．于是，总电流（通过优弧ab R '的电流）为()1111RI n R R NrRnr R nεε==⋅-++． （请读者自行推导此式）则通过G 的电流为()11121RR n n i I I R nr R N n R n r rnε===+⎡⎤-+⎣⎦+． （请读者自行推导此式）解法（2）：如题图2中接上G 后，G 的电阻r 与ab R '并联，然后再与ab R 串联，这时总电阻便为()()211ab ab ab n rR rR R R R nr n R n r R '-=+=++-'+．于是，总电流（通过劣弧ab R 的电流）为()()22111RI n rR R N R nr n R n εε==⋅-++-，则通过G 的电流为()()2211n n i N n R n r ε-=⎡⎤-+⎣⎦8．故对于一微扰位移为d 的粒子，有()20π02Q Q r λλε=->F d，粒子做简谐振动，ω=【解析】 【详解】引理：线电荷密度为()0λλ>的无限长带电线，其在距带电线r 处产生的场强大小为02πE rλε=，方向垂直于带电线向外． 证明略．对于本题所给的模型，建立图示坐标．因粒子在x 轴方向上的受力只与粒子x 方向上的微扰有关，在y 方向上的受力，也只与y 方向上的微扰有关，设粒子在x 方向上有微扰位移x d ，则110021212π2πd 22x i i x Q Q F i i d r x r λλεε∞∞==∆=---⎛⎫⎛⎫+-+ ⎪⎪⎝⎭⎝⎭∑∑． 又由于xd r ，则()()110022111121212π2π22x x x i i d d Q Q F i r i r i r i r λλεε∞∞==⎡⎤⎡⎤∆≈--+⎢⎥⎢⎥--⎛⎫⎛⎫⎣⎦⎣⎦-- ⎪ ⎪⎝⎭⎝⎭∑∑ ()()22221100441ππ2121xxi i Q d Q d r i ri λλεε∞∞===-=---∑∑．又22222222221111111111113523456246⎛⎫⎛⎫+++=-++++++-+++ ⎪ ⎪⎝⎭⎝⎭222222*********111234564123⎛⎫⎛⎫=++++++-+++ ⎪ ⎪⎝⎭⎝⎭223ππ468=⨯=，所以，20π2x x Q F d r λε∆=-． 同理，20π2y y Q F d r λε∆=-． 故对于一微扰位移为d 的粒子，有()20π02Q Q rλλε=->F d ，故粒子做简谐振动，ω=9．（1）πx n k a =，1n =，2，3，… （2）y mk b=，1m =，2，3，…（3）12101239102102πb nm nm -->⨯≈⨯ 【解析】 【详解】（1）要使得电磁波在两端形成驻波，则长度应是半波长的整数倍，相位满足：πx k a n =，即πx n k a=，1n =，2，3，…． （2）要使得电磁波在y 方向上的形式稳定为()()(),sin cos x y E x y A k x k y =，则圆柱的周长应为波长的整数倍，相位满足：2π2πy k b m =，即y mk b=，1m =，2，3，…． （3）由W =1210=， 所以，121239102πm m b <，即12101239102102πb nm nm -->⨯≈⨯10．02U 【解析】 【详解】将过程分为三个阶段，记为α、β、γ． 在第一个14周期内，A U 增加，0A D U U >>，因此二极管2D 截止；又因0DB U ≥，二极管1D 保持导通，等效电路如图1所示，在此阶段2D B A U U U ==，记为α然后A U 开始减小，但AD U 保持不变，最初D U 仍然大于零，因此，2D 依然截止．不过D U 正在逐渐减小，所以1D 截止．由于电容上的电荷无处可走，B U 保持不变，AD U 也保持不变．这个阶段一直持续到0D U =，这一过程等效电路如图2所示，记为β．不过，0D U <是不可能的，所以0D U =直至0A U U =-．这一过程等效电路如答图3所示，记为γ．下面A U 又从0U -开始增加，然后AD U 又保持在0U -不变（再次处于β阶段），而B D U U >停留在02U ，直到D U 升至B U ．当D B U U =时β阶段结束． 而后新的α阶段又开始了．每个周期均按αβγβ---的次序通过各个阶段，但是电路并不是随时间周期变化的，这可以从图4中看出．B U 等比地趋近于02U ，即是说00322B U U U -→，034U ，038U ，0316U ，…．这个电路称为电压倍增器 11．见解析 【解析】 【详解】将多谐振荡器电路等效为图示电路，可见电流只在0102U R C U ---回路中流动．假设系统存在稳态，则电容电量为常数，因而电阻上电流为0，则1G 输入电压等于输出电压，这显然矛盾，因而系统不存在稳态．不失一般性，电容初态电压为0，系统初态010U =，因而0212U V =，电路沿顺时针给电容充电（电阻上的电流I 从下向上为正，电容电量Q 右边记为正）．从0C Q Q CU ==时起，图中i U 的大小开始小于6V ，门反转，将此后直到门再次反转的过程记为过程I ：此时0112U V =，020U =，由于电容上电量不突变，所以，006i Q U V C=-=-． 因而电路沿逆时针给电容反向充电，新充入电量为Q ∆．0120Q Q V IR C +∆-=--，即18QV IR C∆=--． i U 不断上升，到达6C U V =时，10C Q Q Q CU =+∆=-时，门反转，此后进入过程Ⅱ．设过程Ⅰ历时t Ⅰ，将18Q V IR C ∆=--与题目中的RC 电路满足的0QU IR C ∆=+类比，过程Ⅰ满足的018U V =，()12QU t V C∆==，则由电容上的电压随时间变化规律()()01t RC U t U e -=-可得：ln 3t RC =Ⅰ．对于过程Ⅱ，此时010U =，0212U V =， 由于电容上电量不突变，所以，11218i Q U V C=-=． 因而电路沿顺时针给电容正向充电，新冲入电量为Q '．1012Q Q V IR C '+∆-=--，即18Q V IR C'∆=+． i U 不断上升，到达6C U V =时，210C Q Q Q CU Q '=+∆==，门再次反转，此后又进入过程Ⅰ．同理可得：1ln 3t RC =． 过程Ⅰ、Ⅱ循环进行．因此得方波的信号周期为2ln3T RC =．12．（1）4klQ （2）22T ==【解析】 【详解】设由变化的磁场产生的涡旋电场大小为E ，则有22ππBE r rt∆⋅=∆， 得到2rE k =⋅，方向垂直于与O 的连线． 则杆上场强分量为2x k E y =-⋅，2y kE d =-⋅．（1）由于上下电量相反，y 方向的场强为定值，故钉子在y 方向不受力．在x 方向上，其所受电场力（考虑到上下对称）为202d 224l k Q klQF y y l ⎛⎫=⨯-⋅⋅= ⎪⎝⎭⎰．故钉子压力为4klQ．（由于电场和y 坐标成正比，因而也可以使用平均电场计算电场力） （2）设绝缘棒转过一微小角度θ，此时，y 方向的电场力会提供回转力矩．（由于力臂是一阶小量，横坐标变化引起的电场力改变也是一阶小量，忽略二阶以上小量，因而不必计算电场力改变量产生的力矩．由于电场几乎是均匀的，所以正电荷受力的合力力臂为4lθ⋅） 244k l kdlQ M d Q θθ=-⋅⋅⋅⋅=-，而M I θ=，则04kdlQ Iθθ+=．这是简谐方程，故绝缘棒的运动是简谐运动，其周期为22T == 13．（1）12AB R r =，78AC R r =（2）241916C rααω=+ 【解析】 【分析】 【详解】（1）将题图1所示的电阻网络的A 、B 两点接入电路时，可以发现D 、E 等势点，于是DC 、DE 、CE 可去掉．所以，12AB R r =． 将A 、C 接入电路时，将原电路进行等效变化，如图甲所示．11711283122AC R r rr r =+=+． （2）将题图1等效为图所示三端网络．由（1）知1122AB R R r ==，1278AC R R R r +==，解得114R r =，258R r =． 所以图所示虚线框内的等效阻抗为121211121324154496448i Z r r r i L αααω-⎛⎫⎪++=++= ⎪+ ⎪+⎝⎭． 电路的总复导纳()()()()()22222222214964213244964111213216213216Y i C i C Z rr ααααωωαααα⎛⎫+++ ⎪=+=⋅+-⋅⎪++++⎝⎭为使功率因数为1，则复导纳虚部为0．所以，()()2222244964141916213216C r rαααωαωαα+=⋅=⋅+++ 14．(1) 201221211π2I N r I r μΦ= (2) ()2201212522213π2N N r r Ivx r x με=+ (3) 201221π2N N r I Q r R μ= 【解析】 【详解】6.【解析.如图所示，半径为a 的线圈中通以I 的电流，则中轴线上距圆心x 处的磁感强度为()22π003222022d d 4π2aa I I l B B a x a x μμ===++⎰⎰（1）两线圈在同轴共面位置时，1a r =，0x =，当大线圈中通有1I 的电流时，有010112I B N r μ=⋅因为21r r ，所以，212022πB N r Φ=⋅，则201221211π2I N r I r μΦ=（2）当两环中心相距x 时，有()220121211232221π2N N r r I r xμΦ=+，121M I Φ=，12MI Φ=， ()22012122121522213πd d d d d d 2N N r r Ivx x t x t r x μεΦΦ=-=-⋅=+ （3）d d q I t =220122012211ππ1d 1d d d d 0d 22N N r I N N r I Q q I t t t R R t R r r R μμε⎛⎫Φ⎛⎫====-⋅=-=⎪ ⎪⎝⎭⎝⎭⎰⎰⎰⎰15．112310.465AB I R I I I '⨯==Ω'''++【解析】【分析】 【详解】将该网络压扁，如图1所示，除AB ，BC ，CD ，DA 间各边电阻为1Ω外，其余电阻为12Ω现在我们讨论MNPQ 的内部电阻我们将RSTL 的内部电阻等效为图2所示电路，其中a ，b 为待定值，由于RSTL 与MNPQ全等，则有如图所示的等价关系，此等价关系即1212MQ MQ MP MP R R R R =⎧⎪⎨=⎪⎩ 下标的1代表图3，2代表图4（1）MP R 的分析①1MP R ，由对称性，去掉NS ，SL ，LQ 得1112112MP ab a b R ab a b ⎛⎫+⋅ ⎪+⎝⎭=⎛⎫++⎪+⎝⎭ ②2MP R ，由对称性，去掉NQ ，得2MP abR a b=+，从而112112ab ab a b ab a b a b ⎛⎫+⋅ ⎪+⎝⎭=+⎛⎫++⎪+⎝⎭，解得12ab a b =+ （2）MQ R 的分析①1MQ R ．如图5所示，取回路MNPQM ，MRLQM ，RSTLR ，RLTR ，QLTPQ 得()()13412255256452566225643301110222334001110222I I I I I I aI I I I I I aI a I I I bI I a I I I I I -+=⎧⎪⎪---=⎪⎪-++-=⎨⎪----=⎪⎪+----=⎪⎩解得1626364655166721162582482562376252222531332225b ab a b a I I a b a b a I I a b ab a b a I I a b a a I I a b b a I I a ⎧++++⎪=⎪+⎪⎪+++⎪=⎪+⎪⎪⎪++++⎨=⎪+⎪⎪++⎪=⎪+⎪⎪++⎪=⎪+⎩ 故1122316167211626016246460MQ b ab a b I a R b I I I ab a b a++++==++++++ ②2MP R 如图6所示，由回路MNPQM ，MQPM 得()798789300I I I a aI bI aI ⎧--=⎨--=⎩，解得7898322a b I I a a b I I a +⎧=⎪⎪⎨+⎪=⎪⎩， 故()27789344MQ a b a aI R I I I a b+==+++．于是有()166721163 6044162464601 2b ab a b a b a a b a b ab a b aab a b⎧++++⎪+=⎪+⎪++++⎨⎪⎪=⎪+⎩⑧⑨ 令1x a =，由⑨得)11x b=- ⑩由⑩代入⑧化简有2210x x --=．则1x =±又0a >，则0x >，所以，1x =，所以，)1a b ⎧=Ω⎪⎨=Ω⎪⎩于是ABCD 如图7所示，同上步骤可得：1618.93I I ''=，2614.55I I ''=，367.19I I ''=，462.64I I ''=，5610.57I I ''=．则112310.465ABI R I I I '⨯==Ω'''++ 16．(1) 2mA D I = (2) 211116mW U P R == 【解析】 【详解】(1)设每只二极管两端的电压为D U ，通过二极管的电流为D I ，则有1222D D D U U I R R ε⎛⎫=-+ ⎪⎝⎭代入题设数据得()31.50.2510V D D U I =-⨯这是一个在图c 上横轴截距为1.5，纵轴截距为6，斜率为一4的直线方程，绘于c 图可获一直线（称为二极管的负载线）．因D U 、D I 还受二极管D 的伏安线限制，故二极管必然工作在负载线与伏安曲线的交点P 上，如图c 所示．此时二极管两端的电压和电流分别为1V D U =，2mA D I =．(2)电阻1R 上的电压124V D U U ε=-=．其功率211116mW U P R ==．【点睛】对于非线元件的伏安特性曲线，一般无法用函数方式表述，用图解的方式确定其静态工作点应该是不二的选择．物理问题中涉及非线性元件或过程时，通过图解法来确定其工作点，应该是这类问题的通行做法．17．110A I =（方向为11I 的方向），25A I =（方向为21I 的方向）；11200W P =，2600W P =-． 【解析】 【分析】 【详解】这个电路的结构，不能简单地等效为一个串联、并联电路．要计算这种较复杂的电路，可有多种解法．下面提供两种较为常用的方法．方法一：用基尔霍夫定律解．如图乙所示，设各支路的电流分别为1I 、2I 、3I ． 对节点1：1230I I I --+=． ① 对回路1：112212I r I r εε-=-． ② 对回路2：2232I r I R ε+=． ③ 解①②③式求得()2121122110A r R R I rr r R r Rεε+-==++，()121212215A r R R I r r r R r Rεε+-==-++，2112312215A r r I r r r R r Rεε-==++．2I 为负值，说明实际电流方向与所设方向相反．各发电机输出的功率分别为2111111200W P I I r ε=-=，221111600W P I I r ε=-=-．这说明第二台发电机不仅没有输出功率，而且还要吸收第一台发电机的功率． 方法二：利用电源的独立作用原理求解．当只考虑发电机1ε的作用时，原电路等效为如图丙所示的电路，由图可知()2111122182A r R I rr r R r Rε+==++，2111280A RI I r R==+． 当只考虑发电机2ε的作用时，原电路等效为如图丁所示的电路． 由图可知将()1222122175A r R I r r r R r Rε+==++122172A R I I r R==+ 两次求得的电流叠加，可得到两台发电机的实际电流分别为11112827210A I I I =-=-=（方向为11I 的方向），2212280755A I I I =-=-=（方向为21I 的方向）．同理，可解得各发电机的输出功率11200W P =，2600W P =-．【点睛】(1)从本题计算结果看出，将两个电动势和内电阻都不同的电源并联向负载供电未必是好事，这样做会形成两电源并联部分的环路电流，使电源发热．(2)运用基尔霍夫定律解题时，对于一个复杂的含有电源的电路，如果有n 个节点、p 条支路所组成，我们可以对每一支路任意确定它的电流大小和方向，最后解出值为正说明所设电流方向与实际方向一致，所得值为负则说明所设电流方向与实际方向相反．这个电路中共有p 个待求电流强度．在n 个节点中任意选取其中()1n -个节点，根据基尔霍夫第一定律，列出节点电流方程组，再选择()1m p n =--个独立回路，根据基尔霍夫第二定律，列出回路电压方程组，从而得到p 个方程即可求解．(3)处理复杂的电路的方法有很多，各种方法的优点与不足是在比较中领会的，对于某一道具体的试题，该用何种方法，取决于你的经验与临场的判断．事实上，这些方法也不存在优劣之分，只是在具体的过程中可能存在繁易的差别．18．(1) 00.659AC R R = (2)0EG R =【解析】【分析】【详解】(1)先考察B 、D 连线上的节点．由于这些节点都处于从A 到C 途径的中点上，在A 、C 两端接上电源时，这些节点必然处在一等势线上．因此可将这些节点“拆开”，将原网络等效成如图2所示网络．接着可将网络沿A 、C 连线对折叠合，使原来左、右对称的金属丝、节点相互重合，从而又等效成如图3所示网络．注意到图3中A 、C 间网络与J 、I 间网络在形式上的相似性，而图3且后者恰好是前者在线度上缩小12的结构，因此有 12JI AC R R =． 将折叠后与AE 同长的双金属丝电阻记为1R ，对应地与EH 同长的双金属丝电阻记为2R ，不难算得到1001144R R R =，208R R =． 再将如图3所示网络“量化”成如图4所示网络，其中虚线框内的上、下两端间电阻为1201224R R R R R R '=⋅=+ 于是有2121222122AC AC AC R R R R R R R R ⎛⎫'+ ⎪⎝⎭=+'++解之，得00110.6592AC R R R =-=．(2)能否采用1．中所取的递归方法来求解EG R 呢？由于此时不存在结构相似的内层网络，故不能采用这一方法．解决的方法当然还是有的，这就是利用1．的结果进行简化．据对称性，将原网络中AD 边的中点、BC 边的中点处节点“拆开”，等效成如图5所示网络．此网络中通过E 、G 两端与外正方形连接的内无限小网络与原网络结构相同，只是线度缩短为倍，小网络E 、G 之间的等效电阻便为原网络A 、C 间等效电阻AC R倍．据此，可将图5网络“量化”成图6所示的网络，有101BC AC R R R -⎛⎫=+ ⎪ ⎪⎝⎭ 将1．中算得的AC R 代入后，可得0EG R =【点睛】自相似的结构在物理模型中有很多，但大体都是以无穷、平衡为基础的简化处理．同样，这类试题目前在各类书籍上都有成熟的处理方式，在测试中单独成题的可能性并不太大，但将其融于系统中，考查你对这类问题的处理能力却是极有可能的．19．(1) 12R (2) 38R 【解析】【分析】【详解】(1)电流i 从A 点流入，B 点流出，鉴于网络的对称性，图1中12i i =，34i i =，560i i ==，将D 点断开，断开后的两个小四面体框架的等效电阻同为12R ，电路简化为图2；再由对称性知，E 、F 等势，G 、H 等势，于是网络简化为图3；再由对称性，可在C 点将电阻断开，简化成图4的网络，由串、并关系可得(2)电流从C 点流入，从D 点流出，网络相对于ABD 平面具有对称性，与AB 棱平行的小正方形四个顶点等势，故此正方形的四条边都可拆去，余下部分相对ABD 平面上下对称，可上下合并，等效成如图5所示的网络，而图5的立体网络又可改画成如图6所示的平面网络，网络对C 、D 左右对称，故可折叠成如图7所示的网络，由此可得38CD R R =．。

高考物理电磁学知识点之电磁感应真题汇编及答案解析一、选择题1．穿过一个单匝闭合线圈的磁通量始终为每秒均匀增加2Wb，则（）A．线圈中感应电动势每秒增加2VB．线圈中感应电动势始终为2VC．线圈中感应电动势始终为一个确定值，但由于线圈有电阻，电动势小于2VD．线圈中感应电动势每秒减少2V2．两条平行虚线间存在一匀强磁场，磁感应强度方向与纸面垂直。

边长为0.1m、总电阻为0.005Ω的正方形导线框abcd位于纸面内，cd边与磁场边界平行，如图甲所示。

已知导线框向右做匀速直线运动，cd边于t=0时刻进入磁场。

导线框中感应电动势随时间变化的图线如图乙所示（规定感应电流的方向abcda为正方向）。

下列说法正确的是（）A．磁感应强度的方向垂直纸面向内B．磁感应强度的大小为0.5TC．导线框运动速度的大小为0.05m/sD．在t=0.4s至t=0.6s这段时间内，导线框所受的安培力大小为0.04N3．下列关于教材中四幅插图的说法正确的是（）A．图甲是通电导线周围存在磁场的实验。

这一现象是物理学家法拉第通过实验首先发现B．图乙是真空冶炼炉，当炉外线圈通入高频交流电时，线圈产生大量热量，从而冶炼金属C．图丙是李辉用多用电表的欧姆挡测量变压器线圈的电阻刘伟手握线圈裸露的两端协助测量，李辉把表笔与线圈断开瞬间，刘伟觉得有电击说明欧姆挡内电池电动势很高D．图丁是微安表的表头，在运输时要把两个接线柱连在一起，这是为了保护电表指针，利用了电磁阻尼原理4．如图所示，水平绝缘的桌面上放置一个金属环，现有一个竖直的条形磁铁从圆环左上方沿水平方向快速移动经过正上方到达右上方，在此过程中（）A．圆环一定向右运动B．圆环中的感应电流方向不变C．圆环受到的摩擦力方向不变D．圆环对桌面的压力先减小后增大5．如图所示，abcd是边长为L，每边电阻均相同的正方形导体框，今维持线框以恒定的速度v沿x轴运动，并穿过倾角为45°的三角形匀强磁场区域，磁场的磁感应强度为B，方向垂直纸面向里。

高考物理新电磁学知识点之磁场真题汇编含答案一、选择题1．航母上飞机弹射起飞是利用电磁驱动来实现的。

电磁驱动原理如图所示,在固定线圈左右两侧对称位置放置两个闭合金属圆环，铝环和铜环的形状、大小相同，已知铜的电阻率较小,则合上开关S的瞬间（）A．两个金属环都向左运动B．两个金属环都向右运动C．从左侧向右看，铝环中感应电流沿顺时针方向D．铜环受到的安培力小于铝环受到的安培力2．如图所示，两相邻且范围足够大的匀强磁场区域Ⅰ和Ⅱ的磁感应强度方向平行、大小分别为B和2B。

一带正电粒子（不计重力）以速度v从磁场分界线MN上某处射入磁场区域Ⅰ，其速度方向与磁场方向垂直且与分界线MN成60 角，经过t1时间后粒子进入到磁场区域Ⅱ，又经过t2时间后回到区域Ⅰ，设粒子在区域Ⅰ、Ⅱ中的角速度分别为ω1、ω2，则()A．ω1∶ω2＝1∶1B．ω1∶ω2＝2∶1C．t1∶t2＝1∶1D．t1∶t2＝2∶13．在探索微观世界中，同位素的发现与证明无疑具有里程碑式的意义。

质谱仪的发现对证明同位素的存在功不可没，1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖。

若速度相同的一束粒子由左端射入质谱仪后的运动轨迹如图所示，不计粒子重力，则下列说法中正确的是（）A．该束粒子带负电B．速度选择器的P1极板带负电C．在B2磁场中运动半径越大的粒子，质量越大D ．在B 2磁场中运动半径越大的粒子，比荷q m 越小 4．如图所示，ABC 为与匀强磁场垂直的边长为a 的等边三角形，比荷为e m 的电子以速度v 0从A 点沿AB 边射出（电子重力不计），欲使电子能经过AC 边，磁感应强度B 的取值为A ．B ＜03mv ae B ．B ＜02mv aeC ．B ＞03mv aeD ．B ＞02mv ae5．如图所示，空间某处存在竖直向下的匀强电场和垂直纸面向里的匀强磁场，一个带负电的金属小球从M 点水平射入场区，经一段时间运动到M 点的右下方N 点，关于小球由M 到N 的运动，下列说法正确的是（ ）A ．小球可能做匀变速运动B ．小球一定做变加速运动C ．小球动量可能不变D ．小球机械能守恒6．如图所示，某种带电粒子由静止开始经电压为U 1的电场加速后，射人水平放置，电势差为U 2的两导体板间的匀强电场中，带电粒子沿平行于两板方向从两板正中间射入，穿过两板后又垂直于磁场方向射入边界线竖直的匀强磁场中，则粒子入磁场和射出磁场的M 、N 两点间的距离d 随着U 1和U 2的变化情况为（不计重力，不考虑边缘效应）（ ）A ．d 随U 1变化，d 与U 2无关B ．d 与U 1无关，d 随U 2变化C ．d 随U 1变化，d 随U 2变化D ．d 与U 1无关，d 与U 2无关7．某小组重做奥斯特实验，在一根南北方向放置的直导线的正下方放置一小磁针，如图所示，给导线通入恒定电流，小磁针再次静止时偏转了30°，已知该处地磁场水平分量55.010B T -=⨯，通电直导线在该处产生的磁感应强度大小为（ ）A ．52.910T -⨯B ．57.110T -⨯C ．58.710T -⨯D ．41.010T -⨯ 8．一回旋加速器当外加磁场一定时，可把质子加速到v ，它能把氚核加速到的速度为 （ ）A ．vB ．2vC ．3vD ．23v 9．关于垂直于磁场方向的通电直导线所受磁场作用力的方向，正确的说法是（ ） A ．跟磁场方向垂直，跟电流方向平行B ．跟电流方向垂直，跟磁场方向平行C ．既跟磁场方向垂直，又跟电流方向垂直D ．既不跟磁场方向垂直，也不跟电流方向垂直10．如图所示，矩形线圈abcd 在匀强磁场中可以分别绕垂直于磁场方向的轴P 1和P 2以相同的角速度匀速转动，当线圈平面转到与磁场方向平行时( )A ．线圈绕P 1转动时的电流等于绕P 2转动时的电流B ．线圈绕P 1转动时的电动势小于绕P 2转动时的电动势C ．线圈绕P 1和P 2转动时电流的方向相同，都是a →b →c →dD ．线圈绕P 1转动时dc 边受到的安培力大于绕P 2转动时dc 边受到的安培力11．电荷在磁场中运动时受到洛仑兹力的方向如图所示，其中正确的是（ ） A ． B ． C ． D ． 12．如图所示，有abcd 四个离子，它们带等量的同种电荷，质量不等．有m a ＝m b ＜m c ＝m d ，以不等的速度v a ＜v b ＝v c ＜v d 进入速度选择器后有两种离子从速度选择器中射出，进入B 2磁场，由此可判定( )A ．射向P 1的是a 离子B ．射向P 2的是b 离子C ．射到A 1的是c 离子D ．射到A 2的是d 离子13．无线充电技术已经被应用于多个领域，其充电线圈内磁场与轴线平行，如图甲所示；磁感应强度随时间按正弦规律变化，如图乙所示。

高考物理最新电磁学知识点之磁场全集汇编含答案解析一、选择题1．如图所示为质谱仪的原理图，一束粒子流由左端平行于P 1、P 2射入，粒子沿直线通过速度选择器，已知速度选择器的电场强度为E ，磁感应强度为B 1.粒子由狭缝S 0进入匀强磁场B 2后分为三束，它们的轨道半径关系为132r r r =<，不计重力及粒子间的相互作用力，则下列说法中正确的是（ ）A ．P 1极板带负电B ．能通过狭缝S 0的带电粒子的速率等于1B EC ．三束粒子在磁场B 2中运动的时间相等D ．粒子1的比荷11q m 大于粒子2的比荷22q m 2．对磁感应强度的理解，下列说法错误的是（ ） A ．磁感应强度与磁场力F 成正比，与检验电流元IL 成反比 B ．磁感应强度的方向也就是该处磁感线的切线方向C ．磁场中各点磁感应强度的大小和方向是一定的，与检验电流I 无关D ．磁感线越密，磁感应强度越大3．如图所示，一块长方体金属板材料置于方向垂直于其前表面向里的匀强磁场中，磁感应强度大小为B 。

当通以从左到右的恒定电流I 时，金属材料上、下表面电势分别为φ1、φ2。

该金属材料垂直电流方向的截面为长方形，其与磁场垂直的边长为a 、与磁场平行的边长为b ，金属材料单位体积内自由电子数为n ，元电荷为e 。

那么A ．12IBenb ϕϕ-= B ．12IB enb ϕϕ-=- C ．12IB enaϕϕ-=D ．12IB enaϕϕ-=-4．如图，一带电粒子在正交的匀强电场和匀强磁场中做匀速圆周运动。

已知电场强度为E ，方向竖直向下，磁感应强度为B ，方向垂直于纸面向外。

粒子圆周运动的半径为R ，若小球运动到最高点A时沿水平方向分裂成两个粒子1和2，假设粒子质量和电量都恰好均分，粒子1在原运行方向上做匀速圆周运动，半径变为3R，下列说法正确的是（）A．粒子带正电荷B．粒子分裂前运动速度大小为REB gC．粒子2也做匀速圆周运动，且沿逆时针方向D．粒子2做匀速圆周运动的半径也为3R5．下列关于教材中四幅插图的说法正确的是（）A．图甲是通电导线周围存在磁场的实验。

(word完整版)高中物理电磁感应习题及答案解析(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(word完整版)高中物理电磁感应习题及答案解析(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(word完整版)高中物理电磁感应习题及答案解析(word版可编辑修改)的全部内容。

1．图12—2，甲、乙两图为与匀强磁场垂直放置的两个金属框架，乙图除了一个电阻为零、自感系数为L 的线圈外,其他部分与甲图都相同，导体AB 以相同的加速度向右做匀加速直线运动。

若位移相同，则（ ）A ．甲图中外力做功多B ．两图中外力做功相同C ．乙图中外力做功多D ．无法判断2．图12-1，平行导轨间距为d ，一端跨接一电阻为R ，匀强磁场磁感强度为B ,方向与导轨所在平面垂直。

一根足够长的金属棒与导轨成θ角放置，金属棒与导轨的电阻不计。

当金属棒沿垂直于棒的方向以速度v 滑行时，通过电阻R 的电流强度是（ ）A ．Bdv RB ．sin Bdv RθC ．cos Bdv Rθ D ．sin Bdv R θ3．图12-3,在光滑水平面上的直线MN 左侧有垂直于纸面向里的匀强磁场,右侧是无磁场空间。

将两个大小相同的铜质矩形闭合线框由图示位置以同样的速度v 向右完全拉出匀强磁场。

已知制作这两只线框的铜质导线的横截面积之比是1：2.则拉出过程中下列说法中正确的是（ ）A ．所用拉力大小之比为2：1B ．通过导线某一横截面的电荷量之比是1:1C ．拉力做功之比是1:4D ．线框中产生的电热之比为1：24． 图12—5，条形磁铁用细线悬挂在O 点。

2020年高考物理《电磁学中的功能关系》专题训练一、单项选择题1.如图所示，在绝缘水平面上方存在着足够大的水平向右的匀强电场，带正电的小金属块以一定的初速度从A 点开始沿水平面向左做直线运动，经L 长度到达B 点，速度变为零．在此过程中，金属块损失的动能有23转化为电势能．金属块继续运动到某点C (图中未标出)时的动能和A 点时的动能相同，则金属块从A 开始运动到C 的整个过程中经过的总路程为A ．1.5LB ．2LC ．3LD ．4L【解析】根据题述，小金属块从A 运动到B ，克服摩擦力做功W f ＝13E k ＝fL ，克服电场力做功W E ＝23E k ＝qEL .设小金属块从B 运动到C 经过的路程为s ，由动能定理qEs －fs ＝E k ，解得s ＝3L .金属块从A 开始运动到C 的整个过程中经过的总路程为L ＋s ＝4L ，选项D 正确．【答案】D2.如图所示，质量为m 的金属线框A 静置于光滑水平面上，通过细绳跨过定滑轮与质量为m 的物体B 相连，图中虚线内为一水平匀强磁场，d 表示A 与磁场左边界的距离，不计滑轮摩擦及空气阻力，设B 下降h (h ＞d )高度时的速度为v ，则以下关系中能够成立的是( )A ．v 2＝ghB ．v 2＝2ghC ．A 产生的热量Q ＝mgh －mv 2D ．A 产生的热量Q ＝mgh －12mv 2 【解析】由于线框在磁场内的运动情况未知，故不能判断v 与h 的具体关系，故A 、B 错误；根据题意，线框A 进入磁场的过程克服安培力做功，线框A 产生的热量为Q ，对A 、B 构成的系统，在B 下降h 高度的过程中，据能量转化与守恒定律有mgh ＝12×2mv 2＋Q ，Q ＝mgh －mv 2，故选项C 正确．【答案】C3.如图所示，上下开口、内壁光滑的铜管P 和塑料管Q 竖直放置，小磁块先后在两管中从相同高度处由静止释放，并落至底部，则小磁块( )A ．在P 和Q 中都做自由落体运动B ．在两个下落过程中的机械能都守恒C ．在P 中的下落时间比在Q 中的长D ．落至底部时在P 中的速度比在Q 中的大【解析】由于电磁感应，小磁块在铜管P 中还受到向上的磁场力，而在塑料管中只受到重力，即只在Q 中做自由落体运动，机械能守恒，故A 、B 错误；而在P 中加速度较小，下落时间较长，落至底部的速度较小，故C 正确，D 错误．【答案】C4.如图甲，倾角为θ的光滑绝缘斜面，底端固定一带电量为Q 的正点电荷．将一带正电小物块(可视为质点)从斜面上A 点由静止释放，小物块沿斜面向上滑动至最高点B 处，此过程中小物块的动能和重力势能随位移的变化图象如图乙(E 1和x 1为已知量)．已知重力加速度为g ，静电力常量为k ，由图象可求出( )A ．小物块的带电量B ．A 、B 间的电势差C ．小物块的质量D ．小物块速度最大时到斜面底端的距离【解析】小物块在B 点时E 1＝mgx 1sin θ，解得m ＝E 1gx 1sin θ，选项C 正确；小物块由A到B 的过程中，据动能定理，可得qU AB ＋W G ＝0，由功能关系知W G ＝－E 1，故有qU AB ＝E 1，故只能求得小物块由A 到B 的过程中电场力所做的功(或小物块电势能的减少量)，无法求出小物块的带电量及A 、B 两点间的电势差，选项A 、B 错误；小物块向上运动的过程中，开始时库仑力大于重力沿斜面向下的分力，小物块向上加速，随着向上运动，库仑力减小，当库仑力等于重力沿斜面向下的分力时，小物块的速度达到最大，此时有mg sin θ＝k Qq r2，因q 未知，故无法求得小物块到斜面底端的距离r ，选项D 错误． 【答案】C5.质量为m 、长度为l 的金属棒MN 两端由绝缘且等长轻质细线水平悬挂，处于竖直向下的匀强磁场中，磁感应强度大小为B .开始时细线竖直，当金属棒中通以恒定电流后，金属棒从最低点向右开始摆动，若已知细线与竖直方向的最大夹角为60°，如图所示，则棒中电流( )A.方向由M 向N ，大小为3mg 3Bl B.方向由N 向M ，大小为3mg 3Bl C.方向由M 向N ，大小为3mg Bl D.方向由N 向M ，大小为3mg Bl【答案】B【解析】平衡时两悬线与竖直方向夹角均为θ，故导线受到向右的安培力，根据左手定则，可判断金属棒中的电流方向由N 指向M ；金属棒MN 所受安培力的方向垂直于MN 和磁场方向向右，由于棒向上运动的过程中重力和安培力做功，细线的拉力不做功，设细线的长度为x ，由功能关系得：BIl ·x sin θ－mg (x －x ·cos θ)＝0解方程得：I ＝3mg 3Bl . 6.如图甲所示，左侧接有定值电阻R ＝2 Ω的水平粗糙导轨处于垂直纸面向外的匀强磁场中，磁感应强度B ＝1 T ，导轨间距L ＝1 m.一质量m ＝2 kg ，阻值r ＝2 Ω的金属棒在水平拉力F 作用下由静止开始从CD 处沿导轨向右加速运动，金属棒的v －x 图象如图乙所示，若金属棒与导轨间动摩擦因数μ＝0.25，则从起点发生x ＝1 m 位移的过程中(g ＝10 m/s 2)( )A.金属棒克服安培力做的功W 1＝0.5 JB.金属棒克服摩擦力做的功W 2＝4 JC.整个系统产生的总热量Q ＝4.25 JD.拉力做的功W ＝9.25 J【答案】D【解析】金属棒与导轨间因摩擦产生的热量等于克服摩擦力做的功，为：Q 1＝μmg ·x ＝0.25×2×10×1 J＝5 J ，故B 、C 错误；由v －x 图象得：v ＝2x ，金属棒所受的安培力F ＝B 2L 2v R ＋r ＝B 2L 2·2x R ＋r，代入得：F ＝0.5x ，则知F 与x 是线性关系.当x ＝0时，安培力F 0＝0；当x ＝1 m 时，安培力F 1＝0.5 N ，则从起点发生x ＝1 m 位移的过程中，安培力做功为W 安＝－F x ＝－F 0＋F 12x ＝－0＋0.52×1 J＝－0.25 J ，A 错误；根据动能定理得：W －μmgx ＋W 安＝12mv 2，其中v ＝2 m/s ，μ＝0.25，m ＝2 kg ，代入解得，拉力做的功W ＝9.25 J ，故D 正确.7.质量为m 的带正电小球由空中某点自由下落，下落高度h 后在整个空间加上竖直向上的匀强电场，再经过相同时间小球又回到原出发点，不计空气阻力，且整个运动过程中小球从未落地，重力加速度为g ，则( )A ．从加电场开始到小球返回原出发点的过程中，小球电势能减少了mghB ．从加电场开始到小球下落最低点的过程中，小球动能减少了mghC ．从开始下落到小球运动至最低点的过程中，小球重力势能减少了53mgh D ．小球返回原出发点时的速度大小为7gh【解析】小球先做自由落体运动，然后受电场力和重力向下做匀减速到速度为零，再向上做匀加速回到出发点．设小球下落高度h 用了t 秒，加上电场后小球的加速度大小为a ，加上电场时速度为v ，规定向下为正方向，由运动学公式：12gt 2＋gt ×t －12at 2＝0，解得a ＝3g ，由v 2＝2gh ，解得v ＝2gh ；根据牛顿第二定律，F 电－mg ＝ma ，得F 电＝4mg ，因此，从加电场开始到小球返回原出发点的过程中，电场力做功为W 电＝F 电h ＝4mgh ，根据电场力做功和电势能的关系，可知小球的电势能的减少量为ΔE p ＝4mgh ，故选项A 错误；从加电场开始到小球下落最低点的过程中，小球动能减少量为ΔE k ＝12mv 2－0＝mgh ，选项B 正确；从加电场开始到小球下落最低点的过程中，设下落高度为h ′，由运动学公式：v 2＝2ah ′，解得h ′＝h3，从开始下落到小球运动至最低点的过程中，重力做功为W G ＝mg (h ＋h ′)＝43mgh ，根据重力做功和重力势能的关系，可知小球的重力势能的减少量为ΔE p ′＝43mgh ，选项C 错误；设小球返回到原出发点时的速度为v ′，由动能定理，可得12mv ′2＝3mg (h ＋h ′)，解得v ′＝8gh ，选项D 错误． 【答案】B8.如图所示，平行金属导轨与水平面成θ角，导轨与定值电阻R 1和R 2相连，匀强磁场垂直穿过导轨平面.有一导体棒ab ，质量为m ，导体棒的电阻R 0与固定电阻R 1和R 2的阻值均相等，与导轨之间的动摩擦因数为μ，导体棒ab 沿导轨向上滑动，当上滑的速度为v 时，受到安培力的大小为F .此时( )A.电阻R 1消耗的热功率为Fv 3B.电阻R 0消耗的热功率为Fv6C.整个装置消耗的热功率为μmgv sin θD.整个装置消耗的机械功率为(F ＋μmg cos θ)v【答案】D【解析】设ab 长度为L ，磁感应强度为B ，电阻R 0＝R 1＝R 2＝R .电路中感应电动势E ＝BLv ， ab 中感应电流为：I ＝E R ＋12R ＝2BLv 3R ， ab 所受安培力为：F ＝BIL ＝2B 2L 2v 3R① 电阻R 1消耗的热功率为：P 1＝(12I )2R ＝B 2L 2v 29R ②由①②得：P 1＝16Fv ，电阻R 0和R 1阻值相等，P 0＝I 2R ＝23Fv ，故A 、B 错误；整个装置因摩擦而消耗的热功率为：P f ＝F f v ＝μmg cos θ·v ＝μmgv cos θ，故C 错误；整个装置消耗的机械功率为：P 3＝Fv ＋P f ＝(F ＋μmg cos θ)v ，故D 正确.二 不定项选择题1.(多选)如图所示，竖直平面内有一足够长的宽度为L 的金属导轨，质量为m 的金属导体棒ab 可在导轨上无摩擦地上下滑动，且导体棒ab 与金属导轨接触良好，ab 电阻为R ，其他电阻不计．导体棒ab 由静止开始下落，过一段时间后闭合开关S ，发现导体棒ab 立刻做变速运动，则在以后导体棒ab 的运动过程中，下列说法中正确的是( )A ．导体棒ab 做变速运动期间加速度一定减小B ．单位时间内克服安培力做的功全部转化为电能，电能又转化为内能C ．导体棒减少的机械能转化为闭合电路中的电能和电热之和，符合能的转化和守恒定律D ．导体棒ab 最后做匀速运动时，速度大小为v ＝mgR B 2L 2【解析】导体棒由静止下落，在竖直向下的重力作用下做加速运动．开关闭合时，由右手定则判定，导体中产生的电流方向为逆时针方向，再由左手定则，可判定导体棒受到的安培力方向向上，F ＝BIL ＝B BLv RL ，导体棒受到的重力和安培力的合力变小，加速度变小，物体做加速度越来越小的运动，A 正确；最后合力为零，加速度为零，做匀速运动．由F －mg ＝0得，B BLv R L ＝mg ，v ＝mgR B 2L2，D 正确；导体棒克服安培力做功，减少的机械能转化为电能，由于电流的热效应，电能又转化为内能，B 正确．【答案】ABD2.如图所示，两平行金属板水平放置，板长为L ，板间距离为d ，板间电压为U ，一不计重力、电荷量为q 的带电粒子以初速度v 0沿两板的中线射入，经过t 时间后恰好沿下板的边缘飞出，则( )A ．在前t 2时间内，电场力对粒子做的功为14UqB ．在后t 2时间内，电场力对粒子做的功为38UqC ．在粒子下落的前d 4和后d 4过程中，电场力做功之比为1∶1 D ．在粒子下落的前d 4和后d 4过程中，电场力做功之比为1∶2 【解析】粒子在两平行金属板间做类平抛运动，水平方向做匀速直线运动，竖直方向做初速度为零的匀加速直线运动，在前后两个t2的时间内沿电场线方向的位移之比为1∶3，则在前t 2时间内，电场力对粒子做的功为18Uq ，在后t 2时间内，电场力对粒子做的功为38Uq ，选项A 错，B 对；由W ＝Eq ·s 知在粒子下落的前d 4和后d4过程中，电场力做功之比为1∶1，选项C 对，D 错．【答案】BC3.如图所示，绝缘粗糙斜面体固定在水平地面上，斜面所在空间存在平行于斜面向上的匀强电场E ，轻弹簧一端固定在斜面顶端，另一端拴接一不计质量的绝缘薄板.一带正电的小滑块，从斜面上的P 点处由静止释放后，沿斜面向上运动，并能压缩弹簧至R 点(图中未标出)，然后返回，则( )A.滑块从P 点运动到R 点的过程中，其机械能增量等于电场力与弹簧弹力做功之和B.滑块从P 点运动到R 点的过程中，电势能的减小量大于重力势能和弹簧弹性势能的增加量之和C.滑块返回时能到达的最低位置在P 点的上方D.滑块最终停下时，克服摩擦力所做的功等于电势能的减小量与重力势能增加量之差【答案】BC【解析】在小滑块开始运动到到达R 点的过程中，电场力做的功转化为小滑块的重力势能、弹簧的弹性势能以及内能.滑块从P 点运动到R 点的过程中，其机械能增量等于电场力与弹簧弹力做功、摩擦力做功之和.故A 错误；电场力做的功转化为小滑块的重力势能、弹簧的弹性势能以及内能，所以电势能的减小量大于重力势能和弹簧弹性势能的增加量之和.故B 正确；小滑块运动的过程中，由于摩擦力做功，小滑块的机械能与电势能的和减小，所以滑块返回时能到达的最低位置在P点的上方，不能再返回P点.故C正确；滑块运动的过程中，由于摩擦力做功，小滑块的机械能与电势能的和逐渐减小，所以滑块最终停下时，克服摩擦力所做的功等于电势能的减小量与重力势能增加量、弹性势能增加量之差.故D错误.4.如图所示，光滑绝缘细管与水平面成30°角，在管的上方P点固定一个点电荷＋Q，P 点与细管在同一竖直平面内，管的顶端A与P点连线水平．电荷量为－q的小球(小球直径略小于细管内径)从管中A处由静止开始沿管向下运动，在A处时小球的加速度为a.图中PB⊥AC，B是AC的中点，不考虑小球电荷量对电场的影响．则在＋Q形成的电场中( )A．A点的电势高于B点的电势B．B点的电场强度大小是A点的4倍C．小球从A到C的过程中电势能先减小后增大D．小球运动到C处的加速度为g－a【解析】在正电荷产生的电场中，离电荷越近电势越高，因此B点的电势高于A点的电势，A错误；根据点电荷电场强度的决定式得E A＝kQPA2，E B＝kQPB2，由几何关系得PA＝2PB，解得E B＝4E A，B正确；小球从A到C的过程中，电场力先做正功后做负功，因此电势能先减小后增大，C正确；小球在A、C两处受到的电场力大小相等，对小球受力分析，在A处，由牛顿第二定律得mg sin 30°＋F cos 30°＝ma，在C处，由牛顿第二定律得mg sin 30°－F cos 30°＝ma C，解得a C＝g－a，D正确．【答案】BCD5.如图所示，匀强电场的电场强度为E，方向水平向左，一带电量为＋q，质量为m的物体放在光滑水平面上，在恒力F作用下由静止开始从O点向右做匀加速直线运动，经时间t力F做功60 J，此后撤去力F，物体又经过相同的时间t回到出发点O，设O点的电势能为零，则下列说法正确的是( )A.物体回到出发点的速度与撤去力F时的速度大小之比为2∶1B.恒力F ＝4qEC.撤去力F 时，物体的电势能为45 JD.在撤去力F 之前的任一时刻，动能与电势能之比均为1∶3【答案】ACD【解析】在恒力F 作用下的加速度大小为a 1，撤去恒力F 后的加速度大小为a 2，匀加速运动的位移大小x 1＝12a 1t 2，撤去拉力后的位移大小x 2＝a 1t ·t －12a 2t 2 根据x 1＝－x 2得a 2＝3a 1.根据牛顿第二定律得，a 1＝F －F 电m ，a 2＝F 电m ，联立解得F 电＝qE ＝34F .故B 错误. 6.如图所示，绝缘杆两端固定带电小球A 和B ，轻杆处于水平向右的匀强电场中，不考虑两球之间的相互作用，初始时杆与电场线垂直．现将杆右移，同时顺时针转过90°，发现A 、B 两球电势能之和不变．根据如图给出的位置关系，下列说法正确的是( )A ．A 一定带正电，B 一定带负电B ．A 、B 两球所带电量的绝对值之比q A ∶q B ＝1∶2C ．A 球电势能一定增加D ．电场力对A 球和B 球做功的绝对值相等【解析】电场力做功与路径无关，两个小球在杆右移后两球所在位置处电势都降低，而两个小球组成的系统的电势能之和不变，那么电场力对其中一个做正功，对另一个一定做负功，做功的绝对值相同，两个小球一定带异种电荷，但不能准确判断每一个小球所带电荷的电性，A 、C 错误，D 正确；由电势能变化之和为零得E qB L ＝E qA ·2L ，即|q A |∶|q B |＝1∶2，B 正确．【答案】BD7.如图所示，相距为L 的两条足够长的平行金属导轨，与水平面的夹角为θ，导轨上固定有质量为m ，电阻为R 的两根相同的导体棒，导体棒MN 上方轨道粗糙，下方光滑，整个空间存在垂直于导轨平面向下的匀强磁场，磁感应强度为B .将两根导体棒同时释放后，观察到导体棒MN 下滑而EF 保持静止，当MN 下滑速度最大时，EF 与轨道间的摩擦力刚好到达最大静摩擦力，下列叙述正确的是( )A ．导体棒MN 的最大速度为2mgR sin θB 2L2 B ．导体棒EF 与轨道之间的最大静摩擦力为mg sin θC ．导体棒MN 受到的最大安培力为mg sin θD ．导体棒MN 所受重力的最大功率为m 2g 2R sin 2θB 2L 3【解析】当导体棒MN 匀速运动时速度最大，由平衡条件得mg sin θ＝B 2L 2v 2R，则得最大速度为v ＝2mgR sin θB 2L2，选项A 正确；由题意知，当MN 下滑的速度最大时，EF 与轨道间的摩擦力刚好达到最大静摩擦力，两棒所受的安培力大小相等，方向相反，则对EF 棒，有mg sin θ＋B 2L 2v 2R＝f m ，则可得最大静摩擦力为f m ＝2mg sin θ，选项B 错误；导体棒MN 匀速运动时速度最大，感应电流最大，所受的安培力也最大，由平衡条件可知，最大安培力为F m ＝mg sin θ，选项C 正确；导体棒MN 所受重力的最大功率为P m ＝mg sin θ·v ＝2m 2g 2R sin 2 θB 2L2，选项D 错误． 【答案】AC8.如图所示，物体A 和带负电的物体B 用跨过定滑轮的绝缘轻绳连接，A 、B 的质量分别是m 和2m ，劲度系数为k 的轻质弹簧一端固定在水平面上.另一端与物体A 相连，倾角为θ的斜面处于沿斜面向上的匀强电场中，整个系统不计一切摩擦.开始时，物体B 在一沿斜面向上的外力F ＝3mg sin θ的作用下保持静止且轻绳恰好伸直，然后撤去外力F ，直到物体B 获得最大速度，且弹簧未超过弹性限度，则在此过程中( )A.对于物体A 、B 、弹簧和地球组成的系统，电场力做功等于该系统增加的机械能B.物体A 、弹簧和地球所组成的系统机械能增加量等于物体B 电势能的减少量C.B 的速度最大时，弹簧的伸长量为3mg sin θRD.撤去外力F 的瞬间，物体B 的加速度为3g sin θ2【答案】AC【解析】根据能量守恒可知，物体A 、弹簧和地球所组成的系统机械能增加量等于物体B 电势能的减少量和B 物体机械能的减小量之和，故B 错误；当B 所受的合力为零时，B 的速度最大，由：kx ＝F 电＋2mg sin θ 解得弹簧的伸长量为：x ＝3mg sin θk，故C 正确；开始时，外力F 作用在B 上，B 处于静止状态，对B 分析可知：F －2mg sin θ－F 电＝0解得：F 电＝mg sin θ.当撤去外力瞬间，对AB 整体分析，整体受到的合力为：F 合＝F 电＋2mg sin θ＝3mg sin θ由F 合＝3ma 可得 a ＝g sin θ，故D 错误.三 非选择题1.如图所示，倾角为60°的倾斜平行轨道与竖直面内的平行圆形轨道平滑对接，轨道之间距离为L ，圆形轨道的半径为r .在倾斜平行轨道的上部有磁感应强度为B 的垂直于轨道向上的匀强磁场，磁场区域足够大，圆形轨道末端接有一电阻值为R 的定值电阻．质量为m 的金属棒从距轨道最低端C 点高度为H 处由静止释放，运动到最低点C 时对轨道的压力为7mg ，不计摩擦和导轨、金属棒的电阻，求：(1)金属棒通过轨道最低端C 点的速度大小； (2)金属棒中产生的感应电动势的最大值；(3)金属棒整个下滑过程中定值电阻R 上产生的热量； (4)金属棒通过圆形轨道最高点D 时对轨道的压力的大小．【解析】(1)设金属棒通过轨道最低端C 点的速度为v C ，轨道对金属棒的支持力为F C ，金属棒对轨道的压力为F C ′，由牛顿第二定律可知F C －mg ＝mv 2Cr而F C ＝F C ′＝7mg解得v C ＝6gr .(2)由于磁场区域足够大，金属棒在重力和安培力作用下加速运动，当安培力等于重力沿倾斜轨道向下的分力时，速度最大，此时金属棒中产生的感应电动势最大．由mg sin 60°＝BILI ＝E R解得感应电动势的最大值E ＝3mgR2BL. ⑥(1分) (3)由能量守恒定律，在金属棒的整个下滑过程中电阻器R 上产生的热量等于金属棒损失的机械能，所以Q ＝mgH －12mv 2C联立③⑦得Q ＝mg (H －3r )(4)金属棒由C 点运动到D 点，根据机械能守恒，有 12mv 2C ＝12mv 2D ＋mg ·2r金属棒通过圆形轨道最高点D 时，设轨道对金属棒竖直向下的压力为F D ，由牛顿第二定律有F D ＋mg ＝mv 2Dr联立解得F D ＝mg由牛顿第三定律可知金属棒通过圆形轨道最高点D 时对轨道的压力为mg . 【答案】(1)6gr (2)3mgR2BL(3)mg (H －3r )(4)mg 2.如图所示，在竖直平面内有一质量为2m 的光滑“∏”形线框DEFC ，EF 长为L ，电阻为r ；FC ＝ED ＝2L ，电阻不计.FC 、ED 的上半部分(长为L )处于匀强磁场Ⅰ区域中，且FC 、ED 的中点与其下边界重合.质量为m 、电阻为3r 的金属棒用最大拉力为2mg 的绝缘细线悬挂着，其两端与C 、D 两端点接触良好，处在磁感应强度为B 的匀强磁场Ⅱ区域中，并可在FC 、ED 上无摩擦滑动.现将“∏”形线框由静止释放，当EF 到达磁场Ⅰ区域的下边界时速度为v ，细线刚好断裂，Ⅱ区域内磁场消失.重力加速度为g .求：(1)整个过程中，线框克服安培力做的功； (2)EF 刚要出磁场Ⅰ时产生的感应电动势；(3)线框的EF 边追上金属棒CD 时，金属棒CD 的动能. 【答案】(1)2mgL －mv 2(2)4mgr BL (3)mg 2L22v2【解析】(1)对∏形线框用动能定理：2mgL －W ＝12·2mv 2－0，W ＝2mgL －mv 2(2)对金属棒CD 受力分析：F Tm ＝mg ＋BIL ，得到I ＝mg BL，E ＝IR 总＝4mgrBL(3)对金属棒CD 运动分析：H ＝12gt 2，对∏形线框运动分析：H ＋L ＝vt ＋12gt 2，解得：t＝Lv相遇时CD 棒速度v t ＝0＋gt ＝gL v ，此时动能为E k ＝12mv 2t ＝mg 2L22v23.如图所示，绝缘光滑水平面与半径为R 的竖直光滑半圆轨道相切于C .竖直直径GC 左侧空间存在足够大匀强电场，其电场强度方向水平向右.GC 右侧空间处处存在匀强磁场，其磁感应强度垂直纸面水平向里.一质量为m ，电荷量为q 的带正电滑块(可视为质点)在A 点由静止释放，滑块恰好能通过圆周的最高点G 进入电场.已知匀强电场场强大小为E ＝mgq，AC 间距为L ＝4R ，重力加速度为g .求：(1)滑块在G 点的速度v G ；(2)匀强磁场的磁感应强度B 的大小； (3)滑块落回水平面的位置距离C 点的距离x . 【答案】(1)2gR (2)3m2qgR(3)2R 【解析】(1)研究A 到G 过程，由动能定理知：4EqR －2mgR ＝mv2G 2代入可得：v G ＝2gR(2)在G 点，对滑块有：mg ＋qv G B ＝mv2G R代入可得：B ＝3m2q g R(3)设回到电场之后的飞行时间为t ，水平位移为x 竖直方向：2R ＝gt 22水平方向：x ＝v G t －12at 2其中：a ＝Eq m联立可得：x ＝2R .4.如图所示，光滑绝缘水平面AB 与倾角θ＝37°，长L ＝5 m 的固定绝缘斜面BC 在B 处平滑相连，在斜面的C 处有一与斜面垂直的弹性绝缘挡板。

高考物理最新电磁学知识点之电磁感应专项训练及解析答案一、选择题1．如图所示，一个圆形线圈的匝数为N，半径为a，线圈平面与匀强磁场垂直，且一半处在磁场中。

在Δt时间内，磁感应强度的方向不变，大小由B均匀地增大到2B。

在此过程中，线圈中产生的感应电动势为（）A．2NBatπ∆B．22NBatπ∆C．2Batπ∆D．22Batπ∆2．如图所示，用粗细均匀的同种金属导线制成的两个正方形单匝线圈a、b，垂直放置在磁感应强度为B的匀强磁场中，a的边长为L，b的边长为2L。

当磁感应强度均匀增加时，不考虑线圈a、b之间的影响，下列说法正确的是（）A．线圈a、b中感应电动势之比为E1∶E2＝1∶2B．线圈a、b中的感应电流之比为I1∶I2＝1∶2C．相同时间内，线圈a、b中产生的焦耳热之比Q1∶Q2＝1∶4D．相同时间内，通过线圈a、b某截面的电荷量之比q1∶q2＝1∶43．如图所示，MN和PQ为竖直方向的两平行长直金属导轨，间距l为0.4m，电阻不计。

导轨所在平面与磁感应强度B为0.5T的匀强磁场垂直。

质量m为6.0×10-3kg电阻为1Ω的金属杆ab始终垂直于导轨，并与其保持光滑接触。

导轨两端分别接有滑动变阻器R2和阻值为3.0Ω的电阻R1。

当杆ab达到稳定状态时以速率v匀速下滑，整个电路消耗的电功率P为0.27W。

则（）A．ab稳定状态时的速率v=0.4m/sB．ab稳定状态时的速率v=0.6m/sC．滑动变阻器接入电路部分的阻值R2=4.0ΩD．滑动变阻器接入电路部分的阻值R2=6.0Ω4．两条平行虚线间存在一匀强磁场，磁感应强度方向与纸面垂直。

边长为0.1m、总电阻为0.005Ω的正方形导线框abcd位于纸面内，cd边与磁场边界平行，如图甲所示。

已知导线框向右做匀速直线运动，cd边于t=0时刻进入磁场。

导线框中感应电动势随时间变化的图线如图乙所示（规定感应电流的方向abcda为正方向）。

下列说法正确的是（）A．磁感应强度的方向垂直纸面向内B．磁感应强度的大小为0.5TC．导线框运动速度的大小为0.05m/sD．在t=0.4s至t=0.6s这段时间内，导线框所受的安培力大小为0.04N5．如图所示，把金属圆环在纸面内拉出磁场，下列叙述正确的是（）A．将金属圆环向左拉出磁场时，感应电流方向为逆时针B．不管沿什么方向将金属圆环拉出磁场时，感应电流方向都是顺时针C．将金属圆环向右匀速拉出磁场时，磁通量变化率不变D．将金属圆环向右加速拉出磁场时，受到向右的安培力6．如图所示，一带铁芯线圈置于竖直悬挂的闭合铝框右侧，与线圈相连的导线abcd内有水平向里变化的磁场．下列哪种变化磁场可使铝框向左偏离 ( )A．B．C．D．7．如图所示为地磁场磁感线的示意图，在北半球地磁场的竖直分量向下。