初中数学竞赛辅导资料(18)正整数简单性质的复习含答案
- 格式:doc
- 大小:232.00 KB
- 文档页数:12

初中数学竞赛辅导资料3质数 合数甲内容提要1 正整数的一种分类: 质数的定义:如果一个大于1的正整数,只能被1和它本身整除,那么这个正整数叫做质数质数也称素数.合数的定义:一个正整数除了能被1和本身整除外,还能被其他的正整数整除,这样的正整数叫做合数.2 根椐质数定义可知① 质数只有1和本身两个正约数,② 质数中只有一个偶数2如果两个质数的和或差是奇数那么其中必有一个是2,如果两个质数的积是偶数那么其中也必有一个是2,3任何合数都可以分解为几个质数的积.能写成几个质数的积的正整数就是合数.乙例题例1两个质数的和等于奇数a a ≥5.求这两个数解:∵两个质数的和等于奇数∴必有一个是2所求的两个质数是2和a -2.例2己知两个整数的积等于质数m, 求这两个数解:∵质数m 只含两个正约数1和m,又∵-1-m=m∴所求的两个整数是1和m 或者-1和-m.例3己知三个质数a,b,c 它们的积等于30求适合条件的a,b,c 的值解:分解质因数:30=2×3×5适合条件的值共有: ⎪⎩⎪⎨⎧===532c b a ⎪⎩⎪⎨⎧===352c b a ⎪⎩⎪⎨⎧===523c b a ⎪⎩⎪⎨⎧===253c b a ⎪⎩⎪⎨⎧===325c b a ⎪⎩⎪⎨⎧===235c b a 应注意上述六组值的书写排列顺序,本题如果改为4个质数a,b,c,d 它们的积等于210,即abcd=2×3×5×7那么适合条件的a,b,c,d 值共有24组,试把它写出来.例4试写出4个连续正整数,使它们个个都是合数.解:本题答案不是唯一的设N 是不大于5的所有质数的积,即N =2×3×5那么N +2,N +3,N +4,N +5就是适合条件的四个合数即32,33,34,35就是所求的一组数.本题可推广到n 个.令N 等于不大于n+1的所有质数的积,那么N +2, N +3,N +4,……N +n+1就是所求的合数.丙练习31, 小于100的质数共___个,它们是__________________________________ 2, 己知质数P 与奇数Q 的和是11,则P =__,Q =__3, 己知两个素数的差是41,那么它们分别是_____4, 如果两个自然数的积等于19,那么这两个数是___如果两个整数的积等于73,那么它们是____如果两个质数的积等于15,则它们是_____5, 两个质数x 和y,己知 xy=91,那么x=__,y=__,或x=__,y=__. 6, 三个质数a,b,c 它们的积等于1990.那么 ⎪⎩⎪⎨⎧===c b a7, 能整除311+513的最小质数是__8,己知两个质数A 和B 适合等式A +B =99,AB =M.求M 及B A +AB 的值 9,试写出6个连续正整数,使它们个个都是合数.10,具备什么条件的最简正分数可化为有限小数11,求适合下列三个条件的最小整数:① 大于1 ②没有小于10的质因数 ③不是质数12,某质数加上6或减去6都仍是质数,且这三个质数均在30到50之间,那么这个质数是___13,一个质数加上10或减去14都仍是质数,这个质数是__.。

第十八讲平移、对称、旋转趣题引路】如图18-1,已知△ABC内有一点M,沿着平行于边BC的直线运动到CA边上时,再沿着平行于AB的直线运动到BC边时,又沿着平行于AC直线运动到AB边时,再重复上述运动,试证:点M最后必能再经过原来的出发点证明设点M运动过程中依次与三角形的边相遇于点A1,B1,B2,C2,C3,A3,A4,B5,….易知△AC2B₂≌△A1CB1≌△A3C3B.按点M平移的路线,△A C2B2可由△A1CB1平移得到;△A3C3B可由△AC2B2平移得到;△A1CB1可由△A3C3B平移得到,此时,A3应平移至A4,所以A4与A1重合.而这时的平移方向恰与点M开始平移时的方向一致,因此从A3平移到A1的过程中必经过点M,这表明在第七步时,点M又回到了原来的出发点.图18-1知识拓展】1.平移、对称和旋转是解决平面几何问题常用的三种图形变换方法,它们零散地分布在初中几何教材之中.例如,平行四边形的对边可以看成是平行移动而形成,这里的平行移动,就是平移变换.2.一般地,把图形F上的所有点都按照一定的方向移动一定距离形成图形F'.则由F到F'的变换叫做平移变换,简称平移.由此可知,线段平移可以保持长短、方向不变,角、三角形等图形平移保持大小不变.将平面图形F变到关于直线l成轴对称的图形F',这样的几何变换简称为对称,它可使线段、角大小不变.3.将平面图形F绕着平面内的一个定点O旋转一个定角a到图形F',由F到F'的变换简称为旋转.旋转变换下两点之间的距离不变,两直线的夹角不变,且对应直线的夹角等于旋转角.4.运用平移、对称或旋转变换,能够集中图形中的已知条件,沟通各条件间的联系.例1 已知:如图18-2,△ABC中,AD平分∠CAB,交BC于D,过BC中点E作AD的平行线交AB于F,交CA的延长线于C.求证:2ACAB=CG=BF.图18-2解析直接证三角形全等或者用角平分线定理显然不能解决问题.注意到要证式的形式,条件中又有角平分线和中点,如果能切分BF、CG,使分出的两部分一部分是AB的一半,余下的是AC的一半,问题就解决了.由中点,我们不难想到中位线,两条有推论效力的辅助线(EH和EI)就产生了,H、I切分了BF、CG,由平行线性质∠1=∠2=∠3=∠4=∠6,再由中位线定理,等腰三角形的判定定理,切分后的结论不难证明.略证过E作AC、AB的平行线交AB、AC于H、I,由平行线性质及已知条件得,∠1=∠2=∠3=∠4=∠6, ∴EI =GI ,EH =FH .∵E 为BC 中点,EH ∥AC ,EI ∥AB , ∴EI =2AB =BH ,EH =2AC=CI , ∴EI =GI =2AB=BH , FH =EH =2AC=CI . 由于BF =BH +FH , CG =GI +CI , ∴2ACAB =BF =CG .例2 如图18-3,E 是正方形ABCD 的BC 边上的一点,F 是∠DAE 的平分线与CD 的交点,求证:AE =FD +BE .图18-3解析 表面上看所要证等式的各边分布在正方形不同的边上,欲证它们之间的关系,似乎不可能.但我们可以将某一条边作适当的延伸,使等量关系转移(比如证某两个三角形全等,中位线的关系等).此题中可将FD 延长至G ,使得DG =BE ,于是易证△AGD ≌△AEB ,则将AE 与AG ,BE 与GD 联系了起来,转而只需证明AG =GF ,即只要证明△AGF 为等腰三角形即可,由∠1=∠2,∠3=∠4及AB ∥CD 即证得.略证 延长FD 至G 使DG =BE , ∵△ADG ≌△ABE ,∴AG =AE ,GD =BE ,∠1=∠2. 又∵ ∠3=∠4, ∴∠1+∠4=∠2+∠3. 由于DC ∥AB ,∴∠DFA =∠2+∠3, ∴∠1+∠4=∠DFA , ∴GF =AG .即GD +DF =BE +FD =AE .例3 已知∠MON =40°,P 为∠MON 内一点,A 为OM 上一点,B 为ON 上的点,则△PAB 的周长取最小值时,求∠APB 的度数.图18-4解析 如图18-4,若在OM 上A 点固定,不难在ON 上找出点B (B 为P 关于ON 的对称点P ''与A 点的连线与ON 的交点),同样若在ON 上B 点已固定,则点P 关于OM 的对称点P'与B 点的连线与OM 交于A ,因此A 、B 应为P'P ''与0M 、ON 的交点,这时可求得∠A .解 作P'为P 关于OM 的对称点,P ''为P 关于ON 的对称点,连接P'P ''分别交OM 、ON 于A 、B 两点,则△PAB 周长为最小,这时△ABP 的周长等于P'P ''的长(连接两点间距离最短).∵OM P P ⊥',ON P P ⊥''垂足分别为C 、D , ∴∠OCP =∠ODP =90°. ∵∠M O N=40°,∴∠CPD =180°-40°=140°.∴∠PP'P ''=∠P P ''P'=180°-140°=40°.由对称性可知:∠PAB =2∠P',∠PBA =2∠P '', ∴∠APB =180°-(∠PAB -∠PBA )=180°-(2∠P'-2∠P '')=100°.例4 如图18-5,在ABC 中,BC =h ,AB +AC =l ,由B ,C 向∠BAC 外角平分线作垂线,垂足为D 、E , 求证:BD ·CE =定值.图18-5解析 BC =h 是定值,AB +AC =l 是定值,要证BD ·CE 是定值,设法使BD ·CE 用h ,l 的代数式来表示,充分利用DE 是BAC 的外角平分线,构造对称图形,再利用勾股定理。

2020北京 初二数学竞赛 数论专题:整数的整除性质(含答案)1. 下面这个41位数20555L 123个2099L 23个能被7整除,问中间方格代表的数字是几? 解析 因为5555555111111=⨯,9999999111111=⨯,11111137111337=⨯⨯⨯⨯,所以555555和999999都能被7整除,那么由18个5和18个9分别组成的18位数,也能被7整除.而原数=185230555000L L 123123个个1851890999+L L 123123个个,因此右边的三个加数中,前后两个数都能被1整除,那么只要中间的能被7整除,原数就能被7整除.把拆成两个数的和:5599BA B +.因为7|55300,7|399336+=.评注 记住111111能被7整除很有用.2. 一位魔术师让观众写下一个六位数a ,并将a 的各位数字相加得b ,他让观众说出a b -中的5个数字,观众报出1、3、5、7、9,魔术师便说出余下的那个数,问那个数是多少?解析 由于一个数除以9所得的余数与这个数的数字和除以9所得的余数相同,所以a b -是9的倍数.设余下的那个数为x ,则()9|13579x +++++,即 ()9|7x +,由于09x ≤≤,所以,2x =.3. 若p 、q 、21p q -、21q p-都是整数,并且1p >,1q >.求pq 的值. 解析 若p q =,则212112p p q p p--==- 不是整数,所以p q ≠.不妨设p q <,于是2121212p q q q q q--<<=≤, 而21p q -是整数,故211p q-=,即21q p =-.又 214334q p p p p--==- 是整数,所以p 只能为3,从而5q =.所以3515pq =⨯=.4. 试求出两两互质的不同的三个正整数x 、y 、z 使得其中任意两个的和能被第三个数整除.解析 题中有三个未知数,我们设法得到一些方程,然后从中解出这些未知数.不妨设x y z <<,于是y z x +、z x y +、x y z+都是正整数.先考虑最小的一个:12x y z z z z++<=≤, 所以1x y z+=,即z x y =+.再考虑z x y +,因为()|y z x +,即()|2y y x +,所以|2y x ,于是2212x y y y <=≤, 所以21x y=,即2y x =,从而这三个数为x 、2x 、3x .又因为这三个数两两互质,所以1x =.所求的三个数为1、2、3.5. 证明:三个连续奇数的平方和加1,能被12整除,但不能被24整除.解析 要证明一个数能被12整除但不能被24整除,只需证明此数等于12乘上一个奇数即可.设三个连续的奇数分别为21n -、21n +、23n +(其中n 是整数),于是 ()()()()22222121231121n n n n n -+++++=++. 所以 ()()()22212|212123n n n ⎡⎤-++++⎣⎦. 又()2111n n n n ++=++,而n 、1n +是相邻的两个整数,必定一奇一偶,所以()1n n +是偶数,从而21n n ++是奇数,故()()()22224212123n n n ⎡⎤-++++⎣⎦Œ. 6. 若x 、y 为整数,且23x y +,95x y +之一能被17整除,那么另一个也能被17整除. 解析 设23u x y =+,95x y =+.若17|u ,从上面两式中消去y ,得3517v u x -=.① 所以 17|3v .因为(17,3)=1,所以17|v 即17|95x y +.若17|v ,同样从①式可知17|5u .因为(17,5)=1,所以17|u ,即17|23x y +.7. 设n 是奇数,求证:60|6321n n n ---.解析 因为260235=⨯⨯,22、3、5是两两互质的,所以只需证明22、3、5能整除6321n n n ---即可.由于n 是奇数,有22|62n n -,22|31n +,所以22|6231n n n ---;又有3|63n n -,3|21n +,所以3|6321n n n ---;又有5|61n -,5|32n n +,所以5|6321n n n ---.所以60|6321n n n ---.评注 我们通常把整数分成奇数和偶数两类,即被2除余数为0的是偶数,余数为1的是奇数.偶数常用2k 表示,奇数常用21k +表示,其实这就是按模2分类.又如,一个整数a 被3除时,余数只能是0、1、2这三种可能,因此,全体整数可以分为3k 、31k +、32k +这三类形式,这是按模3分类.有时为了解题方便,还常把整数按模4、模5、模6、模8等分类,但这要具体问题具体处理.8. 设n 为任意奇正整数,证明:15961000270320n n n n +--能被2006整除.解析 因为200621759=⨯⨯,所以为证结论成立,只需证n 为奇正整数时,15961000270320n n n n +--能被2、17、59整除.显然,表达式能被2整除.应用公式,n 为奇数时,()()121n n n n n a b a b a a b b ---+=+-++L ,()()121n n n n n a b a b a a b b ----=-+++L .由于159610005944+=⨯,2703205910+=⨯,所以15961000270320n n n n +--能被59整除.又159627013261778-==⨯,10003206801740-==⨯,所以15961000270320n n n n +--能被17整除.9. 若整数a 不被2和3整除,求证:()224|1a -.解析 因为a 既不能被2整除,也不能被3整除,所以,按模2分类与按模3分类都是不合适的.较好的想法是按模6分类,把整数分成6k 、61k +、62k +、63k +、64k +、65k +这六类.由于6k 、62k +、64k +是2的倍数,63k +是3的倍数,所以a 只能具有61k +或65k +的形式,有时候为了方便起见,也常把65k +写成61k -(它们除以6余数均为5).故a 具有61k ±的形式,其中k 是整数,所以()()222161136121231a k k k k k -=±-=±=±. 由于k 与31k ±为一奇一偶(若k 为奇数,则31k ±为偶数,若k 为偶数,则31k ±为奇数),所以()2|31k k ±,于是便有()224|1a -.10. 求证:31n +(n 为正整数)能被2或22整除,但不能被2的更高次幂整除. 解析 按模2分类.若2n k =为偶数,k 为正整数,则()22313131n k n +=+=+. 由3k 是奇数,()23k 是奇数的平方,奇数的平方除以8余1,故可设()2381k l =+,于是 ()3182241n l l +=+=+,41l +是奇数,不含有2的因数,所以31n +能被2整除,但不能被2的更高次幂整除. 若21n k =+为奇数,k 为非负整数,则()()()22131313313811461n k k l l ++=+=⋅+=++=+. 由于61l +是奇数,所以此时31n +能被22整除,但不能被2的更高次幂整除.11. 设p 是质数,证明:满足22a pb =的正整数a 、b 不存在.解析 用反证法.假定存在正整数a 、b ,使得22a pb =.令() , a b d =,1a a d =,1b b d =,则()11 , 1a b =.所以222211a d pb d =,2211a pb =,所以21|p a .由于p 是质数,可知,1|p a .令12a pa =,则22221a p pb =,所以2221pa b =.同理可得,1|p b .即1a 、1b 都含有p 这个因子,这与()11 , 1a b =矛盾.12. 如果p 与2p +都是大于3的质数,那么6是1p +的约数.解析 每一整数可以写成6n 、61n -、61n +、62n -、62n +、63n +中的一种(n 为整数),其中6n 、62n -、62n +、63n +在1n ≥时都是合数,分别被6、2、2、3整除.因此,质数p 是61n -或61n +的形式.如果()611p n n =+≥,那么()263321p n n +=+=+是3的倍数,而且大于3,所以2p +不是质数.与已知条件矛盾.因此()611p n n =-≥.这时16p n +=是6的倍数.评注 本题是将整数按照除以6,所得的余数分为6类.质数一定是61n +或61n -的形式.当然,反过来,形如61n -或61n +的数并不都是质数.但可以证明形如61n -的质数有无穷多个,形如61n +的质数也有无穷多个.猜测有无穷多个正整数n ,使61n -与61n +同为质数.这是孪生质数猜测,至今尚未解决.13. 已知a 、b 是整数,22a b +能被3整除,求证:a 和b 都能被3整除.证 用反证法.如果a 、b 不都能被3整除,那么有如下两种情况:(1)a 、b 两数中恰有一个能被3整除,不妨设3|a ,3b Œ.令3a m =,31b n =±(m 、n 都是整数),于是()222222996133321a b m n n m n n +=+±+=+±+,不是3的倍数,矛盾.(2)a ,b 两数都不能被3整除.令31a m =±,31b n =±,则()()2222223131961961a b m n m m n n +=++±=±++±+()22333222m n m n =+±±+,不能被3整除,矛盾.由此可知,a 、b 都是3的倍数.14. 若正整数x 、y 使得2x x y+是素数,求证:x y ≤. 解析 设2x p x y =+是素数,则()py x x p =-,所以()|p x x p -,故|p x ,或者|p x p -,故可得|p x ,且p x <.令x kp =,k 是大于1的整数,则()1y x k x =-≥.15. 证明:形如abcabc 的六位数一定被7、11、13整除.解析 100171113abcabc abc abc =⨯=⨯⨯⨯. 由此可见,abcabc 被7、11、13整除.16. 任给一个正整数N ,把N 的各位数字按相反的顺序写出来,得到一个新的正整数N ',试证明:N N '-被9整除.解析 N 除以9,与N 的数字和除以9,所得余数相同.N '除以9,与N '的数字和除以9,所得余数相同.N 与N '的数字完全相同,只是顺序相反,所以N 与N '的数字和相等.N 除以9与N '除以9,所得的余数相同,所以N N '-被9整除.17. 19991999199919991999N =L 144424443连写个.求N 被11除所得的余数.解 显然,N 的奇数位数字和与偶数位数字和的差为()1999999119998⨯+--=⨯.19998⨯除以11的余数与88⨯除以11的余数相同,即余数为9.从而N 除以11,所得的余数为9.18. 在568后面补上三个数字,组成一个六位数,使它能被3、4、5分别整除.符合这些条件的六位数中,最小的一个是多少?解析 要命名这个六位数尽可能小,而且能被5整除,百位数字和个位数字都应选0.这样,已知的五个数位上数字之和是5+6+8+0+0=19.要使这个六位数能被3整除,十位上可填2、5、8.由能被4整除的数的特征(这个数的末两位数应该能被4整除)可知,应在十位上填2.这个六位数是568020.19. 已知四位数abcd 是11的倍数,且有b c a +=,bc 为完全平方数,求此四位数. 解析 在三个已知条件中,b c a +=说明给出b 和c ,a 就随之给定,再由11|abcd ,可定d .而bc 为完全平方数,将b 和c 的取值定在两位平方数的十位和个位数字范围中,只要从这个范围中挑选符合要求的即可.由bc 完全平方数,只可能为16、25、36、49、64、81这六种情况.由b c a +=,此时相应的a 为7、7、9、13、10、9.其中13和10显然不可能是四位数的千位数字. 在716d 、725d 、936d 、981d ,这四种可能性中,由11|abcd ,应有()()11|d b a c +-+.()()11|176d +-+时,d 可为1;()()11|275d +-+时,这种d 不存在;()11|396d +-+时,d 可为1;()11|891d +-+时,d 可为2.故满足条件的四位数有:7161、9361、9812.评注 bc 为完全平方数,表示bc 是两位整数,0b ≠,因此,不考虑00、01、04、09这四种情况,否则还应加上1012、4048、9097这三个四位数.20. 用0,1,2,…,9这十个数字组成能被11整除的最大的十位数是多少?解析 因为0+1+2+…+9=45.这个最大十位数若能被11整除,其奇数位上数字之和与偶数位上的数字之和的差(大减小)为0或11的倍数.由于这十个数字之和是45(奇数),所以这个差不可能是0、22、44(偶数).若这个差为33,则只能是396-,但0+1+2+3+4=10,即最小的五个数字之和都超过6,不可能.若这个差为11,()4511228+÷=,452817-=.如果偶数位为9、7、5、3、1,其和为25;奇数位为8、6、4、2、0,其和为20.交换偶数位上的1与奇数位上的4,可得偶数位上的数为9、7、5、4、3,奇数位上的数为8、6、2、1、0.于是所求的最大十位数为9876524130.21. 一个六位数88的倍数,这个数除以88所得的商是多少?解析 设这个六位数为1234A B ,因为它是88的倍数,而88811=⨯,8与11互质,所以,这个六位数既是8的倍数,又是11的倍数.由1234A B 能被8整除,可知34B 能被8整除(一个数末三位组成的数能被8整除,这个数就能被8整除),所以B 是4.由能被11整除的数的特征(一个数奇数位数字之和与偶数位数字之和的差能被11整除,这个数就能被11整除),可知奇数位数字之和与偶数位数字之和的差()()234144A A ++-++=-能被11整除,则40A -=,即4A =.124344881413÷=. 所以,这个六位数是124344,它除以88的商是1413.22. 如果六位数105整除,那么,它的最后两位数是多少?解析 因为这个六位数能被105整除,而105357=⨯⨯,3、5、7这三个数两两互质,所以,这个六位数能同时被3、5、7整除.根据能被5整除的数的特征,它的个位数可以是0或5.根据能被3整除的数的特征,可知这个六位数有如下七种可能:199320,199350,199380,199305,199335,199365,199395.而能被7整除的数的特征是:这个数的末三位数字所表示的数与末三位以前的数字所表示的数的差(以大减小)能被7整除.经试算:395199196-=,196能被7整除.所以,199395能被105整除,它的最后两位数是95.23. 形如1993199319931993520n L 1442443个,且能被11整除的最小数是几? 解析 本题实质上确定n 的最小值.利用被11整除的数的特征:偶数位数字之和与奇位数字之和的差能被11整除.该数的偶数位数字之和为122n +,奇数位数字之和为105n +,两者之差为()12210523n n n +-+=-.要使()11|23n -,不难看出最小的7n =,故所求最小数为71993199319931993520L 1442443个. 24. 是否存在100个不同的正整数,使得它们的和与它们的最小公倍数相等?解析 存在满足条件的100个数.事实上,对任意正整数()3n ≥,下述n 个数3,23⨯,223⨯,…,223n -⨯,13n -,它们的最小公倍数为123n -⨯,和为221222132323233323233n n n n ----+⨯+⨯++⨯+=+⨯++⨯+L L 33211113232333323n n n n n -----=+⨯++⨯+==+=⨯L L .所以,这几个数的和等于它们的最小公倍数.取100n =,可知存在符合要求的100个数.。

初中数学竞赛辅导资料(18)整式的整除内容提要1. 定义:如果一个整式除以另一个整式所得的商式也是一个整式,并且余式是零,则称这个整式被另一个整式整除。
2. 根据被除式=除式×商式+余式,设f(x),p(x),q(x)都是含x 的整式,那么 式的整除的意义可以表示为:若f(x)=p(x)×q(x), 则称f(x)能被 p(x)和q(x)整除例如∵x 2-3x -4=(x -4)(x +1),∴x 2-3x -4能被(x -4)和(x +1)整除。
显然当 x=4或x=-1时x 2-3x -4=0,3. 一般地,若整式f(x)含有x –a 的因式,则f(a)=0反过来也成立,若f(a)=0,则x -a 能整除f(x)。
4. 在二次三项式中若x 2+px+q=(x+a)(x+b)=x 2+(a+b)x+ab 则p=a+b,q=ab在恒等式中,左右两边同类项的系数相等。
这可以推广到任意多项式。
例题例1己知 x 2-5x+m 能被x -2整除,求m 的值。
x -3解法一:列竖式做除法 (如右) x -2 x 2-5x+m由 余式m -6=0 得m=6 x 2-2x解法二:∵ x 2-5x+m 含有x -2 的因式 -3x+m∴ 以x=2代入 x 2-5x+m 得 -3x+622-5×2 +m=0 得m=6 m -6解法三:设x 2-5x+m 除以x -2 的商是x+a (a 为待定系数)那么 x 2-5x+m =(x+a)(x -2)= x 2+(a-2)x -2a根据左右两边同类项的系数相等,得⎩⎨⎧=--=-m a a 252 解得⎩⎨⎧=-=63m a (本题解法叫待定系数法) 例2 己知:x 4-5x 3+11x 2+mx+n 能被x 2-2x+1整除求:m 、n 的值及商式解:∵被除式=除式×商式 (整除时余式为0)∴商式可设为x 2+ax+b得x 4-5x 3+11x 2+mx+n =(x 2-2x+1)(x 2+ax+b )=x 4+(a-2)x 3+(b+1-2a)x 2+(a-2b)x+b根据恒等式中,左右两边同类项的系数相等,得⎪⎪⎩⎪⎪⎨⎧==-=-+-=-n b m b a a b a 12112152 解得⎪⎪⎩⎪⎪⎨⎧=-==-=4113n m n b a ∴m=-11, n=4, 商式是x 2-3x+4例3 m 取什么值时,x 3+y 3+z 3+mxyz (xyz ≠0)能被x+y+z 整除?解:当 x 3+y 3+z 3+mxyz 能被x+y+z 整除时,它含有x+y+z 因式令x+y+z=0,得x=-(y+z),代入原式其值必为0即[-(y+z)]3+y3+z3-myz(y+z)=0把左边因式分解,得-yz(y+z)(m+3)=0,∵yz≠0, ∴当y+z=0或m+3=0时等式成立∴当x,y(或y,z或x,z)互为相反数时,m可取任何值,当m=-3时,x,y,z不论取什么值,原式都能被x+y+z整除。

第18章 整数几何18.1.1★已知ABC △的两条高长分别是5、15,第三条高的长数,求这条高之长的所有可能值.解析 由面积知,三条高的倒数可组成三角形三边,这是它们的全部条件. 设第三条高为h ,则111,155111.515h h⎧+>⎪⎪⎨⎪+>⎪⎩ 解得151545h <<,h 可取4、5、6、7这四个值. 18.1.2★已知ABC △的三边长分别为3AB n x =+,2BC n x =+,CA n x =+,且BC 边上的高AD 的长为n ,其中n 为正整数,且01x <≤,问:满足上述条件的三角形有几个? 解析 注意AB 为ABC △之最长边,故90B ∠<︒,设BD y =,CD z =,则0y >,而z 可正可负.AB D C由2y z n x +=+,及()()()22223242y z n x n x n x x -=+-+=+⋅,得4y z x -=,32ny x =+,由勾股定理,知()222332n x n n x ⎛⎫++=+ ⎪⎝⎭,展开得12n x =,由01x <≤及n 为正整数,知1n =,2,…,12,这样的三角形有12个.18.1.3★已知一个直角三角形的三条边均为正整数,其中一条直角边不超过20,其外接圆半径与内切圆半径之比为52∶,求此三角形周长的最大值.解析设该直角三角形直角边长为a 、b ,斜边为c ,则外接圆半径2cR =,内切圆半径2a b cr +-=,不妨设20a ≤. 由条件知52c a b c =+-,557a b c +=,平方,得()()222225249a b ab a b ++=+,即()2212250a b ab +-=,()()34430a b a b --=,于是3a k =,4b k =,5c k =,或4a k =,3b k =,5c k =,周长为12k ,k 为正整数.k 的最大值为6,此时各边为18、24、30,周长最大值为72.18.1.4★ABC △为不等边三角形,60A ∠=︒,7BC =,其他两边长均为整数,求ABC △的面积.A BCx y60°解析设AB x =,AC y =,则由余弦定理,有2249x y xy +-=.由条件x y ≠,不妨设x y <,则AB 为ABC △之最小边,x 只能取值1、2、3、4、5、6,分别代入,发现当3x =或5时,8y =,其余情形均无整数解.于是1sin 602ABC S xy =︒=△. 18.1.5★★一点P 与半径为15的圆的圆心距离是9,求经过P 且长为整数的弦的条数. 解析 如图,O e 半径为15,9OP =,过P 的弦ST 长为整数,APB 为直径,6AP =,24PB =,则144SP TP PA PB ⋅=⋅=,因此24ST SP TP =+≥.又30ST AB =≤,故这样的弦共有()302412212-+⨯-=条,其中与AB 垂直的弦及AB 各一条,其余的弦每种长度有两条(关于AB 对称).18.1.6★★在直角三角形ABC 中,各边长都是整数,90C ∠=︒,CD 为边AB 上的高,D 为垂足,且3BD p =(p 奇素数),求ACAB的值(用p 表示). C解析由2BC BD AB =⋅知2BD BC ,故设2BC p t =(t 为正整数),则2BA pt =,又由勾股定理,知22442AC p t p t =-,故tp AC .设AC kpt =,代入得()()222p t k t k t k =-=+-,易知只能有2t k p +=,1t k -=,解得212p t +=,212p k -=,于是2211AC p AB p -=+. 18.1.7★★设正三角形ABC ,M 、N 分别在AB 、AC 上,MN BC ∥,两端延长MN ,交ABC △外接圆于P 、Q ,若PM 、MN 、AB 长均为正整数,求AB 的最小值. 解析 如图, 易知NQ PM =也是整数.设AM x =,BM y =,PM NQ z ==,则MN x =,于是由相交弦定理,得()xy z x z =+,2z x y z=-.APQM NB C设y ks =,z kt =,(),k y z =,s t >,(),1s t =,则2kt x s t=-,由于()2,1s t t -=,故s t k -,要使2t AB x y k ks s t=+=+-达到最小,k 得取s t -,于是()2AB t s t s =+-.由于s t >,2s ≥,1t ≥,知()223t s t s t s +-+≥≥.当1AM =,2BM =时AB 取到最小值3,此时1PM =.18.1.8★★已知凸四边形ABCD 的四边长是两两不相等的整数,对边乘积之和等于四边形面积的两倍,且22250AD BC +=,求该四边形面积、对角线长度.解析 不妨设AB α=,BC b =,CD c =,DA d =,AC 与BD 交于O ,则sin 2ABCD AC BD AOB S ac bd AC BD ⋅⋅∠==+⋅≥,于是由托勒密定理,知A 、B 、C 、D 必共圆,且满足AC BD ⊥.又由已知条件,22250b d +=,22250a c +=.经搜索知250表为平方和只有两组:22515+和22913+.由对称性,不妨设5a =,13b =,15c =,9d =,则19622ABCD ac bdS AC BD +=⋅==.由余弦定理,因cos cos 0BAD BCD ∠+∠=,得222222591315045195BD BD +-+-+=,得BD =AC18.1.9★★是否存在一个三边长恰是三个连续正整数,且其中一个内角等于另一个内角2倍的ABC △?证明你的结论. 解析 存在满足条件的三角形.当ABC △的三边长分别为6a =,4b =,5c =时,2A B ∠=∠.如图,当2A B ∠=∠时,延长BA 至点D ,使AD AC b ==.连结CD ,ACD △为等腰三角形.CD A因为BAC ∠为ACD △的一个外角,所以2BAC D ∠=∠.由已知,2BAC B ∠=∠,所以B D ∠=∠.所以CBD △为等腰三角形.又D ∠为ACD △与CBD △的一个公共角,有~ACD CBD △△,于是AD CD CD BD =,即b aa b c=+,所以()2a b b c =+.而()26445=⨯+,所以此三角形满足题设条件,故存在满足条件的三角形. 评注满足条件的三角形是唯一的.若2A B ∠=∠,可得()2a b b c =+.有如下三种情形:(ⅰ)当a c b >>时,设1a n =+,c n =,1b n =-(n 为大于1的正整数),代入()2a b bc =+,得()()()21121n n n +=--,解得5n =,有6a =,4b =,5c =;(ⅱ)当c a b >>时,设1c n =+,c n =,1b n =-(n 为大于1的正整数),代入()2a b bc =+,得()212n n n =-⋅.解得2n =,有2a =,1b =,3c =,此时不能构成三角形;(ⅲ)当a b c >>时,设1a n =+,b n =,1c n =-(n 为大于1的正整数),代入()2a b b c =+,得()()2121n n n +=-,即2310n n --=,此方程无整数解.所以,三边长恰为三个连续的正整数,且其中一个内角等于另一个内角的2倍的三角形存在,而且只有三边长分别为4、5、6构成的三角形满足条件.18.1.10★★三边长为连续整数、周长不大于100、且面积是有理数的三角形共有多少个? 解析 设三角形三边依次为1n -、n 、1n +,则333n ≤≤,()131122p n n n n =-+++=,S △==于是()234n -是平方数,令()()22343n k -=,得2243n k -=,则32n ≤,224102034033n k -==≤,18k ≤.又k 不可能是奇数,否则()222343n k k =+≡,得2243n k -=,则32n ≤,224102034033n k -==≤,18k ≤.又k 不可能是奇数,否则()22343mod 4n k =+≡,将2k =,4,6,8,10,12,14,16,18代入,发现仅当2k =,8时满足要求.因此这样的三角形共有两个,三边长依次为3、4、5与13、14、15.18.1.11★★某直角三角形边长均为整数,一直角边比斜边小1575,求其周长的最小值. 解析 设直角三角形直角边长a 、b ,斜边为1575a +,则 ()2221575a b a +=+,()2157521575b a =+.由于221575357=⨯⨯,设105b k =,则2721575k a =+,设7a s =,则22225k s =+,于是k 的最小值为17,此时32s =,224a =,1785b =,1799c =.此时的最小周长为3808. 18.1.12★★已知ABC △,AD 是角平分线,14AB =,24AC =,AD 也是整数,求AD 所有可取的值.AEB DC解析 如图,作DE AB ∥,E 在AC 上,则易知AE ED =. 又ED CD AC AB BC AB AC==+,故 22AB ACAD AE DE ED AB AC⋅<+==+33617.6819==…, 故17AD ≤.又当17AD ≤时,不难通过AED △构造出ABC △,故AD 所有可取的值为1,2, (17)18.1.13★面积为c 的正方形DEFG 内接于面积为1的正三角形ABC ,其中a 、b 、c 是整数,且b 不能被任何质娄的平方整除,求a cb-的值.ADGB E F C解析设正方形DEFG 的边长为x ,正三角形ABC 的边长为m ,则2m ,由ADG ABC △∽△,可得xx m -=.解得()3x m =.于是()222348x m ==.由题意得28a =,3b =,48c =,所以203a cb -=-. 17.1.14★★如图,AD 是ABC △的高,四边形PQRS 是ABC △的内接正方形,若BC ab =(即两位数),SRc =,ADd =,且a 、b 、c 、d 恰为从小到大的4个连续正整数,求ABC S △的所有可能值.AS RP D Q解析易知11SR AR CR SR BC AC AC AD ==-=-,于是有110c c a b d +=+,或11111132a a a +=+++,移项,得()()1111123a a a =+++,或2650a a -+=,解得1a =或5.于是有两解: 12,3,4;BC SR AD =⎧⎪=⎨⎪=⎩56,7,8.BC SR AD =⎧⎪=⎨⎪=⎩易知这两组数据都符合要求,故24ABC S =△或224.18.1.15★★已知ABC △中,B ∠是锐角.从顶点A 向BC 边或其延长线作垂线,垂足为D ;从顶点C 向AB 边或其延长线作垂线,垂足为E .当2BD BC 和2BEAB均为正整数时,ABC △是什么三角形?并证明你的结论. 解析设2BD m BC =,2BEn AB=,m 、n 均为正整数,则 244cos 4BD BE mn B AB BC=⋅⋅=<, 所以,1mn =,2,3. (1)当1mn =时,1cos 2B =,60B ∠=︒,此时1m n ==.所以AD 垂直平分BC ,CE 垂直平分AB ,于是ABC △是等边三角形.(2)当2mn =时,cos B =45B ∠=︒,此时1m =,2n =,或2m =1n =,所以点E 与点A 重合,或点D 与点C 重合.故90BAC ∠=︒,或90BCA ∠=︒,于是ABC △是等腰直角三角形.(3)3mn =时,cos B =,30B ∠=︒,此时1m =,3n =,或3m =,1n =.于是AD 垂直平分BC ,或CE 垂直平分AB .故30ACB ∠=︒,或30BAC ∠=︒,于是ABC △是顶角为120︒的等腰三角形.18.1.6★★某直角三角形两直角边长均为整数,周长是面积的整数倍(就数字上讲),问问这样的直角三角形有多少个?解析 设直角边分别为a 、b ,则斜边c =,由条件知它是有理数,故必定是整数.设2ka b ab +=,k 为正整数,于是k =.由于a b +1、2或4,记作k '.由a b k +-'=()2220ab k a b k -'++'=,()()22a k b k k -'-'=',1k '=时无解;2k '=时,有()()222a b --=,{a ,b }={3,4};4k '=时,()()448a b --=,{a ,b }={5,12}或{6,8},所以这样的直角三角形共有3个.18.1.17★★在等腰ABC △中,已知AB AC kBC ==,这里k 为大于1的自然数,点D 、E 依次在AB 、AC 上,且DB BC CE ==,CD 与BE 相交于O ,求使OCBC为有理数的最小自然数k .ADEBCO解析如图,连结DE ,则DE BC ∥,11DE AD AB BC BC AB AB k -===-,1k DE BC k-=. 由于四边形DBCE 为等腰梯形,则由托勒密定理(或过D 、E 作BC 垂线亦可),2222121k k CD CD BE DE BC DB CE BC BC BCk k --=⋅=⋅+⋅=+=,又21CO BC kCD DE BC k ==+-,于是CO BC =k 与21k -互质,由题设知其必须均为平方数,1k >,25k =适合,这是满足要求的最小自然数.18.1.18★★★对于某些正整数n 来说,只有一组解xyz n =(不计顺序),这里,x 、y 、z是正整数且可构成三角形的三边长,这样的()100n ≤共有多少个? 解析显然,当n p =(素数)时无解;当2n p =或1时只有一组解(1,p ,p )或(1,1,1);当n pq =(p 、q 为不同素数)时无解;当4n p =(p 为大于3的素数)时也无解.剩下的数为8,12,16,18,24,27,30,32,36,40,42,45,48,50,54,56,60,63,64,66,70,72,75,78,80,81,84,88,90,96,98,99,100. 易验证,无解的n 有:30,42,54,56,63,66,70,78,88,99;唯一解的n 有:8,12,16,18,24,27,32,40,45,48,50,75,80,81,84,90,96,98;不止一组解的n 有:36,60,64,72,100.注意:判定无解的主要依据是,abc n =,c ab >时无解,困为1c ab a b ++≥≥. 因此,有解的n 共有23个.18.1.19★★面积为整数的直角三角形周长为正整数k ,求k 的最小值,并求此时这个直角三角形的两条直角边的可取值(如不止一组解,只需举了一组即可).解析设该直角三角形的直角三角形周长分别为a 、b ,则112ab ≥,a b +≥2,2k a b =+,故5k ≥.下令5k =,2ab =,如有解,则可.()5a b -+,平方得()222225102a b a b a b ab +=-++++.取2ab =,得29,102.a b ab ⎧+=⎪⎨⎪=⎩因此a 、b 为方程21029200x x -+=的根,解得a 、bk 的最小值是5.18.1.20★★若ABC △的三边长a 、b 、c 均为整数,且140abc =,求ABC △内切圆半径. 解析 不妨设a b c ≤≤,于是7c ≥.又14011c a b ab c<++=+≤,故140c c ≤,得10c ≤.于是c 只可能为7或10. 7c =时,20ab =,只可能4a =,5b =,()182p a b c =++=,内切圆半径r =. 10c =时,14ab =,没有满足要求的解.18.1.21★★证明:若a 、b 、c 是一组勾股数()222a b c +=,则存在正整数k 、u 、v 、u v >,(),1u v =使得()22c k u v =+,而()22a k u v =-,2b kuv =;或2a kuv =,()22b k u v =-.解析222a b c +=,设(a ,b ,c )k =,则1a ka =,1b kb =,1c kc =,222111a b c +=.易知1a 、1b 、1c 两两互质;1a 与1b 不可能同偶,否则12a ,1b ,1c ;1a 与1b 也不会同奇,否则()212mod 4c =,矛盾.于是1a 与1b 必一奇一偶,不妨设1a 奇而1b 偶,于是1c 为奇数.从而()()211111a c b c b =+-,11c b +与11c b -必互质,否则有一奇素数11|p c b +,11c b -,得|2p c ,12b ,故|p (1c ,1b ),与(1c ,1b )=1矛盾. 于是可设2111c b u +=,2111c b v -=,(1u ,1v )=1,且1u 、1v 均为奇数,解得221111122u v u v c +-⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭,11111222u v u v b +-=⋅⋅,221111122u v u v a +-⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭,令112u v u +=,112u v v -=,即得结论. 18.1.22★★★如图,F 、E 在ABC △的边AB 、AC 上,FE 的延长线与BC 的延长线交于D ,求证:AF 、BF 、CB 、CD 、AE 、EC 、FE 、ED 的长度不可能是1~8的排列. 解析 如果1EF =,则1AE AF EF -<=,得AE AF =,矛盾,故1EF ≠,同理AF 、AE 、ED 、CD 、EC 都不等于1.AFE GDCB因此1只可能等于FB 或BC 之长,不失对称性,设1BF =,则1FD BD BF -<=,FD BD =,作CG AB ∥,G 在ED 上,四边形FBCG 乃一等腰梯形,于是EG FG EF BC EF =-=-为正整数.又1EG EC CG BF -<<=,故EG EC =,但BFD ∠为等腰三角形DFB 的底角,90BFD <︒∠,18090EGC BFD =︒->︒∠∠,为EGC △的最大内角,EC EG >,矛盾,因此结论证毕.18.1.23★★★已知梯形ABCD 中,AD BC <,E 、F 分别在AB 、CD 上,EF AD BC ∥∥,ED BF ∥,如果AD 、EF 、BC 均为正整数,称该梯形为“整数梯形”.现对于正整数n ,有正整数x x <′<y ′<y ,x y x +=′+y ′=n ,且x 、y 为一“整数梯形”的上、下底, x ′、y ′为另一“整数梯形”的上、下底,求n 的最小值.解析 如图,由AED EFD △∽△,DEF FBC △∽△,得AD AE DF EFEF BE FC BC===,得EF =,于是问题变为求最小的n ,使xy 与x ′y ′均为平方数.A DEFB Cxy 、x ′y ′不可能都为4,故至少有一组≥9,显然另一组也不可能为4,于是xy ,x ′y ′≥9.如果xy 或x ′y ′25≥,则10n =≥.若xy 或x ′y ′=9或16,则19n =+或2810+=.于是n 的最小值为10,1x =,x ′=2,y ′=8,y =9.18.1.24★★★求证:存在无穷多个每边及对角线长均为不同整数的、两两不相似的凸四边形.ABDPC解析 如图,作圆内接四边形ABCD ,AC 与BD 垂直于P ,设a 为一整数,2a >,4AP a =,24BP a =-,241DP a =-,则24AB a =+,241AD a=+,,由此知()()224414aa CP a--=,而由ABP DCP △∽△,BPC APD △∽△知,()224414a BC a a -=+,()224144a CD a a -=+.同时乘以系数4a ,得()244AB a a =+,()2441AD a a =+,()()22441BC a a =-+,()()22414CD a a =-+,4244AC a a =-+,()2201BD a a =-.易知上述6个多项式无二者恒等,于是任两者相等只能得有限个a ,但正整数有无限个,因此有无限个a ,使6个多项式两两不等,又当a →+∞时,0BDAC→,因此有无限个这样的凸四边形两两不相似. 18.1.25★★★已知PA 、PB 为圆的切线,割线过P ,与圆交于M 、N ,与AB 交于S ,若PA 、PM 、MS 、SN 均为正整数,求PA 的最小值. PMABSN解析 如图,易知有PM PNMS SN=(调和点列). 设PM a =,MS b =,SN c =,则()b a b c ac ++=,()b c b c a b+=-,从而PA == 设a ks =,b kt =,k =(a ,b ),则(s ,t )=1,s t >,s tc kts t+=-,PA =易见(s t +,s t -)=1,则s 、t 一奇一偶.于是由(()t s t +,s t -)=1,得|s t k -,且由PA 为整数知2s t x +=,2s t y -=,x 、y 为奇数.因为|s t k -,于是k 的最小值为s t -,()c t s t =+,PA sxy ==,当s =1,2,3,4时,t 无解(即PA 不是整数),故5s ≥,又3x ≥,1y ≥,于是PA ≥15,当a =5,b =4,c =36时取到15PA =.若(s t +,s t -)=2,此时s 、t 同奇,k 的最小值为2s t-,此时()2t s t c +=,PA =22s t x +=,22s t y -=,当1s =,3时,无t 使PA 为整数,于是5s ≥,又x y >,所以1y ≥,2x ≥,5210PA sxy =⨯=≥.当5a =,3b =,12c =时取到PA =10. 综上,PA 的最小值是10.18.1.26★★★一圆内接四边形的四边长及对角线长都是整数,求这类四边形中周长最小者. 解析 显然长与宽为4、3的矩形满足要求,其周长=14.若等腰梯形上、下底分别为3、4,腰为2,则由托勒密定理,对角线长为4,满足要求,此时周长为11.故最小周长≤11. 显然对圆内接凸四边形ABCD ,无边长为1.否则若设1AB =,—1AD BD AB <=,得AD BD =,同理AC CB =,于是C 、D 均在AB 中垂线上,构不成凸四边形.因此最小周长≥2×4=8.四边均为2,得正方形,对角线为2,另一边为3,得等腰梯形,10.当周长为10时,显然至少有两边为2.若是2、2、2、4能为2、2、3、3故最小周长为11.18.1.27★★★在Rt ABC △中,90BCA =︒∠,CD 是高,已知ABC △的三边长都是整数,且311BD =,求BCD △与ACD △的周长之比.CB D解析 设ABC △的三边长分别为a 、b 、c .由题设知 2BC BD BA =⋅,故2311a c =.于是设211a l =,得211l c =由勾股定理得11b ==2211l -是 完全平方数,设为()20t t >,则22211l t -=,()()211l t l t -+=.由于0l t l t <-<+,所以21,11.l t l t -=⎧⎨+=⎩解得61,60.l t =⎧⎨=⎩于是21161a =⨯,116160b =⨯⨯. 因为BCD CAD △∽△,所以它们的周长比等于它们的相似比,即1160a b =.18.1.28★★★已知锐角三角形ABC 中,AD 是高,矩形SPQR 的面积是ABC △的1/3,其顶点S 、P 在BC 上,Q 、R 分别在AC 、AB 上,且BC 、AD 及矩形SPQR 的周长均为有理数,求AB ACBC+的最小值. 解析 如图,设ABC △的三边长依次为a 、b 、c ,AD h =,PQ x =,RS y =,则16xy ah =,及1x y AQ CQ a h AC AC+=+=.由条件,知a 、h 、x y +均为有理数. AR QB S D P C由16x aa x+=,得x a =y h =)2a h x y a h ++=-,因此只能有a h =.若过A 作BC 的平行线l ,再作C 关于l 的对称点C ',则AB AC AB AC +=+′≥BC ′=,于是AB ACBC+,仅当AB AC =时取到. 18.1.29★★★★整数边三角形ABC 中,90BAC =︒∠,AD 是斜边上的高,BD 也是整数.若对同一个BD 能长度,有两个不全等的直角整数边三角形ABC 满足要求,求BD 的最小值. 解析 不妨设ABC △的三边长为a 、b 、c ,AD h =,BD d =,首先bch a=为有理数,又222h c d =-为整数,因此h 也是整数.又CD 为整数,故2h d也是整数.又ABD CBA △∽△,故h b d c=. AB D C因此,只需正整数h 、c 、d 满足222h c d =-及2|d h ,这样的整数边三角形就存在.因为此时hcb d=是有理数,而222b h CD =+为整数,从而b 为整数.易知由2|d h 可得2|d c . 设21d d σ=,σ、1d 为正整数,且σ无平方因子,于是由2|h σ及2c 知|h σ,c .设1h h σ=,1c c σ=,代入得422111d c h =-,又由2|d h ,2c 得2211|d h σ,21c σ,今对1d 的任一素因子p ,其在1d 的指数()1s d 不会比1h 的指数高,否则()()111s d s h +≥,()()22112s d s h +≥,而()s σ最多为1,于是()()2211s d s h σ>,这是不可能的.于是11|d h ,同理11|d c .又令112h d h =,112c d c =,代入422111d c h =-得222122d c h =-. 于是对1d 有两组不同的2c 、2h 满足222122d c h =-.经计算18d ≥,故64d ≥.当64d =时,确实有满足要求的两组解:80AB =,60AC =,100BC =,和136AB =,255AC =,289BC =.故BD 的最小值是64.18.1.30★★★★试找一不等边三角形ABC ,使BC 及BC 边上的中线、角平分线、高的长度都是整数,BC 可以是多少(此时的中线、角平分线、高的长度分别为多少)?若要求BC 不是整数,但2BC 是整数,则BC 可为多少(此时中线、角平分线、高的长度分别为多少)? 解析 首先处理BC 为整数的问题,我们选择的是直角三角形ABC ,对应边为a 、b 、c ,中线AM ,角平分线AD ,高AH ,2aAM =,bc AH a =,又ABC ABD ACD S S S =+△△△,得)bc b c AD +,故AD ,于是a 为偶数2k ,b ,c =,mnAH k =而2mn AD m n =+,2222m n k +=,这个方程有解1m =,7n =,5k =,得75AH =,5AM =,74AD =.乘以一个系数20,即得直角三角形ABC ,它的斜边为200,斜边上的中线为100,角平分线为35,高为28. 下面处理BC 为无理数、2BC 为整数的情形,如图,延长AD ,与MP 交于P ,此处MP BC ⊥.易知A 、B 、P 、C 共圆(P 是ABC △外接圆弧»BC之中点). 今从基本勾股数出发构造.取12AH =,13AD =,15AM =,则5DH =,9MH =,4MD =,485MD MP AH HD =⋅=,45255PD AD ==. ABMD HCP易知BPD APB △∽△,于是25211760845525BP PD PA =⋅=⨯=,()22222608448302444425255BC BM PB MP ⎛⎫==-=-= ⎪⎝⎭. 再乘以系数5,得所求三角形的高60AH =,角平分线65AD =,中线75AM =,边BC =是无理数,但15120BC =.18.1.31★★作圆外切凸五边形ABCDE ,现知该五边形每边长均为整数,1AB =,又圆与BC 切于K ,求BK .解析 如图,设CD 、DE 、EA 、AB 分别与圆切于P 、Q 、R 、S .则RE DP ED +=为整数,于是由题设,AR CP +亦为整数,而AR CP AS KC +=+.于是22BK BS BK BS ==+为整数,由于1BS AB <=,故22BS <,221BK BS ==,12BK =. A S RB EQ K CPD。

初中数学竞赛教程21整数的性质整数是数学中非常基本且重要的概念之一、它是全体正整数、负整数和零的集合,用整数集表示为Z,数学符号为Z={...,-3,-2,-1,0,1,2,3,...}。
整数的性质涉及到整数的四则运算、整数的大小比较以及整数的奇偶性等方面。
下面就对整数的性质进行详细介绍。
一、整数的四则运算1.加法:对于整数a和b,它们的和a+b也是一个整数。
加法满足交换律,即a+b=b+a;加法还满足结合律,即(a+b)+c=a+(b+c)。
2.减法:对于整数a和b,它们的差a-b也是一个整数。
3.乘法:对于整数a和b,它们的积a×b也是一个整数。
乘法满足交换律,即a×b=b×a;乘法还满足结合律,即(a×b)×c=a×(b×c)。
4.除法:对于整数a和b,其中b不等于0,a/b的商可能是一个整数,也可能是一个带有小数部分的数。
二、整数的大小比较1.大小关系:对于两个整数a和b,如果a<b,称a小于b;如果a>b,称a大于b;如果a=b,称a等于b。
2.大于0和小于0:正整数都大于零;负整数都小于零。
三、整数的奇偶性1.奇数:整数中,除了能被2整除的数字外,其他的数字都是奇数。
奇数可以表示为2k+1的形式,其中k为任意整数。
2.偶数:能被2整除的数字为偶数。
偶数可以表示为2k的形式,其中k为任意整数。
3.奇数和奇数的和是偶数,奇数和偶数的和是奇数,偶数和偶数的和是偶数。
四、整数的性质定理1.整数的加法性质:对于任意整数a和b,有a+b=b+a,即整数的加法满足交换律。
2.整数的减法性质:对于任意整数a和b,有a-b=a+(-b),即整数的减法可以转化为加法运算。
3.整数的乘法性质:对于任意整数a、b和c,有(a+b)×c=a×c+b×c,即整数的乘法满足分配律。
4.整数的除法性质:对于任意整数a、b和c,如果a=b×c,且b不等于0,则a除以b的余数为0。
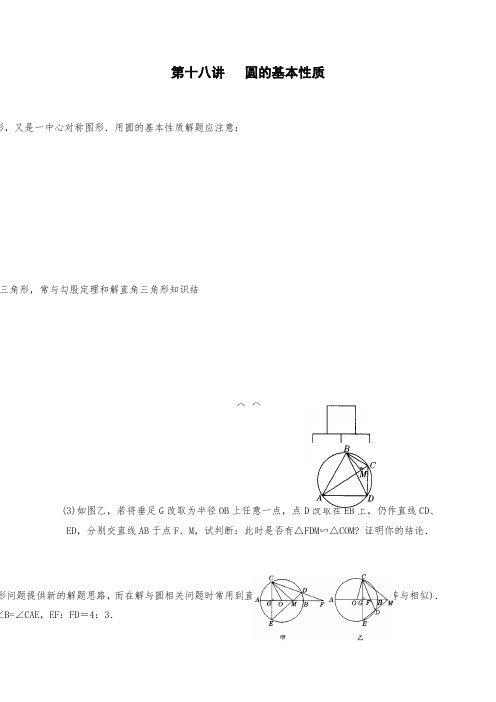
第十八讲圆的基本性质形,又是一中心对称图形.用圆的基本性质解题应注意:
三角形,常与勾股定理和解直角三角形知识结
(3)如图乙,若将垂足G改取为半径OB上任意一点,点D改取在EB上,仍作直线CD、
ED,分别交直线AB于点F、M,试判断:此时是否有△FDM∽△COM? 证明你的结论.
形问题提供新的解题思路,而在解与圆相关问题时常用到直线形的知识与方法(主要是指全等与相似).∠B=∠CAE,EF:FD=4:3.
⌒⌒
⌒
⌒
(3)寻找相似三角形,运用比例线段求出x的值.
圆相关问题的关键.
形A被这些圆所覆盖.
轴对称和中心对称性.
要长、宽都是1cm的正方形小硅片若干.如果晶圆片的直径为10.05cm,问:一张这种晶圆片能否切
中,不写推理过程);
最小值为.
换叫作反演变换,点P与点P′叫做互为反演点.
的周长.
根.
⌒
⌒⌒
⌒。

初中数学竞赛辅导资料倍数约数甲内容提要1两个整数A和B(B≠0),如果B能整除A(记作B|A),那么A 叫做B的倍数,B叫做A的约数。
例如3|15,15是3的倍数,3是15的约数。
2因为0除以非0的任何数都得0,所以0被非0整数整除。
0是任何非0整数的倍数,非0整数都是0的约数。
如0是7的倍数,7是0的约数。
3整数A(A≠0)的倍数有无数多个,并且以互为相反数成对出现,0,±A,±2A,……都是A的倍数,例如5的倍数有±5,±10,……。
4整数A(A≠0)的约数是有限个的,并且也是以互为相反数成对出现的,其中必包括±1和±A。
例如6的约数是±1,±2,±3,±6。
5通常我们在正整数集合里研究公倍数和公约数,几正整数有最小的公倍数和最犬的公约数。
6公约数只有1的两个正整数叫做互质数(例如15与28互质)。
7在有余数的除法中,被除数=除数×商数+余数若用字母表示可记作:A=BQ+R,当A,B,Q,R都是整数且B≠0时,A-R能被B整除例如23=3×7+2则23-2能被3整除。
乙例题例1写出下列各正整数的正约数,并统计其个数,从中总结出规律加以应用:2,22,23,24,3,32,33,34,2×3,22×3,22×32。
解:列表如下正整数正约数个数计正整数正约数个数计正整数正约数个数计21,2231,322×31,2,3,64221,2,43321,3,32322×31,2,3,4,6,126231,2,4,84331,3,32,33422×321,2,3,4,6,9,12,18,369241,2,4,8,165341,3,32,33,345其规律是:设A=a m b n(a,b是质数,m,n是正整数)那么合数A的正约数的个是(m+1)(n+1)例如求360的正约数的个数解:分解质因数:360=23×32×5,360的正约数的个数是(3+1)×(2+1)×(1+1)=24(个)例2用分解质因数的方法求24,90最大公约数和最小公倍数解:∵24=23×3,90=2×32×5∴最大公约数是2×3,记作(24,90)=6最小公倍数是23×32×5=360,记作[24,90]=360例3己知32,44除以正整数N有相同的余数2,求N解:∵32-2,44-2都能被N整除,∴N是30,42的公约数∵(30,42)=6,而6的正约数有1,2,3,6经检验1和2不合题意,∴N=6,3例4一个数被10余9,被9除余8,被8除余7,求适合条件的最小正整数分析:依题意如果所求的数加上1,则能同时被10,9,8整除,所以所求的数是10,9,8的最小公倍数减去1。

装订线初一数学竞赛培优第1讲数论的方法技巧(上)数论是研究整数性质的一个数学分支,它历史悠久,而且有着强大的生命力。
数论问题叙述简明,“很多数论问题可以从经验中归纳出来,并且仅用三言两语就能向一个行外人解释清楚,但要证明它却远非易事”。
因而有人说:“用以发现天才,在初等数学中再也没有比数论更好的课程了。
任何学生,如能把当今任何一本数论教材中的习题做出,就应当受到鼓励,并劝他将来从事数学方面的工作。
”所以在国内外各级各类的数学竞赛中,数论问题总是占有相当大的比重。
数学竞赛中的数论问题,常常涉及整数的整除性、带余除法、奇数与偶数、质数与合数、约数与倍数、整数的分解与分拆。
主要的结论有:1.带余除法:若a,b是两个整数,b>0,则存在两个整数q,r,使得a=bq+r(0≤r<b),且q,r是唯一的。
特别地,如果r=0,那么a=bq。
这时,a被b整除,记作b|a,也称b是a的约数,a是b的倍数。
2.若a|c,b|c,且a,b互质,则ab|c。
3.唯一分解定理:每一个大于1的自然数n都可以写成质数的连乘积,即其中p1<p2<…<p k为质数,a1,a2,…,a k为自然数,并且这种表示是唯一的。
(1)式称为n的质因数分解或标准分解。
4.约数个数定理:设n的标准分解式为(1),则它的正约数个数为:d(n)=(a1+1)(a2+1)…(a k+1)。
5.整数集的离散性:n与n+1之间不再有其他整数。
因此,不等式x<y与x≤y-1是等价的。
下面,我们将按解数论题的方法技巧来分类讲解。
一、利用整数的各种表示法对于某些研究整数本身的特性的问题,若能合理地选择整数的表示形式,则常常有助于问题的解决。
这些常用的形式有: 1.十进制表示形式:n=a n 10n +a n-110n-1+…+a 0; 2.带余形式:a=bq+r ;4.2的乘方与奇数之积式:n=2m t ,其中t 为奇数。
例1 红、黄、白和蓝色卡片各1张,每张上写有1个数字,小明将这4张卡片如下图放置,使它们构成1个四位数,并计算这个四位数与它的各位数字之和的10倍的差。

初中数学竞赛指导数学竞赛中的解技巧分享初中数学竞赛指导:数学竞赛中的解题技巧分享在初中数学竞赛中,掌握一些有效的解题技巧往往能让我们在面对复杂难题时游刃有余,迅速找到解题的突破口。
下面,我将为大家分享一些在初中数学竞赛中常用的解题技巧。
一、仔细审题这是解题的第一步,也是最关键的一步。
很多同学在竞赛中因为紧张或者急于求成,没有认真读懂题目就匆忙下手,结果往往是错误百出或者陷入死胡同。
在审题时,要逐字逐句地读,理解每一个条件和问题的含义。
特别要注意题目中的关键词、限定词和隐藏条件。
例如,“正整数”“不超过”“恰好”等词语往往会对解题产生重要影响。
同时,要善于将文字语言转化为数学语言,画出图形或者列出关系式,帮助我们更直观地理解题目。
二、巧妙运用数学思想1、函数思想函数思想是初中数学竞赛中非常重要的一种思想。
通过建立函数关系,将问题转化为对函数性质的研究,可以使复杂的问题简单化。
例如,对于求最值的问题,可以通过建立函数模型,利用函数的单调性、顶点坐标等性质来求解。
2、方程思想方程是解决数学问题的有力工具。
当遇到等量关系比较明显的问题时,可以设未知数,根据条件列出方程或方程组,然后求解。
比如,行程问题、工程问题等都可以通过方程思想来解决。
3、分类讨论思想当问题的情况不唯一时,需要进行分类讨论。
分类要做到不重不漏,条理清晰。
例如,对于绝对值问题,要根据绝对值内的值的正负情况进行分类讨论;对于等腰三角形的问题,要根据顶角和底角的不同情况进行分类。
4、转化思想将陌生的问题转化为熟悉的问题,将复杂的问题转化为简单的问题,是解决数学竞赛题的常用策略。
比如,将几何问题转化为代数问题,或者将实际问题转化为数学模型。
三、特殊值法当题目中的条件不确定或者比较抽象时,可以采用特殊值法。
选取一些符合条件的特殊值代入题目中进行计算和推理,往往能快速得出答案或者排除错误选项。
例如,对于选择题,如果无法直接得出答案,可以先代入一些简单的特殊值进行验证。

初中数学竞赛辅导资料-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除第一篇 一元一次方程的讨论第一部分 基本方法1. 方程的解的定义:能使方程左右两边的值相等的未知数的值叫做方程的解。
一元方程的解也叫做根。
例如:方程 2x +6=0, x (x -1)=0, |x |=6, 0x =0, 0x =2的解 分别是: x =-3, x =0或x =1, x =±6, 所有的数,无解。
2. 关于x 的一元一次方程的解(根)的情况:化为最简方程ax =b 后, 讨论它的解:当a ≠0时,有唯一的解 x =ab ; 当a =0且b ≠0时,无解;当a =0且b =0时,有无数多解。
(∵不论x 取什么值,0x =0都成立)3. 求方程ax =b (a ≠0)的整数解、正整数解、正数解当a |b 时,方程有整数解;当a |b ,且a 、b 同号时,方程有正整数解;当a 、b 同号时,方程的解是正数。
综上所述,讨论一元一次方程的解,一般应先化为最简方程ax =b第二部分 典例精析例1 a 取什么值时,方程a (a -2)x =4(a -2) ①有唯一的解②无解③有无数多解④是正数解例2 k取什么整数值时,方程①k(x+1)=k-2(x-2)的解是整数?②(1-x)k=6的解是负整数?例3己知方程a(x-2)=b(x+1)-2a无解。
问a和b应满足什么关系?例4a、b取什么值时,方程(3x-2)a+(2x-3)b=8x-7有无数多解?第三部分 典题精练1. 根据方程的解的定义,写出下列方程的解:① (x +1)=0, ②x 2=9, ③|x |=9, ④|x |=-3,⑤3x +1=3x -1, ⑥x +2=2+x2. 关于x 的方程ax =x +2无解,那么a __________3. 在方程a (a -3)x =a 中,当a 取值为____时,有唯一的解; 当a ___时无解;当a _____时,有无数多解; 当a ____时,解是负数。

第18章 整数几何18.1.1★已知ABC △的两条高长分别是5、15,第三条高的长数,求这条高之长的所有可能值. 解析 由面积知,三条高的倒数可组成三角形三边,这是它们的全部条件. 设第三条高为h ,则111,155111.515h h⎧+>⎪⎪⎨⎪+>⎪⎩ 解得151545h <<,h 可取4、5、6、7这四个值. 18.1.2★已知ABC △的三边长分别为3AB n x =+,2BC n x =+,CA n x =+,且BC 边上的高AD 的长为n ,其中n 为正整数,且01x <≤,问:满足上述条件的三角形有几个? 解析 注意AB 为ABC △之最长边,故90B ∠<︒,设BD y =,CD z =,则0y >,而z 可正可负.AB D C由2y z n x +=+,及()()()22223242y z n x n x n x x -=+-+=+⋅,得4y z x -=,32ny x =+,由勾股定理,知()222332n x n n x ⎛⎫++=+ ⎪⎝⎭,展开得12n x =,由01x <≤及n 为正整数,知1n =,2,…,12,这样的三角形有12个.18.1.3★已知一个直角三角形的三条边均为正整数,其中一条直角边不超过20,其外接圆半径与内切圆半径之比为52∶,求此三角形周长的最大值.解析 设该直角三角形直角边长为a 、b ,斜边为c ,则外接圆半径2cR =,内切圆半径2a b cr +-=,不妨设20a ≤. 由条件知52c a b c =+-,557a b c +=,平方,得()()222225249a b ab a b ++=+,即()2212250a b ab +-=,()()34430a b a b --=,于是3a k =,4b k =,5c k =,或4a k =,3b k =,5c k =,周长为12k ,k 为正整数.k 的最大值为6,此时各边为18、24、30,周长最大值为72.18.1.4★ABC △为不等边三角形,60A ∠=︒,7BC =,其他两边长均为整数,求ABC △的面积.A BCx y60°解析设AB x =,AC y =,则由余弦定理,有2249x y xy +-=.由条件x y ≠,不妨设x y <,则AB 为ABC △之最小边,x 只能取值1、2、3、4、5、6,分别代入,发现当3x =或5时,8y =,其余情形均无整数解.于是1sin 602ABC S xy =︒=△. 18.1.5★★一点P 与半径为15的圆的圆心距离是9,求经过P 且长为整数的弦的条数. 解析 如图,O 半径为15,9OP =,过P 的弦ST 长为整数,APB 为直径,6AP =,24PB =,则144SP TP PA PB ⋅=⋅=,因此24ST SP TP =+≥.又30ST AB =≤,故这样的弦共有()302412212-+⨯-=条,其中与AB 垂直的弦及AB 各一条,其余的弦每种长度有两条(关于AB 对称).18.1.6★★在直角三角形ABC 中,各边长都是整数,90C ∠=︒,CD 为边AB 上的高,D 为垂足,且3BD p =(p 奇素数),求ACAB的值(用p 表示). C解析由2BC BD AB =⋅知2BD BC ,故设2BC p t =(t 为正整数),则2BA pt =,又由勾股定理,知22442AC p t p t =-,故tp AC .设AC kpt =,代入得()()222p t k t k t k =-=+-,易知只能有2t k p +=,1t k -=,解得212p t +=,212p k -=,于是2211AC p AB p -=+. 18.1.7★★设正三角形ABC ,M 、N 分别在AB 、AC 上,MN BC ∥,两端延长MN ,交ABC △外接圆于P 、Q ,若PM 、MN 、AB 长均为正整数,求AB 的最小值. 解析 如图, 易知NQ PM =也是整数.设AM x =,BM y =,PM NQ z ==,则M N x =,于是由相交弦定理,得()xy z x z =+,2z x y z=-.APQM NB C设y ks =,z kt =,(),k y z =,s t >,(),1s t =,则2kt x s t=-,由于()2,1s t t -=,故s tk -,要使2t AB x y k ks s t=+=+-达到最小,k 得取s t -,于是()2AB t s t s =+-.由于s t >,2s ≥,1t ≥,知()223t s t s t s +-+≥≥.当1AM =,2BM =时AB 取到最小值3,此时1PM =.18.1.8★★已知凸四边形ABCD 的四边长是两两不相等的整数,对边乘积之和等于四边形面积的两倍,且22250AD BC +=,求该四边形面积、对角线长度. 解析 不妨设AB α=,BC b =,CD c =,DA d =,AC 与BD 交于O ,则sin 2ABCD AC BD AOB S ac bd AC BD ⋅⋅∠==+⋅≥,于是由托勒密定理,知A 、B 、C 、D 必共圆,且满足AC BD ⊥.又由已知条件,22250b d +=,22250a c +=.经搜索知250表为平方和只有两组:22515+和22913+.由对称性,不妨设5a =,13b =,15c =,9d =,则19622ABCD ac bdS AC BD +=⋅==.由余弦定理,因cos cos 0BAD BCD ∠+∠=,得222222591315045195B D B D +-+-+=,得BD =AC18.1.9★★是否存在一个三边长恰是三个连续正整数,且其中一个内角等于另一个内角2倍的ABC △?证明你的结论. 解析 存在满足条件的三角形.当ABC △的三边长分别为6a =,4b =,5c =时,2A B ∠=∠.如图,当2A B ∠=∠时,延长BA 至点D ,使AD AC b ==.连结CD ,ACD △为等腰三角形.CD A因为BAC ∠为ACD △的一个外角,所以2BAC D ∠=∠.由已知,2BAC B ∠=∠,所以B D ∠=∠.所以CBD △为等腰三角形.又D ∠为ACD △与CBD △的一个公共角,有~ACD CBD △△,于是AD CD CD BD =,即b aa b c=+,所以()2a b b c =+.而()26445=⨯+,所以此三角形满足题设条件,故存在满足条件的三角形. 评注满足条件的三角形是唯一的.若2A B ∠=∠,可得()2a b b c =+.有如下三种情形:(ⅰ)当a c b >>时,设1a n =+,c n =,1b n =-(n 为大于1的正整数),代入()2a b b c =+,得()()()21121n n n +=--,解得5n =,有6a =,4b =,5c =;(ⅱ)当c a b >>时,设1c n =+,c n =,1b n =-(n 为大于1的正整数),代入()2a b b c =+,得()212n n n =-⋅.解得2n =,有2a =,1b =,3c =,此时不能构成三角形;(ⅲ)当a b c >>时,设1a n =+,b n =,1c n =-(n 为大于1的正整数),代入()2a b b c =+,得()()2121n n n +=-,即2310n n --=,此方程无整数解.所以,三边长恰为三个连续的正整数,且其中一个内角等于另一个内角的2倍的三角形存在,而且只有三边长分别为4、5、6构成的三角形满足条件.18.1.10★★三边长为连续整数、周长不大于100、且面积是有理数的三角形共有多少个? 解析 设三角形三边依次为1n -、n 、1n +,则333n ≤≤,()131122p n n n n =-+++=,S △==于是()234n -是平方数,令()()22343n k -=,得2243n k -=,则32n ≤,224102034033n k -==≤,18k ≤.又k 不可能是奇数,否则()222343n k k =+≡,得2243n k -=,则32n ≤,224102034033n k -==≤,18k ≤.又k 不可能是奇数,否则()22343mod 4n k =+≡,将2k =,4,6,8,10,12,14,16,18代入,发现仅当2k =,8时满足要求.因此这样的三角形共有两个,三边长依次为3、4、5与13、14、15.18.1.11★★某直角三角形边长均为整数,一直角边比斜边小1575,求其周长的最小值. 解析 设直角三角形直角边长a 、b ,斜边为1575a +,则 ()2221575a b a +=+,()2157521575b a =+.由于221575357=⨯⨯,设105b k =,则2721575k a =+,设7a s =,则22225k s =+,于是k 的最小值为17,此时32s =,224a =,1785b =,1799c =.此时的最小周长为3808. 18.1.12★★已知ABC △,AD 是角平分线,14AB =,24AC =,AD 也是整数,求AD 所有可取的值.AEB DC解析 如图,作DE AB ∥,E 在AC 上,则易知AE ED =. 又ED CD AC AB BC AB AC==+,故 22AB ACAD AE DE ED AB AC⋅<+==+33617.6819==…, 故17AD ≤.又当17AD ≤时,不难通过AED △构造出ABC △,故AD 所有可取的值为1,2, (17)18.1.13★面积为c 的正方形DEFG 内接于面积为1的正三角形ABC ,其中a 、b 、c 是整数,且b 不能被任何质娄的平方整除,求a cb-的值.ADGB E F C解析设正方形DEFG 的边长为x ,正三角形ABC 的边长为m ,则2m ,由ADG ABC △∽△,可得xx m -=.解得()3x m =.于是()222348x m ==.由题意得28a =,3b =,48c =,所以203a cb -=-. 17.1.14★★如图,AD 是ABC △的高,四边形PQRS 是ABC △的内接正方形,若BC ab =(即两位数),SRc =,ADd =,且a 、b 、c 、d 恰为从小到大的4个连续正整数,求ABC S △的所有可能值.AS RP D Q解析易知11SR AR CR SR BC AC AC AD ==-=-,于是有110c c a b d +=+,或1111132a a a +=+++,移项,得()()1111123a a a =+++,或2650a a -+=,解得1a =或5.于是有两解: 12,3,4;BC SR AD =⎧⎪=⎨⎪=⎩56,7,8.BC SR AD =⎧⎪=⎨⎪=⎩易知这两组数据都符合要求,故24ABC S =△或224.18.1.15★★已知ABC △中,B ∠是锐角.从顶点A 向BC 边或其延长线作垂线,垂足为D ;从顶点C 向AB 边或其延长线作垂线,垂足为E .当2BD BC 和2BEAB均为正整数时,ABC △是什么三角形?并证明你的结论. 解析设2BD m BC =,2BEn AB=,m 、n 均为正整数,则 244cos 4BD BE mn B AB BC=⋅⋅=<, 所以,1mn =,2,3. (1)当1mn =时,1cos 2B =,60B ∠=︒,此时1m n ==.所以AD 垂直平分BC ,CE 垂直平分AB ,于是ABC △是等边三角形.(2)当2mn =时,cos B =45B ∠=︒,此时1m =,2n =,或2m =1n =,所以点E 与点A 重合,或点D 与点C 重合.故90BAC ∠=︒,或90BCA ∠=︒,于是ABC △是等腰直角三角形.(3)3mn =时,cos B =,30B ∠=︒,此时1m =,3n =,或3m =,1n =.于是AD 垂直平分BC ,或CE 垂直平分AB .故30ACB ∠=︒,或30BAC ∠=︒,于是ABC △是顶角为120︒的等腰三角形.18.1.6★★某直角三角形两直角边长均为整数,周长是面积的整数倍(就数字上讲),问问这样的直角三角形有多少个?解析 设直角边分别为a 、b ,则斜边c =,由条件知它是有理数,故必定是整数.设2ka b ab +=,k 为正整数,于是k =.由于a b +1、2或4,记作k '.由a b k +-'=()2220ab k a b k -'++'=,()()22a k b k k -'-'=',1k '=时无解;2k '=时,有()()222a b --=,{a ,b }={3,4};4k '=时,()()448a b --=,{a ,b }={5,12}或{6,8},所以这样的直角三角形共有3个. 18.1.17★★在等腰ABC △中,已知AB AC kBC ==,这里k 为大于1的自然数,点D 、E 依次在AB 、AC 上,且DB BC CE ==,CD 与BE 相交于O ,求使OCBC为有理数的最小自然数k .ADEBCO解析如图,连结DE ,则DE BC ∥,11DE AD AB BC BC AB AB k -===-,1k DE BC k-=. 由于四边形DBCE 为等腰梯形,则由托勒密定理(或过D 、E 作BC 垂线亦可),2222121k k CD CD BE DE BC DB CE BC BC BCk k --=⋅=⋅+⋅=+=,又21CO BC kCD DE BC k ==+-,于是CO BC =k 与21k -互质,由题设知其必须均为平方数,1k >,25k =适合,这是满足要求的最小自然数.18.1.18★★★对于某些正整数n 来说,只有一组解xyz n =(不计顺序),这里,x 、y 、z 是正整数且可构成三角形的三边长,这样的()100n ≤共有多少个? 解析显然,当n p =(素数)时无解;当2n p =或1时只有一组解(1,p ,p )或(1,1,1);当n pq =(p 、q 为不同素数)时无解;当4n p =(p 为大于3的素数)时也无解.剩下的数为8,12,16,18,24,27,30,32,36,40,42,45,48,50,54,56,60,63,64,66,70,72,75,78,80,81,84,88,90,96,98,99,100. 易验证,无解的n 有:30,42,54,56,63,66,70,78,88,99;唯一解的n 有:8,12,16,18,24,27,32,40,45,48,50,75,80,81,84,90,96,98;不止一组解的n 有:36,60,64,72,100.注意:判定无解的主要依据是,abc n =,c ab >时无解,困为1c ab a b ++≥≥. 因此,有解的n 共有23个.18.1.19★★面积为整数的直角三角形周长为正整数k ,求k 的最小值,并求此时这个直角三角形的两条直角边的可取值(如不止一组解,只需举了一组即可).解析设该直角三角形的直角三角形周长分别为a 、b ,则112ab ≥,a b +≥2,2k a b =+,故5k ≥.下令5k =,2ab =,如有解,则可.()5a b -+,平方得()222225102a b a b a b ab +=-++++.取2ab =,得29,102.a b ab ⎧+=⎪⎨⎪=⎩因此a 、b 为方程21029200x x -+=的根,解得a 、bk 的最小值是5.18.1.20★★若ABC △的三边长a 、b 、c 均为整数,且140abc =,求ABC △内切圆半径. 解析 不妨设a b c ≤≤,于是7c ≥.又14011c a b ab c<++=+≤,故140c c ≤,得10c ≤.于是c 只可能为7或10. 7c =时,20ab =,只可能4a =,5b =,()182p a b c =++=,内切圆半径r =. 10c =时,14ab =,没有满足要求的解.18.1.21★★证明:若a 、b 、c 是一组勾股数()222a b c +=,则存在正整数k 、u 、v 、u v >,(),1u v =使得()22c k u v =+,而()22a k u v =-,2b kuv =;或2a kuv =,()22b k u v =-.解析222a b c +=,设(a ,b ,c )k =,则1a ka =,1b kb =,1c kc =,222111a b c +=.易知1a 、1b 、1c 两两互质;1a 与1b 不可能同偶,否则12a ,1b ,1c ;1a 与1b 也不会同奇,否则()212mod 4c =,矛盾.于是1a 与1b 必一奇一偶,不妨设1a 奇而1b 偶,于是1c 为奇数.从而()()211111a c b c b =+-,11c b +与11c b -必互质,否则有一奇素数11|p c b +,11c b -,得|2p c ,12b ,故|p (1c ,1b ),与(1c ,1b )=1矛盾. 于是可设2111c b u +=,2111c bv -=,(1u ,1v )=1,且1u 、1v 均为奇数,解得221111122u v u v c +-⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭,11111222u v u v b +-=⋅⋅,221111122u v u v a +-⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭,令112u v u +=,112u v v -=,即得结论. 18.1.22★★★如图,F 、E 在ABC △的边AB 、AC 上,FE 的延长线与BC 的延长线交于D ,求证:AF 、BF 、CB 、CD 、AE 、EC 、FE 、ED 的长度不可能是1~8的排列. 解析 如果1EF =,则1A E A F E F -<=,得A E A F =,矛盾,故1EF ≠,同理AF 、AE 、ED 、CD 、EC 都不等于1.AFE GDCB因此1只可能等于FB 或BC 之长,不失对称性,设1BF =,则1FD BD BF -<=,FD BD =,作CG AB ∥,G 在ED 上,四边形FBCG 乃一等腰梯形,于是EG FG EF BC EF =-=-为正整数.又1EG EC CG BF -<<=,故E G E C =,但BFD ∠为等腰三角形DFB 的底角,90BFD <︒∠,18090EGC BFD =︒->︒∠∠,为EGC △的最大内角,EC EG >,矛盾,因此结论证毕.18.1.23★★★已知梯形ABCD 中,AD BC <,E 、F 分别在AB 、CD 上,EF AD BC ∥∥,ED BF ∥,如果AD 、EF 、BC 均为正整数,称该梯形为“整数梯形”.现对于正整数n ,有正整数x x <′<y ′<y ,x y x +=′+y ′=n ,且x 、y 为一“整数梯形”的上、下底, x ′、y ′为另一“整数梯形”的上、下底,求n 的最小值.解析 如图,由AED EFD △∽△,DEF FBC △∽△,得AD AE DF EFEF BE FC BC===,得E F C =,于是问题变为求最小的n ,使xy 与x ′y ′均为平方数. A DEFB Cxy 、x ′y ′不可能都为4,故至少有一组≥9,显然另一组也不可能为4,于是xy ,x ′y ′≥9.如果xy 或x ′y ′25≥,则10n =≥.若xy 或x ′y ′=9或16,则19n =+或2810+=.于是n 的最小值为10,1x =,x ′=2,y ′=8,y =9.18.1.24★★★求证:存在无穷多个每边及对角线长均为不同整数的、两两不相似的凸四边形.ABDPC解析 如图,作圆内接四边形ABCD ,AC 与BD 垂直于P ,设a 为一整数,2a >,4AP a =,24BP a =-,241DP a =-,则24AB a =+,241AD a=+,,由此知()()224414aa CP a--=,而由ABP DCP △∽△,BPC APD △∽△知,()224414a BC a a -=+,()224144a CD a a -=+.同时乘以系数4a ,得()244AB a a =+,()2441AD a a =+,()()22441BC a a =-+,()()22414CD a a =-+,4244AC a a =-+,()2201BD a a =-.易知上述6个多项式无二者恒等,于是任两者相等只能得有限个a ,但正整数有无限个,因此有无限个a ,使6个多项式两两不等,又当a →+∞时,0BDAC→,因此有无限个这样的凸四边形两两不相似. 18.1.25★★★已知PA 、PB 为圆的切线,割线过P ,与圆交于M 、N ,与AB 交于S ,若PA 、PM 、MS 、SN 均为正整数,求PA 的最小值.PMABSN解析 如图,易知有PM PNMS SN=(调和点列). 设PM a =,MS b =,SN c =,则()b ab c a ++=,()b c b c a b+=-,从而PA = 设a ks =,b kt =,k =(a ,b ),则(s ,t )=1,s t >,s tc kts t+=-,PA =易见(s t +,s t -)=1,则s 、t 一奇一偶.于是由(()t s t +,s t -)=1,得|s t k -,且由PA 为整数知2s t x +=,2s t y -=,x 、y 为奇数.因为|s t k -,于是k 的最小值为s t -,()c t s t =+,PA sxy ==,当s =1,2,3,4时,t 无解(即PA 不是整数),故5s ≥,又3x ≥,1y ≥,于是PA ≥15,当a =5,b =4,c =36时取到15PA =.若(s t +,s t -)=2,此时s 、t 同奇,k 的最小值为2s t-,此时()2t s t c +=,PA =22s t x +=,22s t y -=,当1s =,3时,无t 使PA 为整数,于是5s ≥,又x y >,所以1y ≥,2x ≥,5210PA sxy =⨯=≥.当5a =,3b =,12c =时取到PA =10. 综上,PA 的最小值是10.18.1.26★★★一圆内接四边形的四边长及对角线长都是整数,求这类四边形中周长最小者. 解析 显然长与宽为4、3的矩形满足要求,其周长=14.若等腰梯形上、下底分别为3、4,腰为2,则由托勒密定理,对角线长为4,满足要求,此时周长为11.故最小周长≤11. 显然对圆内接凸四边形ABCD ,无边长为1.否则若设1AB =,—1AD BD AB <=,得AD BD =,同理AC CB =,于是C 、D 均在AB 中垂线上,构不成凸四边形.因此最小周长≥2×4=8.四边均为2,得正方形,对角线为2,另一边为3,得等腰梯形,10.当周长为10时,显然至少有两边为2.若是2、2、2、4能为2、2、3、3故最小周长为11.18.1.27★★★在Rt ABC △中,90BCA =︒∠,CD 是高,已知ABC △的三边长都是整数,且311BD =,求BCD △与ACD △的周长之比.CB D A解析 设ABC △的三边长分别为a 、b 、c .由题设知 2BC BD BA =⋅,故2311a c =.于是设211a l =,得211l c =由勾股定理得11b ==2211l -是 完全平方数,设为()20t t >,则22211l t -=,()()211l t l t -+=.由于0l t l t <-<+,所以21,11.l t l t -=⎧⎨+=⎩解得61,60.l t =⎧⎨=⎩于是21161a =⨯,116160b =⨯⨯. 因为BCD CAD △∽△,所以它们的周长比等于它们的相似比,即1160a b =.18.1.28★★★已知锐角三角形ABC 中,AD 是高,矩形SPQR 的面积是ABC △的1/3,其顶点S 、P 在BC 上,Q 、R 分别在AC 、AB 上,且BC 、AD 及矩形SPQR 的周长均为有理数,求AB ACBC+的最小值. 解析 如图,设ABC △的三边长依次为a 、b 、c ,AD h =,PQ x =,RS y =,则16xy ah =,及1x y AQ CQ a h AC AC+=+=.由条件,知a 、h 、x y +均为有理数. AR QB S D P C由16x a a x+=,得x a =,33y h =,)2a h x y a h ++=-,因此只能有a h =.若过A 作BC 的平行线l ,再作C 关于l 的对称点C ',则AB AC AB AC +=+′≥BC ′,于是AB ACBC+,仅当AB AC =时取到. 18.1.29★★★★整数边三角形ABC 中,90BAC =︒∠,AD 是斜边上的高,BD 也是整数.若对同一个BD 能长度,有两个不全等的直角整数边三角形ABC 满足要求,求BD 的最小值.解析 不妨设ABC △的三边长为a 、b 、c ,AD h =,BD d =,首先bch a=为有理数,又222h c d =-为整数,因此h 也是整数.又CD 为整数,故2h d也是整数.又ABD CBA △∽△,故h b d c=. AB D C因此,只需正整数h 、c 、d 满足222h c d =-及2|d h ,这样的整数边三角形就存在.因为此时hcb d=是有理数,而222b h CD =+为整数,从而b 为整数.易知由2|d h 可得2|d c . 设21d d σ=,σ、1d 为正整数,且σ无平方因子,于是由2|h σ及2c 知|h σ,c .设1h h σ=,1c c σ=,代入得422111d c h =-,又由2|d h ,2c 得2211|d h σ,21c σ,今对1d 的任一素因子p ,其在1d 的指数()1s d 不会比1h 的指数高,否则()()111s d s h +≥,()()22112s d s h +≥,而()s σ最多为1,于是()()2211s d s h σ>,这是不可能的.于是11|d h ,同理11|d c .又令112h d h =,112c d c =,代入422111d c h =-得222122d c h =-. 于是对1d 有两组不同的2c 、2h 满足222122d c h =-.经计算18d ≥,故64d ≥.当64d =时,确实有满足要求的两组解:80AB =,60AC =,100BC =,和136AB =,255AC =,289BC =.故BD 的最小值是64.18.1.30★★★★试找一不等边三角形ABC ,使BC 及BC 边上的中线、角平分线、高的长度都是整数,BC 可以是多少(此时的中线、角平分线、高的长度分别为多少)?若要求BC 不是整数,但2BC 是整数,则BC 可为多少(此时中线、角平分线、高的长度分别为多少)?解析 首先处理BC 为整数的问题,我们选择的是直角三角形ABC ,对应边为a 、b 、c ,中线AM ,角平分线AD ,高AH ,2aAM =,bc AH a =,又ABC ABD ACDS S S =+△△△,得)2bc b c AD =+,故AD b c =+,于是a 为偶数2k ,b =,c =,mn AH k =而2mn AD m n =+,2222m n k +=,这个方程有解1m =,7n =,5k =,得75AH =,5AM =,74AD =.乘以一个系数20,即得直角三角形ABC ,它的斜边为200,斜边上的中线为100,角平分线为35,高为28.下面处理BC 为无理数、2BC 为整数的情形,如图,延长AD ,与MP 交于P ,此处MP BC ⊥.易知A 、B 、P 、C 共圆(P 是ABC △外接圆弧BC 之中点).今从基本勾股数出发构造.取12AH =,13AD =,15AM =,则5DH =,9MH =,4MD =,485MD MP AH HD =⋅=,45255PD AD ==. ABMD HCP易知BPD APB △∽△,于是25211760845525BP PD PA =⋅=⨯=,()22222608448302444425255BC BM PB MP ⎛⎫==-=-= ⎪⎝⎭. 再乘以系数5,得所求三角形的高60AH =,角平分线65AD =,中线75AM =,边BC =是无理数,但15120BC =.18.1.31★★作圆外切凸五边形ABCDE ,现知该五边形每边长均为整数,1AB =,又圆与BC 切于K ,求BK .解析 如图,设CD 、DE 、EA 、AB 分别与圆切于P 、Q 、R 、S .则RE DP ED +=为整数,于是由题设,AR CP +亦为整数,而AR CP AS KC +=+.于是22BK BS BK BS ==+为整数,由于1BS AB <=,故22BS <,221BK BS ==,12BK =. A S RB EQ K CPD。

攀登杯竞赛考试数学复习要点第一节:绝对值第一类题型:去绝对值符号化简.【例1】(1) 若x <﹣2,则|1﹣|1+x||= .(2)已知1=a ,2=b ,3=c ,且c b a >>,那么c b a -+= .(3)非零整数m 、n 满足05=-+n m ,所有这样的整数组),(n m 共有______组.(4)已知d d =-,化简12d d ---所得的结果是________.(5) 若2x+|4-5x |+|1-3x |+4的值恒为常数,则x 取值范围是 .【例2】(1) 如果是非零有理数,且0=++c b a ,那么abc abc c c b b a a +++的所有可能的值为( ).A .0B . 1或1-C .2或2-D .0或2-(2)若c b a 、、为整数,且19919=-+-a c ba ,求cb b a ac -+-+-的值.c b a 、、【例3】化简 (1)12-x (2)31-+-x x (3)1331++--x x第二类题型:含绝对值式子求最值问题.【例4】(1)整数a,b,c,d 满足28,318,510,a b b c c d =+=-=+则7d a +的最小值为(2)设由1到8的自然数写成的序列12,,,,n a a a ⋅⋅⋅则1223347881a a a a a a a a a a -+-+-+⋅⋅⋅+-++的最大值为【例5】已知36)13)(12)(21(=++-++--++z z y y x x ,求z y x 32++的最大值和最小值.【例6】(1)代数式131211++-++x x x 的最小值为_____.(2)代数式4321-+-+-+-a a a a 的最小值为 .(3)If a <b <c ,ac <0 and <<,then the minimum of is .【例7】(1) 代数式122015x x x -+-+⋅⋅⋅+-的最小值是多少? 并求此时x 的范围;(2) 求当12131201x x x x -+-+-+⋅⋅⋅+-取最小值时x 的范围?【例8】已知|x|≤1,|y|≤1,设M=|x+y|+|y+1|+|2y ﹣x ﹣4|,求M 的最大值与最c b a c x b x a x ++-+-小值.【例9】已知y=|2x+6|+|x-1|-4|x+1|,求y 的最大值.第二节: 实数运算【例1的平方根是 .【例2】已知实数a 满足21999,1999a a a -=-=则 .【例3】已知22(4)0,x y -++=求()y xz 平方根.变式:1.已知实数211,,a-b 0,24c a b c c c ab -+=满足则的算术平方根是 .2.=在实数范围内成立,其中a 、x 、y 是两两不相等的实数,则22223x xy y x xy y +--+的值是 .3.已知4,1x y y x +=+则= .4.若,,x y m试求4m-的算数平方根.【例4a,小数部分为b,求2-16ab-8b的立方根.+++⋅⋅⋅+【例5】计算:【例6】由下列等式:===…… 所揭示的规律,可得出一般的结论是 .第三节: 方程及方程组【例1】已知()()063922=+---x m x m 是以x 为未知数的一元一次方程,如果m a ≤,那么m a m a -++的值为_________【例2】已知⎩⎨⎧=-=12y x 是方程⎩⎨⎧=++=-274123ny x y mx 的解,则______________==n m【例3】解方程:(1)()()b x a x a 3512+-=- (2)8453=+-x【例4】解下列方程组(1)()⎩⎨⎧=+=++22422y x y x x (2)⎪⎩⎪⎨⎧-=+=-++441511y x y x【例5】m 取何整数值时,方程组⎩⎨⎧=+=+1442y x my x 的解x 和y 都是整数?【例6】已知关于x ,y 的方程组111456ab bc ca a b b c c a ===+++,,分别求出当a 为何值时,方程组(1)有唯一一组解;(2)无解;(3)有无穷多组解.【例7】已知a 、b 、c 为实数,且求a+b+c 的值.【例8】解方程组12233420152016201620171220162017...1...2017x x x x x x x x x x x x x x +=+=+==+=+=⎧⎨++++=⎩.【例9】已知正数f e d c b a ,,,,,满足41,16,9,4====d abcef c abdef b acdef a bcdef ,161,91==f abcde e abcdf .求()()f d b e c a ++-++的值.【例10】(1) 设,则 .(2) 已知882210322)2()1()1()7()1(++⋅⋅⋅+++++=-+x a x a x a a x x ,则7654321a a a a a a a +-+-+-= .【例11】(1),12=+x x 求200522234+--+x x x x 的值.(2)如果05-2=+x x ,则3223++x x = .【例12】(1)[]x 表示不大于x 的最大整数,若5104=⎥⎦⎤⎢⎣⎡+x ,则x 的取值范围是 (2)解方程:[]21213-=+x xf ex dx cx bx ax x +++++=+23455)13(=-+-+-f e d c b a【例13】(河南省竞赛题)若关于x 的方程9x -17=kx 的解为正整数,则k 的值为k =第四节: 不等式及不等式组【例1】关于x 的不等式06>+--x k 的正整数解为1,2,3,那么k 的取值范围是 .变式1.不等式03≤-a x 的正整数解为1,2,3,那么a 的取值范围是 .2.关于x 的不等式组23(3)1324x x x x a <-+⎧⎪⎨+>+⎪⎩ 有四个整数解,则a 的取值范围是 .3.已知关于x 的不等式组302x a b x -≥⎧⎪⎨<⎪⎩的整数解有且只有4个:-1, 0, 1, 2,那么适合这个不等式组的所有可能的整数对(a,b )共有多少个?【例2】关于x 的不等式05)2(>-+-b a x a b 的解为710<x ,试求032)4(>-+-b a x b a 的解.【例3】若不等式组841x x x m+<-⎧⎨≥⎩的解是x>3,则m 的取值范围是 .变式:若关于x 的不等式组⎪⎩⎪⎨⎧+++01456m <x x >x的解集为4x <,则m 的取值范围是 .【例4】已知不等式125-+x >22+ax 的解是x >21-的一部分,试求a 的取值范围.【例5】若x+y+z=30,3x+y -z=50,x,y,z 均为非负数,求M=5x+4y+2z 的最大值和最小值.【例6】已知非负数a ,b ,c 满足3a+2b+c=5和2a+b-3c=1,若m=3a+b-7c , 求m 的最小值和最大值.【例7】若不等式a x x ≤-+-3312有解,求实数a 的最小值【例8】若方程019971997=--x x a 只有负数根,求a 的取值范围.【例9】若b a ,满足b a s b a 32,75322-==+,求s 的取值范围.【例10】求证:2222111171234n ++++<L【例11】已知19911198311982119811198011+⋅⋅⋅++++=S ,求 S 的整数部分.第五节:应用题【例1】一队旅客乘坐汽车,要求每辆汽车的旅客人数相等.起初每辆汽车乘了22人,结果剩下1人未上车;如果有一辆汽车空着开走,那么所有旅客正好能平均分乘到其他各车上.已知每辆汽车最多只能容纳32人,求起初有多少辆汽车?有多少名旅客?【例2】有一水库,在单位时间内有一定量的水流进,同时也向外放水,按现在的进出水量,水库中的水可使用40天,因最近在水源的地方降雨,流入水库的水量增加20%,如果放水量增加10%,则仍可使用40天,如果按原来的放水量放水,可使用多少天?【例3】有一个两位数,它的十位数字与个位数字的和是8,并且这个两位数除以十位上的数字与个位上的数字的差,所得的商为11,余数为5,求这个两位数.【例4】甲、乙、丙三个容器中盛有含盐比例不同的盐水。

初中数学竞赛知识点总结一、整数1. 整数的概念整数包括正整数、负整数和0。
整数的绝对值表示这个整数到0的距离。
2. 整数的加减法同号两个整数相加或相减,与它们的绝对值的和或差的符号相同;异号两个整数相加或相减,用绝对值相减,结果的符号取绝对值较大的数的符号。
3. 整数的乘法同号两个整数相乘,其积为正;异号两个整数相乘,其积为负。
4. 整数的除法两个不为0的整数相除,商为0时,除数与被除数的符号相同;商不为0时,商的符号与除数与被除数的符号相反。
5. 整数的乘方整数a的n次幂,即a的n次方,是指n个a的乘积。
其中,a是底数,n是指数。
a的0次方等于1。
6. 整数的除法两个整数相除,可以转换为乘法。
例如,a ÷ b = a × (1/b)。
其中,a为被除数,b为除数,1/b为倒数。
7. 整数的分数形式若a和b是整数且b≠0,则数a/b称为有理数。
8. 整数的倍数若b是a的整数倍,则b是a的倍数,a是b的约数。
9. 整数的绝对值整数a的绝对值,记作|a|,是a到0的距离。
如果a≥0,则|a|=a;如果a<0,则|a|=-a。
10. 整数的比大小当两个整数比大小时,可以比较它们的绝对值,绝对值较大的数比较大;若两个数的绝对值相等,则比较它们的正负。
11. 整数的应用整数在实际生活中有着广泛的应用,例如温度的正负、方向的左右等。
整数的应用能够帮助我们更好地理解和解决问题。
二、有理数1. 有理数的概念既包括整数,也包括分数的数为有理数。
2. 有理数的加减法有理数的加减法规则与整数的加减法规则相同。
3. 有理数的乘法有理数的乘法规则与整数的乘法规则相同。
4. 有理数的除法有理数的除法规则与整数的除法规则相同。
5. 有理数的乘方有理数的乘方规则与整数的乘方规则相同。
6. 有理数的应用有理数在实际生活中有着广泛的应用,能够帮助我们更好地理解和解决问题。
三、分数1. 分数的概念分数是用整数除法表示的数,由分子和分母组成。

初中数学竞赛辅导讲义及习题解答含答案共30讲改好278页初中奥数辅导讲义培优计划(星空课堂)第一讲走进追问求根公式第二讲判别式——二次方程根的检测器第三讲充满活力的韦达定理第四讲明快简捷—构造方程的妙用第五讲一元二次方程的整数整数解第六讲转化—可化为一元二次方程的方程第七讲化归—解方程组的基本思想第八讲由常量数学到变量数学第九讲坐标平面上的直线第十讲抛物线第十一讲双曲线第十二讲方程与函数第十三讲怎样求最值第十四讲图表信息问题第十五讲统计的思想方法第十六讲锐角三角函数第十七讲解直角三角形第十八讲圆的基本性质第十九讲转化灵活的圆中角2第二十讲直线与圆第二十一讲从三角形的内切圆谈起第二十二讲园幂定理第二十三讲圆与圆第二十四讲几何的定值与最值第二十五讲辅助圆第二十六讲开放性问题评说第二十七讲动态几何问题透视第二十八讲避免漏解的奥秘第二十九讲由正难则反切入第三十讲从创新构造入手3第一讲走进追问求根公式形如a某2b某c0(a0)的方程叫一元二次方程,配方法、公式法、因式分解法是解一元二次方程的基本方法。
而公式法是解一元二次方程的最普遍、最具有一般性的方法。
求根公式某1,2bb24ac内涵丰富:它包含了初中阶段已学过的全部代数运算;它回答了2a一元二次方程的诸如怎样求实根、实根的个数、何时有实根等基本问题;它展示了数学的简洁美。
降次转化是解方程的基本思想,有些条件中含有(或可转化为)一元二次方程相关的问题,直接求解可能给解题带来许多不便,往往不是去解这个二次方程,而是对方程进行适当的变形来代换,从而使问题易于解决。
解题时常用到变形降次、整体代入、构造零值多项式等技巧与方法。
【例题求解】【例1】满足(n2n1)n21的整数n有个。
思路点拨:从指数运算律、±1的特征人手,将问题转化为解方程。
【例2】设某1、某2是二次方程某2某30的两个根,那么某134某2219的值等于()A、一4B、8C、6D、0思路点拨:求出某1、某2的值再代入计算,则计算繁难,解题的关键是利用根的定义及变形,使多项式降次,如某123某1,某223某2。

初中数学总复习资料答案初中数学总复习资料答案数学是一门需要不断练习和巩固的学科,为了帮助同学们更好地复习数学知识,我们为大家准备了初中数学总复习资料答案。
希望这些答案能够帮助同学们更好地理解和掌握数学知识。
一、整数与有理数1. 整数的概念与性质整数包括正整数、负整数和0,它们在数轴上呈现出对称的特点。
整数的加法、减法和乘法满足结合律、交换律和分配律。
2. 有理数的概念与性质有理数包括整数和分数,它们可以表示为有限小数、无限循环小数和无限不循环小数。
有理数的加法、减法、乘法和除法满足相应的运算规律。
二、代数式与方程式1. 代数式的概念与性质代数式由变量、常数和运算符号组成,可以进行加减乘除等运算。
代数式可以化简、展开和因式分解,方便计算和解题。
2. 方程式的概念与性质方程式是含有未知数的等式,可以通过变换等式的形式来求解未知数的值。
方程式可以是一元一次方程、一元二次方程等,求解方程式需要运用代数运算和方程变形的方法。
三、几何与图形1. 几何图形的基本概念与性质几何图形包括点、线、面以及由它们组成的各种图形,如直线、射线、线段、角、多边形等。
几何图形有不同的性质和特点,可以通过观察和推理来研究和证明。
2. 平面图形的计算平面图形的计算包括计算图形的周长、面积、体积等。
计算平面图形需要掌握相应的计算公式和方法,如长方形的周长和面积公式、圆的周长和面积公式等。
四、函数与图像1. 函数的概念与性质函数是一种特殊的关系,它将一个集合中的每个元素对应到另一个集合中的唯一元素上。
函数可以用图像、表格和公式等形式表示,可以通过函数的性质来进行分析和研究。
2. 图像的绘制与分析图像是函数的可视化表示,可以通过绘制函数的图像来观察和分析函数的性质。
绘制图像需要掌握相应的绘图技巧和方法,如坐标系的绘制、函数图像的绘制等。
五、统计与概率1. 统计的基本概念与方法统计是研究和描述数据的科学,包括数据的收集、整理、分析和解释等过程。

初一数学整数特性复习题和答案一、选择题1. 下列数中是整数的是:A)2.5 B)-1.5 C)3/4 D)0.1答案:B2. 若a为整数且a>0,那么-a的值一定为:A)负整数 B)整数 C)正整数 D)零答案:A3. 若a和b都是整数,那么 (-a) x (-b) 等于:A)ab B)-ab C)a-b D)-a-b答案:A二、填空题1. 对于任意整数a,有a + (____) = a答案:02. 若a为整数,那么-a 的相反数是(____)答案:a3. 若a为整数,且a > 0,那么-a的值是(____)答案:负整数三、解答题1. 已知 a = -3, b = 5,求 a + b 和 a - b 的值。
解答:a + b = -3 + 5 = 2a -b = -3 - 5 = -82. 若 a 为正整数,b 为负整数,且 a > b,那么 a + b 的值是正数还是负数?为什么?解答:a + b 的值是正数。
因为 a 为正整数,b 为负整数,所以 a 的绝对值大于 b 的绝对值,两者相加的结果就是正数。
四、应用题1. 一支队伍向东行走50公里后又向西走30公里,再向东走20公里,最后向西走15公里。
这支队伍最终在起点的东边还是西边?解答:最终在起点的东边。
因为向西走的30公里和15公里相互抵消了,剩余的向东走的距离是50+20=70公里,所以最终在起点的东边。
2. 在数轴上,点A的坐标是-3,点B的坐标是5,求A到B的距离是多少?解答:A到B的距离等于A的坐标与B的坐标的差的绝对值,即| -3 - 5 | = |-8| = 8。
总结:本文复习了初一数学中整数的特性,包括选择题、填空题、解答题和应用题。
通过这些题目的训练,读者可以加深对整数特性的理解,并提高整数运算的能力。
熟练掌握整数的概念和运算规则对于数学学习的后续内容具有重要的基础作用。
初中数学竞赛辅导资料(18)正整数简单性质的复习甲. 连续正整数一. n 位数的个数:一位正整数从1到9,共9个,两位数从10到99,共90个,三位数从100到999共9×102个,那么 n 位数的个数共__________.(n 是正整数)练习:1. 一本书共1989页,用0到9的数码,给每一页编号,总共要用数码___个.2. 由连续正整数写成的数1234……9991000是一个_______位数;100110021003……19881989是_______位数.3. 除以3余1的两位数有____个,三位数有____个,n 位数有_______个.4. 从1到100的正整数中,共有偶数____个,含 3的倍数____个;从50到1000的正整数中,共有偶数____个,含3的倍数____个.二. 连续正整数的和:1+2+3+……+n=(1+n)×2n . 把它推广到连续偶数,连续奇数以及以模m 有同余数的连续数的和.练习:5.计算2+4+6+……+100=__________.6. 1+3+5+……+99=____________.7. 5+10+15+……+100=_________.8. 1+4+7+……+100=____________.9. 1+2+3+……+1989其和是偶数或奇数?答______10. 和等于100的连续正整数共有______组,它们是______________________.11. 和等于100的连续整数共有_____组,它们是__________________________.三. 由连续正整数连写的整数,各位上的数字和整数 123456789各位上的数字和是:(0+9)+(1+8)+…+(4+5)=9×5=45;1234…99100各位数字和是(0+99)+(1+98)+…+(49+50)+1=18×50+1=901.练习:12. 整数 1234……9991000各位上的数字和是_____________.13. 把由1开始的正整数依次写下去,直到第198位为止:位198011121234567891这个数用9除的余数是__________. (1987年全国初中数学联赛题)14. 由1到100这100个正整数顺次写成的数1234……99100中:① 它是一个________位数;② 它的各位上的数字和等于________;③ 从这一数中划去100个数字,使剩下的数尽可能大,那么 剩下的数的前十位是___________________________.四.连续正整数的积:① 1×2×3×…×n 记作n ! 读作n 的阶乘.② n 个连续正整数的积能被n !整除.如:2!|a(a+1), 3!|a (a+1)(a+2), n !|a(a+1)(a+2)…(a+n -1). a 为整数.③ n ! 中含有质因数m 的个数是⎥⎦⎤⎢⎣⎡m n +⎥⎦⎤⎢⎣⎡2m n +…+⎥⎦⎤⎢⎣⎡i m n . [x]表示不大于x 的最大正整数,i=1,2,3… m i ≢n如:1×2×3×…×10的积中,含质因数3的个数是:⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡2310310=3+1=4 练习:15. 在100!的积5的个数是:____16.一串数1,4,7,10,……,697,700相乘的积中,末尾共有零_______个(1988年全国初中数学联赛题)17. 求证:10494 | 1989!18. 求证:4! | a(a 2-1)(a+2) a 为整数五. 两个连续正整数必互质练习:19. 如果n+1个正整数都小于2n, 那么必有两个是互质数,试证之.乙. 正整数十进制的表示法一. n+1位的正整数记作:a n ×10n +a n -1×10n -1+……+a 1×10+a 0其中n 是正整数,且0≢a i ≢9 (i=1,2,3,…n)的整数, 最高位a n ≠0.例如:54321=5×104+4×103+3×102+2×10+1.例题:从12到33共22个正整数连写成A=121314…3233. 试证:A 能被99整除.证明:A=12×1042+13×1040+14×1038+……+31×104+32×102+33=12×10021+13×10020+14×1019+……+31×1002+32×100+33.∵ 100的任何次幂除以9的余数都是1,即100 n =(99+1) n ≡1 (mod 9)∴ A=99k+12+13+14+……+31+32+33 (k 为正整数 )=99 k+(12+33)+(13+32)+…+(22+23)=99k+45×11=99k+99×5.∴A 能被99整除.练习:20. 把从19到80的连结两位数连写成19202122…7980.试证明这个数能被1980整除二. 常见的一些特例 99999个n =10 n -1, 33333个n =31(10 n -1), 9111111= 个n (10 n -1). 例题:试证明12,1122,111222,11112222,……这些数中的任何一个,都是两个相邻的正整数的积.证明:第n 个数是2122221111个个n n =)110(91 -n ×10 n +)110(92-n =)110(91 -n (10 n +2) =331103110+-⨯-n n=)13110(3110+-⨯-n n = 33333个n ×433333)1(个-n . 证毕. 练习:21. 化简 99999个n × 99999个n +199999个n =_______________________________. 22. 化简2122222-1111个个n n =____________________________________________. 23. 求证119901111个是合数. 24. 已知:存在正整数 n,能使数11111个n 被1987整除. 求证:数p= 11111个n 99999个n 88888个n77777个n 和 数q= 111111个+n 919999个+n 818888个+n717777个+n 都能被1987整除. (1987年全国初中数学联赛题)25. 证明: 把一个大于1000的正整数分为末三位一组,其余部分一组,若这两组数的差,能被7(或13)整除,则这个正整数就能被7(或13)整除.26. 求证: 11111个n ×110000个-n 5+1是完全平方数. 丙. 末位数的性质.一.用N (a)表示自然数的个位数. 例如a=124时,N (a)=4; a=-3时,N (a)=3.1. N (a 4k+r )=N (a r ) a 和k 都是整数,r=1,2,3,4.特别的: 个位数为0,1,5,6的整数,它们的正整数次幂的个位数是它本身.个位数是4,9 的正偶数次幂的个位数也是它本身.2. N (a)=N (b)⇔N (a -b)=0⇔10 |(a -b).3. 若N (a)=a 0, N (b)=b 0. 则N (a n )=N (a 0n ); N (ab)=N (a 0b 0).例题1:求①53100 ; 和 ②777的个位数. 解:①N (53100)=N (34×24+4)=N (34)=1②先把幂的指数77化为4k+r 形式,设法出现4的因数.77=77-7+7=7(76-1)+4+3=7(72-1)(74+72+1)+4+3=7×4×12× (74+72+1)+4+3=4k+3∴N(777)=N(74k+3)=N(73)=3.练习:27. 19891989的个位数是______,999的个位数是_______.28. 求证:10 | (19871989-19931991).29. 2210×3315×7720×5525的个位数是______.二. 自然数平方的末位数只有0,1,4,5,6,9;连续整数平方的个位数的和,有如下规律:12,22,32,……,102的个位数的和等于 1+4+9+6+5+5+9+4+0=45.1. 用这一性质计算连续整数平方的个位数的和例题1. 填空:12,22,32,……,1234567892的和的个位数的数字是_______.(1991年全国初中数学联赛题)解:∵12,22,32,……,102的个位数的和等于 1+4+9+6+5+5+9+4+0=45.11到20;21到30;31到40;………123456781到123456789,的平方的个位数的和也都是45. 所以所求的个位数字是:(1+4+9+6+5+5+9+4+0)×(12345678+1)的个位数5.2. 为判断不是完全平方数提供了一种方法例题2. 求证:任何五个连续整数的平方和不能是完全平方数.证明:(用反证法)设五个连续整数的平方和是完全平方数,那么可记作:(n -2)2+(n -1)2+n 2+(n+1)2+(n+2)2=k 2 (n, k 都是整数)5(n 2+2)=k 2 .∵ k 2是5的倍数,k 也是5的倍数.设k=5m, 则5(n 2+2)=25m 2.n 2+2=5m 2.n 2+2是5的倍数,其个位数只能是0或5,那么 n 2的倍数是8或3.但任何自然数平方的末位数,都不可能是8或3.∴假设不能成立∴任何五个连续整数的平方和不能是完全平方数.3.判断不是完全平方数的其他方法例题3. 已知:a 是正整数.求证: a(a+1)+1不是完全平方数证明:∵a(a+1)+1=a 2+a+1,且a 是正整数∴ a 2< a(a+1)+1=a 2+a+1<(a+1)2,∵a 和a+1是相邻的两个正整数,a(a+1)+1介于它们的平方之间∴a(a+1)+1不是完全平方数例题4. 求证:11111个n (n>1的正整数) 不是完全平方数 证明:根据奇数的平方数除以4必余1,即(2k+1)2=4(k+1)+1.但 11111个n =1100111112-个n =4k+11=4k+4×2+3=4(k+2)+3 即11111个n 除以4余数为3,而不是1, ∴它不是完全平方数.例题5. 求证:任意两个奇数的平方和,都不是完全平方数.证明:设2a+1,2b+1(a,b 是整数)是任意的两个奇数.∵(2a+1)2+(2b+1)2=4a 2+4a+1+4b 2+4b+1=4(a 2+b 2+a+b)+2.这表明其和是偶数,但不是4的倍数,故任意两个奇数的平方和,都不可能是完全平方数.三. 魔术数:将自然数N 接写在每一个自然数的右面,如果所得到的新数,都能被N整除,那么N 称为魔术数.常见的魔术数有:a) 能被末位数整除的自然数,其末位数是1,2,5 (即10的一位正约数是魔术数) b) 能被末两位数整除的自然数,其末两位数是10,20,25,50(即100的两位正约数也是魔术数))c) 能被末三位数整除的自然数,其三末位数是100,125,200,250,500(即1000的三位正约数也是魔术数)练习:30. 在小于130的自然数中魔术数的个数为_________.(1986年全国初中数学联赛题)四. 两个连续自然数,积的个位数只有0,2,6;和的个位数只有1,3,5,7,9. 练习:31. 已知:n 是自然数,且9n 2+5n+26的值是两个相邻自然数的积,那么n 的值是:___________________. (1985年上海初中数学竞赛题)丁. 质数、合数1. 正整数的一种分类:⎪⎩⎪⎨⎧).1(.)1( 1然数整除和本身外还能被其他自除合数;然数整除和本身外不能被其他自除质数; 2. 质数中,偶数只有一个是2,它也是最小的质数.3. 互质数:是指公约数只有1的两个正整数. 相邻的两个正整数都是互质数.例题:试写出10个连续自然数,个个都是合数.解:答案不是唯一的,其中的一种解法是:令A=1×2×3×4×5×6×7×8×9×10×11那么A+2,A+3,A+4,A+5,A+6,A+7,A+8,A+9,A+10,A+11就是10个连续数,且个个都是合数.一般地,要写出n 个连续自然数,个个是合数,可用令m=n+1, 那么m !+2, m !+3, m !+4, +……+ m !+n+1 就是所求的合数.∵m !+i (2≢i ≢n+1) 有公约数i.练习:32. 已知质数a , 与奇数b 的和等于11,那么a=___,b=___.33. 两个互质数的最小公倍数是72,若这两个数都是合数,那么它们分别等于____,____.34. 写出10个连续正奇数,个个都是合数,可设m=(10+1)×2, m !=22!那么所求的合数是22!+3,_____,____,____,……35. 写出10个连续自然数,个个都是合数,还可令 N=2×3×5×7×11.(这里11=10+1,即N 是不大于11的质数的积).那么 N+2,N+3,N+4,……N+11就是所求的合数.这是为什么?如果 要写15个呢?36. 已知:x, m, n 都是正整数 . 求证:24m+2+x 4n 是合数.戊.奇数和偶数1.整数的一种分类:⎩⎨⎧)12(.2)02(2,余数为即除以整除的整数奇数:不能被,余数为即除以整除的整数;偶数:能被2. 运算性质:奇数+奇数=偶数, 偶数+偶数=偶数, 奇数+偶数=奇数.奇数×奇数=奇数,偶数×偶数=偶数,奇数×偶数=偶数.(奇数)正整数=奇数,(偶数)正整数=偶数.4. 其他性质:① 两个连续整数必一奇一偶,其和是奇数,其积是偶数.② 奇数的平方被4除余1;偶数的平方能被4整除;除以4余2或3的整数不是平方数.a) 2n (n 为正整数)不含大 于1的奇因数.b) 若两个整数的和(差)是奇数,则它们必一奇一偶.c) 若n 个整数的积是奇数,则它们都是奇数.例1. 设m 与n 都是正整数,试证明m 3-n 3为偶数的充分必要条件是m -n 为偶数.证明:∵m 3-n 3=(m -n )(m 2+mn+n 2).当m -n 为偶数时,不论m 2+mn+n 2是奇数或偶数,m 3-n 3都是偶数;∴m -n 为偶数是m 3-n 3为偶数的充分条件.当m -n 为奇数时,m, n 必一奇一偶,m 2,mn ,n 2三个数中只有一个奇数,∴m 2+mn+n 2是奇数,从而m 3-n 3也是奇数.∴m -n 为偶数,是m 3-n 3为偶数的必要条件.综上所述m 3-n 3为偶数的充分必要条件是m -n 为偶数.例2. 求方程x 2-y 2=1990的整数解.解:(x+y)(x -y)=2×5×199.若x, y 同是奇数或同是偶数,则 x+y ,x -y 都是偶数,其积是4的倍数,但1990不含4的因数,∴方程左、右两边不能相等.若x, y 为一奇一偶,则x -y ,x+y 都是奇数,其积是奇数,但1990不是奇数,∴方程两边也不能相等.综上所述,不论x, y 取什么整数值,方程两边都不能相等.所以 原方程没有整数解本题是根据整数的一种分类:奇数和偶数,详尽地讨论了方程的解的可能性.练习:37. 设n 为整数,试判定n 2-n+1是奇数或偶数.38. 1001+1002+1003+……+1989其和是偶数或奇数,为什么?39. 有四个正整数的和是奇数,那么它们的立方和,不可能是偶数,试说明理由.40. 求证:方程x 2+1989x+9891=0没有整数根.41. 已知: ⎩⎨⎧=⨯⨯⨯⨯=++++.0321321n x x x x x x x x n n ; 求证:n 是4的倍数. 42. 若n 是大于1的整数,p=n+(n 2-1)2)1(1n --试判定p 是奇数或偶数,或奇偶数都有可能. (1985年全国初中数学联赛题)已. 按余数分类1. 整数被正整数 m 除,按它的余数可分为m 类,称按模m 分类.如:模m=2,可把整数分为2类:{2k}, {2k+1} k 为整数,下同模m=3,可把整数分为3类:{3k}, {3k+1},{3k+2}.……模m=9,可把整数分为9类:{9k},{9k+1},{9k+2}.…{9k+8}.2. 整数除以9的余数,与这个整数各位上的数字和除以9的余数相同.如:6372,5273,4785各位数字和除以9的余数分别是0,8,6. 那么这三个数除以9的余数也分别是0,8,6.3. 按模m 分类时,它们的余数有可加,可乘,可乘方的性质.如:若a=5k 1+1, b=5k 2+2.则a+b 除以5 余数 是3 (1+2);ab 除以5余2 (1×2);b 2 除以5余4 (22).例1. 求19891989除以7的余数.解:∵19891989=(7×284+1)1989,∴19891989≡11989 ≡1 (mod 7).即19891989除以7的余数是1.练习:43. 今天是星期一,99天之后是星期________.44. n 个整数都除以 n -1, 至少有两个是同余数,这是为什么?45. a 是整数,最简分数7a 化为小数时,若为循环小数,那么一个循环节最多有几位?4. 运用余数性质和整数除以9的余数特征,可对四则运算进行检验例2. 下列演算是否正确?① 12625+9568=21193 ; ② 2473×429=1060927.解:①用各位数字和除以9,得到余数:12625,9568,21193除以9的余数分别是7,1,7.∵ 7+1≠7, ∴演算必有错.② 2473,429,1060927除以9的余数分别是7,6,7.而7×6=42,它除以9余数为6,不是7,故演算也有错.注意:发现差错是准确的,但这种检验并不能肯定演算是绝对正确.练习:46. 检验下列计算有无差错:①372854-83275=289679 ; ②23366292÷6236=3748.5. 整数按模分类,在证明题中的应用例3. 求证:任意两个整数a 和b ,它们的和、差、积中,至少有一个是3的倍数.证明:把整数a 和b 按模3分类,再详尽地讨论.如果a, b 除以3,有同余数 (包括同余0、1、2),那么a, b 的差是3的倍数;如果a, b 除以3,余数不同,但有一个余数是0,那么a, b 的积是3的倍数;如果a, b 除以3,余数分别是1和2,那么a, b 的和是3的倍数.综上所述任意两个整数a ,b ,它们的和、差、积中,至少有一个是3的倍数.(分类讨论时,要求做到既不重复又不违漏)例4. 已知: p ≣5,且 p 和2p+1都是质数.求证:4p+1是合数.证明:把整数按模3分类. 即把整数分为3k,3k+1,3k+2 (k 为整数)三类讨论∵p 是质数,∴不能是3的倍数,即p ≠3k ;当p=3k+1时, 2p+1=2(3k+1)+1=3(2k+1). ∴ 2p+1不是质数,即p ≠3k+1; 只有当质数p=3k+2时, 2p+1=2(3k+2)+1=6k+5.∴2 p+1也是质数, 符合题设.这时,4p+1=4(3k+2)+1=3(4k+3)是合数. 证毕练习:47. 已知:整数a 不能被2和3整除 . 求证:a 2+23能被24整除.48. 求证:任何两个整数的平方和除以8,余数不可能为6.49. 若正整数a 不是5的倍数. 则a 8+3a 4-4能被100整除.50. 已知:自然数n>2求证:2n -1和2n +1中,如果 有一个是质数,则另一个必是合数.51.设a,b,c 是三个互不相等的正整数,求证 a 3b -ab 3,b 3c -bc 3,c 3a -ca 3三个数中,至少有一个能被10整除. (1986年全国初中数学联赛题)庚. 整数解1. 二元一次方程 ax+by=c 的整数解:当a,b 互质时,若有一个整数的特解⎩⎨⎧==00y y x x 那么可写出它的通解)(00为整数k ak y y bk x x ⎩⎨⎧-=+= 2. 运用整数的和、差、积、商、幂的运算性质整数±整数=整数, 整数×整数=整数,整数÷(这整数的约数)=整数, (整数)自然数=整数3. 一元二次方程,用求根公式,根的判别式,韦达定理讨论整数解.4. 根据已知条件讨论整数解.例1. 小军和小红的生日.都在10月份,且星期几也相同,他们生日的日期的和等于34,小军比小红早出生,求小军的生日.解:设小军和小红的生日分别为x, y ,根据题意,得⎩⎨⎧=+=-347x y k x y (k=1,2,3,4) 2x=34-7k x=17-k 27 k=1, 3时, x 没有整数解;当k=2时, ⎩⎨⎧==.2410y x , 当k=4时,⎩⎨⎧==.313y y x , (10月份没有31日,舍去) ∴小军的生日在10月10日例2. 如果一个三位数除以11所得的商,是这个三位数的各位上的数的平方和,试求符合条件的所有三位数. (1988年泉州市初二数学双基赛题)解:设三位数为100a+10b+c, a, b, c 都是整数,0<a ≢9,0≢b, c ≢9.那么 1191110100c b a b a c b a +-++=++ , 且-8<a -b+c<18. 要使a -b+c 被11整除,其值只能是0和11.( 1)当a -b+c=0时, 得9a+b=a 2+b 2+c 2.以b=a+c 代入,并整理为关于a 的二次方程,得2a 2+2(c -5)a+2c 2-c=0根据韦达定理⎪⎩⎪⎨⎧-=-=+.2522121c c a a c a a , 这是必要而非充分条件. ∵5-c>0, 以c=0, 1, 2, 3, 4 逐一讨论a 的解.当 c=2, 4时,无实数根; 当c=1, 3时,无整数解;只有当c=0时,a=5;或 a=0. (a=0不合题意,舍去)∴只有c=0, a=5, b=5适合∴所求的三位数是550;(2)当a -b+c=11时, 得9a+b+1=a 2+b 2+c 2.以b=a+c 代入,并整理为关于a 的二次方程,得2a 2+2(c -16)a+2c 2-23c+131=0.仿(1)通过韦达定理,由c 的值逐一以讨论a 的解.只有当c=3时, a=8, b=0适合所有条件.即所求三位数为803.综上所述,符合条件的三位数有550和803.练习:52. 正整数x 1, x 2, x 3,……x n 满足等式x 1+x 2+x 3+x 4+x 5=x 1x 2x 3x 4x 4x 5那么 x 5的最大值是________. (1988年全国初中数学联赛题)53. 如果p, q, pq q p 12,12-- 都是整数,.且p>1, q>1, 试求p+q 的值. (1988年全国初中数学联赛题) 54.能否找到这样的两个正整数m 和n ,使得等式m 2+1986=n 2成立. 试说出你的猜想,并加以证明. (1986年泉州市初二数学双基赛题) 55.当m 取何整数时,关于x 的二次方程m 2x 2-18mx+72=x 2-6x 的根是正整数,并求出它的根. (1988年泉州市初二数学双基赛题) 56.若关于x 的二次方程(1+a )x 2+2x+1-a=0的两个实数根都是整数,那么a 的取值是________________. (1989年泉州市初二数学双基赛题) 57.不等边三角形的三条边都是整数,周长的值是28,最大边与次大边的差比次大边与最小边的差大1,适合条件的三角形共有____个,它们的边长分别是:______________________________________________________________. 58.直角三角形三边长都是整数,且周长的数值恰好等于面积的数值,求各边长. 59.鸡翁一,值钱;,鸡母一,值钱三;鸡雏三,值钱一.百钱买百鸡,问鸡翁、鸡母、鸡雏各几何? 60. 甲买铅笔4支,笔记本10本,文具盒1个共付1.69元,乙买铅笔3支,笔记本7本,文具盒1个共付1.26元,丙买铅笔、笔记本、文具盒各1,应付几元? 若1×2×3×4×……×99×100=12 n ×M ,其中M 为自然数,n 为使得等式成立的最大自然数,则M 是( )(A).能被2整除,不能被3整除 . (B).能被3整除,但不能被2整除.(C).被4整除,不能被3整除. (D).不能被3整除,也不能被2整除.(1991年全国初中数学联赛题)参考答案1. 9+90×2+900×3+990×4=68492. 2893 79563. 30,300,3×10n -14. 50, 33, 476, 317 .5.25506.2500.7. 10501. 1717. 9.奇数 (1+1989)×21989 . 10有两组:18,19,20,21,22; 9,10,11,12,13,14,15,16.11.有四组:除上题中的两组外,尚有-8到16;-17到2212. 13501. 13. 余数是6(由1到102刚好是198位).14. (1)192 (2)901 (3)9999978596 15.⎥⎦⎤⎢⎣⎡5100+⎥⎦⎤⎢⎣⎡25100=24 16. 60个. 计算积中含质因数5的个数是:从10,25,40,55,……700这组数中含质因数5的共有(700-10)÷15+1=47; 而25,100,175,……700含有52因数,应各加1个5,共有(100-25)÷75+1=10; 且250,625,含有53因数,应再各加1个5,共有 2个;625 含有54因数,再加1个5. ∴总共是47+10+2+1=60. 17. ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡6251989125198925198951989=379+79+15+3=494 18. 把a(a 2-1)(3a+2)化为a(a+1)(a -1)[(2a+4)+(a -2)]=2(a -1)a(a+1)(a+2)+(a -2)(a -1)a(a+1).19. 根据两个连续整数必互质,把n+1个正整数按非连续数单独分组,因为它们都小于2n,所以最多分为n 组,那么n+1个正整数至少有一个不能单独分组,即与n 组中的一个互质.20. 易证能被20整除,再证能被99整除21. 原数=(10n -1)2+1×10n +(10n -1)=102n 22. 原数=91×(102n -1)-2×91×(10n -1)=……=(3110-n )2=( 个n 2)3333( 23. 原数=91×(101990-1)= 91×(10995+1) (10995-1) =91×(10995+1) (10-1)×N (N 为整数) 24. p= n1111×(103n +9×102n +8×10n +7) q=11111+n ×(103n+3+9×102n+2+8×10n+1+7) ∵10n =9×个n 1111+1, 103n+3,102n+2,10n+1除以个n 1111的余数分别为103,102,10.∴q 的第二因式除以个n 1111的余数分别为1×103+9×102+8×10+7…… 25.设A=103 M+N , 7|(M -N).A=103 M+N=103 M+M -M+N=1001M -(M -N).26. 原数=1)510(9110++⨯-n n =…… 27. 1. 28. 71与33的个位数相同. 29 . 0.30. 9个(1,25,10,20,25,50,100,125).31. 2,6. 可设9n 2+5n+26=m(m+1), 配方,分解因式32. 2,9. 33. 8,9.34. 22!+3,22!+5,22!+7,………22!+19,22!+2135. 可设2×3×5×7×11×13×17, 那么 N+2,N+3,……N+16即所求.36. (22n+1)2+(x 2n )2+2×22n+1×x 2n -4×22n ×x 2n =(22n+1+x 2n )2-(2 ×2m ×x n )2……37. 奇数. 38 奇数 .39. 4个正整数的和为奇数,则这4个数中有1个或3个是奇数.40. 若有奇数根,则奇+奇+奇≠0;若有偶数根,则偶+偶+奇≠0.41. 若n 为奇数,则与(1)矛盾;若n 为偶数,由(1)可知,偶数必成双,再由(2)知n 是4的倍数.42. 奇数 43. 星期二, ∵9 9除以7余数是1.44. 除以整数n -1的余数,最多只有n -1种45. 六位. ∵除以7,余数除0以外,只有6种.46. ①不对,∵用9除的余数 11-7≠5, ②错.8×2=32,除以9余数不是6.47. a=6k ±1, a 2+23=12k(3k ±1)+2448. 把整数按模4分类为4n, 4n+1, 4n+2, 4n+3.其平方后除以8余数分别为0,1,4,1任何两个余数的和都不等于6.49. a 8+3a 4-4=(a 4+4)(a 2+1)(a 2-1), a ≠5k ,则a=5k ±1,5k ±2, a 2 除以5的余数分别为1和4, a 4 除以5余数 均为1.50. 2 n 不是3的倍数,可分别设为3k+1,3k -1.51. (同练习69第10题). 52. 5 53. 854. 不可能.(n+m)(n -m)=1986 按n+m, n -m 同奇,同偶讨论.55. 原方程化为(m 2-1)x 2-6(3m-1)x+72=0, [(m+1)x-12][(m-1)x-6]=0.x 1=112+m ; x 2=16-m . ∵方程的根是自然数, ∴ 11,2,3,4,11,2,3,6.m m +=⎧⎨-=⎩ 0,1,2,3,5,11;2,3,4,7.m m =⎧⎨=⎩ ∴m=2,;或m=3.∴当m=2时,x 1=4; 或 x 2=6. 当 m=3时, x 1=x 2=3.56. a=-3,-2, 0, 1 (x 1+x 2=-a +12, x 1x 2=-1+a+12)57. 有三个,其边长分别是:11,9,8; 12,9,7; 13,9,6.58. 6,8,10或5,12,13.59. 设鸡翁,鸡母,鸡雏一只分别值 x,y,z 钱,则1001531003x y z x y z ++=⎧⎪⎨++=⎪⎩消去一元,得二元一次方程: 7x+4y=200. 求自然数解,得有四组答案:12,8,4,0,4,11,18,25,84;81;78;75.x x x x y y y y z z z z ====⎧⎧⎧⎧⎪⎪⎪⎪====⎨⎨⎨⎨⎪⎪⎪⎪====⎩⎩⎩⎩60.⎩⎨⎧=++=++12673169104 z y x z y x x+y+z=40 .61. 选(A). 根据连续整数的积的性质,100!含因数2共97个,含因数3有48个……。