第4讲 函数、基本初等函数Ⅰ的图像与性质
- 格式:docx
- 大小:314.81 KB
- 文档页数:4
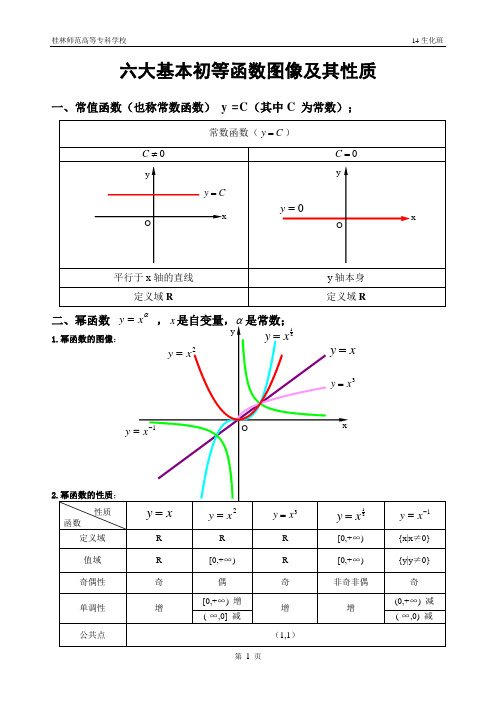
六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。


六大基本初等函数图像及其性质六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 α1.2.幂函数的性质;21xy1)当α为正整数时,函数的定义域为区间为∈x,他们的图形都经过原点,并当α>1时在原点-∞(+∞,)处与x轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数;m时,n为偶数时函数的定义3)当α为正有理数n域为(0, +∞),n为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n图形于x轴相切,如果m<n,图形于y轴相切,且m为偶数时,还跟y轴对称;m,n均为奇数时,跟原点对称;5)当α为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1)当1>a 时函数为单调增,当10<<a 时函数为单调减;2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ; 1xa.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式); a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) nm n m a a a +=⋅ (2) n m n m a a a -=÷(3)()()mn nmnm aaa ==(4) ()n n nb a ab =b.根式的性质; (1)()a a nn= ; (2)当n为奇数时,a a nn =当n 为偶数时,f x xxx g ⎪⎫⎛=1)(⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂; (1))1,,,0(*>∈>=n Z n m a a an m nm (2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 Nab=,那么数b 叫做以a 为底N 的对数,记作bN a=log,其中a 叫做对数的底数,N 叫做真数,式子N alog 叫做对数式。

五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。
如,,,都是幂函数。
没有统一的定义域,定义域由值确定。
如,。
但在内总是有定义的,且都经过(1,1)点。
当时,函数在上是单调增加的,当时,函数在内是单调减少的。
下面给出几个常用的幂函数:的图形,如图1-1-2、图1-1-3。
图1-1-2图1-1-32.指数函数函数称为指数函数,定义域,值域;当时函数为单调增加的;当时为单调减少的,曲线过点。
高等数学中常用的指数函数是时,即。
以与为例绘出图形,如图1-1-4。
图1-1-43.对数函数函数称为对数函数,其定义域,值域。
当时单调增加,当时单调减少,曲线过(1,0)点,都在右半平面内。
与互为反函数。
当时的对数函数称为自然对数,当时,称为常用对数。
以为例绘出图形,如图1-1-5。
图1-1-54.三角函数有,它们都是周期函数。
对三角函数作简要的叙述:(1)正弦函数与余弦函数:与定义域都是,值域都是。
它们都是有界函数,周期都是,为奇函数,为偶函数。
图形为图1-1-6、图1-1-7。
图1-1-6 正弦函数图形图1-1-7 余弦函数图形(2)正切函数,定义域,值域为。
周期,在其定义域内单调增加的奇函数,图形为图1-1-8图1-1-8(3)余切函数,定义域,值域为,周期。
在定义域内是单调减少的奇函数,图形如图1-1-9。
图1-1-9(4)正割函数,定义域,值域为,为无界函数,周期的偶函数,图形如图1-1-10。
图1-1-10(5)余割函数,定义域,值域为,为无界函数,周期在定义域为奇函数,图形如图1-1-11。
图1-1-115.反三角函数反正弦函数,定义域,值域,为有界函数,在其定义域内是单调增加的奇函数,图形如图1-1-12;图1-1-12,为有界函数,在其定义域内为单调减少的非奇非偶函数,图形如图1-1-13;图1-1-13反正切函数,定义域,值域为,为有界函数,在定义域内是单调增加的奇函数,图形如图1-1-14;图1-1-14为有界函数,在其定义域内单调减少的非奇非偶函数。


函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1) 极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性) 极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)等价无穷小(x->0)sinx等价于xarcsinx等价于x tanx等价于x arctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2)数列的夹逼性(1) 数列的夹逼性(2) pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了文案编辑词条B 添加义项?文案,原指放书的桌子,后来指在桌子上写字的人。
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
高中数学基本初等函数图像和性质一次函数(0)y kx b b =+≠的图象和性质二次函数()()20f x ax bx c a =++≠的图像和性质指数函数x y a =(0,1)a a >≠图象和性质对数函数log a y x =(0,1,0)a a x >≠>图像和性质性值域 (),-∞+∞ 恒过定点 ()1,0即log 10a =单调性 在定义域上为减函数 在定义域上为增函数补充性质 “同”正“异”负正弦函数 x y sin =1.定义域:R ;2.值域:[-1,1].3.单调性:在区间[2,2]()22k k k Z ππππ-++∈内,函数单调递增;在区间3[2,2]()22k k k Z ππππ++∈()k Z ∈内,函数单调递减;4.对称性:对称轴2x k ππ=+,对称中心(,0),k k Z π∈.5.周期性:2T π=;6.奇偶性:由sin()sin x x -=-知,正弦函数是奇函数;余弦函数 x y cos =1.定义域:R.2.值域:[-1,1].3.单调性:在区间[]2,2()k k k Z πππ-∈内,函数单调递增;在区间[]2,2()k k k Z πππ+∈内,函数单调递减;4.对称性:对称轴x k π=,对称中心(,0),2k k Z ππ+∈.5.周期性:π=T ;6.奇偶性:由cos()cos x x -=知,余弦函数是偶函数;正切函数 x y tan =1.定义域:⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,2|ππ; 2.值域:R3.单调性:在开区间z k k k ∈⎪⎭⎫ ⎝⎛++-ππππ2,2内,函数单调递增。
4.对称性:对称中心:(,0),2k k Z π∈,没有对称轴. 5.周期性:π=T ;6.奇偶性:由()x x tan tan -=-知,正切函数是奇函数;。
基本初等函数及其性质和图形1.幂函数函数称为幂函数。
如,,,都是幂函数。
没有统一的定义域,定义域由值确定。
如,。
但在内总是有定义的,且都经过(1,1)点。
当时,函数在上是单调增加的,当时,函数在内是单调减少的。
下面给出几个常用的幂函数:的图形,如图1-1-2、图1-1-3。
图1-1-2图1-1-32.指数函数函数称为指数函数,定义域,值域;当时函数为单调增加的;当时为单调减少的,曲线过点。
高等数学中常用的指数函数是时,即。
以与为例绘出图形,如图1-1-4。
图1-1-43.对数函数函数称为对数函数,其定义域,值域。
当时单调增加,当时单调减少,曲线过(1,0)点,都在右半平面内。
与互为反函数。
当时的对数函数称为自然对数,当时,称为常用对数。
以为例绘出图形,如图1-1-5。
图1-1-54.三角函数有,它们都是周期函数。
对三角函数作简要的叙述:(1)正弦函数与余弦函数:与定义域都是,值域都是。
它们都是有界函数,周期都是,为奇函数,为偶函数。
图形为图1-1-6、图1-1-7。
图1-1-6 正弦函数图形图1-1-7 余弦函数图形(2)正切函数,定义域,值域为。
周期,在其定义域内单调增加的奇函数,图形为图1-1-8图1-1-8(3)余切函数,定义域,值域为,周期。
在定义域内是单调减少的奇函数,图形如图1-1-9。
图1-1-9(4)正割函数,定义域,值域为,为无界函数,周期的偶函数,图形如图1-1-10。
图1-1-10(5)余割函数,定义域,值域为,为无界函数,周期在定义域为奇函数,图形如图1-1-11。
图1-1-115.反三角函数反正弦函数,定义域,值域,为有界函数,在其定义域内是单调增加的奇函数,图形如图1-1-12;图1-1-12反余弦函数,定义域为[-1,1],值域为,为有界函数,在其定义域内为单调减少的非奇非偶函数,图形如图1-1-13;图1-1-13反正切函数,定义域,值域为,为有界函数,在定义域内是单调增加的奇函数,图形如图1-1-14;图1-1-14反余切函数,定义域为,值域,为有界函数,在其定义域内单调减少的非奇非偶函数。
2014年高三数学二轮专题第4讲 函数、基本初等函数Ⅰ的图像与性质1.[2013·江西卷改编] 函数y =x ln(1-x )的定义域①是____ 2.[2012·陕西卷] 设函数f (x )=⎩⎪⎨⎪⎧x ,x ≥0,⎝⎛⎭⎫12x ,x <0,②则f (f (-4))=________. 3.[2012·天津卷改编] 函数f (x )=e x -e -x 的奇偶性是③________,单调性是__________. 4.[2013·福建卷改编] 画出函数y =ln(x 2+1)的图像④大致是____________. 5.[2013·安徽卷] 定义在R 上的函数f (x )满足f (x +1)=2f (x ),若当0≤x ≤1时,f (x )=x (1-x ),则当-1≤x ≤0⑤时,f (x )=________.6.[2013·新课标全国卷Ⅱ改编] 设a =log 36,b =log 510,c =log 714,则a ,b ,c 的大小关系⑥是________.⇒ 函数的概念关键词:对应关系、定义域、值域、分段函数,如①②.⇒ 函数性质关键词:单调性、奇偶性、周期性,如③.⇒ 函数图像关键词:函数图像、函数性质、特殊点,如④.⇒ 函数解析式关键词:函数解析式、性质、分段定义域,如⑤.⇒ 基本初等函数Ⅰ关键词:指数函数、对数函数、幂函数、图像、性质,如⑥.► 考向一 函数的概念与表示考向:函数的定义域、值域、最值,分段函数等.考例:2009年T12、2010年T11、2012年T14,近五年新课标全国卷共考查了3次.例1 (1)函数y =x 22-x+lg(2x +1)的定义域是( )A.⎝⎛⎭⎫-12,+∞B.⎝⎛⎭⎫-12,2C.⎝⎛⎭⎫-12,12D.⎝⎛⎭⎫-∞,-12 (2)[2013·福建卷] 已知函数f (x )=⎩⎪⎨⎪⎧2x 3,x <0,-tan x ,0≤x <π2,则f ⎝⎛⎭⎫ f ⎝⎛⎭⎫ π4=____.小结:函数概念的核心是定义域和对应关系,求由解析式给出的函数的定义域就是求使解析式有意义的自变量的取值集合;分段函数求值时注意由内层到外逐次计算,在计算时要随时注意自变量的取值在函数的哪个段上.考向二 函数的基本性质考向:函数的单调性、奇偶性、周期性、最值以及性质的综合运用.考例:2009年T12、2011年T2,近五年新课标全国卷共考查了2次.虽然专门考查函数性质的考题不多,但函数性质在解决函数类试题中具有重要作用.例2 (1)定义域为R 的奇函数f (x ),当x ∈(-∞,0)时f (x )+xf ′(x )<0恒成立,若a =3f (3),b =f (1),c =-2f (-2),则( )A .a >c >bB .c >b >aC .c >a >bD .a >b >c(2)[2013·湖北卷] x 为实数,[x ]表示不超过x 的最大整数,则函数f (x )=x -[x ]在R 上为( )A .奇函数B .偶函数C .增函数D .周期函数方法指导 6.函数的周期性、奇偶性和函数图像对称性的关系函数的奇偶性、函数图像的对称性、函数的周期性有密切的关系.如偶函数y =f (x )的图像关于直线x =a (a ≠0)对称时,根据函数图像的对称性可得函数解析式满足f (a +x )=f (a -x ),以x +a 代x ,得f (2a +x )=f (-x )=f (x ),这样就得到函数y =f (x )的一个周期是2a ;奇函数y =f (x )的图像关于点(a ,0)(a ≠0)对称时,可得f (a +x )=-f (a -x ),以x +a 代x ,得f (2a +x )=-f (-x )=f (x ),也推出2a 是函数y =f (x )的一个周期.变式题 (1)已知函数f (x )对任意x ∈R 都有f (x +4)-f (x )=2f (2),若y =f (x -1)的图像关于直线x =1对称,且f (1)=2,则f (2013)=( )A .2B .3C .4D .0(2)定义在R 上的函数y =f (x )满足f (x )+f ⎝⎛⎭⎫x +32=0,且函数y =f (x +1)的图像关于点(-1,0)成中心对称,若f (1)≥1,f (2)=2a -3a +1,则a 的取值范围是( ) A .-1<a ≤23 B .a <-1 C .a <-1或a ≥23 D .a ≤23► 考向三 函数图像的识别及应用考向:给出函数解析式判断解析式对应的函数图像、根据函数图像使用数形结合思想解决函数问题等.考例:2009年T12、2010年T11、2011年T14、2012年T10、2013年卷ⅠT11,近五年新课标全国卷共考查了5次.例3 (1)[2013·四川卷] 函数y =x 33x -1的图像大致是( )图2-4-(2)已知图像连续的函数f (x )的定义域为[-1,5],部分对应值如下表,f (x )的导函数y =f ′(x )的图像如图2-4-4所示,给出关于f (x )的下列命题:图2-4-4①函数y=f(x)在x=2处取极小值;②函数f(x)在[0,1]上是减函数,在[1,2]上是增函数;③当1<a<2时,函数y=f(x)-a有4个零点;④如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最小值为0.其中所有真命题的序号为________________.方法指导7.解决函数图像识别类试题的基本思想一看函数的定义域、值域;二看函数的性质(单调性、奇偶性、周期性,性质的得出有些要计算和推理);三看特殊函数值,通过特殊函数值对应的图像上的点进行识别判断.小结:本题(1)也可以在研究函数的定义域和函数值为正值的情况下,根据指数函数与幂函数的变化趋势得出,在x→+∞时,f(x)→0,直接得出答案.从函数的导函数的图像上可以得出函数的单调性和极值点,但得不出函数值等具体的数据.变式题(1)函数y=2x-x2的图像为()图2-4-5(2)2012翼装飞行世界锦标赛在张家界举行,某翼人空中高速飞行,图2-4-6反映了他从某时刻开始的15分钟内的速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]-4-7中的()2-4► 考向四 基本初等函数Ⅰ的图像与性质考向:指数函数、对数函数、幂函数的图像与性质及其应用,特别是在分段函数、综合解答题函数图像性质类的题目中使用上述三个函数的图像与性质.考例:2013年T8,近五年新课标全国卷共考查了一次.虽然专门考查该点的试题不多,但指数函数、对数函数和幂函数是构成各式各样函数的基本因素,在函数问题中有举足轻重的作用.例4 (1)设a =212,b =313,c =log 32,则( ) A .b <a <c B .a <b <c C .c <b <a D .c <a <b(2)若实数a ,b ,c 满足log a 2<log b 2<log c 2,则下列关系中不可能成立.....的是( ) A .a <b <c B .b <a <c C .c <b <a D .a <c <b(3)已知函数f (x )=x -4+9x +1,x ∈(0,4),当x =a 时,f (x )取得最小值b ,则函数g (x )=⎝⎛⎭⎫1a |x +b |的图像为( )2-4小结:比较数值大小的基本方法是分段比较,即按照一定的比较标准(如0,1等)先进行第一次划分,再按照函数的性质比较划分后的数值的大小,最后整合得出结果.【最后一练】1已知函数f (x )=|lg x |,若0<a <b ,且f (a )=f (b ),则2a +b 的取值范围是( )A .(2 2,+∞)B .[2 2,+∞)C .(3,+∞)D .[3,+∞) 2函数f (x )的定义域为R ,若f (x +1)与f (x -1)都是奇函数,则( )A .f (x )是偶函数B .f (x )是奇函数C .f (x )=f (x +2)D .f (x +3)是奇函数3 设f (x )=x 3+x ,x ∈R ,当0≤θ≤π2时,f (m sin θ)+f (1-m )>0恒成立,则实数m 的取值范围是( )A .(0,1)B .(-∞,0) C.⎝⎛⎭⎫-∞,12 D .(-∞,1) [利用合情推理与演绎推理解决创新性问题]1.高考试题的选择题或者填空题中有一类是以判断命题真假为背景命制的,在选择题中一般给出四个命题,让考生找出真命题或假命题,在填空题中一般给出三到五个命题,让考生找出其中的真命题或假命题.2.对其中的假命题只要找出其不成立的一个反例即可,这需根据已有知识进行合情推理,再加以具体计算或者论证作出结论;对其中的真命题也往往要先合理的猜测(合情推理)作出判断,再进行演绎推理的证明.[2013·山东卷] 定义“正对数”:ln + x =⎩⎪⎨⎪⎧0,0<x <1,ln x ,x ≥1.现有四个命题: ①若a >0,b >0,则ln +(a b )=b ln +a ;②若a >0,b >0,则ln +(ab )=ln +a +ln +b ;③若a >0,b >0,则ln +⎝⎛⎭⎫a b ≥ln +a -ln +b ; ④若a >0,b >0,则ln +(a +b )≤ln +a +ln +b +ln 2.其中的真命题有________.(写出所有真命题的编号)。