结构力学一二三-精选.pdf
- 格式:pdf
- 大小:374.83 KB
- 文档页数:8


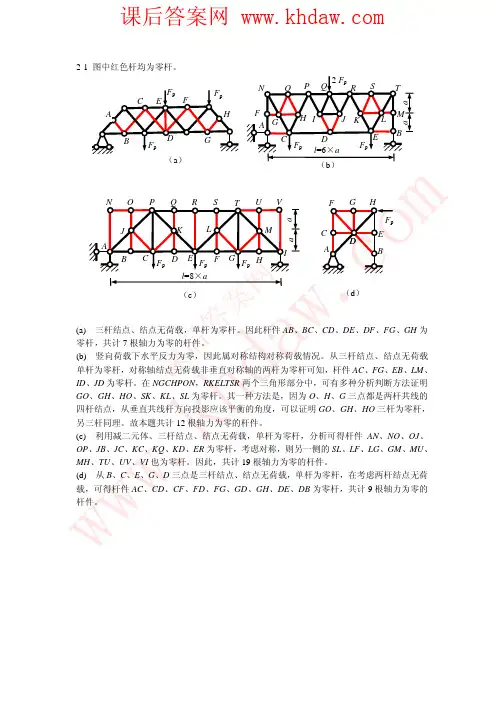


章节平面杆件结构按计算简图分类体系的几何组成与静力性的关系概述几何组成分析举例平面体系的几何组成分析几何组成分析中的几个概念平面体系的计算自由度静定梁和静定刚架静定平面刚架单跨静定梁多跨静定梁绪论几何不变体系和几何可变体系结构力学结构力学的研究对象和任务杆件结构的计算简图几何不变体系的简单组成规则静定结构的一般特性虚功原理和结构位移计算静定结构在荷载作用下的位移计算变形体系的虚功原理平面杆件结构位移计算的一般公式概述各种型式的结构受力特征 静定桁架和组合结构静定平面桁架三种简支桁架的比较概述三铰拱的内力计算三铰拱三铰拱的压力线和合理拱轴空间桁架静定组合结构静定结构在支座位移时的位移计算力法对称性的利用用弹性中心法计算无铰拱用力法计算超静定结构在荷载作用下的内力用力法计算超静定结构在支座位移和温度变化时的内力力法基本概念力法的典型方程超静定结构概述静定结构在温度变化时的位移计算算图乘法线性弹性结构的互等定理超静定结构的位移计算超静定结构内力图的校核超静定结构的一般特性概述截面直杆的转角位移方程位移法的基本概念位移法位移法的典型方程用位移法计算超静定结构在荷载作用下的内力用位移法计算超静定结构在支座位移和温度变化时的内力直接利用平衡条件建立位移法方程矩分配法的基本概念力矩分配法用力矩分配法计算连续梁和无结点线位移的刚架无剪力分配法影响线的概念静力法作静定粱的影响线结点荷载作用下粱的影响线静力法作静定桁架的影响线机动法作静定梁的影响线利用影响线求量值影响线移动荷载最不利位置的确定公路、铁路的标准荷载制及换算荷载简支梁的内力包络图和绝对最大弯矩机动法作连续梁的影响线连续梁的内力包络图知识点章编号节编号知识点编号结构及其分类31374结构力学研究对象31375结构力学的任务31376计算简图的定义31477选取计算简图的一般原则31478实际结构的简化31479平面杆件结构按计算简图分类31580几何不变体系和几何可变体系41681平面体系的几何组成分析41682自由度41783约束41784必要约束与多余约束41785实铰与虚铰41786几何组成分析41787体系的实际自由度S与体系的计算自由度W 41888平面体系的计算自由度算法一——刚片系的W 41889平面体系的计算自由度算法二——铰接链杆体系的W 41890体系的几何组成性质与计算自由度之间的关系41891几何不变体系的简单组成规则41992几何可变体系41993体系的几何组成分析及其步骤42094几何组成分析的方法及举例42095体系的几何组成与静力性的关系42196用截面法求指定截面的内力52297内力图的特征52298用区段叠加法作直杆段的弯矩图52299简支斜梁522100多跨静定梁的组成方式和特点523101多跨静定梁内力计算523102静定平面刚架的类型和特点524103求作静定平面刚架的内力图524104求作静定平面刚架的内力图的要点524105速绘静定平面刚架的弯矩图524106静定梁和静定刚架524107拱的分类625108三铰拱各部分名称625109带拉杆的拱625110三铰拱内力符号规定626111学三铰拱支反力的计算626112三铰拱的内力计算公式626113三铰拱的内力图绘制626114三铰拱的受力特点626115合力多边形627116三铰拱的压力线627117三铰拱的合理拱轴627118桁架的计算简图728119平面桁架的分类728120结点法729121结点平衡的特殊情况729122截面法729123结点法与截面法的联合应用729124对称桁架的受力计算729125静定平面桁架729126简支桁架的受力特点730127三种简支桁架的比较730128空间桁架的支座731129空间桁架的几何组成731130空间桁架的计算方法731131组合结构及其受力特点732132静定组合结构内力的计算方法732133静定组合结构732134各种型式的结构受力特征733135静定梁、刚架内力733136静定结构的一般特性734137位移835138计算位移的目的835139实功836140虚功836141刚体(系)的虚功原理836142变形体系的虚功原理836143虚功原理的两种形式836144实际状态837145虚拟状态837146结构位移计算的一般公式837147单位力设置法837148荷载引起的结构位移计算公式838149梁和刚架的位移计算838150桁架的位移计算838151组合结构的位移计算838152图乘法的适用条件839153图乘法原理839154图乘法的几点说明839155静定结构在支座位移时的位移计算840156温变引起的位移计算841157制造误差引起的位移计算841158功的互等定理842159位移互等定理842160反力互等定理842161反力与位移互等定理842162超静定结构和静定杆件结构分类943163超静定次数的确定943164超静定结构概述943165力法计算超静定结构的思路944166力法的基本未知量、基本结构及基本体944167系、典型方程力法的基本概念944168用力法计算一次超静定结构944169两次超静定结构的力法典型方程945170 n次超静定结构的力法典型方程945171力法典型方程中系数和自由项的计算945172结构的最后内力图945173力法解题步骤946174力法计算超静定梁946175力法计算超静定刚架946176力法计算超静定桁架946177力法计算超静定组合结构946178力法计算铰接排架946179力法计算两铰拱946180支座位移时超静定结构的计算947181温度变化时超静定结构的计算947182对称结构948183对称结构的受力特点948184利用对称性——选择对称的基本体系948185利用对称性——采用半结构948186弹性中心949187荷载作用时的计算949188温度变化时的计算949189支座位移时的计算949190超静定结构位移计算的思路950191荷载作用下超静定结构的位移计算950192支座位移时超静定结构的位移计算950193温度变化时超静定结构的位移计算950194平衡条件的校核951195位移条件的校核951196超静定结构的一般特性952197位移法的基本思路1053198杆端弯矩及杆端位移的正负号规定1054199单跨超静定梁的形常数和载常数1054200转角位移方程1054201位移法的基本未知量1055202位移法的基本结构1055203位移法方程1055204位移法典型方程的建立1056205位移法典型方程中系数及自由项的计算1056206方法位移法计算步骤1057207位移法算例1057208支座位移时位移法的计算1058209温度变化时位移法的计算1058210利用结点和截面平衡条件建立位移法方1059211程转动刚度1160212分配系数和传递系数1160213任意荷载作用时单结点结构的力矩分配1160214法力矩分配法1160215用力矩分配法计算连续梁1161216用力矩分配法计算无结点线位移的刚架1161217无剪力分配法的适用范围1162218无剪力分配法计算步骤和举例1162219移动荷载1263220影响线的定义1263221影响线1263222静力法作影响线的步骤1264223简支梁的影响线1264224影响线与内力图的区别1264225伸臂梁的影响线1264226结点荷载1265227结点荷载作用下影响线的作法1265228静力法作静定桁架的影响线1266229机动法及其原理1267230用机动法作影响线1267231集中荷载作用下的量值1268232分布荷载作用下的量值1268233最不利荷载位置1269234单个移动集中荷载的最不利位置1269235可任意布置的均布荷载的最不利位置1269236行列荷载的最不利位置1269237临界荷载位置的判定1269238铁路标准荷载1270239公路标准荷载1270240换算荷载12702411271242127124312722441272245连续梁的最不利荷载分布1273246连续梁的弯矩包络图1273247连续梁的剪力包络图1273248简支梁的内力包络图机动法作连续梁影响线的原理。
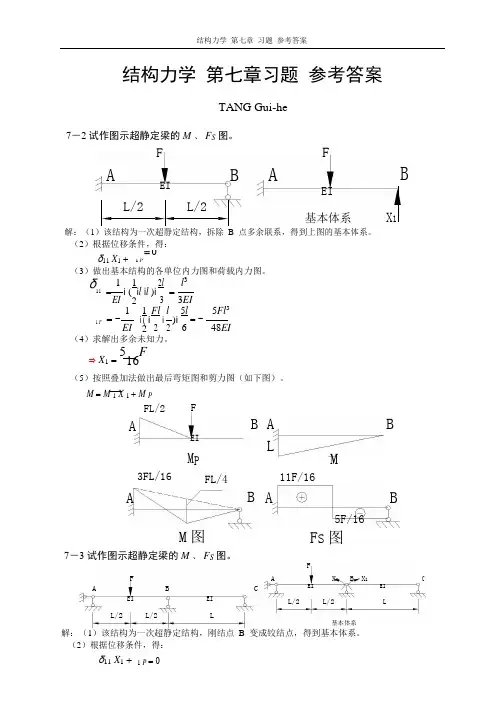
结构力学 第七章 习题 参考答案结构力学 第七章习题 参考答案TANG Gui-he7-2 试作图示超静定梁的M 、 F S 图。
A FFEIBABEIL/2 L/2基本体系X 1解:(1)该结构为一次超静定结构,拆除 B 点多余联系,得到上图的基本体系。
(2)根据位移条件,得:δ11 X 1 + 1 P = 0(3)做出基本结构的各单位内力图和荷载内力图。
δ11 = 11 i l i l )i 2l = l 3i (EI3 3EI2= −1 1 Fl l 5l = − 5Fl 31 Pi ( ii)iEI 2 2 6 48EI2(4)求解出多余未知力。
⇒ X 1 = 516F(5)按照叠加法做出最后弯矩图和剪力图(如下图)。
M = M 1 X 1 + M PFL/2 F ABABEILM PM3FL/16FL/411F/16AABB5F/16M 图 F S 图7-3 试作图示超静定梁的M 、 F S 图。
FFAX 1 B X 1CABCEIEIEIEIL/2 L/2LL/2L/2L基本体系解:(1)该结构为一次超静定结构,刚结点 B 变成铰结点,得到基本体系。
(2)根据位移条件,得:δ11 X 1 + 1 P = 01华南农业大学 水利与土木工程学院(College of water conservancy and Civil Engineering, SCAU )(3)做出基本结构的各单位内力图和荷载内力图。
δ11 = 2 i ( 1 i 1i l )i2= 2lEI 2 33EI1 P= 1 i ( 1 i Fl i l )i 1 = Fl 2EI 2 4 2 16EI(4)求解出多余未知力。
⇒ X 1 = − 3Fl32(5)按照叠加法做出最后弯矩图和剪力图(如下图)。
M = M 1 X 1 + M PF1 B 1ABC ACFL/41M PM3FL/3213F/323F/32BACACBFL/419F/32M 图 F S图7-4 试作图示超静定梁的M 、 F S 图。

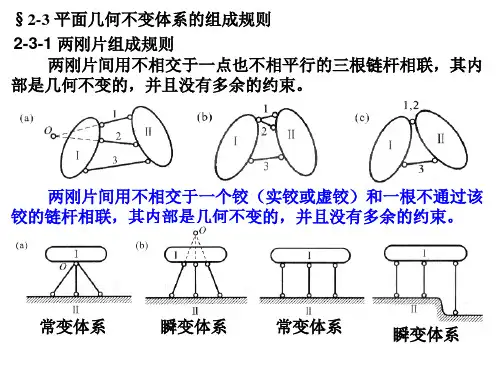

结构力学II试题1、正误判断题 (每题2分,共16分。
正确的标O,错误的标 )1. 矩阵位移法中各类杆件的单元刚度矩阵均具有对称性和奇异性 ( )2. 局部坐标系与整体坐标系之间的坐标变换矩阵T是正交矩阵 ( )3. 简单三角单元的形状函数就是三角单元的面积坐标 ( )4. 简单三角形单元的位移函数中应该包括常数项 ( )5. 两类稳定问题的主要区别是:荷载—位移曲线上是否出现分支点 ( )6. 杆件截面的极限弯矩由极限荷载确定 ( )7. 由于阻尼的存在,任何振动都不会长期持续下去 ( )8. 结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑 ( )二、单项选择题(每题1分,共8分,将选择的字母填在括号内)1. 矩阵位移法的单元刚度方程表示 ( )A.杆端位移与杆端力之间的关系;B.结点位移与结点力之间的关系;C.结点力与杆端力之间的关系D.结点位移与杆端位移之间的关系2. 常应变三角形单元所具有的性质之一是 ( )A. 各单元之间应力连续;B.单元内任意点各插值函数之和等于1;C. 单元的形状函数完全相等;D.单元的形状函数考虑了面外位移;3. 静力法确定完善体系临界荷载的依据是 ( )A.未失稳时的静力平衡条件;B. 失稳时的能量守恒条件;C. 失稳时的静力平衡条件;D. 未失稳时的位移协调条件。
4.极限荷载应满足的条件是 ( )A.单向机构条件 + 内力局限条件;B. 内力局限条件 + 平衡条件;C. 平衡条件 + 单向机构条件;D.平衡条件 + 内力局限条件 + 单向机构条件;5 . 超静定结构的极限荷载的大小 ( )A. 受截面形状影响;B. 受支座移动影响;C. 受温度变化影响;D. 受材料阻尼影响。
6.某单自由度体系当仅刚度EI扩大4倍时,则周期比原周期 ( )A、减小1/4;B、减小1/2 ;C、增大1/4;D、增大1/27. 忽略直杆的轴向变形,图示结构的动力自由度为 ( )A 3;B 5;C 4;D 6。
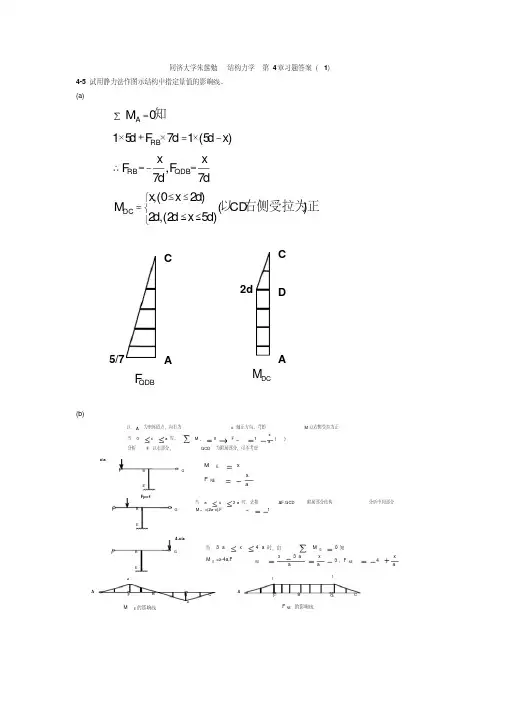

结构⼒学-习题集(含答案)《结构⼒学》课程习题集⼀、单选题1.弯矩图肯定发⽣突变的截⾯是(D )。
A.有集中⼒作⽤的截⾯;B.剪⼒为零的截⾯;C.荷载为零的截⾯;D.有集中⼒偶作⽤的截⾯。
2.图⽰梁中C截⾯的弯矩是( D )。
4m2m4mA.12kN.m(下拉);B.3kN.m(上拉);C.8kN.m(下拉);D.11kN.m(下拉)。
3.静定结构有变温时,(C)。
A.⽆变形,⽆位移,⽆内⼒;B.有变形,有位移,有内⼒;C.有变形,有位移,⽆内⼒;D.⽆变形,有位移,⽆内⼒。
4.图⽰桁架a杆的内⼒是(D)。
A.2P;B.-2P;C.3P;D.-3P。
5.图⽰桁架,各杆EA为常数,除⽀座链杆外,零杆数为(A)。
A.四根;l= a66.图⽰梁A点的竖向位移为(向下为正)(C)。
A.)24/(3EIPl; B.)16/(3EIPl; C.)96/(53EIPl; D.)48/(53EIPl。
PEIEI A l/l/2227. 静定结构的内⼒计算与( A )。
A.EI ⽆关;B.EI 相对值有关;C.EI 绝对值有关;D.E ⽆关,I 有关。
8. 图⽰桁架,零杆的数⽬为:( C )。
A.5;9. 图⽰结构的零杆数⽬为( C )。
A.5;B.6;C.7;D.8。
10. 图⽰两结构及其受⼒状态,它们的内⼒符合( B )。
A.弯矩相同,剪⼒不同;B.弯矩相同,轴⼒不同;C.弯矩不同,剪⼒相同;D.弯矩不同,轴⼒不同。
PP2EI EI EIEI 2EI EIllhl l11. 刚结点在结构发⽣变形时的主要特征是( D )。
A.各杆可以绕结点结⼼⾃由转动; B.不变形; C.各杆之间的夹⾓可任意改变; D.各杆之间的夹⾓保持不变。
12. 若荷载作⽤在静定多跨梁的基本部分上,附属部分上⽆荷载作⽤,则( B )。
A.基本部分和附属部分均有内⼒;B.基本部分有内⼒,附属部分没有内⼒;C.基本部分⽆内⼒,附属部分有内⼒;D.不经过计算,⽆法判断。
第二章平面体系的几何组成分析一、填空题1.2个第一个两个大三角形里面的两个链杆就是多余约束。
直接能看出来。
两个多余约束的不变体系,可以解释为去掉那两个链杆是无多余约束的,所以为两个多余约束.2.瞬变2-2简化如图。
阴影部分,最右侧链杆,大地看作三个刚体。
大地与阴影刚体用左下角铰接,右侧链杆与大地通过两个链杆相连,虚铰位于右下角。
阴影刚体与链杆通过两平行链杆相连,交于无穷远一铰,且两平行链杆与上述两铰的连线平行,因此是几何瞬变的3.无多余约束的几何不变体系1、2、3号链杆看作三个刚体,1、2链杆,1、3链杆分别通过两链杆交于如图两虚铰处。
2、3链杆通过两链杆交于无穷远处一虚铰。
连接2、3的链杆与图中两虚铰的连线不平行,因此上部结构是无多余约束的几何不变体系。
该体系通过一个铰和不过此铰的链杆与大地相连,所有整个体系是无多余约束的几何不变体系二、选择题1.D不难看出左两侧的链杆AC、GE、倾斜短链杆构成的体系几何不变。
同理右侧对称体系几何不变。
分别记作刚片1、刚片2。
大地记作刚片3。
1、2通过A点铰接,大地和1通过C支座和链杆ED相连,交于一虚铰。
刚片2和大地的连接方式类似。
当h=2时,大地和刚片1、2的虚铰分别位于C、B处,与A点位于同一直线上,所以此时为可变体系。
当h无穷大,近似认为ED平行于支座C、B。
此时大地和刚体1、2均相交于无穷远处一虚铰,且两对平行链杆相互平行。
因此此时体系是瞬变的。
除上述两种情况外,体系均满足三铰不共线的原则,因此均是几何不变的,其中链杆AD是多余约束。
2. A体系中有三个刚体,m=3一个连接三个刚体的铰结点,j=2三个固定制作,n=3W=3m-(2j+3n+h)=3*3-(2*2+3*3+0)=-4。
第1章绪论复习思考题1.结构力学的研究对象和具体任务是什么?答:(1)结构力学的研究对象结构力学研究的主要对象是杆系结构。
(2)结构力学的具体任务①研究结构在荷载等因素作用下的内力和位移的计算。
在此基础上,即可利用后续相关专业课程知识进行结构设计或结构验算;②研究结构的稳定计算,以及动力荷载作用下结构的动力反应;③研究结构的组成规则和合理形式等问题。
2.什么是荷载?结构主要承受哪些荷载?如何区分静力荷载和动力荷载?答:(1)荷载的定义荷载是指作用在结构上的主动力。
(2)荷载的分类①按作用时间分为:恒载和活载。
②按荷载的作用位置是否变化分为:固定荷载和移动荷载。
③按荷载对结构所产生的动力效应大小分为:静力荷载和动力荷载。
(3)静力荷载和动力荷载的主要区别荷载是否使结构产生不可忽略的加速度,即是否可以略去惯性力的影响。
若可忽略加速度(惯性力),则为静荷载;若不可忽略加速度(惯性力),则为动荷载。
3.什么是结构的计算简图?如何确定结构的计算简图?答:(1)计算简图的定义结构的计算简图是指略去次要因素,用一个简化图形来代替实际结构的图形。
(2)确定计算简图的方法①杆件的简化,常以其轴线代表。
②支座和结点的简化。
③荷载的简化,常简化为集中荷载及线分布荷载。
④体系的简化,将空间结构简化为平面结构。
4.结构的计算简图中有哪些常用的支座和结点?答:结构的计算简图中常用的支座和结点分别有:(1)常用的支座:活动铰支座、固定铰支座、固定支座、滑动支座。
(2)常用的结点:铰结点、刚结点、组合结点。
5.哪些结构属于杆系结构?它们有哪些受力特征?答:(1)杆系结构的定义杆系结构是指长度远大于其他两个尺度(即截面的高度和宽度)的杆件组成的结构。
杆系结构包括:梁、拱、刚架、桁架、组合结构、悬索结构。
(2)各种杆系结构的受力特征①梁。
梁是一种受弯杆件,其轴线通常为直线,当荷载垂直于梁轴线时,横截面上的内力只有弯矩和剪力,没有轴力。
结构力学的特征1 结构力学简介结构力学是一门研究物体静力学和动力学性质的科学,属于工程力学的范畴。
它主要研究物体在外力作用下的形变、变形能、应力、应变等物理量的关系,并通过计算力学方法获得相应的解析结果。
结构力学的应用非常广泛,例如建筑物、桥梁、轮船、飞机等结构物都需要进行结构力学的计算和分析。
在现代化的工业化进程中,结构力学也成为了极其重要的一门学科。
2 结构力学的基本概念结构力学的基本概念包括以下几个方面:2.1 应力和应变应力和应变是两个非常基本的物理量,它们分别对应了物体受到力的作用下而产生的应力和应变情况。
其中,应力指的是物体内部的力分布情况,而应变指的则是物体在受力情况下的形变情况。
2.2 弹性模量弹性模量是一个非常重要的物理量,它可以衡量材料在受到应力情况下的弹性变形情况。
弹性模量通常是通过材料的荷载-变形关系进行计算的,不同材料的弹性模量会存在差异。
2.3 建构和载荷建构指的是所要计算的结构物,它包括了建筑物、桥梁、管道等,而载荷则是指施加到这些结构物上的力、压力等荷载情况。
在结构力学的计算过程中,建构和载荷都是非常重要的输入参数。
3 结构力学的分析方法结构力学的分析方法主要包括了以下几种:3.1 变分原理变分原理是对结构力学计算的基本原理之一,它通过变分法求解运动方程和边界条件,获得结构物的弯曲、剪切、伸缩等变形情况。
3.2 有限元法有限元法是一种数值计算方法,它将结构物划分成若干个小元素,并通过求解其受载变形情况和应力情况,得到结构物的全局性能参数。
3.3 矩阵分析法矩阵分析法是一种数学分析方法,它将结构物划分成若干个节点,分析节点的受力情况和位移情况,进而求解全局性能参数。
4 结构力学在工业领域的应用结构力学在工业领域的应用非常广泛。
例如,在建筑物建设过程中,通过进行结构力学计算,可以预测房屋的抗风、抗震、抗压等情况,从而保证建筑物的安全性;在机械制造行业中,通过结构力学计算,可以预测机器的静、动态特性,维护机器的正常运行。