数字电子技术基础 综合练习题3

试卷一一、填空题（每空1分，共20分）1、与非门的逻辑功能为。

（全1出0，有0出1）2、数字信号的特点是在时间上和幅值上都是断续变化的，其高电平和低电平常用1和0 来表示。

3、三态门的“三态”指高电平，低电平和高阻状态。

4、逻辑代数的三个重要规则是代入规则、反演规则、对偶规则。

5、为了实现高的频率稳定度，常采用石英晶体振荡器；单稳态触发器受到外触发时进入暂稳态6、同步RS触发器中R、S为高电平有效，基本R、S触发器中R、S 为低电平有效7、在进行A/D转换时，常按下面四个步骤进行，采样、保持、量化、编码。

1. 全1出0，有0出12.时间、幅值、1、03.高电平，低电平，高阻状态4.代入规则对偶规则反演规则5.石英晶体暂稳态6.高低7.采样保持量化编码二、选择题（每题1分，共10分）1、有八个触发器的二进制计数器，它们最多有（）种计数状态。

A、8；B、16；C、256；D、642、下列触发器中上升沿触发的是（）。

A、主从RS触发器；B、JK触发器；C、T触发器；D、D触发器3、下式中与非门表达式为（），或门表达式为（）。

A、Y=A+B；B、Y=AB；C、Y=BA+；D、Y=AB4、十二进制加法计数器需要（）个触发器构成。

A、8；B、16；C、4；D、35、逻辑电路如右图，函数式为（）。

A、F=AB+C；B、F=AB+C；AB+；D、F=A+BCC、F=C6、逻辑函数F=AB+BC的最小项表达式为（）A、F=m2+m3+m6B、F=m2+m3+m7C、F=m3+m6+m7D、F=m3+m4+m77、74LS138译码器有（），74LS148编码器有（）A、三个输入端，三个输出端；B、八个输入端，八个输出端；C、三个输入端，八个输出端；D、八个输入端，三个输出端。

8、单稳态触发器的输出状态有（）A、一个稳态、一个暂态B、两个稳态C、只有一个稳态D、没有稳态1. C2.D3. D A4. C5. A6.C7. A8. A三、判断（每题1分，共10分）：1、逻辑变量的取值，１比0大。

数字电子基础练习题一、选择题1. 在数字电路中，下列哪个逻辑门可以实现“非”运算？（）A. 与门B. 或门C. 非门D. 异或门2. 二进制数1101转换为十进制数是多少？（）A. 13B. 14C. 15D. 163. 在数字电路中，下列哪个器件可以实现数据的存储功能？（）A. 门电路B. 触发器C. 运算器D. 译码器A. 与运算B. 或运算C. 异或运算D. 积运算5. 一个4位二进制数能表示的最大十进制数是多少？（）A. 15B. 16C. 17D. 18二、填空题1. 在数字电路中，逻辑“0”和逻辑“1”分别代表______和______电平。

2. 二进制数1110转换为八进制数是______。

3. 一个触发器可以存储______位二进制信息。

4. 在数字电路中，实现算术运算的电路称为______。

5. n位二进制数可以表示的不同状态有______个。

三、判断题1. 在数字电路中，正逻辑和负逻辑的电压范围是相同的。

（）2. 两个二进制数相加，和的位数一定比被加数和加数的位数多。

（）3. 触发器是数字电路中的基本存储单元。

（）4. 逻辑门电路的输出与输入之间存在线性关系。

（）5. 二进制数和十六进制数之间的转换需要通过十进制数进行。

（）四、简答题1. 请简述数字电路与模拟电路的区别。

2. 什么是逻辑门？请举例说明常见的逻辑门及其功能。

3. 请解释半加器和全加器的区别。

4. 简述二进制数与八进制数之间的转换方法。

5. 请列举至少三种常见的数字电路器件，并说明其功能。

五、综合题1. 给定一个4位二进制数1011，请将其转换为十进制数。

2. 设计一个简单的38译码器电路，并说明其工作原理。

5. 请简述触发器在数字电路中的作用，并以D触发器为例，说明其工作原理。

六、计算题a) 101011b) 11011101c) 111100001a) 25b) 63c) 128a) 1101 + 1011b) 11101 + 10111c) 1001101 + 110111a) 1010 110b) 111100 10101c) 10011011 11011a) 10101111b) 110011001c) 111100001111七、分析题2. 给定一个4位二进制计数器，说明其工作原理，并计算计数器的最大计数值。

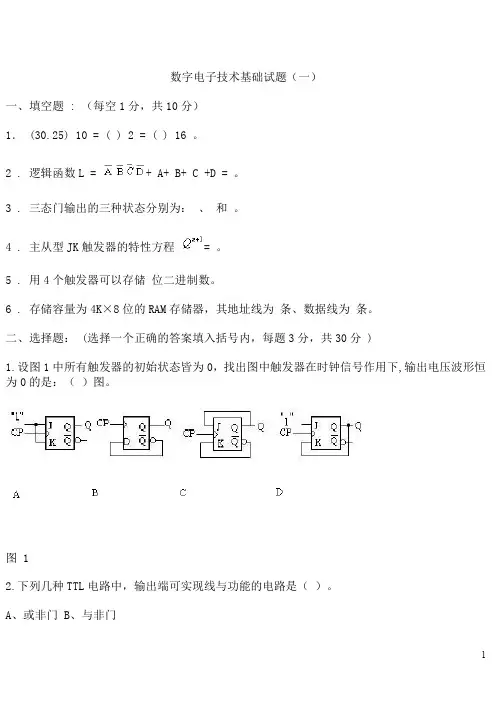
数字电子技术基础试题（一）一、填空题 : （每空1分，共10分）1． (30.25) 10 = ( ) 2 = ( ) 16 。

2 . 逻辑函数L = + A+ B+ C +D = 。

3 . 三态门输出的三种状态分别为：、和。

4 . 主从型JK触发器的特性方程= 。

5 . 用4个触发器可以存储位二进制数。

6 . 存储容量为4K×8位的RAM存储器，其地址线为条、数据线为条。

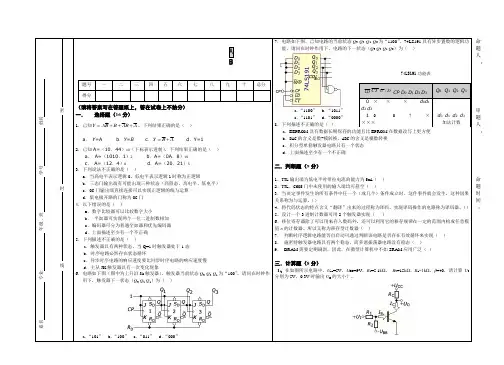
二、选择题： (选择一个正确的答案填入括号内，每题3分，共30分 )1.设图1中所有触发器的初始状态皆为0，找出图中触发器在时钟信号作用下,输出电压波形恒为0的是：（）图。

图 12.下列几种TTL电路中，输出端可实现线与功能的电路是（）。

A、或非门B、与非门C、异或门D、OC门3.对CMOS与非门电路，其多余输入端正确的处理方法是（）。

A、通过大电阻接地（>1.5KΩ）B、悬空C、通过小电阻接地（<1KΩ）D、通过电阻接V CC4.图2所示电路为由555定时器构成的（）。

A、施密特触发器B、多谐振荡器C、单稳态触发器D、T触发器5.请判断以下哪个电路不是时序逻辑电路（）。

图2A、计数器B、寄存器C、译码器D、触发器6．下列几种A/D转换器中，转换速度最快的是（）。

图2A、并行A/D转换器B、计数型A/D转换器C、逐次渐进型A/D转换器D、双积分A/D转换器7．某电路的输入波形 u I 和输出波形 u O 如图 3所示，则该电路为（）。

图3A、施密特触发器B、反相器C、单稳态触发器D、JK触发器8．要将方波脉冲的周期扩展10倍，可采用（）。

A、10级施密特触发器B、10位二进制计数器C、十进制计数器D、10位D/A转换器9、已知逻辑函数与其相等的函数为（）。

A、B、C、D、10、一个数据选择器的地址输入端有3个时，最多可以有（）个数据信号输出。

A、4B、6C、8D、16三、逻辑函数化简（每题5分，共10分）1、用代数法化简为最简与或式Y= A +2、用卡诺图法化简为最简或与式Y= + C +A D，约束条件：A C + A CD+AB=0四、分析下列电路。

数字电子应用技术基础练习题第一部分基础知识一、选择题1．以下代码中为无权码的为。

A. 8421BCD码B. 5421BCD码C.余三码D.格雷码2．以下代码中为恒权码的为。

A.8421BCD码B. 5421BCD码C.余三码D.格雷码3．一位十六进制数可以用位二进制数来表示。

A.１B.２C.４D. 164．十进制数25用8421BCD码表示为。

A.10 101B.0010 0101C.100101D.101015．在一个8位的存储单元中，能够存储的最大无符号整数是。

A.（256）10B.（127）10C.（FF）16D.（255）106．与十进制数（53.5）10等值的数或代码为。

A.(0101 0011.0101)8421BCDB.(35.8)16C.(110101.1)2D.(65.4)87．矩形脉冲信号的参数有。

A.周期B.占空比C.脉宽D.扫描期8．与八进制数(47.3)8等值的数为：A. (100111.011)2B.(27.6)16C.(27.3 )16D. (100111.11)29. 常用的BCD码有。

A.奇偶校验码B.格雷码C.8421码D.余三码10．与模拟电路相比，数字电路主要的优点有。

A.容易设计 B.通用性强C.保密性好D.抗干扰能力强二、判断题（正确打√，错误的打×）1. 方波的占空比为0.5。

（）2. 8421码1001比0001大。

（）3. 数字电路中用“1”和“0”分别表示两种状态,二者无大小之分。

4．格雷码具有任何相邻码只有一位码元不同的特性。

（）5．八进制数（18）8比十进制数（18）10小。

（）6．当传送十进制数5时，在8421奇校验码的校验位上值应为1。

（）7．在时间和幅度上都断续变化的信号是数字信号，语音信号不是数字信号。

（）8．占空比的公式为：q = t w / T,则周期T越大占空比q越小。

（）9．十进制数（9）10比十六进制数（9）16小。

第1章 数字电路基础1.1 (1001010)2=1×26+1×23+1×21=(74)10 (111001)2=1×25+1×24+1×23+1×20=(57)10 1.2 (54)10=(110110)2 (47)10=(101111)2 5427 13 6 3 1 01……MSB10 1 1 0……LSB 2 4723 11 5 2 1 01……MSB 01 1 1 1……LSB1.3 (58A)16 =(0101 1000 1010)2=1×210+1×28+1×27+1×23+1×21=1024+256+128+10=(1418)10 或(58A)16=5×162+8×161+10×160=(1418)10(CE)16 =(1100 1110)2=27+26+14=128+64+14=(206)10 =(0010 0000 0110)8421BCD 1.4 a 1.5 c 1.6 c 1.7 (×) 1.8 (×) 1.9 (√)1.10 ①数字信号：在幅值上，时间上离散的（间断的、不连续的脉冲）信号． ② 数字电路：产生、处理、传输、变换数字信号的电路称为数字电路．③ 数字电路的特点：a ）电路处于开关状态. 与二进制信号要求相一致，这两个状态分别用0和1两个数码表示；b ）数字电路的精度要求不高，只要能区分出两种状态就可以；c ）数字电路研究的问题是逻辑问题，一为逻辑分析，是确认给定逻辑电路的功能，二为逻辑设计，是找到满足功能要求的逻辑电路；d ）研究数字电路的方法是逻辑分析方法，其主要工具是逻辑代数．有代数法和卡诺图法等；e ）数字电路能进行逻辑运算、推理、判断，也能进行算术运算．算术运算也是通过逻辑运算实现的．1.11 ① 位置计数法：将表示数值的数码从左到右按顺序排列起来．它有三个要素a ）基数R ，是指相邻位的进位关系，十进制R =10，即逢十进一，二进制R =2，即逢二进一．b ）数码：表示数字的符号，十进制k i 从0~9共十个．二进制k i 是0和1，十六进制k i 从0~9~A~F 共十六个．c ）位权：数码处于不同位置代表不同的位权，用R i 表示．以小数点前从右到左为i的位号分别为0、1、2、3…，小数点后从左到右i 的位号从–1，–2，–3…来确定R i ．② 按权展开式是将任何进制数表示为十进制数值公式，是系数乘位权的集合，即(N )10=i i i k R ∞=-∞⨯∑． 1.12 ① (3027)10=3×103+2×101+7×100 ② (827)=8×102+2×101+7×100 ③ (1001)2=1×23+1×20④(11101)2=1×24+1×23+1×22+1×20 ⑤ (273)16=2×162 +7×161+3×160 ⑥ (4B5)16=4×162+11×161+5×160 1.13 ① (6)10=(110)2 ② (13)=(1101)2 ③ (39)10=(100111)2 ④ (47)10=(101111)2 1.14 ① (1011)2=(11)10② (110101)2=(53)10③ (4A)16=4×161+10×160=(74)10④ (37)16 =3×161+7×160=(55)10 1.15 ① (10101101)2=(010101101)2=(255)8 =(10101101)2=(AD)16② (100101011)2=(100101011)2=(453)8 =(000100101011)2=(12B)16 ③ ()2=(010*********)2=(2612)8 =(010*********)2=(58A)16 1.16 ① (78)16=(01111000)2=(1111000)2 ② (EC)16=(11101100)2=(11101100)2 ③ (274)16=(001001110100)2=(1001110100)2注：从1.15~1.16均用分组方法，即二进制3位一组可表示1位八进制数；二进制4位一组可表示1位十六进制数．1.17 A =(1011010)2；B =(101111)2； C =(1010100)2；D =(110)2（1）①A +B =(10001001)2②A –B =(101011)2 1011010 + 101111 10001001 1011010 – 101111 101011③C ×D =(111111000)2④C ÷D =(1110)21010100 × 110 0000000 1010100+ 1010100 111111000 1110110 1010100 110 10011100110110 0（2）A=(1011010)2=(90)10B=(101111)2=(47)10①A+B=(137)10=(10001001)2②A–B=(43)10=(101011)2C=(1010100)2=(84)10D=(110)2=(6)10③C×D=(504)10=(111111000)2这说明十进制四则运算的法则在二进制四则运算中也完全适用，对其它进制也一样．1.18 ①[0]8421BCD=(238)10②[10001]8421BCD=(7951)10③[0]8421BCD=(640)101.19 ①逻辑函数：反映因果关系的二值逻辑表达式．原因（条件）为逻辑自变量，结果为逻辑因变量，它们都只有两种状态0和1，用以反映存在不存在，成立不成立，所以它们之间的关系称为（二值）逻辑函数．②与逻辑：表明所有的条件都具备结果才会发生这样的基本逻辑关系为“与”逻辑（逻辑乘）．用式Y=A·B·C…表示．如学生成绩合格与不犯罪与能否毕业的关系即为与逻辑．③或逻辑关系：表明诸多条件中只要有1个以上具备结果就会发生，用Y=A+B+…表示．如去银行办理业务（储蓄），持存款证或持银行卡都可以办理．④非逻辑：是否定的因果关系，即条件具备结果就不能发生，用Y=A表示．如：征兵体检“有病”和“入伍”的关系就是非逻辑．“有病”存在，“入伍”就被否定了，有病不能入伍．1.21 由真值表可以写出最小项与或表达式．方法是将使函数Z为1的几种情况下输入变量的取值组合写成乘积项（变量取值为0写反变量因子，变量取值为1写原变量因子），然后将各乘积项相加，得Z=A B C+A B C+A BC+A B C+A B C1.22Z a=AB AB=A B+A B(摩根定理)=A⊕BZ b=B C AB+= (B⊕C)·AB=(BC+B C)AB=ABC1.24 见教材原文1.5节1.25 a）Z a=∑m(0, 2, 3, 5, 6)=A B C+A B C+A BC+A B C+AB C=A C+B C+A B+A B Cb）Z b =∑m(0, 2, 7, 13, 15, 8, 10)=A B C D+A B C D+A BCD+A B C D+A B C D+AB C D+ABCD=B D+BCD+ABD1.26 （1）Z =A B+B+A B=A B+B=A+B（2）Z =A B C+A+B+C=A B C+A B C++=A B C+A B C=1（3）Z=AB ABC AB AB C+=++=11+=+=AB AB C C（4）Z=A B CD+ABD+A C D=AD(B C+B+C)=AD(C+B+C)=AD·1=AD（5）Z=(A+B)(A CD+AD BC+)A B=(A+B)·A B·(A CD+AD BC+)=0 注：(A+B)A B=A A B+A B·B=0（6）Z=AC(C D+A B)+BC(B AD CE++)=0+BC·(B+AD)·CE=BC(C+E)(B+AD)=(BC E)(B+AD)=BC E+BC E AD=BC E（7）Z=ABC+AC D+A C+CD=C(AB+A D+D)+A C=C(D+A)+A C=AC+CD+A C=A+CD+·(A+B+C)(A+B+C)（8）Z=A+B C=A+B C(A+B+C)(A+B+C)←展开=A+(A B C+B C)(A+B+C)←展开、吸收=A+B C（9）Z =B (A D +A D )+B (AD AD ABCE BC +++) =B (A D +A D )+B (A D +A D ) =A D +A D =A ⊕D（10）Z =AC +A C D +A B E F +B (D ⊕E )+BD E +B D E +BF=A (C +C D )+A B E F +BD E +B D E +BF =AC +AD +F (A B E +B )+B D E +BD E=AC +AD +A E F +BF +BD E +B D E1.27 求反函数Z 和对偶函数Z' （1）Z =AB +C （2）Z =(A +BC )C D Z=(A +B )·C Z=A ·(B +C )+C +D Z' =(A +B )·CZ' =A ·(B +C )+C +D（3）Z =()(+)A C A B AC BC ++ Z =(AC AB A C +++)·(B +C )Z' =(AC AB A C +++)·(B +C ) （4）Z =A D +AC +BCD +C Z=(A +D )·A C +·(B C D ++)·CZ' =(A +D )·A C +·(B C ++D )·C （5）Z =(AC +BD )ABC CD + Z=(A +C )·(B +D )+()()A B C C D +++Z' =(A +C )·(B +D )+()()A B C C D +++ 1.28 用填卡诺图方法写最小项表达式 （1）F 1=A BC +AC +B C =∑m (1, 3, 5, 7)=ABC +A BC +A B C +ABC（2）F 2=A +B +CD =∑m (3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15)=ABCD ABCD ABCD ABCD ABCD ABCD ++++++ABCD ABCD ABCD +++ABCD ABCD ABCD ABCD +++题1.28（1）F 1卡诺图题1.28（2）F 2卡诺图1.29 证明异或关系的正确性 （1）A ⊕0=A ·0+A ·0=A 得证 （2）A ⊕1=A ·1+A ·1=A 得证 （3）A ⊕A =A ·A +A ·A =0 得证 （4）A ⊕A =A ·A +A ·A =1 得证 =A +A =1（5）(A ⊕B )⊕C =(A ⊕B )C +A B C ⊕=ABC ABC ABC ABC +++=∑m (1, 2, 4, 7) A ⊕(B ⊕C ) =A ()B C A B C ⊕+⊕ =A (BC +BC )+A (B C +B C )=ABC ABC ABC ABC +++=∑m (1, 2, 4, 7)左式=右式，得证（6）右式AB ⊕AC =AB ·()()AC ABAC AB A C A B AC ABC ABC +=+++=+ 左式A (B ⊕C )=A (B C +B C )=ABC ABC +得证 （7）左式A ⊕B =A B +AB =AB +AB =中式右式A ⊕B ⊕1=A ⊕(B ⊕1)=A ⊕B =AB AB AB AB +=+=中式 得证．1.30 用卡诺图法将函数化简为与或式． （1）Z ABC ABC ABC ABC =+++ （2）1Z A B AB ABC BC =++++=题1.30（1）的卡诺图题1.30（2）的卡诺图（3）Z ABC AB AD C BD =++++ 填图后，可圈“0”得到ZZ BCD =再对Z 取反，得到ZZ Z BCD B C D ===++（4）Z (A 、B 、C )=∑m (0, 1, 2, 5, 6, 7) Z =AB AC BC ++题1.30（3）的卡诺图题1.30（4）的卡诺图（5）Z (A 、B 、C 、D )=∑m (0, 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 14) Z =B AC AD CD +++（6）Z (A 、B 、C 、D )=∑m (0, 1, 2, 5, 8, 9, 10, 12, 14) Z =BC +BD +AD ACD +题1.30（5）的卡诺图题1.30（6）的卡诺图（7）Z =A C D ABCD ABCD ++++，给定的约束条件为ABCD ABCD ABCD ABCD ++++0ABCD ABCD +=Z=ACD ABCD ABCD ++ =ACD BCD AD ++ （8）Z =()CD A B ABC ACD ⊕++ 给定的约束条件为AB +AC =0Z=ABCD ABCD ABC ACD +++=BD ACD +ACACD题图1.30（7）的卡诺图题图1.30（8）的卡诺图（9）Z=∑m(0, 1, 2, 4)+∑d(3, 5, 6, 7)=1（10）Z=∑m(2, 3, 7, 8, 11, 14)+∑d(0, 5, 10, 15)Z=BD CD AC++题图1.30（9）的卡诺图题图1.30（10）的卡诺图1.31 试用卡诺图法化简下列逻辑图①Z a=ABC ABC BC++=ABC ABC BC++=ABC AC BC②Z b：按逻辑图逐级写函数式，最后得出Z b=A⊕C+(A+B)()+BC AC BD AD=A⊕C+(A+B)()()+++B C AC BD A D=A⊕C+(A+B)ABCD↓展开为与或式=A⊕C+(A+B)(A+B+C+D)=A⊕C+AB+A C+AD+AB+B+BC+BD=A C+A C+AD+B填入卡诺图由卡诺图判断：Z b=AC+AC+AD+B该式已为最简与或式．题图1.31（a）的卡诺图题图1.31（b）的卡诺图1.32 化函数式为与非-与非式，并画出对应的逻辑图．（1）Z1 =AB+BC+AC=AB BC AC++=AB BC AC（2）Z2 =ABC AB BC AB+++=()++ABC AB BC AB=()++++ABC A B BC A B=1ABC=ABC题图1.32（1）题图1.32（2）1.33 用最小项性质证明两个逻辑函数的与、或、异或运算可用卡诺图中对应的最小项分别进行与、或、异或运算来实现．解：命题所给出的结论是正确的．因为当输入变量的取值组合使某一最小项为1时，其他最小项均为0，若两函数相“与”，即Y=Y1·Y2，在对应最小项位置上Y1、Y2均为1时必然使Y 为1；Y1Y2在该位置上有0，则0·0或1·0，Y必然为0，将所有对应最小项作乘运算就实现了Y=Y1·Y2运算．其他运算（或和异或）也是同样的道理．或运算是对应最小项相加；异或运算是对应最小项相异或．。