(完整word版)第五届希望杯六年级一试试题+答案详解

小学六年级“希望杯”全国数学大赛2019-2020年六年级“希望杯”全国数学大赛决赛题（含详细答案）1．计算： 4.5－13×8.13.6＝ 。

2．计算：34 ＋316 ＋364 ＋3256 ＋31024 ＋34096＝ 。

3．若10.5x －10＝36－3y ＝14＋ ,则x ＝ ，y ＝ 。

4．有一类自然数，从第四个数字开始每个数字都恰好等于它前面三个数字的和，直到不能再写为止，如2169，21146等等。

那么这类数中最大的一个数是____________。

5．下面是一串字母的若干次变换。

A B C D E F G H I J第一次变换后为 B C D A F G H I J E 第二次变换后为 C D A B G H I J E F 第三次变换后为 D A B C H I J E F G 第四次变换后为 A B C D I J E F G H……………………………………………………至少经过 次变换后才会再次出现“A 、B 、C 、D 、E 、F 、G 、H 、I 、J ”。

6．把一个棱长为2厘米的正方体在同一平面上的四条棱 的中点用线段连接起来（如右图所示），然后再把正方题 号 一 二 其中： 总 分 13 14 15 16 得 分得分 评卷人x 214体所有顶点上的三角锥锯掉。

那么最后所得的立方体的体积是立方厘米。

7．有一列数，第一个数是5，第二个数是2，从第三个数起每个数都等于它前面两个数中较大数减去较小数的差。

则这列数中前100个数之和等于。

8．在钟面上，当指针指示为6︰20时，时针与分针所组成的较小的夹角为度。

9．小明把五颗完全相同的骰子拼摆成一排（如右图所示），那么这五颗骰子底面上的点数之和是。

10. 有四个房间，每个房间里不少于4人。

如果任意三个房间里的总人数不少于14人，那么这四个房间里的总人数至少有人。

11．如果用符号“[a]”表示数字a的整数部分,例如[5.1]＝5,[ 53]＝1，那么[112000＋12001＋……＋12019]＝。

六年级希望杯初赛试题六年级希望杯初赛试题一、填空题Ⅰ(每题8分，共40分)1、算式(2011-9)÷0.7÷1.1的计算结果是。

2、全世界胡杨90%在中国，中国胡杨90%在新疆，新疆胡杨90%在塔里木，塔里木的胡杨占全世界的%。

3、半径为10、20、30的三个扇形如下放置，S2是S1的倍。

4、50个不同的正整数，它们的总和是2011，那么这些数里奇数至多有个。

5、A、B、C三队比赛篮球，A队以83∶73战胜B队，B队以88∶79战胜C队，C队以84∶76战胜A队，三队中得失分率最高的出线。

一个队的得失分率为(得的总分)/(失的总分)，如，A队得失分率为(83+76)/(73+84)。

三队中队出线。

二、填空题Ⅱ(每题10分，共50分)6、一个边长为120cm的等边三角形被分成了面积相等的五等份，那么，AB=cm。

7、某校六年级学生中男生占52%，男生中爱踢球的占80%，女生中不爱踢球的占70%。

那么，在该校六年级全体学生中，爱踢球的学生占%。

8、在每个方框中填入一数字，使得乘法竖式成立。

已知乘积有两种不同的得数，那么这两个得数的差是。

9、大小相同的金、银、铜、铁、锡正方体各一个，拼成如的`十字，一共有种不同的拼法(旋转后可以重合的拼法看成是相同的拼法)。

10、在右的每个格子中填入1～6中的一个，使得每行、每列所填的数字各不相同。

每个粗框左上角的数和“+”、“-”、“×”、“÷”分别表示粗框内所填数字的和、差、积、商(例如“600×”表示它所在的粗框内的四个数字的乘积是600)。

三、填空题Ⅲ(每题12分，共60分)11、用1、3、5、7、9这五个数字组成若干个合数，每个数字恰好用一次。

那么，这些合数的总和最小是。

12、1盒子高为20cm，底面数据如2，这个盒子的容积是cm3。

(π取3.14)13、一件工程按甲、乙、丙各一天的顺序工作，恰需要整天数工作完毕。

2020年希望杯复赛六年级试题+答案一、 填空题（每小题5分；共60分.）1. 计算：11112123123410+++++++++++L L ；得__________. 2. 某商品单价先上调后；再下降20%才能降回原价.该商品单价上调了__________%.3. 请你想好一个数；将它加5；其结果乘以2；再减去4；得到的差除以2；再减去你最初想好的那个数；最后的计算结果是__________.4. 八进制数12345654321转化为十进数是N ；那么在十进制中；N ÷7与N ÷9的余数的和为__________.5. 小明把一本书的页码从1开始逐页相加；加到最后；得到的数是4979；后来他发现这本书中缺了一张（连续两个页码）.那么；这本书原来有__________页.6. 2015在N 进制下是AABB 形式的四位数；这里A ；B 是N 进制下的不同数码；则N 的值是__________.7. 方程{}{}210x x x x ⎡⎤+=+⎣⎦的所有解的和是__________（其中x ⎡⎤⎣⎦表示不超过x 的最大整数；{}x 表示x 的小数部分）.8. 如图1；将1个大长方形分成了9个小长方形；其中位于角上的3个小长方形的面积分别为9；15和12；则第4个角上的小长方形的面积等于__________.9. 一个魔法钟；一圈有12个大格；每个大格有3个小格；时针每魔法时走一个大格；分针每魔法分走1个小格；每魔法时走两圈.那么；从时针与分针成90º角开始到时针和分针第一次重合；经过了__________魔法分.10. 将1至2015这2015个自然数依次写出；得到一个多位数123456789…20142015；这个多位数除以9；余数是__________.11. 如图2；向装有13水的圆柱形容器中放入三个半径都是1分米的小球；此时水面没过小球；且水面上升到容器高度的25处；则圆柱形容器最多可以装水__________立方分米.（π取3.14）12. 王老师开车从家出发去A 地；去时；前12的路程以50千米/小时的速度行驶；余下的路程行驶速度提高20%；返回时；前13的路程以50千米/小时的速度行驶；余下的路程行驶速度提高32%；结果返回时比去时少用31分钟；则王老师家与A 地相距__________千米.二、 解答题（每小题15分；共60分.）每题都要写出推算过程.13. 二进制是计算技术中广泛采用的一种数制；其中二进制数转换成十进制数的方法如下：210210(101)120212(5)=⨯+⨯+⨯=； 43210210(11011)1212021212(27)=⨯+⨯+⨯+⨯+⨯=； 6543210210(1110111)12121202121212(119)=⨯+⨯+⨯+⨯+⨯+⨯+⨯=； 876543210210(111101111)121212120212121212(495)=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=那么；将二进制数11111011111转化为十进制数；是多少？（注：022222,21n n ↑=⨯⨯⨯=L 1442443）14. 已知寒假一共有29天；小明10天可以完成寒假作业.小明每天可以选择做作业或者不做作业.如果小明在寒假作业完成之前就连续3天不做作业；或者寒假没完成作业；爸爸就会惩罚他.那么小明在不被爸爸惩罚的情况下有多少种度过寒假的安排方式？15. 一个棱长为6的正方体被切割成若干个棱长为整数的小正方体；若这些小正方体的表面积之和是切割前的大正方体的表面积的103倍；求切割成的小正方体中；棱长为1的小正方体的个数.16. 如图3；点M 、N 分别是边长为4米的正方形ABCD 的一组对边AD 、BC 的中点；P 、Q 两个动点同时从M 出发；P 沿正方形的边逆时针方向运动；速度是1米/秒；Q 沿正方形的边顺时针方向运动；速度是2米/秒.求：（1） 第1秒时△NPQ 的面积；（2） 第15秒时△NPQ 的面积；（3） 第2015时△NPQ 的面积.。

2021希望杯四五六年级复赛试题及答案----f032fcf8-7152-11ec-bfcc-7cb59b590d7d2021希望杯四五六年级复赛试题及答案2022希望杯四期；V&period；六年级半决赛问答2021希望杯四、五、六年级复赛试题及答案倒序浏览标题：系统管理员楼主发表于2021-04-1015:59|只看该作者|倒序浏览亲爱的同学们，你们好~萧萧暗笑又来了，也给大家带了新礼物哦（欢呼....~撒花....~~）在上周末（4月8日），希望杯第二轮比赛也结束了。

我不知道学生们在考试中表现如何？不论感觉如何，还是萧萧暗笑的那句老话——考试成绩绝对不是目的，从中获得的经验和提高，才是宝藏。

因为，它能帮助你找到自己的弱点，让你的学习更有针对性。

考试结束了。

我不知道你觉得这次考试怎么样？对于考试的难度、题型等有任何的疑问和想法，都可以留言给我们哦。

我们的老师最近也在积极研究和分析这次考试。

请期待老师们的精彩评论。

没有参加希望杯考试或没有进入复赛的同学，也可以从文库中下载试卷，试着做一做，学习学习，会得到不一样的收获哦~2022希望杯第六级半决赛问答2021希望杯五年级复赛试题及答案2022希望杯第四级半决赛问答（试卷与答案在统一文档中，文档最后一页即是答案）学习是一个不断积累的过程。

你需要有一个明确的计划来推动你的进步。

您不知道如何学习“公共在线课程”中的课程。

看看这个话题~学习视频的同时，可以借鉴这种规划方式，根据自己情况制定适合自己的学习计划，不断的累积、进步。

（单击图片查看详细信息~）。

2019年六年级希望杯试题及答案word版六年级第1试试题解答题目1-应用题Ax比300少30%；y比x多30%；则x y+=483 。

题目2-计算A如果；那么？所表示的图形可以是下图中的 3 。

（填序号）题目3-计算B计算：12113114115=++++++43114。

题目4-应用题A一根绳子；第一次剪去全长的13；第二次剪去余下部分的30%。

若两次剪去的部分比余下的部分多0.4米；则这根绳子原来长 6 米。

题目5-应用题A根据图中的信息可知；这本故事书有 25 页。

题目6-应用题B已知三个分数的和是1011；并且它们的分母相同；分子的比是234::。

那么；这三个分数中最大的是40 99。

题目7-行程B从12点整开始；至少经过55513分钟；时针和分针都与12点整时所在位置的夹角相等。

（如图中的12∠=∠）。

题目8-数论B若三个不同的质数的和是53；则这样的三个质数有 11 组。

题目9-数论B被11除余7；被7除余5；并且不大于200的所有自然数的和是 351 。

题目10-方程B在救灾捐款中；某公司有110的人各捐200元；有34的人各捐100元；其余人各捐50元。

该公司人均捐款 102.5 元。

题目11-几何B如图；圆P 的直径OA 是圆O 的半径；OA BC ⊥；10OA =；则阴影部分的面积是 75 。

（π取3）OBP题目12-几何B如图；一个直径为1厘米的圆绕边长为2厘米的正方形滚动一周后回到原来的位置。

在这个过程中；圆面覆盖过的区域（阴影部分）的面积是 11 平方厘米。

（π取3）题目13-方程A如图；一个长方形的长和宽的比是5:3。

如果长方形的长减少5厘米；宽增加3厘米；那么这个长方形边长一个正方形。

原长方形的面积是 240 平方厘米。

题目14-组合A一次智力测试由5道判断对错的题目组成；答对一道得20分；答错或不答得0分。

小花在答题时每道题都是随意答“对”或“错”；那么她得60分或60分以上的概率是 50 %。

第五届小学“希望杯”全国数学邀请赛六年级 第1试以下每题6分，共120分。

1. 已知31::1.2,:0.75:22a b b c ==,那么:c a = （写成最简单的整数比）2.11111111(1)(1)(1)(1)(1)(1)(1)(1)23456789_____.0.10.20.30.40.50.60.70.80.9--------=++++++++ 3．在下面的算式□中填入四个运算符号+、-、⨯、÷、（每个符号只填一次），则计算结果最大是_______.1□2□3□4□54. 在图1所示的和方格表中填入合适的数,使用权每行、每列以及每条对角线上的 三个数的和相等。

那么标有“★”的方格内应填入的数是_______.5. 过年时，某商品打八折销售，过完年，此商品提价________%可恢复原来的价格。

6．如图2是2003年以来我国日石油需求量和石油供应量的统计图。

由图可知，我国日石油需求量和日石油需求量增长更______(填“大”或“小”)，可见我国对进口石油的依赖程度不断定_______（填“增加”或“减小”）。

7．小红和小明帮刘老师修补一批破损图书。

根据图3中信息计算，小红和 小时一共修补图书______本。

8．一项工程,甲单独完成需要10天,乙单独完成需要15天,丙单独完成需20天,古代合作3天后,甲有其它任务而退出,剩下乙、丙继续工作直至完工。

完成这项工程共用______天。

9．甲、乙两车分别从A 、B 两地同时相向开出，甲车的速度是50千米/时，乙车的速度是40千米/时，当甲车驶过A 、B 距离的13 多50千米时,与乙车相遇.A 、B 两地相距______千米。

10．今年儿子的年龄是父亲年龄的14 ,15年后,儿子的年龄 父亲年龄的511 。

今年儿子______岁。

11．假设地球有两颗卫星A 、B 在各自固定的轨道上环绕地球运行，卫星A 环绕地球一周用145小时，每12．三个数,1,3p p p ++都是质数，它们的倒数和的倒数是_______。

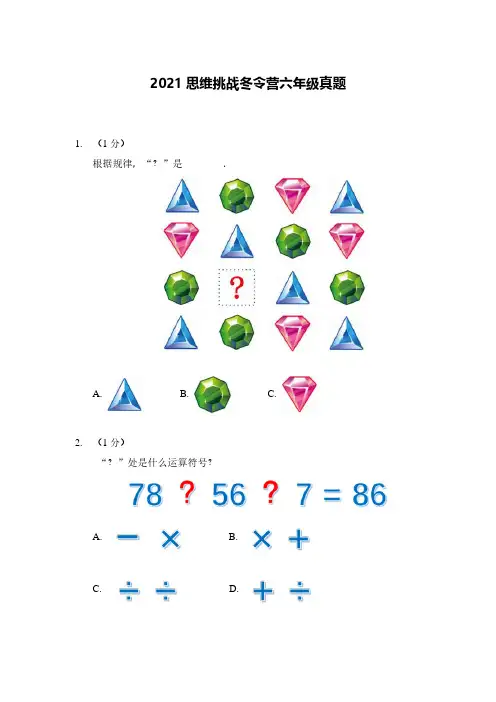
2021思维挑战冬令营六年级真题1.（1分）根据规律，“？”是________．A. B. C.2.（1分）“？”处是什么运算符号？A. B.C. D.根据规律，“？”是________．4.（1分）在字母四阶数独中，每一行、每一列、每一个粗线框里都有A，B，C，D．“？”应该是（）．A. B. C. D.6.（1分）A. B. C. D.8.（1分）“？”处填________．10.（1分）11.（5分）小糊涂遇到一个问题：比较99100，100101，199201的大小．他感到很迷糊，请你帮他找到正确的答案．A.99100>100101>199201B.199201>100101>99100C.99100>199201>100101D.100101>199201>99100E.100101>99100>199201小仙子有一根魔法棒，挥动一下可以让“死”变为“生”，或让“生”变为“死”．一天，小仙子看到4棵树，其中2棵已经枯萎，如下图．她挥动魔法棒希望所有的树都是“生”的状态，可惜魔法棒出了故障，不仅会对她指向的树起作用，也会对相邻的树起作用，那么她至少要挥动________次魔法棒才能实现心愿．13.（5分）森林女巫有一个容积为1升的药瓶，装满药液．每轮操作，把瓶中的药液倒掉一半，再倒入0.5升的水，均匀混合．至少经过________轮操作，瓶中药液的浓度不超过最初时的1 1000．14.（5分）猴山上金丝猴的数量是长尾猴的47．过了几年后，金丝猴的数量变为原来的2倍，长尾猴增加了24只，金丝猴的数量是长尾猴的45，这时金丝猴有________只．15.（5分）两个小黄人凯文和鲍勃从环形跑道同一点同时出发，同向而行，每60秒钟凯文从后面追上鲍勃一次．如果凯文用40秒走完一圈，则鲍勃走完一圈需要________秒．莱洛三角形是一个非常有名的图形，以正三角形的顶点为圆心，以其边长为半径作三条圆弧就可以画出一个莱洛三角形．下图中的莱洛三角形的外周长是314cm，则中心正三角形的边长是________cm．（π取3.14）17.（5分）如图，青青草原有一条圆形步道和两条直步道，两条直步道恰好都通过圆心，圆的半径为50米．慢羊羊村长从A点出发沿步道散步，他要走遍全部的步道再回到A点，至少走________米．（π取3.14）18.（5分）在一场意大利和巴西的足球比赛中，支持意大利队与支持巴西队的观众人数比为5∶4．半场时，由于比分差距过大，有13的观众离场，剩余观众中支持意大利队与支持巴西队的人数比为3∶1．如果离场的观众中有35人支持意大利队，则最初共有观众_______人．对角巷的魔药店进了一批曼德拉草，按100%的利润率来定价，结果只售出30%的曼德拉草．为尽早售出剩下的曼德拉草，魔药店决定打六折销售，结果剩余的曼德拉草销售一空．这批曼德拉草的利润率是________%． 20. （5分）喜羊羊、美羊羊和暖羊羊去寻宝，他们各自都找到了一些金币．喜羊羊的金币数是其他两人金币总数的14，美羊羊的金币数是其他两人金币总数的13，暖羊羊的金币数是176枚．那么他们三人一共找到了________枚金币． 21. （5分）计算：2019202020212020+20212022202120222023202220232024201820192020202111112018201920202021+++++++−+−−+−=________． 22. （5分）2021最多可以表示成________个连续自然数的和．如图，只打开甲，注满一桶水用5小时；只打开乙，排光一桶水用6小时；只打开丙，注满一桶水用3小时；只打开丁，排光一桶水用4小时．开始时桶内没有水，现在按甲、乙、丙、丁、甲、乙、丙、丁……的顺序轮流各开1小时，经过________分钟水桶将注满水．24.（5分）如图，正六边形ABCDEF的面积为125，且CM∶MD=AN∶NM=NP∶PD=2∶3，则△PDE的面积是_________．如图所示，5块相同的小长方形地砖铺成一个大长方形．在此基础上，要铺成一个大正方形，至少再铺________块同样的小长方形地砖．26.（5分）在数字岛上住着很多数，其中有一些六位数都属于一个家族，它们都可以表示为66ABCD，而且它们都能被495整除．这个家族有________个成员．27.（5分）几何王国的广场上有一个由相同的小立方体堆成的建筑，这个建筑从正面看，从左面看，从上面看，看到的视图都相同，如下图所示．那么这个建筑最多由________个小立方体组成．迷糊老师今天上课讲解高斯记号，告诉我们[a ]表示不大于a 的最大整数，例如[1.1]=1，[3]=3，然后计算：1352019202177777⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦________． 29. （5分）在一个神奇的字母王国，人们用字母表示数字．在下面的竖式中，相同的字母表示相同的数字，不同的字母表示不同的数字，那么ABCDEFG 表示的七位数是________．30. （5分）国王让金匠和银匠做钱币，可是只有一个模具，先是金匠做完后，银匠紧接着做．他们共用2小时完成，两人做的钱币恰好一样多．已知他们在第二个小时内做好的钱币比第一个小时多6个，并且每小时银匠比金匠多做8个钱币．那么他们一共做了________个钱币． 31. （5分）粗心的猪八戒在计算2.021165000••⨯时，没注意到循环小数上的小圆点，他的计算结果比正确结果少了________．机械战警在执行任务时遇到一个谜题任务，要求在一个8×8的棋盘中放入一些棋子，每格最多放一枚．那么，最多可以在棋盘中放________枚棋子，使得无论怎样放，总能选出4行4列，这些棋子都在选出的行列中．33.（5分）如图，长方形POQR中嵌入3个相同的正方形．已知PR=8厘米，RQ=10厘米，那么每一个正方形的面积为________平方厘米．朵拉编了一个程序，用计算机按下图所示规律写了100行数，计算机写下的这100行所有数的和是________．56 67 7 78 8 8 89 9 9 9 910 10 10 10 10 10... ... ... ... ... ... ...35.（5分）长寿村有一位老人2021年就101岁啦！如果将老人的年龄作为分子，当年的年份数作为分母，可写出一个分数，如2001年这位老人是81岁，可以写出分数812001．这位老人从1岁至100岁，可以写出100个分数，其中最简分数有________个．36.（5分）公元2222年，为了方便星际旅行，人类要在太阳系的金星、木星、水星、火星、土星这5颗行星之间建设4条航路，每条航路连接其中两颗行星，从其中任意一颗行星出发，都可以到达其他4颗行星．一共有________种不同的建设方案．如图是多多岛上的地图，图上的数表示该段铁路的长度．一天，托马斯和爱德华同时从提茅斯机房出发背向而行，高登在同一时刻也从采石场出发．当托马斯和高登第一次相遇时，爱德华刚好第一次经过采石场；当托马斯和爱德华第一次相遇时，高登刚好第一次经过提茅斯机房．那么，当高登第一次追上爱德华时，托马斯行驶了________km ．38. （5分）小飞侠最近正在研究一些新的运算法则．规定n ※表示不大于n 的所有非零偶数的积，□n 表示不能整除n 的最小自然数．例如：624648=⨯⨯=※，□10=3．如果()13x =※□，那么x 最小是________． 39. （5分）四个海盗分15枚相同的金币，第一个海盗至少要4枚，第二个海盗可以不要，第三个海盗至少要2枚，第四个海盗至少要1枚．共有________种不同的分法． 40. （5分）如果999是212221n ⋯2个的一个因数，那么n 最小是________．答案。

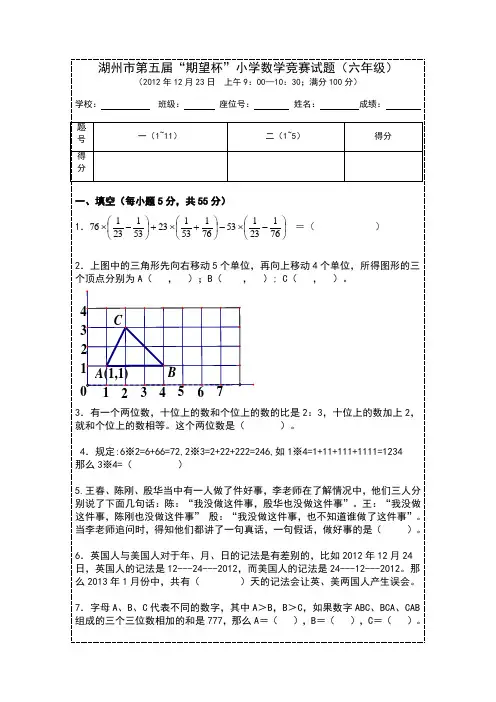
2024 IHC D-6 中文卷1. 将1843化为最简分数，1843= 。

4559 45592. 若正整数k ≥ 2024 , 那么22k−1− 3 − 5 −...− 2019−202 被 3 除所得的余数是。

3. 黑板上写有1 到101 这101 个自然数，现擦去其中一些数，黑板上至多保留个数，才能使黑板上任意两数之和都不能被5 整除。

14. 1+1+1 +... +1的整数部分是。

2004 2005 2006 20245. 有甲、乙两个杯子，甲杯装有纯酒精，乙杯装有纯水，两杯液体质量都是12 千克。

现从甲杯中取出一定量的纯酒精，倒入乙杯并搅拌均匀，再从乙杯中取出一定量的混合液倒入甲杯，此时两杯液体质量仍然都是12 千克。

若此时甲杯中纯酒精和纯水的质量比为5∶1，那么第一次从甲杯中取出的纯酒精是千克。

6. 在数2,3,4,5,6,7,8,9的前面分别添加“＋”或“－”号，使得10 10 10 10 10 10 10 10它们的和等于1。

有种不同的添加方法。

7.如图，F 和G 是△ABC 边BC 上两点，满足BF:FG:GC=2:2:1, 连接AF、AG, 在AF 上取点D，CD 与AG 相交于点E，△DAB 与△ACE 的面积分别是324 和243。

则△ABC 的面积是。

8.幸福小学通过微信小程序对“小天才科普大使”进行票选，每人限投一票。

小华查看了投票结果，发现投票总人数是400，其中小华所在班级代表的投票占48%。

第二天她再次登录该网站时，发现小华所在班级代表的投票率上升到62%，则此时投票总人数至少为人。

9.如果某一天是周四且日期尾数是4，则称这一天为“巧合日”，如2023 年12 月14日是周四，这一天是“巧合日”。

则2023 年一共有个“巧合日”。

10.如图，△ABC 的三条边满足AC : BC : AB = 3:4:5，E 和D 是AC 和BC 上的点，AE :EC=BD : DC = 2:3，F 和G 是AB 上的点，FG : AB=3:5，连接DF、EG 相交于点O，则阴影部分与△ABC 的面积比是。

壹新希望杯（2011年）小学六年级数学邀请赛试卷及解析答（满分120分，时间120分钟）一、填空题（每题5分，共60分）1、计算：=-+••114154.0625.3________________. 解析：原式=625.3+••54.0-••63.1=625.2+（••54.1-••63.1）=625.2+••90.0=••09715.2或 原式=8823911108291115115829=-=-+ 2、对于任意两个数x 和y ，定义新运算◆和⊗，规则如下：x ◆y =y x y x 22++，x ⊗y =3÷+⨯y x y x ；如 1◆2=221212⨯++⨯，1⊗2=5115632121==+⨯， 由此计算••63.0◆=⊗)2114(__________. 解析：=⊗)2114(345.465.045.14==+⨯，而11463.0=••，所以原式=25173211132112342114341142=++=⨯++⨯3、用4根火柴，在桌面上可以拼成一个正方形；用13根火柴可以拼成四个正方形；…，如图1，拼成的图形中，若最下面一层有15个正方形，则需火柴__________根。

解析：第二个图形比第一个图形多9根火柴，第三个图形比第二个图形多13根火柴，经尝试，第四个图形比第三个图形多17根火柴，而最下面一层有15根火柴的是第8个图形，所以共需要火柴4+(9+13+17+21+25+29+33)=151根。

4、若自然数N 可以表示城3个连续自然数的和，也可以表示成11个连续自然数的和，还可以表示成12个连续自然数的和，则N 的最小值是_________。

（注：最小的自然数是0）解析：因为奇数个连续自然数之和等于中间数乘以数的个数，所以N 能被3和11整除，也就是能被33整除；因为偶数个连续自然数之和等于中间两个数的平均值乘以数的个数，所以N 等于一个整数加上0.5再乘以12，也就是被12除余6，最小为66。

2022 思维挑战冬令营六年级真题1. “？”处是（）．2. “？”=．3. 图中最小的正方形边长为1，则最大的正方形边长为．4. 图中的数字6 对应的是（）．5. “？”处填．6. 在字母四阶数独中，每一行、每一列、每一个粗线框里都有A，B，C，D．“？”应该是（）．7. “？”=．8.9. 下图中的红色积木多还是蓝色积木多？A.红色B.蓝色10. 最轻的是（）．11. “？”处的图形是哪一个？（）12. 两个循环小数相乘：□ 0.16 20.12469计算结果小数点后第2022 位上的数字是 ． 13. 等式中的 a 和 b 都是自然数，b = ．1 □ 22 73 1 a a 1 b 14. 计算：1 1 1 1 1 ... 12 23 34 45 2021 2022 □ 1 1 1 1 1 (1 )(1 )(1 )(1 )...(1 ) 2 3 4 5 2022 1 2 3 29 30 36 3636 25 2525 约分后得到整数，那么 m + n 最大是 15. m 个36n 个25 16. 九位数ABCABCBBB 能被 1~18 中任何一个自然数整除，且数字 A 、B 、C 互不相同，则三位数ABC = ．17. 在长寿星上，所有人的寿命都是 1000 岁．乐乐、弟弟、爷爷三人的年龄各不相同，并且今年、明年和后年乐乐的年龄都是弟弟年龄的整数倍，爷爷的年龄也都是乐乐年龄的整数倍．乐乐今年 岁．18. 虎王召集森林动物开会，会议室圆桌周围有28 个座位，其中一些座位已经有动物就座．正要入座的小猴发现，无论它坐在哪个座位上都会与某个已经19. 纪录片《中国通史》共100 集．小明只看了连续的47 集；爸爸只看了连续的65 集；奶奶只有18 集没看过，且其中没有多于3 集连续的情况．那么小明、爸爸和奶奶都看过的最少有集．20. 在4×4 的方格中有16 枚棋子，每枚棋子都是一面黑色，一面白色．规定：将一组2×2 方格里的4 枚棋子各翻转一次称为“一次操作”．最初全部16枚棋子的黑色面朝上，如左图．最少经过次操作，可出现右图所示的情况．21. 正着读和反着读一样的数称为回文数．如121 是三位回文数，5665 是四位回文数．两个四位回文数相加，得到的和是一个五位回文数，这样的四位回文数有对．（注：两个数算做1对，并且两个数没有顺序，如2和3，22. 水中的9 条鱼都标有元气值，两只小猫各钓到一条鱼，这两条鱼的总元气值有种不同的情况．23. 魔法学校的课程分为9 级，学员从第1 级开始学习，学完第9 级就可以成为魔法师．学习过程中允许跳级，但每次最多跳一级，并且第1 级和第9 级是必修课程．在2022 寒季来临前，有一批学员成为魔法师，但他们学习的课程24. 猪猪侠玩闯关游戏，每道关卡会遭遇怪兽、机甲或法师这三种攻击类型中的一种，战胜方可通关．在一次游戏中猪猪侠连闯了10 关，其中没有连续的同关攻击类型的排10种类型的攻击，而他遇到怪兽的关卡不止一关．那么这列有种可能情况．25. 有100 张卡片，上面分别写有1~100．妙妙拿走一些卡片后，米奇发现余下的卡片虽然不够100 张，但仍然能够找到1~100 的任何一个数，因为一些卡片可以倒过来看，比如倒过来看是，倒过来看是．那么妙妙最多拿走了张卡片．（注：0 不能作为首位数字出现）卡片上的数字写法如下：26. 下图是北京市行政区划图，现给这张图染色，有4 种颜色供选择，要求每个区域染一种颜色，并且相邻区域颜色不同，共有种染色方法．27. 从2022 的因数中任意取出两个数相加，它们的和大于202 的概率是（）．1 45125811141728A. B. C. D. E.28. 42 的正方形被分割成四个周长相同的小长方形，则阴影部分的面积边长为为．29. 如图，在梯形ABCD 中，EF 和MN都平行于底边，且AB∶CD=1∶2，CE∶EM∶MB=1∶2∶3，若阴影部分的总面积是10，则梯形ABCD 的面积是．30. 8 个小正八边形的边长都是60，它们贴在一个大正八边形的内侧，并且8 个小八边形的总面积占了大正八边形面积的一半．大正八边形的边长为31. 如图，正方形ABCD 的四个顶点在圆O 上，圆O 的半径为10．以A 为圆心，AB 为半径画大圆，则阴影部分的面积是．（π 取3.14）32. 如图，点P、Q、R、S、T、U 将半径为20 厘米的大圆六等分，大圆内部有一个半径为10 厘米的同心圆．在内外圆之间连线，围出阴影区域，且阴影区33. 一个等腰梯形上、下底边分别长10、20，腰长8．将梯形分别绕着上底、下底旋转一周，得到的两个旋转体的体积之和是（）．A．1170πB．1200πC．1250πD．1280π34. 赫尔墨斯号飞船从地球前往火星，全程80%的时间内每小时飞行45 万千米，2的时间内每小时飞行42 万千米，其余时间内每小时飞行36 万千米．全全程15程的平均速度是每小时万千米．35. 皮皮鲁和鲁西西喜欢冒险，他们来到小人国，这时皮皮鲁和鲁西西的身高相同．当他们从小人国回到正常世界，皮皮鲁的身高增加了20%，鲁西西的身高增加了20 cm．当他们从正常世界来到大人国，皮皮鲁的身高增加了20 cm，鲁西西的身高增加了20%．在大人国，鲁西西比皮皮鲁高cm．36. 莫顿农场和莱茵农场的面积比是3∶2，并且都只种植玉米和黄豆，两个农场种植玉米和黄豆的总面积之比是7∶3，莫顿农场种植玉米和黄豆的面积比是4∶1，那么莱茵农场种植玉米和黄豆的面积比是（）．A．9∶8B．10∶7C．11∶9D．8∶537. 用奇数表示齿轮凸起的部分，称为齿1，齿3，……用偶数表示齿轮凹槽的部分，称为槽2，槽4，……如图，齿轮A 的槽12 和齿轮B 的齿21 咬合，齿轮B 的齿13 和齿轮C 的槽合时，齿轮B 和C 咬合的位置是（）．A.齿轮B 的槽12 和齿轮C 的齿3B.齿轮B 的槽12 和齿轮C 的齿15C.齿轮B 的槽12 和齿轮C 的齿7D.齿轮B 的齿15 和齿轮C 的槽1038. 老虎、狮子和花豹赛跑，它们同时从起跑线出发．当狮子跑到终点时，老虎离终点还有15 米，花豹离终点还有35 米；当老虎跑到终点时，花豹离终点还有22 米．赛道的长度是米．39. 多多岛的小火车们勤快地忙碌着．托马斯和培西从机房前往码头，爱德华从码头前往火车站，他们都是到达目的地后立即返回出发地，往返一次后结束工作．三辆小火车同时出发，当爱德华到达火车站时，托马斯也刚好经过火车站，而这时培西只行驶了45 km；当爱德华回到码头时，托马斯刚好又经过火车站．这时托马斯的蒸汽机出故障，他仍坚持行驶但速度减半，恰好在机房和码头铁路线的中点迎面遇到了培西．那么，机房到码头铁路线的长度为km．40. 从1~9 中选择合适的数字填入方格，每个数字在每行、每列以及每个宫格中只出现一次，且满足相邻两格之间的大于或小于号所表示的大小关系．“？”答案题目 1 2 3 4 5 6 7 8 9 10 答案A68B8A5B A B 题目11 12 13 14 15 16 17 18 19 20 答案D2720211030671036题目21 22 23 24 25 26 27 28 29 30 答案3636341498164224D54018240题目31 32 33 34 35 36 37 38 39 40 答案414928A444C A1652257。