初等几何研究第一章习题的答案(1)
- 格式:pdf
- 大小:2.22 MB
- 文档页数:10
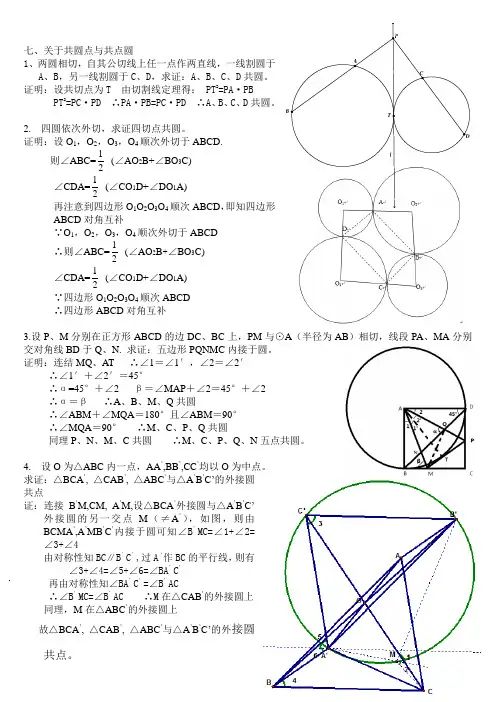
七、关于共圆点与共点圆1、两圆相切,自其公切线上任一点作两直线,一线割圆于A 、B ,另一线割圆于C 、D ,求证:A 、B 、C 、D 共圆。
证明:设共切点为T 由切割线定理得: PT 2=PA·PBPT 2=PC·PD ∴PA·PB=PC·PD ∴A、B 、C 、D 共圆。
2. 四圆依次外切,求证四切点共圆。
证明:设O 1,O 2,O 3,O 4顺次外切于ABCD.则∠ABC=12(∠AO 2B+∠BO 3C) ∠CDA=12(∠CO 1D+∠DO 1A) 再注意到四边形O 1O 2O 3O 4顺次ABCD ,即知四边形ABCD 对角互补∵O 1,O 2,O 3,O 4顺次外切于ABCD∴则∠ABC=12(∠AO 2B +∠BO 3C) ∠CDA=12(∠CO 1D+∠DO 1A) ∵四边形O 1O 2O 3O 4顺次ABCD∴四边形ABCD 对角互补3.设P 、M 分别在正方形ABCD 的边DC 、BC 上,PM 与⊙A (半径为AB )相切,线段PA 、MA 分别交对角线BD 于Q 、N. 求证:五边形PQNMC 内接于圆。
证明:连结MQ 、AT ∴∠1=∠1′,∠2=∠2′∴∠1′+∠2′=45°∴α=45°+∠2 β=∠MAP +∠2=45°+∠2∴α=β ∴A 、B 、M 、Q 共圆∴∠ABM +∠MQA =180°且∠ABM =90°∴∠MQA =90° ∴M 、C 、P 、Q 共圆同理P 、N 、M 、C 共圆 ∴M 、C 、P 、Q 、N 五点共圆。
4. 设O 为△ABC 内一点,AA ’,BB ’,CC ’均以O 为中点。
求证:△BCA ’, △CAB ’, △ABC ’与△A ’B ’C’的外接圆共点证:连接B ’M,CM, A ’M,设△BCA ’外接圆与△A ’B ’C’外接圆的另一交点M (≠A ’),如图,则由BCMA ’,A ’MB ’C ’内接于圆可知∠B ’MC=∠1+∠2=∠3+∠4由对称性知BC ∥B ’C ’,过A ‘作BC 的平行线,则有∠3+∠4=∠5+∠6=∠BA ’C ’再由对称性知∠BA ’C ’=∠B ’AC∴∠B ’MC=∠B ’AC ∴M 在△CAB ’的外接圆上同理,M 在△ABC ’的外接圆上故△BCA ’, △CAB ’, △ABC ’与△A ’B ’C’的外接圆共点。

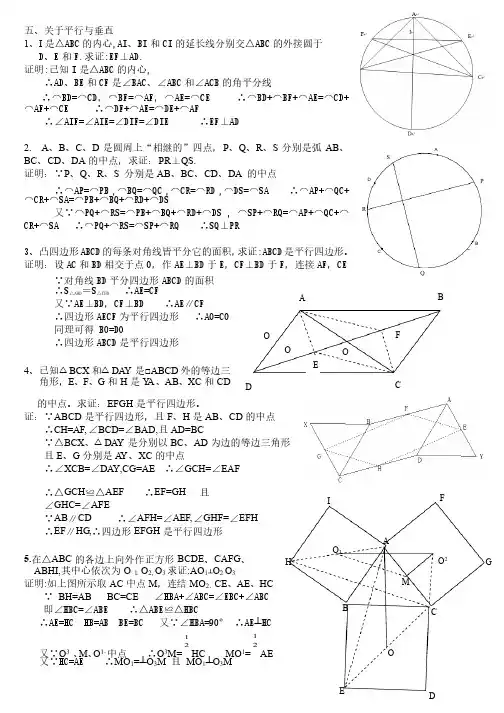
五、关于平行与垂直五、关于平行与垂直 1、I 是△是△ABC ABC 的内心的内心,AI ,AI ,AI、、BI 和CI 的延长线分别交△的延长线分别交△ABC ABC 的外接圆于的外接圆于D 、E 和F.F.求证求证求证:EF :EF :EF⊥⊥AD.AD. 证明证明::已知I 是△是△ABC ABC 的内心的内心, ,∴AD AD、、BE 和CF 是∠是∠BAC BAC BAC、∠、∠、∠ABC ABC 和∠和∠ACB ACB 的角平分线的角平分线 ∴⌒∴⌒BD=BD=BD=⌒⌒CD CD,⌒,⌒,⌒BF=BF=BF=⌒⌒AF AF,⌒,⌒,⌒AE=AE=AE=⌒⌒CE CE ∴⌒∴⌒∴⌒BD+BD+BD+⌒⌒BF+BF+⌒⌒AE=AE=⌒⌒CD+⌒AF+AF+⌒⌒CE CE ∴⌒∴⌒∴⌒DF+DF+DF+⌒⌒AE=AE=⌒⌒DE+DE+⌒⌒AF∴∠∴∠AIF=AIF=AIF=∠∠AIE=AIE=∠∠DIF=DIF=∠∠DIE DIE ∴∴EF EF⊥⊥AD2. A 、B 、C 、D 是圆周上“相继的”四点,P 、Q 、R 、S 分别是弧AB 、BC 、CD 、DA 的中点,求证:PR ⊥QS. 证明:∵P 、Q 、R 、S 分别是AB 、BC 、CD 、DA 的中点的中点 ∴⌒∴⌒AP=AP=AP=⌒⌒PB ,⌒BQ=BQ=⌒⌒QC ,⌒CR=CR=⌒⌒RD ,⌒DS=DS=⌒⌒SA SA ∴⌒∴⌒AP+AP+AP+⌒⌒QC+⌒CR+CR+⌒⌒SA=SA=⌒⌒PB+PB+⌒⌒BQ+BQ+⌒⌒RD+RD+⌒⌒DS DS又∵⌒又∵⌒PQ+PQ+PQ+⌒⌒RS=RS=⌒⌒PB+PB+⌒⌒BQ+BQ+⌒⌒RD+RD+⌒⌒DS , DS , ⌒⌒SP+SP+⌒⌒RQ=RQ=⌒⌒AP+AP+⌒⌒QC+QC+⌒⌒CR+CR+⌒⌒SA SA ∴⌒∴⌒PQ+PQ+PQ+⌒⌒RS=RS=⌒⌒SP+SP+⌒⌒RQ RQ ∴SQ SQ⊥⊥PR PR3、凸四边形ABCD 的每条对角线皆平分它的面积,求证求证:ABCD :ABCD 是平行四边形。

《初等数论》各章习题参考解答第一章习题参考解答1.解:因为25的最小倍数是100,9的最小倍数是,所以满足条件的最小正整数11111111100a =。
2.解:3在100!的分解式中的指数()1001001001003100!33113148392781⎡⎤⎡⎤⎡⎤⎡⎤=+++=+++=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦, 在100!的分解式中的指数()1001001001001002100!50251261942481664⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=++++=++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,∴ ()9448474847100!2343123,,61k k k k =⋅⋅=⋅⋅=⋅=。
故 max 47n =,min 3M k =,(),61k =。
故 当M 最小值是3的倍数,但不是2的倍数。
3.解:112121n n n n x x ++++++等价于()()21221n n n x x x ++-+-,从而3x ³(n 就不会太大,存在反向关系)。
由()()22121n nn x x x -+-?+,得()()2212n n n x x -+?,即()()()121122nn x x -+?。
若2n ³,则()()()()251221114242nn x xx x-?+??,导致25140x x -+?,无解。
所以,只有1n =,335314x x x +-?,只能是37,14x +=,从而4,11x =。
综上所述,所求正整数对()()(),4,111,1x n =、。
4.解:按题意,2m n >>,记*,m n k k N =+?;则()222211111n n k nk n k k a a a a a a a a a a a a +++-+-?-+--++-22211111n k k n k k a a a a a a a a a ++?---+?-+-,故 存在无穷多个正整数a 满足2111n k k a a a a ++-+-。

三、关于比例相似形⒈从 ABCD 的各顶向不过该顶的对角线引垂线,垂足为E 、F 、G 、H,求证: (ⅰ)EFGH 是 ; (ⅱ) EFGH ∽ ABCD. 证明:(1)∵AE ⊥BD DH ⊥AC ∴A 、D 、E 、H 四点共圆(视角相等)∴∠OEH=∠OAD同理 ∠OGF=∠OCB 又∵AD ∥BC ∴∠OAD=∠OCB ∴∠OEH=∠OGF ∴EH ∥GF 同理 EF ∥GH ∴四边形EFGH 为平行四边形(ⅱ)∵△OEH ∽△OAD ∴.OD OHOA OE =∴BDFH AC EG =EFGH 与 ABCD 对角线夹角相等且对角线又成比例 ∴ EFGH ∽ ABCD3.已知:AD 是△ABC 的中线,过C 的一直线分别交AD 、AB 与E 、F 。
求证:AE ·BF=2AF ·ED 证明:延长CF 至点H ,使得CE=EH 连结BH ∵点D 是BC 上的中点 ∴DE 是△CBH 的中位线即DE ∥BH 且DE= 21BH ∵DE ∥BH ∴∠CED=∠CHB=∠AEF ∠AFE=∠BFH∴△AFE ∽△BFH∴BFAFBH AE =,且BH=2ED ∴AE ·BF=2AF ·ED DACBEFGG H4.直线l 与□ABCD 的边AB 、AD 和对角线AC 依次相交于E 、F 和G 。
求证:AGACAF AD AEAB =+ 证明:连结BF 、BE 、CF 和CE , ∵SS SS AEFACF AEFABF AEAB ==SS SS AEFACE AEFADE AFAD==∴AGACAG GC AG AFADAE AB SS SSS SAEFCEFAEFAEFACEACF=+=+=+=+5. AB 证明:作CD 的延长线到点H ,使得AH 垂直CH 作点C 的延长线,使得CP 垂直ABABCP AD AC DH CH CP AD AC AB BP AP DH CH BP DH AP CH CPB AHD CBP DAC APH CBAD CPB AHD DH CH CP AD DH CH DH CH AD DH CH AD CH DH AD CH AH AC ⋅+=+⋅+==+=+==∆≅∆∴∠=∠=∠==∠=∠+⋅+=-++=-+=+-=+=222222222222222 )( 90)( ))(( )( )( 故有又6.AD 是Rt △ABC 斜边上的高,作DE ⊥AB 于E,DF ⊥AC 于F.求证:AD 3=BC •BE •CF证明:∵ AD 2=BD •DC, BD 2=BE •BA, CD 2=CF •CA,B∴ AD 4=BE •CF •AB •AC=BE •CF •BC •AD 约去AD,得AD 3=BC •BE •CF7.在△ABC 中,∠A=60°,∠B=80°。
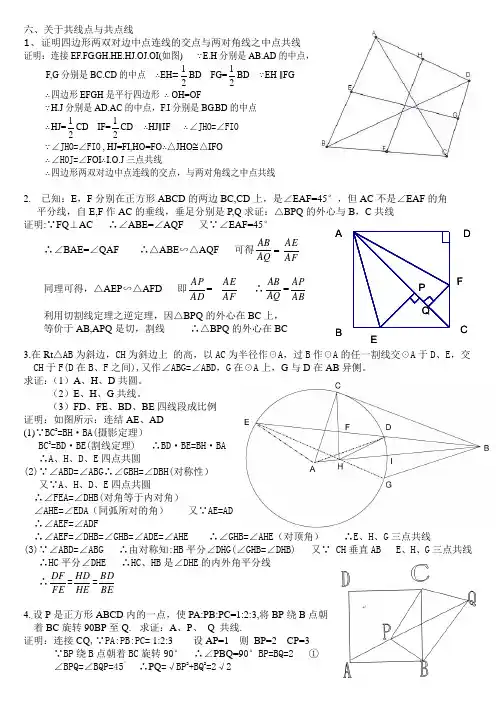
六、关于共线点与共点线1、 证明四边形两双对边中点连线的交点与两对角线之中点共线 证明:连接EF.FG.GH.HE.HJ.OJ.OI(如图) ∵E.H 分别是AB.AD 的中点,F,G 分别是BC.CD 的中点 ∴EH =12BD FG=12BD ∵EH ∥FG∴四边形EFGH 是平行四边形 ∴ OH=OF∵H.J 分别是AD.AC 的中点,F.I 分别是BG.BD 的中点∴HJ=12CD IF=12CD ∴HJ ∥IF ∴∠JHO=∠FIO∵∠JHO=∠FIO , HJ=FI,HO=FO ∴△JHO ≅△IFO ∴∠HOJ=∠FOI ∴I.O.J 三点共线∴四边形两双对边中点连线的交点,与两对角线之中点共线2. 已知:E ,F 分别在正方形ABCD 的两边BC,CD 上,是∠EAF=45°,但AC 不是∠EAF 的角 平分线,自E,F 作AC 的垂线,垂足分别是P,Q 求证:△BPQ 的外心与B ,C 共线 证明:∵FQ ⊥AC ∴∠ABE=∠AQF 又∵∠EAF=45°∴∠BAE=∠QAF ∴△ABE ∽△AQF 可得 AQ AB AFAE同理可得,△AEP ∽△AFD 即ADAP=AFAE∴AQ AB =AB AP利用切割线定理之逆定理,因△BPQ 的外心在BC 上, 等价于AB,APQ 是切,割线 ∴△BPQ 的外心在BC3.在Rt △AB 为斜边,CH 为斜边上 的高,以AC 为半径作☉A ,过B 作☉A 的任一割线交☉A 于D 、E ,交 CH 于F(D 在B 、F 之间),又作∠ABG=∠ABD ,G 在☉A 上,G 与D 在AB 异侧。
求证:(1)A 、H 、D 共圆。
(2)E 、H 、G 共线。
(3)FD 、FE 、BD 、BE 四线段成比例 证明:如图所示:连结AE 、AD (1)∵BC 2=BH ·BA(摄影定理)BC 2=BD ·BE(割线定理) ∴BD ·BE=BH ·BA ∴A 、H 、D 、E 四点共圆(2)∵∠ABD=∠ABG ∴∠GBH=∠DBH(对称性) 又∵A 、H 、D 、E 四点共圆∴∠FEA=∠DHB(对角等于内对角)∠AHE=∠EDA (同弧所对的角) 又∵AE=AD ∴∠AEF=∠ADF∴∠AEF=∠DHB=∠GHB=∠ADE=∠AHE ∴∠GHB=∠AHE (对顶角) ∴E 、H 、G 三点共线(3)∵∠ABD=∠ABG ∴由对称知:HB 平分∠DHG(∠GHB=∠DHB) 又∵ CH 垂直AB E 、H 、G 三点共线 ∴HC 平分∠DHE ∴HC 、HB 是∠DHE 的内外角平分线∴FE DF =HE HD =BE BD4..设P 是正方形ABCD 内的一点,使PA:PB:PC=1:2:3,将BP 绕B 点朝 着BC 旋转90BP 至Q. 求证:A 、P 、 Q 共线.证明:连接 CQ ,∵PA:PB:PC= 1:2:3 设AP=1 则 BP=2 CP=3∵BP 绕B 点朝着BC 旋转90° ∴∠PBQ=90°BP=BQ=2 ①∠BPQ=∠BQP=45° ∴PQ =√BP 2+BQ 2=2√2ADC FBE PQ又∵四边形ABCD 是正方形 ∴AB=BC ② ∴∠ABC=∠PBQ= 90°即∠ABP+∠PBC=∠CBQ +∠PBC=90° ∴∠ABP=∠CBQ ③ ∴△ABP ≌△CBQ(由①②③可得到) ∴PA=QC=1又∵PQ 2+QC 2=(2√2)2+12=32=PC 2 ∴∠PQC=90°, ∠BQC=∠PQC+∠BQP=90+45°=135°又∵∠APB=180°-45°=135° ∴∠BQC=∠APB=135° 即A 、P 、Q 共线(∠APB 、∠BQP 是邻补角)5. 在∆ABC 中,D,E,F 分别在AB.BC.CA 上,使得DE=BE,EF=CE.求证:∆ADF 的外心O 在∠DEF 的角平分线上。

大学数学之初等数学研究 ,李长明 ,周焕山版 ,高等教育出版社 习题一1答:原那么:〔1〕A ⊂B〔2〕A 的元素间所定义的一些运算或根本关系 ,在B 中被重新定义。
而且对于A 的元素来说 ,重新定义的运算和关系与A 中原来的意义完全一致。
〔3〕在A 中不是总能施行的某种运算 ,在B 中总能施行。
(4) 在同构的意义下,B 应当是A 满足上述三原那么的最小扩展,而且由A 唯一确定。
方式:〔1〕添加元素法;〔2〕构造法2证明:(1)设命题能成立的所有c 组成集合M 。
a=b ,M 11b 1a ∈∴⋅=⋅∴, 假设bc ac M c =∈,即 ,那么M c c b b bc a ac c a ∈'∴'=+=+=',由归纳公理知M=N ,所以命题对任意自然数c 成立。
〔2〕假设a <b ,那么bc kc ac bc,k)c (a )1(b k a N k =+=+=+∈∃即,,由,使得 那么ac<bc 。
〔3〕假设a>b ,那么ac mc bc ac,m)c (b )1(a m b N m =+=+=+∈∃即,,由,使得 那么ac>bc 。
3证明:(1)用反证法:假设b a b,a b a <>≠或者,则由三分性知。
当a >b 时 ,由乘法单调性知ac >bc. 当a <b 时 ,由乘法单调性知ac<bc.这与ac=bc 矛盾。
那么a=b 。
〔2〕用反证法:假设b a b,a b a =>或者,则由三分性知不小于。
当a >b 时 ,由乘法单调性知ac >bc. 当a=b 时 ,由乘法单调性知ac=bc.这与ac<bc 矛盾。
那么a <b 。
〔3〕用反证法:假设b a b,a b a =<或者,则由三分性知不大于。
当a<b 时 ,由乘法单调性知ac<bc. 当a=b 时 ,由乘法单调性知ac=bc.这与ac>bc 矛盾。

习题二答案1添加元素法和构造法,自然数扩充到整数可以看成是在自然数的基础上添加0到扩大的自然数集,再添加负数到整数集;实数扩充到复数可以看成是在实数的基础上构造虚数单位i 满足12-=i ,和有序实数对),(b a 一起组成一个复数bi a +.2(略)3从数的起源至今,总共经历了五次扩充:为了保证在自然数集中除法的封闭性,像b ax =的方程有解,这样,正分数就应运而生了,这是数的概念的第一次扩展,数就扩展为正有理数集.公元六世纪,印度数学家开始用符号“0”表示零.这是数的概念的第二次扩充,自然数、零和正分数合在一起组成算术数集.为了表示具有相反意义的量,引入了负数.并且直到17世纪才对负数有一个完整的认识,这是数的概念的第三次扩充,此时,数的概念就扩展为有理数集.直到19世纪下半叶,才由皮亚诺、戴德金、维尔斯特拉斯等数学家的努力下构建了严格的实数理论.这是数的概念的第四次扩充,形成了实数集.虚数作为一种合乎逻辑的假设得以引进,并在进一步的发展中加以运用.这是数学概念的第五次扩充,引进虚数,形成复数集.4证明:设集合D C B A ,,,两两没有公共元素d c b a ,,,分别是非空有限集D C B A ,,,的基数,根据定义,若b a >,则存在非空有限集'A ,使得B A A ~'⊃;若d c ≥从而必存在非空有限集'C ,使得D C C ~'⊃,所以)(C A ⋃)(D B ⋃⊃所以集合C A ⋃的基数c a +大于集合D B ⋃的基数d b +,所以d b c a +>+.5(1)解:按照自然数序数理论加法定义,1555555155155)25(2535''=++=++⋅=+⋅=+⋅=⋅=⋅(2)解:按照自然数序数理论乘法定义87)6(])15[()15()25(2535'''''''''===+=+=+=+=+6证明:︒1当2=n 时,命题成立.(反证法)()()()()()()()01121,1111111,111101111111,,2,1,0111,,2,1,0)2(212122121212121212122221212122111112111212222121≥++-+⇒≥++-++≥+-+-≥++++∴≥⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛->-=-++-+-=+++++=>+=≥+++=+++=>≥=︒+++++++++++++++++k k k k k k k k k k k k k k k i k k k k k k i k k i a k a k k a k k a k k a k a a k a a a a a k a a a a a a a a a a a a a a a a a a k i a k n ka a a a a a k i a k k n ,即要证由归纳假设,得,且得,,且时,由当。

《初等数学研究》习题解答第一章 数系1.1 集合论初步·自然数的基数理论习题1.11.证明集合0{|}x x >与实数集对等。
证明:取对应关系为ln y x =,这个函数构成0(,)+∞与(,)-∞+∞的一一对应,所以集合0{|}x x >与实数集对等。
2.证明()()()A B C A B A C = 证明:()x AB C x A ∀∈⇒∈或x B C ∈,x A ⇒∈或(x B ∈且x C ∈),那么有x A ∈或x B ∈同时还有x A ∈或x C ∈,即x A B ∈同时还有x A C ∈,所以()()()()()x A B A C A B C A B A C ∈⇒⊆反过来:()()x AB AC x A B ∀∈⇒∈且x A C ∈,对于前者有x A ∈或者x B ∈;对于后者有x A ∈或者x C ∈,综合起来考虑,x B ∈与x C ∈前后都有,所以应是“x B ∈且x C ∈”即“x B C ∈”,再结合x A ∈的地位“或者x A ∈”以及前后关系有“x A ∈或x BC ∈”即()x A B C ∈,所以()()()()x AB C A B C A B A C ∈⇒⊇所以()()()A B C A B A C =。
3.已知集合A 有10个元素,,B C 都是A 的子集,B 有5个元素,C 有4个元素,B C有2个元素,那么()BA C -有几个元素?解:集合()BA C -如图1所示:由于452(),(),()r C r B r B C ===,所以32(),()r B C r C B -=-=, 从而1028(())r B A C -=-=, 即()BA C -有8个元素4.写出集合{,,,}a b c d 的全部非空真子集。
图1CBA5.证明,按基数理论定义的乘法对加法的分配律成立。
证明:设,,A B C 是三个有限集合,并且B C φ=,记(),(),()a r A b r B c r C ===首先:由于BC φ=,所以A B A C φ⨯⨯=,所以其次:对于(,)(){(,)|,}a x A B C a x a A x B C ∀∈⨯=∈∈,由于x B C ∈,那么若x B ∈,于是(,)a x A B ∈⨯; 若x C ∈,于是(,)a x A C ∈⨯,所以总有(,){(,)|,}{(,)|,}a x a x a A x B a x a A x C A B A C ∀∈∈∈∈∈=⨯⨯即()(())()A BC A B A C r A B C r A BA C ⨯⊆⨯⨯⇒⨯≤⨯⨯反过来:(,)a x A B A C ∀∈⨯⨯,那么(,)a x A B ∈⨯或者(,)a x A C ∈⨯于是有,a A ∈x B ∈或者x C ∈,即,a A ∈x B C ∈,所以(,)()a x A B C ∈⨯即()(())()A BC A B A C r A B C r A BA C ⨯⊇⨯⨯⇒⨯≥⨯⨯所以()a b c ab ac +=+6.在基数理论定义的乘法下,证明1a a ⨯=。

初等几何研究期末试题及答案第一题:已知四边形ABCD中,AB = 6cm,BC = 8cm,∠ABC = 90°,角ADC的度数为60°。
求四边形ABCD的面积。
解析:由题意可知,四边形ABCD为一个平行四边形,且∠ABC = 90°,∠ADC = 60°。
首先,我们可以使用正弦定理求得∠BAC的度数。
根据正弦定理可以得到:sin∠BAC/AB = sin∠ABC/ACsin∠BAC/6 = sin90°/ACsin∠BAC/6 = 1/ACAC = 6/sin∠BAC接下来,我们可以使用余弦定理求得AC的长度。
根据余弦定理可以得到:AC² = AB² + BC² - 2AB·BC·cos∠ABCAC² = 6² + 8² - 2·6·8·cos90°AC² = 100AC = √100AC = 10再次,我们可以使用正弦定理求得AD的长度。
根据正弦定理可以得到:sin∠ADC/AC = sin∠CAD/ADsin60°/10 = sin∠CAD/AD√3/10 = sin∠CAD/ADAD = 10sin∠CAD/√3最后,我们可以计算四边形ABCD的面积。
四边形ABCD可以分成两个三角形,即△ABC和△ACD。
面积公式为:四边形ABCD的面积 = △ABC的面积 + △ACD的面积= (1/2)·AB·AC + (1/2)·AC·AD= (1/2)·6·10 + (1/2)·10·10sin∠CAD/√3= 30 + 50sin∠CAD/√3综上所述,四边形ABCD的面积为30 + 50sin∠CAD/√3。
第二题:已知直角三角形ABC,其中∠B = 90°,AB = 5cm,AC = 12cm。

《初等数学研究》习题解答第一章 数系1.1 集合论初步·自然数的基数理论习题1.11.证明集合0{|}x x >与实数集对等。
证明:取对应关系为ln y x =,这个函数构成0(,)+∞与(,)-∞+∞的一一对应,所以集合0{|}x x >与实数集对等。
2.证明()()()A B C A B A C =证明:()x A B C x A ∀∈⇒∈或x B C ∈,x A ⇒∈或(x B ∈且x C ∈),那么有x A ∈或x B ∈同时还有x A ∈或x C ∈,即x A B ∈同时还有x A C ∈,所以()()()()()x A B A C A B C A B A C ∈⇒⊆反过来:()()x A B A C x A B ∀∈⇒∈且x A C ∈,对于前者有x A ∈或者x B ∈;对于后者有x A ∈或者x C ∈,综合起来考虑,x B ∈与x C ∈前后都有,所以应是“x B ∈且x C ∈”即“x B C ∈”,再结合x A ∈的地位“或者x A ∈”以与前后关系有“x A ∈或x B C ∈”即()x A B C ∈,所以()()()()x A B C A B C A B A C ∈⇒⊇ 所以()()()A B C A B A C =。
3.已知集合A 有10个元素,,B C 都是A 的子集,B 有5个元素,C 有4个元素,B C 有2个元素,那么()B A C -有几个元素?解:集合()B A C -如图1所示:由于452(),(),()r C r B r B C ===,所以32(),()r B C r C B -=-=,图1CBA从而1028(())r B A C -=-=, 即()B A C -有8个元素4.写出集合{,,,}a b c d 的全部非空真子集。
{,}{},{},{},{,},{,},{,},{,},{,},{,},{,,},{,,},{,,},{,,}a b c d a b a c a d b c b d c d a b c a b d a c d b c d5.证明,按基数理论定义的乘法对加法的分配律成立。
初等几何试题及答案详解1. 题目:已知一个等腰三角形的底边长为6cm,两腰相等,且两腰与底边的夹角为60°,求三角形的高。
答案:首先,我们可以将等腰三角形的底边平分,得到两个30°-60°-90°的直角三角形。
根据30°-60°-90°三角形的性质,我们知道较短的直角边(即高)是斜边(即腰)的一半。
因此,高的长度为:\[ \text{高} = \frac{1}{2} \times \text{腰} \]由于两腰相等,且与底边的夹角为60°,我们可以利用余弦定理求出腰的长度。
设腰长为a,则:\[ a^2 = \left(\frac{6}{2}\right)^2 +\left(\frac{6}{2}\right)^2 - 2 \times \frac{6}{2} \times\frac{6}{2} \times \cos(60°) \]\[ a^2 = 9 + 9 - 18 \times \frac{1}{2} \]\[ a^2 = 18 - 9 \]\[ a^2 = 9 \]\[ a = 3 \]所以腰长为3cm。
因此,高的长度为:\[ \text{高} = \frac{1}{2} \times 3 = 1.5 \text{cm} \]2. 题目:一个圆的半径为5cm,求圆的周长。
答案:圆的周长可以通过公式 \( C = 2\pi r \) 来计算,其中 \( r \) 是圆的半径。
将半径 \( r = 5 \) cm 代入公式:\[ C = 2\pi \times 5 \]\[ C = 10\pi \]所以,圆的周长为 \( 10\pi \) cm。
3. 题目:已知一个矩形的长为8cm,宽为6cm,求矩形的对角线长度。
答案:矩形的对角线可以通过勾股定理来计算。
设对角线长度为 \( d \),则:\[ d^2 = \text{长}^2 + \text{宽}^2 \]\[ d^2 = 8^2 + 6^2 \]\[ d^2 = 64 + 36 \]\[ d^2 = 100 \]\[ d = \sqrt{100} \]\[ d = 10 \]所以,矩形的对角线长度为10cm。
习题1答案1.(1) 有两个分量为零;(2)有一个分量为零;(3)y 坐标为3;(4)z 坐标为±5.2.A 位于xOz 面上;B 位于yOz 面上;C 位于z 轴上;D 位于y 轴上.3.A 在Ⅳ卦限;B 在Ⅴ卦限;C 在Ⅷ卦限;D 在Ⅲ卦限.4. (1) (2,-3,1),(-2,-3,-1),(2,3,-1);(2) (2,3,1),(-2,-3,1),(-2,3,-1);(3) (-2,3,1);(1)(a , b , -c ), (-a , b , c ), (a , -b , c );(2) (a , -b , -c ),(-a , b , -c ),(-a , -b , c );(3) (-a , -b , -c );5. 提示:CA =CB =66.(0,1,-2).7. 134+e e ; 123243-+-e e e ; 3243107-+-e e e .8. 提示:2102AB BC CD AB ++=+=a b .9. B (-2,4,-3) 10. 21P P = (-2, -2, -2); 521P P = (-10, -10, -10). 11. =a 3, =b 38, =c 3; 333(,,)333=a , 235(,,)383838-=b ,212(,,)333--=c ;12()()()()1111,,,2222AB BC CD DA =-=+=-=-+a b a b b a a b ..13.24334233CD BC ⎧=-⎪⎪⎨⎪=-⎪⎩l kl k.14.方法1:→+→=→AM OA OM .方法2:提示:延长 O M 至 N ,使 2ON OM =.15.提示:方法1:()()1123OM OA OB OC AM BM CM =+++++.方法2:坐标法.16.提示:→→→+=AM OA OM ,→→→+=BM OB OM ,→→→+=CM OC OM ,→→→+=DM OD OM17.提示:取AC 的中点O ,则OM ,ON 分别为中位线.18.1))(21→→→+=AC AB AD ,→→→-=AB AC BE 21,→→→-=AC AB CF 21.2) 0=++→→→CF BE AD .19.提示:→→+→-=+i 11OP OP OP i i λ.(其中2 λ)20. 提示:A ,B ,C 三点共线,→→→+=OB OA OC μλ其中21.提示:A ,B ,C ,D 四点共面→→→+=CA k BC k AD 21. 22.)(32321r r r ++=→ED 23.提示:过L 作LD=BM .24.提示:证向量共线.25.1)3a -2b +c =,2)5a +6b +c 26.→AB (1,3,3)27.B (3,4,4)28. A (-1,2,4); B (8,-4,-2).29. (1) 3,57++i j k ; (2) 18,10214-++i j k ;(3) cos ∠(a ,b )=3221; sin ∠(a ,b )= 527; tan ∠(a ,b )=533. 30. (1) 10l =; (2) 2l =-.31. (1) 824j k --; (2) j k --; (3) 2 32. (1) 36; (2)3217, 3677. 33. 1.34.(1) 提示:()()()()[]⋅⋅-=-a a b c ac b a ab c a ac b .(2)提示: 因为 m 1m 2,所以,对该平面上任意矢量c =λm 1+μm 2.(3)提示: BC AC AB =-, AD CD CA =- .35.(1)5;(2)-3;(3)72-;(4)11. 36.(1) 32-(2) 222123=++r 14=, r 与a ,b ,c 的夹角分别为arccos 1414,14arccos 7,314arccos .14(3)cos (,)∠=a b 3π (4)40λ=37.解:1)向量a ,b ,c 不共面,c 不能表成a ,b 的线性组合.2)向量a ,b ,c 共面,b a c 3221+= 3)向量a ,b ,c 共面,c 不能表成a ,b 的线性组合.38. B (10,0,513) 39.|AB |=149,AB 边上的中线长:2461,|BC |=292,BC 边上的中线长:352, |AC |=212,AC 边上的中线长:2341.40.1)20 2)11.41.1)x ·y =354,105,2310==y x , 354(,)arccos242550∠=x y 2)x ·y =929,426,2237==y x , 929(,)arccos 952962∠=x y42.(3a +2b )·(2a -5b )=633314-,两向量间的夹角为π43. 43.略. 44.3=OL ,321531+=→OM ,(,)OL OM ∠3215633arccos --=45.D 分AB 的比为1,T 分AB 的中为b a .H 分AB 的线为θθcos 2cos 2ab b ab a--. 46.略.47.略.48. 略.49.1) a ×b=(6, 3 3), S=63;2) a ×b =(12,26, 8) , =2221S ; 3) a ×b = (72, 24, 0),=2410S . . 50.1) (2,1,2), (2, 1, 2).2) (16, 4, 16). 3) 2, 2.4) (3,4,5), (1, 2, 1).51.略.52.四面体的体积596V =. 53.提示:(a, b , c )=0.自我测验题1一、填空题.1.Ⅵ,(4,2,-6), (4,-2,-6),(8,-4,8).2.68,(-5,15,-7),-34,9299.3.求面积、求垂直向量、证明平行问题.4.0⋅=a b ,(),,0=a b c5.在三轴上的射影,1-1对应.二、判断题.1.√2.×3.√4. ×5.×三、计算题.1.1) x 与 y 共线或 x 与 y 中至少有一个为 0 . 2) x 与 y 共线或 x 与 y 中至少有一个为 0 . .2. 3a +3b -5c .3.x =2||b a b b ⨯-a .4.x =ba c ab ⋅⨯+α. 5..096172,22,63=+--z y x四、证明题.1.提示:证AD AB 与共线.2.略.。
第一章 向量代数 习题1.1
1. 试证向量加法的结合律,即对任意向量,,abc成立
()().abcabc 证明:作向量,,ABaBCbCDc(如下图),
则 ()(),abcABBCCDACCDAD ()(),abcABBCCDABBDAD 故()().abcabc 2. 设,,abc两两不共线,试证顺次将它们的终点与始点相连而成一个三角形的充要条件是0.abc 证明:必要性,设,,abc的终点与始点相连而成一个三角形ABC,
则0.abcABBCCAACCAAA 充分性,作向量,,ABaBCbCDc,由于 0,abcABBCCDACCDAD所以点A与D重合,即三向量
,,abc的终点与始点相连构成一个三角形。
AB C a b c
AB C D a b c
ab bc 3. 试证三角形的三中线可以构成一个三角形。 证明:设三角形ABC三边,,ABBCCA的中点分别是,,DEF(如下图),并且记
,,aABbBCcCA,则根据书中例1.1.1,三条中线表示的向量分别是
111(),(),(),222CDcbAEacBFba
所以,111()()()0,222CDAEBFcbacba故由上题结论得三角形的三中线,,CDAEBF可以构成一个三角形。 4. 用向量法证明梯形两腰中点连线平行于上、下底且等于它们长度和的一半。 证明:如下图,梯形ABCD两腰,BCAD中点分别为,EF,记向量,ABaFAb,
则,DFb而向量DC与AB共线且同向,所以存在实数0,使得.DCAB现在,FBba,FCba由于E是BC的中点,所以
1111()()(1)(1).2222FEFBFCbaabaAB且
111(1)()().222FEABABABABDC
七、关于共圆点与共点圆1、两圆相切,自其公切线上任一点作两直线,一线割圆于A、B,另一线割圆于C、D,求证:A、B、C、D共圆。
证明:设共切点为T由切割线定理得:PT2=PA·PBPT2=PC·PD∴PA·PB=PC·PD∴A、B、C、D共圆。
2. 四圆依次外切,求证四切点共圆。
证明:设O1,O2,O3,O4顺次外切于ABCD.则∠ABC=12(∠AO2B+∠BO3C)∠CDA=12(∠CO1D+∠DO1A)再注意到四边形O1O2O3O4顺次ABCD,即知四边形ABCD对角互补∵O1,O2,O3,O4顺次外切于ABCD∴则∠ABC=12(∠AO2B+∠BO3C)∠CDA=12(∠CO1D+∠DO1A)∵四边形O1O2O3O4顺次ABCD ∴四边形ABCD对角互补3.设P、M分别在正方形ABCD的边DC、BC上,PM与⊙A(半径为AB)相切,线段PA、MA 分别交对角线BD于Q、N. 求证:五边形PQNMC内接于圆。
证明:连结MQ、AT∴∠1=∠1′,∠2=∠2′∴∠1′+∠2′=45°∴α=45°+∠2 β=∠MAP+∠2=45°+∠2∴α=β∴A、B、M、Q共圆∴∠ABM+∠MQA=180°且∠ABM=90°∴∠MQA=90°∴M、C、P、Q共圆同理P、N、M、C共圆∴M、C、P、Q、N五点共圆。
4. 设O为△ABC内一点,AA’,BB’,CC’均以O为中点。
求证:△BCA’, △CAB’, △ABC’与△A’B’C’的外接圆共点证:连接B’M,CM, A’M,设△BCA’外接圆与△A’B’C’外接圆的另一交点M(≠A’),如图,则由BCMA’,A’MB’C’内接于圆可知∠B’MC=∠1+∠2=∠3+∠4由对称性知BC∥B’C’,过A‘作BC的平行线,则有∠3+∠4=∠5+∠6=∠BA’C’再由对称性知∠BA’C’=∠B’AC∴∠B’MC=∠B’AC∴M在△CAB’的外接圆上同理,M在△ABC’的外接圆上故△BCA’, △CAB’, △ABC’与△A’B’C’的外接圆共点。