1978全国高考数学试题

1978年高考数学试题1978年高考，是中国高等教育历史上的重要一年，也是中国改革开放的开端。

数学作为高考的一科必考科目，对学生的逻辑思维和数学运算能力有着重要的考察和培养作用。

下面将介绍1978年高考数学试题，并通过例题分析来展示该年的数学考题特点。

第一题：甲、乙、丙三人合伙办工厂，乙出资3万元，占出资总额的40%，丙不出资，甲出其余的钱。

工厂经营了一段时间后亏损严重，无法在规定的时间里按期注资，乙、丙两人共同决定把工厂出售。

乙以工厂10000元的价格买下了丙的全部股权，请你根据已知，回答下列各小题：1）甲在工厂中出资多少元？2）买下工厂时乙对甲的股权占多少比例？解析：1）设甲出资金额为x元，则有：x+3万元 =总出资金额根据题干提供的信息，乙出资了3万元，占总出资额的40%，则有：3万元 = 总出资金额 × 40%由此可以得出：总出资金额 = 3万元 ÷ 40% = 7.5万元所以甲在工厂中出资的金额为总出资金额 - 乙的出资金额，即：x = 7.5万元 - 3万元 = 4.5万元答：甲在工厂中出资4.5万元。

2）买下工厂时，乙对甲的股权比例可以通过乙的出资金额和总出资金额的比例计算得出。

已知乙出资了3万元，总出资金额为7.5万元，所以乙对甲的股权比例为：3万元 ÷ 7.5万元 × 100% = 40%答：买下工厂时，乙对甲的股权占40%。

第二题：已知函数y = ln(x) - ln(x-1)，其中x > 1，下面哪个结论是正确的？A. 函数y = ln(x) - ln(x-1)的定义域是(1, +∞)B. 函数y = ln(x) - ln(x-1)的值域是(-∞, +∞)C. 函数y = ln(x) - ln(x-1)的图象为一直线D. 函数y = ln(x) - ln(x-1)在(1, +∞)上是递减的解析：首先，函数y = ln(x) - ln(x-1)的定义域是使得x和x-1都大于0的实数集，即x > 1。

1978高考试题及答案一、选择题（每题2分，共10分）1. 1978年恢复高考制度，以下哪项不是当年考试科目？A. 语文B. 数学C. 英语D. 物理答案：D2. 1978年高考中，数学试卷的满分是多少分？A. 100分B. 120分C. 150分D. 200分答案：A3. 1978年高考英语试卷中，听力部分的分值占总分的比例是多少？A. 10%B. 20%C. 30%D. 40%答案：B4. 1978年高考语文试卷中，作文题目是关于什么主题的？A. 我的家乡B. 我的理想C. 我的朋友D. 我的老师答案：B5. 1978年高考中，哪个科目的考试时间最长？A. 语文B. 数学C. 英语D. 物理答案：A二、填空题（每题2分，共10分）6. 1978年高考中，数学试卷的最后一题是关于_________的证明。

答案：几何图形7. 1978年高考英语试卷中，阅读理解部分的文章主要讨论了_________。

答案：环境保护8. 1978年高考语文试卷中，文言文阅读材料选自_________。

答案：《史记》9. 1978年高考物理试卷中，实验题考察了_________的测量方法。

答案：电阻10. 1978年高考中，考生需要在_________分钟内完成所有科目的考试。

答案：120三、解答题（每题10分，共20分）11. 1978年高考数学试卷中，有一道题目要求证明勾股定理。

请简述证明过程。

答案：证明过程涉及直角三角形的面积计算，通过比较直角三角形的面积与斜边的平方，得出勾股定理的正确性。

12. 1978年高考英语试卷中，有一道题目要求考生写一篇关于“如何提高学习效率”的短文。

请列出至少三个提高学习效率的方法。

答案：方法一：制定合理的学习计划；方法二：采用有效的记忆技巧；方法三：保持良好的学习环境。

四、作文题（30分）13. 1978年高考语文试卷中，作文题目是“我的理想”。

请以“我的理想”为题，写一篇不少于800字的作文。

1951年至1978年全国高考数学试题汇编及解析1951年全国高考数学试题 第一部分:1.设有方程组x ＋y ＝8,2x －y ＝7,求x,y.2.若一三角形的重心与外接圆圆心重合,则此三角形为何种三角形？3.当太阳的仰角是600时,若旗杆影长为1丈,则旗杆长为若干丈？?,,,,.4=++-=-=-z y x c b a a c zc b y b a x 则各不相等而若5.试题10道,选答8道,则选法有几种？6.若一点P 的极坐标是(r,θ),则它的直角坐标如何？7.若方程x 2＋2x ＋k ＝0的两根相等,则k ＝？8.9.当(x ＋1)(x －2)＜0时,x 的值的范围如何？10.若一直线通过原点且垂直于直线ax ＋by ＋c ＝0,求直线的方程11.(x ＋x 1)6展开式中的常数项如何？12.02cos =θ的通解是什么？13.系数是实数的一元三次方程,最少有几个根是实数,最多有几个根是实数？ 14.15.x 2－4y 2＝1的渐近线的方程如何？16.三平行平面与一直线交于A,B,C 三点,又与另一直线交于A ＇,B ＇,C ＇三点,已知AB ＝3,BC ＝7及A ＇B ＇＝9求A ＇C ＇17.有同底同高的圆柱及圆锥,已知圆柱的体积为18立方尺,求18.已知lg2＝0.3010,求lg5.19.二抛物线y 2＝12x 与2x 2＝3y 的公共弦的长度是多少？ 20.国旗上的正五角星的每一个顶角是多少度？ 第二部分:?345505542=--1.P,Q,R 顺次为△ABC 中BC,CA,AB 三边的中点,求证圆ABC 在A 点的切线与圆PQR 在P 点的切2.设△ABC 的三边BC ＝4pq,CA ＝3p 2＋q 2,AB ＝3p 2＋2pq －q 2,求∠B,并证∠B 为∠A 及∠C 的等3.(1)求证,若方程x 3＋ax 2＋bx ＋c ＝0的三根可排成等比数列, 则a 3c ＝b 3.(2)已知方程x 3＋7x 2－21x －27＝0的三根可以排成等比数列,求三根4.过抛物线顶点任做互相垂直的两弦,交此抛物线于两点,求证此两点联线的中点的轨迹仍为参考答案与试题解析 第一部分1.⎩⎨⎧==35y x2.证:设△ABC 的重心与外接圆的圆心均为O(图1)∵OA ＝OC,E 为AC 的中点,∴BE ⊥AC ；同理,CD ⊥AB,AF ⊥BC 在Rt △ABE 与Rt △ACD 中,∠A为公共角,BE ＝CD ＝R ＋21R ＝23R(R 为外接圆半径),所以△ABE ≌△ACD,AB ＝AC,同理可得AB ＝BC 由此可知△ABC 为等边三角形3.3丈0)()()(:)()(,)(,,:.4=-+-+-=++-=-=-==-=-=-t a c t c b t b a z y x t a c tz c b y t b a x t ac zc b y b a x 由此可得则有设解5.45810=c6.x ＝r θcos ,y ＝r sin7.由Δ＝b 2－4ac ＝0,得k ＝18.9.－1＜x ＜2 10.bx －ay ＝011.由通项公式可求得是T 4＝2012. ).(4为整数k k π±π=θ13.最少是一个,14.原式＝1003)5(4)2(4550554)5(55430)2(=⋅-⋅--⋅⋅-⋅⋅-⋅⋅-+⋅⋅+⋅⋅-15.02=±y x16.如图易证:3011=''∴''''==C A C A B A AC AB AC AB 17.6立方尺18.略:lg5＝1－lg2＝0.699019.解略:解方程组得两公共点为(0,0)及(3,6)故其公共弦长为:5320.解:由图可知:∠AFG ＝∠C ＋∠E ＝2∠C, ∠AGF ＝∠B ＋∠D ＝2∠B,∴∠A ＋∠AFG ＋∠AGF ＝∠A ＋2∠C ＋2∠B ＝5∠A ∴5∠A ＝1800,∴∠A ＝360 第二部分1.证:如图:由AD 是大圆的切线, 可得: ∠1＝∠由RQ ∥BC,可得:∠2＝∠3, 由QP ∥AB,可得:∠3＝∠42.解:由余弦定理可得:.C A B A,-B 60)180(60B 214)23(2)3()4()23(2cos 222222222222的等差中项与是∠∠∠∴∠∠=∠-︒=∠-∠-∠-︒=∠-∠︒=∠∴=⋅-+--+-+=⋅-+=A B B A B C pqq pq p q p pq q pq p BC AB CA BC AB B3.(1) 证:设α,β,γ是方程x 3＋ax 2＋bx ＋c ＝0的三根,由根与系数关系可知:α＋β＋γ＝－aαβ＋βγ＋γα＝b αβγ＝－c又因α,β,γ排成等比数列,于是β2＝αγ33333233a )()()(bc c a b ==αβγ-=β-=⎥⎦⎤⎢⎣⎡γ+β+αβγ+β+α-=⎥⎦⎤⎢⎣⎡γ+β+αβ+βγ+α-=⎥⎦⎤⎢⎣⎡γ+β+α-γα+βγ+αβ=⎪⎭⎫ ⎝⎛此即(2) 解:由⑴可知β3＝－c,∴β3＝27,∴β＝3代入α＋β＋γ＝－7可得α＋γ＝－10,又由α,β,γ成等比数列,∴β2＝αγ, 即αγ＝9,故可得方程组:⎩⎨⎧--=γ--=α=αγ-=γ+α.91,19,910或或可得解之 于是,所求之三根为－9,3,－1或－1,3,－94.证:设抛物线方程为y 2＝2px ……………① 过抛物线顶点O 任作互相垂直的二弦OA 和 OB,设OA 的斜率为k,则直线OB 的斜率为－k 1,于是直线OA 的方程为:y ＝kx ………………………② 直线OB 的方程为:x k y 1-=③设点A(x 1 ,y 1),点B(x 2 ,y 2)由①,②可得:.2,2121k p y kp x ==由①,③可得: x 2＝2pk 2, y 2＝－2pk设P(x,y)为AB 的中点,由上可得:④ ⑤ 由⑤可得:⑥ 由④可知:px 2222k p k p +=,代入⑥,2p -px y 22222222222=-=-⎪⎪⎭⎫ ⎝⎛+=即ppx p k p k p y所以,点P1952年试题 数学试题分两部分 第一部分注意:第一部分共二十题,均答在题纸上,每题的中间印着一道横线,将正确的答案就填写在横线上.例题:若2x －1＝x ＋3,则x ＝ 4 . 本题的正确答案是4,所以在横线上填写4. 1.分解因式:x4－y4＝ .[Key] 第一部分 1. (x －y)(x ＋y)(x2＋y2).pk k py y y pk kp x x x -=+=+=+=22212221 2222222k p p kp y +-=2.若log102x＝2log10x,问x＝ .[Key] 2.2.[Key] 3.－1.[Key] 4.±3.5.[Key] 5.－246.两个圆的半径都是4寸,并且一个圆通过另一圆的圆心,则这两个圆的公共弦之长是寸.[Key]7.三角形△ABC的面积是60平方寸,M是AB的中点,N是AC的中点,则△AMN的面积是平方寸.[Key] 7.15.8.正十边形的一内角是度.[Key] 8.144°9.祖冲之的圆周率π＝ .[Key]10.球的面积等于大圆面积的倍.[Key] 10.4.11.直圆锥之底之半径为3尺,斜高为5尺,则其体积为立方尺.[Key] 11.12π.12.正多面体有种,其名称为 .[Key] 12.5,正四面体,正六面体,正八面体,正十二面体,正二十面体.[Key]14.方程式tan2x＝1的通解为x＝ .[Key]15.太阳仰角为30°时塔影长5丈,求塔高＝ .[Key]16.三角形△ABC之b边为3寸,c边为4寸,A角为30°,则△ABC的面积为平方寸.[Key] 16.3.17.已知一直线经过点(2,－3),其斜率为－１,则此直线之方程式为 .[Key] 17.x＋y＋1＝0.18.若原点在一圆上,而此圆的圆心为点(3,4),则此圆的方程式为 . [Key] 18. x2＋y2－6x－8y＝019.原点至3x＋4y＋1＝0之距离＝ .[Key]20.抛物线y2－8x＋6y＋17＝0之顶点之坐标为 .[Key] 20.(1,－3)第二部分注意:第二部分共四题,均答在后面白纸上.1.解方程式x4＋5x3－7x2－8x－12＝0.[Key] 第二部分1.2,－6,ω,ω2.2.△ABC中,∠A的外分角线与此三角形的外接圆相交于D,求证:BD＝CD.[Key]3.设三角形的边长为a＝4,b＝5,c＝6,其对角依次为A,B,C.(1)求cosC.(2)求sinC,sinB,sinA.(3)问A,B,C三个角各为锐角或钝角？[Key]A,B,C皆为锐角。

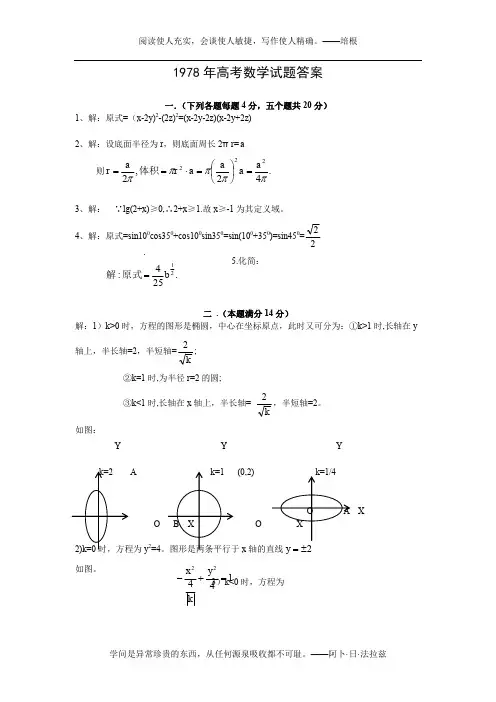
1978年高考数学试题答案一．（下列各题每题4分，五个题共20分） 1、解：原式=（x-2y)2-(2z)2=(x-2y-2z)(x-2y+2z)2、解：设底面半径为r ，则底面周长2πr=a则.42,2222πππππa a a a r a r =⎪⎭⎫ ⎝⎛=⋅==体积3、解： ∵lg(2+x)≥0,∴2+x ≥1.故x ≥-1为其定义域。

4、解：原式=sin100cos350+cos100sin350=sin(100+350)=sin450=225.化简：二 .（本题满分14分）解：1）k>0时，方程的图形是椭圆，中心在坐标原点，此时又可分为：①k>1时,长轴在y 轴上，半长轴=2，半短轴=k2;②k=1时,为半径r=2的圆; ③k<1时,长轴在x 轴上，半长轴=k2，半短轴=2。

如图：y 2=4x 轴的直线2±=y 如图。

3）k<0时，方程为Y Y YA (0,2)XO O .254:.21b =原式解14422=+-y kx这时图形是双曲线，中心在坐标原点，实轴在y 轴上。

如图：三．（本题满分14分）1)证：连CA ，CB ，则∠ACB=900。

∠ACM=∠ABC ∠ACD=∠ABC ∴∠ACM=∠ACD 。

∴△AMC ≌△ADC ∴CM=CD 同理CN=CD 。

∴CD=CM=CN 。

2）∵CD ⊥AB ，∠ACD=900。

∴ CD 2=AD ·DB 由1）知AM=AD ，BN=BD 。

∴CD 2=AM ·BN 。

四．（本题满分12分） 五．（本题满分20分）y=2Xy=-2MCNBD.22log 18log 9log 5log 218log 95log 45log .5log ,518:1818181818183618aba b b -+=++=⋅⋅==∴= 解.43460cos 45cos ;6445sin 34;860sin 34,347545120,45.32,1,32,1:.032)33(x tgC tgA,(2)(1)(2) .33)3)(3-(-1C)A tgAtgC)tg(-(1tgC tgA (1)32120,60.2180:212+=︒+︒=+==︒==︒=∴︒=︒-︒=︒=∴+==<+===+++-+=-=+=++=︒=+︒=∴+=︒=++a b DB AD c b a c C A tgC tgA C A x x x tgAtgC C A B C A B C B A 上的高等于又知则得设解这方程得的两根是可知由而又解六．（本题满分20分）七．（本题满分20分，文科考生不要求作此题） 解：用配方法得：3.设L ：x-y=a 为任一条平行于L 1的直线。

78年高考数学试卷78年高考数学试卷一、前言1978年是中国大规模实施高等教育招生制度的第一年，也是首次使用全国统一命题、全国统一考试的形式进行的高考。

当时，全国共有33个省市参加了高考，共有270万考生。

其中数学是必考科目之一，今年的试卷到底会出现些什么样的内容，让我们一起来看看吧。

二、分析试卷试卷题目全为计算题，从初中课程的知识点出发，共四道大题，计165分。

分别为：填空10分、选择50分、填表10分、作图15分、计算80分。

以下将针对每一大题详细分析。

1. 填空题（10分）本次填空题共有5小题，内容分别为：分类讨论法、证明不等式、概率计算等。

通过填空题可以初步检验考生对于基本概念和基本运算的掌握程度，同时也考察了考生的思维能力和逻辑推理能力。

2. 选择题（50分）选择题是本次试卷的重点，共有20道。

内容覆盖了代数式、函数、三角函数、几何等多个知识点，难度适中。

其中不乏一些需要深刻理解和掌握，同时运用切实的解决方法才能得出答案的题目，如“若$f(x)=\dfrac{p}{q}\sin x+\dfrac{q}{p}\cos x$，则$f(x)$的最小值为多少？”3. 填表题（10分）填表题是本次试卷的突破点，只有1小题，主要考查学生对于函数和曲线的通俗简单的理解。

通过“填表”这种学生常接触和应当熟练掌握的知识来评价学生的综合能力。

4. 作图题（15分）作图题是本次试卷的情境性题目，共有3小题。

主要考查学生的几何学知识和空间感知能力，如投影，当定位球的大小、比率、距离等因素不同时，其在地图上的呈现形状的代数式要如何根据实际情况进行推演。

5. 计算题（80分）计算题是本次试卷的难点之处，共计16道题目。

题目所涉及的知识点包括：函数、三角函数、数列等。

需要细心、耐心、有清晰的思路、思维活跃的学生拿高分。

难度较大，并且需要依照题目所给条件进行思考和推理。

其中一道典型的题目“已知数列$\{a_n\}$满足$a_1=2,a_{n+1}=3a_n+1(n\geqslant 1)$，则$30<a_n<40$的$n$的最小值为多少？”，很多学生会陷入绕弯子的迷茫中，这就考验了学生的“剪枝技术”和“数学想象力”。

山东1978高考数学真题1978年山东高考数学试题是一份历史悠久的文档，记录着当年高考的难度和考查内容。

这份试题反映了当时的教育水平和考试要求，也是一份珍贵的教育资料。

让我们一起来看一下这份题目的内容和解题思路吧。

1. 选择题1. \(\frac{x-y}{a-b} + \frac{y-z}{b-c} + \frac{z-x}{c-a}\) 的值为（\(\)）。

A. 0B. 1C. \(-1\)D. 3解析：将每一个分式化简，可得\(\frac{x-y}{a-b} = \frac{(x-a)-(y-b)}{a-b} = -1\)，同理可得其余两个分式均为\(-1\)，因此答案为C。

2. 方程\(x^2 - 2px + 2 = 0\) 的根之和为（\(\)）A. \(p\)B. \(-p\)C. \(2p\)D. \(-2p\)解析：根据韦达定理可知，根之和为\(2p\)，因此答案为C。

3. 若\(a, b\) 是比\(1\) 略小一些的两个正数，那么\(\sqrt{(1-a)(1-b)}\) 一定小于（\(\)）A. \(ab\)B. \(\frac{a+b}{2}\)C. \(\sqrt{ab}\)D. \(\frac{1}{2}(a+b)\)解析：根据均值不等式，知道\(\sqrt{ab} \leq \frac{a+b}{2}\)，因此答案为C。

4. 一个形状为扇形的卷筒体，其底面半径为\(R\) ，高为\(h\) ，若用它做一个容积为\(1\) 厘米\(^3\)的小球形容器，问底面的圆的半径应该是多少？A. \(\frac{1}{\pi}\sqrt{\frac{3}{2\pi}}\)B.\(\frac{1}{\pi}\sqrt{\frac{1}{2\pi}}\) C. \(\frac{1}{\pi}\sqrt{\frac{1}{\pi}}\) D. \(\frac{1}{\pi}\sqrt{\frac{1}{2\pi}}\)解析：小球形容器的体积为\(\frac{4}{3}\pi r^3\)，令其等于\(1\) 厘米\(^3\)，解得\(R = \frac{1}{\pi}\sqrt{\frac{1}{2\pi}}\)，因此答案为B。

1978年试题注意事项:1.理工科考生要求除作（一）--（四）题和（七）题外,再由（五）、（六）两题中选作一题.文科考生要求作（一）--（四）题,再由（五）、（六）两题中选作一题;不要求作第（七）题.2.考生解题作答时,不必抄题.但须准确地写明题号,例如（一）2、（五）等.（一）1.分解因式:x2-4xy+4y2-4z2.2.已知正方形的边长为a.求侧面积等于这个正方形的面积、高等于这个正方形边长的直圆柱体的体积.（二）已知方程kx2+y2=4,其中k为实数.对于不同范围的k值,分别指出方程所代表图形的类型,并画出显示其数量特征的草图.（三）（如图）AB是半圆的直径,C是半圆上一点,直线MN切半圆于C点,AM⊥MN于M点,BN⊥MN于N点,CD⊥AB于D点. 求证:1)CD=CM=CN;2)CD2=AM·BN.（四）已知log189=a(a≠2),18b=5.求log3645.（五）（本题和第（六）题选作一题）已知△ABC的三内角的大小成（六）已知α、β为锐角,且3sin2α+2sin2β=1,3sin2α-2sin2β=0.（七）（文科考生不要求作此题）已知函数y=x2+(2m+1)x+m2-1（m为实数）.(1)m是什么数值时,y的极值是0?(2)求证:不论m是什么数值,函数图象（即抛物线）的顶点都在同一条直线l1上.画出m=-1、0、1时抛物线的草图,来检验这个结论.(3)平行于l1的直线中,哪些与抛物线相交,哪些不相交?求证:任一条平行于l1而与抛物线相交的直线,被各抛物线截出的线段都相等.1979年试题理工农医类1.若(z-x)2-4(x-y)(y-z)=0,求证:x,y,z成等差数列.2.化简:3.甲、乙二容器内都盛有酒精.甲有公斤υ1公斤，乙有υ2公斤.甲中纯酒精与水(重量)之比为m1:n1,乙中纯酒精与水之比为m2:n2.问将二者混合后所得液体中纯酒精与水之比是多少?4.叙述并且证明勾股定理.5.外国般只,除特许者外,不得进入离我海岸线D以内的区城.设A及B是我们的观测站,A及B间的距离为S,海岸线是过A,B的直线.一外国船在P点.在A站测得∠BAP=α,同时在B站测得∠ABP=β.问α及β满足什么简单的三角函数值不等式,就应当向此未经特许的外国船发出警告,命令退出我海城?6.设三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=直角.求证:△ABC是锐角三角形.7.美国的物价从1939年的100增加到四十年后1979年的500.如果每年物价增长率相同,问每年增长百分之几?(注意:自然对数1nx是以e=2.718…为底的对数.本题中增长率x<0.1,可用自然对数的近似公式:ln(1+x)≈x.取lg2=0.3,ln10=2.3来计算).8.设CEDF是一个已知圆的内接矩形，过D作该圆的切线与CE的延长线相交于点A,与CF的延长线相交于点B.9.试问数列前多少项的和的值是最大?并求出这最大值.(这里取lg2=0.301)10.设等腰△OAB的顶角为2θ,高为h.(1)在△OAB内有一动点P,到三边OA,OB,AB的距离分别为│PD│,│PF│,│PE│并且满足关系│PD│·│PF │=│PE│2.求P点的轨迹.(2)在上述轨迹中定出点P的坐标,使得│PD│+│PE│=│PF│.1980年试题(理工农医类)一、将多项式x5y-9xy5分别在下列范围内分解因式:(1)有理数范围; (2)实数范围 (3)复数范围.二、半径为1、2、3的三个圆两两外切.证明:以这三个圆的圆心为顶点的三角形是直角三角形.三、用解析几何方法证明三角形的三条高线交于一点.(a、b、N都是正数,a≠1,b≠1)五、直升飞机上一点P在地平面M上的正射影是A.从P看地平面上一物体B(不同于A),直线PB垂直于飞机窗玻璃所在的平面N(如图).证明:平面N必与平面M相交,且交线l垂直于AB.(1)写出f(x)的极大值M、极小值m与最小正周期T;(2)试求最小的正整数k,使得当自变量x在任意两个整数间(包括整数本身)变化时,函数f(x)至少有一个值是M 与一个值是m.七、CD为直角三角形ABC中斜边AB上的高,已知△ACD、△CBD、△ABC的面积成等比数列,求∠B(用反三角函数表示).九、抛物线的方程是y2=2x,有一个半径为1的圆,圆心在x轴上运动.问这个圆运动到什么位置时,圆与抛物线在交点处的切线互相垂直.附加题问a、b应满足什么条件,使得对于任意m值来说,直线(L)与椭圆(E)总有公共点.1981年试题(理工农医类)一、设A表示有理数的集合,B表示无理数的集合,即设A={有理数},B={无理数},试写出:(1)A∪B,(2)A∩B.二、在A、B、C、D四位候选人中,(1)如果选举正、副班长各一人,共有几种选法?写出所有可能的选举结果;(2)如果选举班委三人,共有几种选法?写出所有可能的选举结果.三、下表所列各小题中,指出A是B的充分条件,还是必要条件,还是充要条件,或者都不是.四、写出余弦定理(只写一个公式即可),并加以证明.五、解不等式(x为未知数):六、用数学归纳法证明等式对一切自然数n都成立.七、设1980年底我国人口以10亿计算.(1)如果我国人口每年比上年平均递增2%,那么到2000年底将达到多少?(2)要使2000年底我国人口不超过12亿,那么每年比上年平均递增率最高是多少?下列对数值可供选用:lg1.0087=0.00377 lg1.0092=0.00396 lg1.0096=0.00417lg1.0200=0.00860 lg1.2000=0.07918 lg1.3098=0.11720lg1.4568=0.16340 lg1.4859=0.17200 lg1.5157=0.18060八、在120°的二面角P-a-Q的两个面P和Q内,分别有点A和点B.已知点A和点B到棱a的距离分别为2和4,且线段AB=10.(1)求直线AB和棱a所成的角;(2)求直线AB和平面Q所成的角.(1)过点A(2,1)的直线l与所给双曲线交于两点P1及P2,求线段P1P2的中点P的轨迹方程.(2)过点B(1,1)能否作直线m,使m与所给双曲线交于两点Q1及Q2,且点B是线段Q1Q2的中点?这样的直线m如果存在,求出它的方程;如果不存在,说明理由.十、附加题:计入总分.已知以AB为直径的半圆有一个内接正方形CDEF,其边长为1(如图).设AC=a,BC=b,作数列u1=a-b,u2=a2-ab+b2,u3=a3-a2b+ab2-b3,……,uk=ak-ak-1b+ak-2b2-……+(-1)kbk;求证:un=un-1+un-2(n≥3).1982年试题(理工农医类)一、填表:二、(1)求(-1+i)20展开式中第15项的数值;三、在平面直角坐标系内,下列方程表示什么曲线?画出它们的图形.四、已知圆锥体的底面半径为R,高为H.求内接于这个圆锥体并且体积最大的圆柱体的高h(如图).五、设0<x<1,a>0,a≠1,比较│loga(1-x)││loga(1+x)│的大小(要写出比较过程).六、如图:已知锐角∠AOB=2α内有动点P,PM⊥OA,PN⊥OB,且四边形PMON的面积等于常数c2.今以O为极点,∠AOB 的角平分线OX为极轴,求动点P的轨迹的极坐标方程,并说明它表示什么曲线.七、已知空间四边形,ABCD中AB=BC,CD=DA,M,N,P,Q分别是边AB,BC,CD,DA的中点(如图).求证MNPQ是一个矩形.八、抛物线y2=2px的内接三角形有两边与抛物线x2=2qy相切,证明这个三角形的第三边也与x2=2qy相切.九、附加题:计入总分.已知数列a1,a2,…,an,…和数列b1,b2,…,bn,…,其中a1=p,b1=q,an=pan-1,bn=qan-1+rbn-1(n≥2),(p,q,r是已知常数,且q≠0,p>r>0).(1)用p,q,r,n表示bn,并用数学归纳法加以证明;1983年试题(理工农医类)一、本题共5个小题,每一个小题都给出代号为A,B,C,D的四个结论,其中只有一个结论是正确的.把正确结论的代号写在题后的括号内.(1)两条异面直线,指的是(A)在空间内不相交的两条直线.(B)分别位于两个不同平面内的两条直线.(C)某一平面内的一条直线和这个平面外的一条直线.(D)不在同一平面内的两条直线.【】(A)两条相交直线. (B)两条平行直线.(C)两条重合直线. (D)一个点.【】(3)三个数a,b,c不完全为零的充要条件是(A)a,b,c都不是零. (B)a,b,c中最多有一个是零.(C)a,b,c中只有一个是零. (D)a,b,c中至少有一个不是零.【】【】【】(2)在极坐标系内,方程ρ=5cosθ表示什么曲线?画出它的图形.(2)一个小组共有10名同学,其中4名是女同学,6名是男同学.要从小组内选出3名代表,其中至少有1名女同学,求一共有多少种选法.四、计算行列式(要求结果最简):六、如图,在三棱锥SˉABC中,S在底面上的射影N位于底面的高CD上;M是侧棱SC上的一点,使截面MAB与底面所成的角等于∠NSC.求证SC垂直于截面MAB.八、已知数列{a n}的首项a1=b(b≠0),它的前n项的和S n=a1+a2+…+a n(n≥1),并且S1,S2,…,S n,…是一个等比数列,其公比为p(p≠0且│p│<1).(1)证明a2,a3,…,a n…,(即{a n}从第2项起)是一个等比数列.九、(1)已知a,b为实数,并且e<a<b,其中e是自然对数的底,证明ab>b a.(2)如果正实数a,b满足ab=b a,且a<1,证明a=b.1984年试题(理工农医类)一、本题每一个小题都给出代号为A,B,C,D的四个结论,其中只有一个结论是正确的,把正确结论的代号写在题后的括号内.(1)数集X={(2n+1)π,n是整数}与数集Y={(4k±1)π,k是整数}之间的关系是(C)X=Y(D)X≠Y【】(2)如果圆x2+y2+Gx+Ey+F=0与x轴相切于原点,那么(A)F=0,G≠0,E≠0(B)E=0,F=0,G≠0(C)G=0,F=0,E≠0(D)G=0,E=0,F≠0【】(A)一定是零(B)一定是偶数(C)是整数但不一定是偶数(D)不一定是整数【】(4)arccos(-x)大于arccosx的充要条件是(A)x∈(0,1](B)x∈(-1,0)【】(A)是第一象限角(B)是第三象限角(C)可能是第一象限角,也可能是第三象限角(D)是第二象限角【】二、只要求直接写出结果.(1)已知圆柱的侧面展开图是边长为2与4的矩形,求圆柱的体积.(2)函数log0.5(x2+4x+4)在什么区间上是增函数?(6)要排一张有6个歌唱节目和4个舞蹈节目的演出节目单,任何两个舞蹈节目不得相邻,问有多少种不同的排法(只要求写出式子,不必计算).三、本题只要求画出图形.四、已知三个平面两两相交,有三条交线.求证这三条交线交于一点或互相平行.六、(1)设p≠0,实系数一元二次方程z2-2pz+q=0有两个虚数根z1,z2.再设z1,z2在复平面内的对应点是z1,z2.求以z1,z2为焦点且经过原点的椭圆的长轴的长.九、附加题,不计入总分.如图,已知圆心为O、半径为1的圆与直线l相切于点A,一动点P自切点A沿直线l向右移动时,取弧的长为,直线PC与直线1985年试题(理工农医类)一、本题每一个小题都给出代号为A,B,C,D的四个结论,其中只有一个结论是正确的,把正确结论的代号写在题后的括号内.(1)如果正方体ABCD-A′B′C′D′的棱长为a,那么四面体A′-ABD的体积是【】(A)必要条件(B)充分条件(C)充分必要条件(D)既不充分又不必要的条件【】(A)y=x2(x∈R)(B)y=│sinx│(x∈R)(C)y=cos2x(x∈R)(D)y=e sin2x(x∈R)【】(4)极坐标方程ρ=asinθ(a>0)的图象是【】(5)用1,2,3,4,5这五个数字,可以组成比20000大,并且百位数不是数字3的没有重复数字的五位数,共有(A)96个(B)78个(C)72个(D)64个【】二、只要求直接写出结果.(2)设│a│≤1,求arccosa+arccos(-a)的值.(3)求曲线y2=-16x+64的焦点.(5)设函数f(x)的定义域是[0,1],求函数f(x2)的定义域.三、(1)解方程log4(3-x)+log0.25(3+x)=log4(1-x)+log0.25(2x+1).四、如图,设平面AC和BD相交于BC,它们所成的一个二面角为45°,P为面AC内的一点,Q为面BD内的一点.已知直线MQ是直线PQ在平面BD内的射影,并且M在BC上.又设PQ与平面BD所成的角为β,∠CMQ=θ(0°<θ<90°)线段PM的长为a.求线段PQ的长.五、设O为复平面的原点,Z1和Z2为复平面内的两个动点,并且满足:(2)△OZ1Z2的面积为定值S.求△OZ1Z2的重心Z所对应的复数的模的最小值.(1)证明不等式对所有的正整数n都成立.八、设a,b是两个实数,A={(x,y)│x=n,y=na+b,n是整数},B={(x,y)│x=,m,y=3m2+15,m是整数},C={(x,y)│x2+y2≤144}是平面XOY内的点集合.讨论是否存在a和b使得(2)(a,b)∈C同时成立.九、(附加题,不计入总分)已知曲线y=x3-6x2+11x-6.在它对应于x∈[0,2]的弧段上求一点P,使得曲线在该点的切线在y轴上的截距为最小,并求出这个最小值.1986年试题(理工农医类)一、本题每一个小题都给出代号为A,B,C,D的四个结论,其中只有一个结论是正确的,把正确结论的代号写在题后的括号内.(1)在下列各数中,已表示成三角形式的复数是【】(2)函数y=(0.2)-x+1的反函数是(A)y=log5x+1(B)y=log x5+1(C)y=log5(x-1)(D)y=log5x-1【】(A)一条平行于x轴的直线(B)一条垂直于x轴的直线(C)一个圆(D)一条抛物线【】【】(5)给出20个数8791948893918987928690928890918689929588它们的和是(A)1789(B)1799(C)1879(D)1899【】(6)设甲是乙的充分条件,乙是丙的充要条件,丙是丁的必要条件,那么丁是甲的(A)充分条件(B)必要条件(C)充要条件(D)既不充分也不必要的条件【】(7)如果方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)所表示的曲线关于直线y=x对称,那么必有(A)D=E(B)D=F(C)E=F(D)D=E=F【】(8)在正方形SG1G2G3中E、F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE、SF及EF把这个正方形折成一个四面体,使G1、G2、G3三点重合,重合后的点记为G.那么,在四面体S-EFG中必有(A)SG⊥△EFG所在平面(B)SD⊥△EFG所在平面(C)GF⊥△SEF所在平面(D)GD⊥△SEF所在平面【】(9)在下列各图中,y=ax2+bx与y=ax+b(ab≠0)的图象只可能是【】(10)当x∈[-1,0]时,在下面关系式中正确的是【】二、只要求直接写出结果.(3)在xoy平面上,四边形ABCD的四个顶点坐标依次为(0,0)、(1,0)、(2,1)及(0,3),求这个四边形绕x 轴旋转一周所得到的几何体的体积.三、如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A、B的任意一点.求证:平面PAC垂直于平面PBC.四、当sin2x>0时,求不等式log0.5(x2-2x-15)>log0.5(x+13)的解集.五、如图,在平面直角坐标系中,在y轴的正半轴(坐标原点除外)上给定两点A、B.试在x轴的正半轴(坐标原点除外)上求点C,使∠ACB取得最大值.六、已知集合A和集合B各含有12个元素,A∩B含有4个元素,试求同时满足下面两个条件的集合C 的个数:七、过点M(-1,0)的直线l1与抛物线y2=4x交于P1、P2两点.记:线段P1P2的中点为P;过点P和这个抛物线的焦点F的直线为l2;l1的斜率为k.试把直线l2的斜率与直线l1的斜率之比表示为k的函数,并指出这个函数的定义域、单调区间,同时说明在每一单调区间上它是增函数还是减函数.九、(附加题不计入总分)(1)求y=xarctgx2的导数.1987年试题(理工农医类)一、本题每一个小题都给出代号为A,B,C,D的四个结论,其中只有一个结论是正确的,把你认为正确的结论的代号写在题后的括号内.(A)X (B)T (C)φ(D)S【】【】(3)设a,b是满足ab<0的实数,那么(A)│a+b│>│a-b│(B)│a+b│<│a-b│(C)│a-b│<││a│-│b│(D)│a-b│<│a│+│b│【】(4)已知E,F,G,H为空间中的四个点,设命题甲:点E,F,G,H不共面.命题乙:直线EF和GH不相交.那么(A)甲是乙的充分条件,但不是必要条件.(B)甲是乙的必要条件,但不是充分条件.(C)甲是乙的充要条件.(D)甲不是乙的充分条件,也不是乙的必要条件.【】(5)在区间(-∞,0)上为增函数的是【】【】(7)极坐标方程ρ=sinθ+2cosθ所表示的曲线是(A)直线(B)圆(C)双曲线(D)抛物线【】【】二、只要求写出结果.(3)若(1+x)n的展开式中,x3的系数等于x的系数的7倍,求n.(5)在抛物线y=4x2上求一点,使该点到直线y=4x-5的距离为最短.(6)由数字1,2,3,4,5组成没有重复数字且数字1与2不相邻的五位数.求这种五位数的个数.(7)一个正三棱台的下底和上底的周长分别为30cm和12cm,而侧面积等于两底面积之差,求斜高.三、求sin10°sin30°sin50°sin70°的值.四、如图,三棱锥P-ABC中,已知PA⊥BC,PA=BC=L,PA,BC的公垂线ED=h.五、设对所有实数x,不等式恒成立,求a的取值范围.六、设复数z1和z2满足关系式其中A为不等于0的复数.证明:(1)│z1+A││z2+A│=│A│2;七、设数列a1,a2,…,a n,…的前n项的和S n与a n的关系是其中是b与n无关的常数,且b≠-1.(1)求a n和a n-1的关系式;(2)写出用n和b表示a n的表达式;八、定长为3的线段AB的两个端点在抛物线y2=x上移动,记线段AB的中点为M.求点M到y轴的最短距离,并求此时点M的坐标.九、(附加题,不计入总分)(2)设y=xln(1+x2),求y′.1988年试题(理工农医类)一、本题每一个小题都给出代号为A、B、C、D的四个结论，其中只有一个是正确的,把你认为正确的结论的代号写在题后的括号内.(A)1 (B)-1 (C)I (D)-i【】(2)设圆M的方程为(x-3)2+(y-2)2=2,直线L的方程为x+y-3=0,点P的坐标为(2,1),那么(A)点P在直线L上,但不在圆M上(B)点P在圆M上,但不在直线L上(C)点P既在圆M上,又在直线L上(D)点P既不在圆M上,也不在直线L上【】(3)集合{1,2,3}的子集总共有(A)7个 (B)8个(C)6个 (D)5个【】(A)10 (B)5【】(5)在的展开式中,x6的系数是【】(6)函数y=cos4x-sin4x的最小正周期是(A)π(B)2π【】(7)方程的解集是【】(A)圆(B)双曲线右支(C)抛物线(D)椭圆【】(9)如图,正四棱台中,A＇D＇所在的直线与BB＇所在的直线是(A)相交直线(B)平行直线(C)不互相垂直的异面直线(D)互相垂直的异面直线【】【】(11)设命题甲:△ABC的一个内角为60°.命题乙:△ABC的三个内角的度数成等差数列.那么(A)甲是乙的充分条件,但不是必要条件(B)甲是乙的必要条件,但不是充分条件(C)甲是乙的充要条件(D)甲不是乙的充分条件,也不是乙的必要条件【】(12)复平面内,若复数z满足│z+1│=│z-i│,则z所对应的点Z的集合构成的图形是(A)圆(B)直线(C)椭圆(D)双曲线【】(13)如果曲线x2-y2-2x-2y-1=0经过平移坐标轴后的新方程为那么新坐标系的原点在原坐标系中的坐标为(A)(1,1) (B)(-1,-1)(C)(-1,1) (D)(1,-1)【】(14)假设在200件产品中有3件是次品,现在从中任意抽取5件,其中至少有2件次品的抽法有【】(15)如图,二面角αˉABˉβ的平面角是锐角,C是面α内的一点(它不在棱AB上),点D是点C在面β上的射影,点E是棱AB上满足∠CEB为锐角的任意一点,那么(A)∠CEB>∠DEB(B)∠CEB=∠DEB(C)∠CEB<∠DEB(D)∠CEB与∠DEB的大小关系不能确定【】二、只要求直接写出结果.(5)已知等比数列{a n}的公比q>1,并且a1=b(b≠0),求四、如图,正三棱锥S-ABC的侧面是边长为a的正三角形,D是SA的中点,E是BC的中点,求△SDE绕直线SE旋转一周所得到的旋转体的体积.六、给定实数a,a≠0,且a≠1设函数证明(1)经过这个函数图象上任意两个不同的点的直线不平行于x轴;(2)这个函数的图象关于直线y=x成轴对称图形.1989年试题(理工农医类)一、选择题:每一个小题都给出代号为A、B、C、D的四个结论,其中只有一个是正确的,把你认为正确的结论的代号写在题后的括号内.【】(2)与函数y=x有相同图象的一个函数是【】【】【】(A)8 (B)16(C)32 (D)48 【】【】【】(8)已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧,且相距为1,那么这个球的半径是(A)4 (B)3(C)2 (D)5 【】【】【】(11)已知f(x)=8+2x-x2,如果g(x)=f(2-x2),那么g(x)(A)在区间(-1,0)上是减函数(B)在区间(0,1)上是减函数(C)在区间(-2,0)上是增函数(D)在区间(0,2)上是增函数【】(12)由数字1,2,3,4,5组成没有重复数字的五位数,其中小于50000的偶数共有(A)60个(B)48个(C)36个(D)24个【】二、填空题:只要求直接填写结果.(14)不等式│x2-3x│>4的解集是 .(16)已知(1-2x)7=a0+a1x+a2x2+…+a7x7,那么a1+a2+…+a7= .(18)如图,已知圆柱的底面半径是3,高是4,A、B两点分别在两底面的圆周上,并且AB=5,那么直线AB与轴OO＇之间的距离等于 .三、解答题.(Ⅰ)求证:顶点A1在底面ABCD的射影O在∠BAD的平分线上;(Ⅱ)求这个平行六面体的体积.(21)自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.(22)已知a>0,a≠1,试求使方程log a(x-ak)=log a2(x2-a2有解的k的取值范围.(23)是否存在常数a,b,c使得等式对一切自然数n都成立？并证明你的结论.(24)设f(x)是定义在区间(-∞,+∞)上以2为周期的函数,对k∈Z,用I k表示区间(2k-1,2k+1],已知当x∈I0时f(x)=x2.(Ⅰ)求f(x)在I k上的解析表达式;(Ⅱ)对自然数k,求集合M k={a│使方程f(x)=ax在I k上有两个不相等的实根}.1990年试题（理工农医类）一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后括号内.【】(3)如果轴截面为正方形的圆柱的侧面积是S,那么圆柱的体积等于【】(4)方程sin2x=sinx在区间(0,2π)内的解的个数是(A)1(B)2(C)3(D)4【】(5)【】(A){-2,4}(B){-2,0,4}(C){-2,0,2,4}(D){-4,-2,0,4}【】(7)如果直线y=ax＋2与直线y=3x－b关于直线y＝x对称,那么(C)a=3,b=-2(D)a=3,b=6【】(A)圆(B)椭圆(C)双曲线的一支(D)抛物线【】(B){(2,3)}(C)(2,3)(D){(x,y)│y=x+1}【】【】(11)如图,正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别为SC、AB的中点,那么异面直线EF与SA所成的角等于(A)90°(B)60°(C)45°(D)30°【】(12)已知h>0.设命题甲为:两个实数a,b满足│a－b│<2h;命题乙为:两个实数a,b满足│a－1│<h且│b-1│<h.那么(A)甲是乙的充分条件,但不是乙的必要条件(B)甲是乙的必要条件,但不是乙的充分条件(C)甲是乙的充分条件(D)甲不是乙的充分条件,也不是乙的必要条件【】(13)A,B,C,D,E五人并排站成一排,如果B必须站在A的右边（A,B可以不相邻）,那么不同的排法共有(A)24种(B)60种(C)90种(D)120种【】(14)以一个正方体的顶点为顶点的四面体共有(A)70个(B)64个(C)58个(D)52个【】(15)设函数y=arctgx的图象沿x轴正方向平移2个单位所得到的图象为C.又设图象C＇与C关于原点对称,那么C＇所对应的函数是(A)y=-arctg(x-2)(B)y=arctg(x-2)(C)y=-arctg(x+2)(D)y=arctg(x+2)【】二、填空题:把答案填在题中横线上.(17)(x-1)-(x-1)2+(x-1)3-(x-1)4+(x-1)5的展开式中,x2的系数等于.(18)已知{a n}是公差不为零的等差数列,如果S n是{a n}的前n项的和,那(19)函数y=sinxcosx+sinx+cosx的最大值是.(20)如图,三棱柱ABC－A1B1C1中,若E、F分别为AB、AC的中点,平面EB1C1F将三棱柱分成体积为V1、V2的两部分,那么V1:V2＝.三、解答题.7(21)有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12.求这四个数.(23)如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC．DE垂直平分SC,且分别交AC、SC于D、E.又SA＝AB,SB＝BC.求以BD为棱,以BDE与BDC为面的二面角的度数.(24)设a≥0,在复数集C中解方程z2+2│z│＝a.n≥2.(Ⅰ)如果f(x)当x∈(-∞,1]时有意义,求a的取值范围;(Ⅱ)如果a∈(0,1],证明2f(x)<f(2x)当x≠0时成立.1991年试题(理工农医类)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.把所选项前的字母填在题后括号内.【】(2)焦点在(-1,0),顶点在(1,0)的抛物线方程是(A)y2=8(x+1) (B)y2=-8(x+1)(C)y2=8(x-1) (D)y2=-8(x-1) 【】(3)函数y=cos4x-sin4x的最小正周期是【】(4)如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直线共有(A)12对(B)24对 (C)36对 (D)48对【】【】(6)如果三棱锥S-ABC的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点S在底面的射影O在△ABC内,那么O是△ABC的(A)垂心(B)重心 (C)外心 (D)内心【】(7)已知{a n},且a n>0,a2a4+2a3a5+a4a6=25,那么a3+a5的值等于(A)5 (B)10 (C)15 (D)20 【】(A)(0,0),(6,π) (B)(-3,0),(3,0)(C)(0,0),(3,0) (D)(0,0),(6,0) 【】(9)从4台甲型和5台乙型电视机中任意取出3台,其中至少要有甲型与乙型电视机各1台,则不同的取法共有(A)140种(B)84种 (C)70种 (D)35种【】(A)第一象限(B)第二象限(C)第三象限(D)第四象限【】(11)设甲、乙、丙是三个命题.如果甲是乙的必要条件;丙是乙的充分条件但不是乙的必要条件,那么(A)丙是甲的充分条件,但不是甲的必要条件(B)丙是甲的必要条件,但不是甲的充分条件(C)丙是甲的充要条件(D)丙不是甲的充分条件,也不是甲的必要条件【】(A)0 (B)1 (C)2 (D)3 【】(13)如果奇函数f(x)在区间[3,7]上是增函数且最小值为5,那么f(x)在区间[-7,-3]上是(A)增函数且最小值为－5 (B)增函数且最大值为－5(C)减函数且最小值为－5 (D)减函数且最大值为－5 【】(A)1个(B)2个(C)3个(D)4个【】(15)设全集为R,f(x)=sinx,g(x)=cosx,M={x│f(x)≠0},N={x│g(x)≠0},那么集合{x│f(x)g(x)=0}等于【】二、填空题:把答案填在题中横线上.(18)已知正三棱台上底面边长为2,下底面边长为4,且侧棱与底面所成的角是45°,那么这个正三棱台的体积等于.(19)在(ax+1)7的展开式中,x3的系数是x2的系数与x4的系数的等差中项,若实数a>1,那么a= .(20)在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA＝PB＝PC＝a.那么这个球面的面积是.三、解答题.(21)求函数y=sin2x+2sinxcosx+3cos2x的最小值,并写出使函数y取最小值的x的集合.(23)已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC ＝2.求点B到平面EFG的距离.(24)根据函数单调性的定义,证明函数f(x)=-x3+1在(-∞,+∞)上是减函数.(25)已知n为自然数,实数a>1,解关于x的不等式1992年试题(理工农医类)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.把所选项前的字母填在题后的括号内.【】(2)如果函数y=sin(ωx)cos(ωx)的最小正周期是4π,那么常数ω为【】(3)极坐标方程分别是ρ=cosθ和ρ=sinθ的两个圆的圆心距是【】(4)方程sin4xcos5x=-cos4xsin5x的一个解是(A)10°. (B)20°. (C)50°. (D)70°【】(5)已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是(A)6:5. (B)5:4. (C)4:3. (D)3:2 【】个值,则相应于曲线c1、c2、c3、c4的n依次为【】(7)若log a2<log b2<0,则(A)0<a<b<1 (B)0<b<a<1(C)a>b>1 (D)b>a>1 【】(A)20°. (B)70°. (C)110°. (D)160°【】(9)在四棱锥的四个侧面中,直角三角形最多可有(A)1个. (B)2个. (C)3个. (D)4个. 【】(10)圆心在抛物线y2=2x上,且与x轴和该抛物线的准线都相切的一个圆的方程是【】(11)在(x2+3x+2)5的展开式中x的系数为(A)160. (B)240. (C)360. (D)800. 【】(12)若0<a<1,在[0,2π]上满足sinx≥a的x的范围是(A)[0,arcsina]. (B)[arcsina,π-arcsina].【】(13)已知直线l1和l2夹角的平分线为y=x,如果l1的方程是ax+by+c=0(ab>0),那么l2的方程是(A)bx+ay+c=0. (B)ax-by+c=0.(C)bx+ay-c=0. (D)bx-ay+c=0. 【】(14)在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【】(15)已知复数z的模为2,则│z-i│的最大值为【】(A)是奇函数,它在(0,+∞)上是减函数.(B)是偶函数,它在(0,+∞)上是减函数.(C)是奇函数,它在(0,+∞)上是增函数.(D)是偶函数,它在(0,+∞)上是增函数. 【】(17)如果函数f(x)=x2+bx+c对任意实数t都有f(2+t)=f(2-t),那么(A)f(2)<f(1)<f(4). (B)f(1)<f(2)<f(4).(C)f(2)<f(4)<f(1). (D)f(4)<f(2)<f(1). 【】(18)长方体的全面积为11,十二条棱长度之和为24,则这个长方体的一条对角线长为(C)5. (D)6. 【】二、填空题:把答案填在题中横线上.(20)sin15°sin75°的值是.(21)设含有10个元素的集合的全部子集数为S,其中由3个元素组成的(22)焦点为F1(-2,0)和F2(6,0),离心率为2的双曲线的方程是.(23)已知等差数列{a n}的公差d≠0,且a1,a3,a9成等比数列,则三、解答题:解答应写出文字说明、演算步骤.(26)已知:两条异面直线a、b所成的角为θ,它们的公垂线段AA1的长度为d.在直线a、b上分别取点E、F,设A1E=m,AF=n.(27)设等差数列{a n}的前n项和为S n.已知a3=12,S12>0,S13<0.(Ⅰ)求公差d的取值范围.(Ⅱ)指出S1,S2,…,S12中哪一个值最大,并说明理由.1993年试题(理工农医类)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.把所选项前的字母填在题后括号内.(1)如果双曲线的实半轴长为2,焦距为6,那么该双曲线的离心率为【】【】(A)45°(B)60° (C)90° (D)120°【】(A)1 (B)-1 (C)i (D)-i 【】(5)直线bx+ay=ab(a<0,b<0)的倾斜角是【】(6)在直角三角形中两锐角为A和B,则sinAsinB(C)既无最大值也无最小值(D)有最大值1,但无最小值【】(7)在各项均为正数的等比数列{a n}中,若a5a6=9,则log3a1+log3a2+…+log3a10=(A)12 (B)10 (C)8 (D)2+log35 【】(A)是奇函数(B)是偶函数(C)可能是奇函数也可能是偶函数(D)不是奇函数也不是偶函数【】(A)线段(B)双曲线的一支(C)圆弧 (D)射线【】(10)若a、b是任意实数,且a>b,则【】(11)已知集合E={θ│cosθ<sinθ,0≤θ≤2π},F={θ│tgθ<sinθ},那么E∩F为区间【】(12)一动圆与两圆:x2+y2=1和x2+y2-8x+12=0都外切,则动圆圆心的轨迹为(A)抛物线(B)圆(C)双曲线的一支(D)椭圆【】(A)三棱锥(B)四棱锥(C)五棱锥(D)六棱锥【】(14)如果圆柱轴截面的周长l为定值,那么圆柱体积的最大值是【】(A)50项(B)17项(C)16项 (D)15项【】(16)设a,b,c都是正数,且3a=4b=6c,那么【】(17)同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则四张贺年卡不同的分配方式有。

1978高考试题及答案一、选择题（每题2分，共20分）1. 1978年高考是在哪个国家举行的？A. 美国B. 英国C. 中国D. 日本答案：C2. 1978年高考的数学科目中，以下哪个选项是正确的？A. 圆的面积公式为πr²B. 圆的面积公式为2πrC. 圆的周长公式为πr²D. 圆的周长公式为2πr答案：A3. 1978年高考的英语科目中，以下哪个单词的拼写是错误的？A. opportunityB. opportunitysC. opportunitytD. opportunity答案：B4. 1978年高考的物理科目中，以下哪个公式表示了牛顿第二定律？A. F=maB. F=mvC. F=ma²D. F=m/a答案：A5. 1978年高考的化学科目中，以下哪个元素的原子序数是6？A. 碳B. 氧C. 氮D. 氢答案：A6. 1978年高考的历史科目中，以下哪个事件标志着中国改革开放的开始？A. 文化大革命B. 五四运动C. 十一届三中全会D. 辛亥革命答案：C7. 1978年高考的地理科目中，以下哪个国家位于亚洲？A. 巴西B. 阿根廷C. 中国D. 南非答案：C8. 1978年高考的政治科目中，以下哪个原则是中国外交政策的基石？A. 和平共处五项原则B. 单边主义C. 多边主义D. 霸权主义答案：A9. 1978年高考的生物科目中，以下哪个选项是正确的？A. 细胞是所有生物的基本单位B. 病毒不是生物C. 所有生物都有细胞结构D. 病毒是所有生物的基本单位答案：A10. 1978年高考的语文科目中，以下哪个成语的意思是指事情已经过去，不再追究？A. 既往不咎B. 往事如烟C. 过眼云烟D. 烟消云散答案：A二、填空题（每题2分，共20分）1. 1978年高考的语文科目中，著名诗人杜甫的代表作之一是《________》。

答案：春望2. 1978年高考的数学科目中，勾股定理的公式是a² + b² =________。

1978年的高考数学题初中生看了直摇头一脸苦笑1978年高考数学试卷原标题：1978年的高考数学题，初中生看了直摇头，一脸苦笑都说现在是大学扩招的时代，每一年，都有无数高考生被录取进大学，开始自己的大学生活。

于是，有不少人叹息，说过去的大学生，才是真才实学，现在的大学生呢，简直遍地都是，而且就连研究生都快要普及了，唉，大学文凭真的不值钱了呢。

或许，这种感慨也有些道理吧，从上世纪恢复高考以后，不少优秀的学子，进入了大学的校门，想当初那些风华正茂的大学生们，现在早已成为了社会的中坚力量，或者已经退居二线了吧！但他们当年的雄姿英发，依旧令人思念。

不过，在看到了1978年的高考数学题以后，现在的初中生们，却不淡定了，一脸苦笑连连摇头，这是为何呢？先来看看，当年的高考数学题，都考了些什么呢？我们来看看上面两张图，图中的高考数学题，是不是感觉很简单呢？想必不少的初中生，都能计算出来吧！这也让他们很是不平：当年的数学题，为何就这样简单呢？其实呀，由于当时刚刚恢复高考，许多高中生，都没有接受到完整的高中教育，在参加高考的时候，都是凭据自己以前自学过的一些东西，因此，根底都十分差。

再加上当时国家也急需要人才，因此，用现在的目光来看，当年的高考数学题，确实是有些容易吧！因此，在同学们看到这份数学卷时，感慨很多，有的同学，觉得自己读了一个假初中，还有的同学，觉得作为高中生，看来自己有些落后了！不过，任何问题，都要辩证来看吧！当年的高考，不能代表现在的高考生水平。

时代毕竟在前进，在开展，现在的初中生和高中生，更应该迎接挑战，拔高难度，冲击更好的大学才是，对吧！朋友，对此，您是如何看的呢？阅读()。

1978数学试题及答案一、选择题（每题4分，共40分）1. 已知函数f(x) = 2x^3 - 3x^2 + 4x - 5，求f'(x)的值。

A. 6x^2 - 6x + 4B. 6x^2 - 6x + 3C. 6x^2 - 6x + 2D. 6x^2 - 6x + 1答案：A2. 已知函数f(x) = x^2 + 2x + 1，求f(-1)的值。

A. 0B. 1C. 2D. 3答案：B3. 已知函数f(x) = sin(x) + cos(x)，求f'(x)的值。

A. cos(x) - sin(x)B. sin(x) + cos(x)C. -sin(x) + cos(x)D. -sin(x) - cos(x)答案：C4. 已知函数f(x) = e^x，求f'(x)的值。

A. e^xB. -e^xC. e^(-x)D. -e^(-x)答案：A5. 已知函数f(x) = ln(x)，求f'(x)的值。

A. 1/xB. -1/xC. xD. -x答案：A6. 已知函数f(x) = x^2 - 4x + 4，求f(x)的最小值。

A. 0B. 1C. 4D. 8答案：A7. 已知函数f(x) = x^3 - 6x^2 + 11x - 6，求f'(x) = 0的解。

A. x = 1, 2, 3B. x = 2, 3C. x = 1, 3D. x = 1, 2答案：B8. 已知函数f(x) = x^4 - 4x^3 + 6x^2 - 4x + 1，求f'(x)的值。

A. 4x^3 - 12x^2 + 12x - 4B. 4x^3 - 12x^2 + 12x - 1C. 4x^3 - 12x^2 + 12x - 2D. 4x^3 - 12x^2 + 12x - 3答案：A9. 已知函数f(x) = x^2 - 6x + 9，求f(x)的对称轴。

A. x = 3B. x = -3C. x = 0D. x = 6答案：A10. 已知函数f(x) = 2x - 3，求f(2)的值。

1978高考试题及答案一、选择题（每题2分，共10题，满分20分）1. 1978年高考恢复后，下列哪项不是考试科目？A. 语文B. 数学C. 英语D. 体育答案：D2. 1978年高考的考试时间是？A. 7月B. 8月C. 9月D. 10月答案：A3. 1978年高考中，数学科目的满分是多少分？A. 100分B. 120分C. 150分D. 200分答案：B4. 1978年高考中，英语科目的考试形式是什么？A. 笔试B. 口试C. 笔试+口试D. 无英语考试答案：A5. 1978年高考的录取率是多少？A. 5%B. 10%C. 15%D. 20%答案：B6. 1978年高考中，下列哪项不是考试内容？A. 政治B. 历史C. 地理D. 计算机答案：D7. 1978年高考的报名人数是多少？A. 500万B. 600万C. 700万D. 800万答案：C8. 1978年高考中，下列哪项是考试科目？A. 物理B. 化学C. 生物D. 以上都是答案：D9. 1978年高考的考试地点通常在哪里？A. 考生所在城市B. 考生所在省份C. 考生所在学校D. 考生所在班级答案：A10. 1978年高考的录取原则是什么？A. 择优录取B. 按地区分配C. 按分数排序D. 随机抽取答案：A二、填空题（每题2分，共5题，满分10分）1. 1978年高考的语文考试中，作文题目是“________”。

答案：《我在这战斗的一年里》2. 1978年高考的数学考试中，最后一道大题是关于________的。

答案：几何证明3. 1978年高考的英语考试中，听力部分的语速是每分钟________个单词。

答案：1204. 1978年高考的物理考试中，涉及到的实验操作题目是关于________的。

答案：电学5. 1978年高考的化学考试中，涉及到的有机化学题目是关于________的。

答案：苯的结构三、简答题（每题5分，共2题，满分10分）1. 简述1978年高考对于中国教育史的意义。