小学五年级数学上册《小数除法》知识点汇总

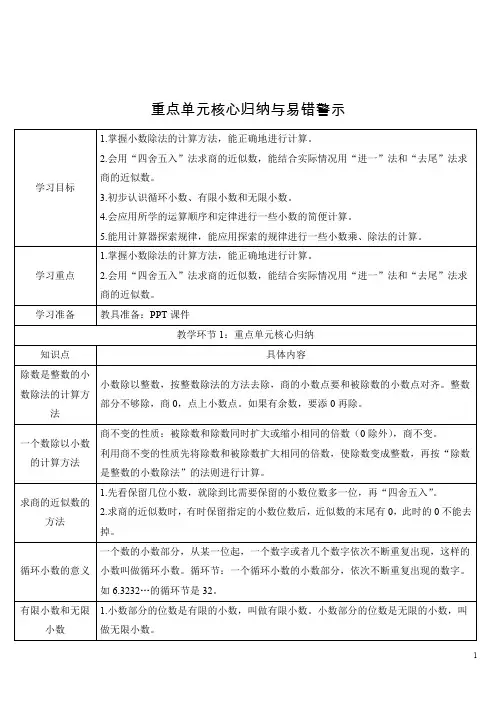
知识点一、除数是整数小数除以整数，按整数除法的方法去除。

商的小数点要和被除数的小数点对齐。

整数部分不够除，商0，点上小数点。

如果有余数，要添0再除。

除得的商的哪一数位上不够商，就在那一位上写0占位。

二、除数是小数一看：看清被除数有几位小数。

二移：把除数和被除数的小数点同时向右移动相同的位数（也就是同时扩大相同的倍数），使除数变成整数，（被除数是不是整数不重要，只要扩大相同倍数就行）。

三算：按照除数是整数的小数除法计算进行计算。

a÷b=c（b≠0），b=1时，a=c；b＞1时，a＞c；b＜1时，a＜c三、商的近似数求商的近似值：计算时要比保留的小数多一位。

取商的近似值的方法：“四舍五入”法、保留商的近似值，小数末尾的0不能去掉。

求积的近似值：计算出整个积的值后再去近似值。

四、循环小数1、循环小数的定义：一个数的小数部分，从某一位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。

2、循环节的定义：一个循环小数的小数部分，依次不断重复出现的一个数字或者几个数字，叫做这个循环小数的循环节。

如5.33……循环节是3。

7.14545……的循环节是45。

3、循环小数必须满足的条件：①必须是无限小数；②一个数字或者几个数字依次不断重复出现。

4、循环小数的记法：①省略后面的“……”号；②在第一个循环节首尾的数字上分别加点。

5、小数分类：可以分为无限小数和有限小数。

小数部分的位数是有限的小数，叫做有限小数。

小数部分是无限的小数叫做无限小数。

循环小数就是无限小数中的一种。

循环小数一定是无限小数，无限小数不一定是循环小数。

五、解决问题应用题中取商的近似值的方法有：“四舍五入”法、“进一法”和“去尾法”。

在解决问题的时候，要根据题目实际情况选择“进一法”和“去尾法”取商的近似值。

练习题一、填空：1.两个数相除时，如果被除数扩大10倍，要使商不变，除数应（）。

2.计算2.025÷1.47时，先将1.47的小数点向（）移动（）位，使它（），再将2.205的小数点向（）移动（）位，最后按除数是整数的除法进行计算。

北师大版小学数学五年级（上册）知识点第一单元小数除法1、除数是整数的小数除法计算法则：除数是整数的小数除法，按照整数除法的法则去除，商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数，就在余数后面添 0 再继续除。

2、除数是小数的小数除法计算法则：除数是小数的除法，先移动除数的小数点，使它变成整数;除数的小数点向右移动几位，被除数的小数点也向右移动几位(位数不够的，在被除数末尾用 0 补足)，然后按照除数是整数的小数除法进行计算。

3、连除的算式可以写成被除数除以几个数的积，但除以几个数的积时，必须给这个相乘的式子加上小括号。

4、在小数除法中的发现：①当除数不为 0 时，除数大于 1 时，商小于被除数。

如：3.5÷5=0.7②当除数不为 0 时，除数小于 1 时，商大于被除数。

如：3.5÷0.5=7(当除数不为 0 时，除数等于 1 时，商等于被除数。

如：3.5÷1=3.55、小数除法的验算方法：①商×除数=被除数(通用)②被除数÷商=除数6、商的近似数：根据要求要保留的小数位数，决定商要除出几位小数，再根据“四舍五入”法保留一定的小数位数，求出商的近似数。

例如：要求保留一位小数的，商除到第二位小数可停下来;要求保留两位小数的，商除到第三位小数停下来……如此类推。

7、循环小数：A、小数部分的位数是有限的小数，叫做有限小数。

如，0.37、1.4135等。

B、小数部分的位数是无限的小数，叫做无限小数。

如 5.3… 7.145145…等。

C 、一个数的小数部分，从某位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。

(如 5.3… 3.12323… 5.7171…)D、一个循环小数的小数部分，依次不断重复的数字，叫做小数的循环节。

(如5.333…的循环节是 3， 4.6767…的循环节是 67，6.9258258…的循环节是258)E、用简便方法写循环小数的方法：①只写一个循环节，并在这个循环节的首位和末位上面记一个小圆点。

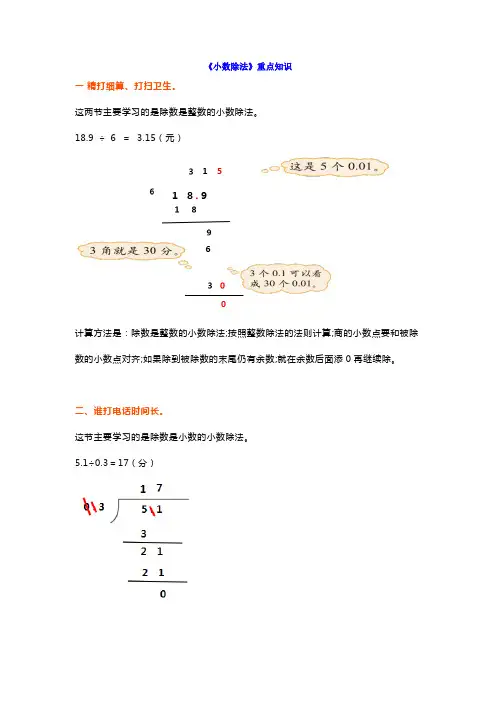
《小数除法》重点知识一精打细算、打扫卫生。

这两节主要学习的是除数是整数的小数除法。

18.9 ÷6 ＝ 3.15（元）计算方法是：除数是整数的小数除法;按照整数除法的法则计算;商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数;就在余数后面添0再继续除。

二、谁打电话时间长。

这节主要学习的是除数是小数的小数除法。

5.1÷0.3＝17（分）计算方法：除数是小数的除法;先移动除数的小数点;使它变成整数;除数的小数点向右移动几位;被除数的小数点也向右移动几位(位数不够的;在被除数末尾用0补足);然后按照除数是整数的小数除法进行计算。

在小数除法中的发现：（1）当除数不为0且大于1时;商小于被除数。

（2）当除数不为0且小于1时;商大于被除数。

（3）当除数不为0且等于1时;商等于被除数。

三、人民币兑换。

这节主要学习积与商的近似值;根据要求要保留的小数位数;决定商要除出几位小数;再根据“四舍五入”法保留一定的小数位数;求出商的近似数。

例如：要求保留一位小数的;商除到第二位小数可停下来;要求保留两位小数的;商除到第三位小数停下来……如此类推。

四、除得尽吗。

这节主要认识循环小数：（1）、小数部分的位数是有限的小数;叫做有限小数。

如：0.3 、3.45 、7.77 这些数都是有限小数。

（2）、小数部分的位数是无限的小数;叫做无限小数。

如2.7272···、3.14159···、3.33333···这些都是无限小数。

（3）、一个数的小数部分;从某位起;一个数字或者几个数字依次不断重复出现;这样的小数叫做循环小数。

（如0.66666···、1.578578···叫做循环小数。

）一个循环小数的小数部分;依次不断重复的数字;叫做小数的循环节。

用简便方法写循环小数的方法：只写一个循环节;并在这个循环节的首位和末位上面记一个小圆点强调。

五年级上册小数乘除法知识点总结第一篇：五年级上册小数乘除法知识点总结五年级上册小数乘除法知识点总结一、小数乘法计算法则：1.列竖式时末位对齐。

2.按照整数乘法算出积。

3.点小数点（如果是小数乘整数，只看小数是几位小数，就从积的末尾起数出几位点上小数点。

如果是小数乘小数，要看两个因数一共有几位小数，再从积的末尾起数出几位点上小数点。

）4.点小数点后，积的末尾有“0”要划掉。

二、小数除法计算法则：列竖式时：①先写除号，再写除数，最后写被除数。

②写时要先看除数是不是整数，如果不是整数，先移动小数点把除数变成整数，除数的小数点向右移动几位，被除数的小数点也向右移动几位。

计算时：①先看整数部分够不够商“1”，不够商“1”要用0占位，再点上小数点。

如果够商“1”，就往下除。

②除数是几位数，先看被除数的前几位，前几位不够再往后多看一位。

③除到哪一位商就写在那一位上面，如果不够商“1”，要用0占位。

④除的过程中，余数一定要比除数小。

⑤最后要检验商的小数点和被除数的小数点有没有对齐。

注意：一列二算三检验。

三、求近似数：保留整数也就是精确到个位，保留一位小数也就是精确到十分位，保留两位小数也就是精确到百分位，保留三位小数也就是精确到千分位。

方法：精确到哪一位，关键看后一位上的数，如果是0、1、2、3、4直接舍去，如果是5、6、7、8、9向前一位进1再舍去。

注意：求商的近似数时要除到比保留的位数多一位。

四、比较大小：乘法：一个数（0除外）乘大于1的数，积比原来的数大。

一个数（0除外）乘小于1的数，积比原来的数小。

除法：除数大于1，商小于被除数。

除数小于1，商大于被除数。

除数等于1，商等于被除数。

注意：被除数不为0。

五、混合运算：1.有括号先算小括号里面的再算小括号外面的。

2.先算乘除法，后算加减法。

3.同级运算按从左往右的顺序依次计算。

简便计算：1.乘法交换律和乘法结合律的运用题型：连乘、两个数相乘其中一个因数是125或25 2.乘法分配律的运用题型：（1）左----右和乘、差乘。

精品资料第一单元小数除法1、除数是整数的小数除法计算法则：除数是整数的小数除法，按照整数除法的法则去除，商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数，就在余数后面添0再继续除。

2、除数是小数的小数除法计算法则：除数是小数的除法，先移动除数的小数点，使它变成整数;除数的小数点向右移动几位，被除数的小数点也向右移动几位(位数不够的，在被除数末尾用0补足)，然后按照除数是整数的小数除法进行计算。

3、在小数除法中的发现：①当除数大于1时，商小于被除数。

如：3.5÷5=0.7②当除数小于1时，商大于被除数。

如：3.5÷0.5=74、小数除法的验算方法：①商×除数=被除数(通用) ②被除数÷商=除数5、商的近似数：根据要求要保留的小数位数，决定商要除出几位小数，再根据“四舍五入”法保留一定的小数位数，求出商的近似数。

例如：要求保留一位小数的，商除到第二位小数可停下来;要求保留两位小数的，商除到第三位小数停下来……如此类推。

6、循环小数问题：A、小数部分的位数是有限的小数，叫做有限小数。

如，0.37、1.4135等。

B、小数部分的位数是无限的小数，叫做无限小数。

如5.3… 7.145145…等。

C、一个数的小数部分，从某位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。

(如5.3… 3.12323… 5.7171…)D、一个循环小数的小数部分，依次不断重复的数字，叫做小数的循环节。

(如5.333…的循环节是3， 4.6767…的循环节是67，6.9258258…的循环节是258)E、用简便方法写循环小数的方法：①只写一个循环节，并在这个循环节的首位和末位上面记一个小圆点。

②例如：只有一个数字循环节的，就在这个数字上面记一个小圆点，5.333…写·作5.3。

有两位小数循环的，就在这两位数字上面，记上小圆点，7.4343…写作··7.4 3。

新北师大版小学数学五年级（上册）知识点第一单元小数除法1、除数是整数的小数除法计算法则：除数是整数的小数除法，按照整数除法的法则去除，商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数，就在余数后面添0再继续除。

2、除数是小数的小数除法计算法则：除数是小数的除法，先移动除数的小数点，使它变成整数;除数的小数点向右移动几位，被除数的小数点也向右移动几位(位数不够的，在被除数末尾用0补足)，然后按照除数是整数的小数除法进行计算。

3、连除的算式可以写成被除数除以几个数的积，但除以几个数的积时，必须给这个相乘的式子加上小括号。

4、在小数除法中的发现：①当除数不为0时，除数大于1时，商小于被除数。

如： 3.5÷5=0.7②当除数不为0时，除数小于1时，商大于被除数。

如： 3.5÷0.5=7当除数不为0时，除数等于1时，商等于被除数。

如： 3.5÷1=3.55、小数除法的验算方法：①商×除数=被除数(通用) ②被除数÷商=除数6、商的近似数：根据要求要保留的小数位数，决定商要除出几位小数，再根据“四舍五入”法保留一定的小数位数，求出商的近似数。

例如：要求保留一位小数的，商除到第二位小数可停下来;要求保留两位小数的，商除到第三位小数停下来……如此类推。

7、循环小数：A、小数部分的位数是有限的小数，叫做有限小数。

如，0.37、1.4135等。

B、小数部分的位数是无限的小数，叫做无限小数。

如5.3… 7.145145…等。

C、一个数的小数部分，从某位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。

(如5.3… 3.12323… 5.7171…)D、一个循环小数的小数部分，依次不断重复的数字，叫做小数的循环节。

(如5.333…的循环节是3， 4.6767…的循环节是67， 6.9258258…的循环节是258)E、用简便方法写循环小数的方法：①只写一个循环节，并在这个循环节的首位和末位上面记一个小圆点②例如：只有一个数字循环节的，就在这个数字上面记一个小圆点， 5.333…写作 5.3 ；有两位小数循环的，就在这两位数字上面，记上小圆点，7.4343…写作7.4 3 ；有三位或以上小数循环的，在首位和末位记上小数点，10.732732…写作10.7328、除法中的变化规律：①商不变性质：被除数和除数同时扩大或缩小相同的倍数( 0除外)，商不变。

五年级数学小数除法知识点归纳（附习题及解析），一定要给孩子看《小数除法》要点知识1、小数除法的意义：已知两个因数的积与其中的一个因数，求另一个因数的运算。

如：0.6÷0.3表示已知两个因数的积0.6，一个因数是0.3，求另一个因数是多少。

2、小数除以整数的计算方法：小数除以整数，按整数除法的方法去除，商的小数点要和被除数的小数点对齐。

整数部分不够除，商0，点上小数点。

如果有余数，要添0再除。

3、除数是小数的除法的计算方法：先将除数和被除数扩大相同的倍数，使除数变成整数，再按“除数是整数的小数除法”的法则进行计算。

注意：如果被除数的位数不够，在被除数的末尾用0补足。

4、在实际应用中，小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数，求出商的近似数。

5、除法中的变化规律：①商不变性质：被除数和除数同时扩大或缩小相同的倍数（0除外），商不变。

②除数不变，被除数扩大（缩小），商随着扩大（缩小）。

③被除数不变，除数缩小，商反而扩大；被除数不变，除数扩大，商反而缩小。

6、(P28)循环小数：一个数的小数部分，从某一位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。

循环节：一个循环小数的小数部分，依次不断重复出现的数字。

如6.3232……的循环节是32.简写作6.327.小数部分的位数是有限的小数，叫做有限小数。

小数部分的位数是无限的小数，叫做无限小数。

小数分为有限小数和无限小数。

易错题解析1、9.97÷4.21的商保留两位小数是( )保留整数是（）。

2.37 22.去掉0.25的小数点，就是把这个数扩大（）；把50.4的小数点向左移动两位，就是把它缩小到原来的（）。

100倍百分之一3、125缩小到它的（）是0.125；（）扩大到它的100倍是0.3。

千分之一 0.0034、0.25除以0.15，当商是1.6时，余数是（）;0.79÷0.04,商是19,余数是（）。

《小数乘除法》知识点归纳一、小数乘法1、小数乘整数意义——求几个相同加数的和的简便运算。

如：1.5×3表示求3个1.5的和的简便运算（或1.5的3倍是多少）。

计算方法：先把小数扩大成整数；按整数乘法的法则算出积；再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

2、小数乘小数意义——就是求这个数的几分之几是多少。

如：1.5×0.8就是求1.5的十分之八是多少（或求1.5的1.8倍是多少）。

计算方法：先把小数扩大成整数；按整数乘法的法则算出积；再看因数中一共有几位小数，就从积的右边起数出几位点上小数点注意：按整数算出积后，小数末尾的0要去掉，也就是把小数化简；位数不够时，要用0占位。

《小数乘除法》知识点归纳3、规律一个数（0除外）乘大于1的数，积比原来的数大；一个数（0除外）乘小于1的数，积比原来的数小。

4、小数乘法的运算定律和性质乘法交换律：axb=b×a乘法结合律：（axb）×c=a×（b×c）三个数相乘，先把前两个数相乘，再和最后一个数相乘，或先把后两个数相乘，再和第一个数相乘，积不变。

乘法分配律∶（a+b）×c=a×c+b×c（a-b）×c=a×c-b×c两个数的和（或者差）同一个数相乘，可以先把这两个数（或者被减数与减数）分别同这个数相乘，再相加（乘加、乘减或者再相减）。

二、小数除法1、小数除法的意义已知两个因数的积与其中的一个因数，求另一个因数的运算如：0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3 求另一个因数的运算。

《小数乘除法》知识点归纳2、小数除以整数的计算方法小数除以整数，按整数除法的方法去除，商的小数点要和被除数的小数点对齐。

整数部分不够除，商0，点上小数点。

如果有余数，要添0再除。

3、除数是小数的除法的计算方法先将除数和被除数扩大相同的倍数，使除数变成整数，再按"除数是整数的小数除法"的法则进行计算。

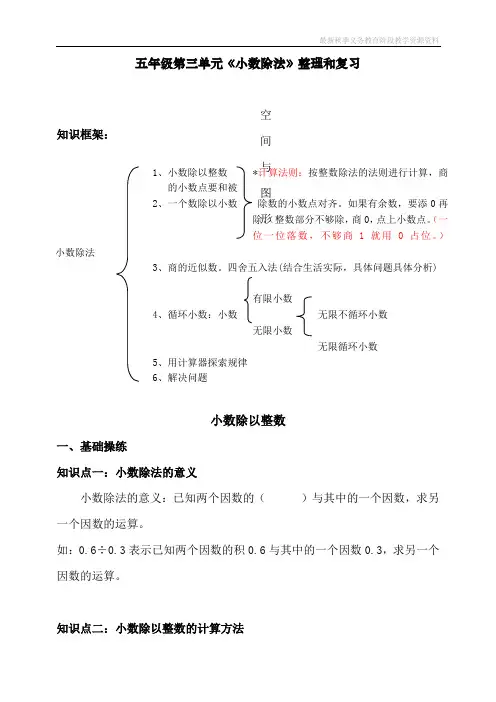
五年级第三单元《小数除法》整理和复习知识框架：小数除以整数一、基础操练知识点一：小数除法的意义小数除法的意义：已知两个因数的（ ）与其中的一个因数，求另一个因数的运算。

如：0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3，求另一个因数的运算。

知识点二：小数除以整数的计算方法1、小数除以整数*计算法则：按整数除法的法则进行计算，商的小数点要和被 2、一个数除以小数 除数的小数点对齐。

如果有余数，要添0再除。

（整数部分不够除，商0，点上小数点。

（一位一位落数，不够商1就用0占位。

）空间与图形3、商的近似数。

四舍五入法(结合生活实际，具体问题具体分析)有限小数4、循环小数：小数 无限不循环小数 无限小数无限循环小数 5、用计算器探索规律 6、解决问题小数除法小数除以整数的计算方法：小数除以整数，按整数除法的方法去除，商的小数点要和被除数的小数点对齐。

整数部分不够除，商写上0，点上小数点。

如果有余数，要添0再除。

【练习】58.89÷13 96÷15 0.465÷15 16.32÷51二、感悟与实践例题1：学校买了13盒白粉笔和10盒彩色粉笔，共付64.5元。

每盒白粉笔2.5元，每盒彩色粉笔多少元？变式练习：一支钢笔的价钱是一支圆珠笔价钱的4倍。

王小东买了一支钢笔和3支圆珠笔，一共花了17.5元。

钢笔和圆珠笔的单价各是多少元？例题2：服装厂做校服。

原来每套服装用布2.2米，现在每套用布节省0.2米。

原来做800套这种服装的布，现在可以做多少套？变式练习：工程队要铺设一条长4.8千米的地下管道，计划用15天完成，实际每天比计划多铺设3.2千米，实际多少天完成任务？变式练习：西平乡修一条长2.1千米的河堤，前15天平均每天修0.086千米。

余下的要9天完成，平均每天修多少千米？三、巩固练习练习1一、口算。

23.6÷10=10÷4=0.36÷3=8.4÷2=40÷50= 6.6÷33 =二、填空。