二元一次方程应用题(百分数)

二元一次方程练习题及答案哎呀，同学们，咱们今天就来好好练练二元一次方程！这可是数学里的“小怪兽”，不过别怕，咱们有“武器”打败它！先来看第一道练习题：小明去买水果，苹果每斤 5 元，香蕉每斤 3 元，他一共买了 10 斤水果，花了 42 元，问小明买了几斤苹果，几斤香蕉？咱们设小明买了 x 斤苹果，y 斤香蕉。

那根据题目条件，可以列出两个方程：x ＋ y ＝ 10 （这表示一共买了 10 斤水果），5x ＋ 3y ＝ 42 （这是花的钱的总数）。

接下来咱们就解这个方程组。

先把第一个方程变形为 x ＝ 10 y ，然后把它代入第二个方程，就得到 5(10 y) ＋ 3y ＝ 42 。

展开括号就是 50 5y ＋ 3y ＝ 42 ，合并同类项就是 50 2y ＝ 42 ，然后移项得到－2y ＝ 42 50 ，也就是－2y ＝－8 ，最后算出 y ＝ 4 。

把 y ＝ 4 代入 x ＝ 10 y ，就能算出 x ＝ 6 。

所以小明买了 6 斤苹果，4 斤香蕉。

再来看这道题：学校组织活动，租了两种车，大巴车每辆能坐 40 人，小巴车每辆能坐 25 人，一共租了 10 辆车，坐了 315 人，问租了几辆大巴车，几辆小巴车？咱们还是设租了 x 辆大巴车，y 辆小巴车。

那方程就是 x ＋ y ＝ 10 ，40x ＋ 25y ＝ 315 。

还是用同样的方法，把第一个方程变成 x ＝ 10 y ，代入第二个方程得到 40(10 y) ＋ 25y ＝ 315 。

展开、合并、移项，一步步算下来，就能算出 x ＝ 5 ，y ＝ 5 。

我记得有一次，我在超市买东西，看到一个小朋友拿着一张纸条，上面写着一些数字和算式，一脸苦恼的样子。

我好奇地凑过去一看，原来也是在做二元一次方程的题目。

他说妈妈给他布置了作业，让他算出买几种不同价格的零食各多少才能刚好花完手里的钱。

我就给他稍微点拨了一下，看着他恍然大悟的表情，我心里可高兴了，感觉自己帮了他一个大忙。

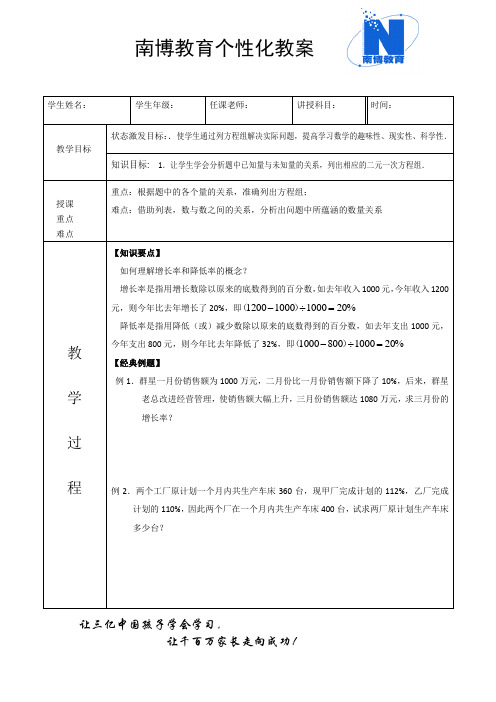
让三亿中国孩子学会学习，学生姓名： 学生年级：任课老师：讲授科目：时间：教学目标状态激发目标：．使学生通过列方程组解决实际问题，提高学习数学的趣味性、现实性、科学性．知识目标: 1．让学生学会分析题中已知量与未知量的关系，列出相应的二元一次方程组．授课 重点 难点重点：根据题中的各个量的关系，准确列出方程组；难点：借助列表，数与数之间的关系，分析出问题中所蕴涵的数量关系教 学 过 程【知识要点】如何理解增长率和降低率的概念？增长率是指用增长数除以原来的底数得到的百分数，如去年收入1000元，今年收入1200元，则今年比去年增长了20%，即%20100010001200=÷-）（降低率是指用降低（或）减少数除以原来的底数得到的百分数，如去年支出1000元，今年支出800元，则今年比去年降低了32%，即%2010008001000=÷-）（ 【经典例题】例1．群星一月份销售额为1000万元，二月份比一月份销售额下降了10%，后来，群星老总改进经营管理，使销售额大幅上升，三月份销售额达1080万元，求三月份的增长率？例2．两个工厂原计划一个月内共生产车床360台，现甲厂完成计划的112%，乙厂完成计划的110%，因此两个厂在一个月内共生产车床400台，试求两厂原计划生产车床多少台？让三亿中国孩子学会学习，例3．某公司存入银行甲、乙两种不同性质的存款共20万元，甲种存款的年利率为1.4%，乙种存款的年利率为3.7%．该公司一年共得利息6250元，求甲、乙两种存款多少万元？例4．某种产品是由A 种原料和B 种原料混 合而成的，其中A 种原料每千克50元，B 种原料每千克40元，据最新消息，这两种原料过几天都要调价，A 种原料价格上涨10%，B 种原料价格下降15%，经核算，产品的成本仍然不变，因而产品不需调价，已知这批产品共1100kg .问A 种原料和B 种原料各需多少？例5．要配制成浓度30%的烧碱溶液50千克，需要浓度为10%和60%的两种烧碱溶液各多少千克？【课堂训练场】1．永盛电子有限公司向工商银行申请了甲、乙两种贷款，共计68万元，每年要付利息8.42万元,甲种贷款每年的利率是12%，乙种贷款每年的利率是13%，求这两种贷款的数额各是多少？若设申请甲种贷款x 万元，乙种贷款y 万元，则列出的方程组应是（ ）A 、⎪⎩⎪⎨⎧=+=+42.81001131001268y x y x B 、⎪⎩⎪⎨⎧=+=+-42.8100121001368y x y x C 、⎪⎩⎪⎨⎧=+=+42.810011310011268y x y x D 、⎪⎩⎪⎨⎧=+=+42.810011210011368y x y x 2．甲、乙两绳共长17m ，如果甲绳减去51，乙绳增加1m ，两条绳子长度相等，求甲、乙的绳长，设甲绳长)(m x ，乙绳长)(m y ．可得方程组（ ）让三亿中国孩子学会学习，A 、⎪⎩⎪⎨⎧+=-=+15117y x y x B 、⎪⎩⎪⎨⎧-=+=+15117y x y x C 、⎪⎩⎪⎨⎧+=-=+15117y x x y x D 、⎪⎩⎪⎨⎧+=-=+15117y x x y x 3．用浓度为30%和15%的盐酸溶液混合配制成浓度为20%的盐酸溶液50千克，问：浓度为30%和15%盐酸溶液各需要多少千克？分别用y x ,表示浓度为30%和15%的盐酸溶液.30%的盐酸溶液 15%的盐酸溶液 混合后20%的盐酸溶液根据上表，你能通过列方程组解决这个问题吗？4．两块试验田去年产花生470kg ，改用良种后，今年产529kg ，已知其中一块田的产量比去年增长16%，第二块田的产量比去年增产10%，这两块田改用良种前每块田的产量分别为多少？今年每块田各增产多少？5．某诚市现有人口42万人，计划一年后城镇人口增加0.8%，农村人口增加1.1%，这样全市人口得增加1%，求这个城镇人口和农村人口分别是多少人?6.某单位去年男员工比女员工多80人，今年经过一次大规模的调整后，女员工增加了20%，男员工减少25%，因此女员工反而比男员工多30人。

二元一次方程组应用题1、用8块相同的长方形拼成一个宽为48厘米的大长方形，每块小长方形的长和宽分别是多少？2、一张桌子由桌面和四条脚组成，1立方米的木材可制成桌面50张或制作桌脚300条，现有5立方米的木材，问应如何分配木材，可以使桌面和桌脚配套？3、一个两位数，十位上的数字比个位上的数字大5，如果把十位上的数字与个位上的数字交换位置，那么得到的新两位数比原来的两位数的一半还少9，求这个两位数？4、某厂第二车间的人数比第一车间的人数的五分之四少30人.如果从第一车间调10人到第二车间，那么第二车间的人数就是第一车间的四分之三.问这两个车间各有多少人？5、共青团中央部门发起了“保护母亲河”行动，某校九年级两个班的115名学生积极参与，已知九一班有三分之一的学生捐了10元，九二班有五分之二的学生每人捐了十元，两班其余的学生每人捐了5元，两班的捐款总额为785元，问两班各有多少名学生?6、某班同学去18千米的北山郊游。

只有一辆汽车，需分两组，甲组先乘车、乙组步行。

车行至A处，甲组下车步行，汽车返回接乙组，最后两组同时到达北山站。

已知车速度是60千米/时，步行速度是4千米/时，求A点距北山的距离。

7、运往灾区的两批货物，第一批共480吨，用8节火车车厢和20辆汽车正好装完；第二批共运524吨，用10节火车车厢和6辆汽车正好装完，求每节火车车厢和每辆汽车平均各装多少吨？8、现要加工400个机器零件，若甲先做1天，然后两人再共做2天，则还有60个未完成；若两人齐心合作3天，则可超产20个.问甲、乙两人每天各做多少个零件？9、一船队运送一批货物，如果每艘船装50吨，还剩下25吨装不完；如果每艘船再多装5吨，还有35吨空位．求这个船队共有多少艘船，共有货物多少吨？10、某校师生到甲、乙两个工厂参加劳动，如果从甲厂抽9人到乙厂，则两厂的人数相同；如果从乙厂抽5人到甲厂，则甲厂的人数是乙厂的2倍，到两个工厂的人数各是多少？11、有一只驳船，载重量是800吨，容积是795立方米，现在装运生铁和棉花两种物资，生铁每吨的体积为0.3立方米，棉花每吨的体积为4立方米，生铁和棉花各装多少吨，才能充分利用船的载重量和容积？12、加工一批零件，甲先单独做8小时，然后又与乙一起加工5小时完成任务。

二元一次方程组的应用板块一：二元一次方程组解的讨论☞二元一次方程组解的三种情况二元一次方程组111222a xb yc a x b y c +=⎧⎨+=⎩ ⑴若1122a b a b ≠，则该方程组有唯一解 ⑵若111222a b c a b c =≠，则该方程组无解 ⑶若111222a b c a b c ==，则该方程组有无数组解 1．如果方程组有唯一的一组解，那么a ，b ，c 的值应当满足（ ）A ．a=1，c=1B ．a ≠bC ．a=b=1，c ≠1D ．a=1，c ≠1【解答】解：根据题意得：，∴1﹣x=，∴（a ﹣b ）x=c ﹣b ，∴x=， 要使方程有唯一解，则a ≠b ，故选B ．2．已知关于x ，y 的方程组，分别求出k ，b 为何值时，方程组：（1）有唯一解；（2）有无数多个解；（3）无解．【解答】解：把y=kx+b 代入y=（3k ﹣1）x+2中，可得：（2k ﹣1）x=b ﹣2，（1）当（2k ﹣1）≠0，即k ≠0.5，方程有唯一解x=，将此x 的值代入y=kx+b 中，得：y=，因而原方程组有唯一一组解； （2）当（2k ﹣1）=0且b ﹣2=0时，即k=0.5，b=2时，方程有无穷多个解，因此原方程组有无穷多组解；（3）当（2k ﹣1）=0且（b ﹣2）≠0时，即k=0.5，b ≠2时，方程无解，因此原方程组无解．板块二、二元一次方程的简单应用☞倍分问题1．（2015•广元）一副三角板按如图方式摆放，且∠1比∠2大50°．若设∠1=x°，∠2=y°，则可得到的方程组为（）A．B．C．D．【解答】解：根据平角和直角定义，得方程x+y=90；根据∠α比∠β的度数大50°，得方程x=y+50．可列方程组为．故选：D．2．（2015•泰安）小亮的妈妈用28元钱买了甲、乙两种水果，甲种水果每千克4元，乙种水果每千克6元，且乙种水果比甲种水果少买了2千克，求小亮妈妈两种水果各买了多少千克？设小亮妈妈买了甲种水果x 千克，乙种水果y千克，则可列方程组为（）A．B．C．D．【解答】解：设小亮妈妈买了甲种水果x千克，乙种水果y千克，由题意得．故选A．3．（2015•盘锦）有大小两种货车，2辆大货车与3辆小货车一次可以运货15.5吨，5辆大货车与6辆小货车一次可以运货35吨．设一辆大货车一次可以运货x吨，一辆小货车一次可以运货y吨，根据题意所列方程组正确的是（）A．B．C．D．【解答】解：设一辆大货车一次可以运货x吨，一辆小货车一次可以运货y吨，由题意得，．故选A．4．（2015•台湾）如图为甲、乙、丙三根笔直的木棍平行摆放在地面上的情形．已知乙有一部分只与甲重迭，其余部分只与丙重迭，甲没有与乙重迭的部分的长度为1公尺，丙没有与乙重迭的部分的长度为2公尺．若乙的长度最长且甲、乙的长度相差x公尺，乙、丙的长度相差y公尺，则乙的长度为多少公尺？（）A ．x+y+3B ．x+y+1C ．x+y ﹣1D ．x+y ﹣3【解答】解：设乙的长度为a 公尺，∵乙的长度最长且甲、乙的长度相差x 公尺，乙、丙的长度相差y 公尺， ∴甲的长度为：（a ﹣x ）公尺；丙的长度为：（a ﹣y ）公尺， ∴甲与乙重叠的部分长度为：（a ﹣x ﹣1）公尺；乙与丙重叠的部分长度为：（a ﹣y ﹣2）公尺，由图可知：甲与乙重叠的部分长度+乙与丙重叠的部分长度=乙的长度，∴（a ﹣x ﹣1）+（a ﹣y ﹣2）=a ，a ﹣x ﹣1+a ﹣y ﹣2=a ，a+a ﹣a=x+y+1+2，a=x+y+3，∴乙的长度为：（x+y+3）公尺，故选：A ．5. 古代有这样一个寓言故事：驴子和骡子一同走，它们驮着不同袋数的货物，每袋货物都是一样重的，驴子抱怨负担太重，骡子说：“你抱怨干嘛？如果你给我一袋，那我所负担的就是你的两倍；如果我给你一袋，我们才恰好驮得一样多！”那么驴子原来所驮货物的袋数是多少？【解答】解：设驴子原来所驮货物的袋数是x ，骡子原来所驮货物的袋数是y ． 由题意得，解得．答：驴子原来所驮货物的袋数是5．☞年龄问题1．小明问王老师的年龄时，王老师说：“我像你这么大时，你才3岁；等你到了我这么大时，我就45岁了．”设王老师今年x 岁，小明今年y 岁，根据题意，列方程组正确的是（ ）A ．B ．C ．D ．【解答】解：王老师今年x 岁，刘俊今年y 岁，可得：， 故选D☞数字问题1. 一个两位数的十位数字与个位数字的和是8，把这个两位数加上18，结果恰好成为数字对调后组成的两位数，求这个两位数．设个位数字为x ，十位数字为y ，所列方程组正确的是（ ）A 、错误!未找到引用源。

二元一次方程应用题及答案1.一位学生问老师年龄，老师回答说：“当我和你一样大时，你还没出生；当你和我一样大时，我已经37岁了。

” 问：老师和学生现在多少岁？2.设长方形的长为x，宽为y，则2(x+y)=44.y=3x+6.解得x=10，y=36.所以该长方形的长是10cm，宽是36cm。

3.设梯形上底长为x，下底长为y，则(x+y)×7/2=56，x=y/3+4.解得x=16，y=40.所以该梯形的上底长为16cm，下底长为40cm。

4.(1) 设一班有x人，二班有y人，则x+y=104，0<x<50，50<y<104，13x+11y=1240.解得x=24，y=80.所以一班有24人，二班有80人。

2) 分班购票共花费13×24+11×80=1240元，合并购票共花费9×104=936元，节省了304元。

3) 由于合并购票更便宜，所以集体购票更合算。

5.(1) 设初一年级人数为x，则45y+15=60(x+1)，45×220=y×300，解得x=90，y=6.所以初一年级有90人，原计划租用45座汽车6辆。

2) 租用9辆60座汽车，每辆车坐5人，每人租金为40元，共花费1800元，更合算。

6.设三人间租了x间，两人间租了y间，则3×25x+2×35y=1510，x+y=50.解得x=20，y=30.所以租了20间三人间，30间两人间。

7.(1) 设正门每分钟可通过x名学生，侧门每分钟可通过y 名学生，则同时开启正门和侧门时，每分钟可通过560/2=280名学生，2x+2y=280.同时开启正门和一道侧门时，每分钟可通过800/4=200名学生，x+y=200/2=100.解得x=40，y=120.所以平均每分钟一道正门和一道侧门各可通过40名和120名学生。

2) 全校学生人数不超过4×8×45=1440人，所以在5分钟内通过560名学生的门不符合安全规定。

浠水县思源实验学校七年级试题利用二元一次方程组解简单的应用题1、李明以两种形式分别储蓄了2000元和1000元，一年后全部取出，扣除利息所得税后可得利息43.92元。

已知这?20％利息金额应交利息所得税＝储蓄的年利率各是多少？（注：公民年两种储蓄的利率的和为3.24％，问这两种2、某班学生参加义务劳动，男生全部挑土，女生全部抬土，这样安排恰需筐68个，扁担40根，问这个班男生、女生各有多少人？3、甲、乙两人做加法，甲将其中一个加数后面多写了一个0，所以得和是2342，乙将同一个加数后面少写了一个0，所得和是65，求原来的两个加数。

4、甲、乙2个工人同时接受一批任务，上午工作的4小时中，甲用了2.5小时改装机器以提高工效，因此，上午工作结束时，甲比乙少做40个零件；下午2人继续工作4小时后，全天总计甲反而比乙多做420个零件，问这一天甲、乙各做多少个零件？5、去年甲、乙两车间计划共完成税利150万元，由于技术革新，生产效率大幅度提高，结果甲车间超额完成税利110％，乙车间超额完成税利120％，两车间一共上缴税利323万元，问甲、乙车间实际上缴税利多少万元？6一列快车长168米，一列慢车长184米，如果两车相向而行，那么两车错车需4秒，如果同向而行，两车错车需16秒钟，求两车的速度。

7、甲、乙两人分别以均匀的速度在周长为600米的圆形轨道上运动，甲的速度较快，当两人反向运动时，每15秒钟相遇一次；当两人同向运动时，每1分钟相遇一次，求各人的速度。

8、某牛奶加工厂现有鲜奶9吨，若在市场上直接销售鲜奶，每吨可获取利润500元；制成酸奶销售，每吨可获取利润1200元；制成奶片销售，每吨可获取利润2000元。

该工厂的生产能力是：如制成酸奶，每天可加工3吨；制成奶片，每天可加工1吨，受人员限制，两种加工方式不可同时进行。

受气温条件限制，这批牛奶必须在4天内全部销售或加工完毕。

为此，该厂设计了两种方案：方案一：尽可能多的制成奶片，其余直接销售鲜奶；方案二：将一部分制成奶片，其余制成酸奶销售，并恰好4天完成。

1、利润问题此类问题常见的等量关系是：利润=售价－进价，总利润=每件商品的利润×销售数量，利润率=利润/进价×100%。

例：某商场销售一批名牌衬衫，现在平均每天可售出20件，每件盈利40元，为了扩大销售量，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果这种衬衫的售价每降低1元，那么衬衫平均每天多售出2件，商场若要平均每天盈利1200元，每件衬衫应降价多少元？分析：假设每件衬衫应降价x元，现每件盈利为（40－x）元，现每天销售衬衫为（20＋2x）件，根据等量关系：每件衬衫的利润×销售衬衫数量=销售利润，可列出方程。

解：设每件衬衫应降价x元根据题意，得（40－x）（20＋2x）=1200解得x1=10，x2=20因尽快减少库存∴取x=20∴每件应降价20元。

答：略2、利息问题此类问题的等量关系是：利率=利息/本金，利息=本金×利率×期数，本息和=本金＋利息=本金×（1＋利率）。

例：某人将2000元人民币按一年定期存入银行，到期后支取1000元用于购物，剩下的1000元及应得利息又全部按一年定期存入银行，若存款的利率不变，到期后本金和利息共1320元，求这种存款方式的年利率（本题不计利息税）分析：假设这种存款方式的年利率为x，2000元存一年后本息和为2000（1＋x）元，支取1000元后，还剩[2000（1＋x）－1000]元，将所剩[2000（1＋x）－1000]元再存入银行一年，到期后本息共1320元，根据本息和=本金×（1＋利率）等量关系可列出方程。

解：设这种存款方式的年利率为x。

根据题意得，[2000（1＋x）－1000]（1＋x）=1320∴(1000+2000x)(1+x)=1320(1+2x)(1+x)=1.32(x+3/4)2=289/400∴x1=－1.6（舍去）， x2=0.1=10%答：略3、与几何图形的面积问题①几何图形的面积问题面积公式是此类问题的等量关系。

二元一次解方程练习题解方程是数学中的重要内容，其中二元一次方程是一种常见的形式。

本文将为您提供一些关于二元一次方程的练习题，以帮助您熟悉解这类方程的方法。

练习题1：解下列二元一次方程组：1）3x + 4y = 102x - y = 12）5x - 2y = 83x + 4y = 2练习题2：求解下列二元一次方程：1）x - y = -22x + 3y = 72）2x + 3y = 14x - y = 11练习题3：请解下列二元一次方程组：1）2x + 5y = 13x - y = 42）4x - y = -3x + 2y = 5练习题4：解下列二元一次方程：1）3x + 2y = 82x - y = 12）4x + 5y = 143x - 2y = -5在解决这些练习题时，我们可以使用不同的方法，如代入法、消元法或图解法。

下面逐一解答这些题目，供您参考。

练习题1：1）首先，我们可以通过消元法解决这个方程组。

将两个方程相加，消去y的系数，得到5x = 11。

然后，将此结果代入第一个方程，解得x = 11/5。

将x的值代入任一方程，求得y的值为3/5。

因此，方程的解为x = 11/5，y = 3/5。

2）对于第二个方程组，我们可以使用代入法。

将第一个方程中的x 表示为y的函数，并代入第二个方程中，最终解得x = 2，y = -3。

因此，方程的解为x = 2，y = -3。

练习题2：1）对于第一个方程组，我们可以使用消元法。

将第一个方程的2倍加到第二个方程上，得到4x + 6y = 14。

然后，将此结果代入第一个方程，解得x = 5，将x的值代入任一方程，求得y的值为-3。

因此，方程的解为x = 5，y = -3。

2）针对第二个方程组，我们可以使用代入法。

将第一个方程中的x 表示为y的函数，并代入第二个方程中，得到2y + 3y = 1。

化简后，解得y = 1/5，将y的值代入任一方程，求得x的值为51/5。

二元一次方程计算题经典题型二元一次方程是初中阶段数学学习中的一个重要内容，掌握二元一次方程的解题方法有助于培养学生的逻辑思维能力和解决问题的能力。

下面将通过几个经典题型来介绍二元一次方程的计算方法。

题型一：解二元一次方程组给定方程组：$$ \\begin{cases} 2x + y = 5 \\\\ x - 3y = -7 \\end{cases} $$求方程组的解。

解析：首先我们可以通过消元法或代入法解方程组。

通过消元法将第二个方程乘以2，得到2x−6y=−14，然后将第一个方程与这个方程相加消去x项，得到−5y=−9，解得$y = \\frac{9}{5}$，将y的值代入第一个方程，可以得到x的值为1。

因此，方程组的解为x=1，$y=\\frac{9}{5}$。

题型二：应用题某商店销售苹果和橙子，已知苹果每斤售价为3元，橙子每斤售价为2元，现共售出50斤，收入为130元。

设苹果销售量为x斤，橙子销售量为y斤，则可以建立如下方程组：$$ \\begin{cases} 3x + 2y = 130 \\\\ x + y = 50 \\end{cases} $$求苹果和橙子的销售量各是多少？解析：同样可以通过消元法或代入法来解决此题。

通过消元法将第二个方程改写为y=50−x，代入第一个方程中得到3x+2(50−x)=130，解得x=20，再将x的值代入y=50−x，可以得到y=30。

因此，苹果的销售量为20斤，橙子的销售量为30斤。

题型三：图形解题已知二元一次方程x+y+1=0，表示一条直线AB，A(1,−2)和B(−1,0)是直线上的两点，求这条直线的方程。

解析：首先通过已知两个点的坐标可以确定直线的斜率。

直线的斜率k可以表示为$\\frac{y_2 - y_1}{x_2 - x_1}$，代入A(1,−2)和B(−1,0)的坐标得到$k =\\frac{0 - (-2)}{(-1) - 1} = 1$。