物理化学(天津大学第四版)课后答案 第六章 相平衡
- 格式:pdf
- 大小:273.82 KB
- 文档页数:13

第一章第一章第一章第一章气体的气体的气体的气体的pVTpVTpVTpVT性质性质性质性质1.1物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
解:根据理想气体方程1.5两个容积均为V的玻璃球泡之间用细管连结,泡内密封着标准状态下的空气。
若将其中的一个球加热到100°C,另一个球则维持0°C,忽略连接细管中气体体积,试求该容器内空气的压力。
解:由题给条件知,(1)系统物质总量恒定;(2)两球中压力维持相同。
标准状态:因此,1.9如图所示,一带隔板的容器内,两侧分别有同温同压的氢气与氮气,二者均可视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽取前后,H2及N2的摩尔体积是否相同?(3)隔板抽取后,混合气体中H2及N2的分压立之比以及它们的分体积各为若干?解:(1)等温混合后即在上述条件下混合,系统的压力认为。
(2)混合气体中某组分的摩尔体积怎样定义?(3)根据分体积的定义对于分压1.11室温下一高压釜内有常压的空气,为进行实验时确保安全,采用同样温度的纯氮进行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解:分析:每次通氮气后至排气恢复至常压p,混合气体的摩尔分数不变。
设第一次充氮气前,系统中氧的摩尔分数为,充氮气后,系统中氧的摩尔分数为,则,。
重复上面的过程,第n次充氮气后,系统的摩尔分数为,因此。
1.13今有0°C,40.530kPa的N2气体,分别用理想气体状态方程及vanderWaals方程计算其摩尔体积。
实验值为。
解:用理想气体状态方程计算用vanderWaals计算,查表得知,对于N2气(附录七),用MatLabfzero函数求得该方程的解为也可以用直接迭代法,,取初值,迭代十次结果1.1625°C时饱和了水蒸气的湿乙炔气体(即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压)总压力为138.7kPa,于恒定总压下冷却到10°C,使部分水蒸气凝结为水。


物理化学天津大学第四版答案【篇一:5.天津大学《物理化学》第四版_习题及解答】ass=txt>目录第一章气体的pvt性质 ....................................................................................................... (2)第二章热力学第一定律 ....................................................................................................... . (6)第三章热力学第二定律 ....................................................................................................... .. (24)第四章多组分系统热力学 ....................................................................................................... . (51)第五章化学平衡 ....................................................................................................... .. (66)第六章相平衡 ....................................................................................................... (76)第七章电化学 ....................................................................................................... (85)第八章量子力学基础 ....................................................................................................... . (107)第九章统计热力学初步 ....................................................................................................... ...... 111 第十一章化学动力学 ....................................................................................................... . (117)第一章气体的pvt性质1.1 物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
第一章气体的pVT性质1.1物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
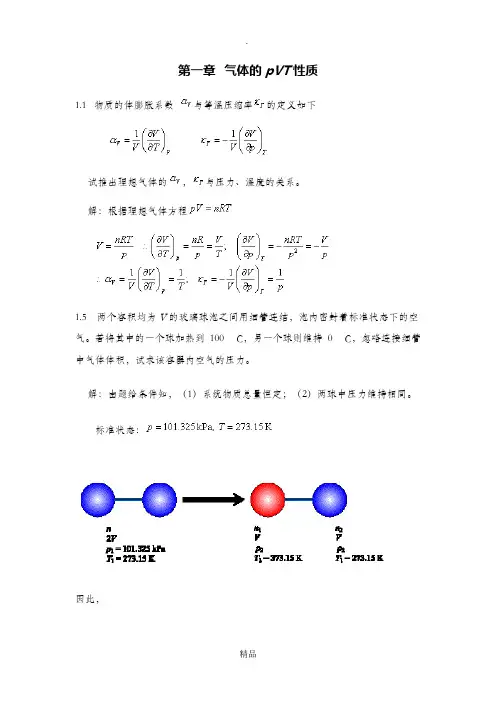
解:根据理想气体方程1.5两个容积均为V的玻璃球泡之间用细管连结,泡内密封着标准状态下的空气。
若将其中的一个球加热到100 C,另一个球则维持0 C,忽略连接细管中气体体积,试求该容器内空气的压力。
解:由题给条件知,(1)系统物质总量恒定;(2)两球中压力维持相同。
标准状态:因此,1.9 如图所示,一带隔板的容器内,两侧分别有同温同压的氢气与氮气,二者均可视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽取前后,H2及N2的摩尔体积是否相同?(3)隔板抽取后,混合气体中H2及N2的分压立之比以及它们的分体积各为若干?解:(1)等温混合后即在上述条件下混合,系统的压力认为。
(2)混合气体中某组分的摩尔体积怎样定义?(3)根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气,为进行实验时确保安全,采用同样温度的纯氮进行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解:分析:每次通氮气后至排气恢复至常压p,混合气体的摩尔分数不变。
设第一次充氮气前,系统中氧的摩尔分数为,充氮气后,系统中氧的摩尔分数为,则,。
重复上面的过程,第n次充氮气后,系统的摩尔分数为,因此。
1.13 今有0 C,40.530 kPa的N2气体,分别用理想气体状态方程及van der Waals 方程计算其摩尔体积。
实验值为。
解:用理想气体状态方程计算用van der Waals计算,查表得知,对于N2气(附录七),用MatLab fzero函数求得该方程的解为也可以用直接迭代法,,取初值,迭代十次结果1.16 25 C时饱和了水蒸气的湿乙炔气体(即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压)总压力为138.7 kPa,于恒定总压下冷却到10 C,使部分水蒸气凝结为水。

第一章气体的pVT性质1.1物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
解:根据理想气体方程1.5两个容积均为V的玻璃球泡之间用细管连结,泡内密封着标准状态下的空气。
若将其中的一个球加热到100 C,另一个球则维持0 C,忽略连接细管中气体体积,试求该容器内空气的压力。
解:由题给条件知,(1)系统物质总量恒定;(2)两球中压力维持相同。
标准状态:因此,1.9 如图所示,一带隔板的容器内,两侧分别有同温同压的氢气与氮气,二者均可视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽取前后,H2及N2的摩尔体积是否相同?(3)隔板抽取后,混合气体中H2及N2的分压立之比以及它们的分体积各为若干?解:(1)等温混合后即在上述条件下混合,系统的压力认为。
(2)混合气体中某组分的摩尔体积怎样定义?(3)根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气,为进行实验时确保安全,采用同样温度的纯氮进行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解:分析:每次通氮气后至排气恢复至常压p,混合气体的摩尔分数不变。
设第一次充氮气前,系统中氧的摩尔分数为,充氮气后,系统中氧的摩尔分数为,则,。
重复上面的过程,第n次充氮气后,系统的摩尔分数为,因此。
1.13 今有0 C,40.530 kPa的N2气体,分别用理想气体状态方程及van der Waals 方程计算其摩尔体积。
实验值为。
解:用理想气体状态方程计算用van der Waals计算,查表得知,对于N2气(附录七),用MatLab fzero函数求得该方程的解为也可以用直接迭代法,,取初值,迭代十次结果1.16 25 C时饱和了水蒸气的湿乙炔气体(即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压)总压力为138.7 kPa,于恒定总压下冷却到10 C,使部分水蒸气凝结为水。

第六章相平衡思考题解答1、答:可能平衡。
相平衡的条件是任一组分在各相的化学势相等。
2、答:不等于零,约为水的饱和蒸气压。
3、答:不变,因为根据相律有:F=C-P+2=1,即蒸气压只是温度的函数。
4、答:是两相,因为二者的物理性质不同。
5、答:是两相,因为从微观的角度来看,粒子之间仍存在界面。
6、答:是一相,因为形成了固溶体(合金)。
7、答:都等于1。
因为C=S-R-R’=3-1-1=1。
8、答:在冰点的自由度不为零。
对于单组分体系C=1,F+P=3,冰点时P=2,故F=1。
9、答:有液体。
根据其相图可知液态存在的条件是T:216.6~304.3K;P:5.11~73pθ。
10、答:是的,此时是三相平衡。
习题解答1. 解:① C=5,P=4,F=3 ② C=5,P=2,F=5 ③ C=2,P=1,F=2 ④ C=2,P=2,F=2 ⑤ C=3,P=2,F=3 2. 解:因甲苯和苯形成理想液态混合物,故两者蒸气分压均可以用拉乌尔定律进行计算。
(1)原来系统为液态,当开始出现气相时,其量极少,可以认为液相组成不变,此时系统的压力p :B A p p p +=B B A A x p x p p ∗∗+=,而1=+B A x x ,联解、整理可得)1(A B A A x p x p p −+=∗∗设甲苯为A ,苯为B ,则459.0)114.78(0.200)078.92(0.200)078.92(0.200)()(111=⋅+⋅⋅=+=−−−mol g g mol g g mol g g M m M m M m x B B A AA A A所以,p=54.22kP a×0.459+136.12kP a×(1-0.459)=98.53kPa 又253.053.98/459.022.54//=×===∗kPa kPa p x p p p y A A A A 故747.0253.011=−=−=A B y y(2)压力降低,液体不断气化,当压力降至某一数值时,则系统内产生极小的一液滴,此时气相组成与未气化前的液体组成相同,即y A =0.459。


第二章 热力学第一定律2.1 1mol 理想气体在恒定压力下温度升高1℃,求过程中系统与环境交换的功。
解:理想气体n = 1mol对于理想气体恒压过程,应用式(2.2.3)W =-p amb ΔV =-p(V 2-V 1) =-(nRT 2-nRT 1) =-8.314J2.2 1mol 水蒸气(H 2O,g)在100℃,101.325kPa 下全部凝结成液态水。
求过程的功。
假设:相对于水蒸气的体积,液态水的体积可以忽略不计。
解: n = 1mol恒温恒压相变过程,水蒸气可看作理想气体, 应用式(2.2.3)W =-p amb ΔV =-p(V l -V g ) ≈ pVg = nRT = 3.102kJ2.3 在25℃及恒定压力下,电解1mol 水(H 2O,l),求过程的体积功。
H 2O(l) = H 2(g) + 1/2O 2(g) 解: n = 1mol恒温恒压化学变化过程, 应用式(2.2.3)W=-p amb ΔV =-(p 2V 2-p 1V 1)≈-p 2V 2 =-n 2RT=-3.718kJ2.4 系统由相同的始态经过不同途径达到相同的末态。
若途径a 的Q a =2.078kJ,Wa=-4.157kJ ;而途径b 的Q b =-0.692kJ 。
求W b .解: 热力学能变只与始末态有关,与具体途径无关,故 ΔU a = ΔU b由热力学第一定律可得 Qa + Wa = Q b + W b ∴ W b = Q a + W a -Q b = -1.387kJ2.5 始态为25℃,200 kPa 的5 mol 某理想气体,经途径a ,b 两不同途径到达相同的末态。
途经a 先经绝热膨胀到 -28.47℃,100 kPa ,步骤的功;再恒容加热到压力200 kPa 的末态,步骤的热。
途径b 为恒压加热过程。
求途径b 的及。
解:先确定系统的始、末态3111061902000001529831485m ...P nRT V =××==32101601000005824431485m ...P nRT V V =××=== kJ .kJ )..(Q W U Δa a 85194225575=+=+=-对于途径b ,其功为kJ .J ..V Δp W b 932706190101602000001-)-(--===根据热力学第一定律2.6 4mol 某理想气体,温度升高20℃, 求ΔH -ΔU 的值。


第六章相平衡6.1指出下列平衡系统中的组分数C,相数P及自由度F。
(1)I2(s)与其蒸气成平衡;(2)CaCO3(s)与其分解产物CaO(s)和CO2(g)成平衡;(3)NH4HS(s)放入一抽空的容器中,并与其分解产物NH3(g)和H2S(g)成平衡;(4)取任意量的NH3(g)和H2S(g)与NH4HS(s)成平衡。
(5)I2作为溶质在两不互溶液体H2O和CCl4中达到分配平衡(凝聚系统)。
解:(1)C = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1.(2)C = 3 – 1 = 2, P = 3, F = C–P + 2 = 2 – 3 + 2 = 1.(3)C = 3 – 1 – 1 = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1.(4)C = 3 – 1 = 2, P = 2, F = C–P + 2 = 2 – 2 + 2 = 2.(5)C = 3, P = 2, F = C–P + 1 = 3 – 2 + 1 = 2.6.2已知液体甲苯(A)和液体苯(B)在90 C时的饱和蒸气压分别为=和。
两者可形成理想液态混合物。
今有系统组成为的甲苯-苯混合物5 mol,在90 C下成气-液两相平衡,若气相组成为求:(1)平衡时液相组成及系统的压力p。
(2)平衡时气、液两相的物质的量解:(1)对于理想液态混合物,每个组分服从Raoult定律,因此(2)系统代表点,根据杠杆原理6.3单组分系统的相图示意如右图。
试用相律分析途中各点、线、面的相平衡关系及自由度。
解:单相区已标于图上。
二相线(F = 1):三相点(F = 0):图中虚线表示介稳态。
6.4已知甲苯、苯在90 ︒C下纯液体的饱和蒸气压分别为54.22 kPa和136.12 kPa。
两者可形成理想液态混合物。
取200.0 g甲苯和200.0 g苯置于带活塞的导热容器中,始态为一定压力下90 ︒C的液态混合物。

第六章相平衡思考题解答1、答:可能平衡。
相平衡的条件是任一组分在各相的化学势相等。
2、答:不等于零,约为水的饱和蒸气压。
3、答:不变,因为根据相律有:F=C-P+2=1,即蒸气压只是温度的函数。
4、答:是两相,因为二者的物理性质不同。
5、答:是两相,因为从微观的角度来看,粒子之间仍存在界面。
6、答:是一相,因为形成了固溶体(合金)。
7、答:都等于1。
因为C=S-R-R’=3-1-1=1。
8、答:在冰点的自由度不为零。
对于单组分体系C=1,F+P=3,冰点时P=2,故F=1。
9、答:有液体。
根据其相图可知液态存在的条件是T:216.6~304.3K;P:5.11~73pθ。
10、答:是的,此时是三相平衡。
习题解答1. 解:① C=5,P=4,F=3 ② C=5,P=2,F=5 ③ C=2,P=1,F=2 ④ C=2,P=2,F=2 ⑤ C=3,P=2,F=3 2. 解:因甲苯和苯形成理想液态混合物,故两者蒸气分压均可以用拉乌尔定律进行计算。
(1)原来系统为液态,当开始出现气相时,其量极少,可以认为液相组成不变,此时系统的压力p :B A p p p +=B B A A x p x p p ∗∗+=,而1=+B A x x ,联解、整理可得)1(A B A A x p x p p −+=∗∗设甲苯为A ,苯为B ,则459.0)114.78(0.200)078.92(0.200)078.92(0.200)()(111=⋅+⋅⋅=+=−−−mol g g mol g g mol g g M m M m M m x B B A AA A A所以,p=54.22kP a×0.459+136.12kP a×(1-0.459)=98.53kPa 又253.053.98/459.022.54//=×===∗kPa kPa p x p p p y A A A A 故747.0253.011=−=−=A B y y(2)压力降低,液体不断气化,当压力降至某一数值时,则系统内产生极小的一液滴,此时气相组成与未气化前的液体组成相同,即y A =0.459。
第六章相平衡6.1指出下列平衡系统中的组分数C,相数P及自由度F。
(1)I2(s)与其蒸气成平衡;(2)CaCO3(s)与其分解产物CaO(s)和CO2(g)成平衡;(3)NH4HS(s)放入一抽空的容器中,并与其分解产物NH3(g)和H2S(g)成平衡;(4)取任意量的NH3(g)和H2S(g)与NH4HS(s)成平衡。
(5)I2作为溶质在两不互溶液体H2O和CCl4中达到分配平衡(凝聚系统)。
解:(1)C = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1.(2)C = 3 – 1 = 2, P = 3, F = C–P + 2 = 2 – 3 + 2 = 1.(3)C = 3 – 1 – 1 = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1.(4)C = 3 – 1 = 2, P = 2, F = C–P + 2 = 2 – 2 + 2 = 2.(5)C = 3, P = 2, F = C–P + 1 = 3 – 2 + 1 = 2.6.2 常见的Na2CO3(s)水合物有Na2CO3∙H2O(s),Na2CO3∙7H2O(s)和Na2CO3∙10H2O(s).(1)101.325kPa下,与Na2CO3水溶液及冰平衡共存的水合物最多能有几种?(2)20℃时,与水蒸气平衡的水合物最多可能有几种?解:(1)C = S – R - R' = 2 – 0 – 0 =2F = C–P + 1 =2 –P + 1= 3 – P ≥0,即P-2≤1,那么能与Na2CO3水溶液及冰平衡共存的水合物最多只有一种。
(2)C = S – R - R' = 2 – 0 – 0 =2F = C–P + 1 =2 –P + 1= 3 – P ≥0,即P-1≤2,那么与水蒸气平衡的水合物最多可能有两种。
6.4 单组分系统碳的想吐(示意图)如附图所示。
第六章 相平衡6.1 指出下列平衡系统中的组分数C ,相数P 及自由度数F 。
(1) I 2(s)与其蒸气成平衡;(2) MgCO 3(s)与其分解产物MgO(s)和CO 2(g)成平衡;(3) NH 4Cl(s)放入一抽空的容器中,与其分解产物NH 3(g)和HCl (g) 成平衡; (4) 取任意量的NH 3(g)和H 2S (g)与NH 4HS(g)成平衡;(5) 过量的NH 4HCO 3(s)与其分解产物NH 3(g),H 2O(g)和CO 2(g) 成平衡; (6) I 2作为溶质在两不互溶液体H 2O 和CCl 4中达到分配平衡(凝聚系统)。
解:(1)C =1,P =2,21F C P =-+=;(2)C =2,P =3,21F C P =-+=; (3)C =1,P =2,21F C P =-+=; (4)C =2,P =2,22F C P =-+=; (5)C =1,P =2,21F C P =-+=; (6)C =3,P =2,12F C P =-+=。
6.2常见的Na 2CO 3(s)水合物有Na 2CO 3•H 2O (s),Na 2CO 3•7H 2O(s)和 Na 2CO 3•10H 2O (s) (1)101.325kPa 下,与Na 2CO 3水溶液及冰平衡共存的水合物最多能有几种? (2)20℃时,与水蒸气平衡共存的水合物最多能可能有几种?解: S =5,R =3,R '=0,C =S -R -R '=2,F =C -P +1=3-P ,F mix =0,P max =3; (1)已有两相(水溶液、冰),只能有一种水合物与其共存; (2)已有一相(水蒸气),有二种水合物与其共存。
6.3已知液体甲苯(A)和液体苯(B)在90℃时的饱和蒸气压为:*A p =54.22kPa 和*B p = 136.12kPa 。
两者可以形成理想溶液。
今有系统组成为B,00.3x =的甲苯-苯混合物5 mol ,在90 ℃下形成气-液两相平衡,若气相组成为B 0.4556y =,求: (1)平衡时液相组成B x 及系统的压力p ; (2)平衡时气、液两相的物质的量n (g),n (l )。
天津大学《物理化学》第四版习题及解答目录第一章气体的pVT性质 (2)第二章热力学第一定律 (6)第三章热力学第二定律 (24)第四章多组分系统热力学 (52)第五章化学平衡 (67)第六章相平衡 (78)第七章电化学 (87)第八章量子力学基础 (110)第九章统计热力学初步 (113)第十一章化学动力学 (120)第一章气体的pVT性质1.1 物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
解:根据理想气体方程1.5 两个容积均为V的玻璃球泡之间用细管连结,泡内密封着标准状态下的空气。
若将其中的一个球加热到100 °C,另一个球则维持0 °C,忽略连接细管中气体体积,试求该容器内空气的压力。
解:由题给条件知,(1)系统物质总量恒定;(2)两球中压力维持相同。
标准状态:因此,1.9 如图所示,一带隔板的容器内,两侧分别有同温同压的氢气与氮气,二者均可视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽取前后,H2及N2的摩尔体积是否相同?(3)隔板抽取后,混合气体中H2及N2的分压立之比以及它们的分体积各为若干?解:(1)等温混合后即在上述条件下混合,系统的压力认为。
(2)混合气体中某组分的摩尔体积怎样定义?(3)根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气,为进行实验时确保安全,采用同样温度的纯氮进行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解:分析:每次通氮气后至排气恢复至常压p,混合气体的摩尔分数不变。
设第一次充氮气前,系统中氧的摩尔分数为,充氮气后,系统中氧的摩尔分数为,则,。
重复上面的过程,第n次充氮气后,系统的摩尔分数为,因此。
1.13 今有0 °C,40.530 kPa的N2气体,分别用理想气体状态方程及van der Waals方程计算其摩尔体积。
第六章相平衡6、1指出下列平衡系统中得组分数C,相数P及自由度F。
(1)I2(s)与其蒸气成平衡;(2)CaCO3(s)与其分解产物CaO(s)与CO2(g)成平衡;(3)NH4HS(s)放入一抽空得容器中,并与其分解产物NH3(g)与H2S(g)成平衡;(4)取任意量得NH3(g)与H2S(g)与NH4HS(s)成平衡。
(5)I2作为溶质在两不互溶液体H2O与CCl4中达到分配平衡(凝聚系统)。
解:(1)C = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1、(2)C = 3 – 1 = 2, P = 3, F = C–P + 2 = 2 – 3 + 2 = 1、(3)C = 3 – 1 – 1 = 1, P = 2, F = C–P + 2 = 1 –2 + 2 = 1、(4)C = 3 – 1 = 2, P = 2, F = C–P + 2 = 2 – 2 + 2 = 2、(5)C = 3, P = 2, F = C–P + 1 = 3 – 2 + 1 = 2、6、2 常见得Na2CO3(s)水合物有Na2CO3∙H2O(s),Na2CO3∙7H2O(s)与Na2CO3∙10H2O(s)、(1)101、325kPa下,与Na2CO3水溶液及冰平衡共存得水合物最多能有几种?(2)20℃时,与水蒸气平衡得水合物最多可能有几种?解:(1)C = S – R R' = 2 – 0 – 0 =2F = C–P + 1 =2 –P + 1= 3 – P ≥0, 即P2≤1,那么能与Na2CO3水溶液及冰平衡共存得水合物最多只有一种。
(2)C = S – R R' = 2 – 0 – 0 =2F = C–P + 1 =2 –P + 1= 3 – P ≥0,即P1≤2,那么与水蒸气平衡得水合物最多可能有两种。
6、4 单组分系统碳得想吐(示意图)如附图所示。
(1)分析图中各点、线、面得相平衡关系及自由度数;(2)25℃,101、325kPa下,碳以什么状态稳定存在?(3)增加压力可以使石墨转换为金刚石。