信号与系统第3章作业解答

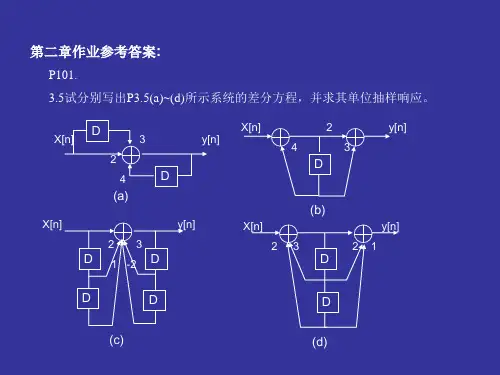
fltnzlults因为是bniif.c EJ.siunwndttjErsincnwtsdt品奇这是咋求的求锯⻮信号ftkocnejnmtcniiffme则⼴哻f则fits品蕊ei哔世这是利⽤指数表示求三⻆函数形式下的⽐⼆ffctldt.FI ff aniiffmcoscnwtgdtiifl ttEjcoscnwtydttf奇㷒依然为奇则为0⼆if Ewscnwtdt2元ㄨ103kHz 6.128X 2X106t1间隔ME巺⼆㗟s不4112X1066.28106带亮13乺烈烈6nfzxi14三次诮波11批t 10⽐红__2.12Et E 4i 1lCniÈffme atdtfcne atdttffze.at dt其中ain⼆弦表ǏF试⻦扣与fun的傅⽴叶变换Fifn Filmfit Alum ut沙井控ult.int坷同样将fun表示⼀下⼆是cult ultt t Al ul ti Ultt则Fl funk Ftw ejwto詏们对于la 来说原因为三⻆以及余弦之积inn则n 01wtionjtoiw zuScilE 2对于⼼来说原⼆Sin 5元右侧的相当于则Sachi ii nl ócw 5元-01W 5到vivre怎么看出来的ht利⽤时域积分把原函看成积分原⽐⽐出⼀吐动deno 个吢砟⼼ólug201W e iwi nameÍjmjw⼆⽆以costing tisinihgznwilosciugtisin int器nomaunt jw求的傅⾥叶变换利⽤傅⾥叶变换的定义式求FlwkfofneiTltftltgeiwtdt.ttcu.int Fxi Eij w W2t恐器加⼀兜圜篮圝噬部⼆品ceiwte Mtice2N.ie可以应leine全部转化为⼼sin之形成三吉xzcoswth.zwszwtfw.zsinz.ru为了求得⽴叶级则要利⽤原tniiFocwilninw.F4从⽽cnet.to cnn.in代⼊上式中则代⼊到了覃⽴叶级数的公式中funÍcneimt⼀H求⼼的傅⾥叶交换则Rcntawhn HIM⼆舙⽅站1jhntl 然后求输⼊信号的得主叶交换在⼀个周期内P fltsejwtdt in哭⼏⼆T T teiwtdtiwlteiwt jeiwtsiEijiMn D 求fun的傅⽴叶级数90i hits dtf.li灬i1第⼀次分布积分⼜弄错了duty卡twsnwitdt ijtwscnw ndt lnwdwscnwnliw.co scnwtsi ǜǐ⼆声n.dz cost 哔_sinc 哔⼆前211叮n华⼆则no 时IAN则An 有加上n 为偶iq ⼥终900则⼈品㹷n 为奇彘流iiwiwiwj.ws对fun 进⾏傉⽴叶交他fun为奇函数外an sc.no求dni ǐǕsincnwmdt.lu 笇d n ⾔Ǖs in2巺七d t ⾔ǜ则所求即为flat fun 不⽤合求iii nt1111111iinnnniiii。

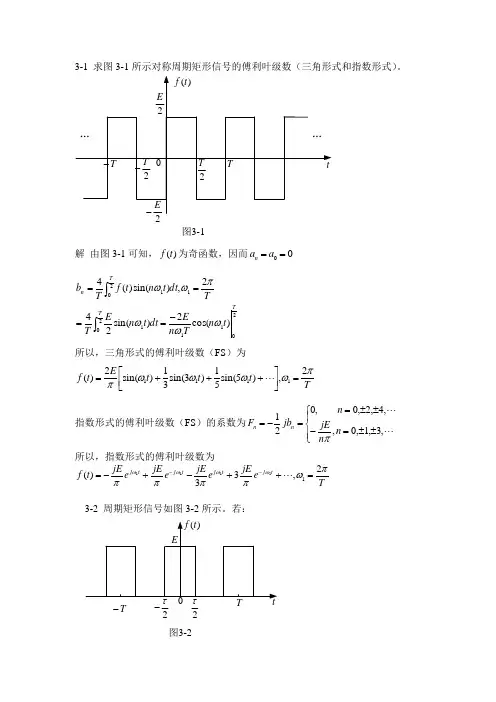
3-1 求图3-1所示对称周期矩形信号的傅利叶级数（三角形式和指数形式）。

图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数（FS ）为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数（FS ）的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。

若：图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。

解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数（FS ）的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数（FS ）为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3）)(1t f 与)(2t f 的基波幅度之比； （4）)(1t f 基波与)(2t f 三次谐波幅度之比。

.第三章作业解答3.1解：420ππω==T ， j a a 4*33-==- 则：t j t j t j t j k tjk ke a e a e a e a ea t x 00000333311)(ωωωωω----∞-∞=+++==∑-)243cos(84cos 443sin 84cos 4)](21[8)(2144422434344434344πππππππππππππ++=-=--⨯++⨯=-++=------t t tt e e je e jejeeet j t j t j t j t jt jt j t j3.3解：)35sin(4)32cos(2)(t t t x ππ++= 则3)32cos(1=→T t π 56)35s i n (2=→T t π故：6],[21==T T lcm T 320ππω==T )(214)(21235353232t j t j t j t j e e je e ππππ---⨯+++=则：20=a 2122==-a a 25j a -= 25j a =- 3.9x[n]波形如下图所示：0 1 4 5 n…- 4 -3则：N=4，220ππω==N ]84[41]}1[8][4{41][41][122302300πππωδδjk n jk n n jk n n jk N n k e e n n e n x e n x N a --=-=->=<+=-+===∑∑∑即：2112133210j a a j a a +=-=-==3.15解：6π=T ，1220==Tπω )(ωj H 如下图所示：则：⎩⎨⎧>≤=9||08||1)(0k k jk H ωtjk k kea t x 0)(ω∑∞-∞==tjk k ktjk k k ea ea jk H t y 00880)()(ωωω∑∑-=∞-∞===而：)()(t y t x =，即：t jk k k tjk k k e a t y ea t x 0088)()(ωω∑∑-=∞-∞====故：当9||≥k 时，0=k a3.22解：（a ）2=T ，ππω==T20 ]|[12121)(11111110dt e te jk dt te dt e t x T a tjk t jk t jk T t jk k ⎰⎰⎰---------===πππωπkjk t jk t jk k j k j k k je k j e jk te k j )1(k ]02[21]|1|[211111-=⎪⎪⎩⎪⎪⎨⎧-=--=---=-----πππππππππ为奇数为偶数021110==⎰-dt t a(注意：与性质验证，由于x(t)是实奇函数，则a k 为纯虚的奇函数，满足： *k k k a a a -=-=- 且：00=a ） (d) 2=T ，ππω==T20 ])1(21[21]21[21)]1(2)([21)(1200k jk t jk T tjk k e dt e t t dt e t x T a --=-=--==---⎰⎰--ππωδδ21)]1(2)([21200-=--=⎰--dt t t a δδ3.28（b ）解：)(21)(21)2cos()32sin(][223232nj n j n jnje e eejn n n x ππππππ--++== )(416/76/6/6/7n j n j n j n j e e e e j ππππ----+=12/2.712/2.12/2.12/2..7(41ππππn j jn jn n j e e e e j----+=⎪⎪⎪⎩⎪⎪⎪⎨⎧++=-++==othersrN rN k j rN rN k j a k 05,11417,141 则：⎪⎩⎪⎨⎧++++==othersrN rN rN rN k a k 05,11,7,141||⎪⎪⎪⎩⎪⎪⎪⎨⎧++=++=-=∠othersrN rN k rN rN k a k 05,1127,12ππ 3.34解：(b)∑∞-∞=--=n nn t t x )()1()(δ其波形如下图所示：其周期T=2，基波频率为：ππω==T20 ⎩⎨⎧=--=-=--==---⎰⎰--是偶数是奇数k 01])1(1[21]1[21)]1()([21)(1200k e dt e t t dt e t x T a k jk t jk T tjk k ππωδδ而：⎪⎩⎪⎨⎧<>==--00)(44||4t et e et h t tt则：240401684141)()(s s s dte e dt e e dt e t h s H st t st t st -=++-=+==--∞-∞--∞∞-⎰⎰⎰故：2)(168)(ππjk jk H -=故：⎪⎩⎪⎨⎧-==∑∞-∞=为偶数为奇数（k k e jk ea jk H t y tjk tjk k k 0)168)()(200πωπω3.357π=T ，1420==Tπω 解：)(ωj H 如下图所示：则：⎩⎨⎧<>=17||017||1)(0k k jk H ωtjk k kea t x 0)(ω∑∞-∞==tjk k k tjk k k ea ea jk H t y 0018||0)()(ωωω∑∑∞=∞-∞===而：)()(t y t x =，即：tjk k ktjk k kea t y ea t x 0018||)()(ωω∑∑∞=∞-∞====故：当18||<k 时，0=k a3.44解：（1）*k k a a =- （2）6=T ，320ππω==T （3）⎩⎨⎧===其他，不为02||1||0k k a k（4）k jk k k a e b t x a t x π--=→--→)3()(k jk k a ea π--= 则：当为偶数k a k 0=结合（3）则：⎩⎨⎧==其他不为01||0k a k（5）帕斯瓦尔关系式：21||21||||12121=⇒=+-a a a （6）211=a 211=-a 则t e e ea e a t x t j t j t j tj 3cos )(21)(333131πππππ=+=+=--- 故：03,1===C B A π。

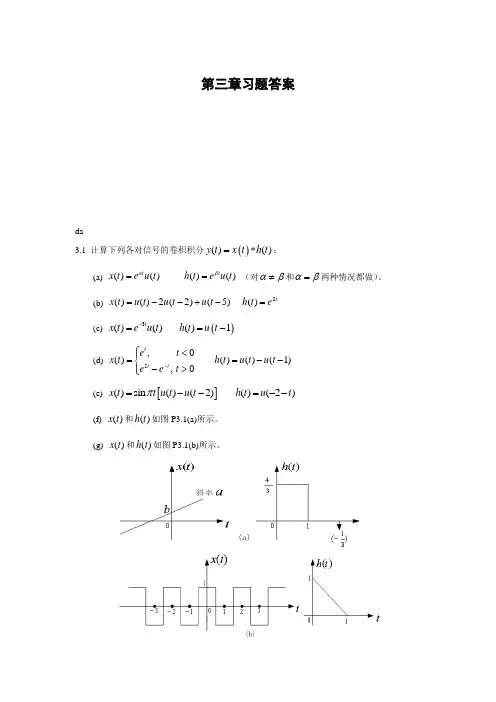
第三章习题答案da3.1 计算下列各对信号的卷积积分()()()y t x t h t =*：(a) ()()()()t tx t e u t h t e u t αβ==（对αβ≠和αβ=两种情况都做）。

(b) 2()()2(2)(5)()tx t u t u t u t h t e =--+-=(c) ()3()()()1tx t eu t h t u t -==-(d) 5,0()()()(1),0tt t e t x t h t u t u t e e t -⎧<⎪==--⎨->⎪⎩(e) []()sin ()(2)()(2)x t t u t u t h t u t π=--=--(f) ()x t 和()h t 如图P3.1(a)所示。

(g) ()x t 和()h t 如图P3.1(b)所示。

图P3.1 解：(a) ()()0()()()(0)t ttty t x t h t eed eed t βτατβαβτττ------=*==>⎰⎰当αβ≠时，()1()()ttey t e u t αβββα----=-当αβ=时，()()t y t te u t α-=(b) 由图PS3.1(a)知， 当1t ≤时，252()2()22(2)2(5)021()22t t t t t y t ed ed e e e ττττ----⎡⎤=-=-+⎣⎦⎰⎰ 当13t ≤≤时，252()2()22(2)2(5)121()22t t t t t y t ed ed e e e ττττ-----⎡⎤=-=-+⎣⎦⎰⎰ 当36t ≤≤时，52()2(5)211()2t t t y t ed e e ττ---⎡⎤=-=-⎣⎦⎰ 当6t >时，()0y t =(c) 由图PS3.1(b)知，当1t ≤时，()0y t = 当1t >时，133(1)01()13t t y t ed e ττ----⎡⎤==-⎣⎦⎰3(1)1()1(1)3t y t e u t --⎡⎤∴=--⎣⎦(d) 由图PS3.1(d)知： 当0t ≤时，11()tt t t y t e d e eττ--==-⎰当01t <≤时，055(1)1014()(2)255t ttt t y t e d e e d e eeτττττ-----=+-=+--⎰⎰当1t >时，555(1)(1)111()(2)2255t tt tt t y t e ed eeeeτττ------=-=-+-⎰(e) 如下图所示：(f) 令()11()(2)3h t h t t δ⎡⎤=+--⎢⎥⎣⎦，则11()()()(2)3y t x t h t x t =*-- 由图PS3.1(h)知，11424()()()()(21)333t t y t x t h t a b d a t b ττ-=*=+=-+⎰2411()(21)(2)()3333a y t tb a t b a t b x t ∴=-+---=+= (g) ()x t 是周期信号，由此可推知()()()y t x t h t =*也是周期的，且周期也为2。

信号与线形系统(第四版)吴大正主编第三章课后习题:3、1试求下列各序列得差分,与。

(1) 解:由题意得 前向差分()()()()()()+⎛⎫⎛⎫∆=+-=+- ⎪ ⎪⎝⎭⎝⎭⎧<-⎪⎪==-⎨⎪+⎪-≥⎩11111220,11,111,02k k f k f k f k U k U k k k k k 后向差分()()()()()()∇=--=---=111f k f k f k kU k k U k U()()()()⎛⎫⎛⎫⎛⎫===-∑∑∑ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=-∞=-∞=-∞111[][2]222k k k kkk f i U k U k U k i i i(2) 解:由题意得 前向差分()()()()()()()∆=+-=++-=+1111f k f k f k k U k kU k U k后项差分()()()()()()()∇=--=---=-1111f k f k f k kU k k U k U k()()()()()1[]kkkk k f i kU k k U k k +===3、2 求下列其次差分方程得解 (1)解:方程得特征根,所以 带入得: 所以解为 (2)解:方程得特征根,所以 带入得: 所以解为: (3)解:方程得特征根,所以 带入得 所以解为 (4)解:方程得特征根,所以 带入得 所以解为3、3 求下列齐次差分方程得解。

(1)()()()()()()()--+---===-=-71162123000,11,23y k y k y k y k y y y解:差分方程得特征方程为()()232716120230λλλλλ-+-=⇒--= 解得特征根其齐次解为 代入初始值, 解得所以其次方程得解为 (2)()()()()()()()()()--+---+-=====2122234000,11,22,35y k y k y k y k y k y y y y解:差分方程得特征方程为 解得特征根方程得齐次解为()cos sin 123422k k y k k C C C C ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭代入初始值解得 齐次方程得解3、4 求下列差分方程所描述得LTI 离散系统得零输入响应 (1)解:零输入响应满足 方程得特征方程解得 则齐次解为 代入初始值解得离散系统得零输入响应为()()()()()14222,02121k k k kzi k k y +=-+=+≥----(2)()()()()()()()212111,23y k y k y k f k f k y y +-+-=---=-=-解:零输入响应满足方程得特征方程解得则齐次解为代入初始值解得离散系统得零输入响应为(3) ()()()()()+-=--=--=-22,12,21y k y k f k y y解:零输入响应满足方程得特征方程,解得则齐次解为代入初始值解得离散系统得零输入响应为3、5 一个乒乓球从离地面10m高处自由下落,设球落地后反弹得高度总就是其下落高度得,令表示其第次反弹所达到得高度,列出其方程并求解。

第2章习题答案2-1 绘出下列各时间函数的波形图。

（1）1()(1)f t tu t =-（2）2()[()(1)](1)f t t u t u t u t =--+-（3）3()(1)[()(1)]f t t u t u t =---- （4）4()[(2)(3)]f t t u t u t =--- （5）5()(2)[(2)(3)]f t t u t u t =---- （6）6()()2(1)(2)f t u t u t u t =--+-解：2-5 已知()f t 波形如图题2-5所示，试画出下列信号的波形图。

t图 题2-5（3）3()(36)f t f t =+ （5）511()36ft f t ⎛⎫=-- ⎪⎝⎭解：t f 3(t)2-5/31-7/3tf 5(t)2-1/21-7/25/2002-6 已知()f t 波形如图题2-6所示，试画出下列信号的波形图。

图 题2-6（4）4()(2)(2)f t f t u t =-- （6）6()(1)[()(2)]f t f t u t u t =--- 解：tf 4(t)2120tf 6(t)21/23/22-7 计算下列各式。

（1）0()()f t t t δ+ （2）00()()d f t t t t t δ∞-∞+-⎰（3）24e (3)d t t t δ-+⎰（4）e sin (1)d tt t t δ∞-+⎰（5）d [e ()]d t t tδ-（6）0()()d f t t t tδ∞-∞-⎰（7）0()()d f t t t tδ∞-∞-⎰（8）00()d 2t t t u t t δ∞-∞⎛⎫--⎪⎝⎭⎰（9）00()(2)d t t u t t t δ∞-∞--⎰（10）(e )(2)d t t t t δ∞-∞++⎰（11）(sin )d 6t t t tδ∞-∞π⎛⎫+- ⎪⎝⎭⎰（12）j 0e [()()]d t t t t t Ωδδ∞--∞--⎰解：(1) 原式0()()f t t δ=(2)原式)2()()(0000t f dt t t t t f =-+=⎰+∞∞-δ(3)原式2334(3)e t dt e δ---=+=⎰(4)原式10sin(1)(1)0((1))e t dt t δδ+∞-=-+=+⎰不在积分区间内(5)原式)()](['0t t e dtd δδ== (6)原式)()()0(00t f dt t t f -=-=⎰+∞∞-δ(7)原式00(0)()()f t t dt f t δ+∞-∞=-=⎰(8)原式⎩⎨⎧><==--=⎰∞+∞-0100)2()2()(000000t t t u dt t t u t t δ(9)原式⎩⎨⎧<>=-=--=⎰∞+∞-0100)()2()(000000t t t u dt t t u t t δ(10)原式22(2)(2)2e t dt e δ+∞---∞=-+=-⎰(11)原式1(sin )()66662t dt ππππδ+∞-∞=+-=+⎰ (12)原式000[()()]1j t j t e t e t t dt e δδ+∞-Ω-Ω-∞=--=-⎰2-8 画出图题2-8所示各信号的偶分量和奇分量的波形。

信号与系统第三版课后习题答案信号与系统第三版课后习题答案信号与系统是电子信息类专业中一门重要的基础课程，它是研究信号的产生、传输、处理和识别的学科。

在学习这门课程时，课后习题是非常重要的，它可以帮助我们巩固所学的知识，并且提高解决问题的能力。

下面是信号与系统第三版课后习题的答案。

第一章：信号与系统的基本概念1. 信号是指随时间、空间或其他独立变量的变化而变化的物理量。

系统是指能够对输入信号进行处理并产生输出信号的物理设备或数学模型。

2. 连续时间信号是在连续时间范围内定义的信号，可以用连续函数表示。

离散时间信号是在离散时间范围内定义的信号，可以用数列表示。

3. 周期信号是指在一定时间间隔内重复出现的信号，具有周期性。

非周期信号是指不具有周期性的信号。

4. 奇对称信号是指关于原点对称的信号，即f(t)=-f(-t)。

偶对称信号是指关于原点对称的信号，即f(t)=f(-t)。

5. 系统的线性性质是指系统满足叠加原理，即对于输入信号的线性组合，输出信号也是这些输入信号的线性组合。

6. 系统的时不变性质是指系统对于不同时间的输入信号，输出信号的特性是不变的。

7. 系统的因果性质是指系统的输出只依赖于当前和过去的输入信号，而不依赖于未来的输入信号。

第二章：连续时间信号与系统的时域分析1. 奇偶分解是将一个信号分解为奇对称和偶对称两个部分的过程。

奇偶分解的目的是简化信号的处理和分析。

2. 卷积是信号处理中常用的一种操作，它描述了两个信号之间的相互作用。

卷积的定义为：y(t) = ∫[x(τ)h(t-τ)]dτ。

3. 系统的冲激响应是指系统对于单位冲激信号的输出响应。

冲激响应可以用来描述系统的特性和性能。

4. 系统的单位阶跃响应是指系统对于单位阶跃信号的输出响应。

单位阶跃响应可以用来描述系统的稳定性和响应速度。

5. 系统的单位斜坡响应是指系统对于单位斜坡信号的输出响应。

单位斜坡响应可以用来描述系统的积分特性。

信号与系统第二版课后答案第一章简介1.1 信号与系统的定义1.1.1 信号的定义信号是对某一现象或信息的描述，可以是物理量、采样值、传感器输出等。

根据信号的不同特性，可以将其分为连续信号和离散信号。

1.1.2 系统的定义系统是对信号加工与处理过程的描述。

系统可以是硬件电路、算法或计算机软件。

根据系统对信号的作用方式，可以将其分为线性系统和非线性系统。

1.2 信号的分类1.2.1 连续信号与离散信号连续信号是在时间上连续变化的信号，可以用数学函数进行描述。

离散信号则是在时间上呈现离散变化的信号，通常通过采样离散化得到。

1.2.2 有限信号与无限信号有限信号是在有限时间内存在的信号，其持续时间有限。

无限信号则是在无限时间内存在的信号，持续时间可以是无限的。

1.3 系统的分类1.3.1 线性系统与非线性系统线性系统满足线性叠加原理，即将输入信号与线性系统的响应相加所得到的输出信号仍然是系统的响应。

非线性系统则不满足线性叠加原理。

1.3.2 因果系统与非因果系统因果系统的输出只与当前和过去的输入有关，不受未来输入的影响。

非因果系统的输出则可能与未来的输入有关。

第二章离散信号与系统2.1 离散信号的表示与性质2.1.1 离散信号的表示离散信号可以通过序列来表示，其中序列是一组按照一定顺序排列的数字。

离散信号可以是有限序列或无限序列。

2.1.2 离散信号的性质离散信号的性质包括幅度、相位、频率、周期性等。

这些性质可以通过变换来描述和分析离散信号。

2.2 离散系统的表示与性质2.2.1 离散系统的表示离散系统可以通过差分方程来表示，其中差分方程描述了输入和输出之间的关系。

离散系统也可以通过单位脉冲响应来描述，单位脉冲响应是当输入为单位脉冲序列时系统的输出。

2.2.2 离散系统的性质离散系统的性质包括稳定性、因果性、线性性等。

这些性质对系统的行为和性能有重要影响。

2.3 离散系统的频域分析2.3.1 傅立叶变换傅立叶变换是一种将信号从时域转换到频域的方法，可以将信号表示为频率的函数。