苏教版七下第八章小结与思考1
- 格式:doc
- 大小:206.50 KB
- 文档页数:4

新苏科版七年级数学下册第八章《小结与思考(1)》导学案执教教师: 课型:复习使用日期:学习[来源学科网]目标 1、 能说出同底数幂的乘法、幂的乘方和积的乘方运算性质;2、 会运用幂的运算性质进行计算,能说出每一步的依据;3、通过具体的例子体会本章学习中体现的从具体到抽象、从特殊到一般的思考问题的方法,渗透转化、化归等思想方法,发展合情推理能力和演绎推理能力.重点难[来源学&科&网]点重点[来源:Z+xx+][来源学#科#网][来源学#科#网]运用幂的运算性质进行计算.难点运用幂的运算性质进行计算.学生活动过程教师导学过程 一、自主学习(独学)任务1:学习了本章的内容,现在回顾一下本章关于同底数幂的乘法、幂的乘方和积的乘方运算的知识点.任务2:想一想学习这三种运算要注意什么?其推导依据是什么? 知识练习:a) 计算: (1)23x x x ⋅⋅ (2)23)()(x x x -⋅⋅-(3))()()(102a b b a b a -⋅-⋅-(4)4523122---⋅-⋅+⋅n n n y y y y y yb) 计算: (1)31)(-m a (2)54])[(y x +(3)325)21(b a - (4)7233323)5()3()(2x x x x x ⋅+-⋅二、合作探究 (对学、群学)例1、下面的计算,对不对,如不对,错在哪里? (1)22)(a a -=- (2) 44)()(x y y x -=- (3) 22)()(a b b a --=- (4) 332)2(x x =-例2、已知m 10=4,n 10=5,求nm 2310+的值.例3、比较332、223和114的大小例4、一个正方体的棱长为mm 2103⨯.求这个正方体的表面积和体积练习:1.比较22221111与11112222大小2.已知32=m,52=n,求nm 24+的值三、拓展提升1.若x =m 2+1,y =3+ m 4,则用x 的代数式表示y 为______.四、当堂检测:1.填空题 (1) 52y y ⋅-=______ (2) 322])2([a ---=______(3) 200820074)25.0(⨯-=______ (5)若107a a a m =⋅,则=m _____2.下列计算结果正确的是 [ ] A .15356)2(x x = B .734)(x x -=- C .6232)2(x x = D .1234])[(x x =-(1) 3.计算题 (1) 999100100)1(5.02-⨯⨯-; (2)123-⋅m m a a (m 是正整数)(3)4235)2(a a a +⋅ (4)23)()()2(a a a ⋅---(5)若nx =3, ny =7,则nxy )(的值是多少? ny x )(32呢?五、小结反思在运用幂的运算性质,首先应确定运算顺序和运算步骤;其次正确地运用性质、法则进行计算,在计算时,应注意符号和指数的变化。


新苏科版七年级数学下册第八章《小结与思考》学案学习目标:1、掌握幂的运算的法则,会运用法则进行运算2、运用科学记数法表示绝对值小于1的数3、会双向应用幂的运算公式学习重难点: 运用法则进行运算、双向应用幂的运算公式学习过程环节学习内容教师活动学生活动自学与检测【出示课题】【出示目标】【自学指导】1.复习第7章(P46—P58)2.仔细看P61,尝试着做一下复习题(每大题选1—2题)。
3.想一想:①每题中都用到哪些公式?②是否可以用不同的方法做一下?【先学】1.学生看书、思考2.检测(板演)建构式生态课堂互动交流与探究【后教】互动1、纠错(学生用彩色粉笔上黑板更正)互动2、讨论(学生小组讨论)互动3、规律总结互动4、板演规范1、用科学计数法表示下列各数(1)14232)71(5)1251(22)2(---++⨯+-(2)a2·a3+(-a2)3-2a(a2)3-2[(a3)3÷a3];互动5、拓展延伸已知:4m = a , 8n = b求: ①22m+3n的值② 24m-6n的值当堂检测【当堂检测】1.填空题(1)52yy⋅-=____(2)23xxx⋅⋅=____(3)31)(-m a=____(4)325)21(ba-=______(4)7233323)5()3()(2xxxxx⋅+-⋅=______2.计算题(1))()(432xxxx⋅÷⋅;(2)yyy⋅÷632)(;(3)999100100)1(5.02-⨯⨯-;(4)])[(2)(2)(333323232aaaaaaa⋅---+⋅;(5))()(xyyxyxyxxy--+-+--232)(2)()(.3、已知32=m,52=n,求nm24+的值教学心得教师的职务是‘千教万教,教人求真’;学生的职务是‘千学万学,学做真人’。
我们发现了儿童有创造力,认识了儿童有创造力,就须进一步把儿童的创造力解放出来。

XX七年级下册数学第八章知识点汇总(苏教版)XX七年级下册数学第八章知识点汇总二元一次方程组判断一个方程是不是二元一次方程,一般要将方程化为一般形式后再根据定义判断。
二元一次方程的解:一个二元一次方程有无数个解,而每一个解都是一对数值。
求二元一次方程的解的方法:若方程中的未知数为x,y,可任取x的一些值,相应的可算出y 的值,这样,就会得到满足需要的数对。
二元一次方程组:两个二元一次方程合在一起,就组成了一个二元一次方程组。
作为二元一次方程组的两个方程,不一定都含有两个未知数,可以其中一个是一元一次方程,另一个是二元一次方程。
二元一次方程组的解:使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值,叫做二元一次方程组的解。
检验一对数值是不是二元一次方程组的解的方法是,将两个未知数分别代入方程组中的两个方程,如果都能满足这两个方程,那么它就是方程组的解。
解二元一次方程组消元:将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
归纳:基本思路:“消元”——把“二元”变为“一元”。
代入消元:将一个未知数用含有另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫做代入消元法,简称代入法。
加减消元法:当两个方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,这种方法叫做加减消元法,简称加减法。
教科书中没有的几种解法加减-代入混合使用的方法:特点:两方程相加减,单个x或单个y,这样就适用接下来的代入消元。
换元法特点:两方程中都含有相同的代数式,换元后可简化方程也是主要原因。
设参数法二元一次方程组二元一次方程:含有两个未知数,并且未知数的指数都是1,像这样的方程叫做二元一次方程,一般形式是ax+by=c。
如果一个方程含有两个未知数,并且所含未知项都为1次方,那么这个整式方程就叫做二元一次方程,有无穷个解,若加条件限定有有限个解。

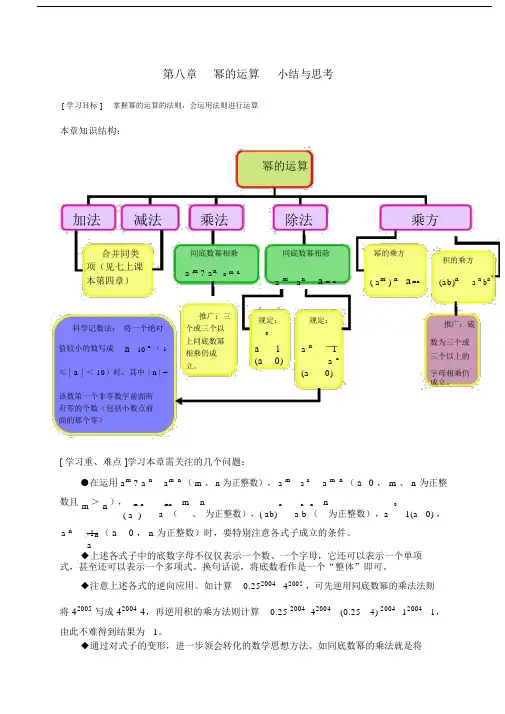
第八章幂的运算小结与思考[ 学习目标 ]掌握幂的运算的法则,会运用法则进行运算本章知识结构:幂的运算加法减法乘法除法乘方合并同类项(见七上课本第四章)科学记数法:将一个绝对值较小的数写成a10 n(1 ≤ | a | <10)时,其中| n | =该数第一个非零数字前面所有零的个数(包括小数点前面的那个零)同底数幂相乘a m ? a n a m n推广:三个或三个以上同底数幂相乘仍成立。
同底数幂相除幂的乘方积的乘方a m a n a m n ( a m ) n a mn (ab)n a nb n规定:规定:推广:底数为三个或a 1 a n 1三个以上的(a 0) a n字母相乘仍(a 0)成立。
[ 学习重、难点 ]学习本章需关注的几个问题:●在运用 a m ? a n a m n( m 、 n 为正整数), a m a n a m n(a 0 ,m、n为正整数且m >n ),m n mn m n n n n n 0( a ) a (、为正整数),( ab) a b (为正整数),a 1(a 0) ,a n 1n ( a 0 ,n为正整数)时,要特别注意各式子成立的条件。
a◆上述各式子中的底数字母不仅仅表示一个数、一个字母,它还可以表示一个单项式,甚至还可以表示一个多项式。
换句话说,将底数看作是一个“整体”即可。
◆注意上述各式的逆向应用。
如计算0.25200442005,可先逆用同底数幂的乘法法则将 42005写成 42004 4,再逆用积的乘方法则计算0.25 200442004(0.25 4) 2004120041,由此不难得到结果为1。
◆通过对式子的变形,进一步领会转化的数学思想方法。
如同底数幂的乘法就是将乘法运算转化为指数的加法运算, 同底数幂的除法就是将除法运算转化为指数的减法运算,幂的乘方就是将乘方运算转化为指数的乘法运算等。
◆在经历上述各个式子的推导过程中,进一步领悟“通过观察、猜想、验证与发现法则、规律”这一重要的数学研究的方法,学习并体会从特殊到一般的归纳推理的数学思想方法。


第八章幂的运算的小结与思考(1) (教案)班级____________姓名____________学号___________备课时间: 主备人:教学目标:1、能说出幂的运算的性质;2、会运用幂的运算性质进行计算,并能说出每一步的依据;3、能说出零指数幂、负整数指数幂的意义,能用熟悉的事物描述一些较小的正数,并能用科学记数法表示绝对值小于1的数;4、通过具体例子体会本章学习中体现的从具体到抽象、特殊到一般的思考问题的方法,渗透转化、归纳等思想方法,发展合情推理能力和演绎推理能力。
教学重点:运用幂的运算性质进行计算教学难点:运用幂的运算性质进行证明规律教学方法:引导发现,合作交流,充分体现学生的主体地位一、系统梳理知识:幂的运算:1、同底数幂的乘法2、幂的乘方3、积的乘方4、同底数幂的除法:(1)零指数幂(2)负整数指数幂请你用字母表示以上运算法则。
你认为本章的学习中应该注意哪些问题?二、例题精讲:例1 判断下列等式是否成立:①(-x)2=-x2,②(-x3)=-(-x)3,③(x-y)2=(y-x)2,④(x-y)3=(y-x)3,⑤x-a-b=x-(a+b),⑥x+a-b=x-(b-a).解:③⑤⑥成立.例2 已知10m=4,10n=5,求103m+2n的值.解:因为103m=(10m)3=43 =64,102n=(10n)2=52=25.所以103m+2n=103m×102n=64×25=1680例3 若x=2m+1,y=3+4m,则用x的代数式表示y为______.解:∵2m=x-1,∴y=3+4m=3+22m.=3+(2m)2=3+(x-1)2=x2-2x+4.例4设<n>表示正整数n的个位数,例如<3>=3,<21>=1,<13×24>=2,则<210>=______.解210=(24)2·22=162·4,∴ <210>=<6×4>=4例5 1993+9319的个位数字是( )A.2 B.4 C.6 D.8解1993+9319的个位数字等于993+319的个位数字.∵ 993=(92)46·9=8146·9.319=(34)4·33=814·27.∴993+319的个位数字等于9+7的个位数字.则 1993+9319的个位数字是6.三、随堂练习:1、已知a=355,b=444,c=533,则有()A.a<b<c B.c<b<aC.c<a<b D.a<c<b2、已知3x=a,3y =b,则32x-y等于( )3、试比较355,444,533的大小.4、已知a=-0.32,b=-3-2,c=(-1/3)-2d=(-1/3)0,比较a、b、c、d的大小并用“,〈”号连接起来。


1、1665年,英国虎克最早研制出光学显微镜,发现了软木薄片由许多小室组成,称为“细胞”。
大多数生物体是由细胞构成,病毒既没有细胞结构又比细胞体积小得多的生物,病毒必须生活在其他生物细胞内,人类流行性感冒、SARS、艾滋病等疾病都是由病毒感染引起的。
细胞是生物体结构和功能的基本单位。
2、观察植物、动物细胞:实验过程玻片标本分类:○1切片——用生物体上切取下来的薄片制成○2涂片——用液体的生物材料(如细菌培养液、血液)经过涂抹制成○3装片——用生物体上取下来的或直接用个体微小的生物如衣藻、水螅、青霉等制成以上三种玻片,都可以制成永久的(永久玻片)和临时的(临时玻片)制作动植物细胞临时装片的基本步骤:植物:擦――滴(清水)——撕(内侧)——展――盖(减少气泡)――染(稀碘液)――吸(吸水纸)动物:擦――滴(0.9%生理盐水)——刮(口腔内侧壁)——涂――盖――染(稀碘液)――吸生理盐水\清水:保持细胞形状;稀碘液:便于寻找和观察细胞,可使细胞结构看得更清楚。
3、细胞基本结构包括细胞膜、细胞质和细胞核。
①细胞膜具有保护细胞内部结构的作用,同时还能控制细胞内外物质的进出。
②细胞质是一种透明的液体,它具有流动性性,这有利于细胞之间和细胞与外界环境之间进行物质交换,是生命活动的重要场所。
③细胞核的染色体上存在生物的遗传物质,主要是一种叫做脱氧核糖核酸的化学物质,即DNA。
克隆羊最像提供细胞核的那只羊。
④植物细胞结构比动物细胞多细胞壁、液泡、叶绿体。
A、植物细胞结构中的细胞壁,位于植物细胞的外层,质地坚韧,保护细胞内部结构和维持细胞形态的作用。
B、植物细胞细胞质内有与细胞呼吸作用有关的线粒体,有与植物光合作用的叶绿体,还有充满细胞液的液泡(切瓜果流出的汁液通常是细胞液)。
C、细胞生命活动所需的能量,大约95%来自线粒体,它被人叫做细胞内供应能量的动力工厂。
4、细胞的生长:生物体的生长现象与细胞的分裂与分化密切相关,一方面,细胞通过分裂增加细胞数量;另一方面,细胞通过生长增大了细胞体积。
初一下册第八章教学解析详解第八章:数与代数本章主要介绍了数与代数的相关内容,包括正数、负数、零、整数等的概念及运算法则,同时还引入了代数中的字母和代数式的概念。
通过学习本章内容,学生将能够理解数与代数的关系,掌握相关的运算法则,为今后的数学学习打下基础。
1. 正数、负数和零本节主要介绍了正数、负数和零的概念及表示法。
学生通过对日常生活中的实际例子的观察和思考,能够理解正数、负数和零的含义,并学会用数轴表示这三种数。
数轴的使用有助于学生直观地理解数的大小关系,并进行简单的比较和运算。
2. 加法与减法法则本节重点介绍了正数、负数和零的加法与减法法则。
通过实际生活中的例子,学生能够体验到正数与正数相加、负数与负数相加、正数与负数相加等不同情况下的结果和规律。
同时,学生还学会了用数轴进行加法与减法运算,并能够根据实际问题进行数学建模和求解。
3. 整数的概念与运算法则本节以正数、负数和零的概念为基础,引入了整数的概念。
学生通过对整数的定义和性质的学习,能够理解整数的特点,并掌握整数的四则运算法则。
此外,本节还介绍了整数的乘方运算,学生通过具体例子的讲解和练习,能够掌握整数乘方运算的规律和方法。
4. 代数式的概念与运算本节引入了代数中的字母和代数式的概念,将学生的思维从具体的数值拓展到抽象的符号。
通过对代数式的定义和性质的学习,学生能够理解代数式的含义和作用,并掌握代数式的基本运算法则。
此外,本节还介绍了代数式的合并同类项和提取公因式的方法,帮助学生进行代数式的化简和计算。
结语通过对初一下册第八章教学解析的详解,我们了解到数与代数的相关概念和运算法则。
这一章的学习对于学生理解数学的抽象概念和推理思维的培养具有重要意义。
在今后的学习中,学生将会进一步运用数与代数的知识解决实际问题,提高数学素养和综合运算能力。
希望同学们能够认真学习并灵活运用本章知识,为今后的学习打下坚实的基础。
七年级下八单元知识点总结本文将对七年级下八单元的知识点进行总结,帮助学生们提高知识点记忆和理解。
一、数学1.1 数与代数在数与代数的学习中,我们需要了解数的概念和性质,常见的数的规律,以及整数和分数的运算;代数学习中,需要掌握开平方、因式分解和解一元一次方程等知识点。
1.2 几何几何学习中,我们需要了解几何图形的类型和特点,几何变换,以及角度的计算等知识点。
1.3 数据与概率在数据与概率的学习中,我们需要了解数据的收集和分析方法,概率的概念和计算,以及统计学的应用等知识点。
二、语文2.1 词汇语文学习中,词汇的掌握是非常重要的。
我们需要了解词汇的基本概念,形音义的关系,以及词语的构成方法等知识点。
2.2 语法语法学习中,需要了解主谓宾的概念和基本结构,各种时态的用法,以及句子成分的分类等知识点。
2.3 文学知识文学知识可以提高学生们的阅读理解能力。
需要了解古代文学作品的基本内容和风格,现代文学的特点和表现手法,以及文化背景和历史背景等知识点。
三、英语3.1 语音英语学习中,语音的掌握是非常关键的。
需要了解英语语音符号的发音和用法,音标的记忆和运用,以及常见发音错误和纠正方法等知识点。
3.2 语法英语语法也是英语学习的重点,需要了解名词、动词、形容词等基础语法知识,以及语态、时态等高级语法知识。
3.3 阅读和写作英语阅读和写作能力的提高是英语学习的最终目标。
需要了解阅读技巧和词汇积累方法,以及写作技巧和文章结构等知识点。
四、物理4.1 运动学在运动学学习中,需要了解质点运动的基本概念和运动规律,包括速度、加速度、位移等物理量的计算方法,以及质点的自由落体运动等知识点。
4.2 力学力学学习中,需要了解牛顿运动定律、重力和弹力等概念,及其在物理学中的应用。
4.3 热学热学学习中,需要了解温度和热量的概念,热力学定律,热传导和热辐射等知识点。
五、化学5.1 元素和化合物化学学习中,需要了解元素和化合物的基本概念,各种元素的性质和分类,以及化合物的组成和命名等知识点。
第八章 单元知识梳理与能力整合一、知识网络结构 二、能力整合三、知识专题讲解 专题一 从特殊到一般的思想方法 例1:阅读材料:求1+2+22+23+24+…22013的值。
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22013+22014将下式减去上式得2S-S=22014-1即S=22014-1即1+2+22+23+24+…+22013=22014-1请你仿照此法计算:(1)1+2+22+23+24+…+210(2)1+3+32+33+34+…+3n (其中n 为正整数).专题二 整体代入思想例2:计算:)(123201*********)12131201012011120121(2012⨯⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯专题三 幂运算法则的灵活运用例3:已知4432=--c b a ,求4)161(84-⨯÷c b a 的值。
1、同底数幂的乘法与除法 (1)相同点:底数不变;不同点:乘法中是指数相加,除法中是指数相减。
(2)除法运算可以转化为乘法运算 n m n m n m a a a a a --=∙=÷2、幂的运算法则既可以正向运用,也可以逆向运用3、对于幂的混合运算,要注意先识别各单元属于哪种幂的运算,再按相关法则进行计算,幂的运算法则之间不能发生混淆。
四、新典型立体分类剖析类型一 幂的运算【例1】计算:(1)234)()()(q p p q q p -∙-÷- (2)524232)()()(a a a ÷∙ (3)⎥⎦⎤⎢⎣⎡--÷∙⎥⎦⎤⎢⎣⎡--222221)()()(m m m x x x(4)01322)14.3(3)21()52(2-+--++-----π【例3】计算:(1)11457)2()25.0(-∙- (2)20001999)532()135(∙ (3)200119972)25.0(48-⨯⨯【例4】已知909999911,999==N M ,那么M 、N 的大小关系是? 【例5】求2007200537⨯的末尾数字类型二 幂的运算法则的逆运用 【例2】计算:401100200920085.0168125.0⨯⨯⨯ 类型三 用科学计数法表示较小的数 【例6】微电子技术的不断进步,时半导体材料的精细加工尺寸大幅度缩小。
8.3小结与思考(1)
班级 姓名 成绩
1:计算:
(1)23x x x ⋅⋅ (2)23)()(x x x -⋅⋅-
(3))()()(102a b b a b a -⋅-⋅- (4)4523122---⋅-⋅+⋅n n n y y y y y y
a) 计算:
(1)31)(-m a (2)54])[(y x +
(3)325)2
1(b a - (4)7233323)5()3()(2x x x x x ⋅+-⋅
3、 典型例题:
例1、下面的计算,对不对,如不对,请改正?
(1)22)(a a -=- (2) 44)()(x y y x -=-
(3) 22)()(a b b a --=- (4) 332)2(x x =-
例2、已知m 10=4,n 10=5,求n m 2310+的值.
解:
例3、若x =m 2+1,y =3+ m 4,则用x 的代数式表示y .
解:
例4、比较332、223和114的大小
解:
例5、一个正方体的棱长为mm 2103⨯.求这个正方体的表面积和体积
解:
4、随堂练习
(1)123-⋅m m a a (m 是正整数) (2)842a a a ⋅⋅
(3)4235)2(a a a +⋅ (4)23)()()2(a a a ⋅---
(5)若107a a a m =⋅,则=m ______
(6)若n x =3, n y =7,则n xy )(的值是多少? n y x )(32呢?
归纳总结:
在运用幂的运算性质,首先应确定运算顺序和运算步骤;其次正确地运用性质、法则进行计算,在计算时,应注意符号和指数的变化。
【课后作业】
1.填空题
(1) 52y y ⋅-=______; (2) 322])2([a ---=______;(3) 200820074)25.0(⨯-=______.
2.选择题
(1)计算31)](2[---n x 等于 [ ]
A .332--n x
B .16--n
C .338-n x
D .338--n x
(2)下述各式中计算正确的是 [ ]
A .824)(ab ab =
B .1052632y y y =⋅
C .642)()(x x x -=-⋅-
D .322233)()(b a b a =
(3)计算)2
3()1()2(221999223y x y x -⋅-⋅--的结果应该等于 [ ] A .10103y x B .10103y x - C .10109y x D .10109y x -
(4) 7x 等于 [ ]
A .52)()(x x -⋅-
B .)()(52x x ⋅-
C .)()(43x x -⋅-
D .5)()(x x ⋅-
(5)在下面各式中的括号内填入3a 的是 [ ]
A .12a =( 2)
B .12a =( 5)
C .12a =( 4)
D .12a =( 6)
(6)下列计算结果正确的是 [ ]
A .15356)2(x x =
B .734)(x x -=-
C .6232)2(x x =
D .1234])[(x x =-
(7)计算323)4()5.2(a a -⋅-的结果应等于 [ ]
A .9400a -
B .9400a
C .940a -
D .940a
(8)计算22)(x x -⋅-等于 [ ]
A .4422)()(x x x =-=-+
B .42222x x x x -=-=⋅-+
C .42222)(x x x x -=-=-⋅-+
D .42222x x x x -=-=⋅-⨯
3.计算题
(1) 999100100)1(5.02-⨯⨯-; (2) ])[(2)(2)(333323232a a a a a a a ⋅---+⋅;
(3) )
()(x y y x y x y x x y --+-+--232)(2)()(.
4、比较22221111与11112222大小
5、已知32=m ,52=n ,求n m 24+的值。