弹性模量与硬度关系
- 格式:pdf
- 大小:337.42 KB
- 文档页数:8

1、弹性模量:(1)定义弹性模量:材料在弹性变形阶段内,正应力与对应得正应变得比值。
材料在弹性变形阶段,其应力与应变成正比例关系(即符合胡克定律),其比例系数称为弹性模量。
“弹性模量”就是描述物质弹性得一个物理量,就是一个总称,包括“杨氏模量”、“剪切模量”、“体积模量”等。
所以,“弹性模量”与“体积模量”就是包含关系。
一般地讲,对弹性体施加一个外界作用(称为“应力”)后,弹性体会发生形状得改变(称为“应变”),“弹性模量”得一般定义就是:应力除以应变。
例如:线应变——对一根细杆施加一个拉力F,这个拉力除以杆得截面积S,称为“线应力”,杆得伸长量dL除以原长L,称为“线应变”。
线应力除以线应变就等于杨氏模量E=( F/S)/(dL/L)剪切应变——对一块弹性体施加一个侧向得力f(通常就是摩擦力),弹性体会由方形变成菱形,这个形变得角度a称为“剪切应变”,相应得力f除以受力面积S称为“剪切应力”。
剪切应力除以剪切应变就等于剪切模量G=( f/S)/a体积应变——对弹性体施加一个整体得压强p,这个压强称为“体积应力”,弹性体得体积减少量(dV)除以原来得体积V称为“体积应变”,体积应力除以体积应变就等于体积模量: K=P/(dV/V) 在不易引起混淆时,一般金属材料得弹性模量就就是指杨氏模量,即正弹性模量。
单位:E(弹性模量)吉帕(GPa)(2)影响因素弹性模量就是工程材料重要得性能参数,从宏观角度来说,弹性模量就是衡量物体抵抗弹性变形能力大小得尺度,从微观角度来说,则就是原子、离子或分子之间键合强度得反映。
凡影响键合强度得因素均能影响材料得弹性模量,如键合方式、晶体结构、化学成分、微观组织、温度等。
因合金成分不同、热处理状态不同、冷塑性变形不同等,金属材料得杨氏模量值会有5%或者更大得波动。
但就是总体来说,金属材料得弹性模量就是一个对组织不敏感得力学性能指标,合金化、热处理(纤维组织)、冷塑性变形等对弹性模量得影响较小,温度、加载速率等外在因素对其影响也不大,所以一般工程应用中都把弹性模量作为常数。


弹性模量和硬度的关系
弹性模量和硬度没有紧密联系。
硬度测量的是塑性, 和屈服应力有关。
弹性模量:材料在弹性变形阶段内,正应力和对应的正应变的比值。
材料在弹性变形阶段,其应力和应变成正比例关系(即符合胡克定律),其比例系数称为弹性模量。
弹性模量是描述物质弹性的一个物理量,是一个总称,包括“杨氏模量”、“剪切模量”、“体积模量”等。
所以,“弹性模量”和“体积模量”是包含关系。
弹性模量是工程材料重要的性能参数,从宏观角度来说,弹性模量是衡量物体抵抗弹性变形能力大小的尺度,从微观角度来说,则是原子、离子或分子之间键合强度的反映。
凡影响键合强度的因素均能影响材料的弹性模量,如键合方式、晶体结构、化学成分、微观组织、温度等。
因合金成分不同、热处理状态不同、冷塑性变形不同等,金属材料的杨氏模量值会有5%或者更大的波动。
但是总体来说,金属材料的弹性模量是一个对组织不敏感的力学性能指标,合金化、热处理(纤维组织)、冷塑性变形等对弹性模量的影响较小,温度、加载速率等外在因素对其影响也不大,所以一般工程应用中都把弹性模量作为常数。
强度是指零件承受载荷后抵抗发生断裂或超过容许限度的残余变形的能力。
也就是说,强度是衡量零件本身承载能力(即抵抗失效能力)的重要指标。
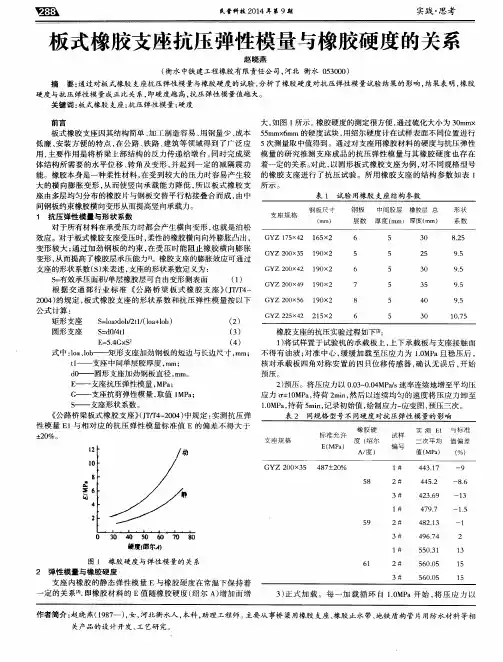

材料硬度-弹性模量-能量耗散之关系沈阳材料科学国家(联合)实验室 高性能陶瓷材料研究部 包亦望编者按:最近,我所沈阳材料科学国家(联合)实验室高性能陶瓷材料研究部包亦望研究员发现并证明了材料硬度-弹性模量-能量耗散三者之间的本征关系,该工作被Acta Materialia 审稿人评价为“确实是对纳米压痕领域的一个新贡献”。
弹性模量和硬度是固体结构材料的两个重要参数,它们之间是否存在本征关系?如果存在,又是怎样的一种关系呢?这个问题一直吸引着材料科学家和机械工程师的兴趣。
从统计的角度来看,通常认为弹性模量随着硬度的增大而增大,但这种趋势没有坚实的理论依据,且并不是对所有材料都适用。
如三元层状陶瓷就具有较低的硬度,而具有较大的弹性模量。
另一个经常用于估算膜的弹性模量的关系为:y y E H σσθ)]3/cos ln(1)[3/2(+=,式中y σ为压缩屈服应力,而θ为压头的半角。
由于此式的理论基础不明确,从而限制了它的应用。
采用此式计算Ti 3SiC 2的弹性模量为1188 GPa ,比实际测量值310 GPa 高很多。
正鉴于此,有必要对硬度和弹性模量之间的关系进行进一步的研究。
位移敏感压痕技术的进步使我们可以根据精确测量得出的载荷——位移曲线数据,来确定材料的弹性模量和硬度值,从而为研究二者之间的关系提供了恰当的实验手段。
另外,Oliver-Pharr 基于弹性接触理论而提出的测试方法使我们能够建立弹性模量和硬度的理论关系。
在对固体材料进行压痕实验时,加载过程中的弹塑性局部变形决定了材料的硬度和外力做功,而卸载过程中的弹性恢复则反映了材料局部的能量耗散和弹性模量。
基于这种思路和应用于卸载过程的弹性接触理论,我们证明了固体材料的弹性模量与硬度之间的关系取决于材料的能量耗散能力(Acta Materialia 52(2004):5397)。
即材料的局部能量耗散越大,则硬度和弹性模量的比值越小,同时压痕周围的弹性恢复也越小。

硬度和弹性模量之间的转换
硬度和弹性模量是材料力学性质的两个重要参数。
硬度是指材料在受力作用下表面的抗压能力,弹性模量则是材料在受力作用下的弹性变形能力。
虽然这两个参数描述的是不同的材料力学性质,但是它们之间存在一定的关联和转换关系。
硬度和弹性模量之间的转换是基于材料在宏观上的弹性变形行
为与微观结构的关系。
在材料受力作用下,如果受到的力越大,材料就会发生更大的弹性变形,这时材料的硬度也会变得更高。
而弹性模量则是反映材料在受力作用下的弹性变形能力,它与材料的硬度呈线性关系。
因此,可以通过硬度值和材料的弹性模量来计算出材料的硬度值。
事实上,硬度和弹性模量之间的转换并不是一种简单的线性关系,因为不同类型的硬度测试所得到的硬度值与材料的弹性模量之间的
关系并不相同。
此外,材料的组成、处理方式和温度等因素也会影响硬度测试结果和弹性模量。
因此,在实际应用中,需要根据具体情况选择合适的转换方法,以获得更准确的结果。
总的来说,硬度和弹性模量是材料力学性质的两个重要参数,它们之间存在一定的关联和转换关系。
在实际应用中,需要根据具体情况选择合适的转换方法,以获得更准确的结果。
- 1 -。
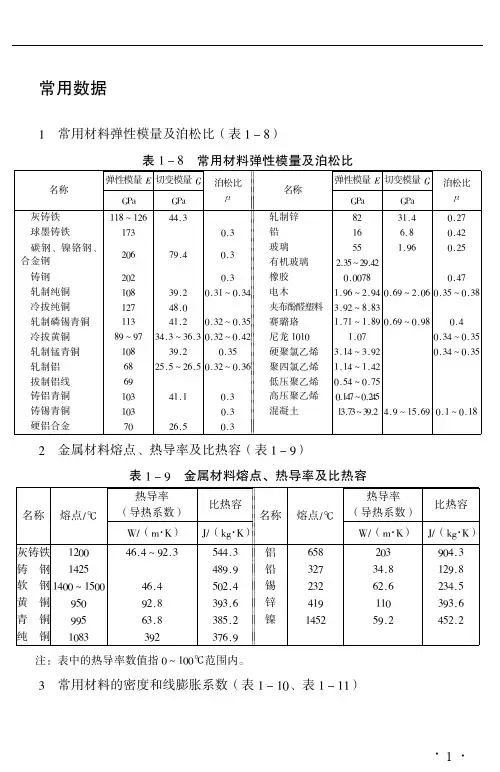
常用数据!常用材料弹性模量及泊松比(表!"#)表!"#!!!!常用材料弹性模量及泊松比名称弹性模量!切变模量"$%&$%&泊松比!名称弹性模量!切变模量"$%&$%&泊松比!!!!!!!!!!!!!!!!!!!!!!!!!灰铸铁!!#’!()**+,球墨铸铁!-,.+,碳钢、镍铬钢、合金钢(.)-/+*.+,铸钢(.(.+,轧制纯铜!.#,/+(.+,!’.+,*冷拔纯铜!(-*#+.轧制磷锡青铜!!,*!+(.+,(’.+,0冷拔黄铜#/’/-,*+,’,)+,.+,(’.+*(轧制锰青铜!.#,/+(.+,0轧制铝)#(0+0’()+0.+,(’.+,)拔制铝线)/铸铝青铜!.,*!+!.+,铸锡青铜!.,.+,硬铝合金-.()+0.+,轧制锌#(,!+*.+(-铅!))+#.+*(玻璃00!+/).+(0有机玻璃(+,0’(/+*(橡胶.+..-#.+*-电木!+/)’(+/*.+)/’(+.).+,0’.+,#夹布酚醛塑料,+/(’#+#,赛璐珞!+-!’!+#/.+)/’.+/#.+*尼龙!.!.!+.-.+,*’.+,0硬聚氯乙烯,+!*’,+/(.+,*’.+,0聚四氯乙烯!+!*’!+*(低压聚乙烯.+0*’.+-0高压聚乙烯.+!*-’.+(*0混凝土!,+-,’,/+(*+/’!0+)/.+!’.+!#(金属材料熔点、热导率及比热容(表!"/)表!"/!!!!!!金属材料熔点、热导率及比热容名称熔点12热导率(导热系数)比热容31(4·5)61(78·5)名称熔点12热导率(导热系数)比热容31(4·5)61(78·5!!)灰铸铁!(..*)+*’/(+,0**+,铝!!)0#(.,/.*+,铸钢!*(0*#/+/铅!!,(-,*+#!(/+#软钢!*..’!0..*)+*0.(+*锡!!(,()(+)(,*+0黄铜/0./(+#,/,+)锌!!*!/!!.,/,+)青铜//0),+#,#0+(镍!!!*0(0/+(*0(+(纯铜!.#,,/(,-)+/注:表中的热导率数值指.’!..2范围内。

材料硬度-弹性模量-能量耗散之关系沈阳材料科学国家(联合)实验室 高性能陶瓷材料研究部 包亦望编者按:最近,我所沈阳材料科学国家(联合)实验室高性能陶瓷材料研究部包亦望研究员发现并证明了材料硬度-弹性模量-能量耗散三者之间的本征关系,该工作被Acta Materialia 审稿人评价为“确实是对纳米压痕领域的一个新贡献”。
弹性模量和硬度是固体结构材料的两个重要参数,它们之间是否存在本征关系?如果存在,又是怎样的一种关系呢?这个问题一直吸引着材料科学家和机械工程师的兴趣。
从统计的角度来看,通常认为弹性模量随着硬度的增大而增大,但这种趋势没有坚实的理论依据,且并不是对所有材料都适用。
如三元层状陶瓷就具有较低的硬度,而具有较大的弹性模量。
另一个经常用于估算膜的弹性模量的关系为:y y E H σσθ)]3/cos ln(1)[3/2(+=,式中y σ为压缩屈服应力,而θ为压头的半角。
由于此式的理论基础不明确,从而限制了它的应用。
采用此式计算Ti 3SiC 2的弹性模量为1188 GPa ,比实际测量值310 GPa 高很多。
正鉴于此,有必要对硬度和弹性模量之间的关系进行进一步的研究。
位移敏感压痕技术的进步使我们可以根据精确测量得出的载荷——位移曲线数据,来确定材料的弹性模量和硬度值,从而为研究二者之间的关系提供了恰当的实验手段。
另外,Oliver-Pharr 基于弹性接触理论而提出的测试方法使我们能够建立弹性模量和硬度的理论关系。
在对固体材料进行压痕实验时,加载过程中的弹塑性局部变形决定了材料的硬度和外力做功,而卸载过程中的弹性恢复则反映了材料局部的能量耗散和弹性模量。
基于这种思路和应用于卸载过程的弹性接触理论,我们证明了固体材料的弹性模量与硬度之间的关系取决于材料的能量耗散能力(Acta Materialia 52(2004):5397)。
即材料的局部能量耗散越大,则硬度和弹性模量的比值越小,同时压痕周围的弹性恢复也越小。

塑料的弹性模量与硬度关系分析塑料是一种广泛应用于制造业和日常生活中的材料。
其中,塑料的弹性模量和硬度是两个重要的力学性质参数。
本文将对塑料的弹性模量与硬度之间的关系进行分析。
引言塑料作为一类具有高度可塑性和可加工性的材料,已被广泛应用于各个领域。
弹性模量和硬度是衡量塑料材料性能的重要指标,对于材料的选择和设计具有重要意义。
一、塑料的弹性模量弹性模量是指材料在受力作用下产生弹性变形时,单位面积内所产生的应力与应变之间的比值。
弹性模量可以用来评估材料的刚性和抗变形能力。
塑料的弹性模量相对较低,主要与其分子结构和内部结构有关。
塑料材料通常由长链高分子聚合物构成,链与链之间通过弱的力相互作用,因此在受力作用下容易发生形变。
不同种类的塑料具有不同的弹性模量值,例如聚乙烯的弹性模量约为0.1-0.8 GPa,而聚酰胺的弹性模量可高达2-4 GPa。
二、塑料的硬度硬度是材料抵抗外界物体对其表面压入的能力。
塑料常用的硬度测试方法有洛氏硬度和巴氏硬度等。
塑料的硬度主要取决于其分子结构、熔融温度以及添加剂等因素。
一般来说,硬度较高的塑料具有较高的熔融温度和较高的强度。
例如,聚碳酸酯是一种硬度较高的塑料,其硬度可达到80-90洛氏硬度(HRL),而聚乙烯的硬度相对较低,一般在30-60HRL之间。
三、弹性模量与硬度的关系塑料的弹性模量和硬度之间存在一定的相关性。
虽然两者的计算方法不同,但可以从宏观上理解其关系。
一方面,弹性模量通常与材料的硬度成正比。
较硬的塑料通常具有较高的弹性模量,反之亦然。
这是因为硬的塑料具有更严密的分子结构,链与链之间的相互作用力更强,因此在受力作用下形变较小。
另一方面,虽然弹性模量和硬度之间存在相关性,但并非线性关系。
不同种类的塑料,在相同硬度下其弹性模量可能存在差异。
这是因为塑料材料的组分和结构多样,不同材料之间的分子链长度、链结构以及添加剂等差异会导致它们具有不同的弹性模量。
结论塑料的弹性模量和硬度是塑料材料性能的重要指标,对于材料的选择和设计具有重要意义。

钢铁制弹簧的材料硬度与弹性模量研究引言:钢铁制弹簧作为一种重要的机械零件,在工业生产中扮演着重要的角色。
其材料的硬度和弹性模量不仅直接影响弹簧的性能和寿命,还与弹簧在工作过程中的安全性和稳定性密切相关。
因此,对钢铁制弹簧的材料硬度和弹性模量进行深入研究,对于弹簧的设计、制造和使用具有重要的意义。
一、材料硬度的研究硬度是材料抵抗外界力量侵蚀的能力,直接反映了材料的硬度和强度。
在钢铁制弹簧的设计和制造过程中,合适的硬度能够保证弹簧具有足够的强度和耐磨性,以满足弹簧在各种工况下的要求。
为了研究钢铁制弹簧的材料硬度,我们可以采用多种方法。
其中,最常用的方法是洛氏硬度试验和布氏硬度试验。
洛氏硬度试验通过将一定负荷加载到试样表面,并测量形成的压痕的直径,来确定材料的硬度。
而布氏硬度试验则是采用压头对材料进行压痕,再根据压痕的大小来判断硬度。
通过进行硬度试验,并与已知材料硬度的标准数据进行对比,可以准确地确定钢铁制弹簧材料的硬度。
二、弹性模量的研究弹性模量是材料表征其弹性性能的重要参数,它代表了材料在受力后恢复原状的能力。
对于钢铁制弹簧来说,合适的弹性模量可以确保弹簧在受力后不会过度变形或失去弹性,从而保证其正常工作。
要研究钢铁制弹簧的弹性模量,我们可以利用材料力学性能测试仪进行拉伸试验。
该试验通过加载试样并在加载过程中测量应力和应变值,进而可以计算出材料的弹性模量。
在拉伸试验中,我们可以选取代表性的样本进行测试,并采用标准的试验方法和参数,以保证测试结果的准确性。
三、材料硬度与弹性模量的关系材料硬度与弹性模量之间存在一定的关系。
一般来说,材料的硬度越高,则其弹性模量通常也会增加。
对于钢铁制弹簧来说,弹性模量的提高意味着弹簧在受力时的刚性增加,有助于弹簧更好地承受外界力量的作用,保持弹簧的结构稳定性。
然而,材料硬度与弹性模量之间的关系并非线性。
研究发现,当材料硬度达到一定程度时,其弹性模量并不随之增加,而是趋于饱和。

硬度和橡胶模量的关系
硬度和橡胶模量是两个不同的物理量,它们之间存在一定的关系,但并不是简单的线性关系。
硬度是指材料抵抗外力压入的能力,通常用邵氏硬度计来测量,单位是邵氏硬度值。
对于橡胶材料,硬度越大,其刚性越强,变形程度越小。
橡胶模量是指橡胶材料在受到外力作用时,应力与应变之比,单位是弹性模量。
橡胶模量的大小反映了橡胶材料在受力时的弹性性能,模量越大,材料的弹性越差。
通常情况下,硬度大的橡胶材料其模量也较大,这是因为硬度的增加会使橡胶分子之间的相互作用力增强,从而使材料的整体弹性模量增加。
但是,如果橡胶材料的硬度过大,可能会导致材料变脆,从而使其模量降低。
另外,橡胶材料的硬度还与其配方有关,不同的配方会导致橡胶材料的硬度不同。
因此,硬度和橡胶模量之间的关系并不是简单的线性关系,而是取决于多种因素。
在实际应用中,需要根据具体的使用环境和要求来选择合适的硬度与模量的橡胶材料。
例如,对于需要承受较大压力的橡胶制品,需要选择硬度较大的材料,以提高其刚性和抗压性能;而对于需要具有较好弹性的橡胶制品,则需要选择硬度较小的材料,以保持其良好的弹性性能。
总之,硬度和橡胶模量之间的关系是一个复杂的问题,需要考虑多种因素。
在实际应用中,需要根据具体的要求来选择合适的硬度与模量的橡胶材料。
永久硬度的概念永久硬度是指在某种外力作用下,物质的形状或结构发生改变并保持在该状态下的程度。
它是一个物质在外力作用下的弹性恢复能力的衡量指标。
永久硬度往往与弹性模量存在一定的关联,弹性模量越高,物质的永久硬度往往也越高。
永久硬度是一个特性,不同物质的永久硬度可以有很大的差异。
例如,在金属材料中,永久硬度可以通过比较金属的塑性变形程度来体现。
当金属受到外力作用时,其原子间的结构会发生一定程度的变化,如果金属能够恢复到原来的形状或结构,那么说明金属的永久硬度较低;反之,如果金属发生可见的形状或结构的改变,并且不能恢复到原来的状态,那么说明金属的永久硬度较高。
永久硬度的存在对于材料的实际应用有着重要的意义。
一方面,较高的永久硬度意味着材料具有较好的刚性和耐久性,能够承受更大的外力作用而不变形或损坏。
这对于一些需要具备较高机械强度的材料来说非常重要,例如建筑结构中的钢材。
另一方面,永久硬度较低的材料在一定程度上能够更好地适应外力的变化,具有较好的可塑性和变形能力。
这对于一些需要具备较好韧性的材料来说非常重要,例如金属线材、橡胶等。
以金属材料为例,永久硬度的提高可以通过材料的合金化、热处理和加工工艺的调整来实现。
通过合金化可以改变金属的晶体结构和原子间的相对位置,从而影响永久硬度。
通过热处理可以改变金属的晶粒尺寸和组织结构,进而改变材料的永久硬度。
通过加工工艺的调整,例如冷轧、冷拔等,也可以增加金属材料的永久硬度。
除了金属材料,永久硬度也适用于其他材料,例如陶瓷材料和塑料材料。
这些材料的永久硬度主要由材料的分子结构和凝固过程中的物理化学参数决定。
对于陶瓷材料来说,其永久硬度往往较高,因为其分子结构具有较高的硬度。
而对于塑料材料来说,其永久硬度往往较低,因为其分子结构具有较低的硬度。
总之,永久硬度是衡量物质在外力作用下形状或结构改变程度的指标。
它对于材料的弹性恢复能力、可塑性和耐久性等方面有着重要的影响。
不同类型的材料具有不同的永久硬度特性,可以通过合金化、热处理和加工工艺等手段来调整材料的永久硬度。
1、弹性模量:(1)定义弹性模量:材料在弹性变形阶段内,正应力和对应的正应变的比值。
材料在弹性变形阶段,其应力和应变成正比例关系(即符合胡克定律),其比例系数称为弹性模量。
“弹性模量”是描述物质弹性的一个物理量,是一个总称,包括“杨氏模量”、“剪切模量”、“体积模量”等。
所以,“弹性模量”和“体积模量”是包含关系。
一般地讲,对弹性体施加一个外界作用(称为“应力”)后,弹性体会发生形状的改变(称为“应变”),“弹性模量”的一般定义是:应力除以应变。
例如:线应变——对一根细杆施加一个拉力F,这个拉力除以杆的截面积S,称为“线应力”,杆的伸长量dL除以原长L,称为“线应变”。
线应力除以线应变就等于杨氏模量E=( F/S)/(dL/L)剪切应变——对一块弹性体施加一个侧向的力f(通常是摩擦力),弹性体会由方形变成菱形,这个形变的角度a称为“剪切应变”,相应的力f除以受力面积S称为“剪切应力”。
剪切应力除以剪切应变就等于剪切模量G=( f/S)/a体积应变——对弹性体施加一个整体的压强p,这个压强称为“体积应力”,弹性体的体积减少量(-dV)除以原来的体积V称为“体积应变”,体积应力除以体积应变就等于体积模量: K=P/(-dV/V)在不易引起混淆时,一般金属材料的弹性模量就是指杨氏模量,即正弹性模量。
单位:E(弹性模量)吉帕(GPa)(2)影响因素弹性模量是工程材料重要的性能参数,从宏观角度来说,弹性模量是衡量物体抵抗弹性变形能力大小的尺度,从微观角度来说,则是原子、离子或分子之间键合强度的反映。
凡影响键合强度的因素均能影响材料的弹性模量,如键合方式、晶体结构、化学成分、微观组织、温度等。
因合金成分不同、热处理状态不同、冷塑性变形不同等,金属材料的杨氏模量值会有5%或者更大的波动。
但是总体来说,金属材料的弹性模量是一个对组织不敏感的力学性能指标,合金化、热处理(纤维组织)、冷塑性变形等对弹性模量的影响较小,温度、加载速率等外在因素对其影响也不大,所以一般工程应用中都把弹性模量作为常数。
硬度和橡胶模量的关系橡胶是一种常见的弹性材料,它具有独特的力学性能,其中硬度和橡胶模量是两个重要的参数。
硬度是衡量材料抵抗变形的能力,而橡胶模量则是衡量材料的刚度。
本文将探讨硬度与橡胶模量之间的关系。
我们需要明确硬度和橡胶模量的定义。
硬度是指材料在受力下抵抗划痕或压痕的能力,常用的硬度测试方法有洛氏硬度、布氏硬度等。
橡胶模量则是指材料在受力下的应力与应变之间的比例关系,可以反映材料的刚度。
硬度和橡胶模量之间存在一定的关联。
一般来说,硬度越大,橡胶模量也越大。
这是因为硬度大的材料在受力下更难发生形变,需要更大的应力才能使其产生应变。
而橡胶模量则是描述材料的刚度,即单位应力下的应变程度。
所以,硬度大的橡胶材料相对来说更加刚硬。
然而,硬度和橡胶模量之间并不是严格的线性关系。
由于橡胶的特殊结构和性质,硬度增加到一定程度后,橡胶模量的增加速度会逐渐减缓。
这是因为橡胶材料在受力下会发生弹性变形和塑性变形,而塑性变形会导致材料的刚度降低。
因此,当硬度增加到一定程度时,橡胶材料的刚度增加速度将会减缓。
橡胶材料的硬度和橡胶模量还受到其他因素的影响。
例如,橡胶的配方、加工工艺和温度等都会对其硬度和橡胶模量产生影响。
不同的橡胶材料具有不同的配方和结构,因此其硬度和橡胶模量也会有所差异。
总结起来,硬度和橡胶模量之间存在一定的关联,硬度大的橡胶材料相对来说更加刚硬。
然而,这种关系并非严格的线性关系,而是受到橡胶材料的特殊结构和性质的影响。
此外,橡胶材料的配方、加工工艺和温度等也会对其硬度和橡胶模量产生影响。
理解硬度与橡胶模量之间的关系有助于我们更好地应用橡胶材料,并在实际工程中选择合适的橡胶材料。