因子分析方法与SPSS

如何利用SPSS做因子分析等分析SPSS是一款强大的统计分析软件，可以用于各种数据分析任务，包括因子分析。

因子分析是一种用于探究观测变量之间关系的统计方法，它可以帮助我们理解数据集中不同变量之间的相关性和结构。

下面是一个简要的关于如何利用SPSS进行因子分析的步骤：1.准备数据首先，需要确保将数据整理成适合因子分析的格式。

确保数据集中的变量是连续型变量，并且不存在缺失值。

如果存在缺失值，需要进行数据处理或进行数据填充。

2.导入数据打开SPSS软件，然后依次选择“File”、“Open”来导入数据文件。

选择正确的文件路径和文件名，然后点击“打开”按钮。

3.创建因子分析模型选择“Analyze”菜单下的“Dimension Reduction”子菜单，然后选择“Factor”。

将需要进行因子分析的变量移至右侧的“Variables”框中，然后点击“OK”按钮。

4.选择因子提取方法5.设置因子提取参数出现因子提取对话框后，可以选择提取的因子数目和提取标准。

默认情况下，SPSS会提取所有可能的因子。

也可以根据实际需要进行调整。

完成设置后，点击“Continue”按钮。

6.选择因子旋转方法因子旋转可帮助我们更好地理解因子结构。

在因子分析向导的旋转选项中，可以选择旋转方法，如正交旋转和斜交旋转等。

选择一个适合你的需求的旋转方法，然后点击“Rotation”按钮。

7.设置旋转参数出现旋转参数对话框后，可以选择旋转的方法和旋转的标准。

默认情况下，SPSS会选择最大方差法和标准负荷量，但你可以根据需要进行调整。

完成设置后，点击“Continue”按钮。

8.检查结果在因子分析向导的“Descriptives”选项中，可以查看因子提取和旋转后的结果。

这些结果包括因子载荷矩阵、公因子方差和解释方差等信息。

仔细检查结果，确保它们符合你的预期。

9.解释结果在进行因子分析后，需要解释因子载荷矩阵以及其他统计结果。

因子载荷矩阵可以告诉你每个变量与每个因子之间的关系。

基于SPSS的主成分分析与因子分析的辨析主成分分析和因子分析是两种常用的多元统计分析方法，用于处理多个变量之间的关系和结构。

尽管它们在一些方面相似，但它们有着不同的目标、假设和应用领域。

主成分分析（PCA）是一种降维技术，旨在将多个相关的变量转化为较少数量的互相无关的新变量，称为主成分。

主成分是原始变量线性组合的结果，它们按照方差的大小递减排序，第一个主成分解释了尽可能多的方差，第二个主成分解释了剩余的方差，依此类推。

主成分分析的目标是找到最重要的成分，以减少数据维度并保留尽可能多的信息。

因子分析（FA）是一种探索性分析方法，旨在找到观察到的变量背后潜在的隐藏因子及其之间的关系。

它假设每个观察到的变量受到几个潜在因子的影响，并通过解释方差-共方差矩阵来确定这些因子。

因子分析的目标是解释数据的系统结构，并识别变量之间的潜在关系。

下面是主成分分析和因子分析的几个区别：1.假设：主成分分析假设所有的变量都是线性相关的，而因子分析假设变量之间存在潜在的隐藏因子。

2.目标：主成分分析的目标是减少数据的维度，使用少量的主成分来解释尽可能多的方差。

因子分析的目标是找出潜在因子，并解释数据的结构。

3.变量解释：在主成分分析中，每个主成分解释了数据中的方差，而在因子分析中，每个因子代表了一个潜在原因，描述了观察到的变量之间的共同性。

4.变换：在主成分分析中，通过线性组合原始变量来创建主成分。

在因子分析中，每个观察到的变量都被假设为由潜在因子和特定的误差项组合而成。

5.前提要求：主成分分析对变量之间的线性关系没有特定的要求，可以处理混合类型的数据。

因子分析假设线性关系是必需的，且数据应满足正态分布。

尽管主成分分析和因子分析在一些方面不同，但它们也有一些共同之处。

它们都可以用于数据降维和构建新的变量，以更好地解释和理解数据。

此外，它们都是无监督学习方法，不需要以前的假设。

在实际应用中，选择主成分分析还是因子分析取决于具体的研究目标和数据属性。

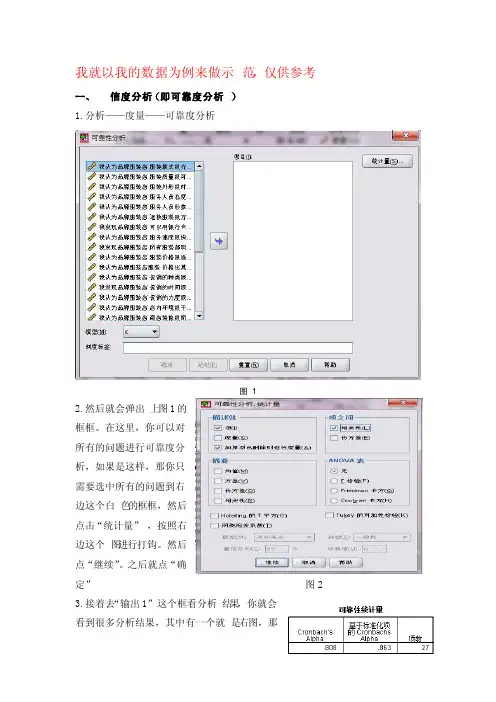
我就以我的数‎据为例来做示‎范，仅供参考一、信度分析（即可靠度分析‎）1.分析——度量——可靠度分析图 12.然后就会弹出‎上图1的框框‎。

在这里，你可以对所有‎的问题进行可‎靠度分析，如果是这样，那你只需要选‎中所有的问题‎到右边这个白‎色的框框，然后点击“统计量”，按照右边这个‎图进行打钩。

然后点“继续”。

之后就点“确定”图23.接着去“输出1”这个框看分析‎结果，你就会看到很‎多分析结果，其中有一个就‎是右图，那第一个0.808就是你‎所选择进行分‎析的数据的信‎度。

如果你想把每‎一个维度的数‎据进行独立的‎信度分析，那道理也是一‎样的。

二、因子分析在做因子分析‎之前首先要判‎断这些数据是‎否适合做因子‎分析，那这里就需要‎进行效度检验‎，不过总共效度‎检验是和因子‎分析的操作同‎步的，意思就是说你‎在做因子分析‎的时候也可以‎做效度检验。

具体示范如下‎：1.分析——降维——因子分析图 2一般来说，咱们做因子分‎析的时候是为‎了把那些具有‎共同属性的因‎子归类成一类‎，说的简单点就‎是要验证咱们‎所选取的每一‎个维度下面的‎题目是属于这‎个维度，而非其他维度‎的。

那一般来说，因子分析做出‎来的结果就是‎你原本有几个‎维度，最终分析结果‎就会归类成几‎个公因子。

2.一般来说，自变量的题目‎和因变量的题‎目是要独立分‎析的。

我的课题是“店面形象对顾‎客购买意愿的‎影响”那自变量就是‎店面形象的那‎些维度，因变量就是顾‎客购买意愿。

3.将要做分析的‎题目选择到右‎边的白框之后‎，就如下图打钩‎：“抽取”和“选项”两个不用管他‎。

然后就点“确定”4.按照上述步骤‎操作下来之后‎，就可以去“输出1”看分析结果。

首先看效度检‎验的结果：这里要看第一‎行和最后一行‎的数据，第一行数据为‎0.756，表明效度较高‎，s ig 为0.000，这两个结果显‎示这份数据完‎全可以做因子‎分析。

那就去看因子‎分析的结果。

《SPSS数据分析教程》——因子分析因子分析（Factor Analysis）是一种常用的统计分析方法，用于研究多个变量之间的相关性和结构关系。

它通过将众多变量转化为相对较少的几个潜在因子，帮助研究者理解和解释数据的结构。

因子分析的目标是通过寻找潜在因子来解释观察到的变量之间的关系。

在因子分析中，变量被假设为由若干个潜在因子和测量误差所决定。

潜在因子是无法直接观测到的，只能通过观测到的变量来推断。

通过因子分析，可以提取出影响变量的潜在因子，从而简化数据分析和数据呈现的复杂度。

因子分析的步骤主要包括：1.设计研究目的和问题。

确定要分析的变量和研究的目标，为分析奠定基础。

2.收集和准备数据。

收集包含需要分析的变量的数据，确保数据的质量，如缺失值处理、异常值处理等。

3.进行初步分析。

对数据进行描述性统计分析，了解各个变量的基本情况，以及变量之间的相关性。

4.进行因子提取。

通过因子提取方法，提取出能够解释大部分变量方差的因子。

常用的因子提取方法有主成分分析法和极大似然估计法等。

5.进行因子旋转。

提取出的因子通常是不易解释和理解的，需要通过因子旋转方法，将因子转化为更容易解释的形式。

常用的因子旋转方法有正交旋转和斜交旋转等。

6.解释因子载荷。

因子载荷表示变量与因子之间的相关性，可以用于解释因子的含义和影响变量的程度。

7.因子得分计算和解释。

通过因子得分计算，可以将观测变量转化为因子得分，从而进一步分析观测变量之间的关系。

8.检验模型合理性。

通过适当的统计方法，检验因子分析模型的合理性和拟合度。

9.解释结果和报告。

根据因子分析的结果，解释潜在因子的含义和变量之间的关系，并撰写报告。

因子分析在很多领域都有广泛的应用，如心理学、教育学、社会学等。

在心理学中，因子分析可以用于构建心理测量量表，如人格特质量表、情绪测量量表等；在市场研究中，可以用于分析消费者的购买动机和偏好等；在教育学中，可以用于分析学生的学习行为和学习成绩等。

因子分析SPSS操作因子分析是一种多变量统计方法，旨在发现潜在的结构和相关性，以便简化数据集并解释变量之间的关系。

SPSS（统计软件包社会科学）是一种广泛使用的统计软件，可以帮助研究人员进行因子分析。

在SPSS中进行因子分析的步骤如下：1.数据准备：-确保数据集已经导入到SPSS中。

-检查和清洗数据，确保数据完整、准确，并且符合因子分析的前提条件。

2.因子分析模型：- 打开SPSS软件并选择“Analyze”菜单。

- 从下拉菜单中选择“Dimension Reduction”>“Factor Analysis”。

3.变量选择：- 从左侧的变量列表中选择要进行因子分析的变量，并将它们移动到右侧的“Variables”框中。

-这些变量应该是连续变量，而非分类变量。

4.因子提取：- 在“Factor Analysis”对话框的“Extraction”选项卡中选择因子提取方法。

- 确定要提取的因子数量。

可以使用Kaiser标准（主成分分析时为特征值大于1）或Scree Plot来指导因子数量的选择。

5.因子旋转：- 进入“Rotation”选项卡，选择适当的因子旋转方法。

- 常用的方法包括Varimax、Promax、Quartimax等。

-因子旋转的目标是最大化因子载荷的简单性和解释性。

6.结果解释：-在因子分析的结果中，可以查看各个变量的因子载荷矩阵，它描述了每个变量在每个因子上的影响程度。

-可以选择将因子载荷阈值设置为一定值，以便筛选出具有较高负载的变量。

-查看每个因子的解释方差，以了解它们对原始变量的解释程度。

7.结果可视化：-可以使用SPSS的图表功能来可视化因子分析结果。

-比如，可以绘制因子载荷矩阵的热图，用不同颜色表示不同的负载水平。

-还可以绘制因子解释方差的条形图，以比较每个因子的贡献程度。

需要注意的是，因子分析在使用时需要考虑以下几点：-样本量必须足够大，一般建议至少大于观测变量数的10倍。

基于SPSS软件的因子分析法及实证分析基于SPSS软件的因子分析法及实证分析引言：随着社会的发展和数据的大规模积累，研究者们面临着海量的数据，如何从中获取有效的信息成为一个亟待解决的问题。

因子分析（Factor Analysis）作为一种数据分析方法，广泛应用于心理学、社会学、教育学、市场营销等领域。

本文将介绍基于SPSS软件的因子分析法以及实证分析的基本原理和步骤。

一、因子分析法概述因子分析法是一种通过统计方法对变量进行降维的分析技术。

它的目的是通过寻找共同的变异性，将一组相关的变量转化为一组较少的潜在因子。

这使得复杂的数据集可以被简化为更容易理解和分析的几个潜在因子。

二、因子分析法的基本原理1. 主成分分析（Principal Component Analysis，PCA）主成分分析是因子分析的一种方法，旨在寻找数据中的最主要的一些因素。

它通过对协方差矩阵进行特征分解，得到特征值和特征向量。

特征值表示对应的特征向量的重要程度，特征向量表示潜在因子与原始变量之间的关系。

2. 公因子分析（Common Factor Analysis，CFA）公因子分析是另一种常用的因子分析方法。

它假设观测变量受到共同的潜在因子影响，同时还存在独立的特殊因素。

公因子分析通过最大似然估计或最小方差法估计因子载荷矩阵，找出与潜在因子最相关的观测变量。

三、基于SPSS软件的因子分析步骤1. 数据准备采集研究数据后，首先需要将数据导入SPSS软件，并保证数据的可靠性和完整性。

2. 数据检查与整理对数据进行检查，确保数据的完整性和一致性。

如有缺失值或异常值，可以选择删除或进行数据插补等处理。

3. 因子分析模型选择根据具体问题和数据特点，选择适合的因子分析模型，如主成分分析或公因子分析。

4. 因子提取通过SPSS软件进行因子提取。

在主成分分析中，可以根据特征值-特征向量矩阵选择特征值大于1的主成分，将其作为因子。

在公因子分析中，可以根据因子载荷矩阵确定合适的因子个数。

基于SPSS统计软件的因子分析法及实证分析基于SPSS统计软件的因子分析法及实证分析一、引言因子分析法是一种常用的数据降维分析方法，旨在通过识别出观测变量之间的潜在因子结构，以更简洁的方式解释数据的变异。

同时，SPSS统计软件作为一种强大的分析工具，提供了直观的界面和丰富的功能，可以便捷地进行因子分析。

二、因子分析法原理因子分析法的核心思想是将大量的变量转化为潜在的少数几个因子，这些因子能够解释观测变量之间的共同方差。

具体步骤如下：1. 数据准备：需要一组观测变量，这些变量应该是连续变量，并且样本量要足够大。

2. 制定假设：设定因子数量或某些特定的加载限制。

3. 提取因子：使用SPSS的因子分析功能进行因子提取，常用的方法有主成分分析和极大似然估计法。

4. 因子旋转：对提取出的因子进行旋转，以使得因子更具解释性，常用的方法有正交旋转和斜交旋转。

5. 因子解释：根据各个因子的载荷以及因子之间的相关关系，解释这些潜在因子代表的含义。

三、SPSS软件的因子分析功能SPSS软件提供了丰富的因子分析功能，使用者可以根据自身需求进行定制化的分析。

具体步骤如下：1. 导入数据：首先需将需要进行因子分析的数据导入SPSS软件中。

2. 变量选择：根据研究目的和实际情况，选择需要进行因子分析的变量。

3. 因子提取：选择适当的因子提取方法，并设置主成分个数或提取的因子个数。

4. 因子旋转：选择适当的因子旋转方法，并设定旋转的目标。

5. 结果解释：根据因子载荷矩阵和因子之间的相关关系解释因子的意义，并给出结论。

四、实证分析为了进一步说明因子分析法在实证研究中的应用，以消费者偏好研究为例进行实证分析。

1. 数据收集：收集消费者对不同品牌产品的评价数据，包括外观、品质、价格、口碑等多个变量。

2. 数据处理：将收集到的数据导入SPSS软件中，并进行数据清洗和预处理，确保数据的准确性和一致性。

3. 因子分析：运用SPSS的因子分析功能，提取潜在因子结构，并进行因子旋转以获得更具解释性的结果。

基于SPSS统计软件的因子分析法及实证分析一、本文概述随着信息技术的迅猛发展，数据分析已经成为众多领域决策和研究的核心工具。

其中，因子分析法作为一种降维技术，在提取和分析大量数据中的潜在结构、识别并解释关键变量间的关联性方面，展现出强大的实用性。

本文旨在探讨基于SPSS统计软件的因子分析法及其在实证分析中的应用。

我们将首先介绍因子分析法的基本原理及其在统计学中的地位，然后详细阐述在SPSS软件中实现因子分析的步骤和方法，最后通过实证分析案例来展示因子分析法在解决实际问题中的应用效果。

本文的目的不仅在于为读者提供一套系统的因子分析操作指南，更希望通过实证分析来揭示因子分析法在实际研究中的价值，为相关领域的学者和实践者提供有益的参考和启示。

二、因子分析法的理论基础因子分析法是一种多元统计分析方法，它的理论基础主要源自于数理统计学、线性代数以及心理测量学等领域。

该方法通过研究众多变量之间的内部依赖关系，找出控制所有变量的少数几个随机变量去描述多个变量或因素之间的联系。

这些少数几个随机变量被称为“因子”或“潜在变量”，它们能够反映原有变量的大部分信息。

因子分析法的核心在于通过降维技术简化数据结构，即通过对原始变量的相关矩阵或协方差矩阵内部结构的研究，找出能够解释大部分变量变异的少数几个公共因子。

这些公共因子是原始变量的线性组合，彼此之间互不相关，并且每个原始变量都可以表示为这些公共因子的线性组合加上一个特殊因子。

特殊因子代表了原始变量中不能被公共因子解释的部分。

因子分析法的数学模型可以表示为： = AF + ε，其中是原始变量向量，A是因子载荷矩阵，F是公共因子向量，ε是特殊因子向量。

因子载荷矩阵A的元素j表示第i个原始变量在第j个公共因子上的载荷，即第i个原始变量与第j个公共因子之间的相关程度。

在因子分析过程中，通常需要进行几个关键步骤，包括：计算相关矩阵或协方差矩阵，估计因子载荷矩阵，进行因子旋转以改善因子的解释性，以及计算因子得分以便进行后续的统计分析。

主成分分析与因子分析详细的异同和SPSS软件1.目的不同：主成分分析的目的是通过将原始变量转化为一组线性无关的主成分来解释数据的变异；而因子分析的目的是通过将原始变量解释为一组潜在的因子来揭示数据背后的结构。

2.数据处理方式不同：主成分分析是以变量为基础进行分析，对变量进行线性组合，通过找到方差最大的主成分来解释原始数据；而因子分析是以样本为基础进行分析，通过将变量分解为共同因子和唯一因素来解释原始数据。

3.解释度不同：主成分分析主要关注每个主成分所解释的原始数据的方差贡献率，即主成分的量变解释；而因子分析主要关注因子与原始变量之间的相关性解释，即因子的质变解释。

4.假设不同：主成分分析假设主成分是线性组合变量，变量之间相互独立；而因子分析假设变量是从潜在因子派生出来的，潜在因子之间可以相关。

SPSS软件是一种功能强大的统计分析工具，可用于进行主成分分析和因子分析。

1.打开SPSS软件并导入数据集。

2.选择“分析”菜单，然后选择“降维”子菜单，再选择“主成分”或“因子”。

3.在主成分分析或因子分析对话框中，选择需要进行分析的变量，并选择相应的分析方法和选项（例如，提取条件、旋转方法等）。

4.点击“确定”按钮，SPSS将根据选择的参数进行分析，并生成结果报告。

5.解读结果报告，包括各个主成分或因子的【特征值】、【所解释的方差】、【载荷矩阵】等。

6.根据需求进行进一步分析和解释，例如提取特定数量的主成分或因子，对主成分或因子进行旋转等。

总之，主成分分析和因子分析是常用的数据降维和特征提取方法，它们在目的、数据处理方式、解释度和假设等方面存在一定的异同。

在使用SPSS进行主成分分析和因子分析时，需要选择合适的参数和方法，并解读分析结果以获得有效的结论。

因子分析的SPSS实现因子分析是一种多变量统计分析方法，用于挖掘多个观察变量之间的潜在维度。

它可以帮助我们减少数据的维度，理解变量之间的关系，并揭示隐藏的结构。

SPSS（统计包统计学软件）是一种广泛使用的统计分析软件，可用于实现因子分析。

下面是在SPSS中执行因子分析的一般步骤：1.准备数据：导入数据文件并确保数据格式正确。

数据应以行列表示个体，以列列表示观察变量。

2.选择因子分析方法：SPSS提供了几种因子分析方法，包括主成分分析和因子分析。

选择适当的方法是根据研究目的和数据性质来确定的。

3.执行因子分析：-在SPSS菜单栏中，选择"分析"，然后选择"降维"，再选择"因子"。

-在因子分析对话框中，选择要分析的变量，并将它们添加到“因子分析变量”列表中。

-在“因子分析变量”列表下方的“因子分析可选命令”中，选择所需的选项，如旋转方法、提取因子数等。

4.选择因子数：因子数是指在因子分析中用于解释变量之间关系的维度数。

选择因子数时，可以根据很多方法进行判断，如Kaiser准则、断裂点法和平行分析等。

在SPSS中，可以使用不同的提取因子数方法，比如特征值大于1和Scree plot。

5.旋转因子：在因子分析中，因子可以进行旋转以提高解释性。

旋转方法包括正交旋转和斜交旋转。

查找可解释因素的最初结构后，可根据数据和研究目的选择适当的旋转方法。

6.结果解读：通过SPSS生成的输出结果，我们可以获得一些关键信息，如特征值、共方差解释总量、因子载荷矩阵、因子之间的相关性等。

根据这些结果，我们可以解读因子分析的结果，并利用它们做进一步的研究。

需要注意的是，因子分析是一种复杂的统计方法，需要在进行因子分析之前对相关性和样本适应性进行检查。

此外，还需要在解释因子分析结果时小心，尽量确保结果的解释合理可靠。

总之，SPSS是一种功能强大的软件工具，可用于执行因子分析以及其他各种统计分析。

使用SPSS软件进行因子分析和聚类分析的方法因子分析和聚类分析是一种常用的数据分析方法，可以用于数据降维和分组。

SPSS是一款常用的统计软件，提供了丰富的分析工具和函数，可以方便地进行因子分析和聚类分析。

一、因子分析：因子分析是一种多变量分析方法，可以将一组相关的变量转化为少数几个互相独立的综合变量，称为因子。

因子分析可以用于降低数据的维度，提取主要的因素，并分析因素之间的关系。

以下是使用SPSS软件进行因子分析的步骤：1.打开SPSS软件，并导入要进行因子分析的数据集。

2.菜单栏选择“分析”-“降维”-“因子”。

3.在弹出的因子分析对话框中，选择要进行因子分析的变量，将其添加到“因子”框中。

4.在“提取”选项中，选择提取的因子个数。

可以根据实际需求和经验进行选择。

5. 在“旋转”选项中，选择旋转方法。

常用的旋转方法有方差最大旋转（Varimax），斜交旋转（Oblique）等。

6.点击“确定”按钮，进行因子分析。

7.SPSS会生成因子载荷矩阵、解释方差表、因子得分等结果。

可以根据因子载荷矩阵和解释方差表来解释因子的含义和解释度。

8.根据具体需求和分析目的，可以进行因子得分的计算和因子分组的分析。

二、聚类分析：聚类分析是一种无监督学习方法，可以将一组样本数据自动分成若干互不相交的群组，称为簇。

聚类分析可以用于数据的分组和群体特征的分析。

以下是使用SPSS软件进行聚类分析的步骤：1.打开SPSS软件，并导入要进行聚类分析的数据集。

2.菜单栏选择“分析”-“分类”-“聚类”。

3.在弹出的聚类分析对话框中，选择要进行聚类分析的变量，将其添加到“变量”框中。

可以选择多个变量进行分析。

4.在“距离”选项中，选择计算样本间距离的方法。

常用的方法有欧几里得距离、曼哈顿距离等。

5. 在“聚类方法”选项中，选择聚类算法的方法。

常用的方法有层次聚类（Hierarchical Clustering）、K均值聚类（K-means）等。

SPSS是一种专业的统计分析软件，被广泛应用于社会科学研究、市场调查、医学和生物科学研究等领域。

因子分析是SPSS中常用的一种统计方法，用于发现变量之间的内在关系和结构。

本文将介绍如何利用SPSS进行因子分析，以及因子分析的基本原理和操作步骤。

1. 数据准备在进行因子分析之前，首先需要准备好数据。

数据可以采用多种方式获取，例如调查问卷、实验记录、观测数据等。

在SPSS中，数据通常以Excel或CSV格式导入。

导入数据后，需要对数据进行清洗和变量筛选，确保数据质量和可靠性。

2. 因子分析的基本原理因子分析是一种多变量分析方法，用于发现变量之间的潜在结构和相关关系。

它可以将多个变量转化为少数几个因子，以便更好地理解和解释变量之间的关系。

因子分析的基本原理是通过主成分分析或最大方差法，提取共性因子和特殊因子，从而揭示变量之间的内在结构。

3. 因子分析的操作步骤在SPSS中进行因子分析的操作步骤如下：（1）导入数据：使用“文件”菜单中的“导入数据”功能，将数据文件导入到SPSS中。

（2）选择因子分析：在“分析”菜单中选择“因子分析”，弹出因子分析对话框。

（3）选择变量：在因子分析对话框中，选择需要进行因子分析的变量，并设置相应的参数。

（4）提取因子：在因子分析对话框中，选择提取因子的方法和标准，并进行因子提取。

（5）旋转因子：在因子分析对话框中，选择旋转方法和标准，并进行因子旋转。

（6）解释因子：根据因子载荷矩阵和方差解释率，解释提取的因子结构和含义。

4. 因子分析的结果解释在进行因子分析后，需要对结果进行解释和分析。

通常可以根据因子载荷矩阵、方差解释率和特征根等指标来解释因子的结构和含义。

此外，还可以使用因子得分和因子得分图表来对因子进行解释和可视化呈现。

5. 因子分析的应用因子分析在实际应用中具有广泛的应用价值，可以用于变量降维、变量筛选、变量融合等多个方面。

例如，在市场调查中，可以利用因子分析发现消费者的偏好和需求；在医学研究中，可以利用因子分析发现疾病的相关因素和病因；在社会科学研究中，可以利用因子分析发现社会现象的内在结构和相关因素。

因子分析的SPSS实现因子分析（Factor Analysis）是统计学中一种常用的多变量分析方法，用于将具有相关性的一组变量归纳为较小数量的互相关联的构成因子。

SPSS是一种流行的统计分析软件，提供了方便易用的功能，可以方便地进行因子分析。

在SPSS中进行因子分析的步骤如下：步骤1：加载数据首先打开SPSS软件，并加载需要进行因子分析的数据。

可以选择从文件中导入数据，或者直接将数据复制粘贴到SPSS的数据视图中。

确保数据在SPSS中正确加载并显示。

步骤2：选择变量在"变量视图"或"数据视图"中，选择需要进行因子分析的变量。

可以使用鼠标按住Ctrl键或Shift键选择多个变量。

选择的变量应该是互相关的，即它们之间应该存在其中一种相关性。

步骤3：进行因子分析在SPSS的菜单栏中选择"分析"，然后选择"数据降维"，再选择"因子"。

在弹出的对话框中，将选中的变量移动到"因子"框中。

可以选择不同的因子提取方法，如主成分法、最大似然法等。

此外，还可以设置因子提取的标准，如特征值、累计方差等。

步骤4：解释因子在因子分析完成后，SPSS提供了多种方法来解释因子。

其中，最常用的方法是因子旋转。

通过旋转因子，可以使得因子在解释上更直观和可解释，同时减少因子之间的相关性。

SPSS提供了多种旋转方法，如正交旋转（如变换等）和斜交旋转（如极大方差法）。

可以根据实际需求选择合适的旋转方法。

步骤5：解释因子载荷因子载荷提供了每个变量与每个因子之间的相关性信息。

在SPSS的因子分析结果中，可以查看因子载荷矩阵，该矩阵显示了每个变量与每个因子的相关系数。

通常认为绝对值大于0.3或0.4的载荷系数比较重要。

步骤6：因子得分计算因子得分计算用于将原始变量转换为因子得分，以进行后续的分析和解释。

在SPSS中，可以通过计算函数来计算因子得分，方法如下：1.在菜单栏中选择"变量视图"，在需要计算因子得分的变量旁边添加一个新的变量。

因子分析SPSS操作因子分析是一种常用的统计方法，用于探索多个变量之间的潜在关系。

它能够帮助研究人员识别出变量之间的关联，从而提取出共同的因素。

SPSS软件是一种广泛使用的统计分析工具，提供了强大的因子分析功能。

下面将详细介绍如何在SPSS中进行因子分析。

首先，在SPSS中打开要进行因子分析的数据集。

确保数据集包含需要进行因子分析的变量。

接下来，选择"分析"菜单，然后选择"尺度"，再选择"因子"。

这会打开"因子分析"对话框。

在"因子分析"对话框中，将需要进行因子分析的变量移动到右侧的框中，通过单击变量名称，再单击右侧的"箭头"按钮，将其添加到因子分析的变量列表中。

在"因子分析"对话框中，有几个选项需要设置。

首先是"提取方法"，它决定了如何提取因子。

常用的方法有主成分分析和最大似然估计。

主成分分析通常用于连续变量，最大似然估计用于分类变量。

选择一个适当的方法。

其次，是选择"旋转方法"，它决定了如何旋转因子。

常用的方法有方差最大化和直角旋转。

方差最大化旋转使得每个因子解释的变异最大化，直角旋转使得因子之间不相关。

根据研究目的选择一个合适的旋转方法。

最后，设置"因子的数目"，它决定了最终提取几个因子。

通常，根据因子的方差解释度和解释的变量数目来决定提取几个因子。

可以尝试提取不同数目的因子，然后根据结果进行选择。

点击"确定"按钮后，SPSS会进行因子分析，并在输出窗口中显示结果。

输出结果包括因子的提取度、因子载荷矩阵、解释的方差比例等。

根据因子载荷矩阵可以判断变量与因子之间的关系。

载荷大于0.3或0.4的变量与因子有较强的关联。

可以根据载荷大小对因子进行命名，进一步解释因子所代表的潜在构念。

因子分析spss因子分析是一种常用的统计方法，用于研究变量之间的关系及其对整体的影响。

它的主要作用是将复杂的数据降维并提取出主要因素，从而简化分析过程。

本文将介绍因子分析的基本概念、原理、假设、步骤以及在SPSS软件中的操作方法。

一、因子分析的基本概念因子分析是一种多变量分析方法，通过寻找一组潜在的共同因素来解释观测变量之间的相关性。

它可以帮助我们理解变量之间的内在关系，并减少数据的复杂性。

二、因子分析的原理因子分析的基本原理是将一组观测变量转化为一组潜在的共同因素。

它假设每个观测变量都受到多个潜在因素的共同影响，并且通过因子载荷来衡量这种影响的强度。

三、因子分析的假设因子分析需要满足以下假设：1. 每个观测变量都是由多个潜在因素共同影响的。

2. 潜在因素之间相互独立。

3. 每个观测变量与潜在因素之间存在线性关系。

4. 观测误差是独立的。

四、因子分析的步骤1. 收集数据并确定分析目的。

2. 进行数据清洗和预处理，包括缺失值处理和异常值处理。

3. 进行合适的因子提取方法。

常用的因子提取方法包括主成分分析和极大似然估计。

4. 确定因子个数。

可以通过观察解释方差贡献和层次图来确定因子个数。

5. 进行因子旋转。

常用的旋转方法包括方差最大旋转和直角旋转。

6. 解释因子载荷。

通过观察因子载荷矩阵来解释变量与潜在因素之间的关系。

7. 计算因子得分。

将观测变量代入因子载荷矩阵，计算每个观测变量的因子得分。

8. 进行因子可靠性和效度检验。

可以使用内部一致性系数和构效效度来评估因子模型的可靠性和效度。

9. 进行结果解读和报告。

五、SPSS中的操作方法在SPSS软件中，进行因子分析的操作步骤如下：1. 打开SPSS软件并导入数据文件。

2. 选择"分析"菜单下的"数据降维"，然后选择"因子"。

3. 在因子分析对话框中，选择需要进行因子分析的变量，并选择因子提取方法和旋转方法。

2020·9（下）157信息科技探索作者简介：肖志芳，实验师，井冈山大学电子与信息工程学院，研究方向为统计分析。

因子分析在SPSS软件中的数据应用解析肖志芳摘 要 SPSS 是有关数据统计分析的一种软件，但当前学界对于它的因子的分析过程仍存在一些疑惑。

文章结合J 市某高校的调研数据，对SPSS 软件进行应用计算，对因子分析的过程进行解析。

关键词 SPSS ；因子分析；数据应用中图分类号 TP3 文献标识码 A 文章编号 1674-6708（2020）267-0157-02作为一项可以从多个变量中抽取共性因子的统计分析技术，因子分析能够揭示复杂又庞大的变量之间的关系，能够从可观测的多个变量中归纳总结出较少个数的因子，以便进行最大程度、最有效的解释并概括这些观测变量的信息，从而计算出事物之间的相关性。

1 因子分析的实例应用本文选取了J 市某高校关于大学生学习倦怠的调查数据，拟对该份数据使用SPSS 应用分析，在对该调查数据进行SPSS 标准化数据处理后如表1所示。

该调查数据共有16个变量，其中T01=我能精力充沛地学习，T02=我不知道该干什么，T03=我很想放弃学习，T04=我在学习中经常能够达到所制定的目标，T05=我在一天的学习结束后感到非常疲劳，T06=学不学我都无所谓，T07=我学习时忘记一切，T08=我最近学习精疲力尽，T09=学习体会不到成就，T10=学习对我没有意义，T11=我能够很好地应付考试，T12=我上课感觉很累，T13=无所谓的态度学习，T14=我有效地解决学习中的问题，T15=我可以做到轻松地应对学习方面的问题，T16=对于所学知识我可以很好掌握。

本案例拟从这16个变量中归纳出较少数量的因子，以便进行有针对性的分析问题、解决问题。

在进行因子分析之前，需要对SPSS 中的因子载荷、因子的方差贡献以及公因子方差等作用进行一些了解[1]。

要理解因子载荷的绝对值与其相关性成正比趋势[2]。