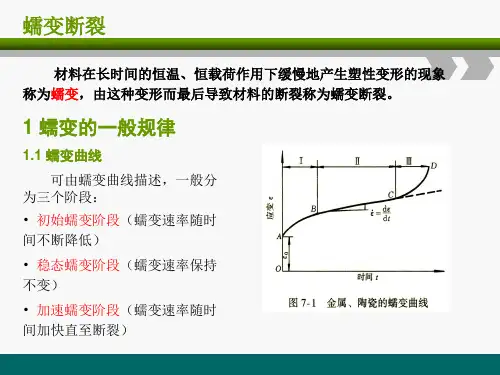
蠕变图谱

4.4蠕变分析4.4.1 蠕变理论4.4.1.1 定义蠕变是率相关材料非线性，即在常荷载作用下，材料连续变形的特性。

相反如果位移固定，反力或应力将随时间而变小，这种特性有时也称为应力松驰，见图4-18a。

图4-18应力松弛和蠕变蠕变的三个阶段如图4-18b所示。

在初始蠕变阶段，应变率随时间而减小，这个阶段一般发生在一个相当短的时期。

在第二期蠕变阶段，有一个常应变率，所以应变以常速率发展，在第三期蠕变阶段，应变率迅速增加直到材料失效。

由于第三期蠕变阶段所经历的时间很短，材料将失效，所以通常情况下，我们感兴趣的是初始蠕变和第二期蠕变。

ANSYS程序中的蠕变行为用来模拟初始蠕变和第二期蠕变。

蠕变系数可以是应力、应变、温度、时间或其它变量的函数。

在高温应力分析中(如核反应堆等)，蠕变分析非常重要。

例如，假设在核反应堆中施加了预荷载，以保证与相邻部件保持接触而不松开。

在高温下过了一段时间后，预荷载将降低(应力松驰)，可能使接触部件松开。

对于一些材料如预应力砼，蠕变也可能十分重要。

最重要的是要记住，蠕变是永久变形。

4.4.1.2 理论介绍蠕变方程：我们通过一个方程来模拟蠕变行为，此方程描述了在实验中观测到的主要特征（特别是在一维的拉伸实验中）。

这个方程以蠕应变率的方式表示出来，其形式如下：上式中，A、B、C、D是从实验中得到的材料常数，常数本身也可能是应力，应变，时间或温度的函数，这种形式的方程被称为状态方程。

上式中，当常数D为负值时，蠕应变率随时间下降，材料处于初始蠕变阶段，当D为0时，蠕应变率为常值，材料处于第二期蠕变阶段。

对于2－D或3－D应力状态，使用VON Mises方程计算蠕应变率方程中所使用的标量等效应力和等效应变。

对蠕变方程积分时，我们使用经过修改的总应变，其表达式为:经过修改的等效总应变为:其等效应力由下式算出：其中：G=剪切模量＝等效蠕应变增量由程序给出的某一种公式进行计算，一般为正值，如果在数据表中，则使用的是衰减的蠕应变率而不是常蠕变率，但这个选项一般不被推荐，因为在初始蠕变所产生的应力为主的情况下，它可能会严重的低估蠕变值。

第23例材料蠕变分析实例—受拉平板本例简单地介绍了蠕变的概念及蠕变材料模型的创建方法，简单地介绍了结构蠕变分析的方法、步骤及要点。

23.1蠕变简介蠕变是指金属材料在长时间的恒温、恒载作用下，持续发生缓慢塑性变形的行为，大多数金属材料在高温下都会表现出蠕变行为。

如果材料发生了蠕变，在恒载作用下结构会发生持续变形；如果结构承受恒位移，则应力会随时间而减小，即产生应力松弛。

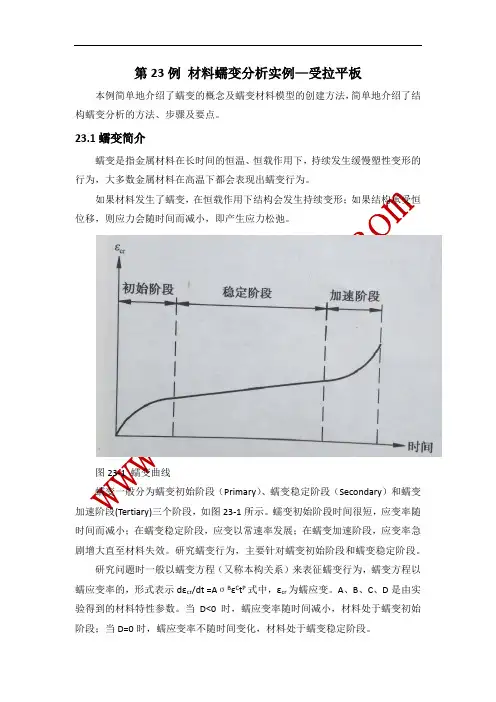
图23-1 蠕变曲线蠕变一般分为蠕变初始阶段（Primary）、蠕变稳定阶段（Secondary）和蠕变加速阶段(Tertiary)三个阶段，如图23-1所示。

蠕变初始阶段时间很短，应变率随时间而减小；在蠕变稳定阶段，应变以常速率发展；在蠕变加速阶段，应变率急剧增大直至材料失效。

研究蠕变行为，主要针对蠕变初始阶段和蠕变稳定阶段。

研究问题时一般以蠕变方程（又称本构关系）来表征蠕变行为，蠕变方程以蠕应变率的，形式表示dεcr/dt =AσBεC t P式中，εcr为蠕应变。

A、B、C、D是由实验得到的材料特性参数。

当D<0时，蠕应变率随时间减小，材料处于蠕变初始阶段；当D=0时，蠕应变率不随时间变化，材料处于蠕变稳定阶段。

在ANSYS中，有一个蠕应变率库供选择。

23.2问题描述一矩形平板，左端固定，右端作用有恒定压力p=100MPa，矩形平板尺寸如图23-2所示，材料的弹性模量为2xl05MPa，泊松比为0.3，蠕变稳定阶段蠕变方程dεcr/dt =C1σC2。

C2，式中，C1=3.125 x10-14，C2=5。

试分析平板右端的位移随时间的变化情况。

提示：为避免出现较小值，力单位用N，长度单位用mm，时间单位为h。

图23-2受拉矩形平板23.3分析步骤23.3.1改变任务名拾取菜单Utility Menu→File→Change Jobname，弹出如图23-3所示的对话框，在“[/FJLNAM]”文本框中输入EXAMPLE23，单击“OK”按钮。

1 蠕变的概念岩石的变形不仅表现出弹性和塑性，而且也具有流变性质，岩石的流变包括蠕变、松弛和弹性后效。

岩石的流变性是指岩石应力应变关系随时间而变化的性质。

蠕变是当应力不变时，变形随时间增加而增长的现象。

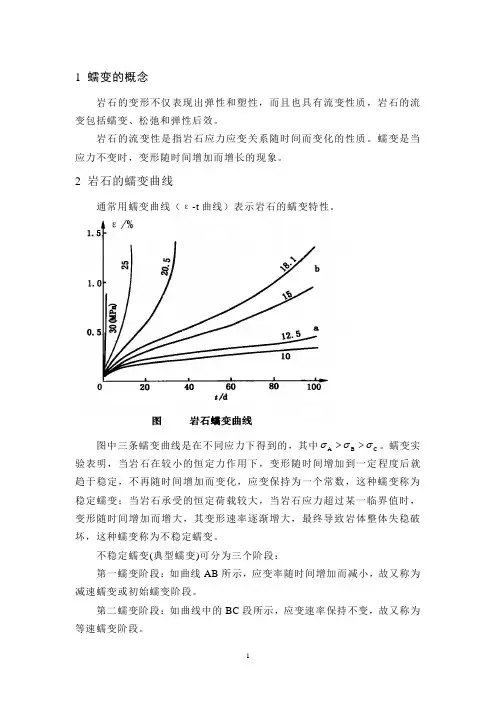
2 岩石的蠕变曲线通常用蠕变曲线（ε-t 曲线）表示岩石的蠕变特性。

图中三条蠕变曲线是在不同应力下得到的，其中C B A σσσ>>。

蠕变实验表明，当岩石在较小的恒定力作用下，变形随时间增加到一定程度后就趋于稳定，不再随时间增加而变化，应变保持为一个常数，这种蠕变称为稳定蠕变；当岩石承受的恒定荷载较大，当岩石应力超过某一临界值时，变形随时间增加而增大，其变形速率逐渐增大，最终导致岩体整体失稳破坏，这种蠕变称为不稳定蠕变。

不稳定蠕变(典型蠕变)可分为三个阶段：第一蠕变阶段：如曲线AB 所示，应变率随时间增加而减小，故又称为减速蠕变或初始蠕变阶段。

第二蠕变阶段：如曲线中的BC 段所示，应变速率保持不变，故又称为等速蠕变阶段。

第三蠕变阶段：如曲线中的CD段所示，应变速率迅速增加直到岩石破坏，故又称为加速蠕变阶段。

一种岩石既可以发生稳定蠕变也可发生不稳定蠕变，这取决于岩石应力的大小。

超过某一临界应力时，蠕变向不稳定蠕变发展；小于此临界应力时，蠕变按稳定蠕变发展。

通常称此临界应力为岩石的长期强度。

3实例3.1 层状岩坡蠕变破坏综合工程地质条件、力的作用方式及边坡具体破坏形式，在考虑时间效应的基础上，杨晓华，陈沅江[1] 对层状岩质边坡的蠕变破坏类型及其所致因素进行了分析探讨，将层状岩质边坡的蠕变破坏分为如下五种主要类型。

3.1.1 水平层状边坡座落式剪切蠕变破坏该类蠕变破坏发生在构造活动区水平或近水平岩层边坡中。

当边坡最终形成后，由于其高度很大，上部破碎岩体的自重应力亦很大，边坡在该自重应力的作用下时常会发生沿边坡下部的水平或近水平软弱夹层蠕动滑移的座落式滑坡。

故这种边坡的蠕变破坏一般首先表现为边坡上部岩体的较大水平剪切位移，当边坡开挖到一定深度时又将表现为垂直剪切位移，一定时间后便将发生沿边坡后缘已形成的滑移面的座落式剧滑。

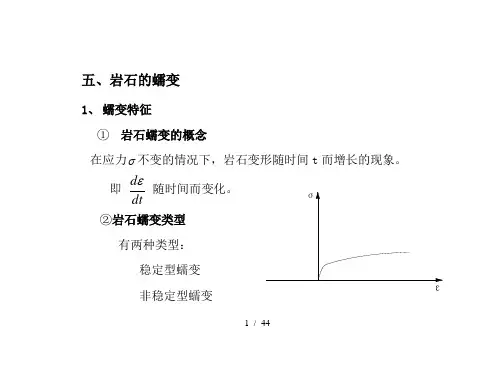
1 / 44五、岩石的蠕变1、 蠕变特征① 岩石蠕变的概念在应力σ不变的情况下，岩石变形随时间t 而增长的现象。

即 dtd ε随时间而变化。

②岩石蠕变类型 有两种类型：稳定型蠕变 非稳定型蠕变a、稳定型蠕变应力作用下，随时间递减，dε零，即0=dt域稳定。

一般在较小应力下或硬岩中。

b、非稳定型蠕变：岩石在恒定应力作用下，岩石变形随时间不断增长，直至破坏。

一般为软弱岩石或应力较大。

2 / 44③蠕变曲线变化特征三个阶段：Ⅰ阶段：初期蠕变。

d曲，应变速率dt小。

属弹性变形。

Ⅱ阶段：等速蠕变。

应变－时间曲线近似直线，应变随时间呈近于等速增长。

出现塑性。

3 / 44Ⅲ阶段：加速蠕变。

应变－时间曲线向上弯曲，其应变速率加快直至破坏。

应指出，并非所有的蠕变都能出现等速蠕变阶段，只有蠕变过程中结构的软化和硬化达到动平衡，蠕变速率才能保持不变。

在Ⅰ阶段，如果应力骤降到零，则ε－t曲线具有PQR形式，曲线从P 点骤变到Q点，PQ＝ε为瞬时弹性变形，而后随时间慢慢退到应变为e零，这时无永久变形，材料仍保持弹性。

在Ⅱ阶段，如果把应力骤降到零，则会出现永久变形，其中TU＝ε。

e4 / 44有直接关系。

变速度变化缓慢，稳定。

率增大。

蠕变速率越大，反之愈小。

5 / 446 / 44岩石长期强度：指 岩石由稳定蠕变转为非稳定蠕变时的应力分界值。

即，岩石在长期荷载作用下经蠕变破坏的最小应力值(∞σ或∞τ) 岩石极限长期强度：指长期荷载作用下岩石的强度。

2、 蠕变经验公式由于岩石蠕变包括瞬时弹性变形、初始蠕变、等速蠕变和加速蠕变，则在荷载长期作用下，岩石蠕变的变形ε可用经验公式表示为：ε＝e ε+)(t ε+t M +)(t T εe ε－瞬时变形；)(t ε－初始蠕变；t M －等速蠕变；)(t T ε－加速蠕变。

7 / 44对于前两个阶段，目前的经验公式主要有三种： ①幂函数取n t A t ⋅=)(ε第一阶段：n e t A ⋅+=εε；第二阶段：)(11t t M t A n e -+⋅+=εε，t ＞1tA 、n 是试验常数，其值取决于应力水平、材料特性以与温度条件。

蠕变试验曲线
蠕变试验曲线是一种用于研究材料在长时间持续加载下发生蠕变变形的曲线。

蠕变变形指的是材料在常温下在一定应力下，随着时间的推移而发生的持续变形现象。

蠕变试验曲线通常分为三个阶段：初蠕变阶段、稳态蠕变阶段和加速蠕变阶段。

在初蠕变阶段，材料经历了一个快速的蠕变变形阶段，曲线呈现出一个陡峭的下坡。

稳态蠕变阶段是指材料的蠕变速率逐渐稳定在一个较低的水平，曲线呈现出一个相对平缓的下坡。

加速蠕变阶段是指材料的蠕变速率开始逐渐增加，曲线会再次变得陡峭。

通过分析蠕变试验曲线，可以评估材料的蠕变特性，包括蠕变强度、蠕变速率和蠕变寿命等。

蠕变试验曲线在材料工程领域的应用非常广泛，可以帮助工程师设计更可靠的材料和结构，提高产品的寿命和性能。

典型的蠕变曲线
典型的蠕变曲线分为四个阶段：
1. 瞬间变形阶段（0a）：在这个阶段，变形量在施加拉应力的瞬间发生。

如果应力超过金属在试验温度下的弹性极限，瞬间变形由弹性变形（0a'）和塑性变形（aa'）组成。

2. 初始蠕变阶段（ab）：在这个阶段，曲线呈下凹型。

特点是应变最初随时间增大较快，但其应变速率随时间迅速递减，到b点达到最小值。

3. 等速蠕变阶段（bc）：在这个阶段，曲线呈近似直线，即应变随时间近似等速增加，直至c点。

4. 加速蠕变阶段（cd）：在这个阶段，蠕变加速发展直至岩块破坏。

蠕变曲线可以反映金属在恒定温度和恒定拉应力下的变形随时间变化的规律。

不同的金属和合金在不同的条件下所得到的蠕变曲线不尽相同，但它们都有一些共同的特征。

把这些共同特征表示出来的蠕变曲线称为典型蠕变曲线。

蠕变蠕变具体描述发展阶段蠕变蠕变图1表示在三个不同的恒定应力作用下，材料的应变ε随时间t变化的典型蠕变曲线。

曲线的终端表示材料发生断裂。

t=0时的应变表示加载结束时的即时应变，它包括弹性应变和塑性应变。

蠕变曲线可分为三个阶段，如图2所示：I为非定常蠕变阶段，应变率随时间的增加而减小；II为定常蠕变阶段，应变率保持常值；在最末阶段Ⅲ，应变率随时间而增大，最后材料在t时刻发生断裂。

通常，升高温度或增加应力会使蠕变加快并缩短达到断裂的时间。

若应力较小或温度较低，则蠕变的第二阶段(Ⅱ)持续较久，甚至不出现第三阶段（Ⅲ），如图1中对应的蠕变曲线；相反，若应力较大或温度较高，则蠕变的第二阶段（Ⅱ）较短，甚至不出现，如图1中对应的蠕变曲线。

蠕变理论发展现状蠕变目前，还没有一个适用于一切材料的统一蠕变理论。

对金属材料目前主要有老化理论、强化理论和蠕变后效理论。

如以表示蠕变的应变（为t=0时的应变），表示蠕变应变率，则对于单向受力情形，这些理论的不同在于：老化理论认为，在恒应力的条件下，时间t以显函数出现于蠕变应变的表达式之中，即p。

强化理论认为，蠕变应变率主要取决于蠕变应变，即有。

蠕变后效理论则认为，蠕变现象实质上是塑性后效，去除应力之后，后效应变是不可恢复的，若以塑性变形规律为基础，可将分解为两部分：蠕变等号右端第一项为基本部分；第二项为后效影响部分，K称为影响函数，它是在τ时刻的单位时间内，单位应力在此后时刻t所引起的变形。

上述各关系式可推广到三向应力状态，但都只在一定条件下近似反映出材料的蠕变性能。

蠕变的微观机制对于不同的材料是不同的。

引起多晶体材料蠕变的原因据认为是原子晶间位错引起的点阵的滑移以及晶间的滑移等。

材料在恒拉应力作用下，经过一定时间t以后发生断裂的现象称为蠕变断裂。

在给定温度下，使材料经过规定时间发生断裂的应力值称为持久强度。

表示恒应力σ随断裂时间t的变化曲线称为持久强度曲线。

在三向应力状态下，一般采用最大正应力（或经适当修正，以考虑剪应力的影响）作为等效应力来绘制持久强度曲线。