06全国高中物理竞赛-质心问题
- 格式:ppt
- 大小:1.51 MB
- 文档页数:16

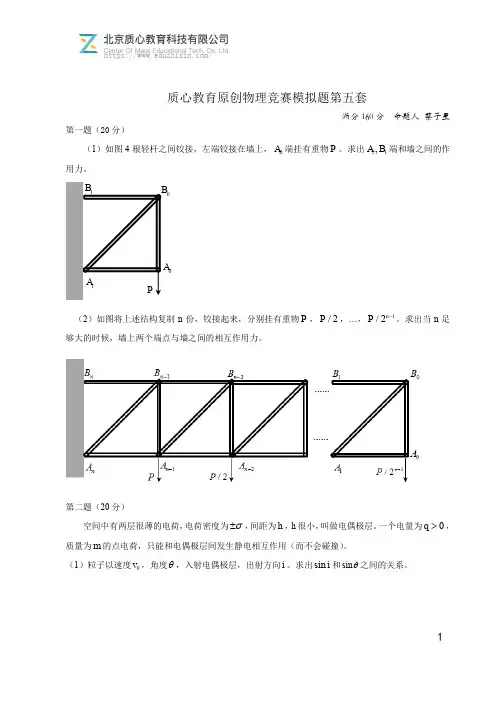
1质心教育原创物理竞赛模拟题第五套满分160分 命题人 蔡子星第一题(20分)(1)如图4根轻杆之间铰接,左端铰接在墙上,0A 端挂有重物P 。
求出11,A B 端和墙之间的作用力。
(2)如图将上述结构复制n 份,铰接起来,分别挂有重物P ,/2P ,…,1/2n P -。
求出当n 足够大的时候,墙上两个端点与墙之间的相互作用力。
第二题(20分)空间中有两层很薄的电荷,电荷密度为σ±,间距为h ,h 很小,叫做电偶极层。
一个电量为0q >,质量为m 的点电荷,只能和电偶极层间发生静电相互作用(而不会碰撞)。
(1)粒子以速度0v ,角度θ,入射电偶极层,出射方向i 。
求出sin i 和sin θ之间的关系。
PA 0B 1B 1A2(2)将电偶极层弯成离心率为e 的双曲面形状,左边为正电荷,两个焦点沿着x 轴方向,要求所有平行于与x 轴方向入射的粒子都能汇交与焦点,则粒子速度,电偶极层厚度,电荷密度之间应当满足什么关系? 第三题(20分)空间中有沿着z 方向的磁场,磁场大小随着时间和空间变化,满足0cos()B B t kx ω=-。
一个桌面在0z =平面上,平面上有一个沿着x-y 方向正放的线框,线框边长为l ,总电阻为R 。
(1)假设线框相对于桌面静止,线圈的左端位于0x =的位置,求出线框中电动势随着时间的变化关系。
(2)若线框质量为m ,摩擦系数为μ,线框是否可能相对于桌面沿着x 方向做匀速直线运动?如果可能求出参数之间应当满足的条件,如果不可以,写明理由。
(以下不是考题:找到三个这样的线框,沿着x 轴发成一排,相邻两个之间用长度为'l 的绝缘木棒连接,问这三个线框是否可能一起做匀速直线运动,如果可以求出各参数应当满足条件,如果不可以写明理由。
)第四题(20分)一个金属球壳,半径为R ,质量为M ,带电量为Q ,初始时刻自由的静止在空间中。
球壳的一端有一个小洞。
球心与小洞的连线方向视为轴线方向。


话题1:重心与质心的确定一、平行力的合成与分解物体所受的几个力的作用线彼此平行,且不作用于一点,即为平行力(系)。
在平行力的合成或分解的过程中,必须同时考虑到力的平动效果和转动效果,后者要求合力和分力相对任何一个转轴的力矩都相同。
两个同向平行力的合力其方向与两个分力方向相同,其大小等于分力大小之和。
其作用线在两个分力作用点的连线上。
合力作用点到分力作用点的距离与分力的大小成反比。
例如:两个同向平行力A F 和B F ,其合力的大小A B F F F =+,合力作用点O 满足A B AO F BO F ⋅=⋅的关系。
两个反向平行力的合力其方向与较大的分力方向相同,其大小等于分力大小之差。
其作用线在两个分力作用点的连线的延长线上,且在较大的分力的外侧。
合力作用点到分力作用点的距离与分力的大小成反比。
例如:两个反向平行力A F 和B F 的合成其合力的大小B A F F F =-(假如B A F F >,则F 和B F 同向)其合力的作用点满足A B AO F BO F ⋅=⋅的关系。
一个力分解成两个平行力,是平行力合成的逆过程。
二、重心和质心重心是重力的作用点。
质心是物体(或由多个物体组成的系统)质量分布的中心。
物体的重心和质心是两个不同的概念,当物体远离地球而不受重力作用时,重心这个概念就失去意义,但质心却依然存在。
对于地球上体积不太大的物体,由于重力与质量成正比,重心与质心的位置是重合的。
但当物体的高度和地球半径比较不能忽略时,两者就不重合了,如高山的重心比质心要低一些。
在重力加速度g 为常矢量的区域,物体的重心是惟一的(我们讨论的都是这种情形),BF AF FO BA BF AF F OBA重心也就是物体各部分所受重力的合力的作用点,由于重力与质量成正比,重力合力的作用点即为质心,即重心与质心重合。
求重心,也就是求一组平行力的合力作用点。
相距L ,质量分别为12,m m 的两个质点构成的质点组,其重心在两质点的连线上,且与12,m m 相距分别为1L ,2L :1122m L m L = 12L L L +=2112m LL m m =+1212m LL m m =+均匀规则形状的物体,其重心在它的几何中心,求一般物体的重心,常用的方法是将物体分割成若干个重心容易确定的部分后,再用求同向平行力合力的方法找出其重心。

质心教育原创物理竞赛模拟题第三套满分160分 命题⼈人 蔡⼦子星、唐鹏、肖虓第一题(22分)一个质量为m 的人站在长度为l 质量为M 的木板上,木板和地面摩擦系数为µ。
要求人在不同的位置都能将自己和木板拉离地面(木板绕着右方端点转起来,而不发生滑动,人的脚和木板之间用胶水黏起来,不会分离和滑动)。
问摩擦系数µ应当满足的关系。
取m /M=2。
第二题(20分)【梯子不用时请横放】一个梯子用完了,靠在墙上,小明同学不小心一脚踢到了梯子上,将梯子踢飞了,脚肿了不要紧,要紧的时砸到了花花草草,甚是不安。
现在我们来粗略还原一下现场。
为了简化问题,将梯子视为质量为M 、长度为L 的匀质棒子,竖直靠在墙上。
梯子与地面、墙面的摩擦系数忽略不计,小明同学的脚视为质量为m 的质点。
脚的初速度方向也平行于墙与地面的交线,脚踢到梯子时,碰撞点为梯子的最下方,视为完全非弹性碰撞,且碰撞时间非常短,之后由于小明疼痛难耐,脚不再与梯子接触。
(均匀棒绕质心的转动惯量为I=ML 2/12)1)求小明以初速0v 踢完梯子瞬间梯子的运动状态。
2)若小明这一脚踢得很重,刚刚踢完,梯子就直接“飞”起来了(即接触点与地面分离),问脚的初速度至少为多少。
第四题(20分)【三叶草】一根特殊的弹簧,原长为0,当长度0x R <<时,弹力为6F kx =−,当长度2R x R <<时,弹力F kx =−。
将弹簧一端连在在光滑水平桌面上的固定点上,可自由转动,另一端系着质量为m 的小球。
现在将小球拉至2R 位置,并以垂直于弹簧的初速0v =释放。
(1)求出小球最靠近原点的时候的速度大小,以及和原点的距离。
(2)求出从释放小球到小球第一次最靠近原点的过程中,弹簧的方向转过了多少角度。
(3)定性描绘小球的轨迹。
第五题(20分)【某科学的超电磁炮】御坂美琴的绝招之一是高速射出硬币以打击目标,现在我们建立简单模型对其进行分析。





质心教育物理竞赛课程
在当今科技飞速发展的时代,物理学科的重要性日益凸显,而竞赛课程则为培养学生物理素养、激发创新精神提供了一个广阔的平台。
质心教育物理竞赛课程正是这样一门课程,它通过设置丰富的竞赛内容、灵活的竞赛形式,为学生们提供了一个提高物理素养、培养创新思维的良好途径。
质心教育物理竞赛课程内容丰富,涵盖了高中物理竞赛的全部知识点,包括力学、电磁学、热学、光学、相对论、量子力学等多个领域。
在课程内容的选择上,质心教育物理竞赛课程注重了与实际生活的紧密联系,将理论知识与实际应用相结合,使学生们在掌握知识的同时,也能积累一些实用的物理知识。
质心教育物理竞赛竞赛形式灵活,竞赛题目设置多样,既有选择题、问答题,也有计算题、综合题。
这种多样化的竞赛题目设置不仅有助于激发学生们的思维活跃度,还能有效提高学生们的解题能力。
此外,质心教育物理竞赛还为学生们提供了模拟竞赛环节,让
学生们可以在模拟竞赛中锻炼自己的解题能力,为今后的学习打下坚实的基础。
质心教育物理竞赛课程旨在培养学生们的创新精神,鼓励学生们敢于挑战、积极创新。
在课程中,学生们不仅可以通过对知识的深入理解和掌握,来提高自己的物理素养。
还可以通过参加竞赛,与其他学生们进行交流,分享各自对物理学习的见解,从而激发学生们更多的创新想法。
总之,质心教育物理竞赛课程是一门为提高学生物理素养、培养创新精神量身打造的课程。
在课程内容、竞赛形式等方面都做了充分的准备,为学生们提供了一个良好的学习平台。
通过学习这门课程,学生们不仅可以提高自己的物理素养,还可以培养创新精神和良好的团队合作精神,为将来的学习打下坚实的基础。
话题1:重心与质心的确定一、平行力的合成与分解物体所受的几个力的作用线彼此平行,且不作用于一点,即为平行力(系)。
在平行力的合成或分解的过程中,必须同时考虑到力的平动效果和转动效果,后者要求合力和分力相对任何一个转轴的力矩都相同。
两个同向平行力的合力其方向与两个分力方向相同,其大小等于分力大小之和。
其作用线在两个分力作用点的连线上。
合力作用点到分力作用点的距离与分力的大小成反比。
例如:两个同向平行力A F 和B F ,其合力的大小A B F F F =+,合力作用点O 满足A B AO F BO F ⋅=⋅的关系。
两个反向平行力的合力其方向与较大的分力方向相同,其大小等于分力大小之差。
其作用线在两个分力作用点的连线的延长线上,且在较大的分力的外侧。
合力作用点到分力作用点的距离与分力的大小成反比。
例如:两个反向平行力A F 和B F 的合成其合力的大小B A F F F =-(假如B A F F >,则F 和B F 同向)其合力的作用点满足A B AO F BO F ⋅=⋅的关系。
一个力分解成两个平行力,是平行力合成的逆过程。
二、重心和质心重心是重力的作用点。
质心是物体(或由多个物体组成的系统)质量分布的中心。
物体的重心和质心是两个不同的概念,当物体远离地球而不受重力作用时,重心这个概念就失去意义,但质心却依然存在。
对于地球上体积不太大的物体,由于重力与质量成正比,重心与质心的位置是重合的。
但当物体的高度和地球半径比较不能忽略时,两者就不重合了,如高山的重心比质心要低一些。
在重力加速度g v为常矢量的区域,物体的重心是惟一的(我们讨论的都是这种情形),BF AF FO BA BF AF F OBA重心也就是物体各部分所受重力的合力的作用点,由于重力与质量成正比,重力合力的作用点即为质心,即重心与质心重合。
求重心,也就是求一组平行力的合力作用点。
相距L ,质量分别为12,m m 的两个质点构成的质点组,其重心在两质点的连线上,且与12,m m 相距分别为1L ,2L :1122m L m L = 12L L L +=2112m LL m m =+1212m LL m m =+均匀规则形状的物体,其重心在它的几何中心,求一般物体的重心,常用的方法是将物体分割成若干个重心容易确定的部分后,再用求同向平行力合力的方法找出其重心。
高中物理竞赛题含答案一、选择题1. 以下哪个物理量是标量?(A)A. 功B. 力C. 速度D. 位移答案:A2. 下列哪个图示了一个物体的加速度随时间的变化呈现为匀加速的情况?(D)A.B.C.D.答案:D3. 光速在真空和介质中的大小关系为:(B)A. 光速在真空与介质中大小相等B. 光速在真空中大于介质中C. 光速在介质中大于真空中D. 光速在介质中与真空中无关答案:B4. 两个球分别从10米和20米的高度落下,它们同时落地。
它们落地时哪个球的速度更大?(A)A. 速度相同B. 10米高度的球速度更大C. 20米高度的球速度更大D. 无法确定答案:A5. 如下图,取自然长度为l、未受拉伸前横截面面积为S的弹性绳,悬挂一质量为m的物体,当物体静止时,绳的长度为l0。
如果物体做振动,振动小于一定范围时,弹性绳对物体做的回复力F正比于振动小的幅度x,弹性系数k即为它的比例系数。
当振动进一步扩大超过一定范围时,弹性绳不能完全回复原状态,即绳有一定的塑性。
当振动到达最大时,弹性绳的长度变为l',则l'与l的变化关系正确的是:(D)A. l' = l(1+x)B. l' = l(1-x)C. l' = l(1+x^2)D. l' = l(1+x)^2答案:D6. 有一小车运动,其初始速度为12米/秒,加速度为8米/秒²,运动的时间为5秒,则小车所运动的距离是(B)A. 180米B. 1800米C. 2800米D. 3520米答案:B二、填空题1. 一个在半径为R的圆形轨道上做匀速圆周运动的质点,速率为v,则此质点的向心加速度为______,受到的向心力为______。
答案:v²/R,mv²/R2. 一个在平面直角坐标系中做匀加速直线运动的物体,其速度可以表示为v=at,物体在t=1时的位移为2米,则它在t=2时的位移为______米。
质心教育物理竞赛课程
质心教育物理竞赛课程是一门面向物理竞赛准备的高质量教育课程。
该课程的目标是帮助学生全面提高物理学科知识和能力,以应对各类物理竞赛的挑战。
该课程的内容涵盖了物理竞赛常见的各个领域,包括力学、电磁学、光学、热学、核物理等。
课程内容深入浅出,既有理论知识的讲解,又有实际问题的解析和解决方法的分享。
通过学习这门课程,学生可以更加深入地理解物理学的基本原理,培养应用物理学知识解决实际问题的能力。
此外,质心教育物理竞赛课程还注重培养学生的实践能力和解决问题的思维方式。
课程中会引导学生进行各类实验和实际操作,以增强他们的实际操作能力和动手能力。
同时,课程还会针对竞赛中常见的解题思路和解题技巧进行讲解和实践,帮助学生更好地应对物理竞赛的挑战。
质心教育物理竞赛课程的特点是教学资源丰富,课程设置灵活。
学生可以根据自己的实际情况选择学习的内容和学习的深度。
而且,课程中还会提供大量的模拟竞赛题目和竞赛经验分享,帮助学生更好地熟悉竞赛形式和提高竞赛技巧。
总之,质心教育物理竞赛课程旨在为学生提供一套全面高效的物理竞赛准备方案,帮助他们充分发展物理学科能力,取得优异的竞赛成绩。
该课程的教学团队由物理学专业背景和丰富竞赛经验的教师组成,为学生提供专业的指导和支持。