下载文档原格式
不等式的表示与解答（知识点总结）一、基本概念不等式是数学中常见的一种关系式，用于比较两个数的大小关系。
不等号的种类包括大于号(>)、小于号(<)、大于等于号(≥)和小于等于号(≤)。
不等式可以由数字、变量和运算符组成，例如：2x + 3 > 5，其中2x + 3和5是表达式，>是不等号，整个表达式称为一个不等式。
二、不等式的表示形式根据不等号的种类和式子的形式，不等式可以分为以下几种表示形式：1. 明确表示的不等式：例如 x > 3，表示x的取值范围大于3。
2. 含有未知数的不等式：例如 2x + 3 > 5，表示未知数x的取值范围满足2x + 3大于5。
3. 绝对值不等式：例如 |x - 3| > 2，表示x距离3的绝对值大于2。
4. 分数不等式：例如 1/x < 2，表示x的倒数小于2。
三、一元一次不等式的解法一元一次不等式是指只含有一个未知数的一次式，并且不等式成立范围是实数集合。
解一元一次不等式需要以下步骤：1. 整理不等式，将未知数放在一边，常数放在另一边，使不等式成为“未知数 > (或<) 常数”的形式。
2. 对于系数为正数的情况，不等式的解集为从第一个系数所在的数开始到无穷(∞)。
3. 对于系数为负数的情况，不等式的解集为从无穷(∞)到第一个系数所在的数。
四、一元二次不等式的解法一元二次不等式是指含有一个未知数的二次式，并且不等式成立范围是实数集合。
解一元二次不等式需要以下步骤：1. 整理不等式，将未知数放在一边，常数放在另一边，使不等式成为“未知数 > (或<) 0”的形式。
2. 解一元二次不等式需要先求出其对应的二次函数的顶点和开口方向。
3. 判断顶点是否在不等式的解集中，若在，则解集为顶点所在的区间；若不在，则根据开口方向确定解集。
五、不等式的组合与求解1. 不等式的组合：当给出多个不等式时，需要将它们整合成一个集合表示，根据逻辑运算符(如与、或)来连接不等式。
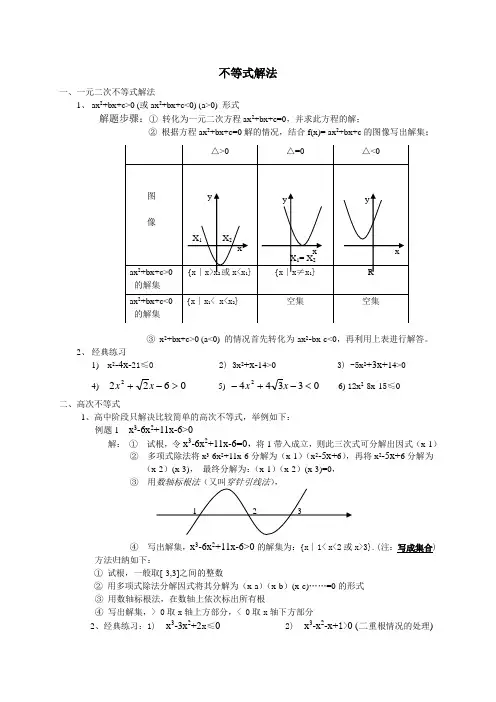
不等式解法一、一元二次不等式解法1、 ax 2+bx+c>0 (或ax 2+bx+c<0) (a>0) 形式解题步骤：① 转化为一元二次方程ax 2+bx+c=0，并求此方程的解；② 根据方程ax 2+bx+c=0解的情况，结合f(x)= ax 2+bx+c 的图像写出解集；③ x 2+bx+c>0 (a<0) 的情况首先转化为-ax 2-bx-c<0，再利用上表进行解答。
2、 经典练习1) x 2-4x-21≤0 2) 3x 2+x-14>0 3) -5x 2+3x+14>04) 06222>-+x x 5) 033442<-+-x x 6) 12x 2-8x-15≤0二、高次不等式1、高中阶段只解决比较简单的高次不等式，举例如下：例题1 x 3-6x 2+11x-6>0解： ① 试根，令x 3-6x 2+11x-6=0，将1带入成立，则此三次式可分解出因式（x-1）② 多项式除法将x 3-6x 2+11x-6分解为（x-1）（x 2-5x+6），再将x 2-5x+6分解为 （x-2）(x-3)， 最终分解为：（x-1）（x-2）(x-3)=0，③④ 写出解集，x 3-6x 2+11x-6>0的解集为：{x ∣1< x<2或x>3}.(注：写成集合) 方法归纳如下：① 试根，一般取[-3,3]之间的整数② 用多项式除法分解因式将其分解为（x-a ）（x-b ）(x-c)……=0的形式③ 用数轴标根法，在数轴上依次标出所有根④ 写出解集，> 0取x 轴上方部分，< 0取x 轴下方部分2、经典练习：1) x 3-3x 2+2x ≤0 2) x 3-x 2-x+1>0 (二重根情况的处理)。
不等式一、知识点：1. 实数的性质：0>-⇔>b a b a ；0<-⇔<b a b a ；0=-⇔=b a b a ．2. 不等式的性质：性 质内 容对称性 a b b a >⇔<，a b b a <⇔>． 传递性 a b >且b c a c >⇒>．加法性质 a b a c b c >⇒+>+；a b >且c d a c b d >⇒+>+．乘法性质 ,0a b c ac bc >>⇒>；0a b >>，且00c d ac bd >>⇒>>． 乘方、开方性质 0,n n a b n N a b *>>∈⇒>；0,n n a b n N a b *>>∈⇒>．倒数性质 11,0a b ab a b>>⇒<．3. 常用基本不等式：条 件结 论 等号成立的条件a R ∈20a ≥ 0a = ,a R b R ∈∈ 222a b ab +≥，2()2a b ab +≤，222()22a b a b ++≥ a b =0,0>>b a基本不等式： 2a b ab +≥常见变式：2≥+b a a b ； 21≥+aa ab =0,0>>b a2211222b a b a ab b a +≤+≤≤+ a b =4.利用重要不等式求最值的两个命题：命题1：已知a ，b 都是正数，若ab 是实值P ，则当a=b=时，和a ＋b 有最小值2.命题2：已知a ，b 都是正数，若a ＋b 是实值S ，则当a=b=2s时，积ab 有最大值42s .注意：运用重要不等式求值时，要注意三个条件：一“正”二“定”三“等”，即各项均为正数，和或积为定值，取最值时等号能成立，以上三个条件缺一不可.5.一元二次不等式的解法：设a>0,x 1x 2是方程ax 2+bx+c=0的两个实根，且x 1≤x 2，则有结论：ax 2+bx+c>0⇔2040a ab ac >⎧=⎨-<⎩或检验；ax 2+bx+c<0⇔2040a ab ac <⎧=⎨-<⎩或检验 6. 绝对值不等式（1）｜x ｜＜a （a ＞0）的解集为：{x ｜－a ＜x ＜a}； ｜x ｜＞a （a ＞0）的解集为：{x ｜x ＞a 或x ＜－a}。
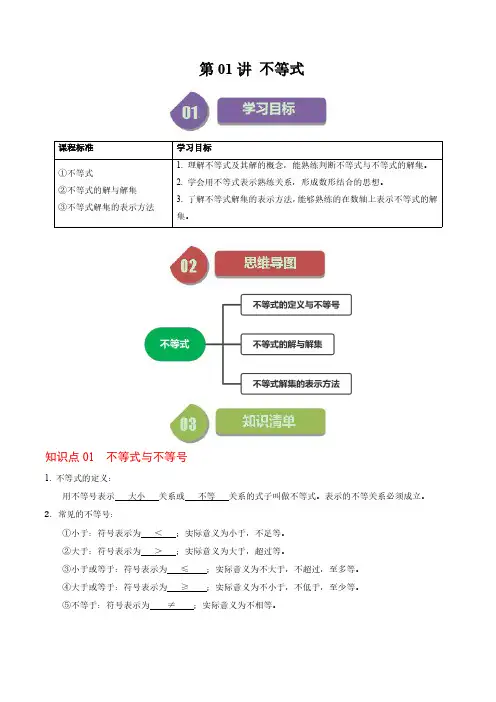
第01讲不等式课程标准学习目标①不等式②不等式的解与解集③不等式解集的表示方法1.理解不等式及其解的概念，能熟练判断不等式与不等式的解集。
2.学会用不等式表示熟练关系，形成数形结合的思想。
3.了解不等式解集的表示方法，能够熟练的在数轴上表示不等式的解集。
知识点01不等式与不等号1.不等式的定义：用不等号表示大小关系或不等关系的式子叫做不等式。
表示的不等关系必须成立。
2.常见的不等号：①小于：符号表示为＜；实际意义为小于，不足等。
②大于：符号表示为＞；实际意义为大于，超过等。
③小于或等于：符号表示为≤；实际意义为不大于，不超过，至多等。
④大于或等于：符号表示为≥；实际意义为不小于，不低于，至少等。
⑤不等于：符号表示为≠；实际意义为不相等。
3.列不等式：审清题意，弄清关键词的含义，找出已知量与未知量以及他们之间存在的关系，然后用不等式将不等关系表示出来。
4.常见的不等式基本语言与符号表示：若a 是正数表示为0＞a ；若a 是负数表示为0＜a ；若a 是非正数表示为0≤a ；若a 是非负数表示为0≥a ；若b a ，是同号表示为0＞ab ；若b a ，是异号表示为＜ab ；【即学即练1】1．下列数学式子：①﹣3＜0；②2x +3y ≥0；③x ＝1；④x 2﹣2xy +y 2；⑤x +1≠3；其中是不等式的有（）A ．5个B ．4个C ．3个D ．2个【分析】根据不等式的定义：用不等号连接的式子是不等式，逐个进行判断即可．【解答】解：①﹣3＜0，是不等式，符合题意；②2x +3y ≥0，是不等式，符合题意；③x ＝1，是等式，不符合题意；④x 2﹣2xy +y 2，是多项式，不符合题意；⑤x +1≠3，是不等式，符合题意；综上：是不等式的有①②⑤，共3个．故选：C ．【即学即练2】2．“x 为正数”的表达式是（）A ．x ＜0B ．x ＞0C ．x ≥0D ．x ≤0【分析】正数即为大于0的数，据此可列出不等式．【解答】解：∵正数是指大于0的数，∴x 是正数，即x ＞0，故选：B ．【即学即练3】3．小明网购了一本《好玩的数学》，同学们想知道书的价格，小明让他们猜．甲说：“至少13元．”乙说：“至多10元．”丙说：“至多8元．”小明说：“你们三个人都说错了”．则这本书的价格x （元）所在的范围为（）A．8＜x＜10B．10＜x＜12C．x＞10D．10＜x＜13【分析】根据甲说：“至少13元．”乙说“至多10元．”丙说“至多8元．”小明说：“你们三个人都说错了．”可以得到相应的不等式组，从而可以得到x的取值范围．【解答】解：∵甲说：“至少13元．”乙说“至多10元．”丙说“至多8元．”∴，可得无解，∵三人都说错了，∴10＜x＜13．故选：D．知识点02不等式的解与解集1.不等式的解的定义：能使不等式成立的未知数的值，叫做不等式的解。
不等式题型及解题方法不等式是数学中常见的一种问题，其解题方法也多种多样。
不同的不等式题型需要采用不同的解题方法才能得出正确的答案。
下面将介绍一些常见的不等式题型及其解题方法。
一、一次不等式一次不等式是指只含有一次项的不等式，如：ax + b > c。
解这种不等式可以采用以下步骤：1. 移项，将不等式中的常数项移到右边，将未知数的系数移到左边，得到ax > c - b。
2. 如果a > 0，则解为x > (c - b)/a；如果a < 0，则解为x <(c - b)/a。
二、二次不等式二次不等式是指含有二次项的不等式，如：ax + bx + c > 0。
解这种不等式可以采用以下步骤：1. 将不等式化为标准形式，即将常数项移到左边，得到ax + bx + c - 0 > 0。
2. 求出方程的根，即x1和x2，根据二次函数的性质可知，当x < x1或x > x2时，函数值大于0。
3. 根据a的正负性分别讨论，如果a > 0，则解为x < x1或x > x2；如果a < 0，则解为x1 < x < x2。
三、绝对值不等式绝对值不等式是指含有绝对值的不等式，如：|x - a| > b。
解这种不等式可以采用以下步骤：1. 将绝对值拆开，得到x - a > b或x - a < -b。
2. 分别解出不等式两边的未知数，得到x > a + b或x < a - b。
四、分式不等式分式不等式是指不等式中含有分式的不等式，如：(ax + b)/(cx + d) > 0。
解这种不等式可以采用以下步骤：1. 将不等式转化为分子和分母的符号相同的形式，即当分子和分母同为正数或同为负数时，不等式成立。
2. 分别讨论分子和分母的正负性，得到不等式的解集。
以上是一些常见的不等式题型及其解题方法，当然，不同的不等式题型还有其他的解题方法，需要根据实际情况进行分析和求解。
完整版的不等式知识点和基本题型不等式是数学中一种重要的关系符号，它用来描述数值之间的大小关系。
以下是不等式的基本知识点和常见题型：1. 不等式基本概念- 不等式是指在两个数之间用不同的关系符号来表示大小关系，比如大于（>）、小于（<）、大于等于（≥）、小于等于（≤）等。
- 不等式的解集是使不等式成立的所有实数的集合。
2. 不等式的性质- 若 a > b，则 b < a。
- 若 a > b 且 b > c，则 a > c。
- 若 a > b 且 a > 0，则 ac > bc（c > 0）。
- 若 a > b 且 c < 0，则 ac < bc（c < 0）。
- 若 a > b 且c ≠ 0，则 ac > bc。
3. 不等式的解法- 在不等式两边同时加（减）相同的数，不等式的方向不变。
- 在不等式两边同时乘（除）正数，不等式的方向不变。
- 在不等式两边同时乘（除）负数，不等式的方向反向。
- 若不等式两边有平方根，应考虑正负情况。
4. 不等式的常见题型4.1. 一元一次不等式- 形如 ax + b > c 或 ax + b < c 的不等式，其中 a、b、c 为常数，x 为变量。
- 解法类似一元一次方程，通过移项和化简来求解。
4.2. 一元一次绝对值不等式- 形如 |ax + b| > c 或 |ax + b| < c 的不等式，其中 a、b、c 为常数，x 为变量。
- 需要根据绝对值的定义来分情况讨论和求解。
4.3. 二元一次不等式- 形如 ax + by > c 或 ax + by < c 的不等式，其中 a、b、c 为常数，x、y 为变量。
- 解法类似于解一元一次不等式，通过移项和化简来求解。
4.4. 二次不等式- 形如 ax^2 + bx + c > 0 或 ax^2 + bx + c < 0 的不等式，其中 a、b、c 为常数，x 为变量。
初一数学不等式题型及解题方法一、不等式的基本概念1.不等式符号及含义不等式是指两个数之间大小关系的一种表示方法。
不等号符号包括大于（>）、小于（<）、大于等于（≥）、小于等于（≤）等。
其中，大于（>）表示左边的数比右边的数大；小于（<）表示左边的数比右边的数小；大于等于（≥）表示左边的数大于或等于右边的数；小于等于（≤）表示左边的数小于或等于右边的数。
2.不等式的解解不等式的过程就是求出不等式中未知数的取值范围。
一般情况下，我们通过对不等式进行变形、化简，再利用一些不等式性质和数轴上的图示可以求出不等式的解集。
解不等式的过程也包括反证法、分段讨论等方法。
二、不等式的性质不等式有一些特殊的性质，了解这些性质有助于我们更好地理解和运用不等式。
1.不等式的性质①两个相等的数之间没有大小关系，所以两个相等数代入一个不等式时不等式的成立与否是无法判断的。
②不等式两边同时加（减）一个相同的数，不等式仍然成立。
即如果a>b，则a+c>b+c。
③不等式两边同时乘（除）一个正数，不等式的方向不变。
即如果a>b，c>0，则a×c>b×c。
④不等式两边同时乘（除）一个负数，不等式的方向改变。
即如果a>b，c<0，则a×c<b×c。
2.不等式的转化不等式的转化是指将不等式进行变形、化简，以便更好地求解。
①不等式中可以进行加减、乘除、倒数、取对数等运算，但要注意符号的变化，需根据不等式的大小关系来进行变换。
②对于含绝对值的不等式，也可以通过转化为分段函数的方式来求解。
即根据不同的不等式形式，将绝对值进行分段讨论，再求解不等式。
三、不等式的解题方法1.一元一次不等式一元一次不等式是指只含有一个未知数和一次项的不等式，通常可以用数轴解题法、图像法、代入法等方法来求解。
①数轴解题法：首先将不等式化简，再根据不等式的方向在数轴上做出相应的标记，并根据不等式的特点来判断解集的范围。
不等式常见题型及解析题一、一元一次不等式1.问题描述解不等式$a x+b>c$，其中$a>0$。
2.解法分析根据不等式的性质，我们可以将不等式转化为等价的形式:$$ax+b=c$$然后确定不等式的解集。
（1）当$a>0$时将不等式转化为等式，我们得到$ax+b=c$，解得$x=\fr ac{c-b}{a}$。
此时，对于任意一个满足$c-b>0$的$x$，都可以使得$a x+b>c$，所以解集为$\le ft(\fr ac{c-b}{a},+∞\ri gh t)$。
（2）当$a<0$时将不等式转化为等式，我们得到$ax+b=c$，解得$x=\fr ac{c-b}{a}$。
此时，对于任意一个满足$c-b<0$的$x$，都可以使得$a x+b<c$，所以解集为$\le ft(-∞,\f r ac{c-b}{a}\r igh t)$。
（3）当$a=0$时此时，不等式退化为$b>c$或$b<c$，没有变量$x$，所以不存在解。
二、一元二次不等式1.问题描述解不等式$a x^2+bx+c>0$，其中$a>0$。
2.解法分析和一元一次不等式类似，我们可以将不等式转化为等价的形式:$$ax^2+b x+c=0$$然后确定不等式的解集。
（1）当$a>0$时判断二次函数$a x^2+b x+c$的图像与$x$轴的交点数：-当判别式$Δ=b^2-4a c$大于0时，二次函数与$x$轴有两个交点，此时不等式的解集为$\le ft(-∞,x_1\ri gh t)\c up\le ft(x_2,+∞\ri g ht)$，其中$x_1$和$x_2$分别为二次方程$a x^2+b x+c=0$的两个根。
-当判别式$Δ=b^2-4a c$等于0时，二次函数与$x$轴有一个交点，此时不等式的解集为$\ma th bb{R}$，即全体实数的集合。
-当判别式$Δ=b^2-4a c$小于0时，二次函数与$x$轴没有交点，此时不等式的解集为空集。
不等式讲义最新考纲：1.理解绝对值的几何意义，并了解下列不等式成立的几何意义及取等号的条件：(1)|a ＋b |≤|a |＋|b |(a ，b ∈R )．(2)|a －b |≤|a －c |＋|c －b |(a ，b ∈R ).2.会利用绝对值的几何意义求解以下类型的不等式：|ax ＋b |≤c ，|ax ＋b |≥c ，|x －c |＋|x －b |≥a .3.了解柯西不等式的几种不同形式，理解它们的几何意义，并会证明.4.通过一些简单问题了解证明不等式的基本方法：比较法、综合法、分析法、反证法、放缩法、数学归纳法．1．含有绝对值的不等式的解法(1)|f (x )|>a (a >0)⇔f (x )>a 或f (x )<－a ；(2)|f (x )|<a (a >0)⇔－a <f (x )<a ；(3)对形如|x －a |＋|x －b |≤c ，|x －a |＋|x －b |≥c 的不等式，可利用绝对值不等式的几何意义求解．2．含有绝对值的不等式的性质|a |－|b |≤|a ±b |≤|a |＋|b |.问题探究：不等式|a |－|b |≤|a ±b |≤|a |＋|b |中，“＝”成立的条件分别是什么？提示：不等式|a |－|b |≤|a ＋b |≤|a |＋|b |，右侧“＝”成立的条件是ab ≥0，左侧“＝”成立的条件是ab ≤0且|a |≥|b |；不等式|a |－|b |≤|a －b |≤|a |＋|b |，右侧“＝”成立的条件是ab ≤0，左侧“＝”成立的条件是ab ≥0且|a |≥|b |.3．基本不等式定理1：设a ，b ∈R ，则a 2＋b 2≥2ab .当且仅当a ＝b 时，等号成立．定理2：如果a 、b 为正数，则≥，当且仅当a ＝b 时，等号成立．a ＋b 2ab 定理3：如果a 、b 、c 为正数，则≥，当且仅当a ＝b ＝c 时，a ＋b ＋c 33abc 等号成立．定理4：(一般形式的算术—几何平均值不等式)如果a 1、a 2、…、a n 为n 个正数，则≥，当且仅当a 1＝a 2＝…＝a n 时，等号成立．a 1＋a 2＋…＋a nn n a 1a 2…a n 4．柯西不等式(1)柯西不等式的代数形式：设a ，b ，c ，d 为实数，则(a 2＋b 2)·(c 2＋d 2)≥(ac ＋bd )2，当且仅当ad ＝bc 时等号成立．(2)若a i ，b i (i ∈N *)为实数，则()()≥(i b i )2，当且仅当b i ＝0(i ＝n ∑i ＝1a 2i n ∑i ＝1b 2i n ∑i ＝1a 1,2，…，n )或存在一个数k ，使得a i ＝kb i (i ＝1,2，…，n )时，等号成立．(3)柯西不等式的向量形式：设α，β为平面上的两个向量，则|α|·|β|≥|α·β|，当且仅当这两个向量同向或反向时等号成立．1．判断正误(在括号内打“√”或“×”)(1)对|a ＋b |≥|a |－|b |当且仅当a >b >0时等号成立．( )(2)对|a －b |≤|a |＋|b |当且仅当ab ≤0时等号成立．( )(3)|ax ＋b |≤c (c >0)的解等价于－c ≤ax ＋b ≤c .( )(4)不等式|x －1|＋|x ＋2|<2的解集为Ø.( )(5)若实数x 、y 适合不等式xy >1，x ＋y >－2，则x >0，y >0.( )[答案] (1)× (2)√ (3)√ (4)√ (5)√2．不等式|2x －1|－x <1的解集是( )A ．{x |0<x <2}B ．{x |1<x <2}C ．{x |0<x <1}D ．{x |1<x <3}[解析] 解法一：x ＝1时，满足不等关系，排除C 、D 、B ，故选A.解法二：令f (x )＝Error!则f (x )<1的解集为{x |0<x <2}．[答案] A3．设|a |<1，|b |<1，则|a ＋b |＋|a －b |与2的大小关系是( )A ．|a ＋b |＋|a －b |>2B ．|a ＋b |＋|a －b |<2C ．|a ＋b |＋|a －b |＝2D ．不能比较大小[解析] |a ＋b |＋|a －b |≤|2a |<2.[答案] B4．若a ，b ，c ∈(0，＋∞)，且a ＋b ＋c ＝1，则＋＋的最大值为( )a b c A ．1 B ． 2C. D ．23[解析] (＋＋)2＝(1×＋1×＋1×)2≤ (12＋12＋12)(a ＋b ＋c )a b c a b c ＝3.当且仅当a ＝b ＝c ＝时，等号成立．13∴(＋＋)2≤3.a b c ＋＋的最大值为.故应选C.a b c 3[答案] C5．若存在实数x 使|x －a |＋|x －1|≤3成立，则实数a 的取值范围是________．[解析] 利用数轴及不等式的几何意义可得x 到a 与到1的距离和小于3，所以a 的取值范围为－2≤a ≤4.[答案] －2≤a ≤4考点一 含绝对值的不等式的解法解|x －a |＋|x －b |≥c (或≤c )型不等式，其一般步骤是：(1)令每个绝对值符号里的代数式为零，并求出相应的根．(2)把这些根由小到大排序，它们把定义域分为若干个区间．(3)在所分区间上，去掉绝对值符号组成若干个不等式，解这些不等式，求出它们的解集．(4)这些不等式解集的并集就是原不等式的解集．解绝对值不等式的关键是恰当的去掉绝对值符号．(1)(2015·山东卷)不等式|x －1|－|x －5|<2的解集是( )A ．(－∞，4)B ．(－∞，1)C ．(1,4)D ．(1,5)(2)(2014·湖南卷)若关于x 的不等式|ax －2|<3的解集为Error!，则a ＝________.[解题指导] 切入点：“脱掉”绝对值符号；关键点：利用绝对值的性质进行分类讨论．[解析] (1)当x <1时，不等式可化为－(x －1)＋(x －5)<2，即－4<2，显然成立，所以此时不等式的解集为(－∞，1)；当1≤x ≤5时，不等式可化为x －1＋(x －5)<2，即2x －6<2，解得x <4，又1≤x ≤5，所以此时不等式的解集为[1,4)；当x >5时，不等式可化为(x －1)－(x －5)<2，即4<2，显然不成立，所以此时不等式无解．综上，不等式的解集为(－∞，4)．故选A.(2)∵|ax －2|<3，∴－1<ax <5.当a >0时，－<x <，与已知条件不符；1a 5a当a ＝0时，x ∈R ，与已知条件不符；当a <0时，<x <－，又不等式的解集为Error!，故a ＝－3.5a 1a[答案] (1)A (2)－3用零点分段法解绝对值不等式的步骤：(1)求零点；(2)划区间、去绝对值号；(3)分别解去掉绝对值的不等式；(4)取每个结果的并集，注意在分段时不要遗漏区间的端点值．对点训练已知函数f (x )＝|x ＋a |＋|x －2|.(1)当a ＝－3时，求不等式f (x )≥3的解集；(2)若f (x )≤|x －4|的解集包含[1,2]，求a 的取值范围．[解] (1)当a ＝－3时，f (x )＝Error!当x ≤2时，由f (x )≥3得－2x ＋5≥3，解得x ≤1；当2<x <3时，f (x )≥3无解；当x ≥3时，由f (x )≥3得2x －5≥3，解得x ≥4；所以f (x )≥3的解集为{x |x ≤1或x ≥4}．(2)f (x )≤|x －4|⇔|x －4|－|x －2|≥|x ＋a |.当x ∈[1,2]时，|x －4|－|x －2|≥|x ＋a |⇔4－x －(2－x )≥|x ＋a |⇔－2－a ≤x ≤2－a .由条件得－2－a ≤1且2－a ≥2，即－3≤a ≤0.故满足条件的a 的取值范围为[－3,0]．考点二 利用绝对值的几何意义或图象解不等式对于形如|x －a |＋|x －b |>c 或|x －a |＋|x －b |<c 的不等式，利用绝对值的几何意义或者画出左、右两边函数的图象去解不等式，更为直观、简捷，它体现了数形结合思想方法的优越性．|x －a |＋|x －b |的几何意义是数轴上表示x 的点与点a 和点b 的距离之和，应注意x 的系数为1.(1)(2014·重庆卷)若不等式|x －1|＋|x ＋2|≥a 2＋a ＋2对任意实数x 恒成立，12则实数a 的取值范围是________．(2)不等式|x ＋1|－|x －2|>k 的解集为R ，则实数k 的取值范围是__________．[解题指导] 切入点：绝对值的几何意义；关键点：把恒成立问题转化为最值问题．[解析] (1)∵|x －1|＋|x ＋2|≥|(x －1)－(x －2)|＝3，∴a 2＋a ＋2≤3，解得≤a ≤.12－1174－1＋174即实数a 的取值范围是.[－1－174，－1＋174](2)解法一：根据绝对值的几何意义，设数x ，－1,2在数轴上对应的点分别为P ，A ，B ，则原不等式等价于PA －PB >k 恒成立．∵AB ＝3，即|x ＋1|－|x －2|≥－3.故当k <－3时，原不等式恒成立．解法二：令y ＝|x ＋1|－|x －2|，则y＝Error!要使|x＋1|－|x－2|>k恒成立，从图象中可以看出，只要k<－3即可．故k<－3满足题意．[答案] (1) (2)(－∞，－3)[－1－174，－1＋174]解含参数的不等式存在性问题，只要求出存在满足条件的x即可；不等式的恒成立问题，可转化为最值问题，即f(x)<a恒成立⇔a>f(x)max，f(x)>a恒成立⇔a<f(x)min.对点训练(2015·唐山一模)已知函数f(x)＝|2x－a|＋a，a∈R，g(x)＝|2x－1|.(1)若当g(x)≤5时，恒有f(x)≤6，求a的最大值；(2)若当x∈R时，恒有f(x)＋g(x)≥3，求a的取值范围．[解] (1)g(x)≤5⇔|2x－1|≤5⇔－5≤2x－1≤5⇔－2≤x≤3；f(x)≤6⇔|2x－a|≤6－a⇔a－6≤2x－a≤6－a⇔a－3≤x≤3.依题意有，a－3≤－2，a≤1.故a的最大值为1.(2)f(x)＋g(x)＝|2x－a|＋|2x－1|＋a≥|2x－a－2x＋1|＋a＝|a－1|＋a，当且仅当(2x－a)(2x－1)≤0时等号成立．解不等式|a－1|＋a≥3，得a的取值范围是[2，＋∞)．考点三 不等式的证明与应用不等式的证明方法很多，解题时既要充分利用已知条件，又要时刻瞄准解题目标，既不仅要搞清是什么，还要搞清干什么，只有兼顾条件与结论，才能找到正确的解题途径．应用基本不等式时要注意不等式中等号成立的条件．(2015·新课标全国卷Ⅱ)设a ，b ，c ，d 均为正数，且a ＋b ＝c ＋d ，证明：(1)若ab >cd ，则＋>＋；a b c d (2)＋>＋是|a －b |<|c －d |的充要条件．a b c d [解题指导] 切入点：不等式的性质；关键点：不等式的恒等变形．[证明] (1)因为(＋)2＝a ＋b ＋2，(＋)2＝c ＋d ＋2，a b ab c d cd 由题设a ＋b ＝c ＋d ，ab >cd 得(＋)2>(＋)2.a b c d ＋>＋.a b c d (2)①若|a －b |<|c －d |，则(a －b )2<(c －d )2，即(a ＋b )2－4ab <(c ＋d )2－4cd .因为a ＋b ＝c ＋d ，所以ab >cd .由(1)得＋>＋.a b c d ＋>＋，则(＋)2>(＋)2，即a b c d a b c d a ＋b ＋>c ＋d ＋2.ab cd 因为a ＋b ＝c ＋d ，所以ab >cd .于是(a －b )2＝(a ＋b )2－4ab <(c ＋d )2－4cd ＝(c －d )2.因此|a －b |<|c －d |.＋>＋是|a －b |<|c －d |的充要条件．a b c d分析法是证明不等式的重要方法，当所证不等式不能使用比较法且与重要不等式、基本不等式没有直接联系，较难发现条件和结论之间的关系时，可用分析法来寻找证明途径，使用分析法证明的关键是推理的每一步必须可逆．对点训练(2014·新课标全国卷Ⅱ)设a 、b 、c 均为正数，且a ＋b ＋c ＝1.证明：(1)ab ＋bc ＋ac ≤；13(2)＋＋≥1.a 2b b 2c c 2a[证明] (1)由a 2＋b 2≥2ab ，b 2＋c 2≥2bc ，c 2＋a 2≥2ca 得a 2＋b 2＋c 2≥ab ＋bc ＋ca .由题设得(a ＋b ＋c )2＝1，即a 2＋b 2＋c 2＋2ab ＋2bc ＋2ca ＝1.所以3(ab ＋bc ＋ca )≤1，即ab ＋bc ＋ca ≤.13(2)因为＋b ≥2a ，＋c ≥2b ，＋a ≥2c ，a 2b b 2c c 2a故＋＋＋(a ＋b ＋c )≥2(a ＋b ＋c )，a 2b b 2c c 2a即＋＋≥a ＋b ＋c .a 2b b 2c c 2a所以＋＋≥1.a 2b b 2c c 2a———————方法规律总结————————[方法技巧]1．绝对值不等式求解的根本方向是去除绝对值符号．2．绝对值不等式在求与绝对值运算有关的最值问题时需灵活运用，同时还要注意等号成立的条件．3．在证明不等式时，应根据命题提供的信息选择合适的方法与技巧．如在使用柯西不等式时，要注意右边为常数．[易错点睛]1．对含有参数的不等式求解时，分类要完整．2．应用基本不等式和柯西不等式证明时要注意等号成立的条件．课时跟踪训练(七十)一、填空题1．不等式|2x －1|<3的解集为__________．[解析] |2x －1|<3⇔－3<2x －1<3⇔－1<x <2.[答案] (－1,2)2．若不等式|kx －4|≤2的解集为{x |1≤x ≤3}，则实数k ＝__________.[解析] ∵|kx －4|≤2，∴－2≤kx －4≤2，∴2≤kx ≤6.∵不等式的解集为{x |1≤x ≤3}，∴k ＝2.[答案] 23．不等式|2x ＋1|＋|x －1|<2的解集为________．[解析] 当x ≤－时，原不等式等价为－(2x ＋1)－(x －1)<2，即－3x <2，x >－12，此时－<x ≤－.当－<x <1时，原不等式等价为(2x ＋1)－(x －1)<2，即x <0，23231212此时－<x <0.当x ≥1时，原不等式等价为(2x ＋1)＋(x －1)<2，即3x <2，x <，此1223时不等式无解，综上，原不等式的解为－<x <0，即原不等式的解集为.23(－23，0)[答案] (－23，0)4．已知关于x 的不等式|x －1|＋|x |≤k 无解，则实数k 的取值范围是__________．[解析] ∵|x －1|＋|x |≥|x －1－x |＝1，∴当k <1时，不等式|x －1|＋|x |≤k 无解，故k <1.[答案] (－∞，1)5．(2015·西安统考)若关于实数x 的不等式|x －5|＋|x ＋3|<a 无解，则实数a 的取值范围是________．[解析] |x －5|＋|x ＋3|≥|(x －5)－(x ＋3)|＝8，故a ≤8.[答案] (－∞，8]6．(2015·重庆卷)若函数f (x )＝|x ＋1|＋2|x －a |的最小值为5，则实数a ＝__________.[解析] 当a ＝－1时，f (x )＝3|x ＋1|≥0，不满足题意；当a <－1时，f (x )＝Error!f (x )min ＝f (a )＝－3a －1＋2a ＝5，解得a ＝－6；当a >－1时，f (x )＝Error!f (x )min ＝f (a )＝－a ＋1＋2a ＝5，解得a ＝4.[答案] －6或47．若关于x 的不等式|a |≥|x ＋1|＋|x －2|存在实数解，则实数a 的取值范围是__________．[解析] ∵f (x )＝|x ＋1|＋|x －2|＝Error!∴f (x )≥3.要使|a |≥|x ＋1|＋|x －2|有解，∴|a |≥3，即a ≤－3或a ≥3.[答案] (－∞，－3]∪[3，＋∞)8．已知关于x 的不等式|x －a |＋1－x >0的解集为R ，则实数a 的取值范围是__________．[解析] 若x －1<0，则a ∈R ；若x －1≥0，则(x －a )2>(x －1)2对任意的x ∈[1，＋∞)恒成立，即(a －1)[(a ＋1)－2x ]>0对任意的x ∈[1，＋∞)恒成立，所以Error!(舍去)或Error!对任意的x ∈[1，＋∞]恒成立，解得a <1.综上，a <1.[答案] (－∞，1)9．设a ，b ，c 是正实数，且a ＋b ＋c ＝9，则＋＋的最小值为__________．2a 2b 2c[解析] ∵(a ＋b ＋c )(2a ＋2b ＋2c )＝[()2＋()2＋()2]a b c [(2a )2＋(2b )2＋(2c )2]≥2＝18，(a ·2a ＋b ·2b ＋c ·2c )∴＋＋≥2，∴＋＋的最小值为2.2a 2b 2c 2a 2b 2c[答案] 210．(2014·陕西卷)设a ，b ，m ，n ∈R ，且a 2＋b 2＝5，ma ＋nb ＝5，则 m 2＋n 2的最小值为________．[解析] 由柯西不等式，得(a 2＋b 2)(m 2＋n 2)≥(am ＋bn )2，即5(m 2＋n 2)≥25，∴m 2＋n 2≥5，当且仅当an ＝bm 时，等号成立．∴的最小值为.m 2＋n 25[答案] 511．对任意x ，y ∈R ，|x －1|＋|x |＋|y －1|＋|y ＋1|的最小值为__________．[解析] ∵|x －1|＋|x |＋|y －1|＋|y ＋1|＝(|1－x |＋|x |)＋(|1－y |＋|1＋y |)≥|(1－x )＋x |＋|(1－y )＋(1＋y )|＝1＋2＝3，当且仅当(1－x )·x ≥0，(1－y )·(1＋y )≥0，即0≤x ≤1，－1≤y ≤1时等号成立，∴|x －1|＋|x |＋|y －1|＋|y ＋1|的最小值为3.[答案] 312．若不等式|x ＋1|－|x －4|≥a ＋，对任意的x ∈R 恒成立，则实数a 的取4a值范围是________．[解析] 只要函数f (x )＝|x ＋1|－|x －4|的最小值不小于a ＋即可．由于||x ＋1|4a－|x －4||≤|(x ＋1)－(x －4)|＝5，所以－5≤|x ＋1|－|x －4|≤5，故只要－5≥a ＋即4a可．当a >0时，将不等式－5≥a ＋整理，得a 2＋5a ＋4≤0，无解；当a <0时，4a将不等式－5≥a ＋整理，得a 2＋5a ＋4≥0，则有a ≤－4或－1≤a <0.综上可知，4a实数a 的取值范围是(－∞，－4]∪[－1,0)．[答案] (－∞，－4]∪[－1,0)二、解答题13．已知不等式2|x －3|＋|x －4|<2a .(1)若a ＝1，求不等式的解集；(2)若已知不等式的解集不是空集，求a 的取值范围．[解] (1)当a ＝1时，不等式即为2|x －3|＋|x －4|<2，若x ≥4，则3x －10<2，x <4，∴舍去；若3<x <4，则x －2<2，∴3<x <4；若x ≤3，则10－3x <2，∴<x ≤3.83综上，不等式的解集为Error!.(2)设f (x )＝2|x －3|＋|x －4|，则f (x )＝Error!作出函数f (x )的图象，如图所示．由图象可知，f (x )≥1，∴2a >1，a >，即a 的取值范围为.12(12，＋∞)14．(2015·新课标全国卷Ⅰ)已知函数f (x )＝|x ＋1|－2|x －a |，a >0.(1)当a ＝1时，求不等式f (x )>1的解集；(2)若f (x )的图象与x 轴围成的三角形面积大于6，求a 的取值范围．[解] (1)当a ＝1时，f (x )>1化为|x ＋1|－2|x －1|－1>0.当x ≤－1时，不等式化为x －4>0，无解；当－1<x <1时，不等式化为3x －2>0，解得<x <1；23当x ≥1时，不等式化为－x ＋2>0，解得1≤x <2.所以f (x )>1的解集为Error!.(2)由题设可得，f (x )＝Error!所以函数f (x )的图象与x 轴围成的三角形的三个顶点分别为A ，B (2a ＋1,0)，C (a ，a ＋1)，△ABC 的面积为(a ＋1)2.(2a －13，0)23由题设得(a ＋1)2>6，故a >2.23所以a 的取值范围为(2，＋∞)．15．设函数f (x )＝|x －1|＋|x －a |.(1)若a ＝－1，解不等式f (x )≥3；(2)如果∀x ∈R ，f (x )≥2，求a 的取值范围．[解] (1)当a ＝－1时，f (x )＝|x －1|＋|x ＋1|，f (x )＝Error!作出函数f (x )＝|x －1|＋|x ＋1|的图象．由图象可知，不等式f (x )≥3的解集为Error!.(2)若a ＝1，f (x )＝2|x －1|，不满足题设条件；若a <1，f (x )＝Error!f (x )的最小值为1－a ；若a >1，f (x )＝Error!f (x )的最小值为a －1.∴对于∀x ∈R ，f (x )≥2的充要条件是|a －1|≥2，∴a 的取值范围是(－∞，－1]∪[3，＋∞)．16．(2015·福建卷)已知a >0，b >0，c >0，函数f (x )＝|x ＋a |＋|x －b |＋c 的最小值为4.(1)求a ＋b ＋c 的值；(2)求a 2＋b 2＋c 2的最小值．1419[解] (1)因为f (x )＝|x ＋a |＋|x －b |＋c ≥|(x ＋a )－(x －b )|＋c ＝|a ＋b |＋c ，当且仅当－a ≤x ≤b 时，等号成立．又a >0，b >0，所以|a ＋b |＝a ＋b ，所以f (x )的最小值为a ＋b ＋c .又已知f (x )的最小值为4，所以a ＋b ＋c ＝4.(2)由(1)知a ＋b ＋c ＝4，由柯西不等式得(4＋9＋1)≥(14a 2＋19b 2＋c 2)2＝(a ＋b ＋c )2＝16，(a 2×2＋b 3×3＋c ×1)即a 2＋b 2＋c 2≥.141987当且仅当＝＝，12a 213b 3c 1即a ＝，b ＝，c ＝时等号成立．8718727故a 2＋b 2＋c 2的最小值为.141987。
不等式的类型及解法一、一元一次不等式一元一次不等式是指只含有一个未知数的一次方程，形如ax+b>0或ax+b<0的不等式，其中a和b为已知实数，且a≠0。
解法：1. 将不等式转化为等式，即ax+b=0，求得方程的解x0。
2. 根据a的正负性，将解x0进行分类讨论：- 当a>0时，若x>x0，则ax+b>0；若x<x0，则ax+b<0。
- 当a<0时，若x>x0，则ax+b<0；若x<x0，则ax+b>0。
二、一元二次不等式一元二次不等式是指含有一个未知数的二次方程，形如ax^2+bx+c>0或ax^2+bx+c<0的不等式，其中a、b和c为已知实数，且a≠0。
解法：1. 将不等式转化为等式，即ax^2+bx+c=0，求得方程的解x1和x2。
2. 根据a的正负性和二次函数的凸凹性，将解x1和x2进行分类讨论：- 当a>0时，若x1<x<x2，则ax^2+bx+c>0；若x<x1或x>x2，则ax^2+bx+c<0。
- 当a<0时，若x<x1或x>x2，则ax^2+bx+c>0；若x1<x<x2，则ax^2+bx+c<0。
三、绝对值不等式绝对值不等式是指含有绝对值符号的不等式，形如|f(x)|>g(x)或|f(x)|<g(x)，其中f(x)和g(x)为已知函数。
解法：1. 对于|f(x)|>g(x)，将不等式拆分为两个不等式：f(x)>g(x)和f(x)<-g(x)。
2. 分别解出这两个不等式的解集，然后求并集即为原不等式的解集。
四、分式不等式分式不等式是指含有分式的不等式，形如f(x)/g(x)>0或f(x)/g(x)<0，其中f(x)和g(x)为已知函数。
解法：1. 将分式不等式转化为分子和分母的符号相同的不等式：f(x)g(x)>0或f(x)g(x)<0。
不等式的解法1、一元一次不等式ax b >方法：通过去分母、去括号、移项、合并同类项等步骤化为ax b >的形式，若0a >,则bx a>；若0a <,则bx a<；若0a =,则当0b <时，x R ∈；当0b ≥时，x ∈∅。
【例1-1】（1）2133ax ->解：此时，因为a 的符号不知道，所以要分：a =0，a >0, a <0这三种情况来讨论. 由原不等式得a x >1, ①当a =0时，⇒ 0>1.所以，此时不等式无解. ② 当a >0时，⇒ x >a 1, ③当a <0时，⇒x <a1. 【例1-2】已知不等式0)(6)23(<-++b a x b a 与不等式01)1(322<+-++-a a x a a 同解，解不等式0)3(2)2(3>-+-a b x b a 。
解：R a ∈，012>+-a a ∴ 01)1(322<+-++-a a x a a 的解为31-<x ∴ )(6)23(b a x b a --<+中0)23(>+b a ∴ 解b a b a x 23)(6+--< 由题意ba b a 23)(631+--=-∴ 043>=b a 代入所求：062>--b bx ∴ 3-<x要注意：当一元一次不等式中未知数的系数是字母时，要分未知数的系数等于0、大于0、小于0这三种情况来讨论.2、一元二次不等式的解集（联系图象）。
尤其当0∆=和0∆<时的解集你会正确表示吗？ 基本步骤：① 把二次项系数a 化为正②求对应的一元二次方程的根（先考虑十字相乘法，不能因式分解的再考虑用求根公式）③利用二次函数的图像（下图，三个“二”的关系）求出对应的解集，用集合或区间表示设0a >,12,x x 是方程20ax bx c ++=的两实根，且12x x <，则其解集如下表：二次函数、方程20ax bx c ++>20ax bx c ++≥ 20ax bx c ++< 20ax bx c ++≤0∆>1{|x x x <或 2}x x >1{|x x x ≤或2}x x ≥12{|}x x x x << 12{|}x x x x ≤≤0∆={|}2b x x a≠-Rφ {|}2b x x a=-0∆<R Rφ φ【例2-1】解下列关于x 的不等式：(1) 2x 2-3x -5>0； (2) 3x 2-4x -1≤0； (3) x 2-2x +1≤0； (4) x 2-2x +1>0； (5) x 2-2x +3>0； (6) x 2-2x +3≤0. 解析：（1）（2）代表判别式大于0的一元二次不等式的题目.只不过（1）对应的一元二次方程容易因式分解求两根，（2）就不容易用十字相乘法因式分解，此时需要用一元二次方程的求根公式或者配成完全平方的形式来求两根.（3）（4）代表判别式等于0的一元二次不等式的题目.（5）（6）代表判别式小于0的一元二次不等式的题目.（1）因为对此不等式对应的一元二次方程x 22-3x -5=0因式分解得(2x -5)(x +1)=0. 所以该方程的两根为：x 1=25,或x 2=-1. 又因为此不等式对应的一元二次函数y =2x 2-3x -5的抛物线开口向上， 所以，根据“大于在两边，小于在中间”的原理， 可以直接写出不等式2x 2-3x -5>0的范围： x >25，或x <-1； （2）与上题解法类似.∵3x 2-4x -1=0的判别式∆=42-4⋅3⋅(-1)=28>0, ∴一元二次方程3x 2-4x -1=0有两个不同的实数根为 x 1=372+, 或x 2=372-. ∴此不等式中x 的取值范围是372-≤x ≤372+； （3）∵x 2-2x +1=0的判别式∆=0.∴x 2-2x +1=0有两个相等的实数根， x 1=x 2=1.所以，根据“大于在两边，小于在中间”的原理，不等式x 2-2x +1≤0中x 的取值范围是 1≤x ≤1,即x =1； （4）与（3）类似分析，可知不等式x 2-2x +1>0中x 的取值范围是x >1，或x <1,即x ≠1；（5）因为方程x 2-2x +3=0的判别式∆<0.所以方程x 2-2x +3=0没有实数根.此时，就不能根据“大于在两边，小于在中间”的原理了， 这时，可以用配成完全平方式的方法.∵x 2-2x +3=x 2-2x +1+2=21）（-x +2>0， ∴不等式x 2-2x +3>0中x 的取值范围是 x ∈R ；（6）与（5）类似分析，可知不等式x 2-2x +3≤0中x 的取值范围是空集. 【例2-2】解下列关于x 的不等式：22232(1)(1)0(2)()0(3)10.x a x a x a a x a ax ax -++>-++≤++≤；；解析：这是与一元(一)二次不等式有关的含有参数的不等式题型，常考的有两种形式：易因式分解求根的形式和不易（能）因式分解求根的形式. 解这类题的关键是：把参数a 以正确的情况来分类讨论，然后再用解一元一（二）次不等式的基本方法来做. ；，或时，当，或时，当时，当）（易知原不等式因式分解，所以，方法一：因为本题容易a x x a x a x a x a x a x <><<>>≠=>--⇔11.11.11.0)1()1(一；以下讨论的情况同方法三种情况讨论了所以，我们就可以分这；；把数轴分为三部分：此时，只能取一个值这样）（即，令判别式系数为常数，我们只要方法二：因为二次项的..11111.1.04102<>==⇒=-+=∆=∆a a a a a a a；原不等式的解为：时，时，即当原不等式的解为：时，，或时，即当，或时，原不等式的解为：，或时，即当原不等式系来讨论即可只要根据两根的大小关，所以，解求出对应方程的两根类似，两者都易因式分与a x a a a a a x a a a a a x x a a a a a x a x ≤≤<<<≤≤<>>=====≤--⇔22222210.01.1010.0))((.)1()2(（3）式对应的方程不易因式分解求出根，判别式的符号不能确定，并且x 2的系数含有参数. 这说明对应方程根的情况不能确定，该不等式也不一定为一元二次不等式. 综合上述分析，我们应以x 2的系数为0以及判别式为0时，得出的参数a 值作为讨论的依据. 求出的参数a 把数轴分为几部分，相应的就分几种情况来讨论..444000.40040.0022>=<<=<==⇒=-=∆=a a a a a a a a a a a x ；；；；值把数轴分为五部分：值一共有两个，这两个所以，求出的，或，即再令判别式，即的系数为令由上面的分析，我们就容易知道讨论的依据了..24240..24,24.00.210)12(01444..0102212222122aaa a x a a a a x a x x aa a a x a a a a x a x x x x a a -+-≤---≥<<-+-=---=>∆<-=⇒≤+⇒≤++⇔=≤⇔=，或时，原不等式的解为：所以，当且此时或两根为：对应的一元二次方程的别式数的图像开口向下，判时，对应的一元二次函当时，原不等式当集为空集所以，此时不等式的解时，原不等式当.24244...04..,0402212aaa a x a a a a a x x a a -+-≤≤--->>>∆><∆<<时，原不等式的解为：所以，当只不过的两根方程的根仍为上面所求此时，对应的一元二次别式数的图像开口向上，判时，对应的一元二次函当为空集所以，原不等式的解集无根即对应的一元二次方程别式数的图像开口向上，判时，对应的一元二次函当总结：对于这种类型中易因式分解求出两根的题型，我们先因式分解求出两根，然后再以两根的大小来进行分类讨论；当不易因式分解求出两根时，我们应以x 2的系数为0以及判别式为0时，得出的参数a 值作为讨论的依据.求出的参数a 把数轴分为几部分，相应的就分几种情况来讨论，在每一种情况里就变成了解基本的不等式的题型.注意：每一种情况的内部既不能取交集，所有情况的结果也不能取并集，最终结果只能分类回答！要与前面所讲述的题型中“一种情况内部取交集，把所有情况的结果取并集，最后得到的才是（不）等式的解集”的原则进行区别和联系.3、简单的一元高次不等式的解法：数轴穿根法： 基本步骤：⑴ 将不等式右边化为０，左边分解成若干个一次因式或二次不可分因式的积. ⑵ 把每个因式的最高次项系数化为正数.⑶ 将每个一次因式的根从小到大依次标在数轴上.⑷ 从右上方依次通过每个点画出曲线，遇到奇次因式的根对应的点，曲线穿过数轴；遇到偶次因式的根对应的点，曲线不穿过数轴，仍在数轴同侧迂回. 即规律“奇穿偶不穿”.⑸ 根据曲线就可以知道函数值符号变化规律. 【例3-1】解下列关于x 的不等式：22211)(2)(3)0(2)(21)(31)(41)0(3)(3(1)(2304(1)(1)(2)0.x x x x x x x x x x x x x ---≤++-+≥-+-->+-+<（）（；；））；（）解析：这种类型的不等式如果用上述的方法1，分类讨论可以做出来，但是比较复杂，而且易出现错误.所以，常用数轴表根法(又称零点分段法)来做这类题.所谓数轴标根法，就是用一条曲线代替列表讨论，这条曲线虽不能准确表达出函数的图象，但能体现出函数值的符号变化规律．即：曲线与x 轴的交点将x 轴分成若干区域，曲线在x 轴上方所对应区间内的x 值，使函数值大于0 ；曲线在x 轴下方所对应区间内的x 值，使函数值小于0 ；曲线与x 轴的交点所对应的x 值，使 函数值等于0.按照上述的方法，易解出以上各题.参考答案：；或）（；或）（4131,21232,11≤≤--≤≤≤≤x x x x .1,12)4(3,1)3(-≠<<-≠->x x x x 且；且4. 分式不等式的解法：一般不能去分母，但分母恒为正或恒为负时可去分母。
基本步骤：（1）标准化：移项．．、通分．．使右边为0，即)()(x g x f >0(或)()(x g x f <0)；)()(x g x f ≥0(或)()(x g x f ≤0)的形式， （2）转化为整式不等式（组）⎩⎨⎧≠≥⇔≥>⇔>0)(0)()(0)()(;0)()(0)()(x g x g x f x g x f x g x f x g x f（3）分解因式，并使每一个因式中最高次项的系数为正，最后用标根法求解。
