当前位置：文档之家 › 10-3 基尔霍夫定律的相量形式

10-3 基尔霍夫定律的相量形式

  • 格式：ppt
  • 大小：317.00 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

最新电工学电力学课程第八章《电路定律的相量形式》

最新电工学电力学课程第八章《电路定律的相量形式》




由相量形式KVL有 : V V 1 V 2 600 8090 (V)
（2）相量图解法
60 j80 10053.1 (V) 故 : |V | 100(V)
相量法的三个基本公式


UR RIR


U L jL IL

1
UC

j
C
IC
以上公式是在电压、电流关联参考方向的条件
错误的写法
1 u
C i
1
C

U I
(2) 容抗的绝对值和频率成反比。
0, XC , 直流开路( 隔直作用) ;
XC
, XC 0, 高频短路（旁路作用）;

(3) 由于容抗的存在使电流领先电压。
4、受控源 如果受控源（线性）的控制电压或电流是正弦量， 则受控源的电压或电流将是同一频率的正弦量。
i 超前u 90° I
0
所示，反映电压电流瞬时 值关系的波形图如图(b)所示。由此图可以看出电容电流超 前于电容电压90°，当电容电压由负值增加经过零点时，其 电流达到正最大值。
容抗
I= CU
U 1
I C
容抗的物理意义：
X
C
定义

1
C
(1) 表示限制电流的能力；
相量关系
+
U R R I
U R
-
有效值关系：UR = RI 相位关系：u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
+ u (t)
u(t) L di(t)
第5章正弦电流电路的稳态分析-4基尔霍夫定律、电路相量模型和电阻电感电容串并联

第5章正弦电流电路的稳态分析-4基尔霍夫定律、电路相量模型和电阻电感电容串并联


2 2 U UR UX
I
由UR 、UX 、U 构成的电压三角形与阻抗三角形相似。
R、L、C 串联电路的性质 Z=R+j(wL-1/wC)=|Z|∠ |Z| = U/I = u-i +
U
I
R
jwL
+ UL 1 jω C
U
.
+.
UC

-
wL > 1/w C ， >0，电路为感性。 wL<1/w C ， <0，电路为容性。 wL=1/w C ， =0，电路为电阻性
.
560 V U
+. -
UC
-
jw L j2π 3 104 0.3 103 j56.5 1 1 j j j26.5 4 6 wC 2π 3 10 0.2 10
1 Z R jω L j 15 j56.5 j26.5 33.5463.4 o Ω ωC
正弦电流电路的稳态分析
第四讲（总第二十讲）
基尔霍夫定律的相量形式和电路的相量模型 电阻、电感和电容串并联的电路
基尔霍夫定律的相量形式和电路的相量模型
一、基尔霍夫定律的相量形式
同频率的正弦量加减可以用对应的相量形式来进行 计算。因此，在正弦电流电路中，KCL和KVL可用相应 的相量形式表示。
i(t ) 0 u(t ) 0
I I

U
I
U
i
R
例
L + uL C
+ u -
已知：R=15, L=0.3mH, C=0.2F,
+ u 5 2 sin( wt 60)V, f 3 104 Hz uC 求 i , uR , uL , uC 。 -
基尔霍夫定律的相量形式.

基尔霍夫定律的相量形式.


电压相量，如图(c)所示，从相量图上容易看出各正弦电压
的相位关系。
值得注意的是回路中全部电压有效值之代数和并不一
定等于零，本题中 US=10U1+U2+U3=6+8+12=26
即一般说来
n
Uk 0
k 1Biblioteka 关于复数的几个公式1. 假设复数 c rθ a jb
则有 c a2 b2 θ arctan b a
uk (t) Re[U kme jt ] Re[ 2U k e jt ]
代入KVL方程中得到
n uk (t) n Re[Ukmejt ] 0
k 1
k 1
n
n
uk (t) Re[
2Uke jt ] 0
k 1
k 1
由于上式适用于任何时刻t，其相量关系也必须成立，
j ej180 cos180 jsin180 1 1 j2 ej180 1180
模型，图中各电流参考方向均与时域模型相同，仅将
时域模型中各电流符号 iS、i、i1、i2 用相应的相量符
号 IS、I、I1、I2 表示，并计算出电流相量 。
I1 1060 A
I2 5 90 A
列出图(b)相量模型中结点1的KCL方程，其相量形式
为
I I1 I2 0
§8－3 基尔霍夫定律的相量形式
一、基尔霍夫电流定律的相量形式
基尔霍夫电流定律(KCL)叙述为：对于任何集中参数 电路中的任一结点，在任何时刻，流出该结点的全部支路 电流的代数和等于零。其数学表达式为
n
ik (t) 0
k 1
假设电路中全部电流都是相同频率ω的正弦电流，则 可以将它们用振幅相量或有效值相量表示为以下形式
第3章习题解答

第3章习题解答

解：线圈的电路模型如图3.12所示。当线圈接在48V的直流电源上，电感相当于短路状态，由题设，可求出线圈的等效电阻为
当线圈改接在交流电源上时，阻抗模
感抗
电感
3.7当30V的直流电压加到某一线圈上时，消耗的功率为150W；改用230V的交流电压加到同一线圈上时，消耗的功率为3174W。求此线圈的感抗。
谐振频率
品质因数
谐振特征
电路呈纯阻性，阻抗最小，电流最大。
电阻电压等于电源电压，电感、电容上的电压大小相等、方向相反。
电路局部过电压，有可能会出现电感电压UL（电容电压UC）远远大于电源电压U的现象，因此，串联谐振又称为电压谐振。
电源不输出无功功率，电感与电容间进行能量交换。
(2)并联谐振
谐振的条件
两个正弦量之间的相位差为
（2） ，
波形图及相量图如图3.8所示
3.3两正弦交流电流分别为 ， ，试用相量法及相量图法求i=i1+i2的瞬时值三角函数式。
解：(1)相量法求解，采用幅值相量
（2）相量图法求解，如图3.9所示。
3.4图3.10所示为某电路中电压和电流的波形图。试分别写出它的三角函数表达式、相量形式，做出相量图，并求出其相位差。
3.2典型例题分析
例3.1下列各式是否正确？为什么？
（1）
（2）
（3）
（4）
解：（1）式不正确。 是随时间做正弦变化的正弦电流，而 为表示该电流的相量，两者是不相等的。但相量表示了正弦电流的幅值和初相位，所以正弦量可以用相量表示。
（2）式正确。根据欧拉公式，可得
“Im”表示取复数虚部，而复数 的虚部就是 。
2.阻抗及其串、并联
（1）.当n个阻抗如图3.3（a）所示串联时，等效阻抗Z为
电工学版课后答案秦曾煌

电工学版课后答案秦曾煌

图3-1 t rad f /3145014.322=⨯⨯==πωAt i Vt u )90314sin(2)45314sin(310︒-=︒+=︒=︒--︒=-=135)90(45i u ψψϕs T x 0075.0501360135360135=⨯︒︒=︒︒=25A t i i t A t t i f ）（，时，）（︒+=∴︒=∴===+=+⨯===3040sin 10305sin 10040sin 10)40sin(225402πψψψπψπππω︒∠=∠︒∠=︒∠=︒∠⨯︒∠=⋅+=+-+=-+=+++=+1.877.145657.51.53101.9857.5645657.51.531042)44()86(1210)44()86(21212121A A A A j j j A A j j j A A 2121)2(;)60sin(10,)sin(5)1(i i i A t i A t i +=︒+==ωω︒∠=︒∠+︒∠=+=︒∠=︒∠=∙∙∙∙∙89.4023.13601005)2(;6010,05)1(2121m m m m m I I I A I A I A I A I V U 25,10,22021===第三章习题3-1 已知正弦电压和正弦电流的波形如图3-1所示,频率为50Hz ，试指出它们的最大值、初相位以及它们之间的相位差，并说明哪个正弦量超前，超前多少度？超前多少时间？解： u 、i 的表达式为即：u 比i 超前135°，超前2-1 某正弦电流的频率为20Hz ，有效值为 A ，在t =0时，电流的瞬时值为5A ，且此时刻电流在增加，求该电流的瞬时值表达式。

解：3-3 已知复数A 1=6+j8Ω，A 2=4+j4Ω，试求它们的和、差、积、商。

解：3-4 试将下列各时间函数用对应的相量来表示。

解：3-5 在图3-2所示的相量图中，已知 ，它们的角频率是ω，试写出各正弦量的瞬时值表达式及其相量。

基本元件的相量形式(3)

基本元件的相量形式(3)


电流与电压同相
电工基础
三、电感元件的相量形式： 电感元件的相量形式：
i
L
Z L = ωL∠90 = jωL = j 2πfL
ɺ I
ZL
相量图
+
u
−
ɺ U
ϕi
ɺ I
+
ɺ U
−
i (t ) = I m sin(ωt + ϕi ) A u (t ) = U m sin(ωt + ϕ u )V
u(t ) = L ⋅
Q=
ωt
t
2 UC
XC
电 源
i 电
源
(var) : 电容元件 电
u
电工基础
例：求电流及电容元件的电压和无功功率，并画相量图。 求电流及电容元件的电压和无功功率，并画相量图。 ɺ ZC C = 10µF i C I
+
u
解： X C =
− u (t ) = 100 2 sin(1000t + 30 )V
ɺ UC
电工基础
u (t ) = U m sin(ωt + ϕ u )V
ϕ
ɺ I +1
电流与电压同相
ɺ I = I∠ϕi (A) ɺ U = U∠ϕ u (V )
ɺ U Z= ɺ = Z ∠ϕ z I
u(t ) = R ⋅ i(t )
= R ⋅ I m sin(ωt + ϕ i )
大小关系： 大小关系： m = R ⋅ I m U
ϕ z = ϕu − ϕi
电工基础
电感元件的功率： 电感元件的功率：
1）瞬时功率: 瞬时功率:
p ( t ) = u ( t )i ( t )
电路相量法和正弦稳态电路的分析

电路相量法和正弦稳态电路的分析


故
图 (c):以 电 感 与 电 容 的 并 联 电 压 为 参 考 相 量
I2.82A 8
U C 3 0 1 A 3 0 0 V I I C I L j - 2 j = - j A , U U R U C 4 0 j + 3 0 = 5 0 5 3 . 1 V
6.2 正弦量的相量表示法
2、正弦量的相量表示
i(t) Im c(o t si)2 Ic ( to s i)
Re
2
Ie
j(t
i
)


Re
2
Ie
ji
e
jt

Re

2

I
e
jt


Re I m
e
jt



其中：



UjLI jXLI
感抗： XL L 有效值： U LI 相位： u i 90
U j
u
I
i

I
j L
t

U
O
1
i O
电压超前于电流 90°
u
6.3 正弦稳态电路的相量模型
例题 电路中已标明电压表和电流表的读数，试求电压 u 和电流 i 的有效值。
60V
6.3 正弦稳态电路的相量模型
例题 已L=知3如H，图所C示=5电路1中0-3Fi S 。 试0 . 求2 c 电o （ s 压 ut R 、4 u5 L） A 和,u C 1 0 r 。a d / s , R 2 0 ,
R
根据
iS +
uR –
C
电路定理的相量形式

电路定理的相量形式


i(t ) 10 2 cos( 5t 36.9 )A
0
U _ I
+
I
1
-j10 15 j20
I2
返 回
I3
上 页 下 页
3. 电容元件相量形式的VCR
iC(t)
+ u(t) -
时域形式： uC (t ) 2U sin(t Ψ u ) duC (t ) iC (t ) C 2CU cos( t Ψ u ) C dt π 2CU sin( t Ψ u ) 2 相量形式：
1 jωC
A0 ＝I0max=?
3. Z1 jX L , Z 2为何参数
A0 ＝?
A0 Z1 A1 A2 Z2
U
A0 ＝I0min=?
解
1. I 0 82 62 10A
2. Z 2 R，I 0 max 8 6 14A 3. Z 2 jX C , I 0 min 8 6 2A
|XC| 容抗和频率成反比
0， |XC| 直流开路(隔直) ，|XC|0 高频短路

1 I jX I UC C C jC
相量表达式
I C j CU C
返 回 上 页 下 页
波形图及相量图
电流超前 电压900
iC
pC u
IC
u
U
o 瞬时 功率
第三节 电路基本定律的相量形式
1. 基尔霍夫定律的相量形式
同频率的正弦量加减可以用对应的相量形式 来进行计算。因此，在正弦电流电路中，KCL和 KVL可用相应的相量形式表示：
i(t ) 0
I 0
U 0
u (t ) 0
电路基本定律的相量形式

电路基本定律的相量形式


uC －
RI 100 0.5 245 50 245 U R
jX I U C C j100 0.5 245 50 2 45
i sin( 100t 45) A u R 100 sin( 100t 45) V u C 100 sin( 100t 45) V
i
2
解：
1000V U s 1 1 XC 100 6 C 100 100 10
+
us －
+
R C uR －
+
U U U s R C
RI U R U U RI jX I U s R C C ( R jX C ) I jX I U C C U 1000 1000 s I 0.5 245A R jX C 100 j100 100 2 45
2、电感元件
di 电感元件伏安关系： u L dt 根据相量运算的规则1、规则3和规则4 ，有：
jLI jX I U L
U 、 I I 代入，得： 将U u i U u j LI i LI ( i 90)
U LI X L I
u i 90
i
L
+ u － (a) 电感元件
U
θ u θ i
I
感抗：XL=ωL，与频率成正比。
(b) 相量图
du 电感元件伏安关系： i C dt 根据相量运算的规则1、规则3和规则4 ，有：
3、电容元件
jCU I
U 、 I I 代入上式，得： 将U u i I i j CU u CU ( u 90)
基尔霍夫定律的相量形式

基尔霍夫定律的相量形式


相量形式的推导
01
通过三角函数和复数的关系，将交流电路中的电压和电流用相 量表示。
02
利用相量图，通过几何方法分析电路，得出各支路电流和元件
上电压的关系。
通过相量的运算（加、减、乘、除等），推导出电路的阻抗、
03
导纳等参数，进而求解交流电路的各种问题。
相量形式的应用场景
交流电路分析
控制系统分析
利用相量形式分析交流电路，可以方便地 得出各支路电流和元件上电压的关系，计 算电路的功率、阻抗、导纳等参数。
3
相量形式的图解分析
通过相量图，可以直观地表示出电压和电流的相 位关系以及元件之间的相互作用，方便理解和分 析电路。
相量形式的优势与局限性
优势 • 简化了交流电路的计算过程。
• 通过相量图可以直观地理解电路的工作原理。
相量形式的优势与局限性
相量形式的优势与局限性
01
局限性
02
• 对于瞬态分析或非线性分析，相量形式可能不够 精确或复杂。
为了更好地适应这一发展趋势，需要进一步深入研究基尔霍夫定律的相量形式在复杂交流电路中的应用， 包括对非线性元件的处理、多频段电路的分析以及高性能计算在交流电路分析中的应用等。
此外，随着智能电网和物联网技术的发展，交流电路的应用领域也在不断扩展，需要进一步探索基尔霍 夫定律的相量形式在智能电网和物联网中的应用。
基尔霍夫定律的相量形式
contents
目录
• 引言 • 基尔霍夫定律的相量形式 • 相量形式与正弦稳态电路 • 相量形式在交流电路分析中的作用 • 基尔霍夫定律的相量形式与实际应用 • 结论
01 引言
基尔霍夫定律的重要性
在电路分析中，基尔霍夫定律 是基本的定律之一，它为电路 分析提供了基础。
电工与电子技术电路定理的相量形式

电工与电子技术电路定理的相量形式


i(t) =10 2 cos(5t + 36.90 )A
ɺ U _ ɺ I
+
ɺ I
1
-j10Ω 15Ω j20Ω
ɺ I2
返 回
ɺ I3
上 页 下 页
jω L 相量关系： 相量关系：
ɺ ɺ ɺ UL = jωL IL = jXL IL
Ψu=Ψi +90°
返 回 上 页 下 页
相量模型
有效值关系： UL=ω L IL 相位关系： 相位关系：
感抗和感纳
XL=ωL=2πfL，称为感抗，单位为 (欧姆) 称为感抗，单位为Ω 欧姆) BL=1/ω L =1/2πfL， 称为感纳，单位为 S 称为感纳 感纳，
ɺ IC
Ψu
ɺ UC
ωt
pC = uCiC = 2UC IC cos(ω t +Ψu ) sin( ω t +Ψu ) = UC IC sin 2(ω t +Ψu )
瞬时功率以2ω交变，有正有负， 瞬时功率以 交变，有正有负，一周期 交变 内刚好互相抵消，表明电容只储能不耗能。 内刚好互相抵消，表明电容只储能不耗能。 有功功率P 有功功率 P=0
1 ωC
ɺ IC
+ ɺ UC -
−j
相量模型
ɺ ɺ 相量关系： 相量关系： ɺC = 1 IC = −j 1 IC U jωC ωC 1 IC 有效值关系： UC = 有效值关系： ωC 相位关系： 相位关系： Ψu=Ψi -90°
返 回 上 页 下 页
容抗与容纳
XC=1/ω C， 称为容抗，单位为 Ω(欧姆) 称为容抗， (欧姆) Β C = ω C， 称为容纳，单位为 S 称为容纳，
返 回 上 页 下 页

第四节 正弦交流电路的复数计算及三相电路的计算

60 53.13 (V )
U L j LI 240 36.87 (V )
U C
I
1
j C
160 143 .13 (V )
电路的相量图
一、相量图
相关的电压和电流相量在复平面上组成。 在相量图上，除了按比例反映各相量的模外， 最重要的是确定各相量的相位关系。
二、相量图的画法
选择某一相量作为参考相量， 而其他有关相量就根据它来加以确定。 参考相量的初相可取为零， 也可取其他值，视不同情况而定。
• 1、掌握正弦量的三要素和有效值 • 2、掌握电感、电容元件电流电压关系的
相量形式及基尔霍夫定律的相量形式 • 3、掌握阻抗、导纳、有功功率、无功功
率、视在功率和功率因数的概念 • 4、熟练掌握正弦电路分析的相量方法
• 5、了解频率特性的概念
预备知识——复数
一、复数的形式
1、代数形式
F = a + jb
1、串联电路
取电流为参考相量，从而确定各元件的电压相量； 表达KVL的各电压相量可按向量求和的方法作出。 2、并联电路 取电压为参考相量，从而确定各元件的电流相量； 表达KCL的各电流相量可按向量求和的方法作出。 3、串并联电路 从局部开始
以上一节中例题为例
I 4 53.13 ( A) U R 60 53.13 (V ) U L 240 36.87 (V ) UC 160 143 .13 (V )
2、角频率ω
i
反映正弦量变化的快慢
Im
单位 rad/s ωT=2π ω=2πf
2π O
π 2π ωt
i
f=1/T
频率f 的单位为赫兹（Hz）
周期T的单位为秒（s）
工频，即电力标准频率：f =50Hz,

基尔霍夫定律的验证的实验报告

1.电压电流电流的参考方向可以任意指定，分析时：若参考方向与实际方向一致，则i>0，反之i<0。

电压的参考方向也可以任意指定，分析时：若参考方向与实际方向一致，则u>0反之u<0。

2．功率平衡一个实际的电路中，电源发出的功率总是等于负载消耗的功率。

3．全电路欧姆定律：U=E-RI4．负载大小的意义：电路的电流越大，负载越大。

电路的电阻越大，负载越小。

5．电路的断路与短路电路的断路处：I＝0，U≠0 电路的短路处：U＝0，I≠0 。

基尔霍夫定律：1．几个概念：支路：是电路的一个分支。

结点：三条（或三条以上）支路的联接点称为结点。

回路：由支路构成的闭合路径称为回路。

网孔：电路中无其他支路穿过的回路称为网孔。

2．基尔霍夫电流定律：（1）定义：任一时刻，流入一个结点的电流的代数和为零。

或者说：流入的电流等于流出的电流。

（2）表达式：i进总和=0 或：i进=i出（3）可以推广到一个闭合面。

3．基尔霍夫电压定律（1）定义：经过任何一个闭合的路径，电压的升等于电压的降。

或者说：在一个闭合的回路中，电压的代数和为零。

或者说：在一个闭合的回路中，电阻上的电压降之和等于电源的电动势之和。

电位的概念（1）定义：某点的电位等于该点到电路参考点的电压。

（2）规定参考点的电位为零。

称为接地。

（3）电压用符号U表示,电位用符号V表示（4）两点间的电压等于两点的电位的差。

（5）注意电源的简化画法。

四．理想电压源与理想电流源1．理想电压源（1）不论负载电阻的大小，不论输出电流的大小，理想电压源的输出电压不变。

理想电压源的输出功率可达无穷大。

（2）理想电压源不允许短路。

2．理想电流源（1）不论负载电阻的大小，不论输出电压的大小，理想电流源的输出电流不变。

理想电流源的输出功率可达无穷大。

（2）理想电流源不允许开路。

3．理想电压源与理想电流源的串并联（1）理想电压源与理想电流源串联时，电路中的电流等于电流源的电流，电流源起作用。

电子科大《电路分析》第10章 正弦稳态分析


解： 2f 100 rad / s
u1 (t ) 50 cos(100t 30)V u2 (t ) 100 cos(100t 150)V
今后我们所见到的正弦波无非以三种形式来描述：
u2 (t ) 100 cos(100t 150)V I1m 560 A 2. I m I m I cos I sin I1m 6 j 7 A 3. I m m m
§10-4 三种基本电路元件伏安关系的相量形式
电阻:
U m RI m ,
U RI
U RI ,
u i
同相 正交
正交
电感:
U m jLI m ,
U jLI
U LI ,
u i 90
I jCU
电容:
I m jCU m ,
12 90,13 210, 23 120
13 150
规定相位差
二、正弦电压电流的相量表示
由欧拉公式有:
e
j
cos j sin
e
j (t )
cos(t ) j sin( t )
U e j 令U m m
§10-3 基尔霍夫定律的相量形式
虽然相量法将微分方程在正弦激励下的特解化成了
复数方程的求解，但对高阶电路，微分方程的建立仍是
一件很困难的工作。
对正弦激励下的电路，能否象直流激励下的电阻电 路那样，用观察法直接写出复数方程，回答是肯定的. 只要引入KCL, KVL和元件VCL的相量形式及相量模 型，就可以将电阻电路的所有分析方法推广到正弦稳态 电路。
一、简单推导
i1 i2 i3 0

基尔霍夫定律的相量形式


独立电源电路
独立电源电路是一种特殊的电路配置，其中有一个或多个独立的电源提供电 流和电压。我们将探讨如何应用基尔霍夫定律解决独立电源电路中的问题。
综合电路的求解和例子
在实际应用中，电路往往是复杂的，由串联、并联和独立电源组成。在这一 部分中，我们将应用基尔霍夫定律的相量形式来解决综合电路的分析问题。
基尔霍夫定律的相量形式
基尔霍夫定律是电路理论中的基本定律之一。它描述了电路中电流和电压之 间关系。在本节中，我们将深入研究基尔霍夫定律的相量形式。
基尔霍夫定律的概述
基尔霍夫定律是基本电路定律，用于分析和解决复杂电路中的电流和电压问题。它有两个关键概念：电 流守恒和电压守恒。
基尔霍夫定律的公式
基尔霍夫定律的公式有两个部分：基尔霍夫第一定律和基尔霍夫第二定律。 第一定律描述了电流守恒，第二定律描述了电压守恒。
电路定义及术语
在学习基尔霍夫定律之前，我们需要了解一些基本电路术语，如电流、电压、电阻和电源。这些概念在 电路分析中起着关键作用。
串联电路的求解和例子
在串联电路中，多个电阻依次连接在一起，形成一个回路。使用基尔霍夫定律的相量形式可以轻松求解 串联电路的电流和电压。
并联电路的求解和例子
在并联电路中，多个电阻同时连接在一个节点上，形成分支。基尔霍夫定律 的相量形式可以帮助我们分析并联电路的电流和电压分布。

基尔霍夫定律的相量形式

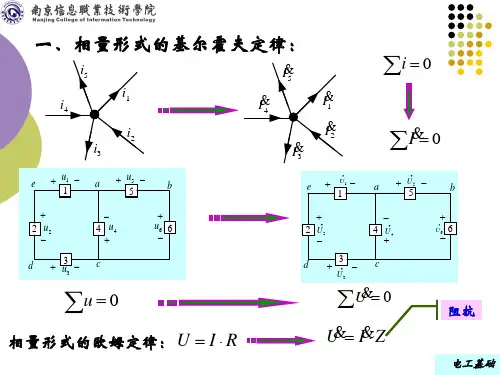
基尔霍夫定律的相量形式
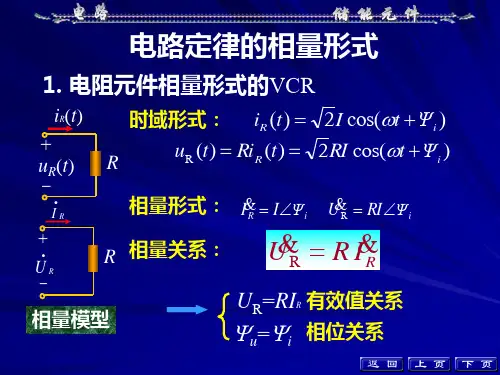
电阻、电容和电感中电压电流的时域关系式，以及相应的相量表达式。

对于简洁电路，我们已知电路中电压和电流均为与所施加的激励源同频率的正弦量。

此结论可推广到线性稳态的简单正弦沟通电路中去。

对于简单的线性电路，假如全部激励源均为同一频率的正弦函数，则各支路的电流和电压都为和激励源有相同频率的正弦函数，都可以表示为相量形式，在电路计算中可采纳相量计算的方法。

基尔霍夫节点电流定律的时域表达式为
（1）
由于全部电流均为相同频率的正弦函数，依据本章第三节内容推导，可把时域求和的表达式转化为相量求和形式
（2）
此式表明，对于任一节点，流出节点的电流相量之和等于零。

此即为相量形式的基尔霍夫节点电流定律。

基尔霍夫电压定律指出，电路中任一闭合回路的各支路电压降之和为零，即
（3）
可得相量形式的基尔霍夫电压定律
（4）
把节点电流或回路电压的相量作成相量图，可得到一个闭合的相量多边形。

在计算分析正弦沟通电路中，可利用上述两个定律及相量关
系。

下面举几个例子加以说明。

例1 图1a的电路中，已知，，求的值。

解：由基尔霍夫电压定律，得：
，图1b中画出了电压的相量图。

图1。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

由于上式适用于任何时刻t，其相量关系也必须成立， 即
U km 0
k 1 n
n
(10 16) (10 17)
U
k 1
k
0
这就是相量形式的KVL定律，它表示对于具有相同频 率的正弦电流电路中的任一回路，沿该回路全部支路电压
相量的代数和等于零。在列写相量形式KVL方程时，对于
e jt ] Re[ 2U e jt ] uk (t ) Re[U km k
代入KVL方程中得到 uk ( ) Re[U km e jt ] 0
k 1 n k 1 n
n
n
uk (t ) Re[ 2U k e jt ] 0
k 1 k 1
e jt ] Re[ 2I e jt ] ik (t ) Re[I km k
代入KCL方程中得到
ik (t ) Re[ I kme jt ] 0
k 1 k 1
n
n
ik (t ) Re[ 2 I k e jt ] 0
k 1 k 1
n
n
参考方向与回路绕行方向相同的电压取“ ＋”号，相反的 电压取“ －”号。 值得特别注意的是沿任一回路全部支路电压振幅(或有 效值)的代数和并不一定等于零，即一般来说
U
k 1
n
km
0
U
k 1
n
k
0
例10-7 电路如图10-13(a)所示，试求电压源电压uS(t)和相 应的电压相量，并画出相量图。已知
4
电路分析中采用符号 应用欧拉公式
j 1
可以得到

e jθ cos jsin θ θ

e
j90
cos90 jsin 90 j
j90
j 1 e e
j90
190

cos(90 ) jsin(90 ) j 1 j90 j e 1 90 j e
由于上式适用于任何时刻t，其相量关系也必须成立， 即
I
k 1
n
km
0
(10 14)
I
k 1
n
k
0
(10 15)
相量形式的KCL定律表示对于具有相同频率的正弦电 流电路中的任一结点，流出该结点的全部支路电流相量的 代数和等于零。在列写相量形式KCL方程时，对于参考方
向流出结点的电流取“ +”号，流入结点的电流取“ -”号。 特别注意的是
由此可求得
U S U1 U 2 U 2 6180 890 120 6 j8 12 6 j8 1053.1 V
写出相应的电压瞬时值表达式
uS (t ) 10 2 cos(t 53.1 )V
值得注意的是回路中全部电压有效值之代数和并不一
§10－3 基尔霍夫定律的相量形式
一、基尔霍夫电流定律的相量形式
基尔霍夫电流定律(KCL)叙述为：对于任何集总参数 电路中的任一结点，在任何时刻，流出该结点的全部支路 电流的代数和等于零。其数学表达式为
i
k 1
n
k
(t ) 0
假设电路中全部电流都是相同频率ω的正弦电流，则
可以将它们用振幅相量或有效值相量表示为以下形式
模型，图中各电流参考方向均与时域模型相同，仅将 时域模型中各电流符号 iS、i、i1、i 2 用相应的相量符
号 I S、I、I 1、I 2 表示，并计算出电流相量 。
I1 1060 A
为
I 2 5 90 A
列出图(b)相量模型中结点1的KCL方程，其相量形式
3+j4=? 5
X Y

53.1
注意：
CASIO fx-100
553.1=?
5 P R 53.1
3 X Y 4
3+j4=?
DEG
表示 度数
SHARP EL-5812
3
X Y 4
r
5
X Y
53.1
SHARP EL-5812
5=?
5
X Y 53.1
xy 3 X Y
解：根据图(a)所示电路的时域模型，画出图(b)所示的相量 模型，并计算出电压相量。
U1 6 180 V U 890 V
2
U 3 120 V
对于图(b)相量模型中的回路，以顺时针为绕行方向， 列出的相量形式KVL方程
US U1 U 2 U3 0
u1 (t ) 6 2 costV u2 (t ) 8 2 cos(t 90 )V u3 (t ) 12 2 costV
图 10-13
u1 (t ) 6 2 costV u2 (t ) 8 2 cos(t 90 )V u3 (t ) 12 2 costV
I I1 I 2 0
由此可得
I I1 I2 1060 5 90 5 j8.66 j5 5 j3.66 6.236.2 A
写出相应的电流瞬时值表达式
i(t ) 6.2 2 cos( t 36.2 )A
j180
cos180 jsin180 1
2 j180
1 j e
1180

值得特别提出的是在正弦电流电路中流出任一结点的
全部电流有效值之代数和并不一定等于零，例如本题中的
I=6.2I1+I2=10+5=15。
本题也可以用作图的方法求解。在复数平面上，画出
已知的电流相量，再用向量运算的平行四边形法则，求得
电流相量，如图(c)所示。相量图简单直观，虽然不够精确， 还是可以用来检验复数计算的结果是否基本正确。 从相量图上容易看出电流i超前于电流i2，超前的角度 为36.2+90=126.2。 容易看出 I=6.2I1+I2=10+5=15 即
I
k 1
n
k
0
二、基尔霍夫电压定律的相量形式
基尔霍夫电压定律(KVL)叙述为：对于任何集中参数 电路中的任一回路，在任何时刻，沿该回路全部支路电压 代数和等于零。其数学表达式为
u (t ) 0
k 1 k
n
假设电路中全部电压都是相同频率ω的正弦电压，则 可以将它们用有效值相量表示如下：
U
k 1
n
k
0
关于复数的几个公式 1. 假设复数 则有
2
c rθ a jb
2
b c a b θ arctan a a r cos b r sin
2. 假设复数 则有
c1 r1θ 1, c2 r2θ
c1c2 r1r2θ 1 θ c1 r1 θ 1 θ c2 r2
定等于零，本题中的 US=10U1+U2+U3=6+8+12=26。
本题也可以用作图的方法求解。在复数平面上，画出 已知的电压相量，再用向量运算的平行四边形法则，求得 电压相量，如图(c)所示，从相量图上容易看出各正弦电压 的相位关系。
值得注意的是回路中全部电压有效值之代数和并不一
定等于零，本题中 US=10U1+U2+U3=6+8+12=26 即一般说来
I
k 1
n
km
0
I
k 1
n
k
0
例10-6 电路如图10-12(a)所示,已知
i1 (t ) 10 2 cos( t 60 ) A

i2 (t ) 5 2 sin t A
试求电流i(t)及其有效值相量。
图 10-12
解：根据图(a)所示电路的时域模型，画出图(b)所示的相量
2 2
2
3. 假设复数
c1 a1 jb1, c2 a2 jb2
c1 c2 (a1 a2 ) j(b1 b2 ) c1 c2 (a1 a2 ) j(b1 b2 )
则有
要求掌握计算器进行复数两种形式的转换。
举例
CASIO fx-100 3 RP 4