下载文档原格式
2019年温州市重点中学自主招生模拟试题数学试卷（考试时间120分钟，满分150分）一.选择题（每题5分，共50分） 1.下列数中不属于有理数的是（ ）A.1B.21C.22D.0.11132.如图，在矩形中截取两个相同的圆作为圆柱的上．下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长和宽分别为y 和x ，则y 与x 的函数图象大致是（ ）A. B. C. D.3.如果把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正 方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中， 符合这一规律的是（ ） A 、13 = 3+10 B 、25 = 9+16 C 、49 = 18+31 D 、36 = 15+214.a 、b 、c 均不为0，若0<=-=-=-abc cxz b z y a y x ，则),(bc ab p 不可能在（ ） A 、第一象限B 、第二象限C 、第三象限D 、第四象限5.如图，在平面直角坐标系中，⊙P 的圆心是（2，a ）（a ＞2），半径为2，函数y=x 的图象被⊙P 截得的弦AB 的长为23， 则a 的值是（ ）A 、22B 、22+C 、23+2D 、23+6.如图，在Rt△ABC 中，∠ACB=90º，∠A=30º，BC=2，将△ABC 绕点C 按顺时针方向旋转n 度后，得到△EDC，此时，点D 在AB 边 上，斜边DE 交AC 边于点F ，则n 的大小和图中阴影部分的面积 分别为（ ）A 、30，2B 、60，2C 、60，32D 、60，3 7.如图一个长为m 、宽为n 的长方形（m ＞n ）沿虚线剪开， 拼接成图2，成为在一角去掉一个小正方形后的一个大正方形，则去掉的小正方形的边长为（ ） A 、2m n - B 、m －n C 、2mD 、2n8.抛物线2x y =上有三点P 1、P 2、P 3，其横坐标分别为t ，t +1，t +3，则△P 1P 2P 3的面积为（ ）． A.1 Ｂ. 2 Ｃ. 3 Ｄ.4 9.已知直线483y x =-+与x 轴、y 轴分别交于点A 和点B ，M 是OB 上的一点，若将△ABM 沿AM 折叠，点B 恰好落在x 轴上的点B '处，则直线AM 的函数解析式是( )A.821+-=x yB.831+-=x y C.321+-=x y D.331+-=x y10.正五边形广场ABCDE 的边长为80米，甲、乙两个同学做游戏，分别从A 、C 两点处同时出发，沿A-B-C-D-E-A 的方向绕广场行走，甲的速度为50米/分，乙的速度为46米/分，则两人第一次刚走到同一条边上时（ ）． Ａ.甲在顶点A 处 Ｂ.甲在顶点B 处 C.甲在顶点C 处 Ｄ.甲在顶点D 处二.填空题（每题6分，共36分）11.分解因式：22242y xy x ++=________________.12.如图，在平面直角坐标系中，反比例函数)0,0(>>=k x xky的图象经过点A （1, 2），B （m ，n ）（m ＞1），过点B 作 y 轴的垂线,垂足为C.若△ABC 面积为２，则点B 的坐标 为________.13.如右图，是一回形图，其回形通道的宽和OB 的长均 为1，回形线与射线OA 交于A 1，A 2，A 3，…．若从O 点到A 1点的回形线为第1圈（长为7），从A 1点到A 2 点的回形线为第2圈，…，依次类推．则第11圈的长 为 ．14.今有一副三角板（如图1），中间各有一个直径为4cm 的圆洞，现将三角板a 的30º角的B /y xMOB AA 3A 2A 1BAO那一头插入三角板b 的圆洞内（如图2），则三角板a 通过三角板b 的圆洞的那一部分的最大面积为 cm 2（不计三角板的厚度，精确到0.1cm 2）．15.如图，等腰梯形MNPQ 的上底长为2，腰长为3，一个 底角为60°．正方形ABCD 的边长为1，它的一边AD 在MN 上，且顶点A 与M 重合．现将正方形ABCD 在梯 形的外面沿边MN 、NP 、PQ 进行翻滚，翻滚到有一个顶 点与Q 重合时，点A 所经过的路线与梯形MNPQ 的三边 MN 、NP 、PQ 所围成图形的面积是________．16.如图，在矩形ABCD 中，AB=2，BC=4，⊙D 的半径为1．现将一个直角三角板的直角顶点与矩形的对称中心O 重合，绕着O 点转动三角板，使它的一条直角边与⊙D切于点H ，此时两直角边与AD 交于E ，F 两点，则tan EFO ∠的值为 ． 三.解答题（共6小题，分别为8,10,10,10,12，14分，共64分） 17.设数列 ,1,,12,1,,13,22,31,12,21,11kk k -，问：（1）这个数列第2010项的值是多少？（2）在这个数列中，第2010个值为1的项的序号是多少？ 18.如图，在梯形ABCD 中，AB ∥CD ，⊙O 为内切圆，E 为切点，（Ⅰ）求AOD ∠的度数；（Ⅱ）若8=AO cm ，6=DO cm ，求OE 的长． .19.请设计三种方案：把一个正方形剪两刀，使剪得的三块图形能够拼成一个三角形，并且使拼成的三角形既不是直角三角形也不是等腰三角形，画出必要的示意图，并附以简要的文字说明．20.某商场在促销期间规定：商场所有商品按标价的80%出售，同时，当顾客在该商场内消费满一定金额后，可按如下方案获得相应金额的奖券：消费金额w （元）的范围 200≤w ＜400 400≤w ＜500 500≤w ＜700 700≤w ＜900 … 获得奖券的金额（元）30 60 100 130 …图1baA BDCEO根据上述促销方法，顾客在该商场购物可以获得双重优惠。
最大最全最精的教育资源网绝密★启用前浙教版 2018-2019 学年度要点高中自主招生数学模拟试卷题号一二三总分得分注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题）评卷人得分一．选择题（共8 小题， 4*8=32 ）1．如图，一条信息可经过网络线由上（ A 点）往下（沿箭头方向）向各站点传递，比如信息要到b2点可由经a1的站点送到，也可由经a2的站点送到，共有两条传递门路，则信息由 A 点传达到d3的不一样门路中，经过站点b3的概率为（）A ．B．C．D．2．已知 x+y＝， |x|+|y|＝ 5，则 x﹣y 的值为（）A ．B．C．D．3．因为货源紧缺，小王、小李两名商贩连续两次以不一样的价钱在同一企业购进了 A 型香米，两次的购置单价分别为a、 b（ a＜ b，单位：元 /千克），小王的采买方式为：每次购进 c 千克大米；小李的采买方式为：每次购进d 元的大米（ d＞c），若只考虑采买单价，以下结论正确的选项是（）A ．小王合算B ．小李合算C．同样合算 D ．没法确立谁更合算4．如图中矩形 ABCD 的四个极点位于双曲线y＝上，且 S ABCD＝ 2，则 x A＝（）A ．B．C．D．5．正整数 a、 b 知足 a+b≤ 10，则 ab＞ 20 的概率为（）A ．B．C．D．6．当 x 知足﹣ 3≤ x≤﹣ 2 时，不等式＞ 3x﹣ 1 恒建立，则 a 的取值范围为（）A ．a＞﹣ 3B．a＞﹣ 5C． a＜﹣ 3D． a＜﹣ 57．若对于 x 的方程＝有绝对值同样，符号相反的两个根，则m 的值应为（）A ．c B．C．D．8．若干人共同买一箱香烟，以后考虑到抽烟污染环境，有害健康，有15 人戒烟，余下每人要多分担15 元，到决定付款时，又有 5 人不买，最后余下的每人又多增添10 元，则开始准备购置香烟的人数是多少（）A ．40B．35C． 37D． 45第Ⅱ卷（非选择题）卷人得分二．填空（共8 小， 4*8=32 ）9．如，∠ MON 两上分有A， C， E 及 D， F， B 六个点，且 S△OAB＝ S△ABC＝ S△BCD＝ S△CDE＝S △ DEF＝1，S△CDF ＝．10．如有蓄每1000 券中，有一等 1 ，金 500 元，二等10 ，金 100 元，三等50 ，金20 元，念100 ，金 5 元．某人一券，他得许多于20 元的概率．11．如，点 P 在双曲y＝上，以P心的⊙ P与两坐都相切，E y 半上的一点，PF ⊥ PE 交 x 于点 F， OF OE 的是．12．++⋯+＝．13．方程的解．14．如， 1 的等三角形ABC ，D、 E 分是 BC、CA 上的点，且有BD ＝CE ，AD 与 BE 交于点 F，若 AD⊥CF ， BD．15．已知方程，＝．16．察以下各式：＝1＝1（1）；＝1＝1（）；＝1＝1（）；⋯算：+++⋯+＝．卷人得分三．解答（共 6 小， 56 分）17．（ 8 分）若对于x 的不等式只有4个整数解，求 a 的取范．18．（ 8 分）壮五金商铺准从宁云机械厂甲、乙两种部件行售．若每个甲种部件的价比每个乙种部件的价少 2 元，且用 80 元甲种部件的数目与用100 元乙种部件的数目相同．（ 1）求每个甲种部件、每个乙种部件的价分多少元？（ 2）若五金商铺本次甲种部件的数目比乙种部件的数目的 3 倍少 5 个，两种部件的数目不超95 个，五金商铺每个甲种部件的售价钱12 元，每个乙种部件的售价钱15 元，将本次的甲、乙两种部件所有售出后，可使售两种部件的利（利＝售价价）超 371 元，19．（ 10 分）对于 x 的方程 9x 29sinA?x 2＝ 0 的两根的平方和是 1，此中∠ A 角△ ABC 的一个内角．（ 1）求 sinA 的 ；（ 2）若△ ABC 的两 m 、 n 足方程 y 2 6y+k 2+4k+13＝ 0（k 常数），求△ ABC 的第三 ．20．（ 10 分）如 ， AB 是 ⊙ O 的直径，直BM 点 B ，点 C 在右半 上移 （与点 A 、 B 不重合）， 点C 作 CD ⊥ AB ，垂足 D ， 接 CA 、CB ，∠ CBM ＝∠ BAC ，点 F 在射 BM 上移（点 M 在点 B 的右 ），在移 程中始 保持OF ∥ AC ．（ 1）求 ： BM⊙O 的切 ；（ 2）若 CD 、FO 的延 订交于点E ，判断能否存在点E ，使得点 E 恰幸亏 ⊙ O 上？若存在， 求∠ E ；若不存在， 明原因；（ 3） 接 AF 交 CD 于点 G ， k ＝， ： k 的 能否随点C 的移 而 化？并 明你的 ．21．（ 10 分）（ 1）已知 n ＝那么 1+2+3+ ⋯ +n ＝++ +⋯ +，即 1+2+3+ ⋯+n ＝＝．模拟上述乞降 程，n 2＝，确立a 与b 的 ，并 算22 22的 果．1 +2 +3 +⋯ +n（2） 1中，抛物y ＝ x 2，直 x ＝ 1 与 x 成底 1 的曲 三角形，其面S ， 利用若干矩形面 和来迫近 ．① 将底 3 平分，建立3 个矩形（ 2），求其面S 3 ；② 将底 n 平分，建立 n 个矩形（如3），求其面 和S n 并化 ；③ 考 当 n 充足大 S n 的迫近状况，并 出 S 的正确 ．（ 3） 算4 中抛物 y ＝ 2x 2与直 y ＝ 2x+4所 成的暗影部分面 ．22．（ 10 分）如图 1，已知直线EA 与 x 轴、 y 轴分别交于点 E 和点 A（ 0，2），过直线EA 上的两点F 、G 分别作 x 轴的垂线段，垂足分别为M（ m， 0）和 N（ n，0），此中m＜0， n＞ 0．（1）假如 m＝﹣ 4， n＝ 1，试判断△ AMN 的形状；（2）假如 mn＝﹣ 4，（ 1）中相关△ AMN 的形状的结论还建立吗？假如建立，请证明；假如不建立，请说明原因；（3）如图 2，题目中的条件不变，假如 mn＝﹣ 4，而且 ON＝ 4，求经过 M、A、N 三点的抛物线所对应的函数关系式；（4）在（ 3）的条件下，假如抛物线的对称轴l 与线段 AN 交于点 P，点 Q 是对称轴上一动点，以点P、Q、 N 为极点的三角形和以点M 、A、 N 为极点的三角形相像，求切合条件的点Q 的坐标．参照答案与试题分析一．选择题（共8 小题）1．如图，一条信息可经过网络线由上（ A 点）往下（沿箭头方向）向各站点传递，比如信息要到b2点可由经a1的站点送到，也可由经a2的站点送到，共有两条传递门路，则信息由 A 点传达到d3的不一样门路中，经过站点b3的概率为（）A．B．C．D．【剖析】依据题意画出树状图，从而利用概率公式，求出答案．【解答】解：画树状图得：所以共有 6 种状况，则经过站点b3的概率为：．应选： A．【评论】本题考察树状图法求概率，要点是获得抵达目的地应走的路口，列齐所有的可能状况．2．已知 x+y＝，|x|+|y|＝5，则x﹣y的值为（）A．B．C．D．【剖析】依据绝对值的性质，可得答案．【解答】解：当 x＞ 0， y＞ 0 时， x+y＝ 5与x+y＝2矛盾，当 x＜ 0， y＜0 时， x+y＝﹣ 5与x+y＝2矛盾，应选： D ．【评论】 本题考察了实数的性质，利用绝对值得性质是解题要点，要分类议论，以防遗漏．3．因为货源紧缺，小王、小李两名商贩连续两次以不一样的价钱在同一企业购进了A 型香米，两次的购置单价分别为 a 、 b （ a ＜ b ，单位：元 /千克），小王的采买方式为：每次购进c 千克大米；小李的采买方式为：每次购进d 元的大米（ d ＞c ），若只考虑采买单价，以下结论正确的选项是（）A ．小王合算B ．小李合算C ．同样合算D ．没法确立谁更合算【剖析】 分别表示出小王与小李两次购置香米的均匀价钱，利用作差法比较即可．【解答】 解：依据题意得：小王两次购置香米的均匀价钱为＝元 /千克，小李两次购置香米的均匀价钱为＝ 元 /千克，∴﹣ ＝ ＝ ，∵（ a ﹣ b ）2＞ 0， 2（a+b ）＞ 0，∴﹣ ＞0，即 ＞ ，则小李的购置方式合算．应选： B ．【评论】 本题考察了分式的混淆运算，以及作差法比较大小，娴熟掌握运算法例是解本题的要点．4．如图中矩形 ABCD 的四个极点位于双曲线 y ＝ ABCD ＝ 2，则 x A ＝（）上，且 SA ．B ．C ．D ．【剖析】 设 A （ x ， ），依据题意C （﹣ x ，﹣）， D （ ，x ），依据矩形的面积公式获得AD ?CD＝ 2，从而获得 ? ＝ 2，解得 x 2＝，求得【解答】 解：设 A （ x ，），依据题意 C （﹣ x ，﹣）， D （ ， x ），∵S 矩形 ABCD ＝2，∴ AD?CD ＝2 ，∴? ＝ 2 ，∴ （ x ﹣ ）? （ x+ ）＝ 2 ，解得： x 2＝或 x 2＝（不合题意舍去），∴ x 1＝， x 2＝，∴ ＝ ， ＝ ，∵点 A 在第一象限，∴ x A ＝ ，应选： A ．【评论】 本题考察了反比率函数与一次函数的交点问题，反比率函数与正比率函数的交点对于原点对称；反比率函数的比率系数等于在它上边的点的横纵坐标的积，三角形面积公式以及点到直线的距离公式等知识点．5．正整数 a 、 b 知足 a+b ≤ 10，则 ab ＞ 20 的概率为（）A ．B ．C ．D ．【剖析】 依据正整数 a 、 b 知足 a+b ≤10，能够写出所有的可能性，而后依据ab ＞ 20，能够获得知足条件的可能性，从而能够获得ab ＞ 20 的概率，本题得以解决．【解答】 解：∵正整数 a 、 b 知足 a+b ≤10，∴ a ＝ 1 时， b ＝ 1， 2， 3， 4， 5， 6， 7， 8， 9；a ＝ 2 时，b ＝ 1， 2，3， 4， 5， 6， 7， 8；a ＝ 3 时，b ＝ 1， 2，3， 4， 5， 6， 7；a ＝ 4 时，b ＝ 1， 2，3， 4， 5， 6；a ＝ 5 时，b ＝ 1， 2，3， 4， 5；a ＝ 6 时，b ＝ 1， 2，3， 4；a ＝ 8 时，b ＝ 1， 2；a ＝ 9 时，b ＝ 1；∴共有 1+2+3+4+5+6+7+8+9 ＝ 45 种，∵ ab ＞ 20，∴ a ＝ 3 时， b ＝ 7； a ＝ 4， b ＝ 6； a ＝ 5 时， b ＝ 5； a ＝ 6 时， b ＝ 4；a ＝ 7 时， b ＝ 3；即 ab ＞ 20 的共有 5 种，∴ ab ＞ 20 的概率为：，应选： C ．【评论】 本题考察概率公式， 解题的要点是能够写出所有的可能性和知足条件的可能性，会用概率公式计算概率．6．当 x 知足﹣ 3≤ x ≤﹣ 2 时，不等式 ＞ 3x ﹣ 1 恒建立，则 a 的取值范围为（）A ．a ＞﹣ 3B ．a ＞﹣ 5C ． a ＜﹣ 3D ． a ＜﹣ 5【剖析】 先依据 x 的取值范围确立出 x+1 的符号，再由不等式恒建立用a 表示出 x 的取值范围，从而可得出结论．【解答】 解：∵ x 知足﹣ 3≤ x ≤﹣ 2，∴ x+1＜ 0．∵不等式＞ 3x ﹣1 恒建立，∴ 3x 2+4x ﹣ a ＜（ x+1）（ 3x ﹣ 1），∴ x ＜．∵﹣ 3≤ x ≤﹣ 2，∴＞﹣ 2，∴ a ＞﹣ 3．应选： A ．【评论】 本题考察的是不等式的性质，熟知不等式的两边同时乘以（或除以）同一个负数，不等号的方向改变是解答本题的要点．7．若对于 x 的方程＝ 有绝对值同样，符号相反的两个根，则m 的值应为（ ）A ．cB ．C ．D ．最大最全最精的教育资源网【解答】 解：去分母得：（ x 2﹣ bx ）（ m+1）＝（ ax ﹣ c ）（ m ﹣ 1），整理得：（ m+1） x 2﹣ b （m+1） x ＝ amx ﹣ ax ﹣ cm+c ，即（ m+1） x 2﹣（ bm+b+a ﹣am ）x+cm ﹣c ＝ 0，由方程有绝对值同样，符号相反的两个根，获得＝ 0，整理得： m ＝，应选： D ．【评论】 本题考察了分式方程的解，解题的要点是理解“方程有绝对值同样，符号相反的两个根”即为两根之和为 0．8．若干人共同买一箱香烟，以后考虑到抽烟污染环境，有害健康，有15 人戒烟，余下每人要多分担15 元，到决定付款时，又有5 人不买，最后余下的每人又多增添10 元，则开始准备购置香烟的人数是多少（）A ．40B ．35C ． 37D ． 45【剖析】 设开始准备购置香烟的有x 人，每人的花销为y 元，依据一箱香烟的价钱不变联合总价＝人数×每人出的钱数即可得出对于x 、y 的二元一次方程组，解之即可得出结论．【解答】 解：设开始准备购置香烟的有x 人，每人的花销为 y 元，依据题意得：，即，解得：．应选： A ．【评论】 本题考察了二元一次方程组的应用，依据一箱香烟的钱数不变列出对于x 、 y 的二元一次方程组是解题的要点．二．填空题（共 8 小题）9．如图，∠ MON 两边上分别有A ， C ， E 及 D ， F ，B 六个点，且 S △OAB ＝ S △ABC ＝ S △BCD ＝ S △ CDE ＝S △DEF＝ 1，则 S △CDF ＝．【剖析】 由 S △ OAB ＝ S △ABC ＝ S △BCD ，可得线段 BD 与线段 OB 的关系，由 S △DEF＝S △ OED ，可得线段DF 与线段 OB 的关系，由 S △ BCD ＝ 1，可得 a?h 的值，即可得 S △ CDF 的值．需要更完好的资源请到新世纪教育网学校租用教师免费下载∵S△OAB＝ S△ABC＝ S△BCD，∴BD ＝ a，∵S△DEF＝ S△OED，∴ DF ＝OD＝（a+0.5 a）＝a，∵S△BCD＝× BD ?h＝× a?h＝ 1，∴a?h＝ 4，∴ S△CDF＝ DF ?h＝×a?h＝．故答案为：．【评论】本题主要考察了面积及等积变换，解题的要点是求出DF 与 OB 之间的关系．10．如有奖积蓄每1000 张奖券中，有一等奖 1 张，奖金 500 元，二等奖10 张，奖金 100 元，三等奖50 张，奖金20 元，纪念奖100 张，奖金 5 元．某人买一张奖券，则他得奖许多于20 元的概率为．【剖析】第一依据题意，当这个人起码获得三等奖时，他得奖许多于20 元；而后依据概率公式，用一、二、三等奖的数目和除以奖券的总量，求出他得奖许多于20 元的概率为多少即可．【解答】解：（ 1+10+50 ）÷ 1000＝ 61÷ 1000＝∴他得奖许多于20 元的概率为．故答案为：．【评论】本题主要考察了概率公式的应用，要娴熟掌握，解答本题的要点是要明确：随机事件 A 的概率 P（ A）＝事件 A 可能出现的结果数÷所有可能出现的结果数．11．如图，点 P 在双曲线y＝上，以P为圆心的⊙ P与两坐标轴都相切，E 为 y 轴负半轴上的一点，PF ⊥ PE 交 x 轴于点 F，则 OF﹣ OE 的值是2．【剖析】利用 P 点在双曲线 y＝上且以 P 为圆心的⊙ P 与两坐标轴都相切求出P 点，再利用向量的垂直时的性质列出OE 与 OF 之间的关系即可．作过切点的半径，结构全等三角形，找寻与结论或条件中相关系的等量线段，从而逐渐研究未知结果．【解答】解：法一：设E（ 0． y）， F （ x， 0）此中 y＜ 0， x＞ 0∵点 P 在双曲线 y＝上，以 P 为圆心的⊙ P 与两坐标轴都相切∴ P（，）又∵ PF⊥PE∴由向量垂直性质可得×（﹣ y） + ×（﹣x）＝ 0∴x+y＝ 2又∵ OE＝ |y|＝﹣ y，OF＝ x∴OF ﹣ OE＝ x+y＝2 ．法二：设⊙ P 与 x 和 y 轴分别相切于点A 和点 B，连结 PA、 PB．则 PA⊥ x 轴， PB ⊥ y 轴．并设⊙ P 的半径为 R．∴∠ PAF＝∠ PBE ＝∠ APB＝90°，∵PF ⊥PE，∴∠ FPA＝∠ EPB ＝ 90°﹣∠ APE，又∵ PA＝ PB，∴△ PAF≌△ PBE （ ASA），∴AF ＝BE∴OF ﹣ OE＝（ OA+AF ）﹣（ BE﹣ OB）＝ 2R，∵点 P 的坐标为（ R， R），∴R＝，需要更完好的资源请到新世纪教育网学校租用教师免费下载解得 R ＝或 （舍去），∴ OF OE ＝2 ． 故答案 ： 2 ．【点 】 本 主要考 反比率函数及向量的 合运用，同学 要熟 掌握． 12．++⋯+＝7 ．【剖析】 先分母有理化．而后归并即可．【解答】 解：原式＝++⋯ +＝++⋯+＝＝103＝ 7．故答案7．【点 】 本 考 了二次根式的混淆运算：先把各二次根式化 最 二次根式，而后 行二次根式的乘除运算，再归并即可．13．方程 的解 或 ．【剖析】 由方程 ① 可得 y ＝，由方程 ② 得 y ＝，即可得 ＝ ，解之可得 x 的，再代入y ＝求得 y 即可．【解答】 解： ，由 ① 得： y ＝，由 ② 得： y ＝， ∴ ＝，∴ 7x （ x+1）＝ 6（ x+1）（ x 2x+1），∴（ 2x 3）（ 3x 2）＝ 0，解得： x ＝ 或 x ＝ ，当 x ＝， y ＝ 8；当 x ＝， y ＝ 27；∴方程组的解为：或 ，故答案为：或 ．【评论】 本题主要考察了高次方程组的解法，波及因式分解中的提取公因式和立方和公式以及用十字相乘法进行分解因式，对方程中的每一个方程正确的变形是解题的要点．14．如图，边长为1 的等边三角形 ABC ，D 、 E 分别是 BC 、CA 上的点，且有BD ＝CE ，AD 与 BE 交于点 F ，若 AD ⊥CF ，则 BD 长为．【剖析】 依据题意推知△ ADB ≌△ BEC （ SAS ），联合全等三角形的性质和相像三角形的判断获得：△ AEF ∽△ ADC ，由此得出比率式，再由勾股定理列出方程，联立方程组求出 BD 的长度．【解答】 解：∵三角形 ABC 是等边三角形，∴ AB ＝BC ，∠ C ＝∠ ABD ＝ 60°，在△ ADB 和△ BEC 中，∴△ ADB ≌△ BEC （ SAS ），∴∠ BAD ＝∠ CBE ，又∵ BD ＝ CE ，∴∠ BAD +∠ABF ＝ 60°，即∠ AFE ＝60°．在△ AEF 和△ ADC 中，∠ AFE ＝∠ ACB ，∠ DAC ＝∠ EAF ，∴△ AEF ∽△ ADC ，∴＝ ．设 BD ＝ x ， DF ＝m ， DA ＝n ，则 x 2＝ mn ①＝，∴ n 2﹣ mn ＝ 1﹣ x ②又∵ AD ⊥ CF ，∴ AC 2﹣ AF 2＝ CD 2﹣ DF 2，∴ 12﹣（ n ﹣m ）2＝（ 1﹣ x ） 2﹣ m 2③ ．由 ①②③ 可得： x ＝ ，即 BD ＝ ．故答案是：．【评论】 本题考察了等边三角形的性质，全等三角形的判断和性质，相像三角形的判断和性质，勾股定理等知识点的应用，题目比较好，难度偏大．15．已知方程组 ，则 ＝ 3 ．【剖析】 设 a ＝ ， b ＝ ，从而将方程组转变为 ，再将第一个方程平方并展开利用加减消元法求出ab 的值，从而得解．【解答】 解：设 a ＝， b ＝，则 x+y ＝（ x+1） +（ y ﹣ 2） +1 ＝ 20，所以，（ x+1） +（ y ﹣2）＝ 19，22即 a +b ＝ 19，所以，方程组可化为，22① 平方得， a +2ab+b ＝25③ ，③ ﹣② 得， 2ab ＝ 6，解得 ab ＝ 3，所以，＝ ?＝ ab ＝ 3．故答案为： 3．【评论】 本题主要考察解无理方程的知识点，去掉根号把无理式化成有理方程是解题的要点， 注意观察方程的结构特色，利用换元法求解更简易．16．察看以下各式：＝1＝1（1）；＝1＝1（）；＝1＝1（）；⋯算：+++⋯+＝2014．【剖析】依据意将待求算式打开可得1（ 1）+1（）+1（）+⋯+1（）＝ 1× 2015（ 1+++⋯ +），即可得答案．【解答】解：依据意得原式＝1（1）+1（）+1（）+⋯+1（）＝ 1× 2015（ 1+++⋯+）＝ 2015＝ 2014，故答案： 2014．【点】本主要考数字的化律，弄清目所列等式的律并熟掌握有理数的混淆运算是解的关．三．解答（共 6 小）17．若对于x 的不等式只有4个整数解，求 a 的取范．【剖析】第一利用不等式的基天性解不等式，再从不等式的解集中找出合适条件的整数解，在确定字母的取范即可．【解答】解：由①得： x＜ 21，由②得： x＞ 2 3a，∵不等式组只有 4 个整数解，∴不等式组的解集为：2﹣ 3a＜ x＜ 21，即不等式组只有 4 个整数解为20、19、18、17，且知足 16≤ 2﹣3a＜17，∴﹣ 5＜ a≤﹣．【评论】本题考察不等式组的解法及整数解确实定．解不等式要用到不等式的性质：（1）不等式的两边加（或减）同一个数（或式子），不等号的方向不变；（2）不等式两边乘（或除以）同一个正数，不等号的方向不变；（3）不等式的两边乘（或除以）同一个负数，不等号的方向改变．18．跃壮五金商铺准备从宁云机械厂购进甲、乙两种部件进行销售．若每个甲种部件的进价比每个乙种部件的进价少 2 元，且用 80 元购进甲种部件的数目与用 100 元购进乙种部件的数目同样．（ 1）求每个甲种部件、每个乙种部件的进价分别为多少元？（ 2）若该五金商铺本次购进甲种部件的数目比购进乙种部件的数目的 3 倍还少 5 个，购进两种部件的总数目不超出95 个，该五金商铺每个甲种部件的销售价钱为12 元，每个乙种部件的销售价钱为 15 元，则将本次购进的甲、乙两种部件所有售出后，可使销售两种部件的总收益（收益＝售价﹣进价）超出 371 元，经过计算求出跃壮五金商铺本次从宁云机械厂购进甲、乙两种部件有几种方案？请你设计出来．【剖析】（ 1）要点语是“用80 元购进甲种部件的数目与用100 元购进乙种部件的数目同样”可依据此列出方程．（ 2）本题中“依据进两种部件的总数目不超出95 个”可得出对于数目的不等式方程，依据“使销售两种部件的总收益（收益＝售价﹣进价）超出371 元”看俄得出对于收益的不等式方程，构成方程组后得出未知数的取值范围，而后依据取值的不一样状况，列出不一样的方案．【解答】解：（ 1）设每个乙种部件进价为x 元，则每个甲种部件进价为（x﹣2）元．由题意得：．解得： x＝ 10．查验：当x＝ 10 时， x（ x﹣ 2）≠ 0∴x＝ 10 是原分式方程的解．每个甲种部件进价为： x﹣ 2＝10﹣ 2＝ 8答：每个甲种部件的进价为8 元，每个乙种部件的进价为10 元．（ 2）设购进乙种部件 y 个，则购进甲种部件（ 3y ﹣ 5）个．由题意得：解得： 23＜y ≤ 25∵ y 为整数∴ y ＝ 24 或 25．∴共有 2 种方案．方案一：购进甲种部件 67 个，乙种部件 24 个；方案二：购进甲种部件 70 个，乙种部件 25 个．【评论】 本题考察了分式方程的应用、 一元一次不等式组的应用， 列分式方程解应用题与所有列方程解应用题同样，要点在于正确地找出相等关系，这是列方程的依照．本题要注意（ 2）中未知数的不一样取值可视为不一样的方案．2的两根的平方和是1，此中∠ A 为锐角△ ABC 的一个内角．19．对于 x 的方程 9x ﹣ 9sinA?x ﹣ 2＝ 0（ 1）求 sinA 的值；（ 2）若△ ABC 的两边长 m 、 n 知足方程 y 2﹣ 6y+k 2+4k+13＝ 0（k 为常数），求△ ABC 的第三边．【剖析】 （1）依据一元二次方程根与系数的关系及完好平方公式，即可求出sinA 的值；（ 2）依据根的鉴别式第一求出k 的值，而后分两种状况： ① ∠ A 是底角； ② ∠ A 是顶角，分别求出△ ABC 的第三边的长度．【解答】 解：（ 1）设对于 x 的方程 9x 2﹣ 9sinA?x ﹣ 2＝ 0 的两根为 x 1， x 2，则 x 1+x 2＝ sinA ， x 1?x 2＝﹣ ．2 2 2 2 ．∴ x 1 +x 2 ＝（ x 1+x 2） ﹣ 2x 1?x 2＝ sin A+∵方程 9x 2﹣ 9sinA?x ﹣ 2＝ 0 的两根的平方和是 1，∴ sin 2A+ ＝ 1，∴ sinA ＝±，∵∠ A 为锐角，∴ sinA ＝；22（ 2）依题意，知 m 、 n 是方程 y ﹣ 6y+k +4k+13 ＝ 0 的两根，则△≥ 0，∴（ k+2） 2≤0，2又∵（ k+2） ≥ 0，把 k ＝﹣ 2 代入方程，得 y 2﹣ 6y+9＝ 0，解得 y ＝ 3，∴ m ＝ n ＝ 3，∴△ ABC 是等腰三角形．分两种状况： ① ∠ A 是底角； ② ∠ A 是顶角．① 当∠ A 是底角时，如图，△ ABC 中， AB ＝ BC ＝ 3，作底边 AB 上的高 BD ，则 AB ＝ 2AD ．在直角△ ABD 中，∵ sinA ＝，∴＝，∴ BD ＝ ，∴AD ＝＝2，∴ AC ＝ 4；② 当∠ A 是顶角时，如图，△ ABC 中， AB ＝ AC ＝ 3，作腰 AC 上的高 BD ．在直角△ ABD 中，∵ sinA ＝，∴＝ ，∴ BD ＝ ，∴AD ＝＝2，∴ CD ＝AC ﹣AD ＝1．在直角△ ABD 中，∵∠ BDC ＝ 90°， ∴ BC ＝＝ ．综上可知，△ ABC 的第三边的长度为4 或 ．【评论】本题主要考察了根的鉴别式，根与系数的关系，等腰三角形的性质，三角函数的定义，综合性强，难度较大．20．如图， AB 是⊙ O 的直径，直线BM 经过点 B，点 C 在右半圆上挪动（与点A、B 不重合），过点C作 CD ⊥ AB，垂足为 D，连结 CA、CB，∠ CBM ＝∠ BAC，点 F 在射线 BM 上挪动（点 M 在点 B 的右侧），在挪动过程中一直保持OF∥ AC．（ 1）求证： BM 为⊙O 的切线；（ 2）若 CD 、FO 的延伸线订交于点E，判断能否存在点E，使得点 E 恰幸亏⊙ O 上？若存在，求∠ E；若不存在，请说明原因；（ 3）连结 AF 交 CD 于点 G，记 k＝，试问：k的值能否随点 C 的挪动而变化？并证明你的结论．【剖析】（1）依据题意得出∠OBM ＝ 90°，再利用切线的判断方法得出答案；（ 2）第一利用全等三角形的判断方法得出△EOD ≌△ CAD（ ASA），从而得出∠ E 的度数；（ 3）第一得出△ ADC∽△ OBF ，从而求出△ ADG∽△ ABF ，再利用相像三角形的性质得出，＝＝，推出 DG＝ GC，由此即可解决问题．【解答】（1）证明：由题意知∠ACB＝90°，∴∠ OBM ＝∠ ABC+∠ CBF ＝∠ ABC +∠ BAC ＝180°﹣∠ ACB＝ 90°，∴OB⊥ BM，∴BM 为⊙O 的切线；（2）解：假定存在点 E，如图 1，∵CD⊥AB，∴DE＝DC，∵OF∥AC，∴∠ ACE＝∠ CEF ，在△ EOD 和△ CAD 中，∴△ EOD ≌△ CAD（ ASA），∴OD ＝ DA，在Rt△ OED 中，sin∠ OED ＝＝＝＝，∴∠ E＝ 30°；（ 3）解：如图1，点 E 存在， k 的值不会变化，k＝，原因：∵点 C 在右半圆上挪动（与点A、 B 不重合），且AC∥OF ，∴∠ CAD ＝∠ FOB ，∵∠ ABF ＝ 90°， DC ⊥ AB，∴∠ ADC ＝∠ ABF ，∴∠ ADC ＝∠ ABF ，∴△ ADC ∽△ OBF ，∴＝，又∵∠ DAG ＝∠ BAF ，∠ ADG ＝∠ ABF ＝ 90°，∴△ ADG ∽△ ABF ，∴＝，又∵ AB＝ 2OB，∴＝，即＝＝，∴DC ＝ 2DG ，即 DG＝ GC，∴k＝＝．【点 】此 主要考 了全等三角形的判断与性 和相像三角形的判断与性 以及切 的判断与性等知 ，得出△ADG ∽△ ABF 是解 关 ，属于中考常考 型．21．（ 1）已知 n ＝那么 1+2+3+ ⋯ +n ＝+ + +⋯ +，即 1+2+3+ ⋯+n ＝＝．模拟上述乞降 程，n 2＝，确立a 与b 的 ，并 算22 22的 果．1 +2 +3 +⋯ +n（2） 1中，抛物y ＝ x 2，直 x ＝ 1 与 x 成底 1 的曲 三角形，其面S ， 利用若干矩形面 和来迫近 ．① 将底 3 平分，建立3 个矩形（ 2），求其面 S 3 ；② 将底 n 平分，建立 n 个矩形（如3），求其面 和S n 并化 ；③ 考 当 n 充足大 S n 的迫近状况，并 出 S 的正确 ．（ 3） 算4 中抛物 y ＝ 2x 2与直 y ＝ 2x+4所 成的暗影部分面 ．【剖析】 （ 1）将 n 2＝通分化 ，依据恒等式的性 ，列出方程即可解决 ．再模拟例 即可解决 ．（ 2） ① 依据矩形的面 公式即可即可．② 依据矩形的面 公式以及（1）中的 即可即可．③ 由 S n ＝2222＝＝ + +，因 n 充足大（ 1+2 +3+⋯ +n ）＝，、靠近于 0，所以 S n 的 迫近于．（ 3）如 4 中， 抛物 y ＝ 2x 2与直 y ＝2x+4 的交点 A 、B ，作 AE ⊥ x 于 E ，BF ⊥ x 于 F ．曲 三角形AEO 的面S 1，曲 三角形OBF 的面S 2．第一利用迫近法求出 S 1、 S 2，再根据 S 阴＝ S 梯形 AEFB S 1 S 2 算即可．【解 答 】 解 ： （ 1 ） ∵ n 2＝＝＝，∴ a ＝ 2， b ＝ 1 等式建立．∴ 1 22 2 2＝++ ⋯＝+2 +3 +⋯ +n ．（2）① S 3＝22 2 （ 1 2 2 2）＝．?（）+ ?（）+ （ ） ＝ +2 +3② 由① 可知 S n ＝2 2 2 2．（ 1 +2 +3 +⋯ +n ）＝③ ∵S n ＝ 2 2 2 2＝ ＝ ++ ，（ 1 +2 +3 +⋯ +n ）＝ ∵ n 充足大 ，、 靠近于 0，∴ S n 的 迫近于 ，∴ S ＝ ．（ 3）如 4 中， 抛物 y ＝ 2x 2与直 y ＝2x+4 的交点 A 、B ，作 AE ⊥ x 于 E ，BF ⊥ x 于 F ． 曲 三角形 AEO 的面 S 1，曲 三角形 OBF 的面 S 2．∴ A（ 1， 2）， B（ 2， 8）， E（ 1， 0）， F（ 2， 0），将底 EO 分红 n 平分，建立n 个矩形1＝?2?（）22?2?（2＝（ 1+2 2 22），S+ ?2?（） +⋯+）+3 +⋯ +n由（ 2）可知 S1迫近于，同理可得 S2迫近于，∴ S 阴＝ S 梯形AEFB S1 S2＝?3＝ 9．【点】本考二次函数合，矩形的性、迫近法求面等知，解的关是理解意，学会模拟例解决，属于新目，中考．22．如 1，已知直EA 与 x 、 y 分交于点 E 和点 A（0， 2），直 EA 上的两点F、 G 分作 x 的垂段，垂足分M（ m， 0）和 N（n， 0），此中m＜ 0， n＞ 0．（1）假如 m＝ 4， n＝ 1，判断△ AMN 的形状；（2）假如 mn＝ 4，（ 1）中相关△ AMN 的形状的建立？假如建立，明；假如不建立，明原因；（3）如 2，目中的条件不，假如 mn＝ 4，而且 ON＝ 4，求 M、A、N 三点的抛物所的函数关系式；（4）在（ 3）的条件下，假如抛物的称l 与段 AN 交于点 P，点 Q 是称上一点，以点P、Q、 N 点的三角形和以点M 、A、 N 点的三角形相像，求切合条件的点Q 的坐．【剖析】（1）依据勾股定理能够求出AM． AN， MN 的度，依据勾股定理的逆定理就能够求出三角形是直角三角形．（2） AM ．AN，MN 的度能够用 m，n 表示出来，依据 m， n 的关系就能够明．（3） M、 A、 N 的坐已知，依据待定系数法局能够求出二次函数的分析式．需要更完好的资源请到新世纪教育网学校租用教师免费下载求出 Q 1Q 2 获得切合条件的点的坐标．【解答】 解：（ 1）△ AMN 是直角三角形．依题意得 OA ＝2， OM ＝ 4， ON ＝1，∴ MN ＝ OM+ON ＝ 4+1＝ 5在 Rt △ AOM 中， AM ＝＝ ＝在 Rt △ AON 中， AN ＝＝＝∴ MN 2＝ AM 2+AN 2∴△ AMN 是直角三角形（解法不唯一）．（2 分）（ 2）答：（ 1）中的结论还建立．依题意得 OA ＝2， OM ＝﹣ m ， ON ＝ n∴ MN ＝ OM+ON ＝ n ﹣m∴ MN 2＝（ n ﹣ m ） 2＝n 2﹣ 2mn+m 2∵ mn ＝﹣ 4∴ MN 2＝ 2 2 2 2+n ﹣ 2×（﹣ 4）+m ＝ n +m 8又∵在 Rt △AOM 中， AM ＝ ＝＝在 Rt △ AON 中， AN ＝＝＝∴ AM 2+ 2＝22 2 2+AN 4+m +4+ n ＝n +m8∴ MN 2＝2+2AM AN∴△ AMN 是直角三角形．（解法不唯一）（ 2 分）（ 3）∵ mn ＝﹣ 4， n ＝ 4， ∴ m ＝﹣ 1．方法一：设抛物线的函数关系式为y ＝ ax 2+bx+c ．∵抛物线经过点 M （﹣ 1， 0）、 N （ 4， 0）和 A （ 0， 2）∴．∴．∴所求抛物线的函数关系式为 y ＝﹣x 2+x+2．方法二：设抛物线的函数关系式为+﹣y ＝ a （x 1）（ x 4）．∵抛物线经过点 A （ 0， 2）∴﹣ 4a ＝ 2 解得 a ＝﹣∴所求抛物线的函数关系式为y ＝﹣ （ x+1）（ x ﹣4）即 y ＝﹣ x 2+x+2．（ 2 分）（ 4）抛物线的对称轴与 x 轴的交点 Q 1 切合条件， ∵ l ⊥ MN ，∠ ANM ＝∠ PNQ 1，∴ Rt △ PNQ 1∽Rt △ ANM∵抛物线的对称轴为直线x ＝ ，∴ Q 1（ ， 0）（ 2 分）∴ NQ 1＝4﹣ ＝ ．过点 N 作 NQ 2⊥ AN ，交抛物线的对称轴于点Q 2．∴ Rt △ PQ 2N 、Rt △ NQ 2Q 1、 Rt △PNQ 1 和 Rt △ANM 两两相像 ∴即 Q 1Q 2＝∵点 Q 2 位于第四象限，∴ Q 2（ ，﹣ 5）（ 2 分）所以，切合条件的点有两个，分别是 Q 1（ ， 0）， Q 2（ ，﹣ 5）．（解法不唯一）浙教版2018-2019学年度重点高中自主招生数学模拟试卷最大最全最精的教育资源网【评论】本题主要考察了勾股定理的逆定理，待定系数法求函数的分析式．以及相像三角形的性质，对应边的比相等．需要更完好的资源请到新世纪教育网学校租用教师免费下载。
第 1 页 共 4 页22018年高中自主招生考试数学模拟试题（满分：120 分时间：120 分钟）一、选择题。
（每小题 4 分，共 24 分）1. 若正方形的外接圆半径为 2，则其内切圆半径为（ ）A. B.2 C. 2 2D.1 2. 如图，在△ABC 中，AC ⊥BC ，∠ABC ＝30°，点 D 是 CB 延长线上的一点，且 BD ＝BA ，则tan ∠DAC 的值为（ ）A.2＋B.2C.3＋D.3 A MPONB第 2 题图第 3 题图第 5 题图3. 如图，正方形 ABCD 中，E 为 CD 的中点，EF ⊥AE ，交 BC 于点 F ，则∠1 与∠2 的大小关系 为 （ ）A.∠1＞∠2B.∠1＜∠2C.∠1=∠2D.无法确定4. 若点 M (－7，m )、N (－8，n )都是函数 y ＝－(k 2＋2k ＋4)x ＋1（k 为常数）的图象上，则 m 和n 的大小关系是（ ）A.m ＞nB.m ＜nC.m ＝nD.不能确定5. 如图，点 P 为定角∠AOB 的平分线上的一个定点，且∠MPN 与∠AOB 互补．若∠MPN 在绕点 P 旋转的过程中，其两边分别与 OA ，OB 相交于 M 、N 两点，则以下结论：（1）PM ＝PN 恒成立，（2）OM ＋ON 的值不变，（3）四边形 PMON 的面积不变，（4）MN 的长不变，其中正确的 个 数 为 （ ）A.4B.3C.2D.16. 在平面直角坐标系内，直线 AB 垂直于 x 轴于点 C （点 C 在原点的右侧），并分别与直线 y ＝23333第 2 页 共 4 页2 3 2 x 和双曲线 y ＝ 1x相交于点 A 、B ，且 AC ＋BC ＝4，则△OAB 的面积为（）A.2 ＋3 或 2 －3B. ＋1 或 －1C.2 －3D. －1二、填空题。
（每小题 4 分，共 24 分）7. 一个人把四根绳子紧握在手中，仅在两端露出它们的头和尾，然后随机地把一端的四个头中的某两个相接，另两个相接，把另一端的四个尾中的某两个相接，另两个相接，则放开手后四根 绳子恰好连成一个圈的概率是．8. 有 4 张看上去无差别的卡片，上面分别写着 2，3，4，6，小红随机抽取 1 张后，放回并混在一起，再随机抽取 1 张，则小红第二次取出的数字能够整除第一次取出的数字的概率为．9. 如图，在直角三角形 ABC 中，AB =3，BC =4，∠ABC =90°，过 B 作 BA 1⊥AC ，过 A 1 作 A 1B 1⊥BC ，得阴影直角三角形 A 1B 1B ；再过 B 1 作 B 1A 2⊥AC ，过 A 2 作 A 2B 2⊥BC ，得阴影直角三角形 A 2B 2B 1；…，如此无限下去，请猜测这样得到的所有阴影三角形的面积之和为．AHDE GBFCQ第 9 题图 第 10 题图第 11 题图10. 如图，四个全等的直角三角形与中间的小正方形拼成的一个大正方形，如果大正方形的面积是 13，小正方形的面积是 1，直角三角形的两条直角边长分别为 a ，b ，则（a +b ）2 的值是 ．11. 如图，将矩形 ABCD 沿 GH 对折，点 C 落在 Q 处，点 D 落在 AB 边上的 E 处，EQ 与 BC相交于点 F ．若 AD ＝8，AB ＝6，AE ＝4，则△EBF 周长的大小为 ．12. 观察下列各式： 2 = 1 - 1 ， 2 = 1 - 1 2 = 1 - 1 ……请利用你所得结论，化简 1⨯ 3 1 3 2 ⨯ 4 2 4 ， 3 ⨯ 5 3 5 ，代 数 式 21⨯ 3＋ 2 2 ⨯ 4 ＋ 2 3 ⨯ 5 ＋…＋ 2 n (n + 2) （n ≥3 且为整数），其结果为．三、解答题。
2018年温州瓯海中学提前招生模拟考试数学试题（满分120分，考试时间：100分钟）第Ⅰ卷（选择题）评卷人得分一、选择题（共10小题，满分40分，每小题4分）1．对于两个数，M=2018×20 192 019，N=2019×20182 018．则（）A．M=N B．M＞N C．M＜N D．无法确定2．（2017•芜湖一中自主招生）已知，，则的值为（）A．3 B．4 C．5 D．63．（2015•黄冈中学自主招生）已知实数x、y、z满足x2+y2+z2=4，则（2x﹣y）2+（2y﹣z）2+（2z﹣x）2的最大值是（）A．12 B．20 C．28 D．364．（2017•延平区校级自主招生）设方程（k+1）x2+2x+1=0的两根为x1、x2，若+2，则满足条件的整数k的值有（）A．无数个B．﹣2，﹣1，0 C．﹣1，0 D．﹣2，05．（2017•余姚中学自主招生）如图，在Rt△ABC中，∠C=90°，AC=3，以AB 为一边向三角形外作正方形ABEF，正方形的中心为O，且OC=4，那么BC 的长等于（）A．3B．5 C．2D．第5题第7题第9题6．（2017•江阴中学自主招生）对于方程x2﹣2|x|+2=m，如果方程实根的个数为3个，则m的值等于（）A．1 B．C．2 D．2.57．如图，已知直线y=﹣x+3分别与x轴，y轴交于A，B两点，与双曲线y=交于E，F两点．若AB=3EF，则k的值是（）A． B．2 C．D．8．（2017•奉化中学自主招生）在△ABC中，AB=AC=a，BC=b，∠A=36°，记m=，则m、n、p的大小关系为（）A．m＞n＞p B．p＞m＞n C．n＞p＞m D．m=n=p9．（2014•成都七中自主招生）如图，在边长为1的正方形ABCD中，E、F分别为线段AB、AD、上的动点，若以EF为折线翻折，A点落在正方形ABCD所在的A′点的位置，那么A'所有可能位置形成的区域面积为（）A．B．C．﹣1 D．﹣110．（2015•慈溪中学自主招生）如图，已知长方体ABCD﹣A1B1C1D1，AB=2，AD=1，AA1=2，P是棱A1B1上任意一点，Q是侧面对角线AB1上一点，则PD1+PQ 的最小值是（）A．3 B．C．D．1+第10题第Ⅱ卷（非选择题）请点击修改第Ⅱ卷的文字说明评卷人得分二、填空题（共5小题，满分25分，每小题5分）11．多项式6x3﹣11x2+x+4可分解为．12．设的整数部分为x，小数部分为y，则的值为．13．（2018•枣庄八中自主招生）已知有理数x满足：，若|3﹣x|﹣|x+2|的最小值为a，最大值为b，则ab=．14．正方形ABCD的中心为O，面积为1989cm2．P为正方形内一点，且∠OPB=45°，PA：PB=5：14．则PB=．第14题第15题15．（2017•奉化中学自主招生）如图，AB为半圆的直径，C是半圆弧上任一点，正方形DEFG的一边DG在直线AB上，另一边DE过△ABC的内切圆圆心I，且点E在半圆弧上，已知DE=9，则△ABC的面积为．评卷人得分三、解答题（共5小题，满分55分）16．（8分）（2016•杭州中国美院附中自主招生）如图，点E是菱形ABCD对角线CA的延长线上任意一点，以线段AE为边作一个菱形AEFG，且∠EAG=∠BAD，连接EC，GD．（1）求证：EB=GD；（2）若∠DAB=60°，AB=2，AG=，求GD的长．第16题17．（10分）（2017•芜湖一中自主招生）方程x2﹣kx+k﹣2=0有两个实数根x1，x2，且0＜x1＜1，2＜x2＜3，求k的取值范围．18．（10分）（2016•黄冈中学自主招生）如图，四边形ABCD为正方形，⊙O过正方形的顶点A和对角线的交点P，分别交AB、AD于点F、E．（1）求证：DE=AF；（2）若⊙O的半径为，AB=，求的值．第18题19．（12分）（2016•邯郸一中自主招生）如图，在平面直角坐标系xoy中，直线y=x+3交x轴于A点，交y轴于B点，过A、B两点的抛物线y=﹣x2+bx+c交x 轴于另一点C，点D是抛物线的顶点．（1）求此抛物线的解析式；（2）点P是直线AB上方的抛物线上一点，（不与点A、B重合），过点P作x 轴的垂线交x轴于点H，交直线AB于点F，作PG⊥AB于点G．求出△PFG的周长最大值；（3）在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M，使得△ABM与△ABD的面积相等？若存在，请求出此时点M的坐标；若不存在，请说明理由．第19题20．（15分）（2017•奉化中学自主招生）如图，在直角坐标系中，⊙M外接于矩形OABC，AB=12，BC=16，点A在x轴上，点C在y轴上．（1）写出点A、B、C及M的坐标；（2）过点C作⊙M的切线交x轴于点P，求直线PC的解析式；（3）如果E为线段PC上一动点（运动时不与P、C重合），过点E作直线EF 交PA于点F．①直线EF将四边形PABC的周长平分，设E点的纵坐标为t，△PEF的面积为S，求S关于t的函数关系式，并求自变量t的取值范围；②是否存在直线EF将四边形PABC的周长和面积同时平分？若能，请求出直线EF的解析式；若不能，请说明理由．第20题2018年温州瓯海中学提前招生模拟考试数学试题参考答案与试题解析一、选择题（共10小题，满分40分，每小题4分）1．对于两个数，M=2018×20 192 019，N=2019×20 182 018．则（）A．M=N B．M＞N C．M＜N D．无法确定【解析】M=2018×（20 190 000+2019）=2018×20 190 000+2018×2019=2018×2019×10000+2018×2019=2019×20180 000+2018×2019，N=2019×（20 180 000+2018）=2019×20180 000+2019×2018，所以M=N．故选：A．2．已知，，则的值为（）A．3 B．4 C．5 D．6【解析】∵a===+2，b==﹣2，∴a2+b2=（a﹣b）2+2ab=42+2×（5﹣4）=18，∴==5，故选：C．3．已知实数x、y、z满足x2+y2+z2=4，则（2x﹣y）2+（2y﹣z）2+（2z﹣x）2的最大值是（）A．12 B．20 C．28 D．36【解析】∵实数x、y、z满足x2+y2+z2=4，∴（2x﹣y）2+（2y﹣z）2+（2z﹣x）2=5（x2+y2+z2）﹣4（xy+yz+xz）=20﹣2[（x+y+z）2﹣（x2+y2+z2）]=28﹣2（x+y+z）2≤28∴当x+y+z=0时（2x﹣y）2+（2y﹣z）2+（2z﹣x）2的最大值是28．故选：C．4．设方程（k+1）x2+2x+1=0的两根为x1、x2，若+2，则满足条件的整数k的值有（）A．无数个B．﹣2，﹣1，0 C．﹣1，0 D．﹣2，0【解析】∵方程（k+1）x2+2x+1=0有实数根，∴，解得：k≤0且k≠﹣1．∵方程（k+1）x2+2x+1=0的两根为x1、x2，∴x1+x2=﹣，x1x2=．∵+2，即k+1+2≥﹣k﹣1，解得：k≥﹣2，∴﹣2≤k≤0且k≠﹣1，∴满足条件的整数k为﹣2或0．故选：D．5．如图，在Rt△ABC中，∠C=90°，AC=3，以AB为一边向三角形外作正方形ABEF，正方形的中心为O，且OC=4，那么BC的长等于（）A．3B．5 C．2D．【解析】如图，作EQ⊥x轴，以C为坐标原点建立直角坐标系，CB为x轴，CA为y轴，则A（0，3）．设B（x，0），由于O点为以AB一边向三角形外作正方形ABEF的中心，∴AB=BE，∠ABE=90°，∵∠ACB=90°，∴∠BAC+∠ABC=90°，∠ABC+∠EBQ=90°，∴∠BAC=∠EBQ，在△ABC和△BEQ中，∴△ACB≌△BQE（AAS），∴AC=BQ=3，BC=EQ，设BC=EQ=x，∴O为AE中点，∴OM为梯形ACQE的中位线，∴OM=，又∵CM=CQ=，∴O点坐标为（，），根据题意得：OC=4=，解得x=4，则BC=5．故选：B．6．对于方程x2﹣2|x|+2=m，如果方程实根的个数为3个，则m的值等于（）A．1 B．C．2 D．2.5【解析】原方程可化为x2﹣2|x|+2﹣m=0，解得|x|=1±，∵若1﹣＞0，则方程有四个实数根，∴方程必有一个根等于0，∵1+＞0，∴1﹣=0，解得m=2．故选：C．7．如图，已知直线y=﹣x+3分别与x轴，y轴交于A，B两点，与双曲线y=交于E，F两点．若AB=3EF，则k的值是（）A． B．2 C．D．【解析】作FH⊥x轴，EC⊥y轴，FH与EC交于D，如图，∵直线y=﹣x+3分别与x轴，y轴交于A，B两点，∴A点坐标为（3，0），B点坐标为（0，3），OA=OB，∴△AOB为等腰直角三角形，∴AB=OA=3，∴EF=AB=，∴△DEF为等腰直角三角形，∴FD=DE=EF=1，设F点横坐标为t，代入y=﹣x+3，则纵坐标是﹣t+3，则F的坐标是：（t，﹣t+3），E点坐标为（t+1，﹣t+2），∴t（﹣t+3）=（t+1）•（﹣t+2），解得t=1，∴E点坐标为（2，1），∴k=2×1=2．8．在△ABC中，AB=AC=a，BC=b，∠A=36°，记m=，则m、n、p的大小关系为（）A．m＞n＞p B．p＞m＞n C．n＞p＞m D．m=n=p【解析】作底角B的角平分线交AC于D，易推得△BCD∽△ABC，所以=，即CD=，AD=a﹣=b（△ABD是等腰三角形）因此得a2﹣b2=ab，∴n====m，p====m，∴m=n=p．故选：D．9．如图，在边长为1的正方形ABCD中，E、F分别为线段AB、AD、上的动点，若以EF为折线翻折，A点落在正方形ABCD所在的A′点的位置，那么A'所有可能位置形成的区域面积为（）A．B．C．﹣1 D．﹣1【解析】如图，以EF为折线翻折，A点落在正方形ABCD所在的A′点的位置，那么A′所有可能位置形成的图形是图中阴影部分．∴S阴=2•S扇形BAC﹣S正方形ABCD=﹣1，故选：D．10．如图，已知长方体ABCD﹣A1B1C1D1，AB=2，AD=1，AA1=2，P是棱A1B1上任意一点，Q是侧面对角线AB1上一点，则PD1+PQ的最小值是（）A．3 B．C．D．1+【解析】将正方形展开，取A1B1C1D1及ABB1A1两个面，过点D1作D1Q⊥AB1于点Q，D1Q交A1B1于点P，此时PD1+PQ取最小值D1Q．∵ABB1A1为正方形，∴∠D1AQ=45°．在Rt△D1QA中，AD1=AA1+A1D1=3，∠D1QA=90°，∠D1AQ=45°，∴D1Q=sin∠D1AQ•AD1=．故选：B．二、填空题（共5小题，满分25分，每小题5分）11．多项式6x3﹣11x2+x+4可分解为（x﹣1）（3x﹣4）（2x+1）．【解析】6x3﹣11x2+x+4，=6x3﹣6x2﹣5x2+x+4，=6x2（x﹣1）﹣（5x2﹣x﹣4），=6x2（x﹣1）﹣（x﹣1）（5x+4），=（x﹣1）（6x2﹣5x﹣4），=（x﹣1）（3x﹣4）（2x+1）．12．设的整数部分为x，小数部分为y，则的值为5．【解析】∵==，而0＜＜1，∴x=2，y=，∴=4+×2×+（）2=4++=5．故答案为5．13．已知有理数x满足：，若|3﹣x|﹣|x+2|的最小值为a，最大值为b，则ab=5．【解析】解不等式：不等式两边同时乘以6得：3（3x﹣1）﹣14≥6x﹣2（5+2x）去括号得：9x﹣3﹣14≥6x﹣10﹣4x移项得：9x﹣14﹣6x+4x≥3﹣10即7x≥7∴x≥1∴x+2＞0，当1≤x≤3时，x+2＞0，则|3﹣x|﹣|x+2|=3﹣x﹣（x+2）=﹣2x+1则最大值是﹣1，最小值是﹣5；当x＞3时，x+2＞0，则|3﹣x|﹣|x+2|=x﹣3﹣（x+2）=x﹣3﹣x﹣2=﹣5，是一定值．总之，a=﹣5，b=﹣1，∴ab=5故答案是：5．14．正方形ABCD的中心为O，面积为1989cm2．P为正方形内一点，且∠OPB=45°，PA：PB=5：14．则PB=42cm．【解析】连接OA，OB，∵正方形ABCD的中心为O，∠OPB=45°，∴∠OAB=∠OPB=45°，∠OBA=45°，∴O，P，A，B四点共圆，∴∠APB=∠AOB=180°﹣45°﹣45°=90°，在△PAB中由勾股定理得：PA2+PB2=AB2=1989，由于PA：PB=5：14，设PA=5x，PB=14x，（5x）2+（14x）2=1989，解得：x=3，∴PB=14x=42．故答案为：42cm．15．如图，AB为半圆的直径，C是半圆弧上任一点，正方形DEFG的一边DG 在直线AB上，另一边DE过△ABC的内切圆圆心I，且点E在半圆弧上，已知DE=9，则△ABC的面积为81．【解析】设⊙I切AC与M，切BC于N，半径为r，则AD=AM，CM=CN=r，BD=BN，r=（AC+BC﹣AB），∵AB为半圆的直径，∴∠ACB=90°，∴AB2=AC2+BC2，∴AD•DB=AM•BN=（AC﹣r）（BC﹣r）=[AC﹣（AC+BC﹣AB）][BC﹣（AC+BC ﹣AB）]=（AC﹣BC+AB）（AB+BC﹣AC）=（AB2﹣AC2﹣BC2+2AC•BC）=AC•BC，由射影定理得AD•DB=DE2=81，∴S△ABC=AC•BC=81，故答案为：81．三．解答题（共5小题，满分55分）16．如图，点E是菱形ABCD对角线CA的延长线上任意一点，以线段AE为边作一个菱形AEFG，且∠EAG=∠BAD，连接EC，GD．（1）求证：EB=GD；（2）若∠DAB=60°，AB=2，AG=，求GD的长．【解析】（1）证明：∵∠EAG=∠BAD，∴∠EAG+∠GAB=∠BAD+∠GAB，∴∠EAB=∠GAD，在△AEB和△AGD中，∵∴△AEB≌△AGD，∴EB=GD；（2）连接BD交AC于点P，则BP⊥AC，∵∠DAB=60°，∴∠PAB=30°，∴BP=AB=1，AP==，AE=AG=，∴EP=2，∴EB==，∴GD=．17．方程x2﹣kx+k﹣2=0有两个实数根x1，x2，且0＜x1＜1，2＜x2＜3，求k的取值范围．【解析】∵方程x2﹣kx+k﹣2=0有两个实数根x1，x2，且0＜x1＜1，2＜x2＜3，∴二次函数y=x2﹣kx+k﹣2如图所示，∴x=0，y=k﹣2＞0；x=1，y=1﹣k+k﹣2＜0；x=2，y=4﹣2k+k﹣2＜0；x=3，y=9﹣3k+k﹣2＞0，而△=k2﹣4（k﹣2）=（k﹣2）2+4＞0，∴2＜k＜3.5，即k的取值范围为2＜k＜3.5．18．如图，四边形ABCD为正方形，⊙O过正方形的顶点A和对角线的交点P，分别交AB、AD于点F、E．（1）求证：DE=AF；（2）若⊙O的半径为，AB=，求的值．【解析】（1）证明：连接EP、FP，如图，∵四边形ABCD为正方形，∴∠BAD=90°，∠BPA=90°∴∠FPE=90°，∴∠BPF=∠APE，又∵∠FBP=∠PAE=45°，∴△BPF≌△APE，∴BF=AE，而AB=AD，∴DE=AF；（2）连EF，∵∠BAD=90°，∴EF为⊙O的直径，而⊙O的半径为，∴EF=，∴AF2+AE2=EF2=（）2=3①，而DE=AF，DE2+AE2=3；又∵AD=AE+ED=AB，∴AE+ED=②，由①②联立起来组成方程组，解之得：AE=1，ED=或AE=，ED=1，所以：或．提示：（1）连接EF、EP、FP，可证明△AEP≌△BFP（2）设：AE=x，ED=AF=y可得：和x2+y2=3，解得x=，y=1或x=1，y=，所以：或．19．如图，在平面直角坐标系xoy中，直线y=x+3交x轴于A点，交y轴于B 点，过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C，点D是抛物线的顶点．（1）求此抛物线的解析式；（2）点P是直线AB上方的抛物线上一点，（不与点A、B重合），过点P作x 轴的垂线交x轴于点H，交直线AB于点F，作PG⊥AB于点G．求出△PFG的周长最大值；（3）在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M，使得△ABM与△ABD的面积相等？若存在，请求出此时点M的坐标；若不存在，请说明理由．【解析】（1）∵直线AB：y=x+3与坐标轴交于A（﹣3，0）、B（0，3），代入抛物线解析式y=﹣x2+bx+c中，∴∴抛物线解析式为：y=﹣x2﹣2x+3；（2）∵由题意可知△PFG是等腰直角三角形，设P（m，﹣m2﹣2m+3），∴F（m，m+3），∴PF=﹣m2﹣2m+3﹣m﹣3=﹣m2﹣3m，△PFG周长为：﹣m2﹣3m+（﹣m2﹣3m），=﹣（+1）（m+）2+，∴△PFG周长的最大值为：．（3）点M有三个位置，如图所示的M1、M2、M3，都能使△ABM的面积等于△ABD的面积．此时DM1∥AB，M3M2∥AB，且与AB距离相等，∵D（﹣1，4），∴E（﹣1，2）、则N（﹣1，0）∵y=x+3中，k=1，∴直线DM1解析式为：y=x+5，直线M3M2解析式为：y=x+1，∴x+5=﹣x2﹣2x+3或x+1=﹣x2﹣2x+3，∴x1=﹣1，x2=﹣2，x3=，x4=，∴M1（﹣2，3），M2（，），M3（，）．20．如图，在直角坐标系中，⊙M外接于矩形OABC，AB=12，BC=16，点A 在x轴上，点C在y轴上．（1）写出点A、B、C及M的坐标；（2）过点C作⊙M的切线交x轴于点P，求直线PC的解析式；（3）如果E为线段PC上一动点（运动时不与P、C重合），过点E作直线EF 交PA于点F．①直线EF将四边形PABC的周长平分，设E点的纵坐标为t，△PEF的面积为S，求S关于t的函数关系式，并求自变量t的取值范围；②是否存在直线EF将四边形PABC的周长和面积同时平分？若能，请求出直线EF的解析式；若不能，请说明理由．【解析】（1）A（16，0），B（16，12），C（0，12），M（8，6）．（2）连接CM．∵CM是圆半径，PC是切线，∴PC⊥CM，K PC×K CM=﹣1，解得K PC=，由点斜式写出解析式为y=x+12．（3）①作EN⊥x轴于N．根据（2）中的直线解析式求得P（﹣9，0）．则PC=15．则四边形ABCP的周长是15+9+16+16+12=68．又点E的纵坐标是t，则PE=t，∵直线EF将四边形PABC的周长平分，则PF=34﹣t，则S=×t（34﹣t）=﹣+17t∵点E为PC上一动点（运动时不与P、C重合），∴0＜t＜12，∵点F在PA上，∴0＜PF≤AP，∵OP=9，OA=16，∴AP=25，∴0＜PF≤25，∵PF=34﹣t，∴0＜34﹣t≤25，∴7.2≤t＜27.2∵0＜t＜12∴7.2≤t＜12即：S=×t（34﹣t）=﹣+17t（7.2≤t＜12）；②因为四边形ABCP的面积=×（16+16+9）×12=246．若把四边形的面积等分，则S=123．有﹣+17t=123，此方程无实数根，故不存在直线EF将四边形PABC的周长和面积同时平分．。
2019年温州永嘉中学提前自主招生选拔模拟考试数学试题（满分：120分时间：100分钟）一、选择题（共8小题，满分32分，每小题4分）1．任意选择一对有序整数（b，c），其中每一个整数的绝对值小于或等于5，每一对这样的有序整数被选择的可能性是相等的．方程x2+bx+c＝0没有相异正实根的概率是（）A．B．C．D．2．若（a2+b2）（a2+b2﹣2）＝8，则a2+b2的值为（）A．4或﹣2 B．4 C．﹣2 D．﹣43．将一副三角板如下图摆放在一起，连接AD，则∠ADB的正切值为（）A．B．C．D．4．已知实数x，y，z适合x+y＝6，z2＝xy﹣9，则z＝（）A．±1 B．0 C．1 D．﹣15．已知a、b、c为自然数，且a2+b2+c2+42＜4a+4b+12c，且a2﹣a﹣2＞0，则代数式的值为（）A．1 B．C．10 D．116．如图，在Rt△ABC中，∠C＝90°，AC＝3，以AB为一边向三角形外作正方形ABEF，正方形的中心为O，且OC＝4，那么BC的长等于（）A．3B．5 C．2D．7．如果对于某一特定范围内的任意允许值，p＝|1﹣2x|+|1﹣3x|+…+|1﹣9x|+|1﹣10x|的值恒为一常数，则此值为（）A．2 B．3 C．4 D．58．如图，直线y＝x+m交双曲线y＝于A、B两点，交x轴于点C，交y轴于点D，过点A作AH⊥x轴于点H，连结BH，若OH：HC＝1：5，S△ABH ＝1，则k的值为（）A．1 B．C．D．二、填空题（共7小题，满分35分，每小题5分）9．若多项式x2﹣y2+3x﹣7y+k可以分解成两个一次因式的乘积，则k＝．10．设x﹣y﹣z＝19，x2+y2+z2＝19，则yz﹣zx﹣xy＝．11．符号“f”表示一种运算，它对一些数的运算如下：，，，，…，利用以上运算的规律写出f（n）＝（n为正整数）；f（1）•f（2）•f（3）…f（200）＝．12．已知P是中心为O的正方形ABCD内一点，AP⊥BP，OP＝，P A＝6，则正方形ABCD的边长是．13．在平面直角坐标系中，横坐标与纵坐标都是整数的点（x，y）称为整点，如果将二次函数的图象与x轴所围成的封闭图形染成红色，则此红色区域内部及其边界上的整点个数有个．14．在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y＝x 的图象被⊙P截得的弦AB的长为，则a的值是．15．设[x]表示不超过x的最大整数（例如：[2]＝2，[1.25]＝1），已知0≤a≤1，且满足，则[10a]＝．三、解答题（共5小题，满分53分）16．（8分）设＝a（a≠0），求的值．17．（10分）永嘉中学高一段组织了围棋比赛，共有10名选手进入了决赛，决赛阶段实行单循环赛（即每两名参赛选手都要赛一局，且每局比赛都决出胜负），若一号选手胜a1局，输b1局；二号选手胜a2局，输b2局，…，十号选手胜a10局，输b10局．试比较a12+a22+…+a102与b12+b22+…+b102的大小，并叙述理由．18．（10分）如图，四边形ABCD为圆内接四边形，对角线AC、BD交于点E，延长DA、CB交于点F，且∠CAD＝60°，DC＝DE．求证：（1）AB＝AF；（2）A为△BEF的外心（即△BEF外接圆的圆心）．19．（12分）如图，在平面直角坐标系中，直角梯形OABC的顶点A、B的坐标分别是（5，0）、（3，2），点D在线段OA上，BD＝BA，点Q是线段BD上一个动点，点P的坐标是（0，3），设直线PQ的解析式为y＝kx+b．（1）求k的取值范围；（2）当k为取值范围内的最大整数时，若抛物线y＝ax2﹣5ax的顶点在直线PQ、OA、AB、BC围成的四边形内部，求a的取值范围．20．（13分）已知抛物线y＝ax2+bx+c经过点（1，2）．（1）若a＝1，抛物线顶点为A，它与x轴交于两点B，C，且△ABC为等边三角形，求b的值；（2）若abc＝4，且a≥b≥c，求|a|+|b|+|c|的最小值．2019年温州重点高中提前自主招生选拔模拟考试数学试题参考答案与试题解析一、选择题（共8小题，满分32分，每小题4分）1．任意选择一对有序整数（b，c），其中每一个整数的绝对值小于或等于5，每一对这样的有序整数被选择的可能性是相等的．方程x2+bx+c＝0没有相异正实根的概率是（）A．B．C．D．【解析】∵任意选择一对有序整数（b，c），其中每一个整数的绝对值小于或等于5，∴b与c可取的整数分别为：﹣5，﹣4，﹣3，﹣2，﹣1，0，1，2，3，4，5共11种情况，∴有序整数（b，c）共有：11×11＝121（种），∵若方程x2+bx+c＝0有相异正实根，则需：△＝b2﹣4c＞0，﹣b＞0，c＞0，∴方程x2+bx+c＝0有相异正实根的有：（﹣5，1），（﹣5，2，），（﹣5，3），（﹣5，4），（﹣5，5），（﹣4，1），（﹣4，2），（﹣4，3），（﹣3，1），（﹣3，2）共10种情况，∴方程x2+bx+c＝0没有相异正实根的情况有：121﹣10＝111（种），∴方程x2+bx+c＝0没有相异正实根的概率是：．故选：C．2．若（a2+b2）（a2+b2﹣2）＝8，则a2+b2的值为（）A．4或﹣2 B．4 C．﹣2 D．﹣4【解析】设a2+b2为x，可得：x（x﹣2）＝8，解得：x1＝4，x2＝﹣2，因为a2+b2的值为非负数，所以a2+b2的值为4，故选：B．3．将一副三角板如下图摆放在一起，连接AD，则∠ADB的正切值为（）A．B．C．D．【解析】作AE⊥BD，交DB的延长线于点E．由题意可得：∠ABE＝∠CBD＝45°，设AE＝1，则AB＝∴BC＝，∵Rt△BCD是等腰直角三角形，∴BD＝，∴DE＝1+，∴tan∠ADB＝1÷（+1）＝．故选：D．4．已知实数x，y，z适合x+y＝6，z2＝xy﹣9，则z＝（）A．±1 B．0 C．1 D．﹣1【解析】∵实数x、y、z满足x+y＝6，z2＝xy﹣9即xy＝z2+9，∴以x，y为根的二次方程为t2﹣6t+z2+9＝0，其中△＝36﹣4（z2+9）＝﹣4z2≥0，所以z＝0．故选：B．5．已知a、b、c为自然数，且a2+b2+c2+42＜4a+4b+12c，且a2﹣a﹣2＞0，则代数式的值为（）A．1 B．C．10 D．11【解析】由a2﹣a﹣2＞0，a为自然数，可知a＞2，将化a2+b2+c2+42＜4a+4b+12c为（a﹣2）2+（b﹣2）2+（c﹣6）2＜2，因为（a﹣2）2、（b﹣2）2、（c﹣6）2都大于0，当a≥4时，上式不成立，所以自然数a只能取值为3．当a＝3时，代入上式，得：（b﹣2）2+（c﹣6）2＜1，所以只能使（b﹣2）2＝0，（c﹣6）2＝0，即b＝2，c＝6，所以＝1．故选：A．6．如图，在Rt△ABC中，∠C＝90°，AC＝3，以AB为一边向三角形外作正方形ABEF，正方形的中心为O，且OC＝4，那么BC的长等于（）A．3B．5 C．2D．【解析】如图，作EQ⊥x轴，以C为坐标原点建立直角坐标系，CB为x轴，CA 为y轴，则A（0，3）．设B（x，0），由于O点为以AB一边向三角形外作正方形ABEF的中心，∴AB＝BE，∠ABE＝90°，∵∠ACB＝90°，∴∠BAC+∠ABC＝90°，∠ABC+∠EBQ＝90°，∴∠BAC＝∠EBQ，在△ABC和△BEQ中，∴△ACB≌△BQE（AAS），∴AC＝BQ＝3，BC＝EQ，设BC＝EQ＝x，∴O为AE中点，∴OM为梯形ACQE的中位线，∴OM＝，又∵CM＝CQ＝，∴O点坐标为（，），根据题意得：OC＝4＝，解得x＝4，则BC＝5．故选：B．7．如果对于某一特定范围内的任意允许值，p＝|1﹣2x|+|1﹣3x|+…+|1﹣9x|+|1﹣10x|的值恒为一常数，则此值为（）A．2 B．3 C．4 D．5【解析】∵P为定值，∴P的表达式化简后x的系数为0；由于2+3+4+5+6+7＝8+9+10；∴x的取值范围是：1﹣7x≥0且1﹣8x≤0，即≤x≤；所以P＝（1﹣2x）+（1﹣3x）+…+（1﹣7x）﹣（1﹣8x）﹣（1﹣9x）﹣（1﹣10x）＝6﹣3＝3．故选：B．8．如图，直线y＝x+m交双曲线y＝于A、B两点，交x轴于点C，交y轴于点D，过点A作AH⊥x轴于点H，连结BH，若OH：HC＝1：5，S△ABH＝1，则k的值为（）A．1 B．C．D．【解析】设OH＝a，则HC＝5a，∴C（6a，0）代入y＝﹣x+m，得m＝3a，设A点坐标为（a，n）代入y＝﹣x+m，得n＝﹣a+3a＝a，∴A（a，a），代入y＝得，∴k＝a2，∴y＝，解方程组，可得：，，∴A点坐标为（a，a），B点坐标为（5a，a），∴AH＝a，∴S△ABH＝×a×（5a﹣a）＝5a2，∵S△ABH＝1，∴5a2＝1，即a2＝，∴k＝×＝．故选：B．二、填空题（共7小题，满分35分，每小题5分）9．若多项式x2﹣y2+3x﹣7y+k可以分解成两个一次因式的乘积，则k＝﹣10．【解析】∵x2﹣y2+3x﹣7y+k＝（x+）2﹣（y+）2＝（x++y+）（x+﹣y﹣）＝（x+y+5）（x﹣y﹣2），又∵（x+y+5）（x﹣y﹣2）＝x2﹣y2+3x﹣7y﹣10，∴k＝﹣10．故答案为：﹣10．10．设x﹣y﹣z＝19，x2+y2+z2＝19，则yz﹣zx﹣xy＝171．【解析】将x﹣y﹣z＝19两边平方得：（x﹣y﹣z）2＝361，即x2+y2+z2﹣2xy﹣2xz+2yz＝361，∵x2+y2+z2＝19，∴x2+y2+z2﹣2xy﹣2xz+2yz＝19+2（yz﹣xy﹣xz）＝361，则yz﹣xy﹣xz＝＝171．答案为：171．11．符号“f”表示一种运算，它对一些数的运算如下：，，，，…，利用以上运算的规律写出f（n）＝1+（n为正整数）；f（1）•f（2）•f（3）…f（200）＝20301．【解析】∵f（1）＝1+，f（2）＝1+，f（3）＝1+，f（4）＝1+，…，∴f（n）＝1+；∵f（n）＝1+＝，∴f（1）•f（2）•f（3）…f（200）＝×××…××＝＝20301．故答案为：1+；20301．12．已知P是中心为O的正方形ABCD内一点，AP⊥BP，OP＝，P A＝6，则正方形ABCD的边长是10或2．【解析】如图1，过O作OH⊥AP于H，∵四边形ABCD是正方形，AP⊥BP，∴∠AOB＝∠APB＝90°，∴A，B，O，P四点共圆，∴∠BPO＝∠BAO＝45°，∴∠OPH＝45°，∴PH＝OH＝1，∴AH＝7，∴AO＝＝5，∴AB＝AO＝10；如图2，过O作OH⊥BP于H，∵四边形ABCD是正方形，AP⊥BP，∴∠AOB＝∠APB＝90°，∴A，B，P，O四点共圆，∴∠OPH＝∠BAO＝45°，∴PH＝OH＝1，设BP＝m，AB＝x，∴（m+1）2+1＝（）2，m2+62＝x2，解得：m＝4，x＝＝2，∴AB＝2，综上所述：正方形ABCD的边长是10或2，故答案为：10或2．13．在平面直角坐标系中，横坐标与纵坐标都是整数的点（x，y）称为整点，如果将二次函数的图象与x轴所围成的封闭图形染成红色，则此红色区域内部及其边界上的整点个数有25个．【解析】将该二次函数化简得，y＝﹣[（x﹣4）2﹣]，令y＝0得，x＝或．则在红色区域内部及其边界上的整点为（2，0），（3，0），（4，0），（5，0），（6，0），（2，1），（2，2），（3，1），（3，2），（3，3），（3，4），（3，5），（4，1），（4，2），（4，3），（4，4），（4，5），（4，6），（5，1），（5，2），（5，3），（5，4），（5，5），（6，1），（6，2）共25个，故答案为：25．14．在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y＝x的图象被⊙P截得的弦AB的长为，则a的值是．【解析】过P点作PE⊥AB于E，过P点作PC⊥x轴于C，交AB于D，连接P A．∵AB＝2，∴AE＝，P A＝2，∴PE＝1．∵点D在直线y＝x上，∴∠AOC＝45°，∵∠DCO＝90°，∴∠ODC＝45°，∴∠PDE＝∠ODC＝45°，∴∠DPE＝∠PDE＝45°，∴DE＝PE＝1，∴PD＝．∵⊙P的圆心是（2，a），∴点D的横坐标为2，∴OC＝2，∴DC＝OC＝2，∴a＝PD+DC＝2+．故答案为：2+．15．设[x]表示不超过x的最大整数（例如：[2]＝2，[1.25]＝1），已知0≤a≤1，且满足，则[10a]＝6．【解析】∵1＜a+＜2，∴[a+]＝1，∵，0≤a≤1，∴[a+]＝[a+]＝…＝[a+]＝0，[a+]＝[a+]＝…＝[a+]＝1，∴0＜a+＜1，1≤a+＜2，∴0＜a＜，0.6≤a＜1，∴0.6≤a＜，∴[10a]＝6．故答案为6．三、解答题（共5小题，满分53分）16．（8分）设＝a（a≠0），求的值．【解析】∵a≠0，＝a，∴＝，即x+＝∵＝x2+1+＝（x+）2﹣1＝（﹣1）2﹣1＝﹣＝∴＝17．（10分）永嘉中学高一段组织了围棋比赛，共有10名选手进入了决赛，决赛阶段实行单循环赛（即每两名参赛选手都要赛一局，且每局比赛都决出胜负），若一号选手胜a1局，输b1局；二号选手胜a2局，输b2局，…，十号选手胜a10局，输b10局．试比较a12+a22+…+a102与b12+b22+…+b102的大小，并叙述理由．【解析】依题意可知，a1+b1＝9，a2+b2＝9，a3+b3＝9…，且a1+a2+…+a10＝b1+b2+…+b10＝45，∴（a12+a22+…+a102）﹣（b12+b22+…b102）＝（a12﹣b12）+（a22﹣b22）+…+（a102﹣b102）＝（a1+b1）（a1﹣b1）+（a2+b2）（a2﹣b2）+…+（a10+b10）（a10﹣b10）＝9[（a1+a2+…+a10）﹣（b1+b2+…+b10）]＝0，∴a12+a22+...+a102＝b12+b22+ (102)18．（10分）如图，四边形ABCD为圆内接四边形，对角线AC、BD交于点E，延长DA、CB交于点F，且∠CAD＝60°，DC＝DE．求证：（1）AB＝AF；（2）A为△BEF的外心（即△BEF外接圆的圆心）．【解析】证明：（1）∠ABF＝∠ADC＝120°﹣∠ACD＝120°﹣∠DEC＝120°﹣（60°+∠ADE）＝60°﹣∠ADE，而∠F＝60°﹣∠ACF，（6分）因为∠ACF＝∠ADE，（7分）所以∠ABF＝∠F，所以AB＝AF．（2）四边形ABCD内接于圆，所以∠ABD＝∠ACD，又DE＝DC，所以∠DCE＝∠DEC＝∠AEB，所以∠ABD＝∠AEB，所以AB＝AE．∵AB＝AF，∴AB＝AF＝AE，即A是三角形BEF的外心．19．（12分）如图，在平面直角坐标系中，直角梯形OABC的顶点A、B的坐标分别是（5，0）、（3，2），点D在线段OA上，BD＝BA，点Q是线段BD上一个动点，点P的坐标是（0，3），设直线PQ的解析式为y＝kx+b．（1）求k的取值范围；（2）当k为取值范围内的最大整数时，若抛物线y＝ax2﹣5ax的顶点在直线PQ、OA、AB、BC围成的四边形内部，求a的取值范围．【解析】（1）直线y＝kx+b经过P（0，3），∴b＝3，∵B（3，2），A（5，0），BD＝BA，∴点D的坐标是（1，0），∴BD的解析式是y＝x﹣1（1≤x≤3），依题意，得，∴x＝，∴1≤≤3，解得﹣3≤k≤﹣；（2）∵﹣3≤k≤﹣，且k为最大整数，∴k＝﹣1，则直线PQ的解析式为y＝﹣x+3，又∵x＝﹣＝﹣＝，＝＝﹣a，∴抛物线y＝ax2﹣5ax的顶点坐标是（，﹣a），对称轴为x＝，解方程组，得，即直线PQ与对称轴为x＝的交点坐标为（，），∴＜﹣a＜2，解得﹣＜a＜﹣．20．（13分）已知抛物线y＝ax2+bx+c经过点（1，2）．（1）若a＝1，抛物线顶点为A，它与x轴交于两点B，C，且△ABC为等边三角形，求b的值；（2）若abc＝4，且a≥b≥c，求|a|+|b|+|c|的最小值．【解析】（1）由题意，a+b+c＝2，∵a＝1，∴b+c＝1抛物线顶点为A（﹣，c﹣）设B（x1，0），C（x2，0），∵x1+x2＝﹣b，x1x2＝c，△＝b2﹣4c＞0∴|BC|＝|x1﹣x2|＝＝＝∵△ABC为等边三角形，∴﹣c＝即b2﹣4c＝2•，∵b2﹣4c＞0，∴＝2，∵c＝1﹣b，∴b2+4b﹣16＝0，b＝﹣2±2所求b值为﹣2±2．（2）∵a≥b≥c，若a＜0，则b＜0，c＜0，a+b+c＜0，与a+b+c＝2矛盾．∴a＞0．∵b+c＝2﹣a，bc＝∴b，c是一元二次方程x2﹣（2﹣a）x+＝0的两实根．∴△＝（2﹣a）2﹣4×≥0，∴a3﹣4a2+4a﹣16≥0，即（a2+4）（a﹣4）≥0，故a≥4．∵abc＞0，∴a，b，c为全大于0或一正二负．①若a，b，c均大于0，∵a≥4，与a+b+c＝2矛盾；②若a，b，c为一正二负，则a＞0，b＜0，c＜0，则|a|+|b|+|c|＝a﹣b﹣c＝a﹣（2﹣a）＝2a﹣2，∵a≥4，故2a﹣2≥6当a＝4，b＝c＝﹣1时，满足题设条件且使不等式等号成立．故|a|+|b|+|c|的最小值为6．。
最大最全最精的教育资源网 505绝密★启用前浙教版2018-20佃学年重点高中自主招生数学模拟试卷题号 -一- -二二三总分得分注意事项： 1 •答题前填写好自己的姓名、班级、考号等信息 2 •请将答案正确填写在答题卡上第I卷（选择题） 请点击修改第1卷的文字说明 评卷人 得分 .选择题（共 8小题，4*8=32 ） 1 •实数b 满足|b|v 3,并且有实数a , a v b 恒成立，a 的取值范围是（ ）A •小于或等于3的实数B •小于3的实数C •小于或等于-3的实数D •小于-3的实数 2 •代数式，..• ' |的最小值为（ ） A . 12 B . 13 C . 14 D . 11 3 .已知关于x 的方程 二^- ■有正根，则实数 a 的取值范围是（ ）x-3 A . a v 0 且a 工―3 B . a >0 C . a v — 3 4 •如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为 D • a v 3 且 a 工-32 16cm ，则该半圆的半径为（ B • 9 cm 5 •如图：将一个矩形纸片ABCD ,沿着BE 折叠，使C 、D 点分别落在点 C 1, D 1处•若/ C 1BA = 50°, 则/ ABE 的度数为（ D最大最全最精的教育资源网6 .观察图中正方形四个顶点所标的规律，可知2012应标在（）7 . 100人共有2000元人民币，其中任意 10人的钱数的和不超过 380元. 元. A . 216B . 218C . 238D . 2368 .如图，正方形 ABCD 的边AB = 1,丨|和「'都是以1为半径的圆弧，则无阴影两部分的面积之差HA .——'B . 1 -C .- 1 D . 1——2 1436第U 卷（非选择题）评卷人得分.填空题（共 8小题，4*8=32 ）B . 20C . 25°D . 30° 第1个正方形 第2个正方形 第3个正方形 第4个正方形A .第 502个正方形的左下角B .第 502个正方形的右下角C .第 503个正方形的左上角D .第 503个正方形的左下角那么一个人最多有（最大最全最精的教育资源网9.两个反比例函数y=L, y = 一在第一象限内的图象如图所示.点P i, P2, P3、…、P2007在反比例X K函数y=2!上，它们的横坐标分别为x i、X2、X3、…、X2007,纵坐标分别是1, 3, 5…共2007个连X续奇数，过P i, P2, P3、…、P2007分别作y轴的平行线，与y= 的图象交点依次为Q i (x i', y i')、Q i (X2‘，y2‘)、…、Q2 (X2007’，y2007‘)，贝U |P2007Q2007|= ___________ .ii .已知x= —TT；「，贝y x2 3+i2x的算术平方根是_______ .i2.如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“T”方向排列，如(i, 0), (2,0),( 2, i),( 3, 2),( 3, i),( 3, 0)( 4, 0)根据这个规律探索可得，第i00个点的坐标为_______ .f(5J)/\ \ \ ft：：：0(LC q t0) L：£：(4t0)庄°2i3.如图，已知二次函数y i = ax+bx+c(0)与一次函数y2= kx+m (k z0)的图象相交于点A (22, 4) , B (8, 2),则关于x的不等式ax + ( b - k) x+c- m>0的解集是_________________最大最全最精的教育资源网14. 在平面直角坐标系中，横坐标与纵坐标都是整数的点（x, y）称为整点，如果将二次函数■■■■■ - ■-——的图象与x轴所围成的封闭图形染成红色，则此红色区域内部及其边界上的整点个数有 _______ 个.15•如图所示：两个同心圆，半径分别是■■二和虫上，矩形ABCD边AB, CD分别为两圆的弦，当矩形ABCD面积取最大值时，矩形ABCD的周长是 ___________ .16. 如图，Rt△ ABC 中，/ BCA = 90°,/ BAC= 30°, AB = 6. △ ABC 以点B 为中心逆时针旋转，使点C旋转至AB边延长线上的C'处，那么AC边转过的图形（图中阴影部分）的面积是_____________评卷人得分三•解答题（共5小题，56分）17. （10分）如图，四边形ABCD为圆内接四边形，对角线AC、BD交于点E，延长DA、CB交于点F，且/ CAD = 60 °，DC = DE .求证：（1）AB= AF ;（2） A BEF的外心（即△ BEF外接圆的圆心）.18. ( 10分)一个家庭有 3个孩子，(1)求这个家庭有2个男孩和1个女孩的概率； (2 )求这个家庭至少有一个男孩的概率.19. ( 12分)如图，0A 和0B 是O O 的半径，并且 0A 丄OB . P 是OA 上的任意一点，BP 的延长线 交O 0于点Q ,点R 在0A 的延长线上，且 RP = RQ . (1) 求证：RQ 是O 0的切线； (2) 求证：0B 2= PB?PQ + 0P 2;(3) 当RA W 0A 时，试确定/ B 的取值范围.20. ( 12分)如图1, 一张三角形纸片 ABC ,/ ACB = 90°, AC = 8, BC = 6.沿斜边 AB 的中线CD 把这张纸片剪成厶 AC 1D 1和厶BC 2D 2两个三角形(如图2)，将纸片厶AC 1D 1沿直线D 2B (AB )方 向平移(点A 、D 1、D 2、B 始终在同一直线上)，当点 D 1与点B 重合时，停止平移.在平移过程 中，C 1D 1与BC 2交于点E , AC 1与C 2D 2、BC 2分别交于点F 、P .(1 )当厶AC 1D 1平移到如图3所示的位置时，猜想图中的D 1E 与D 2F 的数量关系，并证明你的猜想； (2)设平移距离 D 2D 1为x ,A AC 1D 1与厶BC 2D 2重叠部分面积为y ,请写出y 与x 的函数关系式，21. (12分)平面上有n 个点(n 》3, n 为自然数)，其中任何三点不在同一直线上.证明:S3定存在三点，以这三点作为顶点的三角形中至少有一个内角不大于参考答案与试题解析一•选择题（共8小题）1 •实数b满足|b|v 3,并且有实数a, a v b恒成立，a的取值范围是（）A •小于或等于3的实数B •小于3的实数C •小于或等于-3的实数D •小于-3的实数【分析】熟悉绝对值的意义，根据绝对值的意义求得b的取值范围，再根据a, b的关系求得a的取值范围.最大最全最精的教育资源网【解答】解：T |b|v 3,「.- 3 v b v 3,又•/ a v b,••• a的取值范围是小于或等于- 3的实数.故选：C.【点评】此题考查了绝对值的有关内容，用几何方法借助数轴来求解，更直观，且不容易遗漏，体现了数形结合的优点.2.代数式.J | ；+ .二•.的最小值为()A . 12 B. 13 C. 14 D. 11【分析】先将原式可化为(；「订'一+ | .T '' ;「，代数式的值即P(x, 0)到A (0,- 2)和B (12, 3)的距离之和，显然当P为“ x轴与线段AB交点”时，PA+PB= AB最短.【解答】解：如图所示：设P点坐标为P (x, 0), 原式可化为*『斗小］_占-■：.-, 即*上寸二―占一匸AP,心上_二宀：—」亠BP,AB = '■ !，'= 13.代数式，... ，.‘|的最小值为13.故选：B.【点评】解答此题，要弄清以下问题：1、定义：一般地，形如1 (a> 0)的代数式叫做二次根式.当a> 0时，表示a的算术平方根，当a= 0时，* i』=0,当a小于0时，二次根式无意义.2、性质： .'=|a|.童+冋3.已知关于x的方程「有正根，则实数a的取值范围是( )A . a v 0 且a 工―3 B. a > 0 C. a v - 3 D . a v 3 且a^—3【分析】首先解方程求得方程的解，根据方程的解是正数，即可得到一个关于a的不等式，从而求得a的范围.最大最全最精的教育资源网【解答】解：去分母得：x+a=- x+3即2x= 3 - a解得x=-2根据题意得：->2解得：a v 3■/ x - 3工0,.・.X M 3,即3,2解得a M- 3 ,二 a v 3 且a M- 3.故选：D.【点评】本题主要考查了分式方程的解的符号的确定，正确求解分式方程是解题的关键.【解答】解：如图，圆心为A,设大正方形的边长为根据对称性可知AE = BC = x, CE = 2x;2T小正方形的面积为16cm ,•••小正方形的边长EF = DF = 4,2 2 2 2 2由勾股定理得，R = AE +CE = AF +DF ,即x2+4x2=( x+4) 2+42,解得，x= 4或-2 (舍去)，• R= ：Hcm .故选：C.16cm2，则该半圆的半径为（）D. -V :「cmACE中，利用勾股定理即可求解.2x,圆的半径为R,【分析】已知小正方形的面积即可求得边长，在直角厶【点评】本题利用了勾股定理，正方形的性质求解.5.如图：将一个矩形纸片ABCD ,沿着BE折叠，使C、D点分别落在点C1, D1处.若/ C〔BA= 50°,则/ ABE 的度数为（ ）BCA . 15 °B . 20 °C . 25°【分析】根据折叠前后对应角相等可知. 【解答】解：设/ ABE = x , 根据折叠前后角相等可知，/ C i BE =Z CBE = 50° +x ,所以 50° +x+x = 90°, 解得x = 20°. 故选：B .【点评】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴 对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等. 6 .观察图中正方形四个顶点所标的规律，可知2012应标在（）3 ---------- 2 7r ----------------- 6 11 ---------- 10 15 ---------- 44[ ---------- 1 S' ----------- 15 121 -------------- 9第1个正方形 第2个正方形 第3个正方形A .第502个正方形的左下角B .第502个正方形的右下角C .第503个正方形的左上角D .第503个正方形的左下角【分析】 观察各正方形左下角的数字可知，这些数都是 2个正方形左下角 8= 2 X 4,第3个正方形左下角 【解答】 解：I 2012= 503 X 4, ••• 2012应标在第503个正方形的左下角， 故选：D .【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力. 对于找规律的题目首先应找D . 30°厲 ------ 13 第4个正方形4的倍数，第1个正方形左下角4= 1X 4，第 12= 3X 4，…，由此得出一般规律.出哪些部分发生了变化，是按照什么规律变化的.通过分析找到各部分的变化规律后直接利用规律求解.最大最全最精的教育资源网7.100人共有2000元人民币，其中任意10人的钱数的和不超过380元.那么一个人最多有（）元.A. 216B. 218C. 238D. 236【分析】由于共有2000元人民币，10人不超过380元，则其余90人钱数的和不少于1620元，再根据抽屉原理可知存在9人的钱数的和不少于162元，【解答】解：任意10个人的钱数的和不超过380元，（1）•••任意90个人的钱数的和不少于1620元，由抽屉原理，存在9人的钱数的和不少于162元，（2）（1）-（2）, 一个人最多能有218元.故选：B.【点评】本题考查了推理与论证，解答此题要熟悉抽屉原理------ 把多于kn个东西任意分放进n 个空抽屉（k是正整数），那么一定有一个抽屉中放进了至少k+1个东西.8•如图，正方形ABCD的边AB= 1,丨|和：都是以1为半径的圆弧，则无阴影两部分的面积之差A . B. 1 - C. - 1D. 1-2436【分析】图中1、2、3、4图形的面积和为正方形的面积，1、2和两个3的面积和是两个扇形的面积，因此两个扇形的面积的和-正方形的面积=无阴影两部分的面积之差，即川-1 =360兀——-12丄【解答】解：如图：正方形的面积=S1+S2+S3+S4；①两个扇形的面积=2S3+S1+S2；②© 金“曰c S S S90兀X1X2 1兀 t②-①，得：S3 - S4= S扇形-S正方形= —1 == .360 2故选：A.最大最全最精的教育资源网 【分析】要求出|P 2007Q 2007|的值，就要先求|Qy 2007-Py 2007|的值，因为纵坐标分别是 I , 3, 5…，共2007个连续奇数，其中第2007个奇数是2X 2007 - i = 40I3,所以P 2007的坐标是(PX 2007, 40I3), 那么可根据P 点都在反比例函数 y = 乂上，可求出此时 PX 2007的值，那么就能得出P 2007的坐标，3然后将P 2007的横坐标代入y =二中即可求出Qy 2007的值.那么|P 2007Q 2007|= |Qy 2007 - Py 2007|,由此X可得出结果.【解答】 解：由题意可知：P 2007的坐标是(PX 2007, 40I3),c面积之间的联系是解题的关键. 二.填空题(共8小题)9•两个反比例函数y =二，y =上在第一象限内的图象如图所示•点P i , P 2, P 3、…、P 2007在反比例函数y =二上，它们的横坐标分别为x 1> x 2、x 3、…、x 2007，纵坐标分别是1, 3, 5…共2007个连续奇数，过P i , P 2, P 3、…、P 2007分别作y 轴的平行线，与y = J 的图象交点依次为 Q i (x i ',y i '）、 Q i （X 2‘，y 2‘）、…、 Q 2 （X 2007', y 2007‘），贝V|P 2007Q 2007|= -^-3—2【点评】本题主要考查了扇形的面积计算公式及不规则图形的面积计算方法.找出正方形内四个图形最大最全最精的教育资源网 又T P2007 在y= —上，最大最全最精的教育资源网 40134ri1 ? dfil m|P 2007Q 2007|= |Py 2007 - Qy 2007|= |4013_ | = 故答案为：；一 【点评】本题的关键是找出 P 点纵坐标的规律，以这个规律为基础求出 P 2007的横坐标，进而求出Q 2007的值，从而可得出所求的结果.3210.多项式 6x - 11x +X+4 可分解为(X - 1)( 3X -4)( 2x+1).22232232【分析】 将-11x 分为-6x 和-5x 两部分，原式可化为 6x - 6x - 5x +x+4, 6x - 6x 可提公因式， 分为一组，-5X 3+X +4可用十字相乘法分解，分为一组. 【解答】 解：6x 4- 11X 2+X +4,322=6x - 6x - 5x +x+4,2 2=6x 2 (x - 1) -( 5x 2- x - 4),2=6x (x - 1) -( x - 1)( 5x+4),2=(x - 1) ( 6x - 5x - 4),=(x - 1)( 3x - 4)( 2x+1).【点评】本题考查了用分组分解法进行因式分解，要考虑分组后还能进行下一步分解，把-11x 2分成2 2-6x 和-5x 两部分是解题的关键，也是难点. 11 .已知x = |, . | | ' - |，则x +12x 的算术平方根是_2'.【分析】 观察题目，可用借助于整体思想，设 — =a ,----- = b ，进行替换，加以解答.【解答】解：设-^= a , — = b .则-._i ，〔-1.又 4 =| ._] = a 3b 3,3故原式=x (x +12),=(a 2b - ab 2 ) ( a 4b 2 - 2a 3『+a 2b 4+12), =(a 2b - ab 2 ) ( a 4b 2 - 8+a 2b 4+12), =(a 2b - ab 2 )( a 4b 2+a 2b 4+4),而 QX 2007 (即 PX 2007)在 y=-l 上，所以 Qy 2007=0x20074013最大最全最精的教育资源网 = 打厂 _ ■打丨 ■ I ', =4 X 2= 8.则其算术平方根是 2 _. 故答案为：2 -.【点评】此题主要考查了立方根、算术平方根的定义，解题时注意运用公式简便计算(a+b ) (a - b )=a 5- b 2;( a - b )( a 2+ab+b 2)= a 6- b 3.同时注意用一个字母可以表示一个较复杂的数的整体 思想. 12. 如图，在平面直角坐标系中，有若干个整数点，其顺序按图中 0),( 2,1),( 3, 2),( 3, 1),( 3, 0)( 4, 0)根据这个规律探索可得，第坐标为(14, 8)【分析】横坐标为1的点有1个，纵坐标只是0;横坐标为2的点有2个，纵坐标是0或1;横坐标 1, 2…横坐标为奇数，纵坐标从大数开始数；横坐标为偶数, 则从0开始数.100个点在此行上，横坐标就为 14,纵坐标为从第92个点向上数8个点，即为8; 故第100个点的坐标为(14, 8). 故填(14, 8).【点评】 本题考查了学生阅读理解及总结规律的能力，找到横坐标和纵坐标的变化特点是解题要点.213. 如图，已知二次函数 y 1 = ax +bx+c (0)与一次函数 y 2= kx+m (0)的图象相交于点 A (5 、2, 4) , B (8, 2),则关于 x 的不等式ax + ( b - k ) x+c- m >0的解集是x v- 2或x >8 .2 2/2 2“T”方向排列，女口( 1,0), (2,100个点的 为3的点有3个，纵坐标分别是 0, 【解答】 解：因为1+2+3+…+13 = 91, 所以第91个点的坐标为(13, 12).因为在第14行点的走向为向上，故第2【解答】解：ax + (b- k) x+c-m>0,2可整理为ax +bx+c> kx+m,•••两函数图象相交于点 A (- 2, 4), B ( 8, 2),•••不等式的解集是x v- 2或x>&故答案x v - 2 或x> 8.【点评】本题主要考查了二次函数与不等式的关系，解答该题时，要具备很强的读图能力.14. 在平面直角坐标系中，横坐标与纵坐标都是整数的点( x, y)称为整点，如果将二次函数■■■■- - ■-——的图象与x轴所围成的封闭图形染成红色，则此红色区域内部及其边界上的整点个数有25 个.【分析】找到函数图象与x轴的交点，那么就找到了相应的x的整数值，代入函数求得y的值，那么就求得了y的范围.【解答】解：将该二次函数化简得，y=-[ (x- 4) 2-—丄],4令y= 0得，x=l—或二2 2则在红色区域内部及其边界上的整点为( 2, 0),( 3, 0),( 4, 0),( 5, 0),( 6, 0),( 2,1), (2, 2), (3, 1),( 3, 2), (3, 3), (3, 4),( 3, 5),( 4, 1),( 4, 2),(4, 3),( 4, 4), (4, 5),( 4, 6), (5, 1), (5, 2),( 5, 3),( 5, 4),( 5,5), (6, 1), (6, 2)共25个，故答案为:25.【点评】本题涉及二次函数的图象性质，解决本题的关键是得到相对应的x的值.15•如图所示：两个同心圆，半径分别是-:和虫上，矩形ABCD边AB, CD分别为两圆的弦，当矩形ABCD面积取最大值时，矩形ABCD的周长是16+12 「.最大最全最精的教育资源网【分析】此题首先能够把问题转化到三角形中进行分析. 根据锐角三角函数的概念可以证明三角形的面积等于相邻两边的乘积乘以夹角的正弦值，根据这一公式分析面积的最大值的情况•然后运用勾股定理以及直角三角形的斜边上的高等于两条直角边的乘积除以斜边求得长方形的长和宽，进一步求得其周长.【解答】解：连接OA , OD，作0P丄AB于P, OM丄AD于M , 0N丄CD于N .根据矩形的面积以及三角形的面积公式发现：矩形的面积是三角形AOD的面积的4倍.因为0A, 0D的长是定值，则/ AOD的正弦值最大时，三角形的面积最大，即/ AOD = 90°,贝U AD = 6二, 根据三角形的面积公式求得0M = 4,即卩AB= &则矩形ABCD的周长是16+12匚.【点评】本题考查的是矩形的定理以及垂径的性质，考生应注意运用勾股定理来求得边长继而才能求出周长.16. 如图，Rt△ ABC 中，/ BCA = 90°,/ BAC= 30°, AB = 6. △ ABC 以点B 为中心逆时针旋转，使点C旋转至AB边延长线上的C'处，那么AC边转过的图形（图中阴影部分）的面积是9nC 5 A【分析】根据旋转变换的性质可得△ ABC与厶A' BC '全等，从而得到阴影部分的面积=扇形ABA' 的面积-小扇形CBC '的面积.【解答】解：根据旋转变换的性质，△ ABC◎△ A' BC'，•// BCA = 90°，/ BAC= 30 °，AB = 6，BC = - AB= 3，C 5 2【点评】本题考查了扇形的面积计算，解题的关键是看出阴影部分的面积的表示等于两个扇形的面积的差，还考查了直角三角形中30°角所对的直角边等于斜边的一半的性质.三•解答题（共5小题）17. 如图，四边形ABCD为圆内接四边形，对角线AC、BD交于点E,延长DA、CB交于点F，且/CAD = 60°, DC = DE .求证：（1）AB= AF ;（2） A BEF的外心（即△ BEF外接圆的圆心）.【分析】（1）根据圆内接四边形的性质和三角形的内角和定理进行证明；（2）根据三角形的外心到三角形的三个顶点的距离相等的性质只需证明AB= AF = AE，根据等腰三角形的性质和判定进行证明.【解答】证明：（1）Z ABF = Z ADC = 120°-/ ACD = 120°-/ DEC=120° -（60° +/ADE ）= 60°-/ ADE , （ 4 分）而/ F = 60°-/ ACF , （ 6 分）因为/ ACF = / ADE , （7 分）所以/ ABF = / F，所以AB = AF .（8 分）（2）四边形ABCD内接于圆，所以/ ABD = / ACD , （10分）又DE = DC，所以/ DCE = / DEC = / AEB ,（12 分）所以/ ABD = / AEB,所以AB= AE.（14分）•/ AB = AF ,AB = AF = AE，即A是三角形BEF的外心.（16分）【点评】综合运用了圆内接四边形的性质、三角形的内角和定理以及三角形的外心的性质.18. 一个家庭有3个孩子，(1)求这个家庭有2个男孩和1个女孩的概率；(2 )求这个家庭至少有一个男孩的概率.【分析】画树状图展示所有8种等可能的结果数，再找出有2个男孩和1个女孩的结果数和至少有个男孩的结果数，然后根据概率公式求解.【解答】解: 画树状图为：男女男女男女Z\八八男女男女男女男女共有8种等可能的结果数；(1 )有2个男孩和1个女孩的结果数为3,所以有2个男孩和1个女孩的概率= ;8(2)至少有一个男孩的结果数为7, 所以至少有一个男孩的概率=厂.8【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.19 .如图，0A和0B是O O的半径，并且0A丄OB . P是0A上的任意一点，BP的延长线交O O于点Q,点R在0A的延长线上，且RP= RQ.(1)求证：RQ是O 0的切线；2 2(2)求证：0B2= PB?PQ + 0P2;(3)当RA W 0A时，试确定/ B的取值范围.【分析】(1)要证明RQ是O O的切线只要证明/ OQR= 90°即可；(2)先证明△ BCP AQP，从而得到PB?PQ = PC?PA，整理即可得到OB2= PB?PQ + OP2;(3)分别考虑当RA= OA时或与A重合时，/ B的度数，从而确定其取值范围.【解答】证明：(1)连接OQ;•/ OB = OC, PR= RQ;•••/ OBP = Z OQP,Z RPQ = Z RQP;•••/ OBP + Z BPO = 90°,/ BPO=Z RPQ;•••/ OQP + / RQP = 90°;即/ OQR = 90°,• RQ是O O的切线.证明：(2)延长AO O O交于点C;•// BPC =/ QPA, / BCP = / AQP,•••△BCPAQP ,2 2• PB?PQ= PC?FA=( OC + OP)( OA - OP) = ( OB+OP)( OB - OP)= OB2- OP2,2 2• OB = PB?PQ+OP .解：(3)当RA= OA 时，/ R= 30°,易得/ B = 15°，当R与 A 重合时，/ B = 45°;•/ R是OA延长线上的点，• R与A不重合，•••/ B工45°;又••• RA W OA,•/ B V 45°, • 15°W B V 45 ° .最大最全最精的教育资源网【点评】此题考查了学生对切线的判定及相似三角形的判定等知识点的综合运用.20.如图1, 一张三角形纸片ABC,/ ACB = 90°, AC= 8, BC = 6.沿斜边AB的中线CD把这张纸片剪成△AC1D1和厶BC2D2两个三角形(如图2)，将纸片厶AC1D1沿直线D2B(AB)方向平移(点A、D1、D2、B始终在同一直线上)，当点D1与点B重合时，停止平移.在平移过程中，C1D1与BC2交于点E，AC1与C2D2、BC2分别交于点F、P.(1)当厶AC1D1平移到如图3所示的位置时，猜想图中的D1E与D2F的数量关系，并证明你的猜想；(2)设平移距离D2D1为x，A AC1D1与厶BC2D2重叠部分面积为y，请写出y与x的函数关系式，【分析】(1)由题意可得C1D1 = C2D2= BD2= AD1，根据两直线平行，同位角相等，及等腰三角形的性质，可得到AD2= D2F ;同理：BD1= D1E，即可得出D1E = D2F .(2)由题意，D2D1 = x，贝U D1E= BD1 = D2F= AD2= 5 - x，在△ BC2D2 中，C2到BD2 的距离就是△94ABC的AB边上的高，根据△ ABC的面积可得高为——，设△ BED1的BD1边上的高为h，可证△5BC2D2SA BED1，所以…;分别表示出△ BED1和V△ FC2P的面积，根据重叠部分面积为y= S A BC2D2 - S^BED 1 - S^FC2P，可求出y与x的函数关系式，求出最大值即可；【解答】解：(1) D1E= D2F.T C1D1 〃C2D2，•••/ C1 = / AFD2，又•••/ ACB = 90°，CD是斜边上的中线，• - DC = DA = DB，即C1D1=C2D2=BD2= AD1，.•./ C i = Z A,•••/ AFD2=/ A,••• AD2= D2F ;同理：BD1 = D I E,又••• AD1= BD2,• AD i - D I D2= BD2 - D i D2,• AD2= BD1,•- D i E= D2F;(2)由题意得AB= 10, AD 1 = BD2= C i D 1 = C2D2= 5,又••• D2D1 = x,•- D1E= BD1= D2F = AD2= 5- x,•- C2F = C1E= x,在厶BC2D2中，C2到BD2的距离就是△ ABC的AB边上的高, •根据△ ABC的面积可得高为 1 ,5设厶BED1的BD1边上的高为h,可证△ BC2D2S^ BED1,h•* 24（57 S 1 …厂、八12 *•- ，S A BED1= , ' —L：• _=千:-，又C1 + Z C2= 90° ,•/ FPC2= 90° ,又C2=Z B , sinB=…,cosB= ,5 5•F，F，S AFC2P=4r PC2X PF = ^^ , _ ,• y= S A BC2D2 - S A BED1 - S A F C2P==S\ABC - :'_ -■■■，2 25 25•y= J 八丄=—：一-•函数y的最大值是8.【点评】本题主要考查了相似三角形的判定与性质、平移的性质和二次函数的最值等知识，本题涉及的知识点较多，考查了学生的综合运用能力.21 .平面上有n个点（n>3, n为自然数），其中任何三点不在同一直线上.证明：一定存在三点,以这三点作为顶点的三角形中至少有一个内角不大于180°n【分析】题目中的n个点中不妨设这两个点为A i、A2,则可以分当/ A2A i An> 180°—___ 和n 当/ A2A l A n< 180° -「；「两种情况进行讨论•根据三角形的内角和定理就可以证出.n【解答】解：如图，在这n个点中，必存在这样的两点，使其它各点均在这两点所在直线同侧，设这两个点为A i、A2,其它各点按逆时针方向设为A3、A4、A n.(1)当/ A2A l A n> 180°- —时，连接A2A n.n在厶A1A2A n 中，/ A1A2A n+Z A1A n A2= 180 -/ A2A1A n< … 一 -----------n则/ A2A1A n、/ A1A n A2中必有一个角不大于—：；(2)当/ A2A1A n< 180°- 一L ------ 时，/ A2A1A3+ / A3A1A4+ / A4A1A5+…+/A n- 1A1A n< 180°-n2XlS0en则在这n- 2个角中，必有一个角不大于一一【点评】本题的难度较大，分情况讨论是解题的关键.=ab (a - b ) a b (a +b +ab ),。
2019届温州市重点中学自主招生模拟试题数学试卷（考试时间120分钟，满分150分）一.选择题（每题5分，共50分） 1.下列数中不属于有理数的是（ ）A.1B.21C.22D.0.11132.如图，在矩形中截取两个相同的圆作为圆柱的上．下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长和宽分别为y 和x ，则y 与x 的函数图象大致是（ ）A. B. C. D.3.如果把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正 方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ） A 、13 = 3+10 B 、25 = 9+16 C 、49 = 18+31 D 、36 = 15+214.a 、b 、c 均不为0，若0<=-=-=-abc cxz b z y a y x ，则),(bc ab p 不可能在（ ） A 、第一象限B 、第二象限C 、第三象限D 、第四象限5.如图，在平面直角坐标系中，⊙P 的圆心是（2，a ）（a ＞2），半径为2，函数y=x 的图象被⊙P 截得的弦AB 的长为， 则a 的值是（ ）A 、B 、2+C 、错误！未找到引用源。
6.如图，在Rt△ABC 中，∠ACB=90º，∠A=30º，BC=2，将△ABC 绕 点C 按顺时针方向旋转n 度后，得到△EDC，此时，点D 在AB 边 上，斜边DE 交AC 边于点F ，则n 的大小和图中阴影部分的面积 分别为（ ）A 、30，2B 、60，2C 、60、60，3 7.如图一个长为m 、宽为n 的长方形（m ＞n ）沿虚线剪开， 拼接成图2，成为在一角去掉一个小正方形后的一个大 正方形，则去掉的小正方形的边长为（ ） A 、2m n - B 、m －n C 、2mD 、2n8.抛物线2x y =上有三点P 1、P 2、P 3，其横坐标分别为t ，t +1，t +3，则△P 1P 2P 3的面积为（ ）． A.1 Ｂ. 2 Ｃ. 3 Ｄ.4 9.已知直线483y x =-+与x 轴、y 轴分别交于点A 和点B ，M 是OB上的一点，若将△ABM 沿AM 折叠，点B 恰好落在x 轴上的点B '处，则直线AM 的函数解析式是( )A.821+-=x yB.831+-=x y C.321+-=x y D.331+-=x y10.正五边形广场ABCDE 的边长为80米，甲、乙两个同学做游戏，分别从A 、C 两点处同时出发，沿A-B-C-D-E-A 的方向绕广场行走，甲的速度为50米/分，乙的速度为46米/分，则两人第一次刚走到同一条边上时（ ）． Ａ.甲在顶点A 处 Ｂ.甲在顶点B 处 C.甲在顶点C 处 Ｄ.甲在顶点D 处二.填空题（每题6分，共36分）11.分解因式：22242y xy x ++=________________. 12.如图，在平面直角坐标系中，反比例函数)0,0(>>=k x xky的图象经过点A （1, 2），B （m ，n ）（m ＞1），过点B 作 y 轴的垂线,垂足为C.若△ABC 面积为２，则点B 的坐标 为________.13.如右图，是一回形图，其回形通道的宽和OB 的长均 为1，回形线与射线OA 交于A 1，A 2，A 3，…．若从O 点到A 1点的回形线为第1圈（长为7），从A 1点到A 2 点的回形线为第2圈，…，依次类推．则第11圈的长 为 ．14.今有一副三角板（如图1），中间各有一个直径为4cm 的圆洞，现将三角板a 的30º角的那一头插入三角板b的圆洞内（如图2），则三角板a 通过三角板b 的圆洞的那一部分的最大面积为 cm 2（不计三角板的厚度，精确到0.1cm 2）．15.如图，等腰梯形MNPQ 的上底长为2，腰长为3，一个底角为60°．正方形ABCD 的边长为1，它的一边AD 在MN 上，且顶点A 与M 重合．现将正方形ABCD 在梯 形的外面沿边MN 、NP 、PQ 进行翻滚，翻滚到有一个顶 点与Q 重合时，点A 所经过的路线与梯形MNPQ 的三边 MN 、NP 、PQ 所围成图形的面积是________．16.如图，在矩形ABCD 中，AB=2，BC=4，⊙D 的半径为1．现将一个直角三角板的直角顶点与矩形的对称中心O图1ba切于点H ，此时两直角边与AD 交于E ，F 两点，则tan EFO ∠的值为 ． 三.解答题（共6小题，分别为8,10,10,10,12，14分，共64分） 17.设数列 ,1,,12,1,,13,22,31,12,21,11kk k -，问：（1）这个数列第2010项的值是多少？（2）在这个数列中，第2010个值为1的项的序号是多少？18.如图，在梯形ABCD 中，AB ∥CD ，⊙O 为内切圆，E 为切点， （Ⅰ）求AOD ∠的度数；（Ⅱ）若8=AO cm ，6=DO cm ，求OE 的长． .19.请设计三种方案：把一个正方形剪两刀，使剪得的三块图形能够拼成一个三角形，并且使拼成的三角形既不是直角三角形也不是等腰三角形，画出必要的示意图，并附以简要的文字说明．20.某商场在促销期间规定：商场所有商品按标价的80%出售，同时，当顾客在该商场内消费满一定金额后，可按如下方案获得相应金额的奖券：根据上述促销方法，顾客在该商场购物可以获得双重优惠。
2018年温州中学自主招生综合素质测试物理试卷一、单项选择题(本题共7小题,每小题5分,共35分,在每小给出的选项中,只有一个选项是符合题目要求的)1、2018年初全国出现大面积的降温降雪,路面结冰,路政部门在结冰的路面上撒工业盐,它的主要作用是（）A.增加车胎与路面的摩擦,防止汽车打滑B.通过盐与冰发生化学反应,去除路面结冰C.降低冰的熔点使冰融化D.利用盐的吸水功能使路面保持干燥2、如图所示,一个立方体铁块固定于水中,当水面上方的大气压强增大时,下列说法正确的是（）A.立方体上表面受到水的压力增大B立方体上表面受到水的压力不变C立方体受到水的浮力增大D立方体左侧面受到水的压力不变第2题图3、如图所示,向右匀速运动的车厢里有一个三棱柱,斜面AB和AC相同,车厢中的人将两个相同的物体甲、乙分别从两斜面顶端静止释放,则下列说法正确的是( )A两物体同时到达底端B.甲物体先滑到底端C.乙物体先滑到底端D.上述三种情况均有可能4、如图所示,AB与凸透镜的主光轴OA垂直,与主光轴的交点A到光心O的距离大于一倍焦距且小于两倍焦距,当点光源从A点开始以恒定的速度v沿着虚线向B运动,则关于点光源通过透镜所成像的运动,下列说法正确的是（）A.与点光源的运动方向相反且大于vB.与点光源的运动方向相同且大于vC.与点光源的运动方向相反且小于vD.与点光源的运动方向相同且小于v5若有一电源，其电流强度与标识为“3v、2.5w”的手电筒灯珠的额定电流相同，当该电流从头到脚流过人体，下列说法正确的是（）A人基本上没有任何感觉B人会有轻微的“麻”的感觉c人会受到严重伤害，并危及生命D上述三种情况因人而异，都有可能6、有一块体积为10cm3，密度为3.5g/cm3橡皮泥，可将橡皮泥成任意形状。
然后放入盛有水的容器中，已知容器足够大，容器中的水足够深，水的密度为1.0g/cm3,g=10N/kg.则下列说法正确是的（）A橡皮泥受到的浮力不可能为0.2NB橡皮泥受到的浮力一定为0.1NC橡皮泥受到的浮力可能为0.35ND橡皮泥受到的浮力可能为0.4N7、当冷却的电炉接电压恒定的电源后，电炉的电阻丝逐渐得通红起来，下列关于这一过程的说法正确的是（）A、电阻丝的电功率逐渐增大B、电阻丝的电功率减小C、电阻丝的电功率保持不变D、电阻丝的电功率先减小后增大二、填空题(本题共8小题，共38分）8、已知1纳米=10埃米，则1埃米_________米路径ABCDE，最终到达点9、如图所示为等高线地形图，体重为50kg的小明从A点沿着路径ABCDE，最终到达E点，则此过程中重力对小明做功为________________焦耳。
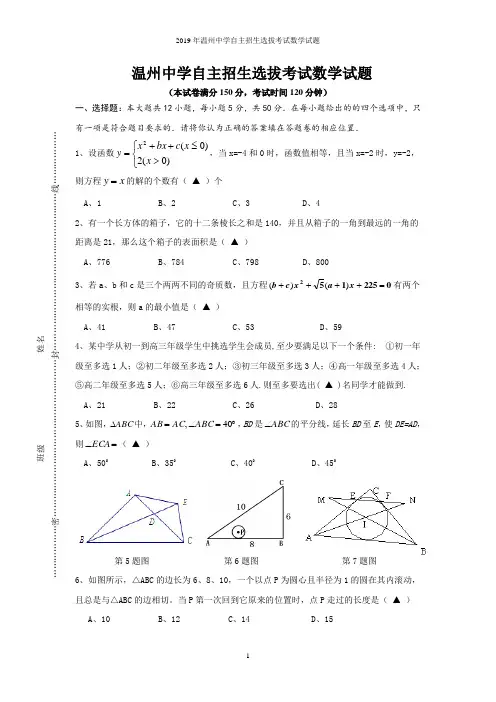
温州中学自主招生选拔考试数学试题（本试卷满分150分，考试时间120分钟）一、选择题：本大题共12小题，每小题5分，共50分．在每小题给出的的四个选项中，只有一项是符合题目要求的．请将你认为正确的答案填在答题卷的相应位置．1、设函数⎩⎨⎧>≤++=)0(2)0(2x x c bx x y ，当x=-4和0时，函数值相等，且当x=-2时，y=-2，则方程x y =的解的个数有（ ▲ ）个A 、1B 、2C 、3D 、42、有一个长方体的箱子，它的十二条棱长之和是140，并且从箱子的一角到最远的一角的距离是21，那么这个箱子的表面积是（ ▲ ）A 、776B 、784C 、798D 、8003、若a 、b 和c 是三个两两不同的奇质数，且方程0225152=++++x a x c b )()(有两个相等的实根，则a 的最小值是（ ▲ ） A 、41B 、47C 、53D 、594、某中学从初一到高三年级学生中挑选学生会成员,至少要满足以下一个条件: ①初一年级至多选1人；②初二年级至多选2人；③初三年级至多选3人；④高一年级至多选4人；⑤高二年级至多选5人；⑥高三年级至多选6人.则至多要选出( ▲ )名同学才能做到. A 、21 B 、22 C 、26 D 、285、如图，ABC ∆中，︒=∠=40,ABC AC AB ，BD 是ABC ∠的平分线，延长BD 至E ，使DE=AD ，则=∠ECA （ ▲ ）A 、500B 、350C 、400D 、450第5题图 第6题图 第7题图6、如图所示，△ABC 的边长为6、8、10，一个以点P 为圆心且半径为1的圆在其内滚动，且总是与△ABC 的边相切。
当P 第一次回到它原来的位置时，点P 走过的长度是（ ▲ ） A 、10 B 、12 C 、14 D 、15班级____________________ 姓名____________________………………密………………………………………………封………………………………………………线………………7、如图，在Rt △ABC 中，∠ACB=090，内切圆⊙I 切AC,BC 于E,F ，射线BI 、AI 交直线EF 于点M 、N ，设S △AIB =S 1，S △MIN =S 2 ，则21S S 的值为（ ▲ ） A 、 23 B 、2 C 、25D 、38、将20个乒乓球（不加区分）装入5个不同的盒子里，要求不同的盒子中的球数互不相同，且盒子都不空，一共有（ ▲ ）种不同装法。
第一套：满分120分2020-2021年浙江温州中学初升高自主招生数学模拟卷一．选择题（共6小题，满分42分）1. （7分）货车和小汽车同时从甲地出发，以各自的速度匀速向乙地行驶，小汽车到达乙地后，立即以相同的速度沿原路返回甲地，已知甲、乙两地相距180千米，货车的速度为60千米/小时，小汽车的速度为90千米/小时，则下图中能分别反映出货车、小汽车离乙地的距离y （千米）与各自行驶时间t （小时）之间的函数图象是【 】A. B. C. D.2. （7分）在平面直角坐标系中，任意两点规定运算：①；②；③当x 1= x 2且y 1=y 2时，A =B.有下列四个命题：（1）若A (1，2)，B (2，–1)，则，； （2）若，则A =C ； （3）若，则A =C ；()()1122,,，A x y B x y ()1212,⊕=++A B x x y y 1212=⊗+A B x x y y (),31⊕= A B 0=⊗A B ⊕=⊕A B B C =⊗⊗A B B C（4）对任意点A 、B 、C ，均有成立. 其中正确命题的个数为（ ）A. 1个B. 2个C. 3个D. 4个 3．（7分）如图，AB 是半圆直径，半径OC ⊥AB 于点O ，AD 平分∠CAB 交弧BC 于点D ，连结CD 、OD ，给出以下四个结论：①AC ∥OD ；②CE=OE ；③△ODE ∽△ADO ；④2CD 2=CE •AB ．正确结论序号是（ ）A ．①②B ．③④C ．①③D ．①④ 4. （7分）如图，在△ABC 中，∠ACB =90º，AC =BC =1，E 、F 为线段AB 上两动点，且∠ECF =45°，过点E 、F 分别作BC 、AC 的垂线相交于点M ，垂足分别为H 、G ．现有以下结论：①；②当点E 与点B 重合时，；③；④MG •MH =，其中正确结论为（ ）A. ①②③B. ①③④C. ①②④D. ①②③④ 5.（7分）在数学活动课上，同学们利用如图的程序进行计算，发现无论x 取任何正整数，结果都会进入循环，下面选项一定不是该循环的是（ ）A. 4，2，1B. 2，1，4C. 1，4，2D. 2，4，1 6. （7分）如图，在矩形ABCD 中，AB =4，AD =5，AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点，过点D()()⊕⊕=⊕⊕A B C A B C 2AB =12MH =AF BE EF +=12作⊙O 的切线交BC 于点M ，则DM 的长为（ ）A.B. C. D.二．填空题（每小题6分，满分30分）7.（6分）将边长分别为1、2、3、4……19、20的正方形置于直角坐标系第一象限，如图中方式叠放，则按图示规律排列的所有阴影部分的面积之和为 . 8.（6分）如图，三个半圆依次相外切，它们的圆心都在x 轴上，并与直线3y x =相切．设三个半圆的半径依次为r 1、r 2、r 3，则当r 1＝1时，r 3＝ ．9.（6分）如图，将一块直角三角板OAB 放在平面直角坐标系中，B （2，0），∠AOB=60°，点A 在第一象限，过点A 的双曲线为k y x=．在x 轴上取一点P ，过点P 作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ´B ´．（1）当点O ´与点A 重合时，点P 的坐标是 ；（2）设P （t ，0），当O ´B ´与双曲线有交点时，t 的取值范围是 ．1339241332510.（6分）如图，正方形A 1B 1P 1P 2的顶点P 1、P 2在反 比例函数2(0)y x x=>的图象上，顶点A 1、B 1分别在x 轴、y 轴的正半轴上，再在其右侧作正方形P 2P 3A 2B 2，顶点P 3在反比例函数2(0)y x x=>的图象上，顶点A 2在x 轴的正半轴上，则点P 3的坐标为 ．11.（6分）如图，在⊙O 中，直径AB ⊥CD ，垂足为E ，点M 在OC 上，AM 的延长线交⊙O 于点G ，交过C 的直线于F ，∠1=∠2，连结CB 与DG 交于点N ．若点M 是CO 的中点，⊙O 的半径为4，cos ∠BOC=41，则BN= ．三．解答题（每小题12分，满分48分）12.（12分）先化简，再求值：， 其中.13.（12分）如图，点A （m ，m ＋1），B （m ＋3，m －1）都在反比例函数的图象上．（1）求m ，k 的值；32221052422x x x x x x x x --÷++--+-2022(tan 45cos30)21x =-+︒-︒-xky =xO yAB （2）如果M 为x 轴上一点，N 为y 轴上一点， 以点A ，B ，M ，N 为顶点的四边形是平行四边形，试求直线MN 的函数表达式． （3）将线段AB 沿直线进行对折得到线段，且点始终在直线OA 上，当线段与轴有交点时,则b 的取值范围为 （直接写出答案）14.（12分）如图，在Rt △ABC 中，∠ABC=90°，以AB 为直径作⊙O 交AC 于点D ，DE 是⊙O 的切线，连接DE ．（1）连接OC 交DE 于点F ，若OF=CF ，证明：四边形OECD 是平行四边形； （2）若=n ，求tan ∠ACO 的值b kx y +=11B A 1A 11B A x OFCF15.（12分）如图1，抛物线y ＝ax 2＋bx ＋c （a ≠0）的顶点为C （1，4），交x 轴于A 、B 两点，交y 轴于点D ，其中点B 的坐标为（3，0）。
