原子物理学第二章

第二章 原子的能级和辐射一、学习要点：1.氢原子光谱：线状谱、可分为若干线系，常见五个线系（记住名称、顺序）。

广义巴尔末公式)11(~22nm R -=ν、光谱项()2nR n T =、并合原则：)()(~n T m T -=ν 2.玻尔氢原子理论：(1)玻尔三条基本假设的实验基础和内容（记熟）实验基础：⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧氢原子光谱爱因斯坦光量子光电效应普朗克能量子黑体辐射-- 三条假设：⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧=-=ππνϕϕ2h n P 2h P 3E E h E E 2......E E 1j i ij j i 21的整数倍，即等于—电子的角动量—能轨道下列条件的轨道才是可，只有满足电子在绕原子核运动中、角动量量子化条件：系：射，其频率满足如下关子形式发射单色辐的另一定态时，才以光具有较低能量的定态跃迁到子从具有较高能量、频率条件：只有当原会发生辐射。

电子虽有加速度，也不，相对应，在这些定态下、这些定态各与一定能量定状态，存在一系列不连续的稳、定态假设：原子只能(2)圆轨道理论（会推导）：氢原子中假设原子核静止，电子绕核作匀速率圆周运动02200202220A 529,04,Z Z 4≈===e m a n a n e m r e e n πεπε;13714,Z Z 40202≈===c e n c n c e n πεααπευ； ()n hcT n hc R n e m E e n -=-=-=∞22224220Z 2Z )41( πε，n ＝１.2.3……(3)实验验证：（a ）氢原子五个线系的形成)11(Z ~,)4(222232042n m R c h e m R e -==∞∞νπεπ (会推导）非量子化轨道跃迁 )(212n E E mv h -+=∞ν （b ）夫－赫实验：装置、.结果及分析；原子的电离电势、激发电势3.类氢离子（+++Li ,He ,正电子偶素.-μ原子等）(1) He +光谱:毕克林系的发现、波数公式、与氢原子巴耳末系的异同等(2)理论处理（会推导）：计及原子核的运动，电子和原子核绕共同质心作匀速率圆周运动ee m M m M +⋅=μ, 正负电荷中心之距Z e n r n 22204μπε =. 能量2242202Z )41(n e En μπε-=，里德伯常数变化M m R R e A +=∞11重氢（氘）的发现4.椭圆轨道理论索末菲量子化条件,q q pdq n h n =⎰ 为整数 a n n b n em a n e m E n p e n ϕϕϕπεπε==-==,Z 4,2Z )41(,2220224220 ，n n n ,,3,2,1;,3,2,1 ==ϕn 一定，n E 一定，长半轴一定，有n 个短半轴，有n 个椭圆轨道（状态），即nE 为n 度简并。

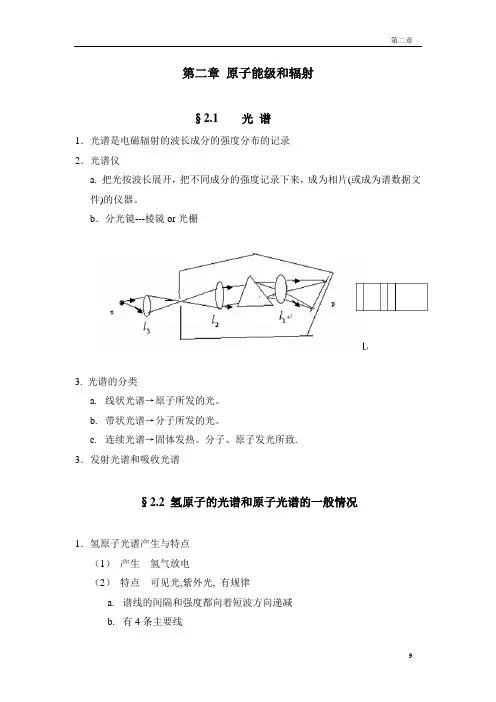
第二章原子能级和辐射§2.1 光谱1．光谱是电磁辐射的波长成分的强度分布的记录2．光谱仪a. 把光按波长展开，把不同成分的强度记录下来，成为相片(或成为谱数据文件)的仪器。

b．分光镜---棱镜or光栅3. 光谱的分类a.线状光谱→原子所发的光。

b.带状光谱→分子所发的光。

c.连续光谱→固体发热。

分子、原子发光所致.3．发射光谱和吸收光谱§2.2 氢原子的光谱和原子光谱的一般情况1．氢原子光谱产生与特点（1）产生氢气放电（2）特点可见光,紫外光, 有规律a.谱线的间隔和强度都向着短波方向递减b.有4条主要线H α 6562.100A , H β 4860.740A H γ 4340.100A , H δ 4101.200AH α H γ H β H δ2. 巴耳末（J.J,.Balmer ）1885年a ．22,3,4,54n B n n λ==⋅⋅⋅- 03645.6B A =,称为巴耳末公式 n 增大,谱线间的间隔减少, n →∞,B λ=,称为系限波长. b ． 1νλ=称为波数2222114411()2n B n B nνλ-==⋅=-2211()3,4,5,2H R n nν=-=⋅⋅⋅7141.0967758*10H R B -==米，称为里德堡(伯)常数 2,2H Rn ν-∞→∞=称为线系限波数３．氢原子光谱的其他谱线系a ． 赖曼系[lyman] 2211(),2,3,4,1H R n nν-=-=⋅⋅⋅b.． 巴耳末系[Balmer] 2211(),3,4,5,2H R n n ν-=-=⋅⋅⋅ c ． 帕形系[ Paschen] 2211(),4,3H R n n ν-=-=⋅⋅⋅ d ． 布喇开系[Brackett] 2211(),5,4H R n n ν-=-=⋅⋅⋅e ． 普丰特系[Pfund] 2211(),6,5H R n n ν-=-=⋅⋅⋅ 普式:①2211()H R m nν-=- 其中：1,2,3,4,m =⋅⋅⋅对于一个m 值,n 可以取如下值:n=m+1,m+2,m+3,… ②光谱项 2()H R T m m =2()HR T n n= ()()T m T n ν-=-规律a ．光谱是线状谱b ．谱线间有一定的关系c ．每一谱线的波数可以表为二光谱之差 结论:所有原子的光谱都具有上述规律§2.3 玻尔的氢原子理论和关于原子的普遍规律原子光谱是如何产生的？从原子光谱规律如何得知原子结构知识? 或者说从解释原子光谱规律可以获得原子的结构知识.一．电子在库仑场中的运动 1. 运动方程库仑力作用,原子核质量远大于电子质量,近似认为核心不动.222014mv ze r r πε= 2．能量原子内部能量=动能+势能 动能 212k E m v =势能 2014p ze E k rπε=-, 0k = r →∞2014p ze E rπε=-222001112442ze ze E mv r rπεπε=-=-3．电子绕核运动频率2vf r π==v =二．经典理论的困难 1. 经典电动力学原理有加速度a 向外辐射能量,且辐射频率=2. 存在的实验事实原子大小1010-m,光谱是线状光谱 3. 经典力学的结论原子大小1410-m ～1510-m ，光谱为连续谱三. 玻尔氢原子理论 1. 理论提出的背景a. 原子大小1010-m, 电子在1010-m 数量级的半径上作稳定轨道运动b. 22R R m n ν-=-是线状光谱 c. 普朗克分析黑体辐射时得出,光的能量是一个单元的整倍数,一个单元是h ν. h —Planck constant=6.6262*3410-J ⋅S, ν---frequency 推测: H 原子:22hcR hcRhc h m nνν==- 左边是能量,右边两项必为能量之差,而且应为辐射前后能量之差.21h E E ν=- 仍采用E 为负值,则: 22h c R E n =-12h c RE m =- 结论: 2h c RE n=-原子能量只能具有一系列的一定数值,分隔,不能连续变化220142ze hcRE r nπε=-=-220142ze r n hcRπε=轨道是分隔的,不连续变化.结论: 从实验事实推知: ⑴.氢原子中的电子只能在一定大小的，彼此分隔的一系列轨道上运动;电子在这样的轨道时,原子具有一定的能量.⑵. 电子从大轨道运动跃迁到小轨道上运动，原子能量就从大变小，多余的能量就放出成为一个光子的能量。

原子物理第2章第三节：玻尔模型从理论上导出里德伯常数：结束目录nextback 氢光谱的解释玻尔假设电子的运动第二章：原子的能级与辐射：玻尔理论第三节：玻尔模型氢原子轨道半径与谱系结束目录nextback氢光谱的解释玻尔假设电子的运动赖曼系n=1n=2n=3n=4n=5r04r09r016r025r0布喇开系巴耳末系帕邢系第二章：原子的能级与辐射：玻尔理论第三节：玻尔模型结束目录nextback氢光谱的解释玻尔假设电子的运动第二章：原子的能级与辐射：玻尔理论第四节：类氢离子光谱结束目录nextback第二章：原子的能级与辐射：玻尔理论毕克林系起初以为是星体上的一种特殊氢，后在实验室中加氦后的氢光谱中观察到，得以确认是氦离子的光谱。

氢光谱类氢光谱第四节：类氢离子光谱结束目录nextba ck第二章：原子的能级与辐射：玻尔理论如果套用玻尔理论，只需要将氢原子理论中的Z改为2，就可得到氦离子的光谱理论公式上式中n1取4，n2取5、6、7、….就与毕克林系规律相同第四节：类氢离子光谱结束目录nextback第二章：原子的能级与辐射：玻尔理论尽管上述结果与观察结果非常一致，但还有一个明显的差别：类氢离子光谱与氢光谱并不完全重合。

这一差别后来被认为是里德伯常数的变化引起的。

考虑原子核的运动，推导出修正后的里德伯常数核的质量有关。

修正后的里德伯常数与观测结果非常一致第四节：类氢离子光谱结束目录nextback第二章：原子的能级与辐射：玻尔理论里德伯常数受核的质量影响的理论曾被用来证实氢的同位素-氘-的存在。

起初有人从原子质量测定估计有原子量为2的氢存在，但如存在，含量应很低，一时难以确认。

1932年尤雷（HCUre y），观察到类氢光谱，通过质量修正，能很好得到解释。

从而确认氘-的存在。

第四节：类氢离子光谱结束目录nextback第二章：原子的能级与辐射：玻尔理论玻尔理论非常成功地解释了氢、类氢离子光谱的规律，一度被人们广泛接受。