拓扑图形
- 格式:pptx
- 大小:291.02 KB
- 文档页数:11

图形拓扑基础1图元这里的图元指的是具有拓扑的图元。
1.1端点(Terminal)图元具有一个或多个端点。
常见的图元和端点如下:1.2设备(Equipment)除了连接连以为,我们都可以认为一个图元就是一个设备。
1.3连接点(ConnectivityNode)连接点,用于连接不同的图元。
一般一个连接点,包含了两个或两个以上的不同设备的端点2拓扑系统拓扑系统是由拓扑设备和节点组成的。
而拓扑设备和节点来源于一张或多张图形。
拓扑设备之间是通过节点关联在一起。
2.1拓扑设备在拓扑图元中,主要分为两类:连接线类、设备类、非设备类。
我所说的拓扑设备一般指,设备类图元。
拓扑设备具有的属性:✧设备性质:电源、地刀、断路器、刀闸等。
✧端点关联节点:指明连接到哪些节点上。
2.2节点结点是用来连接两个或多个端点,图元和图元之间是通过结点连接在一起,习惯上也叫“节点”。
在配网系统中,有时为了提供速度,进行了优化处理:将多个“小节”,点融合一个大“节点”。
节点具有的属性:✧节点编号(ID)✧关联设备端点:连接到哪些拓扑设备上。
2.3配网优化在配网系统中,图元的数量是非常庞大的,目前碰到最大的数据是厦门思明配网,图元数达到仅2,000,000个。
按照一般情况下,拓扑系统是极其庞大,运算速度会受到很大的影响。
在这种情况下,必须进行优化,原则是将小节点糅合成大节点:✧连接线或连接在一起的多条连接线,都归入同一个节点。
✧配网不关系的设备,当通路处理,归入连接线所在的节点。
在接线图的众多图元中,有些是配网关心的,例如:断路器、刀闸、地刀、变压器、用户变、电缆头等;有些则是配网不关心的,例如:电容器、电抗器等。
2.4拓扑模型示例2.4.1接线图2.4.2拓扑模型2.4.3拓扑优化模型3单图拓扑单个图形的拓扑,如:拓扑优化模型4多图拓扑4.1图形接口4.2镜像和原型。


局域网拓扑图局域网拓扑图(Local Area Network Topology),是指在一个局域网中各个网络设备之间的连接方式和结构方式的图示表示。
拓扑图可以帮助网络管理员和工程师清晰地了解局域网的网络架构,并且为网络的设计、维护和故障排除提供指导。
本文将就局域网拓扑图的定义、优点、常见拓扑结构和实例进行讨论。
定义局域网拓扑图是用图形化的方式展示局域网中各个网络设备(如服务器、交换机、路由器、终端设备等)之间的物理连接关系和逻辑通信方式的一种图示表示。
通过拓扑图,我们可以清楚地看到设备之间的连接方式、传输路径以及数据流动的方向。
拓扑图还可以显示设备的名称、IP地址、MAC地址等信息,有助于快速定位故障和进行网络管理。
优点拓扑图具有以下优点:1. 可视化:拓扑图通过图形化的方式表达网络设备之间的连接关系,使得复杂的网络结构一目了然,方便网络管理员和工程师快速理解和管理网络。
2. 故障排除:通过拓扑图,我们可以清楚地看到网络中的哪些设备之间存在故障,从而有针对性地进行故障排除,提高网络的可靠性和稳定性。
3. 规划设计:在局域网升级或者新建网络时,拓扑图可以帮助规划和设计整个网络架构,包括设备的布局、选型以及连接方式等,提高网络的可扩展性和性能。
4. 安全性:拓扑图可以帮助管理员和工程师识别潜在的安全隐患,比如网络中可能存在的盲区、冗余路径等,从而采取相应措施提高网络的安全性。
常见拓扑结构局域网拓扑图常见的结构包括星型拓扑、总线型拓扑、环型拓扑和混合型拓扑等。
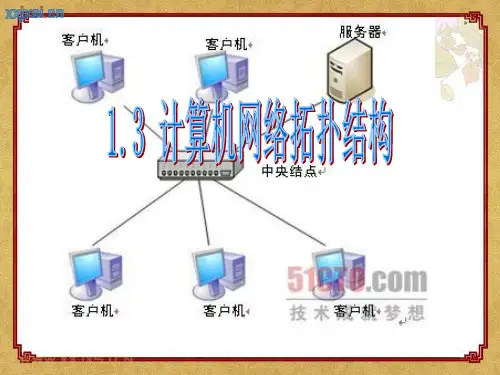
星型拓扑是最常见的拓扑结构之一,将所有的终端设备都连接到一个中心设备(如交换机或者集线器)上。
这样做的好处是易于管理和故障排除,但是如果中心设备发生故障,整个网络将受到影响。
总线型拓扑是将所有的终端设备都连接到一条主干线上,所有设备共享同一条传输介质。
这种结构简单易部署,但是如果主干线发生故障,整个网络将瘫痪。
环型拓扑是将所有的终端设备按照顺序连接成一个环状结构,每个设备都连接两台相邻设备。

拓扑结构图所谓拓扑学(TOPOLOGY)是一种研究与大小、距离无关的几何图形特性的方法。
网络拓扑是由网络节点设备和通信介质构成的网络结构图。
在选择拓扑结构时,主要考虑的因素有:安装的相对难易程度、重新配置的难易程度、维护的相对难易程度、通信介质发生故障时,受到影响的设备的情况.一.基本术语1.节点节点就是网络单元。
网络单元是网络系统中的各种数据处理设备、数据通信控制设备和数据终端设备。
节点分为:转节点,它的作用是支持网络的连接,它通过通信线路转接和传递信息;访问节点,它是信息交换的源点和目标。
2.链路链路是两个节点间的连线。
链路分“物理链路”和“逻辑链路”两种,前者是指实际存在的通信连线,后者是指在逻辑上起作用的网络通路。
链路容量是指每个链路在单位时间内可接纳的最大信息量。
3.通路通路是从发出信息的节点到接收信息的节点之间的一串节点和链路。
也就是说,它是一系列穿越通信网络而建立起的节点到节点的链路.二.常见的网络拓扑结构1.星型结构星型结构的优点是结构简单、建网容易、控制相对简单。
其缺点是属集中控制,主节点负载过重,可靠性低,通信线路利用率低。
一个星型拓扑可以隐在另一个星型拓扑里而形成一个树型或层次型网络拓扑结构。
相对其他网络拓扑来说安装比较困难,比其他网络拓扑使用的电缆要多。
容易进行重新配置,只需移去、增加或改变集线器某个端口的连接,就可进行网络重新配置。
由于星型网络上的所有数据都要通过中心设备,并在中心设备汇集,星型拓扑维护起来比较容易。
受故障影响的设备少,能够较好地处理。
2.总线结构总线结构是比较普遍采用的一种方式,它将所有的入网计算机均接入到一条通信线上,为防止信号反射,一般在总线两端连有终结器匹配线路阻抗,总线结构的优点是信道利用率较高,结构简单,价格相对便宜。
缺点是同一时刻只能有两个网络节点相互通信,网络延伸距离有限,网络容纳节点数有限。
在总线上只要有一个点出现连接问题,会影响整个网络的正常运行。






各种图(流程图,思维导图,UML,拓扑图,ER图)简介流程图1.定义:流程图是对过程、算法、流程的一种图像表示,在技术设计、交流及商业简报等领域有广泛的应用。
2.案例3.计算机语言只是一种工具。
光学习语言的规则还不够,最重要的是学会针对各种类型的问题,拟定出有效的解决方法和步骤即算法。
有了正确而有效的算法,可以利用任何一种计算机高级语言编写程序,使计算机进行工作。
因此,设计算法是程序设计的核心。
对同一个问题,可以有不同的解题方法和步骤。
例如,求1+2+3+…+100,可以先进行1+2,再加3,再加4,一直加到100,也可采取100+(1+99)+(2+98)+…+(49+51)+50=100+50+49×100=5050。
还可以有其它的方法。
当然,方法有优劣之分。
有的方法只需进行很少的步骤,而有些方法则需要较多的步骤。
一般说,希望采用方法简单,运算步骤少的方法。
因此,为了有效地进行解题,不仅需要保证算法正确,还要考虑算法的质量,选择合适的算法。
一个计算问题的解决过程通常包含下面几步:a.确立所需解决的问题以及最后应达到的要求。
必须保证在任务一开始就对它有详细而确切的了解,避免模棱两可和含混不清之处。
b.分析问题构造模型。
在得到一个基本的物理模型后,用数学语言描述它,例如列出解题的数学公式或联立方程式,即建立数学模型。
c.选择计算方法。
如定积分求值问题,可以用矩形法、梯形法或辛普生法等不同的方法。
因此用计算机解题应当先确定用哪一种方法来计算。
专门有一门学科“计算方法”,就是研究用什么方法最有效、最近似地实现各种数值计算的,换句话说,计算方法是研究数值计算的近似方法的。
d.确定算法和画流程图。
在编写程序之前,应当整理好思路,设想好一步一步怎样运算或处理,即为“算法”。
把它用框图画出来,用一个框表示要完成的一个或几个步骤,它表示工作的流程,称为流程图。
它能使人们思路清楚,减少编写程序中的错误。
⽹络拓扑图是⼀种什么图?有什么⽤?拓扑图是指由计算机、打印机、⽹络设备以及其他设备构成的⽹络结构图,⼜称为拓扑结构图,简单来说就是⽤图⽰的⽅式将实物的连接⽅式表现出来。
拓扑图可以简单地分为物理拓扑和逻辑拓扑两种。
物理拓扑是指⽤线缆构成的物理连接;逻辑拓扑是在物理拓扑的基础上实现通信。
拓扑图⽬的是⽤图形传递量化信息,让数量的对⽐更加直观,易于绘制,是⼀种量化图的有效表现形式。
拓扑图常见⽤途拓扑图常见的⽤途有两种:⼀是⽤于电脑⽹络的管理:不考虑电脑的实际位置,只是单纯的表⽰⽹络中的计算机与⽹络设备之间的关系。
⼆是择优或淘汰配置⽅案,减少在思维导图当中不具备操作性的⽅案。
拓扑图模板套⽤⽅法在绘制拓扑图的时候,直接套⽤模板⽆异是⼀种最为简单有效的绘制⽅法。
通过亿图图⽰(Edraw Max),只需简单地⼏步操作,就可以轻松绘制出⼀幅专业实⽤的拓扑图。
第⼀步:登录亿图图⽰官⽹,下载“”软件,或者直接访问在线版亿图图⽰,开始作图。
第⼆步:新建“⽹络拓扑图”。
登录软件或进⼊在线版后依次点击“新建”-“软件/计算机”-“⽹络图”-“拓扑图”,也可直接在搜索栏中检索“拓扑图”,即可从多种类型的图⽰模板中选择⼀个你所需要的模板,双击⿏标左键打开。
第三步:⿏标点击画布中的拓扑图,然后在左侧的属性⾯板中点击思维导图,添加中⼼主题,然后插⼊程序框。
第四步:直接双击⽂本框,替换模板中需要更改的⽂字。
第五步:完成⽹络拓扑图的绘制后,可根据需要点击左侧的保存(快捷键Ctrl S)、下载、打印、分享等按钮。
绘制好的⽹络图还可以储存为各种图⽚格式并导出,除此之外和可以导出为PDF或者是PPT。
拓扑图绘制软件——亿图图⽰是⼀款适⽤于办公,战略规划等的综合办公绘图软件,软件内部含260多种绘图类型,⽽且界⾯简洁,有海量模板素材可以帮助你轻松快速的绘制⽹络拓扑图、思维导图、流程图等图形,可以有效提⾼你的⼯作效率。
亿图图⽰兼容Windows、Mac以及Linux系统平台,如果没有亿图图⽰软件,也可以进⼊亿图官⽹启动亿图在线版作图。
有趣的拓扑学现象嘿,大家好啊!今天咱来聊聊有趣的拓扑学现象。
啥是拓扑学呢?哎呀,其实我一开始也不太明白,后来慢慢了解了一些,才发现这玩意儿还挺有意思的。
简单来说呢,拓扑学就是研究图形在变形过程中不变的性质。
比如说,一个甜甜圈和一个咖啡杯,从拓扑学的角度来看,它们是一样的哦!惊不惊喜,意不意外?我记得有一次,我和朋友去参加一个科普活动。
活动现场有个老师拿着一个橡胶圈,给我们演示拓扑学现象。
他把橡胶圈扭了几下,然后就变成了一个奇奇怪怪的形状。
我们都看得目瞪口呆,这也太神奇了吧!老师还说,这就是拓扑学的魅力,它能让我们看到一些平时看不到的东西。
还有一个很有趣的拓扑学现象,就是莫比乌斯带。
这玩意儿可好玩了。
你知道吗?莫比乌斯带只有一个面和一条边。
听起来很不可思议吧?我自己也动手做了一个莫比乌斯带。
我拿了一张纸条,把一端扭转 180 度,然后再和另一端粘起来。
哇,真的就变成了一个只有一个面和一条边的神奇带子。
我拿着铅笔在上面画,一直画一直画,居然能把整个带子都画满,而且不会重复。
这可把我乐坏了。
另外,还有一个叫克莱因瓶的东西。
这瓶子也很神奇哦!它没有内外之分。
就好像一个瓶子被打通了,然后把里面和外面连在了一起。
我在网上看到过克莱因瓶的图片,那形状真的很奇特。
我就想啊,要是有一个真正的克莱因瓶,那该多好玩啊!可以把东西放进去,然后不知道会从哪里出来呢。
拓扑学现象真的很有趣,它让我们看到了世界的奇妙之处。
虽然有时候我们可能不太理解那些复杂的理论,但是通过一些简单的实验和演示,我们也能感受到拓扑学的魅力。
说不定哪天,我们在生活中也能发现一些有趣的拓扑学现象呢。
嘿嘿,到时候可就有的玩了。
总之啊,拓扑学虽然有点神秘,但也很有趣。
大家有时间可以去了解了解,说不定会给你带来很多惊喜哦!好啦,今天就聊到这里吧。
下次有好玩的事儿,再跟大家分享。
拜拜!。
拓扑几何学摘要:一、拓扑几何学简介1.拓扑几何学的定义2.拓扑几何学的发展历程二、拓扑几何学的基本概念1.拓扑不变量2.连续映射3.拓扑空间三、拓扑几何学的应用1.计算机科学中的拓扑几何学2.物理学中的拓扑几何学3.生物学中的拓扑几何学四、拓扑几何学的前沿研究1.拓扑几何学在数学领域的发展2.拓扑几何学与其他领域的交叉研究正文:拓扑几何学是一门研究几何图形在其形状发生改变时,哪些性质保持不变的数学分支。
它的研究对象包括各种形状的曲线、面和空间,主要关注它们的连续性、收缩和变形等性质。
拓扑几何学在数学、计算机科学、物理学和生物学等领域有着广泛的应用。
拓扑几何学的发展历程可以追溯到古希腊时期,当时的数学家开始研究各种形状的性质。
然而,拓扑几何学作为一个独立的数学分支,是在20 世纪初随着数学研究的深入而逐渐形成的。
如今,拓扑几何学已经成为数学领域中一个重要的研究方向。
在拓扑几何学中,有三个基本概念:拓扑不变量、连续映射和拓扑空间。
拓扑不变量是用来描述几何图形性质的量,如曲线的扭结数、面的亏格等。
连续映射是一个保持拓扑性质的映射,即在映射过程中,图形的拓扑结构不会发生改变。
拓扑空间则是一个具有拓扑性质的集合,其中的元素具有连续性、收缩和变形等性质。
拓扑几何学在许多领域都有广泛的应用。
在计算机科学中,拓扑几何学可以用于图像处理、数据分析和机器学习等领域。
在物理学中,拓扑几何学可以用于描述各种物理现象,如流体力学、电磁学和量子力学等。
在生物学中,拓扑几何学可以用于研究生物分子、细胞和组织的形状和结构。
近年来,拓扑几何学在数学领域的发展越来越快。
一方面,拓扑几何学与其他数学分支的交叉研究取得了丰硕的成果;另一方面,拓扑几何学在物理学、计算机科学等领域的新应用也不断涌现。