总结和分类Mathematica的画图功能

总结和分类Mathematica的画图功能——数学应用软件设计实验报告实验目的：近一步了解和掌握Mathematica的画图功能。

实验内容：对Mathematica的所有画图函数或命令进行总结和分类（对它的一些重要可选项进行说明），并画出一些有趣的图形。

实验环境：Mathematica4.0实验结果：基本作图函数1.画点函数 Point[x,y]2.画线函数 Line[x1,y1,x2,y2]3.画圆函数 Circle[x,y,r]4.画矩形函数 Rectangle5.画多边形函数 Ploygon6.字符输出函数 Text[字符串，输出坐标]7.画离散点图1.绘出由离散点对(n,yn)组成的图 ListPlot[{y1,y2,..}]2.绘出由离散点对(xn,yn)组成的图 ListPlot[{{x1,y1},{x2,y2},..}]3.二维数据阵array的立体高度图 ListPlot3D[array]4.根据可选项，把数据点dd在平面上画出来 ListPlot[dd，选项]画二维函数图像1.标准二维函数作图Plot[函数f，{x,xmin,xmax}，选项]：在区间{x,xmin,xmax}上，按选项的要求画出函数f的图形Plot[{函数1,函数2,…}，{x,xmin,xmax}，选项]：在区间{x,xmin,xmax}上，按选项的要求画出几个函数的图形2.二维参数方程作图ParametricPlot[{x[t]，y[t]}，{t,t0,t1}，选项]：画一个X轴、Y轴坐标为{x[t]，y[t]}，参变量t在[t0，t1]中的参数曲线3.二维等高线图ContourPlot[f[x,y]，{x,x0,x1}，{y,y0,y1}，选项]：画出空间曲面f[x,y]在区域x∈[x0,x1]和y∈[y0,y1]上的等高线图4.二维密度图DensityPlot[f[x,y]，{x,x0,x1}，{y,y0,y1}，选项]：画出空间曲面f[x,y]在区域x∈[x0,x1]和y∈[y0,y1]上的密度图5.二维极坐标方程作图PolarPlot[r[t]，{t,min,max}，选项]：按选项的要求画出极坐标方程为r=r(t)的图形（需要先打开作图软件包，输入“<<Graphics`Graphics`”）6.二维隐函数方程作图ImplicitPlot[隐函数方程，自变量范围，选项]：按选项的要求画出隐函数的方程确定的函数图形（需要先打开作图软件包，输入“<<Graphics`ImplicitPlot`”）画三维函数图像1.标准三维函数作图Plot3D[f[x,y]，{x,x0,x1}，{y,y0,y1}，选项]：在区域x∈[x0,x1]和y∈[y0,y1]上，画出空间曲面f[x,y]2.三维参数方程作图ParametricPlot3D[{x[u,v],y[u,v],z[u,v]}，{u,u0,u1}，{v,v0,v1}，可选项]：画一个X轴坐标为x[u,v]、Y轴坐标为y[u,v]、Z轴坐标为z[u,v]，参变量u在[u0,u1]、v在[v0,v1]中的参数曲面重要可选项1.AspectRatio：设定图形的宽高比2.PlotStyle：确定所画图形的线宽、线形、颜色等特性，如（1）RGBColor[r,g,b]使曲线采用某种颜色（2）GrayLevel[gray]描述颜色的灰度（3）PointSize[相对尺度]表示点的大小（4）Thickness[相对尺度]表示线的宽度3.PlotPoint：设定计算机描点作图时在每个单位长度内取的点数4.PlotRange：表示作图的值域5.PlotLabel：在图形上方居中加注释6.Axes：指定是否显示坐标轴7.AxesLabel：在坐标轴上做标记8.AxesOrigin：指定两个坐标轴的交点位置9.AxesStyle：设定坐标轴的颜色、线宽等选项10.Ticks：给坐标轴加上刻度或给坐标轴上的点加上标记11.GridLinese：用于加网格线12.Background：用于指定背景颜色13.DisplayFunction：指定如何显示图形趣味图形举例二维：Plot[{Sin[x]+Sin[1.6 x],-Sin[x]-Sin[1.6 x]},{x,0,40}]ParametricPlot[{Cos[5 t],Sin[3 t]},{t,0,2 Pi},AspectRatio->Automatic}]<<Graphics`Graphics`PolarPlot[Sin[4 t],{t,0,2 Pi}]ParametricPlot[{t Cos[t],t Sin[t]},{t,0,4 Pi},PlotPoints->250,AspectRatio-> Automatic]<<Graphics`Graphics`PolarPlot[Sin[1000 t],{t,0,2 Pi}]ContourPlot[x^2-y^2,{x,-1,1},{y,-1,1}]ContourPlot[Cos[x y],{x,-5,5},{y,-5,5}]ContourPlot[Sin[x y],{x,-5,5},{y,-5,5},ContourLines->False]Plot[Evaluate[Table [BesselJ[n,x],{n,4}]],{x,0,100}]三维：Plot3D[Sin[x y],{x,0,4},{y,0,4},PlotPoints->40,Mesh->False,FaceGrids->All, AxesIabel->{“Length”, “Width”, “Height”}]Plot3D[Sin[x y] Cos[x y],{x,0,4},{y,0,4},PlotPoints->30]Plot3D[Tan[x y],{x,0,4},{y,0,4},PlotPoints->30]}ParametricPlot3D[{Sin[t],Sin[2 t] Sin[u],Sin[2 t] Cos[u]},{t,-Pi/2, Pi/2},{u,0,2 Pi},Ticks->None]ParametricPlot3D[{Cos[5 t],Sin[3 t],Sin[t]},{t,0,2 Pi}]ParametricPlot3D[{Cos[u] Sin[v],Sin[u] Sin[v],Cos[v]+Log[Tan[v/2]]+0.1*u},{u,0,4Pi},{v,0.001,1},PlotPoints->{64,32}]ParametricPlot3D[{Cos[t](3+Cos[u]),Sin[t](3+Cos[u]),Sin[u]},{t,0,2Pi},{u,0,2Pi}]实验中出现的问题及解决方法：早期图形举例前面的命令都是由Mathematica 4里面的命令直接粘贴到文档中，但是在打印的过程中，这些命令无法正常显示，猜想出现这种情况可能与打印分辨率或者连接打印机的电脑未安装Mathematica软件有关。

mathmatic 基本用法Mathematica是一种强大的数学软件，它具有广泛的数学计算和可视化功能。

基本用法包括使用Mathematica进行数学运算、求解方程、绘制图表等。

1.数学运算：Mathematica可以进行基本的数学运算，如加减乘除、幂运算、三角函数、对数函数等。

例如，可以输入"2+3"得到结果"5"，输入"Sin[π/2]"得到结果"1"。

2.方程求解：Mathematica可以求解各种类型的方程。

例如，可以输入"Solve[x^2 - 3x + 2 == 0, x]"来求解这个二次方程，得到结果"x == 1 || x == 2"。

3.符号计算：Mathematica可以进行符号计算，包括展开、化简、因式分解等。

例如，可以输入"Simplify[(x^2 + x - 6)/(x + 3)]"来化简这个表达式，得到结果"x - 2"。

4.绘图功能：Mathematica可以生成各种类型的图表，包括二维曲线图、三维曲面图、柱状图、散点图等。

例如，可以输入"Plot[Sin[x], {x, 0, 2π}]"来绘制正弦函数的曲线图。

除了基本用法外，Mathematica还有许多其他功能，如矩阵计算、微积分、概率统计、符号推导、动态演示等。

它还提供了大量的内置函数和算法，可以用于求解复杂的数学问题。

使用Mathematica还可以进行科学计算、工程计算、数据分析等各种应用领域。

总之，Mathematica是一款功能强大的数学软件，可以帮助用户进行各种数学计算和可视化操作。

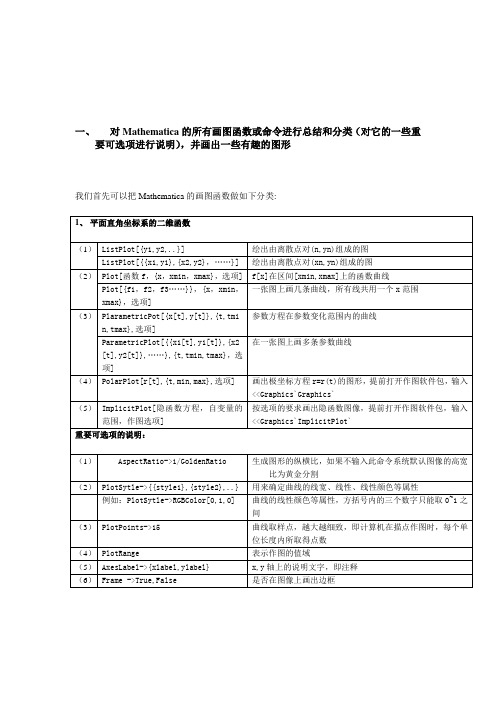
一、对Mathematica的所有画图函数或命令进行总结和分类（对它的一些重要可选项进行说明），并画出一些有趣的图形我们首先可以把Mathematica的画图函数做如下分类:有趣的图形：1、2、三、（1） 这是一个兔子繁殖的模型，一对子兔一个月后成为一对成兔，而成年兔每个月能繁殖一对子兔，这样下去，每个月统计一下成年兔的数目，有如下的关系：月份： 1 2 3 4 5 6 7 8 …… Fn ： 1 1 2 3 5 8 13 21 …… 不难看出：2121;1;1--+===n n n F F F F F 。

这就是著名的裴波那奇数列。

通过数学软件编程，请问第40年、80年有多少成年兔？你能给出几种求裴波那奇数列通项的方法。

满足21--+=n n n F F F 的数列完全由前两项决定，既由向量),(21F F 决定，能否利用线性代数中的子空间和向量线性表示的理论给出它的通项的一种求法。

（2）雌鸟每年只育一只小雌鸟，次年各自又育一只雌鸟，每鸟只能育十次。

请问第30年、100年有多少雌鸟？你能求出第n 年有多少雌鸟吗（通项）？（设鸟都不死）解：（1）、第40年的成年兔： 第80念得成年兔：求斐波那契数列通项的方法： 方法一、（向量线性表示）已知数列： A 0=a ，A 1=b ， F[n+1]=c*F[n]+d*F[n-1] （a=b=c=d1时就是斐波那契数列） 求F[n]的表达式解：这个数列经过整理后可得一个F[n]与F[n-1]的线性组合，即A*F[n]+B*F[n-1]是一个等比数列的形式 令 F[n+1]- k F[n]=p(F[n] - k F[n-1])————————————————————-(1）这样 如果令B[n+1]=F[n+1] – k F[n]，则B[n]（n=1, to n) 是一个等比数列。

(1）=> F[n+1]= p F[n]+k F[n] –pk F[n-1]和 F[n+1]=c*F[n]+d*F[n-1] 比较，可知有 p+k=c ，pk=-d 这样知道 p 和 k 是 x^2 - cx -d=0 的两个根。

mathematica 画函数Mathematica 是一款功能强大的数学软件，可以用于绘制各种函数图形。

下面我将用中文回答您的问题，并且提供超过1200字的解答。

首先，我们需要了解如何使用Mathematica 进行函数绘图。

Mathematica 支持使用Plot 函数来绘制函数图形。

Plot 函数的基本语法为：Plot[f, {x, xmin, xmax}]其中，f 表示要绘制的函数表达式，x 表示自变量，xmin 和xmax 分别表示自变量的取值范围的起始值和结束值。

例如，我们要绘制函数y = x^2，可以使用以下命令：Plot[x^2, {x, -5, 5}]这将绘制出一个函数y = x^2 在x 取值范围为-5 到5 的图形。

Mathematica 还支持在同一张图中绘制多个函数。

可以使用Plot 函数的多个参数来实现。

以下是一个例子：Plot[{x^2, Sin[x]}, {x, -5, 5}]这将同时绘制出函数y = x^2 和函数y = sin(x) 在同一张图中。

除了基本的函数绘制，Mathematica 还支持对函数进行自定义，包括添加标题、坐标轴标签、网格线等。

例如，我们可以使用以下命令添加标题和坐标轴标签：Plot[x^2, {x, -5, 5}, PlotLabel -> "函数图形", AxesLabel -> {"x", "y"}]这将在图形上添加一个标题为“函数图形”，并且在坐标轴上添加x 轴和y 轴的标签。

此外，Mathematica 还支持对函数图形进行进一步的定制，如改变线条颜色、线型、添加图例等。

例如，我们可以使用以下命令改变函数y = x^2 的线条颜色为红色，并添加一个图例：Plot[{x^2, Sin[x]}, {x, -5, 5}, PlotStyle -> {Red, Green},PlotLegends -> {"y = x^2", "y = sin(x)"}]这将绘制出函数y = x^2 为红色，函数y = sin(x) 为绿色，并且在图形中添加一个图例，用于区分这两个函数。

Mathematica绘图总结Mathematica是一个强大的数学工具，它可以广泛应用到数学的各个领域中。

而Mathematica的绘图以其丰富的形式，多样的变化，鲜明的色彩给人以直观的视觉感受，并加深我们对抽象的数学的直观理解。

·二维作图1 基本绘图命令Plot[f,{x,xmin,xmax}，选项]：f[x]在区间[xmin,xmax]上的函数曲线Plot[{fl, f2..},{x,xmin,xmax}，选项]：在同一图形上画几条曲线ListPlot[{y1,y2,..}]：绘出由离散点对(n，yn)组成的图ListPlot[{{x1,y1},{x2,y2},}}：绘出由离散点对(xi,yi)组成的图ParametricPlot[{fx,fy}，{t,tmin,tmax}]：由参数方程在参数变化范围内产生的曲线2常用选项Plot 函数的选项，告诉系统如何显示图形，以及对坐标轴、刻度等细节的处理等。

PlotRange：作图显示的值域范围AspectRatio：图形的纵横比PlotLabel->label：标题文字Axes：分别制定是否画x,y轴AxesLabel->{xlabel,ylabel}：x,y轴上的说明文字AxesOrigin->{x,y}：坐标轴原点位置Frame：是否画边框FrameLabel->{xmlabel,ymlabel,xplabel,yplabel}：边框四边上的文字Ticks：设置坐标轴上刻度的位置lotsytle->{{style1}，{style2},..}：曲线的线性颜色等属性PlotPoints：曲线取样点，越大越细致·三维作图1 基本绘图命令Plot3D[f,{x,xmin,xmax}，{y,ymin,ymax}，选项]：二维函数flx,y]的空间曲面ListPlot3D[array]：二维数据阵array的立体高度图ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}]：三维参数图形ContourPlot[f,{x,xmin,xmax}，{y,ymin,ymax}]：二维函数f在指定区间上的等高线图2常用选项Axes：是否包括轴PlotLabel：在轴上加标志PlotLabel：设置x,y,z 轴的标志AspectRatio：图形的高度与宽度之比ViewPoint：观察曲面所在的点，可以设定任何观察点Boxed True：是否在曲面周围加立体框BoxRatios：三维立体边长比率·等值线图和密度图ContourPlot [f[x,y],{x,xmin,xmax},{y,ymin,ymax},选项]：等值线图Densityplot [f[x,y],{x,xmin,xmax},{y,ymin,ymax},选项]：密度图·用图形元素绘图Point [{x, y}]：点的位置在{x,y}，x 和y 为坐标值Line [{{x1,y1}, {x2,y2},…}]：依次连接相邻两点的线段Rectangle [{xmin,ymin}, {xmax,ymax}]：以{xmin,ymin}和{xmax,ymax}为对角线坐标的填实矩形Polygon [{x1,y1}, {x2,y2},…]：以{x1,y1},{x2,y2},…为顶点的封闭多边形Raster [{{a11,a12,…}, {a21,a22,…},…}]：灰度颜色的矩阵Circle [{x,y}, r]：圆心在{x,y},半径为r 的圆Circle [{x,y}, {rx,ry}]]：圆心在{x,y}, 长短半轴为rx和ry的椭圆Circle [{x,y}, r, {t1,t2}]：从弧度t1 到弧度t2 的圆弧Circle [{x,y}, {rx,rt}, {t1,t2}]：从弧度t1 到弧度t2 的椭圆弧Disk [{x,y}, r]：圆心在{x,y},半径为r 的填实圆Point[{x,y,z}]：点{x,y,z}Line[{{x1,y1,z1},{x2,y2,z2},…}]：通过点{x1,y1,z1},{x2,y2,z2},…的线Pol ygon[{{x1,y1,z1},{x2,y2,z2},…}]：具有指定角的填实多边形Cuboid[{x0,y0,z0},{x1,y1,z1}]：以{x0,y0,z0}和{x1,y1,z1}为对角线的立方体Text [expr,{x,y,z}]：在{x,y,z}处的文本·图形显示Show[graphics,options]：显示一组图形对象，options为选项设置Show[g1，g2…]：在一个图上叠加显示一组图形对象GraphicsArray[{g1，g2,...}]：在一个图上分块显示一组图形对象SelectionAnimate[notebook,t]：把选中的notebook中的图画循环放映·着色及其他GrayLevel[level]：灰度level为0~1间的实数RGBColor[red，green，blue]：RGB颜色，均为0~I间的实数Hue[h，s，b]：亮度，饱和度等，均为0~1间的实数CMYKColor[cyan，magenta,yellow,block]：CMYK颜色Thickness[r]：设置线宽为rPointSize[d]：设置绘点的大小Dashing[{r1, r2...}]画一个单元的间隔长度的虚线ImageSize->{x，y}：显示图形大小(单位为像素)总结：Mathematica中作图的命令繁多复杂，我们要将这些命令熟练掌握，灵活运用，才能做出精美的图案。

Mathematica绘图总结第一篇：Mathematica绘图总结Mathematica绘图总结Mathematica是一个强大的数学工具，它可以广泛应用到数学的各个领域中。

而Mathematica的绘图以其丰富的形式，多样的变化，鲜明的色彩给人以直观的视觉感受，并加深我们对抽象的数学的直观理解。

·二维作图基本绘图命令Plot[f,{x,xmin,xmax}，选项]：f[x]在区间[xmin,xmax]上的函数曲线Plot[{fl, f2..},{x,xmin,xmax}，选项]：在同一图形上画几条曲线ListPlot[{y1,y2,..}]：绘出由离散点对(n，yn)组成的图ListPlot[{{x1,y1},{x2,y2},}}：绘出由离散点对(xi,yi)组成的图ParametricPlot[{fx,fy}，{t,tmin,tmax}]：由参数方程在参数变化范围内产生的曲线2常用选项Plot 函数的选项，告诉系统如何显示图形，以及对坐标轴、刻度等细节的处理等。

PlotRange：作图显示的值域范围AspectRatio：图形的纵横比PlotLabel->label：标题文字 Axes：分别制定是否画x,y轴AxesLabel->{xlabel,ylabel}：x,y轴上的说明文字AxesOrigin->{x,y}：坐标轴原点位置 Frame：是否画边框FrameLabel->{xmlabel,ymlabel,xplabel,yplabel}：边框四边上的文字 Ticks：设置坐标轴上刻度的位置lotsytle->{{style1}，{style2},..}：曲线的线性颜色等属性PlotPoints：曲线取样点，越大越细致·三维作图基本绘图命令 Plot3D[f,{x,xmin,xmax}，{y,ymin,ymax}，选项]：二维函数flx,y]的空间曲面ListPlot3D[array]：二维数据阵array的立体高度图ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}]：三维参数图形ContourPlot[f,{x,xmin,xmax}，{y,ymin,ymax}]：二维函数f在指定区间上的等高线图2常用选项Axes：是否包括轴PlotLabel：在轴上加标志PlotLabel：设置x,y,z 轴的标志AspectRatio：图形的高度与宽度之比ViewPoint：观察曲面所在的点，可以设定任何观察点Boxed True：是否在曲面周围加立体框 BoxRatios：三维立体边长比率·等值线图和密度图ContourPlot [f[x,y],{x,xmin,xmax},{y,ymin,ymax},选项]：等值线图 Densityplot [f[x,y],{x,xmin,xmax},{y,ymin,ymax},选项]：密度图·用图形元素绘图Point [{x, y}]：点的位置在{x,y}，x 和y 为坐标值 Line [{{x1,y1}, {x2,y2},…}]：依次连接相邻两点的线段Rectangle [{xmin,ymin}, {xmax,ymax}]：以{xmin,ymin}和{xmax,ymax}为对角线坐标的填实矩形Polygon [{x1,y1}, {x2,y2},…]：以{x1,y1},{x2,y2},…为顶点的封闭多边形Raster [{{a11,a12,…}, {a21,a22,…},…}]：灰度颜色的矩阵Circle [{x,y}, r]：圆心在{x,y},半径为r 的圆Circle [{x,y}, {rx,ry}]]：圆心在{x,y}, 长短半轴为rx和ry的椭圆Circle [{x,y}, r, {t1,t2}]：从弧度t1 到弧度t2 的圆弧Circle [{x,y}, {rx,rt}, {t1,t2}]：从弧度t1 到弧度t2 的椭圆弧 Disk [{x,y}, r]：圆心在{x,y},半径为r 的填实圆Point[{x,y,z}]：点{x,y,z} Line[{{x1,y1,z1},{x2,y2,z2},…}]：通过点{x1,y1,z1},{x2,y2,z2},…的线Polygon[{{x1,y1,z1},{x2,y2,z2},…}]：具有指定角的填实多边形Cuboid[{x0,y0,z0},{x1,y1,z1}]：以{x0,y0,z0}和{x1,y1,z1}为对角线的立方体 Text [expr,{x,y,z}]：在{x,y,z}处的文本·图形显示Show[graphics,options]：显示一组图形对象，options为选项设置 Show[g1，g2…]：在一个图上叠加显示一组图形对象GraphicsArray[{g1，g2,...}]：在一个图上分块显示一组图形对象SelectionAnimate[notebook,t]：把选中的notebook中的图画循环放映·着色及其他GrayLevel[level]：灰度level为0~1间的实数RGBColor[red，green，blue]：RGB颜色，均为0~I间的实数Hue[h，s，b]：亮度，饱和度等，均为0~1间的实数CMYKColor[cyan，magenta,yellow,block]：CMYK颜色Thickness[r]：设置线宽为r PointSize[d]：设置绘点的大小Dashing[{r1, r2...}]画一个单元的间隔长度的虚线 ImageSize->{x，y}：显示图形大小(单位为像素)总结：Mathematica中作图的命令繁多复杂，我们要将这些命令熟练掌握，灵活运用，才能做出精美的图案。

总结和分类Mathematica的画图功能一、引言简述Mathematica软件及其在数学和科学计算中的地位强调画图功能在Mathematica中的重要性二、Mathematica画图功能概述Mathematica画图功能的基本特点画图功能与其他数学软件的比较三、基本图形绘制点、线、面的绘制基本几何图形的绘制：圆形、矩形、多边形等四、函数图形绘制一元函数图形的绘制多元函数图形的绘制参数方程和极坐标方程图形的绘制五、数据可视化散点图、折线图、柱状图等常见图表的绘制高级数据可视化技术：热图、树状图、网络图等六、三维图形绘制三维空间中点、线、面的绘制三维函数图形的绘制复杂的三维几何体的绘制七、图形的变换与操作平移、旋转、缩放等图形变换图形的合并、拆分与组合图形的动画与交互八、颜色与样式的应用颜色的选择与应用图形样式的定制样式模板的使用九、图形的标注与解释文本标注、数值标注、符号标注图形的标题、图例、坐标轴标签交互式图形的注释与解释十、高级图形绘制技术隐函数图形的绘制轮廓图、等高线图的绘制动态图形与交互式图形的创建十一、图形的输出与导出图形的屏幕显示与打印图形的导出格式：PDF、EPS、PNG等图形的嵌入与分享十二、Mathematica画图功能的应用案例科学计算中的图形应用工程领域的图形应用教育与教学中的图形应用十三、Mathematica画图功能的局限性与改进当前画图功能的局限性用户反馈与改进建议未来画图功能的发展趋势十四、结语总结Mathematica画图功能的核心优势对Mathematica画图功能的综合评价十五、参考文献列出用于撰写文档的相关文献和资料。

个人整理Mathematica 画图命令集二维作图命令：Plot[f,{x,xmin,xmax}] 一维函数f[x]在区间[xmin,xmax]上的函数曲?Plot[,f2.{f1.},{x,xmin,xmax}] 在一张图上画几条曲线ListPlot[{y1,y2,..}] 绘出由离散点对(n,yn)组成的图ListPlot[{{x1,y1},{x2,y2},..}] 绘出由离散点对(xn,yn)组成的图PlarametricPot[{fx,fy},{t,tmin,tmax}] 由参数方程在参数变化范围内的曲线ParametricPlot[{{fx,fy},{gx,gy},...},{t,tmin,tmax}]在一张图上画多条参数曲线选项：PlotRange->{0,1} 作图显示的值域范围AspectRatio->1/GoldenRatio 生成图形的纵横比PlotLabel ->label 标题文字Axes ->{False,True} 分别制定是否画x,y 轴AxesLabel->{xlabel,ylabel}x,y 轴上的说明文字Ticks->None,Automatic,fun 用什么方式画轴的刻度AxesOrigin ->{x,y} 坐标轴原点位置AxesStyle->{{xstyle}, {ystyle}}设置轴线的线性颜色等属性Frame ->True,False 是否画边框FrameLabel ->{xmlabel,ymlabel,xplabel,yplabel} 边框四边上的文字FrameTicks 同Ticks 边框上是否画刻度GridLines 同Ticks 图上是否画栅格线FrameStyle ->{{xmstyle},{ymstyle}设置边框线的线性颜色等属性ListPlot[data,PlotJoined->True] 把离散点按顺序连线PlotSytle->{{style1},{style2},..}曲线的线性颜色等属性PlotPoints->15 曲线取样点，越大越细致三维作图命令：Plot3D[f,{x,xmin,xmax}, {y,ymin,ymax}] 二维函数f[x,y]的空间曲面Plot3D[{f,s}, {x,xmin,xmax}, {y,ymin,ymax}]同上，曲面的染色由s[x,y]值决定ListPlot3D[array] 二维数据阵array 的立体高度图ListPlot3D[array,shades]同上，曲面的染色由shades[数据]值决定ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}] 二元数方程在参数变化范围内的曲线ParametricPlot3D[{{fx,fy,fz},{gx,gy,gz},...},{t,tmin,tmax}]多条空间参数曲线选项：ViewPoint ->{x,y,z} 三维视点，默认为{1.3,-2.4,2}Boxed -> True,False 是否画三维长方体边框BoxRatios->{sx,sy,sz} 三轴比例BoxStyle 三维长方体边框线性颜色等属性Lighting ->True 是否染色LightSources->{s1,s2..} si 为某一个光源si={{dx,dy,dz},color} color 为灯色，向dx,dy,dz 方向照射AmbientLight->颜色函数慢散射光的光源Mesh->True,False 是否画曲面上与x,y 轴平行的截面的截线MeshStyle 截线线性颜色等属性MeshRange->{{xmin,xmax}, {ymin,ymax}}网格范围ClipFill->Automatic,None,color,{bottom,top}指定图形顶部、底部超界后所画的颜色Shading ->False,True 是否染色HiddenSurface->True,False 略去被遮住不显示部分的信息等高线命令：ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}] 二维函数f[x,y]在指定区间上的等高线图ListContourPlot[array] 根据二维数组array 数值画等高线选项：Contours->n 画n 条等高线Contours->{z1,z2,..} 在zi 处画等高线ContourShading -> False 是否用深浅染色ContourLines -> True 是否画等高线ContourStyle -> {{style1},{style2},..}等高线线性颜色等属性FrameTicks 同上密度图命令：DensityPlot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的密度图ListDensityPlot[array] 同上图形显示命令：Show[graphics,options] 显示一组图形对象，options 为选项设置Show[g1,g2...] 在一个图上叠加显示一组图形对象GraphicsArray[{g1,g2,...}]在一个图上分块显示一组图形对象SelectionAnimate[notebook,t]把选中的notebook 中的图画循环放映选项：(此处选项适用于全部图形函数)Background->颜色函数指定绘图的背景颜色RotateLabel -> True 竖着写文字TextStyle 此后输出文字的字体，颜色大小等ColorFunction->Hue 等把其作用于某点的函数值上决定某点的颜色RenderAll->False 是否对遮挡部分也染色MaxBend 曲线、曲面最大弯曲度图元函数Graphics[prim, options] prim 为下面各种函数组成的表，表示一个二维图形对象Graphics3D[prim, options] prim 为下面各种函数组成的表，表示一个三维图形对象SurfaceGraphics[array, shades]表示一个由array 和shade 决定的曲面对象ContourGraphics[array]表示一个由array 决定的等高线图对象DensityGraphics[array]表示一个由array 决定的密度图对象以上定义图形对象，可以进行对变量赋值，合并显示等操作，也可以存盘Point[p] p={x,y}或{x,y,z}，在指定位置画点Line[{p1,p2,..}]经由pi 点连线Rectangle[{xmin, ymin}, {xmax, ymax}] 画矩形Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}]由对角线指定的长方体Polygon[{p1,p2,..}] 封闭多边形Circle[{x,y},r] 画圆Circle[{x,y},{rx,ry}] 画椭圆，rx,ry 为半长短轴Circle[{x,y},r,{a1,a2}] 从角度a1～a2 的圆弧Disk[{x, y}, r] 填充的园、弧等参数同上Raster[array,ColorFunction->f] 颜色栅格Text[expr,coords] 在坐标coords 上输出表达式PostScript["string"] 直接用PostScript 图元语言写Scaled[{x,y,..}] 返回点的坐标，且均大于0 小于1 颜色函数(指定其后绘图的颜色)GrayLevel[level] 灰度level 为0~1 间的实数RGBColor[red, green, blue] RGB 颜色，均为0~1 间的实数Hue[h, s, b] 亮度，饱和度等，均为0~1 间的实数CMYKColor[cyan, magenta, yellow, black] CMYK 颜色其他函数(指定其后绘图的方式)Thickness[r] 设置线宽为rPointSize[d] 设置绘点的大小Dashing[{r1,r2,..}] 虚线一个单元的间隔长度ImageSize->{x, y} 显示图形大小(像素为单位)ImageResolution->r 图形解析度r个dpi 小(像素为单位)ImageResolution->r 图形解析度r个dpiImageMargins->{{left,right},{bottom,top}}四边的空白ImageRotated->False 是否旋转90 度显示。

Mathematic的函数作图总结一、Mathematic做图总结：随着数学的计算技术不断地发展，出现了许多优秀的数学软件。

使用这些数学软件，可以大大地提高我们分析和解决数学问题的能力。

数学软件Mathematica功能比较强大，它集数值计算、公式推导和图形等功能为一体。

可以顺利解决我们在高等数学、线性代数、概率论、最优化、概率统计等一些数学科目中所要经常遇到的一些问题。

Mathematica在操作是必须得注意大小写，内部函数一般要写全称，而且一定是以大写英文字母开头，自定义的变量可以取任意的名称，长度不限但是不可以以数字开头，（）用来表示项的结合顺序，而[]表示函数。

Mathematica的图形函数十分丰富，用它可以画出很复杂的图形，而且只需要寥寥几句就可以，具有十分方便的操作性能。

Mathematica可以用来函数的各类函数画图：例如所有的三角函数，反三角函数，以及各类的特殊函数，各种的复杂函数各种的随机函数等等图形的输出。

函数的各种表示方法（列表法，解析法(直角坐标方程，参数方程，极坐标方程，隐函数)）Mathematic做图分为二维的和三维的二、根据函数维数对Mathematic做图作总结：二维图形：例如：Plot x Sin 1x ,x,0.5,0.5例如：用ImplicitPlot 命令作出221x y xy +=+的图形再例如：用不同颜色画出sin ,arctan ,[4,4]y x y x x ==∈-的图形，并写出命令。

G1Plot Sin x ,x,4,4,PlotStyle RGBColor 0,1,0G2Plot ArcTan x ,x,4,4,PlotStyle RGBColor 1,1,0Show G1,G2由图可以看出 Mathematic可以在一幅图中用多种颜色表示图像图像更清晰明了。

即颜色函数RGBColor[red,green,blue]用PolarPlot命令, 作出曲线3sin8ρϕ=（极坐标表示）的图形。