机械原理课程设计——内燃机设计——凸轮轮廓线程序、图像

格式：doc
大小：52.00 KB
文档页数：4

下载文档原格式

机械原理凸轮轮廓曲线设计

正确确定推杆的位移或摆角
直动推杆：位移等于推杆所在位置与理论廓线的交点和与基圆交点之间的距离。
摆动推杆：角位移等于推杆所在位置与推杆起始位置之间的夹角。
感谢下载
12
已知凸轮的基圆半径r0，角速度
和从动件的运动规律及偏心距e，
设计该凸轮轮廓曲线。
e
s
8 9 10
7 5 3 1
11 12
13 14
1 3 5 7 8 9 11 13 15
120º 60º 90º 90º
设计步骤
A
15
15 1414
13 13 12 11
O kkk91k1011k2k1k381k47kk61k5 5kk4k3k21
感谢下载
9
4.对心直动平底推杆盘形凸轮
对心直动平底推杆凸轮机构中，已知凸
轮的基圆半径r0，角速度ω和推杆的运动规律，
设计该凸轮轮廓曲线。
8’ 7’ 5’ 3’ 1’
1 3 5 78
9’ 11’ 12’
13’ 14’
9 11 13 15
1’ 2’ 3’
12 3 4
5
4’ 5’
15 14’
14
13’ 13
12
10
③①② 确选等定比分反例位转尺移后曲l，从线作动及位件反移尖向
9
顶等曲在分线各各、等运基分圆动点r角0占和，据偏确的距定位圆反置e。转。后对④应于将各各等尖分顶点点的连从接动成件一的
11
条光位滑置曲。线。
10
感谢下载
9
7
3. 对心滚子移动从动件盘形凸轮廓线的设计
已知凸轮的基圆半径r0，
滚子半径rT、凸轮角速度和
运动的轨迹即凸轮的轮廓曲线。

机械原理-凸轮轮廓曲线设计图解法

-ω
3’ 2’ 1’ ω O 1 2
1
2
3
3
直动从动件盘形凸轮轮廓的绘制
1.对心直动尖顶从动件盘形凸轮已知凸轮的基圆半径r0，角速度ω 和从动件的运动规律，设计该凸轮轮廓曲线。
4’ 5’ 6’
-ω ω
3’ 2’ 1’
7’
8’ 5 6 7 8
1 2 3 4
设计步骤: ①作基圆r0。
②反向等分各运动角，得到一系列与基圆的交点。
7’ 5’ 3’ 1’ 1 3 5 78 8’ 9’ 11’ 12’ 13’ 14’ 9 11 13 15
e
-ω
ω 15’ 15 14’14
k12 k11 k10 k9 k15 k14 k13
A
13’
12’
k1 13 k 12 k32 k8 k7k6 k5k4 11 10 9
O
注意：与前不同的是——过各等分点作偏距圆的一系列切线，即是从动件导路在反转过程中的一系列位置线。
11’
10’ 9’
直动平底从动件盘形凸轮轮廓的绘制

直动平底从动件盘形凸轮轮廓的绘制
-

实际廓线
直动平底从动件盘形凸轮轮廓的绘制
-

实际廓线
③过各交点作从动件导路线，确定反转后从动件尖顶在各等分点的位置。 ④将各尖顶点连接成一条光滑曲线。
直动从动件盘形凸轮轮廓的绘制
2.对心直动滚子从动件盘形凸轮已知凸轮的基圆半径r0，滚子半径 rT ，角速度ω 和从动件的运动规律，设计该凸轮轮廓曲线。
3’ 2’ 1’ 7’ 8’ 1 2 3 4 5 6 7 8 4’
-ω
理论轮廓
ω
5’ 6’

机械原理第九章凸轮机构及其设计PPT课件

（2）三角函数运动规律
1）余弦加速度运动规律（简谐运动规律）推程时：s＝h[1－cos(πδ /δ0)]/2 在始、末两瞬时有柔性冲击。
2）正弦加速度运动规律（摆线运动规律）
推程时：s＝h[(δ /δ0)－sin(2π δ /δ0) /(2π)]
6
推杆的运动规律(4/4)
既无刚性冲击，又无柔性冲击。（3）组合型运动规律
§9-4 凸轮机构基本尺寸的确定
1．凸轮机构的压力角（1）凸轮机构中的作用力
推杆等减速推程段： s = h－2h(δ0－δ )2/δ02
在始、中、末三瞬时有柔性冲击。
5
推杆的运动规律(3/4)
3）五次多项式运动规律（3-4-5多项式运动规律）
s＝10hδ 3/δ03－15hδ 4/δ04＋6hδ 5/δ05
既无刚性冲击，又无柔性冲击。
说明对于多项式运动规律，其多项式中待定系数的数目应与边界条件的数目相等，其数目多少应根据工作要求来确定。但当边界条件增多时，会使设计计算复杂，加工精度也难以达到，故通常不宜采用太高次数的多项式。
凸轮廓线设计的方法：作图法和解析法
1．凸轮廓线设计的基本原理无论是采用作图法还是解析法设计凸轮廓线，所依据的基本原理都是反转法原理。例9-2 偏置直动尖顶推杆盘形凸轮机构（1）凸轮的轮廓曲线与推杆的相对运动关系当给整个凸轮机构加一个公共角速度－ω，使其绕凸轮轴心转动时，凸轮将静止不动，而推杆则一方面随其导轨作反转运动，另一方面又沿导轨作预期的往复运动。推杆在这种复合运动中，其尖顶的运动轨迹即为凸轮的轮廓曲线。
式中δ 为凸轮转角；s为推杆位移；C0，C1，C2，…Cn为待定系数，可利用边界条件等来确定。
（1）多项式运动规律 1）一次多项式运动规律（等速运动规律）

《机械原理》第四章凸轮机构与其设计

标准传动函数介绍
刚性机构的输入参数x转变为输出参数y仅与机构几何学有关。此关系在数学上理解为机构的传动函数y=y(x)
标准传动函数f(z)的单位为1,满足定义域 z∈[0,1],值域f(z) ∈[0,1],且满足边界条件f(0)=0, f(1)=1。
当满足f(z)=1-f(1-z)时为对称标准传动函数。
基本概念
行程
从动件往复运动的最大位移，用h表示。
10/16/2020
第四章凸轮机构及其设计
基本概念
推程
从动件背离凸轮轴心运动的行程。
推程运动角
与推程对应的凸轮转角。
10/16/2020
第四章凸轮机构及其设计
基本概念
回程
从动件向着凸轮轴心运动的行程。
回程运动角
与回程对应的凸轮转角。
Knowledge Points
凸轮机构的组成凸轮机构的分类凸轮机构的优点、缺点
10/16/2020
第四章凸轮机构及其设计
凸轮机构的组成
凸轮是具有曲线轮廓或凹槽的构件
凸轮机构一般由凸轮、从动件和机架三个构件组成。
10/16/2020
第四章凸轮机构及其设计
凸轮机构的分类
按照凸轮的形状分类按照从动件的型式分
形锁合
所谓形锁合型，是指利用高副元素本身的几何形状使从动件与凸轮轮廓始终保持接触。
10/16/2020
第四章凸轮机构及其设计
凸轮机构的优点
结构简单、紧凑，占据空间较小；具有多用性和灵活性，从动件的运动规律取决于凸轮轮廓曲线的形状。对于几乎任意要求的从动件的运动规律，都可以毫无困难地设计出凸轮廓线来实现。
10/16/2020

机械原理凸轮凸轮机构及其设计PPT课件

/

2 0
/

2 0
0

后半程：

=
s
=
0
/C2时t 2,=s
=Kh2/2
；
= 0=时1，：s2=：h3，……v =s 0
h
a 4h 2
2h( 0
/

2 0
)2 /
2 0
a

C0=
-sh=,1C：1=4：4h9/…0…, v

4h ( 0

)
/

2 0
0
C2=

)
/

2 0
C0= - h , C1= 4h / 0 ,
a

4h
2
/

2 0
C2=
-2h
/
2 0
结束
推杆常用的运动规律
二、推杆常用的运动规律（以推程为例）
s
5 678
1、多项式运动规律 s C0 C1 C2 2 Cn n
（2）n = 2 等加速等减速运动规律 s C0 C1 C2 2 v ds / dt C1 2C2
结束
凸轮机构的应用和分类
三、凸轮机构的类型
1、按凸轮的形状 →圆柱凸轮、盘形凸轮（移动凸轮） 2、按从动件的运动形式 → 摆动从动件、移动从动件 3、按从动件的形式 → 尖底从动件、平底从动件、滚子从动件
凸轮形状
凸轮 — 具有曲线轮廓或凹槽的构件
从动件形式
结束
凸轮机构的应用和分类
三、凸轮机构的类型
常用于传力不大的场合 4、轮廓加工困难，不过现在借助新的加工设备已经有了很大改善 5、从动件位移量不能过大，否则凸轮体积将会很大；

机械原理课程设计凸轮机构

目录（一）机械原理课程设计的目的和任务 (2)（二）从动件（摆杆）及滚子尺寸的确定 (4)（三） .............................. 原始数据分析5（四） ............. 摆杆的运动规律及凸轮轮廓线方程6（五） ................................ 程序方框图8（六） .............................. 计算机源程序9（七） ....................... 程序计算结果及其分析14（八） .......................... 凸轮机构示意简图16（九） .................................. 心得体会16（十）参考书籍 (18)（一）机械原理课程设计的目的和任务一、机械原理课程设计的目的：1、机械原理课程设计是一个重要实践性教学环节。

其目的在于：进一步巩固和加深所学知识；2、培养学生运用理论知识独立分析问题、解决问题的能力；3、使学生在机械的运动学和动力分析方面初步建立一个完整的概念；4、进一步提高学生计算和制图能力，及运用电子计算机的运算能力。

二、机械原理课程设计的任务：1、摆动从动件杆盘型凸轮机构2、采用图解法设计：凸轮中心到摆杆中心A的距离为160mm,凸轮以顺时针方向等速回转，摆杆的运动规律如表：3、设计要求：①确定合适摆杆长度②合理选择滚子半径rr③选择适当比例，用几何作图法绘制从动件位移曲线并画于图纸上；④用反转法绘制凸轮理论廓线和实际廓线，并标注全部尺寸（用A2图纸）⑤将机构简图、原始数据、尺寸综合方法写入说明书4、用解析法设计该凸轮轮廓，原始数据条件不变，要写出数学模型，编制程序并打印出结果备注：1、尖底（滚子）摆动从动件盘形凸轮机构压力角：临f[acos*M）—I]tan:asin伴°十屮）在推程中，当主从动件角速度方向不同时取“-”号，相同时取“ +” 号。

机械原理凸轮轮廓曲线设计(课堂PPT)

ω，摆动推杆长度l以
及摆杆回转中心与凸轮回转中心的距离d，摆杆角位移方程，设 A8 计该凸轮轮廓曲线。
4’ 3’ 2’ 1’
123 4
5’ 6’
7’ 8’
5 6 78A7φ7A6.Al
B’1 B1
B
r0ω
-ω
A1 φ1
B’2 B’3
B2 B3
120°
B4
φ2 A2
B’4 φ3 A3
90 °
B8
60 °
依据此原理可以用几何作图的方法设计凸轮的轮廓曲线。
反转前反转后
机架不动 - 转动
-ω 1
3’
2’
2
1’
ω1 2
O
33
凸轮转动不动
从动件
- 转动 S移动 S移动 .
4
-ω
A2 A3 A4 A1
A1
A3 A4 A2
ω
ω
A4
S2
A1 A2 A3
ω
S3 A2A3
A1
ω
A4 S4
r0
r0
r0
r0
-ω ω
的从动件的位置。
.
A
O
理论轮廓曲线
8
实际轮廓——凸轮与从动件直接接触的廓线称为凸轮的工作廓线。
理论轮廓——对于滚子从动件，可把滚子圆心看作从动件的尖点，该点的复合运动轨迹称为凸轮的理论廓线。实际廓线是滚子的包络线。
基圆——以凸轮理论轮廓曲线上的最小半径为半径所画的圆。
对于尖顶从动件来说，凸轮的理论轮廓和实际轮廓重合。
多缸内燃机-配气机构
.
1
§4-3 凸轮轮廓曲线的设计
一、凸轮轮廓曲线设计的基本原理二、凸轮轮廓曲线的作图法

3.2凸轮轮廓设计ppt课件

一、凸轮廓线设计方法的基本原理
反转原理：
给整个凸轮机构施以-ω时，不影响各构件之间
的相对运动，此时，凸轮将静止，而从动件尖顶复合
运动的轨迹即凸轮的轮廓曲线。
-ω 1
依据此原理可以用几何作图的方法 3’
设计凸轮的轮廓曲线，
2’
2
1’
ω 1 2 潘存云教授
O
33
设计：潘存云
二、直动从动件盘形凸轮轮廓的绘制
若不满足此条件时：
增大r0 减小rr
4.平底尺寸l 的确定作图法确定： l=2lmax+(5~7)mm
ω
1’ 2’
3’
同理，当导路位于中心左侧时，有：
OP= v/ω = [ds/dt] / [dδ/dt] =[ds/dδ]
∴ CP = ds/dδ
n
+ etgα=(OP+e)/BC
s
B
Dα
=(ds/dδ+e)/(s0+s) 其中： s0= r20 - e2
s0 ω r0
O 潘存云教授
P
C
设计：潘存云
n
∴ tgα = ds/dδ + e
正确偏置：导路位于与凸轮旋转方向ω相反的位置。注意：用偏置法可减小推程压力角，但同时增大了回
程压力角，故偏距 e 不能太大。
错误偏置
n
αB
ω 设潘计存：云潘教存云授
o
e Pn
正确偏置
n B
α
ω0 P 潘存云教授 en
对心布置有：tgα=ds/dδ/ (r0+s）
设计时要求： α≤[α] 于是有：
1.对心直动尖顶从动件盘形凸轮已知凸轮的基圆半径r0，角速度ω和从动件的运动规律，设计该凸轮轮廓曲线。

机械原理-凸轮PPT

第三章凸轮机构及其设计
第一节概述
内燃机配气凸轮机构
自动机床进刀凸轮机构
冲床凸轮机构
绕线机凸轮机构
圆柱凸轮输送机
自动车床凸轮机构
凸轮机构的组成凸轮、从动件和机架。
凸轮机构的适用场合广泛用于各种机械，特别是自动机械、自动控制装置和装配生产线。
凸轮机构的优点结构简单、紧凑、工作可靠，可以使从动件准确实现各种预期的运动规律，还易于实现多个运动的相互协调配合。
凸轮机构选型
度凸设轮计机
构运动学尺
计算从动件位移参数确定凸轮各个转角从动件运动规律设计凸轮机构基本尺寸设计凸轮轮廓曲线设计
凸轮机构的动力学分析与设计
刀具中心轨迹坐标计算
凸轮机构结构设计
第四节凸轮机构运动学参数和基本尺寸的设计
一、工作循环图与凸轮工作转角的确定凸轮的工作转角应当根据机器中各个执行机构动作之间的配合关系，由工作循环图(Working cycle diagram)来确定。
机构刚好发生自锁时的压力角为临界压力角c
c
arctan
(1
2b
1
l ) tan 2
1
凸轮机构能正常工作的重要条件
max [ ] c 推程移动从动件[ ]30º40º；摆动从动件[ ] 40º45º。回程 [ ] 70º80º。
第三节凸轮机构的设计过程
凸轮机构的设计内容
机构运动分配设计
电阻坯件电阻送料机构凸轮
电阻帽送帽压帽机构凸轮
送帽压帽机构凸轮
夹紧机构凸轮
工艺过程
电阻自动压帽机传动系统图
电阻体上料
电阻体夹紧
送帽
压帽
电阻自动压帽机工作循环图

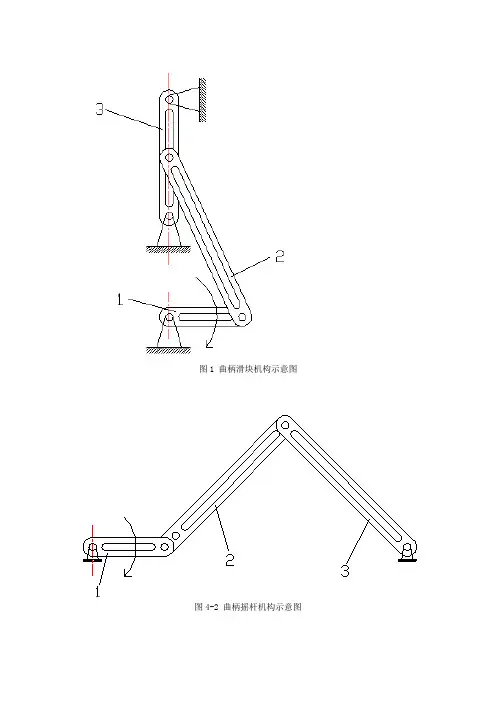
机械原理机构创新设计图例

图1 曲柄滑块机构示意图图4-2 曲柄摇杆机构示意图
图4-3 内燃机机构示意图图4-4 精压机机构示意图
图4-5 牛头刨床机构示意图
图6 两齿轮—曲柄摇杆机构示意图
图7 喷气织机开口机构示意图图4-8 冲压机构示意图
图4-9 筛料机构示意图图4-10 插床机构示意图
图11 凸轮—连杆组合机构示意图图12 凸轮—五连杆机构示意图
图13 行程放大机构示意图图14 自卸货车翻转机构示意图
图15 齿轮齿条—双曲柄滑块机构示意图图16 盘型凸轮（尖端推杆）机构示意图
图17 冲压机构示意图
图18 双摆杆摆角放大机构示意图
图19 双摇杆机构示意图。

机械原理凸轮机构精品ppt课件

38
二、从动件运动规律的选择
1.机器的工作过程只要求凸轮转过一角度时，推杆完成一行程h或φ，对运动规律并无严格要求。
则应选择直线或圆弧等易加工曲线作为凸轮的轮廓曲线。如夹紧凸轮。
φ ω
工件
39
2. 机器的工作过程对推杆运动有要求，则应严格按工作要求的运动规律来设计凸轮廓线。如刀架进给凸轮。
设计：凸轮轮廓曲线。
ω
r0
o
44
μs＝（）mm/mm
8’ 9’
7’
11’
5’ 3’
1’
12’
13’ 14’
12 345 67 8 9 11 13 15
μφ＝（）°/mm
取适当的比例尺μl＝μs
-ω ω
15
o
45
设计步骤：
① 按给定从动件的运动规律绘制从动件的位移线图。 ② 确定从动件尖底的初始位置。 ③ 确定导路在反转过程中的一系列位置。 ④ 确定尖底在反转过程中的一系列位置。 ⑤ 绘制凸轮廓线。
偏置尖底直动从动件盘形
凸轮机构
20
9.从动件的运动线图
从动件的运动规律——从动件的位移、速度和加速度与时间或凸轮转角间的关系。
位移方程 s = f(φ)
速度方程
v
ds dt
ds d
d dt
ds d
加速度方程
a
d
2 s
dt 2
dv dt
dv d
d dt
2
d
2 s
d 2
21
M s1 M1
M’ s1
第一节凸轮机构的类型
一、凸轮机构的组成
内燃机的配气凸轮机构
1

机械原理凸轮机构及其设计PPT精品医学课件

起点： =0 , s=0 , v=0
终点： = 0 , s=h
升程运动规律：
同理，得回程运动规律：
作推程运动线图
h/2
1
2
3
4
5
6
7
8
1
2
3
5
6
7
8
4
推程运动线图
s
O
h
0
0/2
：0 = ：
=(/ 0)
位移线图
速度线图
5
6
7
8
1
2
3
5
6
7
8
4
h /20
0
0/2
v
O
1
2
3
4
2
A
O
B
180º
120º
60º
o
1
2
3
4
5
6
7
8
9
10
（1）作出角位移线图；
（2）作初始位置；
（4）找从动件反转后的一系列位置，得 C1、C2、等点，即为凸轮轮廓上的点。
A1
A2
A3
A5
A6
A7
A8
A9
A10
A4
0
0
0
0
0
0
0
0
0
0
（3）按- 方向划分圆R得A0、 A1、A2等点；即得机架反转的一系列位置；
二．图解法设计凸轮轮廓曲线
1. 对心直动尖端从动件盘形凸轮机构
已知：推杆的运动规律、升程 h；凸轮的及其方向、基圆半径r0
设计：凸轮轮廓曲线
h
s
O
/2
h/2

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

凸轮理论轮廓线与实际轮廓线数据x y x1 y1 0 0 35 0 30 5 -3.06104 34.9879 -2.98506 29.9885 10 -6.16038 34.9373 -5.96929 29.9409 15 -9.32665 34.8075 -8.95079 29.8217 20 -12.5705 34.5372 -11.9229 29.5794 25 -15.8791 34.0528 -14.8684 29.156 30 -19.2135 33.2787 -17.756 28.4959 35 -22.5107 32.1486 -20.5396 27.5536 40 -25.6887 30.6146 -23.163 26.2995 45 -28.6546 28.6546 -25.5658 24.7228 50 -31.3147 26.2762 -27.6908 22.8313 55 -33.5852 23.5166 -29.4895 20.6488 60 -35.4018 20.4392 -30.9252 18.2121 65 -36.727 17.1261 -31.9759 15.5683 70 -37.5544 13.6687 -32.6356 12.7712 75 -37.909 10.1577 -32.9168 9.87707 80 -37.8432 6.67277 -32.8502 6.93899 85 -37.4301 3.27471 -32.4829 3.99979 90 -36.7538 9.84813e-007 -31.8734 1.08708 95 -35.8983 -3.14069 -31.0846 -1.78862 100 -34.9373 -6.16038 -30.1769 -4.6311 105 -33.9248 -9.09012 -29.2009 -7.45161 110 -32.8892 -11.9707 -28.1908 -10.2606 115 -31.7208 -14.7916 -27.1892 -12.6785 120 -30.3109 -17.5 -25.9808 -15 125 -28.6703 -20.0752 -24.5746 -17.2073 130 -26.8116 -22.4976 -22.9813 -19.2836 135 -24.7487 -24.7487 -21.2132 -21.2132 140 -22.4976 -26.8116 -19.2836 -22.9813 145 -20.0752 -28.6703 -17.2073 -24.5746 150 -17.5 -30.3109 -15 -25.9808 155 -14.7916 -31.7208 -12.6785 -27.1892 160 -11.9707 -32.8892 -10.2606 -28.1908 165 -9.05867 -33.8074 -7.76457 -28.9778 170 -6.07769 -34.4683 -5.20945 -29.5442 175 -3.05045 -34.8668 -2.61467 -29.8858 180 -1.87564e-006 -35 -1.60769e-006 -30 185 3.05045 -34.8668 2.61467 -29.8858 190 6.07768 -34.4683 5.20944 -29.5442 195 9.05866 -33.8074 7.76457 -28.9778 200 11.9707 -32.8892 10.2606 -28.1908205 14.7916 -31.7208 12.6785 -27.1892 210 17.5 -30.3109 15 -25.9808 215 20.0752 -28.6703 17.2073 -24.5746 220 22.4976 -26.8116 19.2836 -22.9813 225 24.7487 -24.7487 21.2132 -21.2132 230 26.8116 -22.4976 22.9813 -19.2836 235 28.6703 -20.0752 24.5746 -17.2073 240 30.3109 -17.5 25.9808 -15 245 31.7208 -14.7916 27.1892 -12.6785 250 32.8892 -11.9707 28.1908 -10.2606 255 33.8074 -9.05867 28.9778 -7.76457 260 34.4683 -6.07769 29.5442 -5.20945 265 34.8668 -3.05045 29.8858 -2.61467 270 35 -2.81346e-006 30 -2.41154e-006 275 34.8668 3.05045 29.8858 2.61467 280 34.4683 6.07768 29.5442 5.20944 285 33.8074 9.05866 28.9778 7.76457 290 32.8892 11.9707 28.1908 10.2606 295 31.7208 14.7916 27.1892 12.6785 300 30.3109 17.5 25.9808 15 305 28.6703 20.0752 24.5746 17.2073 310 26.8116 22.4976 22.9813 19.2836 315 24.7487 24.7487 21.2132 21.2132 320 22.4976 26.8116 19.2836 22.9813 325 20.0752 28.6703 17.2073 24.5746 330 17.5 30.3109 15 25.9808 335 14.7916 31.7208 12.6786 27.1892 340 11.9707 32.8892 10.2606 28.1908 345 9.05867 33.8074 7.76457 28.9778 350 6.07769 34.4683 5.20945 29.5442 355 3.05045 34.8668 2.61468 29.8858 360 3.75129e-006 35 3.21539e-006 30 Press any key to continue凸轮理论轮廓线与实际轮廓线数据#include<iostream.h>#include<math.h>#include<iomanip.h>#define PI 3.1415926void main(){double p,x,y,m,n,x1,y1,r=5;//分别代表角度值、理论x、理论y、x对角度的导数，y对角度的导数，实际x，实际y，磙子半径cout<<setw(15)<<"x"<<setw(20)<<"y"<<setw(20)<<"x1"<<setw(20)<<"y1"<<endl;for(p=0;p<=360;p=p+5){if(p<=55){x=-38*sin(p*PI/180)+3*cos(p*PI/55)*sin(p*PI/180);y=38*cos(p*PI/180)-3*cos(p/55*PI)*cos(p*PI/180);m=(38-3*cos(p/55*PI))*cos(p*PI/180)+180/55*3*sin(p*PI/180)*sin(p*PI/55);n=(-38+3*cos(p/55*PI))*sin(p*PI/180)+180/55*3*cos(p*PI/180)*sin(p*PI/55);x1=x-r*n/sqrt((m*m+n*n));y1=y-r*m/sqrt((m*m+n*n));cout<<p<<setw(15)<<x<<setw(20)<<y<<setw(20)<<x1<<setw(20)<<y1<<endl;}else if(p<=110){x=-38*sin(p*PI/180)-3*cos((p-55)*PI/55)*sin(p*PI/180);y=38*cos(p*PI/180)+3*cos((p-55)/55*PI)*cos(p*PI/180);m=(38+3*cos((p-55)/55*PI))*cos(p*PI/180)-180/55*3*sin(p*PI/180)*sin((p-55)*PI/55);n=(-38-3*cos((p-55)/55*PI))*sin(p*PI/180)-180/55*3*cos(p*PI/180)*sin((p-55)*PI/55);x1=x-r*n/sqrt((m*m+n*n));y1=y-r*m/sqrt((m*m+n*n));cout<<p<<setw(15)<<x<<setw(20)<<y<<setw(20)<<x1<<setw(20)<<y1<<endl;}else{ x=-35*sin(p*PI/180);y=35*cos(p*PI/180);m=35*cos(p*PI/180);n=-35*sin(p*PI/180);x1=x-r*n/sqrt((m*m+n*n));y1=y-r*m/sqrt((m*m+n*n));cout<<p<<setw(15)<<x<<setw(20)<<y<<setw(20)<<x1<<setw(20)<<y1<<endl;}}}。