焓湿图详解ppt课件

➢等焓线(为使图线不过密，两坐标轴间夹角为135℃) ➢等温线(干球温度线) ➢等相对湿度线Φ ➢水蒸气分压力线Pq ➢热湿比线
作用：
1.确定湿空气的状态参数；
2.表示湿空气的状态变化过程。
12.04.2020
17
1、2 湿空气的含湿图
等干球温度线
等湿度线
等相对湿度线
(水蒸气分压力线)
等焓线
湿空气焓湿图
实际计算中，在标况下，可近似取ρ=1.2Kg/m3
12.04.2020
9
1、1 湿空气的物理性质
4、含湿量d
基本定义：指1Kg干空气所含有的水蒸气质量，单位为 Kg/Kg·干空气或g/Kg·干空气。
即： d=mq/mg 式中 mq、mg — 分别为水蒸气和干空气的质量，Kg。
➢ 含湿量可以确切地表示空气中实际含有的水蒸气量的多少。 ➢ 空调中常用含湿量的变化来表示空气被加湿或减湿的程度。
12.04.2020
12
1、1 湿空气的物理性质
➢ 相对湿度可近似用湿空气的含湿量与同温度下饱和含湿量
之比来表示，即： Φ≈d/db
➢ 相对湿度是空调中的一个重要参数，相对湿度的大小对人
体的舒适和健康、工业产品的质量都会产生较大的影响。
12.04.2020
13
1、1 湿空气的物理性质
6、比焓h
基本定义：指1Kg干空气的比焓和d/1000Kg水蒸气的比焓的总 和，单位KJ/Kg干空气，取0℃时空气的焓值为零，则 ：
12.04.2020
2
1、1 湿空气的物理性质
12.04.2020
3
1、1 湿空气的物理性质
本节的主要内容
湿空气的组成 湿空气的基本状态参数

mg
由Vg=Vq=V，Tg=Tq=T，
Rg=287 J/(kg·K)，Rq＝46l J/(kg·K)
dRgpq 28p7 q 0.62p2q
Rqpg 46pg 1
pg
当大气压力B一定时，水蒸气分压力Pq只取决于
含湿量d。
精
品
4、相对湿度
Air conditioning
相对湿度：湿空气的水蒸气压力与同温度 下的饱和湿空气中的水蒸气压力之比。
Air conditioning
精 品
Air conditioning
第1.1节 湿空气的物理性质
一、基本概念 大气的组成成分：
水蒸气、氧气、二氧化碳等。 干空气 湿空气
精 品
干空气
Air conditioning
➢ 干空气：由各种气体成分组成，在空调 中被视为稳定的混合物。
➢ 一般将海平面高度的清洁空气成分作为 标准组成。（P4表1-1）
精 品
3、湿空气的含湿量d
Air conditioning
➢ 湿空气的含湿量：
湿空气中的水蒸气密度与干空气密度之比。
d =q/g
=0.622 Pq/Pg =0.622 Pq /(B-Pq) （kg/kg干air）
(1-5)
精 品
湿空气的含湿量d
Air conditioning
➢在湿空气中与l kg干空气同时并存的水蒸气 量称为含湿d 量 m q
精 品
2、湿空气的密度
Air conditioning
单位容积的湿空气所具有的质量，称为密度。
湿空气的密度＝干空气密度 +水蒸气密度
gqR P g g TR P q q T0.00T B 34 0.080P T 1 q 3

8.1 湿空气的物理性质
利下用：相对湿度的定d义式0.〔682-B 82〕P q可P .qb得.b到k含g/湿k量ga的〔()d另8-1一2表c〕达式如
另外，对于湿空气 d0.622Pq kg/kga(d)
对于饱和空气
db
0.6
2 2BP q.P bq
〔8-13a〕
kg/kga()d
BPq. b
g/kg(•da〔) 8-13b〕
8.1 湿空气的物理性质
8.1.2.2 温度
温度是分子动能的宏观结果，是表示湿空气冷热程度的物
理量。湿空气中的干空气和水蒸气总是均匀混合的，故湿空气
温度与干空气温度均相等。目前国际上常用的有绝对温标〔又
t 称开氏温标〕，符号为 T，单位为K；摄氏温标，符号为 ， t 单位为℃；有的国家也采有华氏温标，符号为 ，单位为℉。
8.1 湿空气的物理性质
8.1.2 湿空气物理性质
湿空气的物理性质除和它的组成成分温度、相对湿度、 含湿量及焓等参数来度量和描画。这些参数称为湿空气的形状 参数。 所谓理想气体，就是假设气体分子是一些有弹性的、不占有空 间的质点，分子相互之间没有作用力。通风空调工程中所涉及 湿空气的压力和温度都可以看作属于这个范畴。由于在热力学 中，常温常压下的干空气可视为理想气体；同时，湿空气中水 蒸气含量普通很少，只需几克到几十克，在通风空调中运用的 湿空气，其中水蒸气的质量份额最大不超越5%，而且湿空气 中的水蒸气大多处于过热形状，水蒸气的分压力很小，比容很 大。
下篇 空气调理
单元8 湿空气焓湿图及 运用
【知识点】湿空气的物理性质；湿空气焓湿 图的运用方法及空气参数空气焓湿图确定 方法；热湿比的概念及运用；两种不同形 状空气混合点确实定方法〔几何法和公式 法〕。

iC iD 4.19tDd , d dC dD
显然,参与混合得两种空气得质量比与C点分割两状态联线得
线段长度成反比。据此, 在i－d图上求混合状态时,只需将线段AB
划分成满足GA／GB比例得两段长度,并取C点使其接近空气质量大 得—端,而不必用公式求解。
第四节 焓湿图得应用
图1-14 两种状态空气得混合
第四节 焓湿图得应用
两种空气混合,若混合点处于“结雾区”,则此种状态空气就是 饱与空气加水雾,就是一种不稳定状态。假定饱与空气状态为D,则 混合点C得焓值应为D得焓值与水雾得焓值之与,即:
设有一空气与水直接接触得小室,保证二者有充分得接触表面积与时间,空气以 P,t1,d1,i1状态流入,以饱与状态P, t2,d2,i2流出,由于小室为绝热得,所以对应于每公 斤干空气得湿空气,其稳定流动能量方程式为:
i1＋(d2－d1)iw/1000＝i2 iw＝4、19tw ＝(i2－i1)/(d2－d1)×1000＝ 4、19tw
dA 5、热湿比线
iB iA i i G Q
dB d A d d G W
A
dB B
iB
100%
iA
空气状态变化在i-d图上得表示
第三节 湿球温度与露点温度
一、湿球温度 湿球温度得概念在空气调节中 至关重要
1、热力学湿球温度
理论上,湿球温度就是指在定压绝热条件下,空气与水直接接触达到稳定热湿平 衡时得绝热饱与温度,也称热力学湿球温度。
第三节 湿球温度与露点温度
空气的湿球温度和露点温度
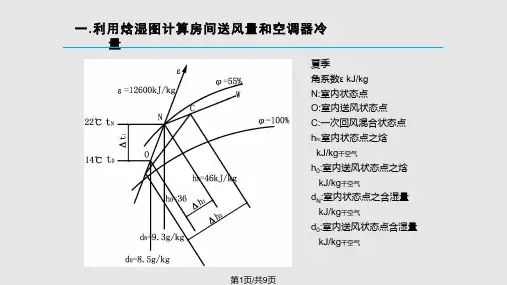
第四节 焓湿图得应用
空气得焓湿图得应用
1、确定空气状态参数 2、表示空气得处理过程(湿空气状态变化过程与
不同状态空气混合过程) 3、确定空气露点温度与湿球温度

5.2.2 湿空气的湿度图 （焓湿图）
在工程计算中，常用的是以湿空气的焓值I为纵坐 标，湿度H为横坐标的焓湿图，即I-H图。
图上共有五种线，图上任一点都代表一定温度t和
湿度Ｈ的湿空气状态。
等湿度线(等H线)： 等焓线(等I线)： 等温线(等t线)： 等相对湿度线（等j线） 水蒸汽分压线：
一、等湿度线(等H线) 一组与纵轴平行的直线。在同一条等H线上，湿空气
一、求空气的状态参数 若已知湿含量H和焓I，在焓湿图中得到Ａ点 H=0.02kg水/kg干空气，I=120kJ/kg干空气
H：沿等H线
.
I：沿等I线
.A

pv：过A点沿等H线交水
汽分压线
tw
td: 沿等H线，交j＝100 td
％沿等t线
tW：沿等I线，交j＝
100％，沿等t线
== 1= 0 01 %0
的露点td不变。即确定了H，就可以确定露点温度td 。
二、 等焓线(等I线) 一组与水平线倾斜135°的直线 。读数范围0~
680kJ/kg绝干气。 三、 干球温度线(等t线)
固定总压下，给定不同的温度t值，以H为自变量，I为因变量， 根据I=(1.88t+2490)H+1.01t作出的曲线。当空气的干球温度t不变 时，I与H成直线关系，故在I-H图中对应不同的t，可作出许多 等t线。 各种不同温度的等温线，其斜率为(1.88t+2490)，故温度 愈高，其斜率愈大。因此，成直线的等t线并不互相平行。
三、湿空气的状态变化过程 1、加热与冷却过程 加热：湿空气的加热与冷却
属等压过程，p不变，H不 变，AB线为一垂直线，沿 等H线由A到达B点，温度
升高，空气的j下降，干燥

送风量
G
Q1 hN h0
W dN d0
kg/ s
1000
式中 Q1 室内冷负荷（室内余热）kw（kJ/s）
W 室内湿负荷（室内余湿）kg/s
确定送风状态点和计算送风量及空调器冷负荷
1)在h-d图(当地气压，广州是101325pa即760mmHg)上找出室 内状态点N
2)根据Q1、W算出ε
3)根据选取的送风温差求出送风温度t0，t0等温线和ε线交点
第2页/共9页
一.利用焓湿图计算房间送风量和空调器冷量
即 h0 dN d0 1000
计算出风量
5)空调器冷负荷Q2=G1Δh2 用以选空调器
例：某空调房间，室内冷负荷为Q1=3.314kw。湿负荷为 0.264g/s即W=0.264/1000kg/s。全年送风状态为tN＝22±1℃， φ=55±5%。当地大气压为101325pa(N/m2).求送风状态点和送
第6页/共9页
二.水电动阀选择
2.1空调器水电动阀
流量系数
Cv
KQv=Cv/1.17 P
其中 Q:水流量（US G P M）
Q 冷负荷（kcal/h）15.84 3600 T
△T：进出水温差
△P：阀全开时的压降。取3～7psi（磅/in2）一般取4
d 25 32 40 50 65 80 100 125 150 Kv 10 16 25 40 63 100 160 250 400
c.空调器湿负荷w＝G(do’-dc’)/1000 kg/s c’为混合状态点 空调器加热量Q热＝GCp(tL-tc’)/1000(kw)Cp：湿空气比热
1.01kJ/kg℃ 若冬季风量小于夏季，可节能，假定to”＝36℃。在ε线上

加强焓湿图的理论学习
• 焓湿图是一种用于描述空气状态变化的图表，其中包含温度、湿度、压力等参 数，可以用于分析空气的加热或冷却过程。加强焓湿图的理论学习，可以帮助 人们更好地理解其背后的原理和数学模型，从而更好地应用它。
• 掌握焓湿图的基本概念和参数：了解焓湿图的基本概念和参数，如温度、湿度、 压力等，以及它们之间的关系，是理解其作用意义的基础。
基于大数据的优化方法
利用大数据技术对大量焓湿图数据进行分析和处理，总结出各种参数对湿空气的影响规律，为优化焓湿图的设计 提供依据。
基于云计算的优化方法
通过云计算平台，可以将焓湿图的计算和分析任务进行分布式处理，提高计算效率和准确性，进一步优化焓湿图 的设计。
绿色能源利用与可持续发展的焓湿图应用研究
备的选型和配置。
其他领域的应用案例
在建筑行业中，焓湿图可用 于建筑通风和空调系统的设 计，提高建筑的舒适度和能效。
在农业领域，焓湿图可用于 指导灌溉和作物保护措施的 实施，提高农作物的产量和
品质。
在医疗领域，焓湿图可用于 指导病房和手术室的空气调 节，提高医疗环境的质量和 安全性。
05
如何提高焓湿图的实践效果
产品研发与设计
在产品研发ห้องสมุดไป่ตู้设计中，焓湿图可以帮助企业了解产品的能量利用和湿 物料的含湿量变化情况，为产品设计和性能优化提供依据。
安全与环保
1 2 3
安全风险评估 焓湿图可用于安全风险评估，帮助企业及时发现 和解决潜在的安全隐患，提高企业的安全性能。
环保监测与评估 焓湿图可用于环保监测和评估，帮助企业了解生 产过程中的环境污染情况，为企业制定更加科学 合理的环保方案提供依据。
控制系统设计
焓湿图可用于控制系统设计，为控制系统提供准确的参数控制和调 节，保证生产过程的稳定性和可靠性。