非线性方程线性化

（整理）计量经济学第四章⾮线性回归模型的线性化第四章⾮线性回归模型的线性化以上介绍了线性回归模型。

但有时候变量之间的关系是⾮线性的。

例如 y t = α 0 + α11βt x + u t y t = α 0 t x e 1α+ u t上述⾮线性回归模型是⽆法⽤最⼩⼆乘法估计参数的。

可采⽤⾮线性⽅法进⾏估计。

估计过程⾮常复杂和困难，在20世纪40年代之前⼏乎不可能实现。

计算机的出现⼤⼤⽅便了⾮线性回归模型的估计。

专⽤软件使这种计算变得⾮常容易。

但本章不是介绍这类模型的估计。

另外还有⼀类⾮线性回归模型。

其形式是⾮线性的，但可以通过适当的变换，转化为线性模型，然后利⽤线性回归模型的估计与检验⽅法进⾏处理。

称此类模型为可线性化的⾮线性模型。

下⾯介绍⼏种典型的可以线性化的⾮线性模型。

4.1 可线性化的模型⑴指数函数模型y t = t t ubx ae + (4.1)b >0 和b <0两种情形的图形分别见图4.1和4.2。

显然x t 和y t 的关系是⾮线性的。

对上式等号两侧同取⾃然对数，得Lny t = Lna + b x t + u t (4.2)令Lny t = y t *, Lna = a *, 则y t * = a * + bx t + u t (4.3) 变量y t * 和x t 已变换成为线性关系。

其中u t 表⽰随机误差项。

010203040501234XY 1图4.1 y t =tt u bx ae+, (b > 0) 图4.2 y t =t+, (b < 0)⑵对数函数模型y t = a + b Ln x t+ u t(4.4)b>0和b<0两种情形的图形分别见图4.3和4.4。

x t和y t的关系是⾮线性的。

令x t* = Lnx t, 则y t = a + b x t* + u t(4.5)变量y t和x t* 已变换成为线性关系。

图4.3 y t = a + b Lnx t + u t , (b > 0) 图4.4 y t = a + b Lnx t + u t , (b < 0)⑶幂函数模型y t= a x t b t u e(4.6) b取不同值的图形分别见图4.5和4.6。

非线性方程线性化的两个条件
一，小偏差理论和小信号理论。

在工程实践中，控制系统都有一个额定的工作状态和工作点，当变量在工作点附近小范围的变化事，满足这个条件。

只有在这个情况下转化之后的误差才足够小。

二，在工作点附近存在各阶倒数和偏导数
一元函数，一个y对应一个x，导数只有一个。

二元函数，一个z对应一个x和一个y，那就有两个导数了，一个是z对x的导数，一个是z对y的导数，称之为偏导，即输入与输出的导数都存在。

这个是能够转化的条件。

浅谈非线性回归模型的线性化广东省惠州市惠阳区崇雅中学高中部 卢瑞勤(516213)回归分析在各个领域中都有十分重要的作用，比如：在财务中可以用回归分析进行财务预测；在医疗检验中可以用回归分析进行病理预报等等。

高中新课标教材就在《必修3》和《选修2-3》中分别增加了《线性回归》和《回归分析》的内容，介绍了求线性回归方程的方法。

但在实际问题中，变量间的关系并非总是线性关系，本文结合本人的教学实践，对教材中的这两部分内容进行适当延伸，谈谈对一些可线性化的非线性回归模型的线性化问题，供各位同行在教学时参考。

一、什么是可线性化的非线性回归模型线性回归模型的基本特征是预报变量可以表示成解释变量和一个系数相乘的和，即预报变量y 可以表示成解释变量i x (i =1，2，3，……)的如下形式：0112233y a a x a x a x =++++，其中变量ix 是以其原型(而不是以ni x 或其它)的形式出现，变量y 是各变量i x 的线性函数。

而有些回归模型不具备这个特点，但是可以通过适当的代数变换转化成这种形式，我们称这类回归模型为可线性化的回归模型。

在本文中，我们只讨论只有一个解释变量可线性化的非线性回归模型的线性化。

二、非线性回归模型的线性化的基本思路非线性回归模线性化的基本思路是：由已知数据，确定解释变量和预报变量，作出散点图，根据经验，确定回归曲线的类型，然后作适当的代数变换，若变换后散点图体现较好的线性关系，即可将其化成线性形式求解，最后还原到原来的回归曲线。

如果回归曲线可用多种形式表示，可以各自将其线性化后求解，再用相关系数2R 进行拟合效果分析，2R 越大，拟合效果越好，所求的回归方程也就越精确。

三、非线性回归模型的线性化的常用方法可线性化的非线性回归模型有以下几种常见类型：(1)双曲线型，其形式为1a b y x =+，其变换为1y y '=， 1x x'=，变换后的形式为y b ax ''=+ (2)幂函数型，其形式为by ax = ，可以变形为ln ln ln y a b x =+，作变换ln y y '= ，ln x x '= ，变换后的形式为y a bx ''=+(3)指数函数型，其形式为bxy ae = ，以变形为ln ln y a bx =+，作变换ln y y '=，ln a a '= ，变换后的形式为y a bx ''=+(4)对数函数型，其形式为ln y a b x =+，作变换ln x x '=，变换后的形式为y a bx '=+ 下面以高中新课标数学教材《选修2-3》一道习题为例加以说明【例】在某地区的一段时间内观察到的不小于某震级x 的地震个数y 数据如下表，试建立回归方程表述二者之间的关系。

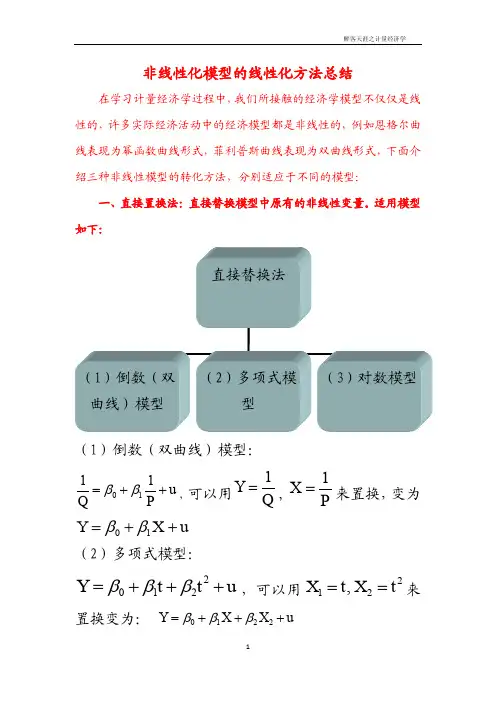
非线性化模型的线性化方法总结在学习计量经济学过程中，我们所接触的经济学模型不仅仅是线性的，许多实际经济活动中的经济模型都是非线性的，例如恩格尔曲线表现为幂函数曲线形式，菲利普斯曲线表现为双曲线形式，下面介绍三种非线性模型的转化方法，分别适应于不同的模型：一、直接置换法：直接替换模型中原有的非线性变量。

适用模型如下：（1）倒数（双曲线）模型：0111u Q P ββ=++，可以用1Y Q =,1X P=来置换，变为01Y X u ββ=++（2）多项式模型：2012Y t t u βββ=+++，可以用212,X t X t ==来置换变为： 0122Y X X u βββ=+++（3）对数模型： 01ln Y X u ββ=++，将1ln X X=带入原式进行置换，得到：011Y X u ββ=++二、函数变换法：通过函数变化，如取对数、移项等方式对原模型进行变形以得到线性化模型：12(,,,)k Y f X X X u =⋅⋅⋅+（1） 幂函数模型：u Q AK L e αβ=，方程两边取对数，得到：ln ln ln ln Q A K L u αβ=+++再对上式进行置换。

（2）指数函数模型：Q uC ab e =，方程两边取对数得到：ln ln ln C a Q b u =++，再对上式进行置换。

三、级数展开法：如CES 函数112()p p u pQ A K L e δδ---=+，方程两边取对数得到：121ln ln ln()p p Q A K L u pδδ--=-++，将式中12ln()p p K L δδ--+在p=0处展开泰勒级数，取关于p 的线性项，即得到一个线性近似式，如取0阶、1阶、2阶项，可得:212121ln ln ln ln [ln()]2K Y A K L p Lδδδδ=++- （备注：无法线性化的模型一般为：12(,,,)k Y f X X X u =⋅⋅⋅+，其中12(,,,)k f X X X ⋅⋅⋅为非线性函数）。

第2章 辅导机械系统机械旋转系统如图所示。

为一圆柱体被轴承支撑并在黏性介质中转动。

当力矩作用于系统时，产生角位移。

求该系统的微分方程式。

解 根据牛顿第二定律，系统的诸力矩之和为22s )()()(T -T (t)dtt d J t T t d θ=- 式中：J ——转动系统的惯性矩；扭矩)()(T s t K t θ=， K ——扭簧的弹性系数； 黏性摩擦阻尼力矩dtt d B t T d )()(θ=，B因此该系统的运动方程式为)()()()(22t T tK dt t d B dt td J =++θθθ （2－2）电气系统电气系统的基本元件是电阻、电容、电感以及电动机等，支配电气系统的基本定律是基尔霍夫电路定律。

图为一具有电阻－电感－电容的无源网络，求以电压u 为输入，u c 为输出的系统微分方程式。

解 根据基尔霍夫电路定律，有 C u R i dtdiL t u +⋅+⋅=)( 而 dtdu Ci c=，则上式可写成如下形式 22u dt du RC dt u d LCC cc =++ （2－3）上式表示了RLC 电路的输入量和输出量之间的关系。

编写控制系统微分方程的一般步骤为：(l) 首先确定系统的输入量和输出量；(2) 将系统划分为若干个环节，确定每一环节的输入量和输出量。

确定输入量和输出量时，应使前一环节的输出量是后一环节的输入量。

(3) 写出每一环节(或元件)描述输出信号和输入信号相互关系的运动方程式；找出联系输出量与输入量的内部关系，并确定反映这种内在联系的物理规律。

而这些物理定律的数学表达式就是环节(或元件)的原始方程式。

在此同时再做一些数学上的处理，如非线性函数的线性化。

考虑忽略一些次要因素。

使方程简化的可能性和容许程度。

(4) 消去中间变量，列出各变量间的关系式。

设法消去中间变量，最后得到只包含输入量和输出量的方程式。

于是，就得到所要建立的元件或系统的数学模型了。

非线性数学模型的线性化1、一般运动方程式化为增量方程式的步骤 以下式为例)()()()(22t ky dt t dy B dtt y d M t F ++= (1) 确定额定点，写出静态方程式：设额定点为(F 。

计量经济学第4章非线性回归模型的线性化（1）多项式函数模型（2）双曲线函数模型（3）对数函数模型（4）生长曲线(logistic) 模型file:li-4-1file:5nonli7（比教材中的模型复杂些）（5）指数函数模型幂数模型file:5nonli3 file:5nonli01 file:li-4-2（6）幂函数模型file:5nonli14第4章非线性回归模型的线性化有时候变量之间的关系是非线性的。

虽然其形式是非线性的但可以通过适当的变换转化为线性模型然后利第章非线性模型的线性线性的，但可以通过适当的变换，转化为线性模型，然后利用线性回归模型的估计与检验方法进行处理。

称此类模型为可线性化的非线性模型可线性化的非线性模型。

以下非线性回归模型是无法用最小二乘法估计参数的。

可采用非线性方法进行估计估计过程非常复杂和困难计可采用非线性方法进行估计。

估计过程非常复杂和困难，计算机的出现大大方便了非线性回归模型的估计。

专用软件使这种计算变得非常容易但本章不是介绍这类模型的估计这种计算变得非常容易。

但本章不是介绍这类模型的估计。

y t = α0 + α11βt x + u t y t = α0tx e1α+ u t下面介绍几种典型的可以做线性化处理的非线性模型。

（第(1)多项式函数模型(1)2版教材第111页）（第3版教材第90页）多项式方程=+++y t = b 0+b 1 x t + b 2 x t 2+ b 3 x t 3+ u t 令x t 1 = x t ，x t 2 = x t 2，x t 3 = x t 3，上式变为+++y t = b 0+b 1 x t 1+ b 2 x t 2+ b 3 x t 3+ u t这是三元线性回归模型。

经济学中的总成本与产品产量曲线与左图相似。

(b 1>0, b 2>0, b 3>0) (b 1<0, b 2>0, b 3<0)(1)多项式函数模型(1)例4.1：总成本与产品产量的关系（课本91页, file:li-4-1)+++y t= b0+b1 x t+ b2 x t2+ b3 x t3+ u t（第2版教材第112页）估计结果见下页（第3版教材第91页）(1)多项式函数模型(1)例4.1：总成本与产品产量的关系（课本91页,file:li-4-1）= 2434.7+ 85.7x t -0.028 x t 2+0.00004 x t3(1.8) (12.0) (-2.8) (9.6)t C ˆ（第R 2= 0.9998, N = 152版教材第114页）（第3版教材第92页）19902003（1990~2003）19902003从散点图看，用多项式方程拟合比较合理。

JMA（Jacobian Matrix and Algebraic）方程是一种用于求解非线性系统的状态估计问题的方法。

它结合了雅可比矩阵（Jacobian Matrix）和代数方法（Algebraic），用于解决系统状态估计问题，尤其是在卡尔曼滤波和扩展卡尔曼滤波（EKF）的框架下。

在非线性系统状态估计问题中，系统的状态转移方程和观测方程通常是非线性的。

JMA方程提供了一种方法来近似这些非线性方程，以便在估计状态时使用线性化的形式。

这种方法的关键在于对非线性方程进行泰勒展开，并保留一阶项，从而得到一个线性化的系统模型。

JMA方程的主要步骤包括：
1. **线性化**：对系统的状态转移方程和观测方程进行泰勒展开，并保留一阶项，从而得到一个线性化的系统模型。

2. **构造雅可比矩阵**：雅可比矩阵包含了线性化模型中状态变量和观测变量对状态转移和观测方程的偏导数。

这个矩阵对于解决线性化后的系统至关重要。

3. **求解线性系统**：使用线性化的系统和雅可比矩阵，可以求解出状态估计问题。

这通常涉及到卡尔曼滤波或EKF框架。

4. **更新估计**：根据新的观测数据，更新状态估计和误差协方差。

JMA方程在工程和科学领域有广泛的应用，特别是在自动驾驶、机器人导航、信号处理等领域。

它提供了一种有效的手段来处理非线性系统的状态估计问题，从而提高系统的性能和可靠性。

第二章控制系统的数学模型第3讲非线性微分方程的线性化王燕舞为什么要进行线性化？严格的说，几乎所有元件或系统的运动方程都是非线性方程，即输入、输出和扰动等之间的关系都是非线性的。

非线性微分方程的求解和控制系统性能研究非常复杂，而线性化后的模型可借助叠加原理的性质，简化系统分析。

因此，研究非线性微分方程的线性化具有较强的工程实用价值。

什么是非线性数学模型的线性化？在一定的条件下或在一定范围内把非线性的数学模型化为线性模型的处理方法。

符合什么条件的系统可以进行线性化呢？▪条件1: 小偏差理论或小信号理论。

在工程实践中，控制系统都有一个额定的工作状态和工作点，当变量在工作点附近作小范围的变化时，就满足这个条件。

▪条件2: 在工作点附近存在各阶导数或偏导数。

如何进行线性化呢？假设微分方程模型中包含非线性函数f(x)如图所示。

设y=f(x)，假设系统在工作点(x 0, y 0), y 0=f(x 0) 附近变化，且在该工作点处各阶导数均存在，在(x 0, y 0)附近将y 展开成泰勒级数：)()()()(000xx x x x f x f x f y -⎥⎦⎤⎢⎣⎡∂∂+==若偏差Δx=x-x 0很小，可忽略级数中高阶无穷小项，上式化为)()()()()()(00000x xK x f x x x x x f x f x f y -+=-⎥⎦⎤⎢⎣⎡∂∂+≈=K 表示y=f(x)曲线在(x 0,y 0)处切线的斜率。

因此非线性函数在工作点处可以用该点的切线方程线性化。

yy=f(x)y 0x 0x ⋯+-⎥⎦⎤⎢⎣⎡∂∂+20022)()(!21x x x x x f xK x f x f y y y ∆=-=-=∆)()(00如何进行线性化呢？小偏差法：在给定工作点的邻域将非线性函数展开为泰勒级数，忽略级数中的高阶项，得到只包含偏差的一次项的线性方程。

液位流体过程。

如图，Q1为流入量，也是输入量；Q 2为流出量；h 为液位高度，为系统输出；C 为液缸的截面积。