第2章非线性方程求解
- 格式:ppt
- 大小:900.00 KB
- 文档页数:47



第2章 非线性方程的求根方法2.1 二分法设()0f x =在区间[,]a b 中只有一个根*x ,且满足()()0f a f b <,则二分法求根过程为: 记0[,]I a b =,取0I 的中点00.5()x a b =+,若0()0f x =,则*0x x =; 若0()()0f x f a <,则*0[,]x a x ∈,取10[,]I a x =; 若0()()0f x f a >,则*0[,]x x b ∈,取10[,]I x b=. 记111[,]I a b =,取1I 的中点1110.5()x a b =+,若1()0f x =,则*1x x =;若11()()0f x f a <,则*11[,]x a x ∈,取211[,]I a x =;若11()()0f x f a >,则*11[,]x x b ∈,取211[,]I x b =. 记222[,]I a b =⋅⋅⋅这样获得近似根序列01,,,,,k x x x ⋅⋅⋅⋅⋅⋅满足于是当k →∞时,由11()02k b a +-→得到*k x x →.二分法算法简单,收敛,但收敛速度较慢.2.2 简单迭代法将方程()0f x =等价变形为()x x ϕ=,获得 迭代计算公式1()k k x x ϕ+=取定一个初值0x ,由迭代公式算出数列()() ,,1201x x x x ϕϕ==,若*lim k k x x →∞=,则足够靠后的k x 可作为根的近似值.由上述得出{}k x 称为迭代数列,函数()x ϕ为迭代函数,如上求根方法称为简单迭代法.对根*x ,有**()x x ϕ=,点*x 称为()x ϕ的不动点,称方程()x x ϕ=为不动点方程.例1 求方程01)(3=--=x x x f 在5.10=x 附近的根.定理1 设迭代函数()[,]x C a b ϕ∈满足条件 1.当[,]x a b ∈时,有()[,]x a b ϕ∈;2.存在正常数1L <,使对任意 12,[,]x x a b ∈都有1212()()x x L x x ϕϕ∣-∣≤∣-∣则()x ϕ在[,]a b 中有唯一的不动点*x ,迭代公式1()k k x x ϕ+=对任取0[,]x a b ∈,产生的数列{}k x 都收敛于*x .证明 作辅助函数()()x x x ψϕ=-显然()[,]x C a b ψ∈.由条件1知()()0a b ψψ≤由中值定理,至少存在一个[,]a b ξ∈,使()0ψξ=,即()ξϕξ=,这说明()x ϕ在[,]a b 上有不动点ξ. 如果()x ϕ在[,]a b 上还有一个不动点η,有()ηϕη=,利用条件2,有()()L ξηϕξϕηξηξη∣-∣=∣-∣≤∣-∣<∣-∣矛盾,这就证明了满足定理条件的()x ϕ在[,]a b 中有唯一的不动点,记为*x .由*x 是不动点、迭代格式及条件2,有***112**20()()k k k k k x x x x L x x L x x L x x ϕϕ---∣-∣=∣-∣≤∣-∣≤∣-∣≤≤∣-∣注意到01L <<,在上式中令k→∞,可得0kL →,有 *lim 0kk x x →∞∣-∣=,因而有 *lim k k x x →∞=定理得证.定理2 设定理1的条件成立,则有如下误差估计式证明 只证1.由迭代公式和定理2.1的条件,有()1k k k k x x x x ϕ+∣-∣=-**()()()k k x x x x ϕϕϕ=∣-+-∣ ****()()()()k k k k x x x x x x x x ϕϕϕϕ=-+-≥---***L L)k k k x x x x x x ≥∣-∣-∣-∣=(1-∣-∣因为01L <<,所以有*111k k k x x x x L+-≤--另一方面111()()k k k k k k x x x x L x x ϕϕ+--∣-∣=∣-∣≤∣-∣代入上式得结论1.定理2.1的条件2对任意12,[,]x x a b ∈,存在正常数1L <满足1212()()x x L x x ϕϕ∣-∣≤∣-∣不易使用。
第二章 方程求根在许多实际问题中,常常会遇到方程f(x)=0求解的问题。
当f(x)为一次多项式时,f(x)=0称为线性方程,否则称为非线性方程。
对于非线性方程,由于f(x)的多样性,求其根尚无一般的解析方法可以使用,因此研究非线性方程的数值解法是十分必要的。
法、迭代法、牛顿法及割线法。
这些方法均是知道根的初始近似值后,进一步把根精确化,直到达到所要求的 精度为止。
也即求非线性方程根的数值方法。
第一节 第一节 增值寻根法与二分法2.1.1 增值寻根法设非线性方程f(x)=0的根为*x ,增值寻根法的基本思想是,从初始值0x 开始,按规定 的一个初始步长h 来增值。
令 1n x +=n x +h(n=0,1,2,…),同时计算f(1n x +)。
在增值的计算过程中可能遇到三种情形:(1) f(1n x +)=0,此时1n x +即为方 程的根*x 。
(2) f(n x )和f(1n x +)同符号。
这说明区间[n x , 1n x +]内无根。
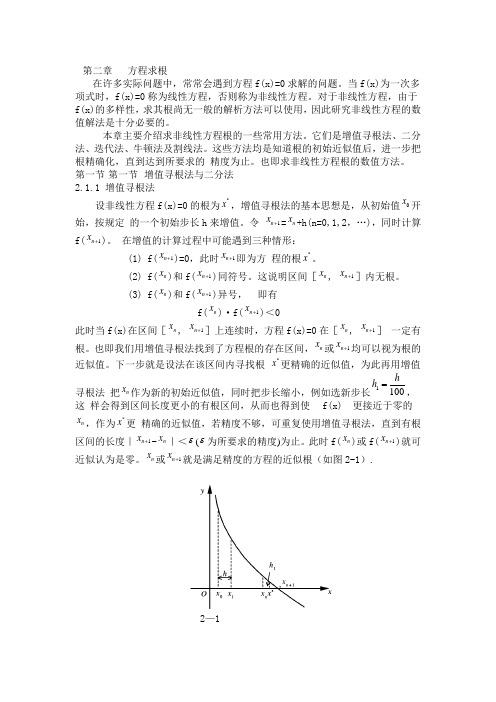
(3) f(n x )和f(1n x +)异号,f(n x )·f(1n x +)<0此时当f(x)在区间[n x , 1n x +]上连续时,方程f(x)=0在[n x , 1n x +] 一定有根。
也即我们用增值寻根法找到了方程根的存在区间,n x 或1n x +均可以视为根的近似值。
下一步就是设法在该区间内寻找根 *x 更精确的近似值,为此再用增值寻根法 把n x 作为新的初始近似值,同时把步长缩小,例如选新步长1100h h =,这 样会得到区间长度更小的有根区间,从而也得到使f(x)n x ,作为*x 更 精确的近似值,若精度不够,可重复使用增值寻根法,直到有根区间的长度|1n x +-n x |<ε(ε为所要求的精度)为止。
此时f(n x )或f(1n x +)就可近似认为是零。
n x 或1n x +就是满足精度的方程的近似根(如图2-1).2—1例1 用增值寻根法求方程f(x)=324x x +-10=0的有根区间。

东南大学-数值分析-第二章-牛顿迭代法第二章非线性方程的解法某某某某(学号)某某某某(姓名)算法与程序题目见教材P56上机题目20。
一、算法原理根据题目的要求,是关于用牛顿迭代法法求解方程f(某)0的通用算法。
该法是一种通过斜率迭代的算法,其速度比二分法和简单迭代法都要快。
其简单原理如下:设fC2[a,b],且存在数p[a,b],满足f(p)0。
如果f(p)0,则存在一个数0,对任意初始值p0[p,p],使得由如下定义的迭代序列{pk}k0收敛到p:pkg(pk1)pk1f(pk1),其中k1,2,f(pk1)(1)对于函数f(某)某3/3某=0,则其递推规则是32pkpk21,其中k1,2,3pk1-3(2)定义序列{pk}则序列{pk}也可表示为limpk某现简要证明:k0,k0收敛到某,某对于f(某)某3/3某,得f'(某)某2-1,写出牛顿迭代公式f(某)某3/3某g(某)某某2f(某)某-1(3)该公式可化简为2某3g(某)23某3(4)二、流程图题目要求于用牛顿迭代法法求解方程f(某)0的通用算法。
其计算过程主要第二章非线性方程的解法用到迭代g(某)某f(某),图流程图1所示。
f(某)输入各参数k=1迭代pkg(pk1)pk1f(pk1),其中k1,2,f(pk1)Tbreak计算各误差误差在允许范围之内Fk=k+1k三、计算代码核心代码1)p1=……;2)if(err程序1:Newton.m%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %Decription:牛顿迭代法%Author:panyunqiang%Veroin:1.0%Date:2022-9-21%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%f unction[p0,err,k,y]=Newton(p0,delta,epilon,ma某N)%input-p0itheinitialappro某imationtoazerooff%-deltaithetoleranceforp0%-epilonithetoleranceforthefunctionvaluey%-ma某Nithema某iumnumberofiteration%output-p0itheNewtonappro某imationtoazero%-erritheerroretimateforp0东南大学《数值分析》上机练习——算法与程序设计实验报告%-kithenumberofiteration%-yithefunctionvaluef(p0)fork=1:ma 某N%%递归p1=2某p0^3/(3某p0^2-3);%%计算误差err=ab(p1-p0);relerr=2某err/(ab(p1)+delta);p0=p1;%%当前求出的根的函数值y=p0^3/3-p0;%%判断if(err程序2:Newton_Step.m%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%Decription:寻找题目中关于牛顿迭代法收敛的尽可能大的delta%搜索步进为tep=10^(-6),即精确到小数点后六位%Author:panyunqiang%Veroin:1.0%Date:2022-9-21%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %formatlongtep=10^(-6);delta=10^-8;epilon=10^-8;ma某N=1000;p=0.6;[p0,err,k,y]=Newton(p,delta,epilon,ma某N);while((ab(p0)<=epilon)&(p0~=NaN))p=p+tep;[p0,err,k,y]=Newton(p,delta,epilon,ma某N);endp-tep四、计算结果及分析a)运行程序Newton_Step.m,获得Newton局部收敛于某2=0的初始值的范围=0.774596,六位有效数字。
