当前位置：文档之家 › 正弦函数、余弦函数的性质对称中心与对称轴多ppt课件

正弦函数、余弦函数的性质对称中心与对称轴多ppt课件

  • 格式：ppt
  • 大小：676.00 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

正弦函数、余弦函数的图象和性质 PPT

正弦函数、余弦函数的图象和性质 PPT

x0
2
3 2 2
sin x 0 1 0 1 0
1+sin x 1 2 1 0 1
2.画出函数y cos x, x0,2 的简图.
x0
2
3 2 2
cos x 1 0 1 0 1
cos x 1 0 1 0 1
1.已知函数y 2cos x 1,作出函数的图象，并根据图象 写出函数的定义域、值域、单调区间、对称轴、对称中 心，并解不等式 2cos x 1 0.
对称中 心 周期
R
1，1
增：
2
2k
,
2
2k
,
k
Z
减：2
2k ,
3 2
2k
,
k
Z
奇函数
x k , k Z
2
k,0, k Z
2
R
1，1
增： 2k，2k ,k Z
减：2k, 2k , k Z
偶函数
x k , k Z
2
k
,
0
,
k
Z
2
1.画出函数y 1sin x, x0,2 的简图.
函数名sin 后面跟的是角，无论角 以何种形式出现，只要整体取定一 个值，就可以得一个正弦值。
根据正弦函数的图象填写下面的表格
函数
y sin x
y cos x
图象
定义域 值域 单调区 间
奇偶性 对称轴
对称中 心 周期
R
1，1
增：
2
2k
,
2
2k
,
k
Z
减：2
2k ,
3 2
2k
,
k
Z
奇函数
x k , k Z

【课件】正弦函数、余弦函数的性质+(2)+课件-高一上学期数学人教A版(2019)必修第一册

【课件】正弦函数、余弦函数的性质+(2)+课件-高一上学期数学人教A版(2019)必修第一册

23
33
4.变式:求函数y sin( 1 x ), x [ , ]的单调递增区间.
23
解 : y sin( 1 x ) sin(1 x ),
23
23
令z 1 x , x [2 ,2 ], 则z [ 4 , 2 ].
23
33
因为y
sin
z,
z
[
4
,
2
]的单调递减区间是[
4
时取得最小值
1;
7.最大值与最小值
由余弦函数的图象知
y1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
余弦函数当且仅当 x _2_k__,_k____Z__ 时取得最大值1,
当且仅当x _____2_k__,_k___Z_时取得最小值 1.
8. 正弦函数、余弦函数的图象和性质
函 数 y sin x, x R
在每个闭区间 [2k , 2k ](k Z ) 上都单调递减,
其值从1减小到－1.
7.最大值与最小值
正弦函数图象知
y1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
正弦函数当且仅当
x
2k , k Z
_2__________
时取得最大值 1,
当且仅当
x
2k , k Z
___2__________
5
)在区间[0,
]上的单调递增区间为(
)
3
A.[5 ,11 ]
12 12
5
、B.[0, 12 ]

正、余弦函数的对称性、最值PPT课件

正、余弦函数的对称性、最值PPT课件

8
2020/1/14
9
研一研·问题探究、课堂更高效
1.4.2（二）
跟踪训练 1 求函数 y＝cos2x＋4sin x 的最值及取到最 大值和最小值时的 x 的集合．
解 y＝cos2x＋4sin x＝1－sin2x＋4sin x
＝－sin2x＋4sin x＋1＝－(sin x－2)2＋5. ∴当 sin x＝1，即 x＝2kπ＋π2，k∈Z 时，ymax＝4； 当 sin x＝－1 时，即 x＝2kπ－π2，k∈Z 时，ymin＝－4. 所以 ymax＝4，此时 x 的取值集合是{x|x＝2kπ＋π2，
其值从1减小到－1。
2020/1/14
3
(一)探究：①正弦函数的最大值和最小值
y
1
3 5
2
2 3
2
O
2
1

2
3 2
2
5 3
2
x

最大值： 当 x
2k 时，有最大值 y 1
2
最小值：当x 2k 时，有最小值y 1
2
2020/1/14
y
1
3 5
2
P'
2 3
2

2
O
1

2
P
3 2
2
5 3
2
x
对称轴： x ,0, , 2
x k ,k Z
对称中心： ( ,0),( ,0),( 3 ,0),( 5 ,0)
22 2
2
( k ,0) k Z
2
2020/1/14
正弦、余弦函数的性质 对称性和最值
2020/1/14

5.4.2 正弦函数、余弦函数的性质(2)课件高一上学期数学人教A版(2019)必修第一册

5.4.2 正弦函数、余弦函数的性质(2)课件高一上学期数学人教A版(2019)必修第一册

例题讲解 LOGO
例5 求下列函数的最大值，最小值，并写出取最值时自变量x的集合．
（1）y cos x 1, x R；（2）y 3sin 2x, x R.
整体代换
【解析】(2)令z＝2x，使函数y＝－3sin 2x取得最大值的x的集合，
就是使y＝sin z取得最小值的z的集合z z
由
2x
z
1
2
探究新知 LOGO
例7 求下列函数的值域：
(1) y 3 2 cos(2x );(2) y cos2 x 4 cos x 5.
3
解：(1) -1 cos(2x ) 1-2 2 cos(2x ) 2,
3
3
1 3 2 cos(2x ) 5，即y=3 2 cos(2x )的值域为[1,5].
3
3
(2) y cos2 x 4 cos x 5 (cos x 2)2 1,
令t cos x,则t [1,1]
y (t 2)2 1在[1,1]上单调递减
当t= 1时，ymax (1 2)2 1 10 当t=1时，ymin (1 2)2 1 2 故y cos2 x 4 cos x 5的值域为[2,10].
课堂练习 LOGO
1.求函数y=2sin( x),x∈R 的单调递增区间；
4
解：y
2 s in(
x)
2sin(x
)
4
4
由 2k x 3 2k (k Z)， 得 3 2k x 7 2k (k Z)
2
42
4
4
故y 2sin( - x)的单调增区间为[3 2k , 7 2k ](k Z ).
课堂练习 LOGO
课堂小结 LOGO
课堂小结

正弦函数、余弦函数的性质-PPT课件

正弦函数、余弦函数的性质-PPT课件

3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
最大值：当 x
2
时，有最大值 y 1
最小值：当x
2
时，有最小值y 1
探究：余弦函数的最大值和最小值
1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
最大值： 当 x 0
时，有最大值 y 1
最小值：当 x
时，有最小值y 1
例2.下列函数有最大、最小值吗？如果有，请写出取最大、最
(1)y cos x 1, x R;
(2)y 3sin 2x, x R.
解（：2）令t=2x,因为使函数y 3sin t,t R取最大值的t的集合是
{t | t 2k , k Z}
由
2x
t
2
2k
得
x k
2
4
所以使函数 y 3sin 2x, x R取最大值的x的集合是 {x | x k , k Z} 4
故 2k 1 x 2k ,
2
2 32
得 5 4k x 4k , k Z.
3
3
则函数y sin(1 x )，x R的单调递增区间是[ 5 4k, 4k]。
23
33
练习：求函数y sin( 1 x)，x R的单调递增区间 32
得 5 4k x 11 4k , k Z.
2
2x k
32
解得：对称轴为 x k ,k Z
12 2
(2) y sin z 的对称中心为 (k ,0) , k Z

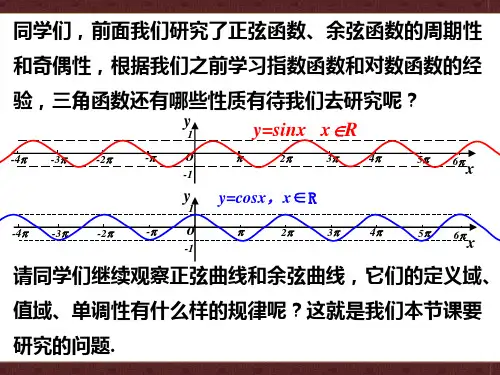
5-4-2 第2课时 正弦函数、余弦函数的性质课件-高一上学期数学人教A版(2019)必修第一册

5-4-2 第2课时 正弦函数、余弦函数的性质课件-高一上学期数学人教A版(2019)必修第一册
π
π
π




由 y＝cosx＋6，x∈0，2，可得 x＋ ∈ ， ，




6 6 3
1

3
∴ − ≤ cos( + ) ≤
2
6
2
1

所以函数的值域为－ ，
2
3
.
2
解三角不等式
当x∈[0，2π]时，求不等式 cos ≥
y


集.
, ∪ [ , ]
值域、单调性有什么样的规律呢？这就是我们本节课要
研究的问题.
学习
目标
1. 理 解 正 弦 函 数 、 余 弦
2.能够利用函数的单调
函数的单调性具有周期
性解决比较函数值的大
性变化的规律，通过一
小以及求函数的最值、
个周期内的单调性进而
值域等问题.
研究在整个定义域上的
性质.
问题1：类比以往对函数性质的研究，正弦函数、余
使函数 y cos x, x R 取得最小值的x的集合
{x | x (2k 1) , k Z}
函数 y cos x 1, x R 的最大值是1+1=2；最小值是
-1+1=0.
例3.下列函数有最大、最小值吗？如果有，请写出取最大、最
小值时的自变量x的集合，并说出最大、最小值分别是什么.


5π
π
π
即 2kπ－ 6 ≤2x≤2kπ＋6(k∈Z)，
令 2kπ－π≤2x－6≤2kπ(k∈Z)，
5π
π
∴kπ－12≤x≤kπ＋12(k∈Z).


5π
π

第五章 第四节 三角函数的图象与性质 课件(共63张PPT)

第五章 第四节 三角函数的图象与性质 课件(共63张PPT)

，解
得 ω＝32 .
法二：由题意，得 f(x)max＝fπ3
2．(必修 4P35 例 2 改编)若函数 y＝2sin 2x－1 的最小正周期为 T，最大
值为 A，则( )
A．T＝π，A＝1
B．T＝2π，A＝1
C．T＝π，A＝2
D．T＝2π，A＝2
A [T＝22π ＝π，A＝2－1＝1.]
3．(必修 4P40 练习 T4 改编)下列关于函数 y＝4cos x，x∈[－π，π]的单 调性的叙述，正确的是( )
求三角函数单调区间的两种方法 (1)代换法：就是将比较复杂的三角函数含自变量的代数式整体当作一个 角 u(或 t)，利用复合函数的单调性列不等式求解．(如本例(1)) (2)图象法：画出三角函数的正、余弦曲线，结合图象求它的单调区间． [注意] 要注意求函数 y＝A sin (ωx＋φ)的单调区间时 ω 的符号，若 ω<0， 那么一定先借助诱导公式将 ω 化为正数．同时切莫漏掉考虑函数自身的定义 域．
又当 x∈[0，π2
]时，f(x)∈[－
2 2
，1]，所以π2
≤ω2π
－π4
≤5π4
，解得
3 2
≤ω≤3，故选 B.
π
π
π
优解：当 ω＝2 时，f(x)＝sin (2x－ 4 ).因为 x∈[0，2 ]，所以 2x－ 4 ∈
π [－ 4
，3π4
π ]，所以 sin (2x－ 4
)∈[－
2 2
，1]，满足题意，故排除 A，C，
B．[kπ，kπ＋π2 ](k∈Z)
C．[kπ＋π6 ，kπ＋23π ](k∈Z)
D．[kπ－π2 ，kπ](k∈Z)
(2)函数 y＝tan x 在－π2，32π 上的单调减区间为__________．

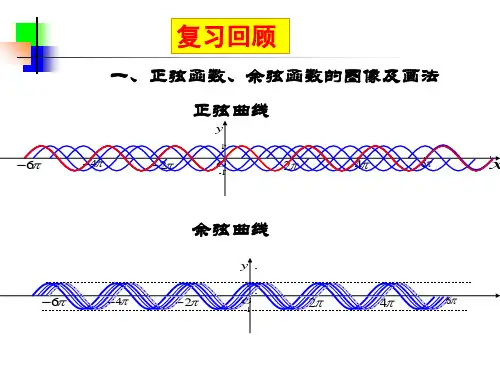
正弦余弦函数的图像性质(周期、对称、奇偶)经典课件25页PPT

正弦余弦函数的图像性质(周期、对称、奇偶)经典课件25页PPT

新知探究 ：
1、正弦函数的单调性 y
1
y
1
2
o
2
o
-1
-1
3
2
2
x x
y=sinx x[0,2]
y
y=sinx xR
-4 -3
-2
1
- o
-1
正弦曲 线
2
3
4
5 6 x
新知探究：
1、正弦函数的单调性
y
-4 -3
-2
- 2
1
o
-1
2
2
3
4
5 6 x
x
2
…
0
…
正 正弦弦函数余.余弦弦函函数的数图象对和称性质性
-
-
-
6
4
2
对称轴：无数条
xk，kZ
2
-
-
-
6
4
2
对称轴：无数条 x=kπ，k∈Z
-
y
正弦 函数 y=sinx的 图象
1-
-
-
-
o - 1-
2
4
6
x
对称中心：无数个
（kπ，0）,k∈Z
y
余 弦函 数 y =co sx的 图象
1-
-
-
-
o
复习回顾
一、正弦函数、余弦函数的图像及画法
正弦曲线
y
1-
-
-
6
4
2
o
-1-
2
4
6
x
6
4
余弦曲线
y-
1
2
o-
-1
2
4
6
探索发现

高三数学正弦余弦函数的性质,图像课件

高三数学正弦余弦函数的性质,图像课件

例1： 求函数
3 cos x y 2 cos x
的值域
解法二： ∵ ∴
2y 3 cos x ( y 1) y 1 1 cos x 1
1 2y 3 1且y 1 y 1
∴
4 函数值域为 2 3，
反函数法
练习：
①若 2 ，则 y 2 cos 2
例3： 求方程lg x sin x的实根的个数
在同一坐标系中作出 y lg x和y sin x的图象如下：
y=sinx
数形结合思想
两图象有三个交点，即方程有三个实数根。
练习：
⒈已知 f ( x) 4m sin x cos 2 x( x R) ,
③ 函数
y 1 2 cos x lg(2 sin x 1) 的定义域为
5 2 k , 2 k , k Z 6 3
例 2： 若函数 f ( x) cos 2 x 2a cos x a 2 2a(0 x )的 最 小 值

2
, 知0 cos x 1, 可 得
1 当0 a 2时, f ( x） 最 小 值 为 a 2 2a 1 2解 得 2 a 2 2 , 此 时f ( x)的 最 大 值 为 1 当a 2时 ，f ( x)的 最 小 值 为 a 2 4a 1 2, 解 得a 3 此 时f ( x)的 最 大 值 为 2 a 0时, f ( x)的 最 小 值 a 2 2a 1 2, 解 得a 1, 显 然 不 成 立
y=sinx xR
ห้องสมุดไป่ตู้
y
1
正弦曲 线
3
-4
-3

高一数学必修第一册正弦函数、余弦函数的性质课件

高一数学必修第一册正弦函数、余弦函数的性质课件

上都单调递减，其值从1减小到-1.
最大值与最小值
【整理】从上述对正弦函数、余弦函数的单调性的讨论中容易得到：

+ ( ∈ ) 时取得最大值1，


当且仅当 = − + ( ∈ ) 时取得最小值-1；

①正弦函数当且仅当 =
②余弦函数当且仅当 = ( ∈ ) 时取得最大值1，
【1】周期性：观察正弦函数的图像，可以发现，在图像上，横坐标每隔2π个单位
长度，就会出现纵坐标相同的点，这就是正弦函数值具有的“周而复始”的
变化规律.实际上，这一点既可以从定义中看出，也能从诱导公式中得到反映.即自
变量 的值加上2π的整数倍时所对应的函数值，与 所对应的函数值相等.数学
上用周期性来定量地刻画这种“周而复始”的规律.
如何用自变量的系数表示上述函数的周期呢？
事实上，令 = + ，那么由 ∈ 得 ∈ ，且函数 = , ∈ 及函数
= , ∈ 的周期都是.
因为 + = + + = +




+ ，所以自变量增加 ，函数值




+ ,
+ ( ∈ ) 上都单调递减，其值从1减小到-1.


单调性


−
−



−



同样的道理结合余弦函数的周期性我们可以知道：
余弦函数在每一个闭区间
在每一个闭区间
− + , ( ∈ ) 上都单调递增，其值从-1增大到1；
, + ( ∈ )
关于y轴对称.所以正弦函数是奇函数，余弦函数是偶函数.

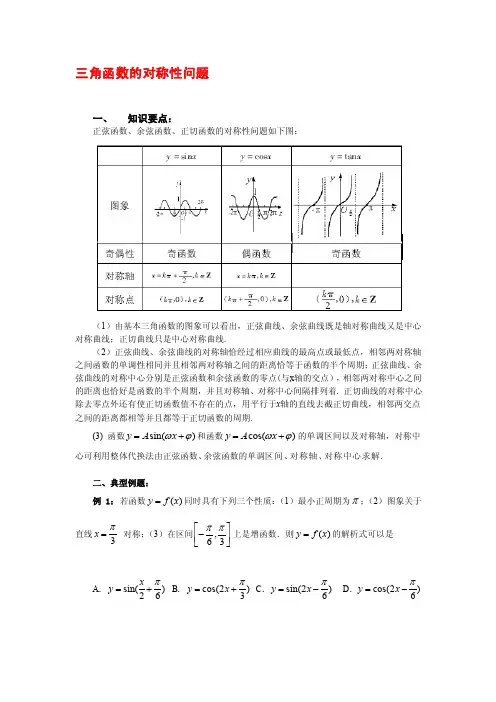
三角函数的对称性问题

三角函数的对称性问题

三角函数的对称性问题一、知识要点：正弦函数、余弦函数、正切函数的对称性问题如下图：（1）由基本三角函数的图象可以看出，正弦曲线、余弦曲线既是轴对称曲线又是中心对称曲线；正切曲线只是中心对称曲线.（2）正弦曲线、余弦曲线的对称轴恰经过相应曲线的最高点或最低点，相邻两对称轴之间函数的单调性相同并且相邻两对称轴之间的距离恰等于函数的半个周期；正弦曲线、余弦曲线的对称中心分别是正弦函数和余弦函数的零点(与x 轴的交点），相邻两对称中心之间的距离也恰好是函数的半个周期，并且对称轴、对称中心间隔排列着. 正切曲线的对称中心除去零点外还有使正切函数值不存在的点，用平行于x 轴的直线去截正切曲线，相邻两交点之间的距离都相等并且都等于正切函数的周期.(3) 函数sin()y A x ωϕ=+和函数cos()y A x ωϕ=+的单调区间以及对称轴，对称中心可利用整体代换法由正弦函数、余弦函数的单调区间、对称轴、对称中心求解.二、典型例题：例1：若函数()y f x =同时具有下列三个性质：（1）最小正周期为π；（2）图象关于直线3x π=对称；（3）在区间,63ππ⎡⎤-⎢⎥⎣⎦上是增函数．则()y f x =的解析式可以是A ．sin()26x y π=+B ．cos(2)3y x π=+C ．sin(2)6y x π=-D ．cos(2)6y x π=-2222π22解析：由最小正周期为π,可排除A, 由图象关于直线3x π=对称,可排除B, 由在区间,63ππ⎡⎤-⎢⎥⎣⎦上是增函数可得答案应为C.评述：本题考查了三角函数的性质及其解析式的探求.三角的复习应充分利用数形结合的思想方法，即借助于图象(或三角函数线)的直观性来获取三角函数的性质，同时利用三角函数的性质来描绘函数的图象，揭示图形的代数本质.例2：已知函数()f x 是定义在)3,3(-上的奇函数，当30<<x 时，)(x f 的图象如图所示，则不等式0cos )(<x x f 的解集是 ( )A ．(3,(0,1)(,3)22ππ--⋃⋃ B ．(,1)(0,1)(,3)22ππ--⋃⋃C ．(3,1)(0,1)(1,3)--⋃⋃D ．(3,(0,1)(1,3)2π--⋃⋃解析: ∵y = cosx 是R 上的偶函数，∴()cos y f x x =是定义在)3,3(-上的奇函数，故只须考察()cos y f x x =在区间(0,3)上的函数值的取正取负的情况，根据函数(),cos y f x y x ==在区间(0,3)上的零点，列表如下：函数()cos y f x x =的图象如上所示，不等式0cos )(<x x f 的解集是三个分离的开区间的并集，即(,1)(0,1)(,3)22ππ--⋃⋃.故应选B.评述：考纲要求“理解正弦函数、余弦函数、正切函数的图像和性质，会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+ϕ)的简图”.命题时将函数图象的叠加作为命题点,这也是近年来高考的一个热点.三、举一反三：1. 函数1cos y x =+的图象 ( )A. 关于x 轴对称B.关于y 轴对称C.关于原点对称D.关于直线x =2π对称答案： B解析:由于函数cos 1y x =+为偶函数，故其图象关于y 轴对称.故应选B.2.将函数y =sin x －3cos x 的图象沿x 轴向右平移a 个单位(a >0)，所得图象关于y 轴对称，则a 的最小值为（ ）A ．76π B ．2π C ．6π D ．3π答案：C解析:由)3sincos 3cos(sin 2cos 3sin ππ⋅-⋅=-=x x x x y 2sin(),3x π=-2sin(),3y x π=-即 函数图象的周期,2π=T 且图象上一个对称中心)0,3(π,结合图象分析知,图象再向右平移6π 后，图象关于y 轴对称,所以a 的最小值为,6π故选C.3. 若函数f (x )＝sin2x ＋a cos2x 的图象关于直线x ＝－π8对称，则a ＝ .答案： a ＝－1解析:∵x 1＝0，x 2＝－π4 是定义域中关于x ＝－π8对称的两点∴f (0)＝f (－π4 ),即0＋a ＝sin(－π2 )＋a cos(－π2), ∴a ＝－1.4.已知函数22()sin 2sin cos 3cos f x x x x x =++，R x ∈.(Ⅰ)求函数()f x 图象的对称中心坐标；(Ⅱ)若11()25x f =，且π<<x 0，求x x sin cos -的值.解析:)2cos 1(232sin 22cos 1)(x x x x f +++-=22cos 2sin ++=x x 2)42sin(2++=πx .令ππk x =+42 知 82ππ-=k x ， Z k ∈.故函数)(x f 的图象的对称中心的坐标为)2,82(ππ-k（Z k ∈）.（II ）由11()25xf =, 得1sin cos 5x +=, 平方得 242sin cos 25x x =- .又).,0(π∈x 故 0s i n>x ， 0cos <x∴7cos sin 5x x -===-即7cos sin 5x x -=-.。

正余弦函数图像和性质PPT课件

正余弦函数图像和性质PPT课件

（2）余弦函数“五点作图法”：
y 1 y=cosx
3 2
2
o
2
-1
3 2
Y=sinx 2 5 3 x
2
五个关 键点：
( 0 ,1),
( ,0 ), 2
( , 1), ( 3 , 0 ) , ( 2 ,1)
2
（3）正、余弦函数图象的关系
cosx=sin(x+
2
y=cosx
y
) sinx=cos( -x)=cos(x- )
定义域 值域 周期性 对称性 单调性
性质的应. 用
3
一.基础知识复习
（一）正、余弦函数图象
“五点作图法”
（1）正弦函数“五点作图法”：
y
1
4
3
2
-
3 2
-
-
2
o
2
3 2
2
3
4 x
-1
五个关键点：
( 0 , 0 ) ,(
2
, 1 ) , ( , 0 ) ,( 3
2
, 1)(, 2 , 0 )
正 余弦函数的图象与性质(1)
y
1
ysinx,x[0,2
3p
π
2
2π
O
p
x
2
-1
思考4：观察函数y=sin在[0，2π]内的 图象，其形状、位置、凸向等有何变化 规律？
《正弦函数、余弦函数的图象和性质》的知识框架
正弦线 正弦函数的图象 平移变换 余弦函数的图象
正弦函数的性质 “五点法”作 图
余弦函数的性质
⑤奇偶性:
奇偶性的y1定义y=：sif f n( ( x x x ) ) ( x ff R( ( x x )) ) ff( ( x x ) ) 为 为 偶 奇 函 函 数 数

课件4：1.3.2 余弦函数、正切函数的图象与性质

课件4：1.3.2 余弦函数、正切函数的图象与性质
|φ|的最小值为|φ|＝2π＋2－ 3 ＝6.


答案：A
3.试比较
23
cos－ 5 π与


17
cos－ 4 π的大小．



23

解：cos－ 5 π＝cos



17

cos－ 4 π＝cos


23
3
3
5 π＝cos(4π＋5π)＝cos 5π，
的图象也可由 y＝cos x 的图象通过变换得到，变换规
律相同．
3.研究函数 y＝Acos (ωx＋φ)的性质时，注意采用整体代换的
思想．如当 ωx＋φ＝2kπ(k∈Z)时，它取得最大值；当 ωx＋φ
＝2kπ＋π(k∈Z)时，它取得最小值.
4.正切函数的图象
π
正切函数有无数多条渐近线，渐近线方程为 x＝kπ＋ ，k∈Z，相邻
∴函数
1

π
π
3
y＝tan－2x＋4的单调递减区间是2kπ－2，2kπ＋2π(k∈Z)，




最小正周期 T＝
π
1＝2π.
－
2
小结 函数 y＝tan(ωx＋φ) (ω>0)的单调区间的求法是把
π
π
ωx＋φ 看成一个整体，解－2＋kπ<ωx＋φ<2＋kπ，k∈Z
即可．当 ω<0 时，先用诱导公式把 ω 化为正值再求单调
(
π
A.6
π
B.4
π
C.3
π
D.2
)
解析：由
f
4π



，0
y＝3cos(2x＋φ)的图象关于点 3

正弦定理和余弦定理 课件(53张)

正弦定理和余弦定理 课件(53张)

a≥b 一解
a>b 一解
上表中,若A为锐角,当a<bsin A时无解;若A为钝角或直角,当a≤b时无解.
3.三角形面积
设△ABC的内角A、B、C所对的边分别为a、b、c,其面积为S.
(1)S=
1 2
ah(h为BC边上的高).
1
(2)S= 2 absin C=
1
1
2 acsin B = 2 bcsin A.
1∶13.
由余弦定理得cos
C=
52
112 132 2 511
<0,所以C为钝角,即△ABC一定是钝角
三角形.
2-2 在△ABC中,内角A,B,C所对的边分别是a,b,c,若c-acos B=(2a-b)cos
A,则△ABC的形状为 ( D )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等腰或直角三角形
A. 6 B. 3 C. 6
D. 3
4.△ABC的内角A,B,C所对的边分别为a,b,c,若a2cos Asin B=b2sin Acos B,
则△ABC的形状为 ( D )
A.等腰直角三角形 B.直角三角形 C.等边三角形 D.等腰三角形或直角三角形
5.若满足条件C=60°,AB= 3 ,BC=a的△ABC有两个,那么a的取值范围是
1 2
absin
C≤
3
3 4
,又S△
ABC>0,所以S△ABC∈
0,
3
3 4
.
解法二:因为 a = b = c =2,
sin A sin B sin C
所以a=2sin A,b=2sin B.
又A+B=
2
3

课件：正弦函数、余弦函数的图像与性质市公开课一等奖省赛课获奖PPT课件

课件：正弦函数、余弦函数的图像与性质市公开课一等奖省赛课获奖PPT课件

2
2
；
（3）由 π2 2kπ 2x π4 π2 2kπ
得 π8 kπ x 3π8 kπ（k Z）. 第20页
由π2 2kπ 2x π4 3π2 2k
得 3π8 kπ x 7π8 kπ （k Z）
函数y
1 2
cos2
x
sin
x
cos
x
3 2
sin2
x
的增区间：[π8 kπ，3π8 kπ] (k Z) ；
回顾：
1. 三角函数是以角（实数）为自变量函数.
y sin x, x R
2. 惯用画图方法: 描点法
y =sinx 过点
( ,sin ),( ,sin ) 6 63 3
而 sin 3 0.866,不便于描点 32
故介绍另一个画法:几何法(即利用三角函 数线画图)
第1页
正弦函数图像
1
cos2
x
sin
x
cos
x
3
sin 2
x，x
R，求
：
2
2
（1）函数的最大值、最小值 ；
（2）函数的最小正周期 ；
（3）函数的单调区间； （4）函数的图象是正弦函数 y sin x 经过怎样的变化得到的？
解：
y
1 2
1
cos 2
2x
1 2
sin
2x
3 2
1
cos 2
2x
1
1 2
sin
2x
1 2
cos 2x
y cos x, x 0,2
图象与x轴交点
(
2
,0)
(
3 2
,0)
图象最低点 ( ,1)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

解：令z 1 x
2
3
函数y sin z的单调增区间
[ 2k , 2k ]
2
2
即 2k 1 x 2k
2
2 32
得 5 4k x 4k (k Z )
3
3
又∵ x [2 , 2 ]
函数y sin(1 x )的单调增区间是 [ 5 , ]
23
33 9
求函数 y sin( 1 x)的单调递增区间。
轴对称：将图象绕对称轴折叠180度后所得的曲 线能够和原来的曲线重合。
5
正弦函数——对称性
●
●
●
●
正弦函数的对称性
正弦函数是轴对称图形吗？
对称轴： x k ,k Z
2
正弦函数是中心对称图形吗？
对称中心（ k ,0) (k Z ) 6
余弦函数——对称性
余弦函数的对称性
余弦函数是轴对称图形吗？
1
函数 图形 定义域 值域 最值
单调性 奇偶性
周期 对称性
y=sinx
y
1
2
0
2
-1
3 2 5 x
2
2
xR
y [1,1]
xx2222kk时时，，yymmaxin
1 1
x[-
2
2k
,
2
2k
]
x[2
2k ,
3
2
2k
]
增函数 减函数
奇函数
2
对称轴： x
2
k
,k
Z
对称中心： (k , 0) k Z
x 4k
3
x
|
x
5
3
4k ,k
Z
使原函数取得最大值的集合是
x
|
x
3
4k
,k
Z
函数y的最大值是
1 2
，
最小值是
1 2
。
3
利用三角函数的单调性，比较下列各组数的的大小.
（3） cos515。 与 cos530。. y 1
0
2
3 2
2
5 2
x
-1
解： cos515 o cos(360 o 155 o ) cos155 o
y=cosx
y
1
0
2
3 2 5 x
2
2
-1
xR
y [1,1]
x 2k 时， ymax 1
x 2k 时，ymin 1
x 2k ,2k 2 增函数 x[2k , 2k ] 减函数
偶函数
2
对称轴： x k , k Z 对称中心：(2 k , 0) k 2 Z
(4)
y
1 2
sin
3
3
111 2x3解：令z 1 x
23
要使y 1 sin z有最大值， 2
必须 z 2k ,k z
2
1 x 2k
2 32
y
1
2
0
2
3 2 5 x
2
2
-1
必要须使y
1 sin 2
z有最小值，
z 2k ,k z
2
1 x 2k
23 2
x 5 4k
3
使原函数取得最小值的集合是
32 为了防止出错，以及计算方便，遇到负号要提出来
反思:
对于求y Asin( x )的单调区间,要注意 0 的情形,将 <0化为 >0,再处理.
10
变式3.求函数y sin( 1 x )的单调增区间.
23
遇到x系数为负的三角函数， 详解：y sin( 1 x ) sin(1 x )
cos530 o cos(360 o 170 o ) cos170 o
因为 0o 155o 170o 180o
且函数y=cos x,x∈[0°,180°]是减函数，所以
cos155o cos170o
即
cos515o cos530o
4
中心对称：将图象绕对称中心旋转180度后所得 的曲线能够和原来的曲线重合。
对称轴：x k (k Z )
余弦函数是中心对称图形吗？
对称中心：x k , k Z
2
7
y
1
•
2
0
求 y sin(2 x -1 )
2
3
2 5
x
2
2
函数的对称轴和对称中心
解（1）令
z
3
2x
则
y sin(2x ) sin z
3
3
y sin z 的对称轴为 z k ,k Z
2
2x k
32
解得：对称轴为 x k ,k Z
12 2
(2) y sin z 的对称中心为 (k ,0) , k Z
z k
2x k
3
x k
62
对称中心为 ( k ,0) ,k Z
62
8
例5 求函数 y sin( 1 x ) ，x [2 , 2 ]
的单调增区间.2 3
23
23
第即一求函 步数一y 定sin要(12 将x x3系)的单 数调化减为区间 正。值，
否2则 2答k 案 12会x 正3 好32相 反2k，, k 出Z现错误。
5 4k x 11 4k , k Z
3
3
所以函数y sin( 1 x )的单调增区间为：
23
[5 4k , 11 4k ], k Z