最优化DFP算法报告

第1篇一、实验目的本次实验旨在通过数值实验，验证不同优化算法在解决特定优化问题时的性能和效率。

实验选取了三种常用的优化算法：黄金分割法、复合形法和进化场优化算法（EFO），分别针对一个典型的无约束优化问题进行实验，并对比分析其性能。

二、实验内容1. 黄金分割法- 基本原理：黄金分割法是一种基于搜索区间分割的优化算法，通过不断缩小搜索区间，寻找最优解。

- 实验设计：选择一个无约束优化问题，设定初始搜索区间，通过迭代计算，逐步缩小搜索区间，直至满足终止条件。

2. 复合形法- 基本原理：复合形法是一种基于几何形状的优化算法，通过迭代构建一个复合形，逐渐逼近最优解。

- 实验设计：选择与黄金分割法相同的优化问题，设定初始复合形，通过迭代调整复合形顶点，直至满足终止条件。

3. 进化场优化算法（EFO）- 基本原理：EFO是一种基于种群的元启发式优化算法，通过模拟自然进化过程，寻找最优解。

- 实验设计：选择与黄金分割法和复合形法相同的优化问题，设定初始种群，通过迭代计算，不断进化种群，直至满足终止条件。

三、实验步骤1. 选择优化问题- 实验选取了如下无约束优化问题：\[ f(x) = \sum_{i=1}^{n} x_i^2, \quad x \in [-5, 5]^n \]- 目标：求解函数 \( f(x) \) 的最小值。

2. 算法实现- 黄金分割法：编写程序实现黄金分割法的基本原理，设置初始搜索区间和终止条件。

- 复合形法：编写程序实现复合形法的基本原理，设置初始复合形和终止条件。

- EFO：编写程序实现EFO算法的基本原理，设置初始种群和终止条件。

3. 实验参数设置- 黄金分割法：设置迭代次数为100，初始搜索区间为 \([-5, 5]\)。

- 复合形法：设置迭代次数为100，初始复合形顶点为随机选取。

- EFO：设置迭代次数为100，初始种群规模为10。

4. 实验结果分析- 对比三种算法的迭代次数、最优解值和收敛速度。

最优化学习报告（写写帮整理）第一篇：最优化学习报告（写写帮整理）最优化学习报告在日常生活中，无论做任何一件事，人们总希望以最少的代价取得最大的效益，也就是力求最好，这就是优化问题。

最优化的问题是奥数中常见的一个问题，因为最优化是在生活中常用的。

例如一件事情要怎么样才能在尽可能节省人力、物力和时间前提下，争取获得在可能范围内的最佳效果。

这个就是需要通过计算来实现!最优化问题不仅具有趣味性，而且由于解题方法灵活，技巧性强，因此对于开拓解题思路，增强数学能力很有益处。

最优化就是在一切可能的方案中选择一个最好的方案以达到最优目标的学科。

最优化问题无处不在。

只要存在选择，就一定存在优化问题。

例如，从甲地到乙地有公路、水路、铁路、航空四种走法，如果我们追求的目标是省钱，那么只要比较一下这四种走法的票价，从中选择最便宜的那一种走法就达到目标。

这是最简单的最优化问题。

生活中还有很多的例子，比如说随着我国经济高速发展，能源短缺的矛盾突现，建设节约性社会是众望所归。

现实生活中，汽车作为代步工具，与我们的生活密切相关。

汽油的使用效率何时最高的问题也是最优化问题，众所周知，汽车的每小时耗油量与汽车的速度有一定的关系。

如何使汽车的汽油使用效率最高（汽油使有效率最高是指每千米路程的汽油耗油量最少）的问题。

此外还有磁盘的最大存储量问题，计算机把数据存储在磁盘上。

磁盘是带有磁性介质的圆盘，并有操作系统将其格式化成磁道和扇区。

磁道是指不同半径所构成的同心轨道，扇区是指被同心角分割所成的扇形区域。

磁道上的定长弧段可作为基本存储单元，根据其磁化与否可分别记录数据0或1，这个基本单元通常被称为比特（bit）。

则一个磁盘它的存储区是半径介于与多少之间的环形区域，磁盘的存储量越大问题。

第三个例子，饮料瓶大小对饮料公司利润的影响，现实生活中你是否注意过，市场上等量的小包装的物品一般比大包装的要贵些？那是不是饮料瓶越大，饮料公司的利润越大？又比如说一个具体的例子，货轮上卸下若干只箱子，总重量为10吨，每只箱子的重量不超过1吨，为了保证能把这些箱子一次运走，问至少需要多少辆载重3吨的汽车?[分析] 因为每一只箱子的重量不超过1吨，所以每一辆汽车可运走的箱子重量不会少于2吨，否则可以再放一只箱子。

最优化方法课程设计报告班级：________________姓名： ______学号： __________成绩：2017年 5月 21 日目录一、摘要.............................. 错误!未定义书签。

二、单纯形算法 .......................... 错误!未定义书签。

1.1 单纯形算法的基本思路................................................................... 错误!未定义书签。

1.2 算法流程图....................................................................................... 错误!未定义书签。

1.3 用matlab编写源程序...................................................................... 错误!未定义书签。

二、黄金分割法 ......................... 错误!未定义书签。

2.1 黄金分割法的基本思路................................................................... 错误!未定义书签。

2.2 算法流程图....................................................................................... 错误!未定义书签。

2.3 用matlab编写源程序...................................................................... 错误!未定义书签。

2.4 黄金分割法应用举例....................................................................... 错误!未定义书签。

最优化方法(Matlab)实验报告—— Fibonacci 法一、实验目的：用MATLAB 程序实现一维搜索中用Fibonacc 法求解一元单峰函数的极小值问题。

二、实验原理：（一）、构造Fibonacci 数列：设数列{}k F ，满足条件：1、011F F ==2、11k k k F F F +-=+则称数列{}k F 为Fibonacci 数列。

（二）、迭代过程：首先由下面的迭代公式确定出迭代点：111(),1,...,1(),1,...,1n k k k k k n k n k k k k k n k F a b a k n F Fu a b a k n F λ---+--+=+-=-=+-=-易验证，用上述迭代公式进行迭代时，第k 次迭代的区间长度缩短比率恰好为1n kn k F F --+。

故可设迭代次数为n ，因此有 11121211221111223231()()......()()n n n n n n n n nF F F F F F b a b a b a b a b a F F F F F F F ------=-=⨯-==⨯-=- 若设精度为L ，则有第n 次迭代得区间长度 111()n n nb a Lb a LF -≤-≤ ，即就是111()nb a L F -≤，由此便可确定出迭代次数n 。

假设第k 次迭代时已确定出区间 [,]k k a b 以及试探点,[,]k k k k u a b λ∈并且k k u λ<。

计算试探点处的函数值，有以下两种可能： （1） 若()()k k f f u λ>，则令111111111,,()()()k k k kk k k k n k k k k k n ka b b f f F a b a F λλμλμμ++++--++++-=====+-计算 1()k f μ+的值。

（2）()()k k f f u λ≤，则令111121111,,()()()k k k kk k k k n k k k k k n ka ab f f F a b a F μμλμλλ++++--++++-=====+-计算1()k f λ+ 的值。

最优化方法实验报告（1）最优化方法实验报告Numerical Linear Algebra And Its Applications学生所在学院：理学院学生所在班级：计算数学10-1学生姓名：甘纯指导教师：单锐教务处2013年5月实验一实验名称：熟悉matlab基本功能实验时间: 2013年05月10日星期三实验成绩：一、实验目的：在本次实验中，通过亲临使用MATLAB，对该软件做一全面了解并掌握重点内容。

二、实验内容：1. 全面了解MATLAB系统2. 实验常用工具的具体操作和功能实验二实验名称：一维搜索方法的MATLAB实现实验时间: 2013年05月10日星期三实验成绩：一、实验目的：通过上机利用Matlab数学软件进行一维搜索，并学会对具体问题进行分析。

并且熟悉Matlab软件的实用方法，并且做到学习与使用并存，增加学习的实际动手性，不再让学习局限于书本和纸上，而是利用计算机学习来增加我们的学习兴趣。

二、实验背景：(一）0.618法（黄金分割法），它是一种基于区间收缩的极小点搜索算法，当用进退法确定搜索区间后，我们只知道极小点包含于搜索区间内，但是具体哪个点，无法得知。

1、算法原理黄金分割法的思想很直接，既然极小点包含于搜索区间内，那么可以不断的缩小搜索区间，就可以使搜索区间的端点逼近到极小点。

2、算法步骤用黄金分割法求无约束问题min (),f x x R ∈的基本步骤如下：（1）选定初始区间11[,]a b 及精度0ε>，计算试探点：11110.382*()a b a λ=+-11110.618*()a b a μ=+-。

（2）若k k b a ε-<，则停止计算。

否则当()()k k f f λμ>时转步骤（3）。

当()()k k f f λμ≤转步骤（4）。

（3）置11111110.382*()k kk k k k k k k k a b b a b a λλμμ+++++++=??=??=??=+-?转步骤（5）（4）置11111110.382*()k k k k k k k k k k a a b a b a μμλλ+++++++=??=??=??=+-?转步骤（5）（5）令1k k =+，转步骤（2）。

最优化基础理论与⽅法⽬录1．最优化的概念与分类 (2)2. 最优化问题的求解⽅法 (3)2.1线性规划求解 (3)2.1.1线性规划模型 (3)2.1.2线性规划求解⽅法 (3)2.1.3 线性规划算法未来研究⽅向 (3)2.2⾮线性规划求解 (4)2.2.1⼀维搜索 (4)2.2.2⽆约束法 (4)2.2.3约束法 (4)2.2.4凸规划 (5)2.2.5⼆次规划 (5)2.2.6⾮线性规划算法未来研究⽅向 (5)2.3组合规划求解⽅法 (5)2.3.1 整数规划 (5)2.3.2 ⽹络流规划 (7)2.4多⽬标规划求解⽅法 (7)2.4.1 基于⼀个单⽬标问题的⽅法 (7)2.4.2 基于多个单⽬标问题的⽅法 (8)2.4.3多⽬标规划未来的研究⽅向 (8)2.5动态规划算法 (8)2.5.1 逆推解法 (8)2.5.2 顺推解法 (9)2.5.3 动态规划算法的优点及研究⽅向 (9)2.6 全局优化算法 (9)2.6.1 外逼近与割平⾯算法 (9)2.6.2 凹性割⽅法 (9)2.6.3 分⽀定界法 (9)2.6.4 全局优化的研究⽅向 (9)2.7随机规划 (9)2.7.1 期望值算法 (10)2.7.2 机会约束算法 (10)2.7.3 相关机会规划算法 (10)2.7.4 智能优化 (10)2.8 最优化软件介绍 (11)3 最优化算法在电⼒系统中的应⽤及发展趋势 (12)3.1 电⼒系统的安全经济调度问题 (12)3.1.1电⼒系统的安全经济调度问题的介绍 (12)3.1.2电⼒系统的安全经济调度问题优化算法的发展趋势 (12)2. 最优化问题的求解⽅法最优化⽅法是近⼏⼗年形成的，它主要运⽤数学⽅法研究各种优化问题的优化途径及⽅案，为决策者提供科学决策的依据。

最优化⽅法的主要研究对象是各种有组织系统的管理问题及其⽣产经营活动。

最优化⽅法的⽬的在于针对所研究的系统，求得⼀个合理运⽤⼈⼒、物⼒和财⼒的最佳⽅案，发挥和提⾼系统的效能及效益，最终达到系统的最优⽬标。

智能优化算法报告总结范文智能优化算法是一种基于机器学习和人工智能技术的高效算法，它能够在解决复杂问题时进行自动优化和调整，以提供最佳解决方案。

本报告将对智能优化算法进行总结和分析，以期探讨其优势、应用领域和未来发展趋势。

首先，智能优化算法具有广泛的应用领域。

无论是供应链管理、资源调配、网络优化还是数据挖掘，智能优化算法都能够提供有效的解决方案。

例如，在供应链管理中，智能优化算法可以通过优化运输路线和库存管理，帮助企业降低成本、提高效率；在数据挖掘中，智能优化算法能够从大量数据中自动挖掘出有用的模式和规律，帮助企业进行精准营销和决策。

其次，智能优化算法具有高效快速的特点。

传统的优化算法可能需要进行大量的计算和试错，耗费大量的时间和资源。

而智能优化算法基于机器学习和人工智能技术，能够通过学习和适应环境快速找到最佳解决方案。

这不仅提高了问题解决的效率，还能够减少人工干预和资源的浪费。

另外，智能优化算法还具有较好的鲁棒性。

在实际应用中，由于问题的复杂性和不确定性，传统的优化算法可能会受到噪声和干扰的影响，导致结果不稳定。

而智能优化算法通过学习和适应能力，能够自动调整算法参数和策略，从而提高算法的鲁棒性和稳定性。

这使得智能优化算法能够在不同的环境下适应并取得可靠的结果。

然而，智能优化算法也存在一些挑战和限制。

首先，智能优化算法的效果受到数据质量和特征表示的影响。

如果输入的数据含有噪声或信息缺失，就会影响算法的性能和结果准确度。

同时，特征表示的选择也会影响算法的优化过程和结果。

因此，在实际应用中，需要提前对数据进行预处理和特征工程，以获得更好的优化效果。

此外，智能优化算法还需要有效的评估和比较方法。

由于问题的多样性和复杂性，不同的优化算法可能适用于不同的问题和场景。

因此，如何评估和比较不同算法的性能和效果是一个挑战。

目前，针对不同问题和领域的评估指标和方法还需要进一步研究和发展，以提供更客观、可靠的评估结果。

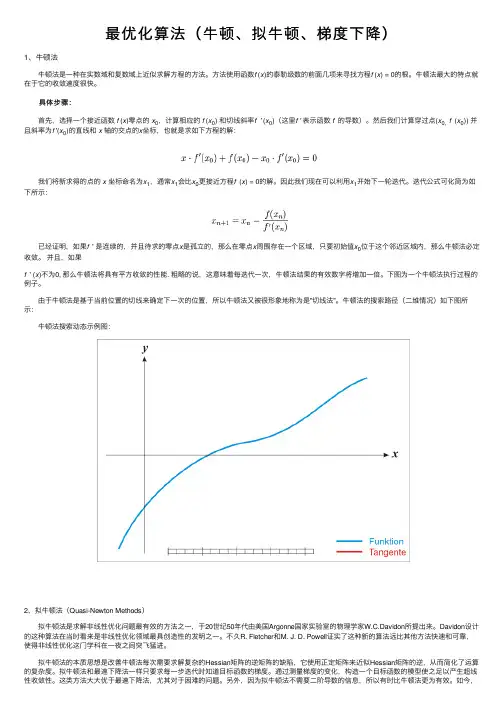
最优化算法（⽜顿、拟⽜顿、梯度下降）1、⽜顿法 ⽜顿法是⼀种在实数域和复数域上近似求解⽅程的⽅法。

⽅法使⽤函数f (x)的泰勒级数的前⾯⼏项来寻找⽅程f (x) = 0的根。

⽜顿法最⼤的特点就在于它的收敛速度很快。

具体步骤： ⾸先，选择⼀个接近函数f (x)零点的x0，计算相应的f (x0) 和切线斜率f ' (x0)（这⾥f ' 表⽰函数f 的导数）。

然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和x 轴的交点的x坐标，也就是求如下⽅程的解： 我们将新求得的点的x 坐标命名为x1，通常x1会⽐x0更接近⽅程f (x) = 0的解。

因此我们现在可以利⽤x1开始下⼀轮迭代。

迭代公式可化简为如下所⽰： 已经证明，如果f ' 是连续的，并且待求的零点x是孤⽴的，那么在零点x周围存在⼀个区域，只要初始值x0位于这个邻近区域内，那么⽜顿法必定收敛。

并且，如果f ' (x)不为0, 那么⽜顿法将具有平⽅收敛的性能. 粗略的说，这意味着每迭代⼀次，⽜顿法结果的有效数字将增加⼀倍。

下图为⼀个⽜顿法执⾏过程的例⼦。

由于⽜顿法是基于当前位置的切线来确定下⼀次的位置，所以⽜顿法⼜被很形象地称为是"切线法"。

⽜顿法的搜索路径（⼆维情况）如下图所⽰： ⽜顿法搜索动态⽰例图：2、拟⽜顿法（Quasi-Newton Methods） 拟⽜顿法是求解⾮线性优化问题最有效的⽅法之⼀，于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。

Davidon设计的这种算法在当时看来是⾮线性优化领域最具创造性的发明之⼀。

不久R. Fletcher和M. J. D. Powell证实了这种新的算法远⽐其他⽅法快速和可靠，使得⾮线性优化这门学科在⼀夜之间突飞猛进。

拟⽜顿法的本质思想是改善⽜顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使⽤正定矩阵来近似Hessian矩阵的逆，从⽽简化了运算的复杂度。

[实验题目]作者姓名(学号: 000000000)摘要: [简要陈述实验的内容]。

[简要介绍使用的方法]。

[简要介绍实验的结果]。

关键词: 群智能算法;1 引言a) 问题背景介绍。

b) 详细描述出其中的优化调度问题。

c) 大体介绍所使用的解决方案（基于如何的想法、有怎样的关键步骤），以及实验效果。

本文后续部分组织如下。

第2节详细陈述使用的方法，第3节报告实验结果，第4节对讨论本文的方法并总结全文。

2 算法设计[算法思路简介][展开详细介绍算法，使得读者可以自行实现。

本节中可该算法，可以自行划分小节]3 实验3.1 实验设置[详细交代实验的设置，如实验环境、运行时间等，使得读者可以重复该实验]3.2 实验结果[可包含参数实验、对比实验等，可以组织在不同的小节中][描述实验获得的客观结果，应当提供适当的图表][给出实验结果并分析][图的格式示例：图左右不环绕文字，占独立的行，居中，标题在图下方]图1 调度时序图[表格格式示例：三线表，居中，标题在表格上方]表1运行结果与运行时间算法运行结果运行时间（秒）PSO 173 111 ACO 222 1002[在提到他人的工作时，需要给出参考文献，例如：“李冬妮等人研究了一种柔性路径下的跨单元调度方法[3].”]4 总结[对本文工作进行总结][讨论本文的方法有何不足和有待提高之处，可能的解决方案有哪些]References: [注意参考文献的格式][1] Li D, Li M, Meng X, et al. A hyperheuristic approach for intercell scheduling with single processing machines and batch processingmachines[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 45(2): 315-325.[2] Li D, Wang Y, Xiao G, et al. Dynamic parts scheduling in multiple job shop cells considering intercell moves and flexible rou tes[J].Computers & Operations Research, 2013, 40(5): 1207-1223.[3] 李冬妮, 肖广雪, 王妍, 等. 一种柔性路径下的跨单元调度方法[J]. 自动化学报, 2012, 38(6): 969-975.。

优化算法调研报告优化算法调研报告一、引言优化算法是一种用于求解最优化问题的方法，其主要目标是找到使目标函数取得极值的最优解。

优化算法在实际应用中广泛使用，例如在工程设计、机器学习、数据分析等领域。

随着计算机计算能力的提高，优化算法在解决实际问题中的重要性越来越凸显。

本报告对几种常见的优化算法进行了调研，并对比了它们的特点和优缺点，旨在为实际应用提供参考。

二、遗传算法遗传算法是一种仿生优化算法，它模拟了生物进化的过程。

遗传算法基于自然选择和遗传变异的原理，通过模拟种群中个体的交叉和变异过程来搜索最优解。

遗传算法的优点是可以在大规模搜索空间中找到全局最优解，但代价是计算复杂度较高，需要较多的计算资源。

此外，遗传算法对问题的表示方式要求较高，需要将问题转化为适应度函数。

三、粒子群优化算法粒子群优化算法是一种模拟鸟群觅食行为的优化算法，其思想是通过模拟粒子在搜索空间中的移动来求解最优解。

粒子群优化算法的优点是收敛速度较快，在求解连续优化问题时具有较好的效果。

但粒子群优化算法对初始参数的敏感性较高，需要进行参数调优才能达到较好的效果。

四、模拟退火算法模拟退火算法是一种基于统计物理学的优化算法，其思想是通过模拟原子在固体退火过程中的行为来求解最优解。

模拟退火算法通过接受较差的解以避免陷入局部最优解，可以在搜索空间中跳出局部极小值，有较好的全局搜索能力。

模拟退火算法适用于求解连续和离散优化问题，但对于高维问题，其计算复杂度较高。

五、遗传模拟退火算法遗传模拟退火算法将遗传算法和模拟退火算法相结合，既有遗传算法的全局搜索能力，又有模拟退火算法的局部搜索能力。

遗传模拟退火算法通过遗传算子和退火策略的结合，可以在搜索过程中通过交叉和变异来实现全局搜索，同时通过温度策略来实现局部搜索。

遗传模拟退火算法具有较好的搜索性能，但计算复杂度较高。

六、小结优化算法是求解最优化问题的一类重要方法，不同的优化算法适用于不同类型的问题。

推荐算法优化方案报告摘要：推荐算法在现代社会中扮演着重要的角色，它们帮助人们发现新的内容、产品和服务。

然而，目前存在的推荐算法仍然存在一些问题，如推荐过于狭窄、个性化程度不够高等。

本报告旨在提出一些优化方案，以改善现有的推荐算法。

1. 引言推荐算法是根据用户的兴趣和行为，为用户提供个性化的推荐内容。

然而，当前的推荐算法往往只基于用户的历史行为，忽略了其他重要的因素。

因此，我们需要一种更加综合的推荐算法来提高推荐的准确性和个性化程度。

2. 数据收集和处理推荐算法的准确性和个性化程度取决于数据的质量和数量。

因此，我们需要收集和处理大量的用户数据。

一种方法是通过用户注册和登录来收集数据，另一种方法是通过分析用户的社交媒体活动来获取数据。

在处理数据时，我们可以使用机器学习和深度学习技术来提取有用的特征。

3. 用户画像建模用户画像是推荐算法的核心组成部分，它描述了用户的兴趣、偏好和行为。

为了提高个性化程度，我们需要建立更加精细的用户画像模型。

除了用户的历史行为，我们还可以考虑用户的社交网络、地理位置和个人信息等因素。

通过综合考虑这些因素，我们可以更准确地了解用户的需求和兴趣。

4. 推荐算法选择当前常用的推荐算法包括协同过滤、内容过滤和混合推荐等。

为了提高推荐的准确性和个性化程度，我们可以选择更加先进的推荐算法，如基于深度学习的推荐算法。

这些算法可以通过学习用户的行为模式和兴趣来提供更准确的推荐结果。

5. 推荐结果评估为了评估推荐算法的性能，我们需要选择合适的评估指标。

常用的评估指标包括准确率、召回率和覆盖率等。

通过对推荐结果进行评估，我们可以了解推荐算法的优劣，并对算法进行改进。

6. 用户反馈和迭代用户的反馈是优化推荐算法的重要依据。

我们可以通过用户调查、用户评价和用户行为分析等方式获得用户的反馈。

根据用户的反馈，我们可以对推荐算法进行迭代和改进，以提供更好的推荐结果。

7. 隐私保护在推荐算法中，用户的隐私是一个重要的考虑因素。

最优化方法上机报告院（系）：理学院专业：信息与计算科学班级：141414学号200914141426姓名：李嵩指导教师：方世成目录一、线性规划 (1)1. 线性规划题目 (1)2. 线性规划求解 (1)3. 线性规划运行结果 (1)二、0.618法 (2)1. 0.618法题目 (2)2. 0.618法程序 (2)3. 0.618法结果 (3)三、最速下降法 (3)1.最速下降法题目 (3)2.最速下降法程序 (3)3.最速下降法运行结果 (4)四、DFP方法 (5)1. DFP算法题目 (5)2．DFP算法程序 (5)3．DFP算法结果 (6)五、二次规划 (6)1.二次规划题目 (6)2.二次规划求解 (6)3.二次规划运行结果 (7)参考文献 (8)一、线性规划1. 线性规划题目max z=1001x +2002xs.t ⎪⎪⎩⎪⎪⎨⎧≥≥=+≤≤+0,01200622005002121121x x x x x x x2. 线性规划求解function myfunc=[-100;-200]; A=[1 1;1 0]; b=[500;200]; Ae=[2 6]; be=1200; lb=[0;0]; ub=[ ]';[x,fval]=linprog(c,A,b,Ae,be,lb,ub); end3. 线性规划运行结果图 11. 0.618法题目计算函数122--x x 极小值；区间 [-1,1];2. 0.618法程序function[x,minf,k]=minHJ(f,a,b,eps) l=a+0.382*(b-a); u=a+0.618*(b-a); k=1; tol=b-a;while tol>eps && k<10000 fl=subs(f,l); fu=subs(f,u); if fl>fu a=l; l=u;u=a+0.618*(b-a); else b=u u=ll=a+0.382*(b-a); end k=k+1;tol=abs(b-a); endif k==10000disp('找不到最优点'); x=NaN; minf=NaN; return; endx=(a+b)/2; minf=subs(f,x);图 2三、最速下降法1.最速下降法题目设(1)()(),9212221x x x f +=(2)()().102122421x x x f +=试讨论最速下降法的收敛速度. 2.最速下降法程序function [x,val,k]=grad(fun,gfun,x0)maxk=5000;rho=0.5;sigma=0.4; k=0;epsilon=1e-5; while(k<maxk)g=feval(gfun,x0); %计算梯度 d=-g; %计算搜索方向if(norm(d)<epsilon),break; endm=0;mk=0;while(m<20) %Armijo 搜索if(feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d) mk=m;break; endm=m+1; endx0=x0+rho^mk*d; k=k+1;endx=x0;val=feval(fun,x0);3.最速下降法运行结果（1图 3 （2）初始点x0=[0 1]’;图 4四、DFP 方法1. DFP 算法题目min ()(),9212221x x x f +=其中().1,2*T x -= 2．DFP 算法程序function [x,val,k]=dfp(fun,gfun,x0) maxk=1e5;rho=0.55;sigma=0.4; epsilon=1e-5;k=0; n=length(x0); Hk=eye(n); %Hk=eye(n); while(k<maxk)gk=feval(gfun,x0); if(norm(gk)<epsilon), break; end dk=-Hk*gk; m=0; mk=0; while(m<20)if(feval(fun,x0+rho^m*dk)<feval(fun,x0)+sigma*rho^m*gk'*dk) mk=m; break; endm=m+1; endx=x0+rho^mk*dk; sk=x-x0; yk=feval(gfun,x)-gk; if(sk'*yk>0)Hk=Hk-(Hk*yk*yk'*Hk)/(yk'*Hk*yk)+(sk*sk')/(sk'*yk); endk=k+1; x0=x; endval=feval(fun,x0); x=x0;3．DFP 算法结果初始值x0=[1 1]’；图 5五、二次规划1.二次规划题目目标函数为：min ()212122212x x x x x x x f ---+=约束条件为：⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+-≤+.0,0,32,22,221212121x x x x x x x x2.二次规划求解进行求解：function [x,lam,fval]=qlagH=[2 -1;-1 2]; c=[-2 -1]’;A=[1 1;-1 2;2 1]; b=[2;2;3];IH=inv(H); AHA=A*IH*A'; IAHA=inv(AHA); AIH=A*IH;G=IH-AIH'*IAHA*AIH;B=IAHA*AIH;C=-IAHA;x=B'*b-G*c;lam=B*c-C*b;fval=0.5*x'*H*x+c'*x;3.二次规划运行结果图 6参考文献[1]孙文瑜,徐成贤,朱德通.最优化方法.北京:高等教育出版社,2010.[2]赖炎连.贺国最优化方法.北京:清华大学出版社,2008.。

最优化学习报告在日常生活中，无论做任何一件事，人们总希望以最少的代价取得最大的效益，也就是力求最好，这就是优化问题。

最优化的问题是奥数中常见的一个问题，因为最优化是在生活中常用的。

例如一件事情要怎么样才能在尽可能节省人力、物力和时间前提下，争取获得在可能范围内的最佳效果。

这个就是需要通过计算来实现!最优化问题不仅具有趣味性，而且由于解题方法灵活，技巧性强，因此对于开拓解题思路，增强数学能力很有益处。

最优化就是在一切可能的方案中选择一个最好的方案以达到最优目标的学科。

最优化问题无处不在。

只要存在选择，就一定存在优化问题。

例如，从甲地到乙地有公路、水路、铁路、航空四种走法，如果我们追求的目标是省钱，那么只要比较一下这四种走法的票价，从中选择最便宜的那一种走法就达到目标。

这是最简单的最优化问题。

生活中还有很多的例子，比如说随着我国经济高速发展，能源短缺的矛盾突现，建设节约性社会是众望所归。

现实生活中，汽车作为代步工具，与我们的生活密切相关。

汽油的使用效率何时最高的问题也是最优化问题，众所周知，汽车的每小时耗油量与汽车的速度有一定的关系。

如何使汽车的汽油使用效率最高（汽油使有效率最高是指每千米路程的汽油耗油量最少）的问题。

此外还有磁盘的最大存储量问题，计算机把数据存储在磁盘上。

磁盘是带有磁性介质的圆盘，并有操作系统将其格式化成磁道和扇区。

磁道是指不同半径所构成的同心轨道，扇区是指被同心角分割所成的扇形区域。

磁道上的定长弧段可作为基本存储单元，根据其磁化与否可分别记录数据0或1，这个基本单元通常被称为比特（bit）。

则一个磁盘它的存储区是半径介于与多少之间的环形区域，磁盘的存储量越大问题。

第三个例子，饮料瓶大小对饮料公司利润的影响，现实生活中你是否注意过，市场上等量的小包装的物品一般比大包装的要贵些？那是不是饮料瓶越大，饮料公司的利润越大？又比如说一个具体的例子，货轮上卸下若干只箱子，总重量为10吨，每只箱子的重量不超过1吨，为了保证能把这些箱子一次运走，问至少需要多少辆载重3吨的汽车?[分析] 因为每一只箱子的重量不超过1吨，所以每一辆汽车可运走的箱子重量不会少于2吨，否则可以再放一只箱子。

最优化实验报告最优化实验报告引言：最优化是一种重要的数学方法，它在各个领域都有广泛的应用。

本实验旨在通过一个具体的案例，探索最优化方法在实际问题中的应用，以及优化算法对问题求解的效果。

一、问题描述：本实验中，我们将研究一个经典的最优化问题：背包问题。

背包问题是一个组合优化问题，目标是在给定的背包容量下，选择一组物品放入背包，使得背包中物品的总价值最大化。

具体来说，我们有一组物品，每个物品有一个重量和一个价值，背包有一定的容量限制。

我们的目标是选择一组物品，使得它们的总重量不超过背包容量，且总价值最大。

二、问题分析：背包问题是一个经典的组合优化问题，可以用多种方法求解。

在本实验中，我们将尝试使用两种常见的最优化算法：贪心算法和动态规划算法。

1. 贪心算法：贪心算法是一种简单但有效的最优化方法。

它每次选择当前看起来最优的解，然后逐步构建最终解。

在背包问题中，贪心算法可以按照物品的单位价值（即价值与重量的比值）进行排序，然后依次选择单位价值最高的物品放入背包。

贪心算法的优点是简单快速，但是它不能保证得到全局最优解。

2. 动态规划算法：动态规划算法是一种更为复杂但准确的最优化方法。

它通过将原问题分解为若干子问题，并保存子问题的解，最终得到全局最优解。

在背包问题中，动态规划算法可以通过构建一个二维表格来保存子问题的解，然后逐步计算出最终解。

动态规划算法的优点是能够得到全局最优解，但是它的时间和空间复杂度较高。

三、实验设计与结果分析：为了验证贪心算法和动态规划算法在背包问题中的效果，我们设计了一个实验。

我们随机生成了一组物品，每个物品的重量和价值都在一定范围内。

然后，我们分别使用贪心算法和动态规划算法求解背包问题，并比较它们的结果。

实验结果显示，贪心算法在求解背包问题时速度较快，但是得到的解并不一定是最优解。

而动态规划算法虽然耗时较长，但是能够得到全局最优解。

这说明在背包问题中，贪心算法是一种可行但不保证最优的方法，而动态规划算法是一种准确但复杂的方法。

最优化方法课程设计报告班级：________________姓名： ______学号： __________成绩：2017年 5月 21 日目录一、摘要 (1)二、单纯形算法 (2)1.1 单纯形算法的基本思路 (2)1.2 算法流程图 (3)1.3 用matlab编写源程序 (4)二、黄金分割法 (7)2.1 黄金分割法的基本思路 (7)2.2 算法流程图 (8)2.3 用matlab编写源程序 (9)2.4 黄金分割法应用举例 (11)三、最速下降法 (11)3.1 最速下降法的基本思路 (11)3.2 算法流程图 (13)3.3 用matlab编写源程序 (13)3.4 最速下降法应用举例 (13)四、惩罚函数法 (17)4.1 惩罚函数法的基本思路 (17)4.2 算法流程图 (18)4.3 用matlab编写源程序 (18)4.4 惩罚函数法应用举例 (19)五、自我总结 (20)六、参考文献 (20)一、摘要运筹学是一门以人机系统的组织、管理为对象，应用数学和计算机等工具来研究各类有限资源的合理规划使用并提供优化决策方案的科学。

通过对数据的调查、收集和统计分析，以及具体模型的建立。

收集和统计上述拟定之模型所需要的各种基础数据，并最终将数据整理形成分析和解决问题的具体模型。

最优化理论和方法日益受到重视，已经渗透到生产、管理、商业、军事、决策等各个领域，而最优化模型与方法广泛应用于工业、农业、交通运输、商业、国防、建筑、通信、政府机关等各个部门及各个领域。

伴随着计算机技术的高速发展，最优化理论与方法的迅速进步为解决实际最优化问题的软件也在飞速发展。

其中，MATLAB软件已经成为最优化领域应用最广的软件之一。

有了MATLAB 这个强大的计算平台，既可以利用MATLAB优化工具箱（OptimizationToolbox）中的函数，又可以通过算法变成实现相应的最优化计算。

关键词：优化、线性规划、黄金分割法、最速下降法、惩罚函数法二、单纯形算法1.1 单纯形算法的基本思路线性规划问题的可行域是n维向量空间Rn中的多面凸集，其最优值如果存在必在该凸集的某顶点处达到。