高考文科数学专题复习导数训练题

文科求函数的导数练习题一、基本初等函数求导1. 求函数 f(x) = x^3 的导数。

2. 求函数 f(x) = 5x^2 的导数。

3. 求函数 f(x) = 3x + 7 的导数。

4. 求函数 f(x) = 1/x 的导数。

5. 求函数f(x) = √x 的导数。

二、复合函数求导6. 求函数 f(x) = (x^2 + 3x + 2)^5 的导数。

7. 求函数f(x) = √(4x^2 9) 的导数。

8. 求函数 f(x) = e^(2x 1) 的导数。

9. 求函数 f(x) = ln(3x + 1) 的导数。

10. 求函数f(x) = sin(πx) 的导数。

三、隐函数求导11. 已知 y = x^2 + 3xy + y^3，求 dy/dx。

12. 已知 x^3 + y^3 = 6xy，求 dy/dx。

13. 已知 e^x + e^y = xy，求 dy/dx。

14. 已知 sin(x + y) = ycosx，求 dy/dx。

15. 已知 lnx + ln(y 1) = x，求 dy/dx。

四、参数方程求导16. 已知参数方程 x = 2t^3，y = t^2 + 1，求 dy/dx。

17. 已知参数方程x = cosθ，y = sinθ，求 dy/dx。

18. 已知参数方程 x = e^t，y = ln(t)，求 dy/dx。

19. 已知参数方程x = 3cosθ，y = 3sinθ，求 dy/dx。

20. 已知参数方程 x = t^2 + 1，y = 2t + 3，求 dy/dx。

五、高阶导数21. 求函数 f(x) = x^4 的二阶导数。

22. 求函数 f(x) = e^x 的二阶导数。

23. 求函数 f(x) = sinx 的三阶导数。

24. 求函数 f(x) = ln(x^2 + 1) 的一阶和二阶导数。

25. 求函数 f(x) = arctanx 的一阶导数。

六、分段函数求导26. 求函数 f(x) = { x^2 + 1, x < 0{ 2x 3, x ≥ 0 的导数。

专题 8：导数（文）经典例题剖析考点一：求导公式。

例 1. f (x) 是 f (x) 1 x3 2x 1 的导函数，则 f ( 1) 的值是。

3解析： f ' x x 2 2 ，所以 f ' 1 1 2 3答案： 3考点二：导数的几何意义。

例 2. 已知函数 y f ( x) 的图象在点 M (1， f (1)) 处的切线方程是 y 1x 2 ，则2f (1) f (1) 。

解析：因为 k 1，所以25，所以 f 1 5 ，所以2 21f ' 1，由切线过点M (1，f (1))，可得点M的纵坐标为2f 1 f ' 1 3答案： 3例 3.曲线y x3 2x2 4x 2 在点 (1， 3) 处的切线方程是。

解析： y' 3x2 4x 4 ，点 (1， 3) 处切线的斜率为k 3 4 4 5 ，所以设切线方程为 y 5x b ，将点 (1， 3) 带入切线方程可得 b 2 ，所以，过曲线上点(1，3) 处的切线方程为：5x y 2 0答案： 5x y 2 0点评：以上两小题均是对导数的几何意义的考查。

考点三：导数的几何意义的应用。

例 4.已知曲线 C ：y x3 3x 2 2x ，直线 l : y kx ，且直线l 与曲线C相切于点x0 , y0 x0 0 ，求直线l的方程及切点坐标。

解析：直线过原点，则 k y0 x0 0 。

由点x0, y0在曲线 C 上，则x0y 0 x 0 3 3x 0 22x 0 ， y 0x 0 23x 0 2。

又 y' 3x 26x 2 ，在x 0x 0 , y 0处 曲 线 C 的 切 线 斜 率 为 k f ' x 03x 0 2 6x 02 ，23x 0 226x 0 2 ，整理得： 2 x 0 3x 0 0 ，解得： x 03 0x 03x 0或 x 02（舍），此时， y 03 ， k1 。

所以，直线 l 的方程为 y1x ，切点坐标是8443 , 3 。

高考文科数学专题复习导数训练题文Newly compiled on November 23, 2020考点一：求导公式。

例1. ()f x '是31()213f x x x =++的导函数，则(1)f '-的值是 。

解析：()2'2+=x x f ，所以()3211'=+=-f 答案：3 考点二：导数的几何意义。

例2. 已知函数()y f x =的图象在点(1(1))M f ，处的切线方程是122y x =+，则(1)(1)f f '+= 。

解析：因为21=k ，所以()211'=f ，由切线过点(1(1))M f ，，可得点M 的纵坐标为25，所以()251=f ，所以()()31'1=+f f 答案：3例3.曲线32242y x x x =--+在点(13)-，处的切线方程是 。

解析：443'2--=x x y ，∴点(13)-，处切线的斜率为5443-=--=k ，所以设切线方程为b x y +-=5，将点(13)-，带入切线方程可得2=b ，所以，过曲线上点(13)-，处的切线方程为：025=-+y x考点三：导数的几何意义的应用。

例4.已知曲线C ：x x x y 2323+-=，直线kx y l =:，且直线l 与曲线C 相切于点()00,y x 00≠x ，求直线l 的方程及切点坐标。

解析： 直线过原点，则()000≠=x x y k 。

由点()00,y x 在曲线C 上，则02030023x x x y +-=，∴2302000+-=x x x y 。

又263'2+-=x x y ，∴ 在()00,y x 处曲线C 的切线斜率为()263'0200+-==x x x f k ，∴26323020020+-=+-x x x x ，整理得：03200=-x x ，解得：230=x 或00=x （舍），此时，830-=y ，41-=k 。

高考文科数学专题复习导数训练题(文)一、考点回顾1 •导数的概念及其运算是导数应用的基础，是高考重点考查的内容•考查方式以客观题为主，主要考查导数的基本公式和运算法则，以及导数的几何意义2. 导数的应用是高中数学中的重点内容，导数已由解决问题的工具上升到解决问题必不可少的工具，特别是利用导数来解决函数的单调性与最值问题是高考热点问题•选择填空题侧重于利用导数确定函数的单调性、单调区间和最值问题，解答题侧重于导数的综合应用，即与函数、不等式、数列的综合应用.3. 应用导数解决实际问题，关键是建立适当的数学模型(函数关系) ，如果函数在给定区间内只有一个极值点，此时函数在这点有极值，而此时不用和端点值进行比较，也可以得知这就是最值.二、经典例题剖析考点一：求导公式1例 1 f/(x)是f(x) x3 2x 1 的导函数，贝y f/(-1) = ________________ .3考点二：导数的几何意义1例2•已知函数y=f(x)的图象在点M(1,f(1))处的切线方程是y x 2，则f(1)・f/(1)=：.2考点三：导数的几何意义的应用例3.已知曲线C ： y = x3-3x2• 2x，直线I : y二kx，且直线l与曲线C相切于点x0，y0 x0 = 0，求直线I的方程及切点坐标.考点四：函数的单调性例4.设函数f(x) =2x3 3ax2 3bx 8c在x =1及x =2时取得极值.(1)求a，b的值及函数f (x)的单调区间；⑵若对于任意的0,3,都有f (x) <c2成立，求c的取值范围.考点五：函数的最值例5.已知a为实数，f(x) =(x2 -4)(x-a).(1)求导数f'(x) ；(2)若孑(-1)=0,求f(x)在区间〔-22上的最值.考点六：导数的综合性问题例6.设函数f (x)二ax3• bx • c(a = 0)为奇函数，其图象在点1, f(1)处的切线与直线x -6y -7 =0垂直，导函数『(x) |min 一-12. (1)求a, b, c的值；⑵求函数f (x)的单调递增区间，并求函数f(x)在L 1,3】上的最大值和最小值.例7.已知f(x)二ax3巾於+cx在区间0,1】上是增函数，在区间(一00,0)(1,亦)上是减函数，又厂'丄〕=3 •12丿2(I)求f (x)的解析式；(n)若在区间[Q m(m O上恒有f (x) < x成立，求m的取值范围.例8•设函数f (x) - -x(x - a) ( x R )，其中a R .(I)当a =1时，求曲线y二f (x)在点(2, f (2))处的切线方程；(n)当a=0时，求函数f(x)的极大值和极小值;(川)当a >3时，证明存在 “[-10 ],使得不等式f(k-cos)> f(k ?_coSx)对任意的x w R 恒成立. 例9.已知f (x) =ax 3 -x 2 bx - c(a,b,c • R)在-：:,0上是增函数，031上是减函数，方程f (x) = 0有三 个实根，它们分别是:-,2, ：.(1)求b 的值，并求实数 a 的取值范围； ⑵求证：二史.2三、 方法总结 (一) 方法总结导数是中学限选内容中较为重要的知识，由于其应用的广泛性，为我们解决所学过的有关函数问 题提供了一般性方法，是解决实际问题强有力的工具.导数的概念及其运算是导数应用的基础，是高 考重点考查的对象.要牢记导数公式，熟练应用导数公式求函数的导数，掌握求导数的方法.应用导 数解决实际问题的关键是要建立恰当的数学模型，了解导数概念的实际背景.应用导数求函数最值及 极值的方法在例题讲解中已经有了比较详细的叙述. (二) 高考预测导数的考查方式以客观题为主，主要考查求导数的基本公式和法则，以及导数的几何意义.也可 以解答题的形式出现，即以导数的几何意义为背景设置成导数与解析几何的综合题.导数的应用是重 点，侧重于利用导数确定函数的单调性和极值、最值、值域问题. 四、 强化训练 2x1.已知曲线y 的一条切线的斜率为 4A . 1B . 2C . 3D . 4322 .函数f (x)二x ax • 3x -9,已知f (x)在x = -3时取得极值，则 a = ( D )(A ) 2( B ) 3( C ) 4( D ) 53 .函数f(x) =2x 2 -1 x 3在区间0,6上的最大值是( A )332 16 A . 3B . 3C . 12D . 94. 三次函数y 二ax 3，x 在内是增函数，贝U( A )1A . a 0B. a 0C. a=1D. a =-36.已知函数f (x^x 3 ax 2 bx c,当x =—1时，取得极大值7；当x =-1时，取得极小值.求这个极小值及a, b, c 的值.32/7.设函数 f (x)二 x bx • cx(x • R).已知 g(x)二 f(x)「f (x)是奇函数.1—，则切点的横坐标为25 .在函数y =x 3 -8x 的图象上，其切线的倾斜角小于'的点中，坐标为整数的点的个数是4A . 3B . 2C . 1D . 0(1)求b,c的值；(2)求g(x)的单调区间与极值8 .用长为18 cm的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为 2 : 1,问该长方体的长、宽、高各为多少时，其体积最大？最大体积是多少？3 '9. 已知函数f x =x 3ax -1, g x = f x -ax-5，其中f x是的导函数.(I) 对满足-1_a_1的一切a的值，都有g x ：：：0,求实数x的取值范围；2 _(II) 设a—m，当实数m在什么范围内变化时，函数y二f x的图象与直线y = 3只有一个公共点. 10. 设函数f (x)二tx2 2t2x t -1(x R, t 0) . (I)求f (x)的最小值h(t);(II) 若h(t) ：：：—2t m对t (0,2)恒成立，求实数m的取值范围.311 .设函数f (x) (a 1)x24ax b(a,b R).31(I)若函数f (x)在x=3处取得极小值一，求a,b的值；(II)求函数f (x)的单调递增区间；2(III) 若函数f (x)在上有且只有一个极值点，求实数a的取值范围.212. 已知二次函数f (x)二ax bx c(a,b,^ R)满足：对任意x R ,都有f (x) >x,且当(1,3)12时，有f (x) <- (x 2)成立.(I)试求f(2)的值；(II)若f(-2)=0,求f (x)的表达式；8(III)在(II)的条件下，若0,=时，f (x) > m x 1恒成立，求实数m的取值范围.2 4a 3 1 2 213. 已知函数f(x) x (3a 2)x 6x, g(x)--ax 4x - m(a, m ：二R).3 2(I) 当a =1,x • 0,3时，求f (x)的最大值和最小值；(II) 当a <2且a=O时，无论a如何变化，关于x的方程f(x)二g(x)总有三个不同实根，求m的取值范围.例题参考答案1 f 3 3 \例 1 3 ;例 2 3 ;例 3 y = _—x —- i;例 4 (1) a=—3,b=4,增区间为(―叫1)(2,七c )；减区间为(1,2 ),4<2 8 丿⑵("一灿9卞)；例 5 ⑴4 ⑵ f(X )max=f(-1)£,f(X )min = f (4)=-10.；2 327例6 (1) a=2,b = _12,C =0. (2)(-QO ,-/2命2^«；f (X )max= f (3) =18 f (X )min = f Q 2)二"8'2 ；例 7 解：(I) f (x^3ax 22bx C ，由已知 f (0) = f (1) =0 ,*2JI I 3a 3a 3c3 2二 f (x) =3ax -3ax ，二 f — 1=——-——=—，二 a = -2，二 f (x) = —2x +3x .\2)42 21(n)令 f (x) < x ，即 _2x 3 3x 2 —x < 0 , x(2x —1)(x —1) > 0 , 0 < x w —或 x > 1 .2又f (x) w x 在区间1.0, m 1上恒成立，.0 ：：： m w 1 .2例8解：(I)当 a=1 时，f (x) =-x(x-1)2 =-x 3 2x 2-x ，得 f(2)=—2，且f (x ^-3x 2 4x -1 , f (2) = -5 .2所以，曲线y =-x(x -1)在点(2, -2)处的切线方程是 y 2 =—5(x -2)，整理得5x • y -8 = 0 .(n)解：f (x) = _x(x — a)2 = -x 3 2ax 2 _ a 2x , f (x) = -3x 2 4ax _ a 2 = —(3x _ a)(x _ a).令f (x) = 0，解得x 二旦或x = a .3由于a = 0，以下分两种情况讨论.(1)因此，函数f (x)在x =旦处取得极小值f i a ，且f i 旦—a 3 ；即C解得 J 3a 2b C =0,c = 0,3ba.I 23 13 丿13 丿27函数f (x)在x = a处取得极大值f (a)，且f (a) = 0 .(2)若，当x变化时，f (x)的正负如下表:因此，函数f (x)在x=a处取得极小值f (a)，且f(a)=0 ；函数f (x)在x=a处取得极大值f a，且f a 4a3.3 「3 丿「3 丿27(川)证明：由a 3，得—1，当-10 1 时，k -cosx < 1, k2-cos2 x < 1 .3由(n)知，f(x)在,1 ］上是减函数，要使f(k -cosx) > f(k2—cos2x) , R2 2 _ 2 2 -只要k -cosx < k -cos x(x R) 即cos x-cosx < k -k(x R) ①( 1 Y 1设g(x) = co€ x-cosx = cosx ，则函数g(x)在R上的最大值为2.要使①式恒成立，必须k2 - k > 2，即k > 2或k < -1.所以，在区间1-1,01上存在k二「1，使得f(k-cosx) > f(k2-cos2x)对任意的x R恒成立.例9解：(1厂f/(x) =3ax2 -2x b, f (x)在-：：,0上是增函数，在0,31上是减函数，所以当x = 0时，f(x)取得极小值，.『(0)=0,. b=0. f(2)=0,. 8a-4 c=0./ 2 2 又方程f (x) = 0有三实根，.a = 0.. f (x)二3ax「2x • b = 0的两根分别为论=0,x2.3a又f (x)在(-°°,0 )上是增函数，在b,3】上是减函数，二f/(x) >0在(—°° ,0 )上恒成立,f / (x) <0在0,3】上恒成立.2 2 * 21由二次函数的性质知，a>0且一 >3^ 0<a <-.故实数a的取值范围为0 -.3a 9 19」(2)，：,2,:是方程f(x) =0的三个实根，则可设f (x) = a(x 7-)(x-2)(x - F) = ax3-a(2 n、「)x2■ a(2二亠:川)x-2—-：E.321又 f (x) = ax 「xbx c(a,b, c R)有 a(d 亠：亠 2) = 1,2,ac 2 R 5 0<a w —，二】“—.9 2强化训练答案：6 •解： f /(x) = 3x 2 2ax b .据题意，—1, 3是方程3x 2 2ax ・b =：0的两个根，由韦达定理得a = —3,b = -9,. f (x) = x 3 —3x 2 —9x •c , f ( _1) =7,. c =2极小值 f(3)=33 —3 32 -9 3 2 =-25加/ 八 f (x )=x 3+bx 2+cxf "(x )=3x 2+2bx + c "由7 .解：(1 )T,.。

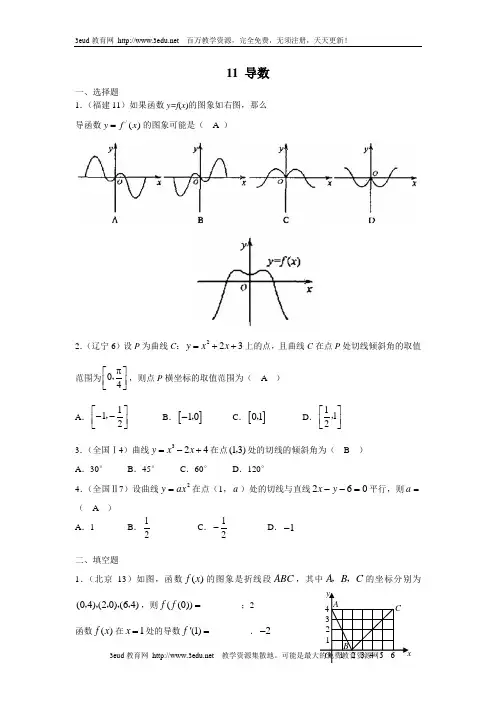
11 导数一、选择题 1．（福建11）如果函数y=f (x )的图象如右图，那么 导函数/()y f x =的图象可能是（ A ）2．（辽宁6）设P 为曲线C ：223y x x =++上的点，且曲线C 在点P 处切线倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦，，则点P 横坐标的取值范围为（ A ）A ．112⎡⎤--⎢⎥⎣⎦，B ．[]10-，C ．[]01，D ．112⎡⎤⎢⎥⎣⎦，3．（全国Ⅰ4）曲线324y x x =-+在点(13)，处的切线的倾斜角为（ B ） A ．30°B ．45°C ．60°D ．120°4．（全国Ⅱ7）设曲线2ax y =在点（1，a ）处的切线与直线062=--y x 平行，则=a （ A ） A ．1B ．12C ．12-D ．1-二、填空题1．（北京13）如图，函数()f x 的图象是折线段ABC ，其中A B C ，，的坐标分别为(04)(20)(64)，，，，，，则((0))f f =_________；2函数()f x 在1x =处的导数(1)f '=_________．2-BCAy12 3 42．（江苏14）13)(3+-=x ax x f 对于[]1,1-∈x 总有0)(≥x f 成立，则a = 4三、解答题10．(山东21)（本小题满分12分） 设函数2132()x f x x eax bx -=++，已知2x =-和1x =为()f x 的极值点．（Ⅰ）求a 和b 的值； （Ⅱ）讨论()f x 的单调性； （Ⅲ）设322()3g x x x =-，试比较()f x 与()g x 的大小． 解：（Ⅰ）因为122()e (2)32x f x x x ax bx -'=+++1e (2)(32)x x x x ax b -=+++，又2x =-和1x =为()f x 的极值点，所以(2)(1)0f f ''-==，因此6203320a b a b -+=⎧⎨++=⎩，，解方程组得13a =-，1b =-． （Ⅱ）因为13a =-，1b =-，所以1()(2)(e1)x f x x x -'=+-，令()0f x '=，解得12x =-，20x =，31x =． 因为当(2)x ∈-∞-，(01)，时，()0f x '<；当(20)(1)x ∈-+∞，，时，()0f x '>．所以()f x 在(20)-，和(1)+∞，上是单调递增的；在(2)-∞-，和(01)，上是单调递减的． （Ⅲ）由（Ⅰ）可知21321()e 3x f x x x x -=--， 故21321()()e (e )x x f x g x x x x x ---=-=-，令1()ex h x x -=-，则1()e1x h x -'=-．令()0h x '=，得1x =，因为(]1x ∈-∞，时，()0h x '≤， 所以()h x 在(]1x ∈-∞，上单调递减． 故(]1x ∈-∞，时，()(1)0h x h =≥； 因为[)1x ∈+∞，时，()0h x '≥， 所以()h x 在[)1x ∈+∞，上单调递增． 故[)1x ∈+∞，时，()(1)0h x h =≥．所以对任意()x ∈-∞+∞，，恒有()0h x ≥，又20x ≥，因此()()0f x g x -≥，故对任意()x ∈-∞+∞，，恒有()()f x g x ≥． 1．（安徽20）（本小题满分12分） 设函数323()(1)1,32a f x x x a x a =-+++其中为实数。

导数文科测试题及答案一、单项选择题（每题3分，共30分）1. 函数y=x^2的导数是（）A. 2xB. x^2C. 2D. x答案：A2. 函数y=3x的导数是（）A. 3B. 3xC. 1D. 0答案：A3. 函数y=x^3的导数是（）A. 3x^2B. x^3C. 3D. x^2答案：A4. 函数y=sin(x)的导数是（）A. cos(x)B. sin(x)C. -sin(x)D. -cos(x)答案：A5. 函数y=e^x的导数是（）A. e^xB. e^(-x)C. 1D. 0答案：A6. 函数y=ln(x)的导数是（）A. 1/xB. xC. ln(x)D. 1答案：A7. 函数y=1/x的导数是（）A. -1/x^2B. 1/x^2C. -1/xD. 1/x答案：A8. 函数y=x^(1/2)的导数是（）A. 1/2x^(-1/2)B. 1/2x^(1/2)C. 1/2D. 2x^(-1/2)答案：A9. 函数y=tan(x)的导数是（）A. sec^2(x)B. tan(x)C. 1D. sec(x)答案：A10. 函数y=arcsin(x)的导数是（）A. 1/sqrt(1-x^2)B. 1/xC. xD. sqrt(1-x^2)答案：A二、填空题（每题4分，共20分）11. 函数y=x^4的导数是________。

答案：4x^312. 函数y=cos(x)的导数是________。

答案：-sin(x)13. 函数y=ln(1+x)的导数是________。

答案：1/(1+x)14. 函数y=x^(-2)的导数是________。

答案：-2x^(-3)15. 函数y=arccos(x)的导数是________。

答案：-1/sqrt(1-x^2)三、解答题（每题10分，共50分）16. 求函数y=x^2-2x+1的导数。

答案：y'=2x-217. 求函数y=e^(2x)的导数。

高二文科导数求导练习题1. 求导函数：f(x) = 3x^2 - 2x + 5我们将使用导数的定义来求解这个练习题。

首先，我们需要确定函数f(x)在给定的区间内是可导的。

在这种情况下，我们不需要担心定义域或间断点。

根据导数的定义，导数f'(x)为函数f(x)在x点的极限值：f'(x) = lim(h->0) [f(x+h) - f(x)] / h我们将使用极限的性质来简化这个表达式。

首先，我们计算f(x+h)：f(x+h) = 3(x+h)^2 - 2(x+h) + 5= 3(x^2 + 2xh + h^2) - 2x - 2h + 5= 3x^2 + 6xh + 3h^2 - 2x - 2h + 5接下来，我们计算f(x+h) - f(x)：f(x+h) - f(x) = (3x^2 + 6xh + 3h^2 - 2x - 2h + 5) - (3x^2 - 2x + 5)= 6xh + 3h^2 - 2h现在我们可以将此结果代入到导数的定义中：f'(x) = lim(h->0) [6xh + 3h^2 - 2h] / h我们可以通过取消分式中的h来简化上述表达式：f'(x) = lim(h->0) 6x + 3h - 2最后，当h趋近于0时，只有常数项6x会影响极限的结果：f'(x) = 6x最后的结果表明，在给定的区间内，函数f(x)的导数f'(x)是6x。

2. 求导函数：g(x) = sqrt(x^3) + 2x与第一个练习题相似，我们将使用导数的定义来求解这个问题。

同样地，我们需要确定函数g(x)在给定的区间内是可导的。

根据导数的定义，导数g'(x)为函数g(x)在x点的极限值：g'(x) = lim(h->0) [g(x+h) - g(x)] / h首先，我们计算g(x+h)：g(x+h) = sqrt((x+h)^3) + 2(x+h)= sqrt(x^3 + 3x^2h + 3xh^2 + h^3) + 2x + 2h接下来，我们计算g(x+h) - g(x)：g(x+h) - g(x) = (sqrt(x^3 + 3x^2h + 3xh^2 + h^3) + 2x + 2h) - (sqrt(x^3) + 2x)= sqrt(x^3 + 3x^2h + 3xh^2 + h^3) + 2x + 2h - sqrt(x^3) - 2x= sqrt(x^3 + 3x^2h + 3xh^2 + h^3) - sqrt(x^3) + 2h现在我们可以将此结果代入到导数的定义中：g'(x) = lim(h->0) [sqrt(x^3 + 3x^2h + 3xh^2 + h^3) - sqrt(x^3) + 2h] / h将分式中的h进行约分，我们可以得到：g'(x) = lim(h->0) [(sqrt(x^3 + 3x^2h + 3xh^2 + h^3) - sqrt(x^3)) / h + 2]当h趋近于0时，我们只需要考虑第一项中的根式部分，其他项不会影响极限的结果：g'(x) = lim(h->0) [(sqrt(x^3 + 3x^2h + 3xh^2 + h^3) - sqrt(x^3)) / h]为了使计算更加便捷，我们将使用导函数的性质。

最新文件---------------- 仅供参考--------------------已改成-----------word 文本 --------------------- 方便更改高考文科数学专题复习导数训练题（文）一、考点回顾1．导数的概念及其运算是导数应用的基础，是高考重点考查的内容．考查方式以客观题为主，主要考查导数的基本公式和运算法则，以及导数的几何意义.2.导数的应用是高中数学中的重点内容,导数已由解决问题的工具上升到解决问题必不可少的工具,特别是利用导数来解决函数的单调性与最值问题是高考热点问题.选择填空题侧重于利用导数确定函数的单调性、单调区间和最值问题,解答题侧重于导数的综合应用,即与函数、不等式、数列的综合应用.3.应用导数解决实际问题,关键是建立适当的数学模型（函数关系）,如果函数在给定区间内只有一个极值点,此时函数在这点有极值,而此时不用和端点值进行比较,也可以得知这就是最值.二、经典例题剖析 考点一：求导公式 例1)(/x f 是1231)(3++=x x x f 的导函数，则=-)1(/f . 考点二：导数的几何意义例2. 已知函数)(x f y =的图象在点))1(,1(f M 处的切线方程是221+=x y ，则=+)1()1(/f f .考点三：导数的几何意义的应用例3.已知曲线,23:23x x x y C +-=直线,:kx y l =且直线l 与曲线C 相切于点()(),0,000≠x y x 求直线l 的方程及切点坐标.考点四：函数的单调性例4.设函数c bx ax x x f 8332)(23+++=在1=x 及2=x 时取得极值.(1)求b a ,的值及函数)(x f 的单调区间；(2)若对于任意的[],3,0∈x 都有)(x f <2c 成立，求c 的取值范围.考点五：函数的最值例5.已知a 为实数，).)(4()(2a x x x f --=(1)求导数)(/x f ；(2)若,0)1(/=-f 求)(x f 在区间[]2,2-上的最值.考点六：导数的综合性问题例6. 设函数)0()(3≠++=a c bx ax x f 为奇函数，其图象在点())1(,1f 处的切线与直线076=--y x 垂直，导函数.12|)(min /-=x f (1)求c b a ,,的值；(2)求函数)(x f 的单调递增区间，并求函数)(x f 在[]3,1-上的最大值和最小值.例7．已知cx bx ax x f ++=23)(在区间[]1,0上是增函数,在区间()()+∞∞-,1,0,上是减函数，又1322f ⎛⎫'= ⎪⎝⎭． （Ⅰ）求()f x 的解析式；（Ⅱ）若在区间[0](0)m m >，上恒有()f x x ≤成立，求m 的取值范围．例8．设函数2()()f x x x a =--（x ∈R ），其中a ∈R ．（Ⅰ）当1a =时，求曲线()y f x =在点(2(2))f ，处的切线方程；（Ⅱ）当0a ≠时，求函数()f x 的极大值和极小值；（Ⅲ）当3a >时，证明存在[]10k ∈-，，使得不等式22(cos )(cos )f k x f k x --≥对任意的x ∈R 恒成立．例9．已知),,()(23R c b a c bx x ax x f ∈++-=在()0,∞-上是增函数,[]3,0上是减函数,方程0)(=x f 有三个实根，它们分别是.,2,βα(1)求b 的值，并求实数a 的取值范围；(2)求证：βα+≥.25三、方法总结 （一）方法总结导数是中学限选内容中较为重要的知识，由于其应用的广泛性，为我们解决所学过的有关函数问题提供了一般性方法，是解决实际问题强有力的工具．导数的概念及其运算是导数应用的基础，是高考重点考查的对象．要牢记导数公式，熟练应用导数公式求函数的导数，掌握求导数的方法．应用导数解决实际问题的关键是要建立恰当的数学模型，了解导数概念的实际背景．应用导数求函数最值及极值的方法在例题讲解中已经有了比较详细的叙述．（二）高考预测导数的考查方式以客观题为主，主要考查求导数的基本公式和法则，以及导数的几何意义．也可以解答题的形式出现，即以导数的几何意义为背景设置成导数与解析几何的综合题．导数的应用是重点，侧重于利用导数确定函数的单调性和极值、最值、值域问题． 四、强化训练1．已知曲线42x y =的一条切线的斜率为21，则切点的横坐标为（ A ）A ．1B ．2C ．3D ．42．函数,93)(23-++=x ax x x f 已知)(x f 在3-=x 时取得极值，则=a （ D ）（A ）2 （B ）3 （C ）4（D ）53．函数32312)(x x x f -=在区间[]6,0上的最大值是（ A ） A ．323B ．163C ．12D ．94．三次函数x ax y +=3在()+∞∞-∈,x 内是增函数，则 （ A ）A ． 0>aB ．0<aC ．1=aD ．31=a 5．在函数x x y 83-=的图象上,其切线的倾斜角小于4π的点中,坐标为整数的点的个数是（ D ）A ．3B ．2C ．1D ．06．已知函数,)(23c bx ax x x f +++=当1-=x 时，取得极大值7；当1-=x 时，取得极小值．求这个极小值及c b a ,,的值．7．设函数).()(23R x cx bx x x f ∈++=已知)()()(/x f x f x g -=是奇函数. （1）求c b ,的值；（2）求)(x g 的单调区间与极值.8．用长为18 cm 的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为2：1，问该长方体的长、宽、高各为多少时，其体积最大？最大体积是多少？9．已知函数()()()331,5f x x ax g x f x ax =+-=--，其中()'f x 是的导函数. (I)对满足11a -≤≤的一切a 的值，都有()0g x <，求实数x 的取值范围；(II)设2a m =-，当实数m 在什么范围内变化时，函数()y f x =的图象与直线3y =只有一个公共点.10．设函数22()21(0)f x tx t x t x t =++-∈>R ，．(I)求()f x 的最小值()h t ； (II)若()2h t t m <-+对(02)t ∈，恒成立，求实数m 的取值范围．11．设函数).,(4)1(3)(23R b a b ax x a x x f ∈+++-= (I)若函数)(x f 在3=x 处取得极小值,21求b a ,的值；(II)求函数)(x f 的单调递增区间； (III) 若函数)(x f 在)1,1(-上有且只有一个极值点，求实数a 的取值范围．12．已知二次函数),,()(2R c b a c bx ax x f ∈++=满足：对任意R x ∈，都有)(x f ≥,x 且当)3,1(∈x 时，有)(x f ≤2)2(81+x 成立．(I)试求)2(f 的值；(II)若,0)2(=-f 求)(x f 的表达式；(III)在(II)的条件下，若[)+∞∈,0x 时，)(x f >412+x m 恒成立，求实数m 的取值范围． 13．已知函数).,(4)(,6)23(213)(223R m a m x ax x g x x a x a x f ∈-+-=++-=(I)当[]3,0,1∈=x a 时，求()f x 的最大值和最小值；(II)当a <2且0≠a 时，无论a 如何变化，关于x 的方程)()(x g x f =总有三个不同实根，求m 的取值范围．例题参考答案例1 3；例2 3；例3 ⎪⎭⎫ ⎝⎛--=83,23,41x y ；例4 (1) ,4,3=-=b a 增区间为()()+∞∞-,2,1,；减区间为()2,1， (2)()()+∞-∞-,91, ；例 5 (1),423)(2/--=ax x x f(2).2750)34()(,29)1()(min max -===-=f x f f x f ； 例6(1).0,12,2=-==c b a (2)()().28)2()(,18)3()(;,2,2,min max-====+∞-∞-f x f f x f ；例7解：（Ⅰ）2()32f x ax bx c '=++，由已知(0)(1)0f f ''==，即0320c a b c =⎧⎨++=⎩，，解得032c b a =⎧⎪⎨=-⎪⎩，．2()33f x ax ax '∴=-，13332422a a f ⎛⎫'∴=-= ⎪⎝⎭，2a ∴=-，32()23f x x x ∴=-+．（Ⅱ）令()f x x ≤，即32230x x x -+-≤，(21)(1)0x x x ∴--≥，102x ∴≤≤或1x ≥．又()f x x ≤在区间[]0m ，上恒成立，102m ∴<≤． 例8解：（Ⅰ）当1a =时，232()(1)2f x x x x x x =--=-+-，得(2)2f =-，且2()341f x x x '=-+-，(2)5f '=-．所以，曲线2(1)y x x =--在点(22)-，处的切线方程是25(2)y x +=--，整理得580x y +-=．（Ⅱ）解：2322()()2f x x x a x ax a x=--=-+-，22()34(3)()f x x ax a x a x a '=-+-=---．令()0f x '=，解得3ax =或x a =． 由于0a ≠，以下分两种情况讨论．（1）若0a >，当x 变化时，()f x '的正负如下表：因此，函数()f x 在3x =处取得极小值3f ⎛⎫ ⎪⎝⎭，且3327f a ⎛⎫=- ⎪⎝⎭；函数()f x 在x a =处取得极大值()f a ，且()0f a =． （2）若0a <，当x 变化时，()f x '的正负如下表：函数()f x 在3ax =处取得极大值3a f ⎛⎫⎪⎝⎭，且34327a f a ⎛⎫=- ⎪⎝⎭．（Ⅲ）证明：由3a >，得13a >，当[]10k ∈-，时，cos 1k x -≤，22cos 1k x -≤． 由（Ⅱ）知，()f x 在(]1-∞，上是减函数，要使22(cos )(cos )f k x f k x --≥，x ∈R 只要22cos cos ()k x k x x --∈R ≤ 即22cos cos ()x x k k x --∈R ≤①设2211()cos cos cos 24g x x x x ⎛⎫=-=-- ⎪⎝⎭，则函数()g x 在R 上的最大值为2．要使①式恒成立，必须22k k -≥，即2k ≥或1k -≤．所以，在区间[]10-，上存在1k =-，使得22(cos )(cos )f k x f k x --≥对任意的x ∈R恒成立．例9解：(1))(,23)(2/x f b x ax x f +-= 在()0,∞-上是增函数，在[]3,0上是减函数，所以当0=x 时，)(x f 取得极小值，.048,0)2(.0,0)0(/=+-∴==∴=∴c a f b f又方程0)(=x f 有三 实根，023)(.02/=+-=∴≠∴b x ax x f a 的两根分别为.32,021ax x == 又)(x f 在()0,∞-上是增函数，在[]3,0上是减函数，)(/x f ∴>0在()0,∞-上恒成立，)(/x f <0在[]3,0上恒成立．由二次函数的性质知，a >0且a 32≥0,3∴<a ≤.92 故实数a 的取值范围为.92,0⎥⎦⎤ ⎝⎛ (2) βα,2, 是方程0)(=x f 的三个实根， 则可设.2)22()2())(2)(()(23αβαββαβαβαa x a x a ax x x x a x f -+++++-=---=又),,()(23R c b a c bx x ax x f ∈++-=有,21,1)2(-=+∴=++aa βαβα 0 <a ≤∴,92βα+≥.25强化训练答案：6．解：b ax x x f ++=23)(2/.据题意，－1，3是方程0232=++b ax x 的两个根，由韦达定理得⎪⎪⎩⎪⎪⎨⎧=⨯--=+-3313231b a∴c x x x x f b a +--=∴-=-=93)(,9,323，2,7)1(=∴=-c f∴极小值25239333)3(23-=+⨯-⨯-=f7．解：（1）∵()32f x x bx cx=++，∴()232f x x bx c'=++。

文科《导数》高考常考题型专题训练1.已知函数/。

）= 6'一。

工一3（。

£/?）（1）若函数段）在函,—1））处的切线与直线木广0平行,求实数”的值;（2）当a=2, k为整数，且当Q1时，“一外/'（x） + 2x + l＞0,求〃的最大值.1 .【解析】(1)由/(x) = "—ax — 3,则/'*・) = "—〃又函数7U）在（1,火1））处的切线与直线片厂0平行，则=（2）当〃=2,且当x＞l 时，&一行（。

”一+ 2x + l>0等价于2）, 2x+l)当x>l 时，k< x + ^—k " - 2 7m j n2x + \，-2X-3)令g(x) = x + ^-则g (幻=—：-------------------e -2 (。

”-2)-再令h(x) = e x - 2x - 3(x > 1),则/(x) = " - 2 > 0 ,所以,〃（x）在（L+o。

）上单调递增，且以l）vO,以2）＞0,所以，/?（x）在（1, 2）上有唯一的零点，设该零点为小,则x°w（l,2）,且e"=2%+3, 当xw。

,,q）时，〃（％）v。

，即g'（x）＜。

：当xw（小，+°°）时，"（x）＞。

，即g'（x）＞0, 所以，g （x）在。

,小）单调递减，在（/，+8）单调递增，2（ +1所以，g（X）min +c - z而x°e（L2）,故一+le（2,3）且"vg（瓦）,又k为整数,所以k的最大值为2.2.已知函数/（x） = 6 + sinx,其中（1）若函数”刈在区间上单调递增，求k的取值范围:⑵若k = l时，不等式/Oarcosx在区间0尚上恒成立，求实数。

的取值范围.2・1解析】(1)由题意，f\x) = k+cosx t(冗5兀।「兀5兀、因为/(”)在区间二；上单调递增，所以工£二：时，/'(x) = Z + cosxNO恒成立，即k 3 6 7 V3 6 yk>—COSX9因为函数)'= -cosx在(工:上单调递增，所以—cosxK—cos^ =无，所以攵之五. (361 6 2 2(2) 〃 = 1 时，/(x) = x + sinx,令g(x) = /(x)—ovcosx = x+sinx-arcosx, xw[o.g],则g(x)A。

高考文科数学导数真题汇编(带答案)高考数学文科导数真题汇编答案一、客观题组4.设函数f(x)在R上可导，其导函数f'(x)，且函数f(x)在x=-2处取得极小值，则函数y=xf'(x)的图象可能是。

5.设函数f(x)=x^2-2x，则f(x)的单调递减区间为。

7.设函数f(x)在R上可导，其导函数f'(x)，且函数f(x)在x=2处取得极大值，则函数y=xf'(x)的图象可能是。

8.设函数f(x)=1/(2x-lnx)，则x=2为f(x)的极小值点。

9.函数y=1/(2x-lnx)的单调递减区间为(0,1]。

11.已知函数f(x)=x^2+bx+c的图象经过点(1,2)，且在点(2,3)处的切线斜率为4，则b=3.12.已知函数f(x)=ax^2+bx+c的图象过点(1,1)，且在点(2,3)处的切线斜率为5，则a=2.二、大题组2011新课标】21.已知函数f(x)=aln(x/b)+2，曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.(1) 求a、b的值；(2) 证明：当x>1，且x≠b时，f(x)>2ln(x/b)。

解析】1) f'(x)=a/(xlnb)+2/x，由于直线x+2y-3=0的斜率为-1/2，且过点(1,f(1))，解得a=1，b=1.2) 由(1)知f(x)=ln(x)+1，所以f(x)-2ln(x/b)=ln(x/b)+1>0，当x>1，且x≠b时，f(x)>2ln(x/b)成立。

2012新课标】21.设函数f(x)=ex-ax-2.(1) 求f(x)的单调区间；(2) 若a=1，k为整数，且当x>0时，(x-k)f'(x)+x+1>0，求k的最大值。

解析】1) f(x)的定义域为(-∞,+∞)，f'(x)=ex-a，若a≤0，则f'(x)>0，所以f(x)在(-∞,+∞)单调递增。

高二数学导数单元练习一、选择题1.一个物体的运动方程为S=1+t+t^2其中s 的单位是米，t 的单位是秒，那么物体在3秒末的瞬时速度是（）A 7米/秒B 6米/秒C 5米/秒D 8米/秒2.已知函数f (x )=ax 2＋c ,且(1)f '=2,则a 的值为（）3()f x ''()()x g x =,5.0，则7．曲线3()2f x x x =+-在0p 处的切线平行于直线41y x =-，则0p 点的坐标为（）A (1,0)B (2,8)C (1,0)和(1,4)--D (2,8)和(1,4)--8．函数313y x x =+-有（）A.极小值-1，极大值1B.极小值-2，极大值3C.极小值-1，极大值3D.极小值-2，极大值29对于R 上可导的任意函数()f x ，若满足'(1)()0x f x -≥，则必有（）A (0)(2)2(1)f f f +<B (0)(2)2(1)f f f +≤14.n 项和的1516 17．2y x =-，请解答下列问题：（1）求)(x f y =的解析式；（2）求)(x f y =的单调递增区间。

18．已知函数323()(2)632f x ax a x x =-++-（1）当2a >时，求函数()f x 极小值；（2）试讨论曲线()y f x =与x 轴公共点的个数。

20.已知1x =是函数32()3(1)1f x mx m x nx =-+++的一个极值点，其中,,0m n R m ∈<，（1）求m 与n 的关系式；（3111） )012n+，所以21n n a n =+，则数列1n a n ⎧⎫⎨⎬+⎩⎭的前n 项和()12122212n n n S +-==--三、解答题：15．解：设切点为(,)P a b ，函数3235y xx =+-的导数为'236y x x =+ 切线的斜率'2|363x a k y a a ===+=-，得1a =-，代入到3235y x x =+-得3b =-，即(1,3)P --，33(1),360y x x y +=-+++=16．解：设小正方形的边长为x 厘米，则盒子底面长为82x -，宽为52x -'2'10125240,0,1,3V x x V x x =-+===令得或，103x =（舍去） (1)18V V ==极大值，在定义域内仅有一个极大值， c bx ax x f ++=24182a =- （20<， 轴有三个交点；()x 的图像与x 轴只有一个交点；综上知，若0,()a f x ≥的图像与x 轴只有一个交点；若0a <，()f x 的图像与x 轴有三个交点。

文科导数练习题一、单项选择题1. 函数f(x) = 2x² + 3x + 1的导数f'(x)为：A. 2x + 3B. 4x + 3C. 4x + 1D. 2x + 12. 函数g(x) = sin(x) - cos(x)的导函数g'(x)为：A. cos(x) + sin(x)B. -cos(x) - sin(x)C. -cos(x) + sin(x)D. cos(x) - sin(x)3. 函数h(x) = ln(x² + 1)的导数h'(x)为：A. 2x/(x² + 1)B. (x² + 1)/(2x)C. x/(x² + 1)D. 2x4. 函数p(x) = e^x - e^(-x)的导函数p'(x)为：A. e^x + e^(-x)B. e^x - e^(-x)C. e^x + e^(-x)D. e^x + e^(-x)5. 函数q(x) = sqrt(2x - 3)的导数q'(x)为：A. 1/sqrt(2x - 3)B. 1/(2sqrt(2x - 3))C. sqrt(2x - 3)D. 1/(2sqrt(2x - 3))二、计算题1. 求函数f(x) = x³ - 3x的导函数f'(x)。

解答：首先，对于多项式函数而言，导数的计算只需要对各项的指数进行乘积运算，然后指数减1即可。

对于f(x) = x³ - 3x，可以分别计算出各项的导数。

f'(x) = 3x² - 32. 求函数g(x) = cos(2x)的导函数g'(x)。

解答：对于三角函数而言，导数的计算需要使用链式法则，即外函数的导数乘上内函数的导数。

对于g(x) = cos(2x)，外函数是cos(x)，内函数是2x。

g'(x) = -sin(2x) * 2= -2sin(2x)3. 求函数h(x) = ln(x + 1)的导函数h'(x)。

高三文科导数练习题1. 某物体运动的位移函数为 $s(t) = 2t^3 - 3t^2 + 6t + 1$，求该物体在 $t=2$ 时的速度和加速度。

解析：位移函数的导数即为速度函数，速度函数的导数即为加速度函数。

我们可以先求位移函数的导数，然后再求导一次得到加速度函数。

首先求位移函数的导数：$s'(t) = \frac{d}{dt}(2t^3 - 3t^2 + 6t + 1)$根据求导法则，我们可以依次对每一项求导：$s'(t) = \frac{d}{dt}(2t^3) - \frac{d}{dt}(3t^2) + \frac{d}{dt}(6t) +\frac{d}{dt}(1)$对于多项式函数的求导，我们可以应用幂函数的导数规则：$s'(t) = 6t^2 - 6t + 6$接下来求速度函数的导数，即加速度函数：$s''(t) = \frac{d}{dt}(6t^2 - 6t + 6)$同样地，我们对每一项应用幂函数的导数规则：$s''(t) = 12t - 6$因此，该物体在 $t=2$ 时的速度为 $s'(2) = 6(2)^2 - 6(2) + 6 = 24$，加速度为 $s''(2) = 12(2) - 6 = 18$。

2. 已知函数 $f(x) = \frac{3}{x^2}$，求 $f'(x)$ 和 $f''(x)$。

解析：首先求 $f(x)$ 的导数 $f'(x)$。

根据导数的定义和商规则：$f'(x) = \frac{d}{dx}\left(\frac{3}{x^2}\right) = \frac{0*x^2 -3*2x}{(x^2)^2} = \frac{-6x}{x^4} = -6\frac{1}{x^3}$接下来求 $f'(x)$ 的导数 $f''(x)$。

高考文科数学专题复习导数训练题（文）一、考点回顾1．导数的概念与其运算是导数应用的基础，是高考重点考查的内容．考查方式以客观题为主，主要考查导数的基本公式和运算法则，以与导数的几何意义.2.导数的应用是高中数学中的重点内容,导数已由解决问题的工具上升到解决问题必不可少的工具,特别是利用导数来解决函数的单调性与最值问题是高考热点问题.选择填空题侧重于利用导数确定函数的单调性、单调区间和最值问题,解答题侧重于导数的综合应用,即与函数、不等式、数列的综合应用.3.应用导数解决实际问题,关键是建立适当的数学模型（函数关系）,如果函数在给定区间内只有一个极值点,此时函数在这点有极值,而此时不用和端点值进行比较,也可以得知这就是最值. 二、经典例题剖析 考点一：求导公式例1)(/x f 是1231)(3++=x x x f 的导函数，则=-)1(/f .考点二：导数的几何意义 例2. 已知函数)(x f y =的图象在点))1(,1(f M 处的切线方程是221+=x y ，则=+)1()1(/f f .考点三：导数的几何意义的应用例3.已知曲线,23:23x x x y C +-=直线,:kx y l =且直线l 与曲线C 相切于点()(),0,000≠x y x 求直线l 的方程与切点坐标.考点四：函数的单调性例4.设函数c bx ax x x f 8332)(23+++=在1=x 与2=x 时取得极值. (1)求b a ,的值与函数)(x f 的单调区间；(2)若对于任意的[],3,0∈x 都有)(x f <2c 成立，求c 的取值范围. 考点五：函数的最值例5.已知a 为实数，).)(4()(2a x x x f --=(1)求导数)(/x f ；(2)若,0)1(/=-f 求)(x f 在区间[]2,2-上的最值.考点六：导数的综合性问题例6. 设函数)0()(3≠++=a c bx ax x f 为奇函数，其图象在点())1(,1f 处的切线与直线076=--y x 垂直，导函数.12|)(min /-=x f (1)求c b a ,,的值； (2)求函数)(x f 的单调递增区间，并求函数)(x f 在[]3,1-上的最大值和最小值.例7．已知cx bx ax x f ++=23)(在区间[]1,0上是增函数,在区间()()+∞∞-,1,0,上是减函数，又1322f ⎛⎫'= ⎪⎝⎭．（Ⅰ）求()f x 的解析式；（Ⅱ）若在区间[0](0)m m >，上恒有()f x x ≤成立，求m 的取值范围．例8．设函数2()()f x x x a =--（x ∈R ），其中a ∈R ．（Ⅰ）当1a =时，求曲线()y f x =在点(2(2))f ，处的切线方程；（Ⅱ）当0a ≠时，求函数()f x 的极大值和极小值；（Ⅲ）当3a >时，证明存在[]10k ∈-，，使得不等式22(cos )(cos )f k x f k x --≥对任意的x ∈R 恒成立．例9．已知),,()(23R c b a c bx x ax x f ∈++-=在()0,∞-上是增函数,[]3,0上是减函数,方程0)(=x f 有三个实根，它们分别是.,2,βα(1)求b 的值，并求实数a 的取值范围；(2)求证：βα+≥.25三、 方法总结 （一）方法总结导数是中学限选内容中较为重要的知识，由于其应用的广泛性，为我们解决所学过的有关函数问题提供了一般性方法，是解决实际问题强有力的工具．导数的概念与其运算是导数应用的基础，是高考重点考查的对象．要牢记导数公式，熟练应用导数公式求函数的导数，掌握求导数的方法．应用导数解决实际问题的关键是要建立恰当的数学模型，了解导数概念的实际背景．应用导数求函数最值与极值的方法在例题讲解中已经有了比较详细的叙述． （二）高考预测导数的考查方式以客观题为主，主要考查求导数的基本公式和法则，以与导数的几何意义．也可以解答题的形式出现，即以导数的几何意义为背景设置成导数与解析几何的综合题．导数的应用是重点，侧重于利用导数确定函数的单调性和极值、最值、值域问题． 四、强化训练1．已知曲线42x y =的一条切线的斜率为21，则切点的横坐标为（ A ）A ．1B ．2C ．3D ．42．函数,93)(23-++=x ax x x f 已知)(x f 在3-=x 时取得极值，则=a （ D ） （A ）2（B ）3 （C ）4 （D ）53．函数32312)(x x x f -=在区间[]6,0上的最大值是（ A ）A ．323B ．163C ．12D ．94．三次函数x ax y +=3在()+∞∞-∈,x 内是增函数，则 （ A ） A ． 0>aB ．0<aC ．1=aD ．31=a5．在函数x x y 83-=的图象上,其切线的倾斜角小于4π的点中,坐标为整数的点的个数是（ D ） A ．3B ．2C ．1D ．06．已知函数,)(23c bx ax x x f +++=当1-=x 时，取得极大值7；当1-=x 时，取得极小值．求这个极小值与c b a ,,的值． 7．设函数).()(23R x cx bx x x f ∈++=已知)()()(/x f x f x g -=是奇函数.（1）求c b ,的值；（2）求)(x g 的单调区间与极值.8．用长为18 的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为2：1，问该长方体的长、宽、高各为多少时，其体积最大？最大体积是多少？9．已知函数()()()331,5f x x ax g x f x ax =+-=--，其中()'f x 是的导函数. (I)对满足11a -≤≤的一切a 的值，都有()0g x <，求实数x 的取值范围； ()设2a m =-，当实数m 在什么范围内变化时，函数()y f x =的图象与直线3y =只有一个公共点.10．设函数22()21(0)f x tx t x t x t =++-∈>R ，．(I)求()f x 的最小值()h t ；()若()2h t t m <-+对(02)t ∈，恒成立，求实数m 的取值范围． 11．设函数).,(4)1(3)(23R b a b ax x a x x f ∈+++-=(I)若函数)(x f 在3=x 处取得极小值,21求b a ,的值；()求函数)(x f 的单调递增区间；() 若函数)(x f 在)1,1(-上有且只有一个极值点，求实数a 的取值范围． 12．已知二次函数),,()(2R c b a c bx ax x f ∈++=满足：对任意R x ∈，都有)(x f ≥,x 且当)3,1(∈x 时，有)(x f ≤2)2(81+x 成立．(I)试求)2(f 的值；()若,0)2(=-f 求)(x f 的表达式；()在()的条件下，若[)+∞∈,0x 时，)(x f >412+x m 恒成立，求实数m 的取值范围．13．已知函数).,(4)(,6)23(213)(223R m a m x ax x g x x a x a x f ∈-+-=++-=(I)当[]3,0,1∈=x a 时，求()f x 的最大值和最小值；()当a <2且0≠a 时，无论a 如何变化，关于x 的方程)()(x g x f =总有三个不同实根，求m 的取值范围．例题参考答案例1 3；例2 3；例3⎪⎭⎫⎝⎛--=83,23,41x y ；例4 (1) ,4,3=-=b a 增区间为()()+∞∞-,2,1,；减区间为()2,1，(2) ()()+∞-∞-,91, ；例5 (1),423)(2/--=ax x x f (2).2750)34()(,29)1()(min max -===-=f x f f x f ；例6 (1).0,12,2=-==c b a (2) ()().28)2()(,18)3()(;,2,2,min max -====+∞-∞-f x f f x f ； 例7解：（Ⅰ）2()32f x ax bx c '=++，由已知(0)(1)0f f ''==，即0320c a b c =⎧⎨++=⎩，，解得032c b a =⎧⎪⎨=-⎪⎩，． 2()33f x ax ax '∴=-，13332422a a f ⎛⎫'∴=-= ⎪⎝⎭，2a ∴=-，32()23f x x x ∴=-+．（Ⅱ）令()f x x ≤，即32230x x x -+-≤，(21)(1)0x x x ∴--≥，102x ∴≤≤或1x ≥． 又()f x x ≤在区间[]0m ，上恒成立，102m ∴<≤．例8解：（Ⅰ）当1a =时，232()(1)2f x x x x x x =--=-+-，得(2)2f =-，且2()341f x x x '=-+-，(2)5f '=-．所以，曲线2(1)y x x =--在点(22)-，处的切线方程是25(2)y x +=--，整理得580x y +-=．（Ⅱ）解：2322()()2f x x x a x ax a x =--=-+-，22()34(3)()f x x ax a x a x a '=-+-=---．令()0f x '=，解得3a x =或x a =．由于0a ≠，以下分两种情况讨论．（1）若0a >，当x 变化时，()f x '的正负如下表：因此，函数()f x 在3ax =处取得极小值3a f ⎛⎫⎪⎝⎭，且34327a f a ⎛⎫=- ⎪⎝⎭；函数()f x 在x a =处取得极大值()f a ，且()0f a =． （2）若0a <，当x 变化时，()f x '的正负如下表：因此，函数()f x 在x a =处取得极小值()f a ，且()0f a =； 函数()f x 在3ax =处取得极大值3a f ⎛⎫⎪⎝⎭，且34327a f a ⎛⎫=- ⎪⎝⎭．（Ⅲ）证明：由3a >，得13a>，当[]10k ∈-，时，cos 1k x -≤，22cos 1k x -≤． 由（Ⅱ）知，()f x 在(]1-∞，上是减函数，要使22(cos )(cos )f k x f k x --≥，x ∈R 只要22cos cos ()k x k x x --∈R ≤ 即22cos cos ()x x k k x --∈R ≤①设2211()cos cos cos 24g x x x x ⎛⎫=-=-- ⎪⎝⎭，则函数()g x 在R 上的最大值为2． 要使①式恒成立，必须22k k -≥，即2k ≥或1k -≤． 所以，在区间[]10-，上存在1k =-，使得22(cos )(cos )f k x f k x --≥对任意的x ∈R 恒成立．例9解：(1))(,23)(2/x f b x ax x f +-= 在()0,∞-上是增函数，在[]3,0上是减函数，所以当0=x 时，)(x f 取得极小值，.048,0)2(.0,0)0(/=+-∴==∴=∴c a f b f又方程0)(=x f 有三 实根，023)(.02/=+-=∴≠∴b x ax x f a 的两根分别为.32,021ax x == 又)(x f 在()0,∞-上是增函数，在[]3,0上是减函数，)(/x f ∴>0在()0,∞-上恒成立，)(/x f <0在[]3,0上恒成立． 由二次函数的性质知，a >0且a32≥0,3∴<a ≤.92故实数a 的取值范围为.92,0⎥⎦⎤ ⎝⎛ (2) βα,2, 是方程0)(=x f 的三个实根，则可设.2)22()2())(2)(()(23αβαββαβαβαa x a x a ax x x x a x f -+++++-=---= 又),,()(23R c b a c bx x ax x f ∈++-=有,21,1)2(-=+∴=++aa βαβα 0 <a ≤∴,92βα+≥.25 强化训练答案：6．解：b ax x x f ++=23)(2/.据题意，－1，3是方程0232=++b ax x 的两个根，由韦达定理得⎪⎪⎩⎪⎪⎨⎧=⨯--=+-3313231b a∴c x x x x f b a +--=∴-=-=93)(,9,323，2,7)1(=∴=-c f ∴极小值25239333)3(23-=+⨯-⨯-=f 7．解：（1）∵()32f x x bx cx=++，∴()232f x x bx c'=++。

导数文科练习题一、多选题1. 若函数 f(x) 的导数存在，下列哪些函数的导数定理成立？A. f(x) - g(x)B. f(x)g(x)C. f(x)/g(x)D. f(g(x))答案：A、B、C2. 函数 f(x) 在点 x = a 的某去心邻域内连续，下列哪些情况下函数f(x) 在点 x = a 处的导数存在？A. f(x) 在点 x = a 处极限存在B. f(x) 在点 x = a 处左导数存在且等于右导数C. f(x) 在点 x = a 处的左导数存在D. f(x) 在点 x = a 处的右导数存在答案：A、B、C、D3. 设函数 f(x)、g(x) 在点 x = a 上连续，下列哪些说法是正确的？A. 若 f(x) 在点 x = a 上可导，那么 g(x) 在点 x = a 上也可导B. 若 f(x) 在点 x = a 上可导，那么 f(x) 在点 x = a 处的导数一定等于 0C. 若 f(x) 在点 x = a 处的导数存在，那么 f(x) 在点 x = a 上连续D. 若 f(x) 在点 x = a 上不连续，那么 f(x) 在点 x = a 处的导数不存在答案：A、C、D二、填空题1. 若函数 f(x) = e^x - x 的切线与 x 轴的交点为 (a, 0)，则 a 的值为__________。

答案：12. 设函数 f(x) = 2x^2 - x，则 f(x) 在点 x = 1 处的导数为 __________。

答案：33. 设函数 y = ax^2 + bx + c 在点 x = 2 处的导数为 4，且曲线在该点的切线方程为 y = 4x - 2，则 c 的值为 __________。

答案：-6三、计算题1. 求函数 f(x) = x^3 - 6x^2 + 9x 的导函数。

解答：首先对 f(x) 求导，得到 f'(x) = 3x^2 - 12x + 9。

答案：f'(x) = 3x^2 - 12x + 92. 求函数 f(x) = 2x^3 - 9x^2 + 12x - 5 在点 x = 1 处的切线方程。

高中文科数学导数大
题练习题
精品文档
收集于网络，如有侵权请联系管理员删除 高中文科数学导数大题练习题
1、设l 为曲线ln :x C y x
=在点(1,0)处的切线． (1)求l 的方程；
(2)证明：除切点(1,0)之外，曲线C 在直线l 的下方．
2、已知函数2()sin cos f x x x x x =++
(1)若曲线()y f x =在点(,())a f a 处与直线y b =相切，求a 与b 的值；
(2)若曲线()y f x =与直线y b =有两个不同交点，求b 的取值范围．
3、已知函数32()331f x x ax x =+++
(1)
求当a =,讨论()f x 的单调性;
(2)若[2,)x ∈+∞时,()0f x ≥,求a 的取值范围.
4、已知函数()ln ()f x x a x a R =-∈
(1)当2a =时，求曲线()y f x =在点(1,(1))A f 处的切线方程；
(2)求函数()f x 的极值．
5、设函数()ln f x x ax =-，()x g x e ax =-，其中a 为实数.若()f x 在()1,+∞上是单调减函数，且()g x 在()1,+∞上有最小值，求a 的范围.
6、已知函数2()ln (,)f x ax bx x a b R =+-∈
(1)设0a ≥，求)(x f 的单调区间
(2)设0a >，且对于任意0x >，()(1)f x f ≥。

试比较ln a 与2b -的大小。

高中文科导数练习题导数是微积分中的重要概念，对于高中文科学生来说，理解和应用导数是必不可少的。

本文将提供一些文科导数的练习题，帮助学生加深对导数的理解和应用。

1. 函数的导数概念考虑函数f(x) = 2x^2 + 3x - 5，求该函数在x=2处的导数。

2. 导数的运算法则已知函数f(x) = sin(x)，g(x) = e^x，求h(x) = f(x) * g(x)的导数。

3. 导数与图像的关系已知函数f(x) = x^3 - 4x^2 + 3x，绘制该函数的图像并找出其关键点，然后根据导数的定义解释这些关键点的意义。

4. 导数在最优化问题中的应用某公司每月生产x件产品，月总成本C(x)与产量的关系由函数C(x) = 0.01x^3 - 0.2x^2 + 30x + 2000给出，求最小月成本对应的产量以及最小月成本。

5. 导数在经济学中的应用考虑市场上一种产品的需求量和价格之间的关系由函数D(p) =2000/p表示，其中p为价格，D(p)为需求量。

求该产品的最大价格以及最大需求量。

6. 导数在物理学中的应用某物体在水平面上以速度v(t) = 3t^2 - 2t + 5移动，其中t为时间。

求该物体的位移函数s(t)以及物体在t=1处的瞬时速度。

7. 函数的高阶导数已知函数f(x) = 2x^3 - 5x^2 + 3x - 2，求该函数的二阶导数。

8. 隐函数求导已知方程x^2 + y^2 = 25，求dy/dx。

9. 反函数求导已知函数f(x) = ln(x)，求f^{-1}(x)的导数。

10. 参数方程求导已知参数方程x = 2t^2，y = 3t，求dy/dx。

以上是一些文科导数的练习题，涵盖了导数的基本概念、运算法则以及在不同领域的应用。

希望通过这些习题的练习，学生们能够加深对导数的理解，提升解决实际问题的能力。

祝学习顺利！总结：本文给出了一系列高中文科导数练习题，涵盖了导数的基本概念、运算法则以及在不同领域的应用。