广西钦州市钦南区2019学年九年级上期末数学模拟试卷(含答案)

2018-2019学年广西钦州市钦南区九年级（上）期末数学模拟试卷一．选择题（共12小题，满分36分，每小题3分）1．已知反比例函数y＝﹣，下列结论中不正确的是（）A．图象必经过点（﹣3，2）B．图象位于第二、四象限C．若x＜﹣2，则0＜y＜3D．在每一个象限内，y随x值的增大而减小2．用配方法解方程x2﹣10x﹣1＝0，正确的变形是（）A．（x﹣5）2＝1B．（x+5）2＝26C．（x﹣5）2＝26D．（x﹣5）2＝24 3．抛物线y＝（x﹣2）2+3的顶点坐标是（）A．（2，3）B．（﹣2，3）C．（2，﹣3）D．（﹣2，﹣3）4．已知△ABC内接于⊙O，OD⊥AC于D，如果∠COD＝32°，那么∠B的度数为（）A．16°B．32°C．16°或164°D．32°或148°5．方程﹣5x2＝1的一次项系数是（）A．3B．1C．﹣1D．06．下列成语中描述的事件必然发生的是（）A．水中捞月B．瓮中捉鳖C．守株待兔D．拔苗助长7．如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠BAC＝20°，求∠P 的度数为（）A．50°B．70°C．110°D．40°8．如图是一个旋转对称图形，以O为旋转中心，以下列哪一个角为旋转角旋转，能使旋转后的图形与原图形重合（）A．60°B．90°C．120°D．180°9．在平面直角坐标系中，平移二次函数y＝x2+4x+3的图象能够与二次函数y＝x2的图象重合，则平移方式为（）A．向左平移2个单位，向下平移1个单位B．向左平移2个单位，向上平移1个单位C．向右平移2个单位，向下平移1个单位D．向右平移2个单位，向上平移1个单位10．一个不透明的盒子中装有5个红球，3个白球和2个黄球，这些球除了颜色外无其他差别，从中随机摸出一个小球，恰好是白球的可能性为（）A．B．C．D．11．当k＜0，x＞0时，反比例函数y＝的图象在（）A．第一象限B．第二象限C．第三象限D．第四象限12．一个圆锥的侧面积是底面积的2倍，则该圆锥侧面展开图的圆心角的度数是（）A．120°B．180°C．240°D．300°二．填空题（共6小题，满分18分，每小题3分）13．在同一平面内，⊙O的直径为2cm，点P到圆心O的距离是3cm，则点P与⊙O的位置关系是．14．若反比例函数的图象经过点（﹣2，3），则这个反比例函数的表达式为．15．二次函数y＝x2+4的最小值是，顶点坐标．16．一元二次方程2x2﹣4x+1＝0有个实数根．17．王江泾是著名的水乡，如图，圆拱桥的拱顶到水面的距离CD为9m，水面宽AB为6m，则桥拱半径OC为m．18．在甲，乙两个不透明口袋中各装有10个和3个形状大小完全相同的红色小球，则从中摸到红色小球的概率是P甲P乙（填“＞”，“＜”或“＝”）；三．解答题（共7小题，满分66分）19．用适当的方法解下列方程：（1）（3x﹣1）2＝（x+1）2；（2）x2﹣2x﹣2＝0．20．某小区利用一块空地修建一个长方形花坛，要使花坛的长比宽多5m，且面积为24m2，长方形花坛的长和宽应各是多少？21．如图，方格纸中的每个小方格都是边长为1的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．（1）试作出△ABC以点C为旋转中心顺时针旋转90°后的图形△A1B1C；（2）以原点O为对称中心，作出与△ABC关于原点O对称的△A2B2C2，并写出点C2的坐标．22．某同学报名参加学校秋季运动会，有以下5个项目可供选择：径赛项目：100m、200m、1000m（分别用A1、A2、A3表示）；田赛项目：跳远，跳高（分别用T1、T2表示）．（1）该同学从5个项目中任选一个，恰好是田赛项目的概率P为；（2）该同学从5个项目中任选两个，求恰好是一个径赛项目和一个田赛项目的概率P1，利用列表法或树状图加以说明；（3）该同学从5个项目中任选两个，则两个项目都是径赛项目的概率P2为．23．如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD⊥CD于点D．（1）求证：AE平分∠DAC；（2）若AB＝4，∠ABE＝60°．①求AD的长；②求出图中阴影部分的面积．24．已知x＝1+2m，y＝1﹣m．（1）若点（x，y）恰为抛物线y＝ax2﹣ax+1的顶点，求a的值；（2）求y关于x的函数表达式；（3）若﹣3≤m≤1，x≤0，求y的取值范围．25．如图，在平面直角坐标系xOy中，直线y＝x+b与双曲线y＝相交于A，B两点，已知A（2，5）．求：（1）b和k的值；（2）△OAB的面积．参考答案一．选择题（共12小题，满分36分，每小题3分）1．【解答】解：A、图象必经过点（﹣3，2），故A正确；B、图象位于第二、四象限，故B正确；C、若x＜﹣2，则y＜3，故C正确；D、在每一个象限内，y随x值的增大而增大，故D正确；故选：D．2．【解答】解：x2﹣10x﹣1＝0，移项，得x2﹣10x＝1，方程两边同时加上25，得x2﹣10x+25＝26，∴（x﹣5）2＝26．故选：C．3．【解答】解：y＝（x﹣2）2+3是抛物线的顶点式方程，根据顶点式的坐标特点可知，顶点坐标为（2，3）．故选：A．4．【解答】解：如图；∵△OAC是等腰三角形，OD⊥AC，∴OD是∠ADC的平分线，（等腰三角形三线合一）∴∠AOC＝2∠COD＝64°；①当点B在优弧AC上时，由圆周角定理知，∠B＝∠AOC＝32°；②当点B在如图点E的位置时，由圆内接四边形的对角互补知，∠E＝180°﹣∠B＝148°；故选：D．5．【解答】解：方程整理得：﹣5x2﹣1＝0，则一次项系数为0，故选：D．6．【解答】解：A、水中捞月是不可能事件，故本选项错误；B、瓮中捉鳖是一定能发生的事件，属必然事件，故本选项正确；C、守株待兔是可能发生也可能不发生的事件，是随机事件，故本选项错误；D、拔苗助长是一定不会发生的事件，是不可能事件，故本选项错误．故选：B．7．【解答】解：∵PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∴∠CAP＝90°，PA＝PB，∴∠PAB＝∠PBA，∵∠BAC＝20°，∴∠PBA＝∠PAB＝90°﹣20°＝70°，∴∠P＝180°﹣∠PAB﹣∠PBA＝180°﹣70°﹣70°＝40°，故选：D．8．【解答】解：O为圆心，连接三角形的三个顶点，即可得到∠AOB＝∠BOC＝∠AOC＝120°，所以旋转120°后与原图形重合．故选：C．9．【解答】解：二次函数y＝x2+4x+3＝（x+2）2﹣1，将其向右平移2个单位，再向上平移1个单位得到二次函数y＝x2．故选：D．10．【解答】解：从中随机摸出一个小球，恰好是白球的概率P＝．故选：B．11．【解答】解：∵在反比例函数y＝中，k＜0，∴函数图象分别在二、四象限，又∵x＞0，∴函数图象在第四象限．故选：D．12．【解答】解：设母线长为R，底面半径为r，∴底面周长＝2πr，底面面积＝πr2，侧面面积＝πrR，∵侧面积是底面积的2倍，∴2πr2＝πrR，∴R＝2r，设圆心角为n，则＝2πr＝πR，解得，n＝180°，故选：B．二．填空题（共6小题，满分18分，每小题3分）13．【解答】解：∵⊙O的直径为2cm，∴半径r＝1cm，∵d＝3，且d＞r，∴点P与⊙O的位置关系是：点P在⊙O外，故答案为：点P在⊙O外．14．【解答】解：把点（﹣2，3）代入y＝得k＝﹣2×3＝﹣6，所以反比例函数解析式为y＝﹣．故答案为y＝﹣．15．【解答】解：二次函数y＝x2+4的最小值是4，顶点坐标（0，4）．故答案为：4；（0，4）．16．【解答】解：∵a＝2，b＝﹣4，c＝1，∴△＝（﹣4）2﹣4×2×1＝8＞0，∴此一元二次方程有两个实数根，故答案为：两．17．【解答】解：连接OA，∵OD⊥AB，∴AD＝AB＝3，在Rt△AOD中，OA2＝OD2+AD2，即OC2＝（9﹣OC）2+32，解得，OC＝5，故答案为：5．18．【解答】解：由题意知，从甲口袋的10个小球中摸出一个小球，是红色小球是必然事件，概率为1；从乙口袋的3个小球中摸出一个小球，是红色小球是必然事件，概率为1；∴P甲＝P乙，故答案为：＝．三．解答题（共7小题，满分66分）19．【解答】解：（1）把右边的项移到左边有：（3x﹣1）2﹣（x+1）2＝0，（3x﹣1+x+1）（3x﹣1﹣x﹣1）＝0，2x（2x﹣2）＝0，∴x1＝0，x2＝1；（2）x2﹣2x﹣2＝0，x2﹣2x＝2，x2﹣2x+1＝3，（x﹣1）2＝3，x﹣1＝±∴x1＝1+x2＝1﹣x．20．【解答】解：设花坛的宽为x米，根据题意得x（x+5）＝24，整理得：x2+5x﹣24＝0解这个方程的x1＝3x2＝﹣8（不合题意舍去），∴x＝3x+5＝8，答：长方形花坛的长为8米，宽为3米．21．【解答】解：（1）如图所示，△A1B1C即为所求；（2）如图所示，△A2B2C2即为所求，点C2的坐标为（﹣4，1）．22．【解答】解：（1）该同学从5个项目中任选一个，恰好是田赛项目的概率P＝；（2）画树状图为：共有20种等可能的结果数，其中一个径赛项目和一个田赛项目的结果数为12，所以一个径赛项目和一个田赛项目的概率P1＝＝；（3）两个项目都是径赛项目的结果数为6，所以两个项目都是径赛项目的概率P2＝＝．故答案为，．23．【解答】（1）证明：连接OE，如图，∵CD与⊙O相切于点E，∴OE⊥CD，∵AD⊥CD，∴OE∥AD，∴∠DAE＝∠AEO，∵AO＝OE，∴∠AEO＝∠OAE，∴∠OAE＝∠DAE，∴AE平分∠DAC；（2）解：①∵AB是直径，∴∠AEB＝90°，∠ABE＝60°．∴∠EAB＝30°，在Rt△ABE中，BE＝AB＝×4＝2，AE＝BE＝2，在Rt△ADE中，∠DAE＝∠BAE＝30°，∴DE＝AE＝，∴AD＝DE＝×＝3；②∵OA＝OB，∴∠AEO＝∠OAE＝30°，∴∠AOE＝120°，﹣S△AOE∴阴影部分的面积＝S扇形AOE﹣S△ABE＝S扇形AOE＝﹣••2•2＝π﹣．24．【解答】解：（1）抛物线y＝ax2﹣ax+1的对称轴为直线x＝，即1+2m＝，∴m＝﹣，即x＝1+2m＝，y＝1﹣m＝，把顶点（，）代入y＝ax2﹣ax+1，得：＝a﹣a+1，解得：a＝﹣1；（2）由x＝1+2m得：m＝x﹣，∴y＝1﹣m＝1﹣（x﹣）＝﹣x+；（3）当x≤0时，1+2m≤0，解得m≤﹣，又﹣3≤m≤1，∴﹣3≤m≤﹣，∴≤1﹣m≤4，则y的范围为≤y≤4．25．【解答】解：（1）∵直线y＝x+b与双曲线y＝相交于A，B两点，已知A（2，5），∴5＝2+b，5＝．解得：b＝3，k＝10．（2）如图，过A作AD⊥y轴于D，过B作BE⊥y轴于E，∴AD＝2．∵b＝3，k＝10，∴y＝x+3，y＝．由得：或，∴B点坐标为（﹣5，﹣2）．∴BE＝5．设直线y＝x+3与y轴交于点C．∴C点坐标为（0，3）．∴OC＝3．＝OC•AD＝×3×2＝3，∴S△AOCS△BOC＝OC•BE＝×3×5＝．＝S△AOC+S△BOC＝．∴S△AOB。

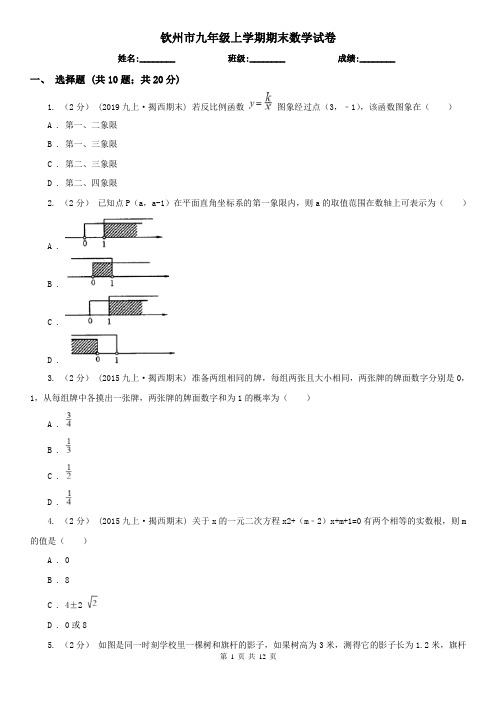
钦州市九年级上学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分） (2019九上·揭西期末) 若反比例函数图象经过点（3，﹣1），该函数图象在（）A . 第一、二象限B . 第一、三象限C . 第二、三象限D . 第二、四象限2. （2分）已知点P（a，a-1）在平面直角坐标系的第一象限内，则a的取值范围在数轴上可表示为（）A .B .C .D .3. （2分） (2015九上·揭西期末) 准备两组相同的牌，每组两张且大小相同，两张牌的牌面数字分别是0，1，从每组牌中各摸出一张牌，两张牌的牌面数字和为1的概率为（）A .B .C .D .4. （2分） (2015九上·揭西期末) 关于x的一元二次方程x2+（m﹣2）x+m+1=0有两个相等的实数根，则m 的值是（）A . 0B . 8C . 4±2D . 0或85. （2分）如图是同一时刻学校里一棵树和旗杆的影子，如果树高为3米，测得它的影子长为1.2米，旗杆的高度为5米，则它的影子长为（）A . 4米B . 2米C . 1.8米D . 3.6米6. （2分） (2015九上·揭西期末) 如图，三角形ABC中，D，E，F分别是AB，AC，BC上的点，且DE∥BC，EF∥AB，AD：DB=1：2，BC=30cm，则FC的长为（）A . 10cmB . 20cmC . 5cmD . 6cm7. （2分）如图，桌面上放着1个长方体和1个圆柱体，按如图所示的方式摆放在一起，其左视图是（）A .B .C .D .8. （2分） (2015九上·揭西期末) 已知点P（1，2）在反比例函数y= 的图象上，过P作x轴的垂线，垂足为M，则△OPM的面积为（）A . 2B . 4C . 8D . 19. （2分）如图，为了估计河的宽度，在河的对岸选定一个目标点P，在近岸取点Q和S，使点P，Q，S在一条直线上，且直线PS与河垂直，在过点S且与PS垂直的直线a上选择适当的点T，PT与过点Q且与PS垂直的直线b的交点为R．如果QS=60m，ST=120m，QR=80m，则河的宽度PQ为（）A . 40mB . 60mC . 120mD . 180m10. （2分） (2015九上·揭西期末) 如图，菱形ABCD的对角线相交于点O，过点D作DE∥AC，且DE= AC，连接CE，OE，连接AE，交OD于点F．若AB=2，∠ABC=60°，则AE的长为（）A .B .C .D .二、填空题 (共6题；共7分)11. （2分）“*”是规定的一种运算法则：a*b=a2﹣2b．那么2*3的值为________ ；若（﹣3）*x=7，那么x=________12. （1分）(2019·广安) 点在第四象限，则x的取值范围是________．13. （1分）(2017·黄冈模拟) 从﹣3，﹣2，﹣1，0，1，3，4这七个数中随机抽取一个数记为a，a的值既是不等式组的解，又在函数y= 的自变量取值范围内的概率是________．14. （1分） (2015九上·揭西期末) 如图，在矩形ABCD中，对角线AC与BD相交于点O，AE⊥BD，垂足为E，ED=3BE，则∠AOB的度数为________．15. （1分） (2015九上·揭西期末) 如图，在矩形ABCD中，E，F分别是边AB，CD上的点，AE=CF，连接EF，BF；EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC，FC=2，则AB的长为________．16. （1分） (2015九上·揭西期末) 如图，正方形ABCD的边长为3，延长CB到点M，使BM=1，连接AM，过点B作BN⊥AM，垂足为N，O是对角线AC，BD的交点，连接ON，则ON的长为________．三、解答题 (共9题；共65分)17. （5分）(2017·文昌模拟) 学校安排学生住宿，若每室住8人，则有12人无法安排；若每室住9人，可空出2个房间．这个学校的住宿生有多少人？宿舍有多少房间？18. （5分）今年,在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况．（售价不低于进价）.请根据小丽提供的信息,解答小华和小明提出的问题．认真阅读上面三位同学的对话,请根据小丽提供的信息．（1）解答小华的问题；（2）解答小明的问题．19. （5分）已知二次函数y=a(x-m)2-2a(x-m)（a,m为常数，且a≠0）.（1）求证：不论a与m为何值，该函数的图象与x轴总有两个公共点；（2）设该函数的图象的顶点为C，与x轴交于A，B两点，当△ABC是等腰直角三角形时，求a的值．20. （10分） (2015九上·揭西期末) 如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与x、y 轴交于点A（1，0），B（0，﹣1）与反比例函数y= 在第一象限内的图象交于点C，点C的纵坐标为1．（1）求一次函数的解析式；（2）求点C的坐标及反比例函数的解析式．21. （5分） (2015九上·揭西期末) 某班从3名男生和2名女生中随机抽出2人参加演讲比赛，求所抽取的两名学生中至少有一名女生的概率．22. （10分） (2015九上·揭西期末) 已知：如图，在矩形ABCD中，对角线AC，BD相交于点O，E是CD中点，连结OE．过点C作CF∥BD交线段OE的延长线于点F，连结DF．求证：（1）△ODE≌△FCE；（2）四边形ODFC是菱形．23. （5分） (2016九上·洪山期中) 某小区在绿化工程中有一块长为20m、宽为8m的矩形空地，计划在其中修建两块相同的矩形绿地，使它们的面积之和为56m2 ，两块绿地之间及周边留有宽度相等的人行通道（如图所示），求人行通道的宽度．24. （5分） (2015九上·揭西期末) 如图，正方形ABCD中，AB=4，E为BC的中点，F为AE的中点，过点F 作GH⊥AE，分别交AB和CD于G，H，求GF的长，并求的值．25. （15分） (2015九上·揭西期末) 如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长交AD于E，交BA的延长线于点F．（1）求证：△APD≌△CPD；（2）求证：△APE∽△FPA；（3）猜想：线段PC，PE，PF之间存在什么关系？并说明理由．参考答案一、选择题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题；共7分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共9题；共65分)17-1、18-1、19-1、20-1、20-2、21-1、22-1、22-2、23-1、24-1、25-1、25-2、25-3、。

广西钦州市九年级上学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）(2019·青岛) 下列四个图形中，既是轴对称图形，又是中心对称图形的是（）A .B .C .D .2. （2分） (2017九上·南平期末) 下列事件是必然事件的是（）A . 在一个标准大气压下，加热到100℃，水沸腾B . 抛一枚硬币，正面朝上C . 某运动员射击一次，击中靶心D . 明天一定是晴天3. （2分）把下列各式分解因式结果为-（x-2y）（x+2y）的多项式是（）A . x2-4yB . x2+4y2C . -x2+4y2D . -x2-4y24. （2分）⊙O的半径为5cm ，点A到圆心O的距离OA=3cm ，则点A与圆O的位置关系为（）A . 点A在圆上B . 点A在圆内C . 点A在圆外D . 无法确定5. （2分）下列说法中正确的个数共有①如果圆心角相等,那么它们所对的弦一定相等．②平面内任意三点确定一个圆．③半圆所对的圆周角是直角．④半圆是弧．A . 1个B . 2个C . 3个D . 4个6. （2分）(2016·余姚模拟) 如图，抛物线y=ax2+bx+c关于原点对称的抛物线是（）A . y=﹣ax2﹣bx+cB . y=ax2﹣bx﹣cC . y=﹣ax2+bx﹣cD . y=﹣ax2﹣bx﹣c7. （2分）某校学生小亮每天骑自行车上学时都要经过一个十字路口，设十字路口有红、黄、绿三色交通信号灯，他在路口遇到红灯的概率为，遇到绿灯的概率为，那么他遇到黄灯的概率为A .B .C .D .8. （2分）如图，抛物线y=ax2+bx+c(a≠0)经过点（－1，0），对称轴为：直线x=1，则下列结论中正确的是（）A . a＞0B . 当x>1时，y随x的增大而增大C . c＜0D . x=3是一元二次方程ax2+bx+c=0(a≠0)的一个根9. （2分）如图，PA切⊙O于点A，PB切⊙O于点B，CD切⊙O于E，若∠APB=50°，则∠COD的度数是（）A . 50°B . 40°C . 25°D . 65°10. （2分）下列说法正确的个数是（）①“对顶角相等”的逆命题是真命题②所有的黄金三角形都相似③若数据1、－2、3、x的极差为6，则x=4 ④方程x2－mx－3=0有两个不相等的实数根⑤已知关于x的方程的解是正数，那么m的取值范围为m＞-6A . 5B . 4C . 3D . 211. （2分）(2017·景泰模拟) 某商品的进价为每件20元．当售价为每件30元时，每天可卖出100件，现需降价处理，且经市场调查：每降价1元，每天可多卖出10件．现在要使每天利润为750元，每件商品应降价（）元．A . 2B . 2.5C . 3D . 512. （2分）如图，该图形围绕点按下列角度旋转后，不能与其自身重合的是（）A . 72°B . 108°C . 144°D . 216°二、填空题 (共6题；共6分)13. （1分）(2017·泰州模拟) 已知m，n是方程x2+2x﹣5=0的两个实数根，则m2﹣mn+3m+n=________．14. （1分）(2019·新宾模拟) 若点与关于原点对称，则的值是________.15. （1分）如图，△ABC为⊙O的内接三角形，AB=1，∠C=30°．则⊙O的内接正方形的面积为________ ．16. （1分） (2016八上·鞍山期末) 如图，在平面直角坐标系中，⊙P与轴相切于点C，⊙P的半径是4，直线被⊙P截得的弦AB的长为，则点P的坐标为________．17. （1分）(2017·贵港模拟) 某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO=8米，母线AB与底面半径OB的夹角为α，，则圆锥的侧面积是________平方米（结果保留π）．18. （1分）如图，AB是半圆O的直径，点C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点P，连接AC，BC，，AD＝3.给出下列结论：①AC平分∠BAD；②△ABC∽△ACE；③AB＝3PB；④S△ABC＝5，②根据两角相等两三角形相似即可判断；③由AB是⊙O的直径，PE是切线，可证得∠PCB＝∠PAC，即可证得△PCB∽△PAC，然后由相似三角形的对应边成比例与PB：PC＝1：2，即可求得答案；④首先过点O作OH⊥AD于点H，则AH＝ AD＝，四边形OCEH是矩形，即可得AE＝ +OC，由OC∥AE，可得△PCO∽△PEA，然后由相似三角形的对应边成比例，求得OC的长，再由△PBC∽△PCA，证得AC＝2BC，然后在Rt△ABC中，AC2+BC2＝AB2 ，可得（2BC）2+BC2＝52 ，即可求得BC的长，继而求得答案；其中正确的是________（写出所有正确结论的序号）.三、解答题 (共8题；共96分)19. （5分） (2017九上·三明期末) 解方程：x2﹣2（x+4）=0．20. （8分） (2016九上·萧山月考) 已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（﹣1，2）、B（﹣2，1）、C（1，1）（正方形网格中每个小正方形的边长是1个单位长度）．（1）△A1B1C1是△ABC绕点________逆时针旋转________度得到的，B1的坐标是________；（2）求出线段AC旋转过程中所扫过的面积（结果保留π）．21. （8分）如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．（1）旋转中心是点________，旋转角度是________度；若连结EF，则△AEF是________三角形；（2）若四边形AECF的面积为25，DE=2，求AE的长．22. （20分） (2015八下·淮安期中) 一只不透明的袋子中有2个红球、3个绿球和5个白球，这些球处颜色外都相同，将球搅匀，从中任意摸出1个球．（1）会出现哪些可能的结果？（2）能够确定摸到的一定是红球吗？（3）你认为摸到哪种颜色的球可能性最大？哪种颜色的球可能性最小？（4）怎样改变袋子中红球、绿球和白球的个数，使摸到这三种颜色的球的概率相同？23. （15分）(2018·牡丹江模拟) 为了迎接“五·一”小长假的购物高峰，某运动品牌服装专卖店准备购进甲、乙两种服装，甲种服装每件进价l80元，售价320元；乙种服装每件进价l50元，售价280元．（1）若该专卖店同时购进甲、乙两种服装共200件，恰好用去32400元，求购进甲、乙两种服装各多少件?（2）该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元，且不超过26800元，则该专卖店有几种进货方案?（3）在(2)的条件下，专卖店准备在5月1日当天对甲种服装进行优惠促销活动，决定对甲种服装每件优惠a(0<a<20)元出售，乙种服装价格不变．那么该专卖店要获得最大利润应如何进货?24. （10分）(2017·蜀山模拟) 一块矩形的草地，长为8m，宽为6m，若将长和宽都增加x m，设增加的面积为y m2 ，（1）求y与x之间的函数关系式；（2）若要使草地的面积增加32m2，长和宽都需增加多少米？25. （15分） (2019九下·天心期中) 如图所示，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB 于点D，CD交AE于点F，过C作CG∥AE交BA的延长线于点G．（1）求证：CG是⊙O的切线．（2）求证：AF＝CF．（3）若sinG＝0.6，CF＝4，求GA的长．26. （15分）(2016·攀枝花) 如图，抛物线y=x2+bx+c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，﹣3）（1）求抛物线的解析式；（2）点P在抛物线位于第四象限的部分上运动，当四边形ABPC的面积最大时，求点P的坐标和四边形ABPC的最大面积．（3）直线l经过A、C两点，点Q在抛物线位于y轴左侧的部分上运动，直线m经过点B和点Q，是否存在直线m，使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似？若存在，求出直线m的解析式，若不存在，请说明理由．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共6题；共6分)13-1、14-1、15-1、16-1、17-1、18-1、三、解答题 (共8题；共96分)19-1、20-1、20-2、21-1、21-2、22-1、22-2、22-3、22-4、23-1、23-2、23-3、24-1、24-2、25-1、25-2、25-3、26-1、26-2、26-3、。

广西钦州市九年级上学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）一同学将方程x2-4x-3=0化成了（x+m）2=n的形式，则m、n的值应为（）A . m=－2，n=7B . m=2，n=7C . m=－2，n=1D . m=2，n=72. （2分） (2019七上·顺德期末) 如图所示的几何体是由七个相同的小正方体组合成的，从上面看到的图形是（）A .B .C .D .3. （2分）将二次函数y=x2+4x﹣8化为y=（x+m）2+n的形式正确的是（）A . y=（x+2）2+8B . y=（x+2）2﹣8C . y=（x+2）2+12D . y=（x+2）2﹣124. （2分）用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.9，下列说法正确的是（）A . 种植10棵幼树，结果一定是“有9棵幼树成活”B . 种植100棵幼树，结果一定是“90棵幼树成活”和“10棵幼树不成活”C . 种植10n棵幼树，恰好有“n棵幼树不成活”D . 种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.95. （2分）(2017·西城模拟) 如图，小明在地面上放了一个平面镜，选择合适的位置，刚好在平面镜中看到旗杆的顶部，此时小明与平面镜的水平距离为2m，旗杆底部与平面镜的水平距离为16m．若小明的眼睛与地面距离为1.5m，则旗杆的高度为（单位：m）（）A .B . 9C . 12D .6. （2分）(2018·来宾模拟) 某班同学毕业时，都将自己的照片向全班其他同学各送一张表示留念，全班共送1892张照片，如果全班有x名同学，根据题意，列出方程为（）A . x（x+1）=1892B . x（x−1）=1892×2C . x（x−1）=1892D . 2x（x+1）=18927. （2分）下列图形中，阴影部分的面积最大的是（）A .B .C .D .8. （2分）小明在操场上练习双杠时，在练习的过程中他发现在地上双杠的两横杠的影子（）A . 相交B . 平行C . 垂直D . 无法确定9. （2分）将二次函数y=x2﹣2x﹣3化成y=（x﹣h）2+k形式，则h+k结果为（）A . ﹣5B . 5C . 3D . ﹣310. （2分）(2013·贵港) 如图，在矩形ABCD中，点E是AD的中点，∠EBC的平分线交CD于点F，将△DEF 沿EF折叠，点D恰好落在BE上M点处，延长BC、EF交于点N．有下列四个结论：①DF=CF；②BF⊥EN；③△BEN是等边三角形；④S△BEF=3S△DEF ．其中，将正确结论的序号全部选对的是（）A . ①②③B . ①②④C . ②③④D . ①②③④二、填空题 (共6题；共6分)11. （1分）三棱柱的三视图如图所示，△EFG中，EF=10cm，EG=16cm，∠EGF=30°，则AB的长为________cm ．12. （1分）若＝，则＝________．13. （1分） (2017九上·平舆期末) 如图，在△ABC中，D是AB边上一点，连接CD，要使△ADC与△ABC相似，应添加的条件是________．14. （1分）已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如表：x…﹣2﹣1012…y…﹣3﹣4﹣305…当y＞0时，则x的取值范围为________．15. （1分）已知关于的一元二次方程有两个实数根和．若时，则 = ________ ．16. （1分）(2014·贵港) 已知点A1（a1 ， a2），A2（a2 ， a3），A3（a3 ， a4）…，An（an ， an+1）（n为正整数）都在一次函数y=x+3的图象上．若a1=2，则a2014=________．三、解答题 (共9题；共98分)17. （5分）(2012·资阳) 先化简，再求值：，其中a是方程x2﹣x=6的根．18. （5分）如图，在▱ABCD中，∠BAD的平分线交CD于点E，交BC的延长线于点F，连接BE，∠F=45°．（1）求证：四边形ABCD是矩形；（2）若AB=14，DE=8，求sin∠AEB的值．19. （5分） (2020九下·汉中月考) 如图，某中学两座教学楼中间有个路灯，甲、乙两个人分别在楼上观察路灯顶端，视线所及如图①所示。

钦州港经济技术开发区中学2018年秋季学期期末考试九年级数学一、选择题1. 下列各式是最简二次根式的是（）A．B．C．D．2. 下列各组数中，能构成直角三角形的是（）A．4，5，6 B．C．6，8，11 D．5，12，233. 已知一次函数y=kx+b的图象如图所示，则k、b的符号是（）A．k＜0，b＜0 B．k＞0，b＜0 C．k＜0，b＞0 D．k＞0，b＞04. 连接对角线互相垂直的四边形的四边中点，所构成的四边形一定是（）A．矩形B．菱形C．正方形D．梯形5. 若的整数部分为x，小数部分为y，则的值是（）A．B．C．D．6.下列说法正确的有（）①4是x3＞1的解；②不等式x2＜0的解有无数个；③x＞5是不等式x+2＞3的解集；④x=3是不等式x+2＞1的解；⑤不等式x+2＜5有无数个正整数解．A．1个B．2个C．3个D．4个7. 若a＜b，则下列各式中一定成立的是（）A．ac＜bc B．a＜b C．a1＜b1 D．8. 如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐的角∠A是120°，第二次拐的角∠B是150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C的大小是（）A．150°B．130°C．140°D．120°9. 如图，一次函数y=k 1 x+b 1 的图象l 1 与y=k 2 x+b 2 的图象l 2 相交于点P，则方程组的解是（）A．B．C．D．10. 如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x≥ax+4的解集为（）A．x≥B．x≤3 C．x≤D．x≥311. “六一”儿童节前夕，某超市用3360元购进A，B两种童装共120套，其中A型童装每套24元，B型童装每套36元．若设购买A型童装x套，B型童装y 套，依题意列方程组正确的是（）A．C．B．D．12. 如果不等式3xm≤0的正整数解为1，2，3，则m的取值范围是（）A．9≤m＜12 B．9＜m＜12 C．m＜12 D．m≥9二、填空题13. 使代数式有意义的x的取值范围是．14.请你写出同时具备下列两个条件的一次函数的表达式（写出一个即可）．（1）y随x的增大而减小；（2）图象经过点（2，8）15. 已知一次函数y=2x+1，则它的图象与坐标轴围成的三角形面积是．16. 如图，在直角坐标系中，正方形A 1 B 1 C 1 O、A 2 B 2 C 2 C 1 、A 3 B 3 C 3 C 2 、…A nB nC n C n 1 的顶点A 1 、A 2 、A 3 、…、A n 均在直线y=kx+b上，顶点C 1 、C 2 、C 3 、…、C n 在x轴上，若点B 1 的坐标为（1，1），点B 2 的坐标为（3，2），那么点B 4 的坐标为．17.一个三角形的三边长分别为15cm、20cm、25cm，则这个三角形最长边上的高是 cm．三、计算题18.19. 计算：．20. 计算或化简：12018××[3(3)2]21. 解不等式组，并把不等式组的解集在数轴上表示出来．答案一、选择题1、B.2、B3、A.4、A5、C．6、B.7、C.8、A.9、A.10、A．11、B. 12.A.二、填空题13、且x≠3. 14、y=x615、. 16、（15，8）17、12．三、计算题18、-2 解:19、===．20、 0 12018（10.5）××[3(3)2]=-1-0.5××[39]………………2分=-1-0.5××[-6]……………………4分=-1+1=0…………………………………………6分21、x＜-4 ．由①得x ＜-4 ………………………………………………1分由②得x ≤15 ………………………………………………3分∴x ＜-4 ………………………………………………4分图略。

广西钦州市九年级上学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）(2019·云南模拟) 若（2，k）是双曲线y＝上的一点，则函数y＝（k﹣2）x的图象经过（）A . 第一、三象限B . 第二、四象限C . 第一、二象限D . 第三、四象限2. （2分）方程的解是（）A .B . ，C . ，D .3. （2分）从1、2、－3三个数中，随机抽取两个数相乘，积是正数的概率是（）A . 0B .C .D . 14. （2分）若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根，则k的取值范围是（）A . k＞-1B . k＞-1且k≠0C . k＜1D . k＜1且k≠05. （2分）如图是一个照相机成像的示意图，如果底片AB宽40mm，焦距是60mm，所拍摄的2m外的景物的宽CD为（）A . 12mB . 3mC . mD . m6. （2分）如图，在中，点D，E分别为AB，AC边上的点，且，CD、BE相较于点O，连接AO并延长交DE于点G，交BC边于点F，则下列结论中一定正确的是（）A .B .C .D .7. （2分）如图所示的支架是由两个长方形构成的组合体，则它的主视图是（）A .B .C .D .8. （2分）(2017·农安模拟) 如图，在平面直角坐标系中，反比例函数y= （x＞0）的图象经过A、B两点，菱形ABCD在第一象限内，边BC于x轴平行．若A、B两点的纵坐标分别为3和1，则菱形ABCD的面积为（）A . 2B . 4C . 2D . 49. （2分） (2014九上·临沂竞赛) 冬至时是一年中太阳相对于地球位置最低的时刻，只要此时能采到阳光，一年四季就均能受到阳光照射．此时竖一根米长的竹杆，其影长为米，某单位计划想建米高的南北两幢宿舍楼（如图所示）．当两幢楼相距多少米时，后楼的采光一年四季不受影响？（）A . 米B . 米C . 米D . 米10. （2分）(2017·衡阳模拟) 如图，菱形OABC的顶点O在坐标原点，顶点A在x轴上，∠B=120°，OA=2，将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置，则点B′的坐标为（）A . （，﹣）B . （﹣，）C . （2，﹣2）D . （，﹣）二、填空题 (共6题；共6分)11. （1分）一元二次方程x2=3的根是________ .12. （1分）(2017·常州模拟) 反比例函数y= 的图象经过点（1，6）和（m，﹣3），则m=________．13. （1分）(2017·谷城模拟) 在﹣1、3、﹣2这三个数中，任选两个数的积作为k的值，使反比例函数的图象在第一、三象限的概率是________．14. （1分）如图，在矩形ABCD中，点E、F分别在AB、DC上，BF∥DE，若AD=12cm，AB=7cm，且AE：EB=5：2，则阴影部分的面积为________ cm215. （1分） (2016·临沂) 如图，在△ABC中，点D，E，F分别在AB，AC，BC上，DE∥BC，EF∥AB．若AB=8，BD=3，BF=4，则FC的长为________．16. （1分）(2016·梅州) 如图，在平行四边形ABCD中，点E是边AD的中点，EC交对角线BD于点F，若S△DEC=3，则S△BCF=________．三、解答题 (共9题；共66分)17. （5分）先化简，再求值：（ +4）÷ ，其中x的值是方程x2+x=0的根．18. （10分） (2017八下·苏州期中) 如图，一次函数的图象与反比例函数的图象交于点A﹙−2，−5﹚、C﹙5，n﹚，交y轴于点B，交x轴于点D．（1）求反比例函数和一次函数的表达式；（2）连接OA、OC．求△AOC的面积．19. （5分）如图，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形．（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）20. （10分）(2017·泸州) 一次函数y=kx+b（k≠0）的图象经过点A（2，﹣6），且与反比例函数y=﹣的图象交于点B（a，4）（1）求一次函数的解析式；（2）将直线AB向上平移10个单位后得到直线l：y1=k1x+b1（k1≠0），l与反比例函数y2= 的图象相交，求使y1＜y2成立的x的取值范围．21. （5分） (2019九上·朝阳期末) 在一个不透明的盒子里装着三张卡片，分别标记为A、B、B ，每张卡片除图案不同外其余均相同，卡片上的图案分别为正方形和等边三角形．从盒子里随机抽出一张卡片，记下图案后放回并搅匀；再随机抽出一张卡片记下图案．用画树状图（或列表）的方法，求两次抽出的卡片上的图案都是等边三角形的概率．22. （10分）(2017·大连模拟) 如图，在平面直角坐标系xOy中，点A、B的坐标分别为（0，3）、（7，0），点C在第一象限，AC∥x轴，∠OBC=45°．（1）求点C的坐标；（2）点D在线段AC上，CD=1，点E的坐标为（n，0），在直线DE的右侧作∠DEG=45°，直线EG与直线BC相交于点F，设BF=m，当n＜7且n≠0时，求m关于n的函数解析式，并直接写出n的取值范围．23. （5分） (2016九上·孝南期中) 某超市经销一种成本为40元/kg的水产品，市场调查发现，按50元/kg 销售，一个月能售出500kg，销售单位每涨0.1元，月销售量就减少1kg，针对这种水产品的销售情况，超市在月成本不超过10000元的情况下，使得月销售利润达到8000元，请你帮忙算算，销售单价定为多少？24. （5分）如图，锐角△ABC中，边BC长为3，高AH长为2，矩形EFMN的边MN在BC边上，其余两个顶点E，F分别在AB，AC边上，EF交AH于点G．（1）求的值；（2）当EN为何值时，矩形EFMN的面积为△ABC面积的四分之一．25. （11分） (2016九上·淅川期中) 如图，已知在矩形ABCD中，AB=a，BC=b，点E是线段AD边上的任意一点（不含端点A、D），连接BE、CE．若a=5，sin∠ACB= ，解答下列问题：（1）填空：b=________；（2）当BE⊥AC时，求出此时AE的长；（3）设AE=x，试探索点E在线段AD上运动过程中，使得△ABE与△BCE相似时，请写x、a、b三者的关系式．参考答案一、选择题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题；共6分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共9题；共66分)17-1、18-1、18-2、19-1、20-1、20-2、21-1、22-1、23-1、24-1、25-1、25-2、25-3、。

钦州市九年级上学期期末数学试卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题；共16分)1. （2分） (2017九下·萧山开学考) 已知线段 a=2，b=8，则 a，b 的比例中项线段为（）A . 16B . ±4C . 4D . ﹣42. （2分）在Rt△ABC中，∠C=90°，BC=3，AB=5，则cosA的值为（）A .B .C .D .3. （2分） (2019九上·深圳期末) 今年3月12日，某学校开展植树活动，某植树小组20名同学的年龄情况如下表：那么这20名同学年龄的众数和中位数分别是（）年龄（岁）1213141516人数14375A . 15，14B . 15，15C . 16，14D . 16，154. （2分）(2017·微山模拟) 如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1，下列结论：①abc＜0；②9a+3b+c=0；③4ac﹣b2＜2a；④2b=3a．其中正确的结论是（）A . ①③B . ②④C . ①④D . ②③5. （2分）(2017·淄博) 在一个不透明的袋子里装有四个小球，球上分别标有6，7，8，9四个数字，这些小球除数字外都相同．甲、乙两人玩“猜数字”游戏，甲先从袋中任意摸出一个小球，将小球上的数字记为m，再由乙猜这个小球上的数字，记为n．如果m，n满足|m﹣n|≤1，那么就称甲、乙两人“心领神会”，则两人“心领神会”的概率是（）A .B .C .D .6. （2分）下列说法中，正确的是（）A . 经过三个点一定可以作一个圆B . 经过四个点一定可以作一个圆C . 经过圆心且平分弦的直线一定垂直于这条弦D . 三角形的外心到三角形各顶点的距离都相等7. （2分）抛物线y=（m﹣1）x2﹣3的图象开口向下，则m的取值范围是（）A . m≠1B . m＞1C . m＜1D . m可取一切实数8. （2分）若二次函数的图象与x轴有两个交点，坐标分别为（， 0），（， 0），且，图象上有一点M（）在x轴下方，则下列判断中正确的是（）．A .B .C .D .二、填空题 (共10题；共10分)9. （1分） (2015九上·龙岗期末) 方程4x（2x+1）=3（2x+1）的解为________．10. （1分）两个相似三角形面积之比为2：7，较大三角形一边上的高为，则较小三角形的对应边上的高为________.11. （1分）(2018·深圳模拟) 一台机床生产一种零件，5天内出现次品的件数为：1，0，1，2，1．则出现次品的方差为________．12. （1分） (2018九上·兴化期中) 如图，一块飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是________．13. （1分）(2016·姜堰模拟) 一个圆锥的侧面积是2πcm2 ，它的侧面展开图是一个半圆，则这个圆锥的高为________ cm．14. （1分） (2018九上·大庆期末) 如图，在锐角△ABC中，以BC为直径的半圆O分别交AB，AC于D，E 两点，且cosA= ，则S△ADE：S四边形DBCE的值为________．15. （1分） (2020九上·平度期末) 已知一元二次方程x2+k-3=0有一个根为-2，则k的值为________。