【思维拓展】数学六年级思维拓展之标数法(附答案)

2022-2023学年小学六年级思维拓展专题 转化单位“1”知识精讲把不同的数量当作单位“1”，得到的分率可以在一定的条件下转化。

如果甲是乙的ab，乙是丙的cd，则甲是丙的acbd；如果甲是乙的ab，则乙是甲的ba；如果甲的ab等于乙的cd，则甲是乙的cd÷ab=bcad，乙是甲的ab÷ab=adbc。

我们必须重视转化训练。

通过转化训练，既可理解数量关系的实质，又可拓展我们的解题思路，提高我们的思维能力。

典例分析【典例01】甲数是乙数的23，乙数是丙数的34，甲、乙、丙的和是216，甲、乙、丙各是多少？解法一：把丙数看所单位“1”那么甲数就是丙数的34×23=12，丙：216÷1+34+34×23=96乙：96×34=72甲：72×23=48解法二：可将“乙数是丙数的34”转化成“丙数是乙数的43”，把乙数看作单位“1”。

乙：216÷23+1+43=72甲：72×23=48丙：72÷34=96解法三：将条件“甲数是乙数的23”转化为“乙数是甲数的32”，再将条件“乙数是丙数的34”转化为“丙数是乙数的43”，以甲数为单位“1”。

甲：216÷1+32+32×43=48乙：48×32=72丙：72×43=96答：甲数是48，乙数是72，丙数是96。

【典例02】红、黄、蓝气球共有62只，其中红气球的35等于黄气球的23，蓝气球有24只，红气球和黄气球各有多少只？解法一：将条件“红气球的35等于黄气球的23”转化为“黄气球的只数是红气球的35÷23=910”。

先求红气球的只数，再求出黄气球的只数。

红气球：(62-24)÷1+35÷23=20(只)黄气球：62-24-20=18(只)解法二：将条件“红气球的35等于黄气球的23”转化为“红气球的只数是黄气球的23÷35= 109”。

数学试题卷 第1页（共4页）六年级数学思维提升试卷（时间：80分钟，满分100分）一、填空题。

（第1-3题每小题3分，第4-7题每小题4分，第8-10题每小题5分，共40分）1. 把2017减去它的21，再减去余下的31，再减去余下的41，依此类推，一直减去余下的20161，那么最后剩下的数是（ ）。

2. 小丁、小钱、小王、小韩、小傅参加学校围棋比赛，而且都进入了前五名。

发奖前，老师让他们猜一猜各自的名次。

小丁说：小钱第三，小王第五；小钱说：小傅第四，小韩第五；小王说：小丁第一，小傅第四；小韩说：小王第一，小钱第二；小傅说：小丁第三，小韩第四。

老师说：每个名次都有人猜对。

那么，获第四名的是（ ）。

3. 甲、乙两位探险者要到沙漠深处探险，他们每天可走25千米，已知每人最多可带一个人20天的食物和水，如果允许将部分食物存放在途中，那么其中一个人最远可走入沙漠（ ）千米。

4. 有一些自然数按照右边规律排列，则上起第10行，左起第8列的数是 （ ）。

5. 如下图，右面的4个图形，只有一个是左边的纸板折叠起来的，这个图形是（ ）。

6. 如图所示的四个圆形跑道，每个跑道长都是1千米。

甲、乙、丙、丁四人同时从交点O 出发，分别沿四个跑道跑步，他们的速度分别是每小时4千米，每小时6千米，每小时8千米，每小时10千米。

从出发到四人再次相遇，四人一共跑了（ ）千米。

7. 有黑色、白色、黄色、银色的筷子各8根，混杂放在一起，黑暗中想从这些筷子中取出颜色不同的三双筷子，至少要取出（ ）根才能保证达到要求。

8. 右图圆锥体底面半径为1.5厘米，AB 长为9厘米，一只甲壳虫从A 点出发绕圆锥表面爬一圈回到A 点，问最短路程是（ ）厘米。

9. 用面积为1、2、3、4的4张长方形纸片拼成如右图所示的长方形。

图中阴影部分的面积是 ( )。

10. 一批工人到甲乙两个工地进行清理工作。

甲工地的工作量是乙工地的工作量的211倍。

上午去甲工地的人数是去乙工地人数的3倍，下午这批工人中有125在乙工地工作，其他工人去甲工地。

小学六年级思维训练专题之7 归纳与推递1、早在公元前300多年前，古希腊著名科学家欧几里德就在他的旷世名著<几何原本》一书中记载了几何学中最基本、最引人人胜的一条著名定理：“三角形的内角和等于180度”，我们的问题是：①四边形的内角和等于多少度（见下图）?答：五边形的内角和等于多少度（见下图）?答：②进一步，如果把多边形的边数记作n，你能够归纳出n边形的内角和的计算公式吗？答：公式为__ __．③在家庭装修中，经常采用各种正多边形（注：正多边形就是各条边均相等且各内角也相等的多边形）的瓷砖搭配出各式各样的地面图案．小明家装修时采用了三种正多边形瓷砖铺地面，这三种型号的瓷砖可以围绕着地面上的一点既不重叠又不产生漏洞的拼接起来．其中一种型号是正方形，另一种型号是正六边形，你知道第三种型号的多边形瓷砖的边数是多少吗？请写出你的计算过程．2、一条直线分一个平面为两部分，二条直线最多分一张平面为四部分，问：五条直线最多分一个平面为多少部分？3、将一个圆形纸片用直线划分成大小不限的若干小纸片，如果要分成不少于50个小纸片，至少要画多少条直线？请说明．4、一个长方形把平面分成两部分，那么三个长方形最多把平面分成部分．5、 n个平面最多钝将空间分成多少个部分？6、如下图所示，第一个三角形的面积是256，取三角形的3条边的中点，连成一个三角形，将中间的三角形挖去，得到第二个图，再将第二个图中每个三角形按照前一个做法得到第三个图，如此下去……，求第五个图形的面积是。

7、在一张长方形纸片内有n个点，加上四个顶点共，n+4个点，这些点中任意三点都不在同一条直线上，（1）n=4时，将长方形纸片剪开，最多可以剪成多少个以这些点为顶点的三角形（画出一个示意图即可作答）．(2)n=2010时，最多可以剪成多少个以这些点为顶点的三角形？并作简要说明．(注意：(1)、(2)中任意两个三角形不重叠）8、在一个圆周上标出一些数，第一次先把圆周二等分，在两个分点旁分别标上和，如图a所示；第二次把两段半圆弧二等分，在分点旁标上相邻两分点旁所标两数的和，如图b 所示，=＋；第三次把4段圆弧二等分，并在4个分点旁标上相邻两分点旁所标两数的和，如图c所示，1=＋，1=＋；如此继续下去，当第八次标完数以后，圆周上所有已标的数的总和是____．9、小凯家住二楼，从一楼到二楼的楼梯共有9阶，小凯上楼时每步可跨1阶、跨2阶、或跨3阶．请问他共有多少种不同的方法上楼？10、仅由数字1和2组成一些数，其中至少有两个数字1相连的数称为“学而思数”，如11，112，1211等都是“学而思数”，而12212就不是“掌而思数”．那么所有六位的学而思数共多少个？11、用1×2小长方形或1×3的小长方形覆盖2×6的方格网（如下图所示），共有不同的盖法。

（尖子生题库）专题16数与形的解题技巧2023六年级数学思维拓展奥数培优讲义（通用版）通过不同事物的某些相似性逆向类推出其他的相似性的方法，叫做逆向类推法。

解答数形结合问题时,先仔细观察算式的特点,找出其中隐含的规律,再解答。

数与形是数学中的两个最古老、也是最基本的研究对象，它们在一定条件下可以相互转化。

数与形是有联系的，这个联系称之为数形结合，或形数结合。

数形结合的思想，其实质是将抽象的数学语言与直观的图像结合起来，关键是代数问题与图形之间的相互转化，它可以使代数问题几何化，几何问题代数化。

数形结合的思想可以使某些抽象的数学问题直观化、生动化，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷。

顶点处。

应选（ ）。

A ．673，左下B ．674，上C ．673，右下D ．674，左下2．用白色和灰色小正方形按下面规律排成大正方形。

……第一幅第二幅第三幅第五幅图一共用了（）个灰色小正方形。

A．19 B．21 C．25 D．363．下图是某晚报“百姓热线”一周内接到热线电话的统计图，其中有关环境保护话题的电话最多，共70个。

则本周“百姓热线”共接到热线电话有（）。

A．350个B．200个C．180个D．150个4．观察数列的排列规律，然后从四个选项中选出你认为最合理的一项，来填补空缺项：1 2 4 8 16（）A．32 B．24 C．64 D．205．仔细分析，后面的第10个方框里有（）个点。

A．36 B．37 C．38 D．406．与1＋3＋5＋7＋9＋5＋3＋1得数相同的算式是（）。

A．42B．52＋32C．52－327．如图的每个正方形中的四个数之间都有相同的规律，请根据此规律，计算出m的值是（）。

A．86 B．74 C．52．中。

A．60 B．50 C．46 D．4517．观察下列图形：第1个图形有6根小棒，第2个图形有11根小棒，第3个图形有16根小棒……，第10个图形有（）根小棒。

01.从六个数字1，2，3，4，5，6中任意选取两个组成两位数，如果其中的6也可以换成9使用，一共可以组成（40）个不同的两位数。

解：组成两位数的情况=普通情况+6作9的情况普通情况：6×5=30;6作9的情况:有一位必选9，剩下的排数位2×5=10;30+10=40(个）02.两个自然数a和b,它们的最大公因数是14，最小公倍数是280，那么它们的和a+b是（294）或（136）。

解：方法：短除模型14xy=280,xy=20;x,y=1;只有两组可能解：൝x=1y=20，ቊx=4y=5；则൝a=14b=280，ቊa=56b=70；则a+b=294或136.03.从7开始，把7的倍数一直写下去，一直到994，成为一个很大的数：71421……987994.这个数是（411）位数。

解：994是7的142倍；7是7的1倍，也是唯一的个位数7的倍数；从7的2倍14一直到7的14倍98，一共有13个是两位数的7的倍数；从7的15倍105一直到7的142倍994，一共有128个是三位数的7的倍数；1×1+2×13+3×128=411(位）。

04.有一泓泉水，泉水不断从泉底涌出，并且每分钟涌出的泉水一样多。

如果用8台抽水机10小时可以把全部的水抽干；如果用12台抽水机6小时可以把全部的水抽干.那么如果用14台抽水机（5）小时可以把全部的水抽干。

解：设一台抽水机一小时抽一份水；则10小时抽了8×10=80份水；6小时抽了12×6=72份水；水速：80−72÷10−6=2份每小时；原来水量：80−10×2=60份水；设14台抽水机x小时抽完所有水14x=60+2xx=505.六（1）班和六（2）班的人数之和在100人左右。

如果排成3列不多不少；如果排成5列少2人；如果排成7列少4人。

这两个班一共有（102）人。

解：将条件用同余式表示：a≡0mod3,a≡2mod5,a≡4mod7;即a最小是3,5,7−3=10206.在▲ABC中，E是AC的中点，且BD=2DC，AD和BE交于F,则▲BDF的面积:四边形DCEF的面积=（8:7）。

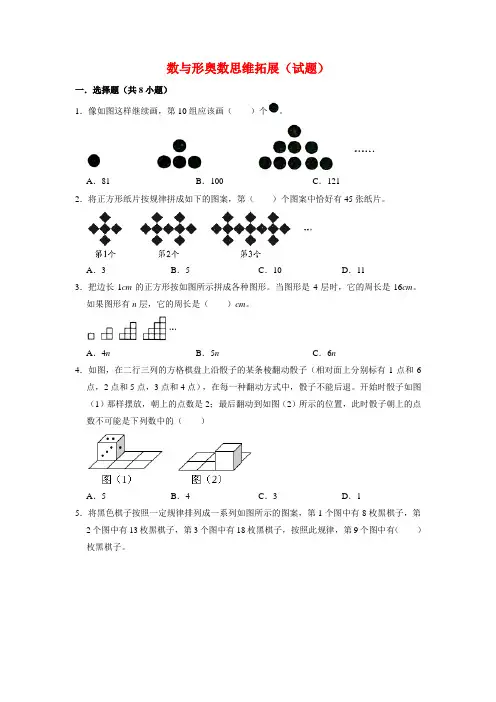
数与形奥数思维拓展（试题）一．选择题（共8小题）1．像如图这样继续画，第10组应该画（）个。

A．81B．100C．1212．将正方形纸片按规律拼成如下的图案，第（）个图案中恰好有45张纸片。

A．3B．5C．10D．113．把边长1cm的正方形按如图所示拼成各种图形。

当图形是4层时，它的周长是16cm。

如果图形有n层，它的周长是（）cm。

A．4n B．5n C．6n4．如图，在二行三列的方格棋盘上沿骰子的某条棱翻动骰子（相对面上分别标有1点和6点，2点和5点，3点和4点），在每一种翻动方式中，骰子不能后退。

开始时骰子如图（1）那样摆放，朝上的点数是2；最后翻动到如图（2）所示的位置，此时骰子朝上的点数不可能是下列数中的（）A．5B．4C．3D．15．将黑色棋子按照一定规律排列成一系列如图所示的图案，第1个图中有8枚黑棋子，第2个图中有13枚黑棋子，第3个图中有18枚黑棋子，按照此规律，第9个图中有（）枚黑棋子。

A．49B．48C．47D．466．把同样的小棒按下面的方式摆放，第9个图形需要（）根小棒。

A．24B．27C．307．观察下面图形的规律，其中第1个图形由4个小正方形组成，第2个图形由7个小正方形组成，第3个图形由10个小正方形组成，…按此规律排列下去，则第n个图形由（）个小正方形组成。

A．4n B．2n﹣1C．3n+1D．3n﹣18．如图所示，用白色小正方形和黑色长方形按照下面的摆法，组成不同的长方形。

当摆5个黑色长方形时，四周需要摆（）个白色小正方形。

A．16B．20C．26D．36二．填空题（共8小题）9．如图，用小棒摆出若干个小正方形。

照这样的规律，摆n个小正方形需要根小棒；用100根小棒可以摆个这样的正方形。

10．观察如图规律，如果一幅图中涂色正方形是6个，那么空白正方形有个。

11．观察下面的图形并填空。

利用你发现的规律直接写出下面算式的结果：1992﹣1982＝12．照此规律画下去，第n个图形共有个■，个□。

六年级思维拓展之标数法1.如图，8个单位正方体拼成的大正方体，沿着面上的格线，从A到B的最短路线共有多少条？2.如图，27个单位正方体拼成的大正方体，沿着面上的格线，从A到B的最短路线共有多少条？3.在下面的街道示意图中，有几处的街区有积水不能通行，那么从A到B的最短路线有多少种？4.一只兔子沿着方格的边从A到B，规定只能往上走或者往右走，但是必须经过一座独木桥MN，这只兔子有多少种不同的走法？5.如图所示，一个花坛的道路由3个圆和5条线段组成，小兔要从A处走到B 处，如果他在圆上只能顺时针方向走，在线段上只能从小圆走向大圆，且每条道路最多走一次，那么小兔可以选择的不同路线有多少条？6.阿雅和天天到图书馆参加活动。

如果他们从学校出发，共有多少种不同的最短路线?7.下图是阿雅学校附近小区的平面图。

今天阿雅放学，要去同学家写作业。

请问：从学校到同学家有多少种不同的最短路线?8.皮皮和天天准备去看望养老院的李奶奶，可是市中心在修路（城市的街道如图所示），他们从学校到养老院最短路线共有几条呢？聪明的小朋友，你们知道吗？9.按图中箭头所示的方向行走，从A点走到B点的不同路线共有多少条?10.如图，一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？参考答案1.【解答】直接用标数法。

从A点出发的三个面左面、下面、前面所标数相等，上面的中间填6，进而中间右填18。

类似的，即可得到到达B段的方法总数有：18×3=542.【解答】共有384条3.【解答】22条4.【解答】18种5.【解答】6条6.【解答】标数法：三步走(1)确定方向；（2）从起点出发的两个方向上每个点标1；（3）其他点来源相加。

如下图所示。

一共有10种不同的最短路线。

7.【解答】3.标数，如下图所示。

一共有10种不同的路线。

8.【解答】标数，不能通过的点打叉或者标0，如下图所示。

一共有132条路线，9.【解答】标数法，如下图所示。

分数、百分数问题奥数思维拓展一．选择题（共6小题）1．一袋洗衣粉，第一周用了全部的，第二周用了全部的25%，还剩1.2千克。

这瓶洗衣粉原来有多少千克？（）A．3.2B．5.6C．3.5D．5.22．汽车厂今年上半年完成计划的75%，下半年完成计划的，汽车厂今年超产（）A．75%B．50%C．25%D．125%3．甲数比乙数多，乙数就比甲数少（）A．12.5%B．37.5%C．60%4．体育用品商店进购一批体育器材，其中足球和篮球的总数是150个，足球的数量占两种球总数的40%．后来又进购了一些足球，此时篮球的数量占两种球总数的，后来又进购了（）个足球．A．90B．70C．605．学校一次课外活动，缺勤人数是出勤人数的10%，后来又有2人因病请假，这时缺勤人数是出勤人数的，这个学校课外活动小组共有（）A．99人B．90人C．100人D．190人6．某厂上半月完成计划的75%，下半月完成计划的，这个月增产（）A．25%B．45%C．30%D．20%二．填空题（共8小题）7．某服装厂计划一个月生产衬衫8000件，结果上半月完成了60%，下半月完成，这个月超量生产件。

8．某超市将商品促销活动，一种书包原价是100元，先降价20%后，又提价这种书包现在的售价是元。

9．湖边种了40棵柳树，是桃树棵数的，榕树的棵数是桃树棵数的65%。

湖边种了棵榕树。

10．工地有水泥120吨，沙子的质量是水泥的40%，又是石子的，石子的质量是吨。

11．运动健身迎亚运，和谐杭州展新韵。

为迎接第十九届杭州亚运会，学校组织教师健步走，张老师已经走了全程的40%，如果再走4千米，已走路程就占全程的。

这次健步走的全程是千米。

12．明彩文具超市新购进180支钢笔，新购进的圆珠笔的数量比钢笔多，新购进的圆珠笔有支；新购进的中性笔比圆珠笔少50%。

新购进的中性笔有支。

13．一堆货物，第一天运走了总数的，第二天运走了总数的25%，剩下的按3：4分配给甲车和乙车。

六年级数学专题思维训练—计数综合1、若4个两两不同的自然数的倒数之和为1，则这样的自然数组（次序不同认为是同共有组，2、如下图所示，在纸上画有A、B、C三点，经过其中任意两点画一条直线，可以画3条直线，如果在纸上画有5个点，其中任意三个点都不在一条直线上，经过每两点画一条直线，可以画____条直线．3、在右下图中，以最短的路径从点P到点Q，请问共有种不同的走法．4、科学家“爱因斯坦”的英文名拼写为“Einstein”，如下图所示，按图中箭头所示方向有种不同的方法拼出英文单词“Einstein”．5、在下图中，用水平或者竖直的线段连接相邻的字母，当沿着这些线段行走时，正好拼出“APPLE”的路线共有多少条？6、甲队和乙队进行的一场足球赛的最终比分是4：2，已知甲队先进一球，而乙队在比赛过程中始终没有领先过，那么两队的入球次序共有种不同的可能．7、如下图所示，27个单位正方体拼成大正方体，沿着面上的格线，从A到B的最短路线共有条．8、国际象棋中“马”的走法如图a所示，位于O位置的“马”只能走到标有×的格中，类似于中国象棋中的“马走日”．如果“马”在8×8的国际象棋棋盘中位于第一行第二列（图b）中标有△的位置），要走到第八行第五列（图b）中标有★的位置），最短路线有条．9、小思从X市开车到y市，她必须遵照下图箭头所指示的方向行驶：请问小思由X市到y市共有多少种不同的路径？10、 A，B两人进行象棋比赛，没有和棋，先比对方多胜三局的一方赢得比赛，如果经过11局比赛A才以7胜4负获胜，那么这11局比赛的胜负排列共有种．（例如：“胜负胜负胜负胜负胜胜胜”是一种胜负排列）11、一个正在行进的8人队列，每人身高各不相同，按从低到高的次序排列．现在他们要变成2列纵队，每列仍然是按从低到高的次序排列，同时要求并排的每两人中左边的人比右边的人要矮，那么，2列纵队有种不同排法．12、有7个相同的小球放人4个不同的盒子中，每个盒子中至少放一个球，则共有种不同的放法．A. 15 B．18 C．20 D．2413、以下图的黑点作为顶点，请问可作出多少个三角形？14、正整数2009的数码和为11，请问在2010到2999之间有多少个自然数其数码和为11 ？15、学学和思思一起洗已摞好的5个互不相同的碗，思思洗好的碗一个一个往上摞，学学再从最上面一个一个地拿走放人碗柜摞成一摞，思思一边洗，学学一边拿，那么学学摞好的碗一共有种不同的摞法。