张仁友_高能物理过程的精确计算
- 格式:pdf
- 大小:3.89 MB
- 文档页数:42


5.2 裂变及其应用1。
知道重核裂变能放出能量,并能计算核能的变化.(重点+难点) 2.了解铀核的裂变特点,知道链式反应.(重点)3.了解裂变反应堆的结构、类型及核电站的工作原理., [学生用书P69])一、铀核的裂变1.定义:重核裂变是用中子轰击铀核时发现的,中子轰击铀—235核,使该核变成处于激发态的复核,并分裂成两块质量差不多的新原子核,同时放出几个中子,称为裂变核反应.2.铀核裂变:用中子轰击铀核时,铀核发生了裂变,铀核裂变的产物是多种多样的,其中一种典型的反应是235U+1,0n→错误!Ba+错误!Kr+3错误!n.92二、链式反应及其条件1.链式反应:铀核裂变时,通常会放出2到3个中子,这些中子可以作为新的“炮弹"轰击其他的铀核,使裂变反应不断地进行下去,这种反应叫做核裂变的链式反应.2.临界体积:能够使铀块发生链式反应的最小体积(或对应的最小质量)称为临界体积(或临界质量).3.链式反应的条件:发生裂变物质的体积大于等于临界体积或裂变物质的质量大于等于临界质量.1.(1)铀核的裂变是一种天然放射现象.()(2)铀块的质量大于临界质量时链式反应才能不停地进行下去.()(3)中子的速度越快,越容易发生铀核裂变.()提示:(1)×(2)√(3)×三、裂变反应堆1.裂变反应堆的基本构造(1)裂变材料(核燃料):浓缩铀.(2)慢化剂(减速剂):通常用石墨、重水或普通水.(3)控制棒:用镉或硼钢制成,用来吸收减速后的中子,控制反应强度.(4)反射层:一般用石墨做材料.(5)热交换器:核反应堆中释放的能量大部分转化为热能,利用水循环,产生高温高压的蒸汽,从而推动蒸汽轮机,带动发电机发电.(6)防护层:由金属套、防止中子外逸的水层以及1~2 m厚的钢筋混凝土构成,可有效地防止射线对人体及其他生物体的侵害.2.列变反应堆的常见类型:重水堆,高温气冷堆,快中子增殖反应堆.3.核电站的工作模式:以核反应堆为能源,用它产生高压蒸汽,取代发电厂的锅炉,从而进行发电.2.(1)在核反应中,中子的速度越大越容易击中铀核.()(2)核反应堆是通过调节中子数目以控制反应速度.( )(3)核反应堆用过的核废料无毒无害.( )提示:(1)×(2)√(3)×铀核裂变及链式反应[学生用书P70]1.发现:1938年12月,德国物理学家哈恩与斯特拉斯曼利用中子轰击铀核时,发现了铀核的裂变,向核能的利用迈出了第一步.2.裂变的解释(1)核子受激发:当中子进入铀235后,便形成了处于激发状态的复核,复核中由于核子的激烈运动,使核变成不规则的形状.(2)核子分裂:核子间的距离增大,因而核力迅速减弱,使得原子核由于质子间的斥力作用而分裂成几块,同时放出2~3个中子,这些中子又引起其他铀核裂变,这样,裂变就会不断地进行下去,释放出越来越多的核能.(3)能量:重核裂变为中等质量的原子核,发生质量亏损,所以放出能量.一般来说,每个核子放出的平均能量约为1 MeV,1 kg 铀全部裂变放出的能量相当于2 500 t优质煤燃烧时释放的能量,裂变时能产生几万度的高温.3.铀核裂变的条件(1)铀块的体积大于临界体积.(2)铀块的质量大于临界质量.以上两个条件满足一个即可.4.裂变过程为什么能放出能量中等大小的原子核的平均结合能最大,这些核最稳定.如果使较重的核分裂成中等大小的核,核子的平均结合能会增加,可以释放出能量.错误!U裂变是很常见的一种重核裂变,它裂变的反应物和生成物有多种,其中有两种很典型的反应是:错误!U+错误!n→错误!Xe +错误!Sr+2错误!n错误!U+错误!n→错误!Ba+错误!Kr+3错误!n在重核裂变过程中,核反应满足电荷数守恒和质量数守恒.但反应前后质量不同,发生了质量亏损,释放出能量.计算一个铀核在上述第二种裂变过程放出的能量.已知m(错误!U)=235。
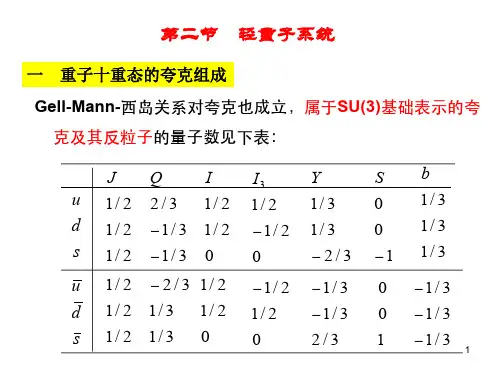

粒子物理I吕才典学科基础课。
需要量子力学基础,电动力学。
主要讲解物质是由什么构成的,构成物质的最小单元是如何相互作用如何相互转化的,同时还涉及宇宙是如何形成和演化的。
通过本课程的学习,希望学生理解粒子物理的标准模型,即按目前的认识水平,构成物质的最小单元是夸克和轻子,自然界存在强相互作用,电磁相互作用,弱相互作用和引力相互作用,此外还要跟踪粒子物理实验的最新进展。
通过本课程的学习使学生为进一步从事粒子物理的研究打下坚实的基础。
主要参考书:1. 章乃森, 《粒子物理学》, 科学出版社, 北京, 1985。
2. 唐孝威等, 《正负电子物理》, 科学出版社, 北京, 1995。
3.高崇寿,曾谨严,《粒子物理和核物理讲座》,高等教育出版社,北京,1994。
教材:D.H. Perkins, Introduction to High Energy Physics, Addison-Wesley Publishing Company Inc, 1972,1982,1987,2000.目录第一章粒子的运动和动力学性质 (4)1.1引言 (4)1.2粒子的运动性质 (7)1.3粒子的运动学描写 (12)1.4相互作用 (19)1.5粒子的分类 (23)第二章对称性和守恒定律 (26)2.1守恒量的一般性质 (26)2.2N OETHER定理 (29)2.3同位旋 (32)2.4奇异数和重子数 (36)2.5P变换(宇称变换) (41)2.6正反粒子(C)变换 (45)2.7G变换 (50)2.8CP变换 (53)2.9全同粒子交换变换 (57)2.10正反粒子组成系统的对称性 (60)2.11守恒定律的回顾 (64)第三章强相互作用和强子结构 (65)3.1重夸克和重夸克偶素 (65)3.3重子八重态 (73)3.4轻介子系统:赝标量介子 (75)3.5轻矢量介子 (78)3.6重味介子 (81)3.7强子的命名规则 (83)3.8顶夸克(TOP) (86)3.9色相互作用—QCD (87)3.10重离子碰撞实验和夸克胶子等离子体 (90)第四章电弱相互作用 (92)4.1弱相互作用的性质 (92)4.2弱相互作用的理论 (97)4.3GIM机制和CKM矩阵 (101)4.4中性K介子的对称性 (105)4.5介子的纯轻子衰变 (111)4.6电弱统一理论 (113)4.7费米子散射过程 (124)第五章超出标准模型的新物理探索 (128)5.1更高电弱对称性的探寻 (129)5.2大统一及超大统一理论 (131)5.3超对称理论等超出标准模型的理论 (134)5.4中微子质量和中微子振荡 (136)第一章粒子的运动和动力学性质1.1 引言世界是由什么组成的?早先的中国人,夏朝(公元前两千年)相信是由金、木、水、火、土(五行)组成西方哲学家(古希腊的Empedocles)在公元前430年认为是由水、火、土和空气组成的,同时代的Democritus认为万物是由大小不同、质量不同、有不可入性的原子组成,原子是“不可再分”的意思。

物理22章知识点总结22.1 电子衍射22.1.1 电子衍射的实验现象电子衍射是指当高速电子穿过晶体或金属薄膜时,会发生衍射现象,表现出干涉条纹的特点。
22.1.2 德布罗意波长德布罗意波长是指用来描述粒子的波动性质的物理量,可以通过德布罗意关系来计算,表达式为λ=h/p,其中λ为德布罗意波长,h为普朗克常量,p为粒子的动量。
22.1.3 配合滤镜配合滤镜是指用来改变电子的能量和波长,从而探测不同物质的衍射图样,通过调节配合滤镜的电压,可以控制电子的能量,进而改变其德布罗意波长。
22.2 光子的波粒二象性22.2.1 光的波粒二象性光既可以表现出波动性,又可以表现出粒子性。
在实验中,光的波动性可以由干涉和衍射来解释,而光的粒子性可以由光电效应和康普顿散射来解释。
22.2.2 波长和频率光的波长和频率之间有着紧密的关系,可以通过光速等于波长乘以频率来表示。
22.2.3 光子的动量和能量光子的动量和能量与其波长和频率之间有着一定的关系,可以通过光子动量公式和光子能量公式来计算。
22.2.4 波包与波束波包是指由不同波长的波构成的波动现象,而波束是一组处于相干状态的波所组成的集合,可以在物理实验中观察到波束的干涉和衍射现象。
22.3 康普顿效应22.3.1 康普顿效应的实验现象康普顿效应是指当X射线与物质相互作用时,X射线会散射出不同波长和动量的光子,导致散射光的能量和波长发生改变。
22.3.2 康普顿公式康普顿公式可以通过光子的波粒二象性来解释,用来描述康普顿效应中散射光的波长和入射光的波长之间的关系,表达式为λ'-λ=h/mc(1-cosθ),其中λ'为散射光的波长,λ为入射光的波长,h为普朗克常量,m为光子的静止质量,c为光速,θ为散射角。
22.3.3 康普顿散射的能量守恒和动量守恒在康普顿散射中,能量守恒和动量守恒是两个重要的物理定律,能够用来解释散射光的能量和动量之间的关系。

第 二 章 热 传 导 方 程§1 热传导方程及其定解问题的提1. 一均匀细杆直径为l ,假设它在同一截面上的温度是相同的,杆的表面和周围介质发生热交换,服从于规律dsdt u u k dQ )(11-= 又假设杆的密度为ρ,比热为c ,热传导系数为k ,试导出此时温度u 满足的方程。
解:引坐标系:以杆的对称轴为x 轴,此时杆为温度),(t x u u =。
记杆的截面面积42l π为S 。
由假设,在任意时刻t 到t t ∆+内流入截面坐标为x 到x x ∆+一小段细杆的热量为t x s xu kt s xu kt s xukdQ xx x x ∆∆∂∂=∆∂∂-∆∂∂=∆+221 杆表面和周围介质发生热交换,可看作一个“被动”的热源。
由假设,在时刻t 到t t ∆+在截面为x 到x x ∆+一小段中产生的热量为()()t x s u u lk t x l u u k dQ ∆∆--=∆∆--=111124π 又在时刻t 到t t ∆+在截面为x 到x x ∆+这一小段内由于温度变化所需的热量为 ()()[]t x s tuc x s t x u t t x u c dQ t ∆∆∂∂=∆-∆+=ρρ,,3 由热量守恒原理得:()t x s u u lk t x s x ukt x s t u c x t ∆∆--∆∆∂∂=∆∆∂∂11224ρ 消去t x s ∆∆,再令0→∆x ,0→∆t 得精确的关系:()11224u u l kxu k t u c --∂∂=∂∂ρ或 ()()11222112244u u l c k xu a u u l c k x u c k t u --∂∂=--∂∂=∂∂ρρρ 其中 ρc k a =22. 试直接推导扩散过程所满足的微分方程。
解:在扩散介质中任取一闭曲面s ,其包围的区域 为Ω,则从时刻1t 到2t 流入此闭曲面的溶质,由dsdt nuDdM ∂∂-=,其中D 为扩散系数,得 ⎰⎰⎰∂∂=21t t sdsdt nuDM 浓度由u 变到2u 所需之溶质为()()[]⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩ∂∂=∂∂=-=2121121,,,,,,t t tt dvdt t uC dtdv t u C dxdydz t z y x u t z y x u C M两者应该相等,由奥、高公式得:⎰⎰⎰⎰⎰⎰⎰⎰ΩΩ∂∂==⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂=21211t t t t dvdt t uC M dvdt z uD z y u D y x u D x M 其中C 叫做孔积系数=孔隙体积。



2023届湖北高考高效提分物理仿真模拟测试练习卷(二)(强化版)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题航天飞机中的物体处于失重状态,是指这个物体( )A.不受地球的吸引力B.受到地球吸引力和向心力的作用而处于平衡状态C.对支持它的物体的压力为零D.受到向心力和离心力的作用而处于平衡状态第(2)题物理学家的科学研究推动了人类文明的进程,关于原子核内部的信息,最早来自天然放射现象。
人们从破解天然放射现象入手,逐步揭开了原子核的秘密。
下列说法正确的是( )A.贝克勒尔发现天然放射现象揭开原子核内部信息,认为原子核是可分的,从原子核内部释放的射线有α射线、β射线、X射线、γ射线B.德国物理学家伦琴首次发现铀和含铀的矿物能够发出α射线C.卢瑟福预言了中子的存在,查德威克通过实验发现了中子D.汤姆孙通过α粒子轰击铍核()获得碳核()的实验发现了中子第(3)题如图甲所示,在高空运行的同步卫星功能失效后,往往会被送到同步轨道上空几百公里处的“墓地轨道”。
运送原理图如图乙所示,失效的卫星在P点进入转移轨道,在Q点进入墓地轨道,则下列判断正确的是( )A.在P点进入转移轨道时要加速,在Q点进入墓地轨道时要减速B.在同步轨道上P点加速度小于在转移轨道上P点加速度C.卫星在墓地轨道上运行周期大于24hD.若要从Q点逃脱地球的引力束缚,则在该处速度必须大于11.2km/s第(4)题一种配有小型风力发电机和光电池的新型路灯功率为120W,风力发电机的风能转化率为,工作原理如图所示,内部的线圈面积为、匝数匝,磁体的磁感应强度为,风叶的半径为,空气的密度为。
太阳垂直照射的单位面积功率为1,光电池板被太阳光直射的等效面积为,光能转化率为。
如果在一个风速稳定的晴天,经3小时的光照和风吹,路灯可正常工作7小时,测得风力发电机输出的电流强度大小为1A。


高二物理高效课堂资料
山东省昌乐一中2017级
高二物理翻转课堂课时学案
课题19.5核力与结合能
编制人刘海龙
审核人曹建民
目标导学
学习目标
了解核力的概念,知道原子核中质子和中子的比例关系;
了解爱因斯坦的质能方程,会根据质能方程和质量亏损的概念计算核反应中释放的核能。
重点
难点
质量亏损及爱因斯坦的质能方程的理解;结合能的概念、爱因斯坦的质能方程、质量与能量的关系。
问题记录自学质疑学案
班级小组姓名使用时间年月日编号
第 1 页
第 3 页
第 4 页。
高二物理高效课堂资料
山东省昌乐一中2017级
高二物理翻转课堂课时学案
课题19.8粒子和宇宙
编制人刘海龙
审核人曹建民
目标导学
学习目标了解聚变反应的特点
知道可控热核反应。
重点
难点
了解有关新粒子的情况
问题记录自学质疑学案
班级小组姓名使用时间年月日编号
第 1 页
【例1】以下说法正确的是( )
A.聚变是裂变的逆反应
B.如果裂变释放能量,则聚变反应必定吸收能量
C.聚变须将反应物加热至数百万度以上高温,显然聚变过程是吸收能量的
D.裂变与聚变均可释放巨大能量
【例2】.关于核衰变和核反应的类型,下列表述正确的有( )
【例3】一个质子和两个中子聚变为一个氚核,已知质子质量m H=1.007 3 u,中子质量m n=1.008 7 u,氚核质量m=3.018 0 u。
(1)写出聚变方程;
(2)释放出的核能多大?
(3)平均每个核子释放的能量是多少?
训练展示学案
第 4 页。
一、填空题1.天文学家测得银河系中氦的含量约为25%。
有关研究表明,宇宙中氦生成的途径有两条:一是在宇宙诞生后2分钟左右生成的;二是在宇宙演化到恒星诞生后,由恒星内部的氢核聚变反应生成的(1)把氢核聚变反应简化为4个氢核(11H )聚变成氦核(42He ),同时放出2个正电子(01e )和2个中微子(0ν),请你写出该氢核聚变反应的方程_____________________,并计算一次反应释放的能量是_____________________J 。
(2)研究表明,银河系的年龄约为173.810s t =⨯,每秒钟银河系产生的能量约为37110J ⨯。
现假定该能量全部来自上述氢核聚变反应,请你尝试估算银河系中氦的含量,并根据你的估算结果,对银河系中氢的主要生成途径作出判断:银河系中的氦主要是______________(选填A 或B )A .宇宙诞生后2分钟左右生成的;B .宇宙演化到恒星诞生后,由恒星内部的氢核聚变反应生成的(可能用到的数据:银河系质量约为41310kg M =⨯,原子质量单位271u 1.6610kg -=⨯,1u 相当于101.510J -⨯的能量,电子质量0.0005 u m =,氦核质量 4.0026u m α=,氢核质量 1.0078u D m =,中微子0ν的质量为零)。
A解析:14012104H He+2e+2ν→ 124.1410J -⨯ A(1)[1][2].根据电荷数守恒、质量数守恒得14012104H He+2e+2ν→由△E =△mc 2得△E =(4m D -m α-2m )c 2=(4×1.0078-4.0026-2×0.0005)×1.66×10-27×(3×108)2J=4.14×10-12J(2)[3].核反应产生的氦的质量:396.110kg Pt m m Eα=⨯=⨯∆ 氦的含量 39416.1102%310m k M ⨯==≈⨯ 由估算结果可知,k ≈2%远小于25%的实际值,所以银河系中的氦主要是宇宙诞生后不久生成的,即选A 。
2024届山东省聊城市百师联盟高三下学期模拟预测高效提分物理试题(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题下列关于天体运动的说法中,正确的是( )A.所有行星绕太阳运行的轨道都是椭圆,太阳在椭圆的一个焦点上B.地心说代表人物哥白尼认为地球是宇宙的中心,其他星球都环绕地球运动C.牛顿由于测出了引力常量而成为第一个计算出地球质量的人D.地球绕太阳公转时,在近日点运行速率最小,在远日点速率最大第(2)题一种折射率为的材料制成如图所示的截面为半圆形的棱镜,一束光线平行射入该棱镜,则下列判断中正确的是( )A.所有光线都能通过该棱镜B.所有光线都不能通过该棱镜C.只有距圆心两侧R范围内的光线才不能通过该棱镜D.只有距圆心两侧R范围内的光线才能通过该棱镜第(3)题下列说法中正确的是( )A.汤姆孙发现电子,表明原子核是可分的B.卢瑟福通过α粒子散射实验证实了在原子核内部存在质子C.在核反应方程+ → +X中,X表示的是质子D.质子与中子结合成氘核的过程中会释放能量第(4)题如图所示,两小球分别从半径大小为的半圆轨道顶端和斜面顶端以大小相等的初速度同时水平抛出,已知半圆轨道的半径与斜面竖直高度相等,斜面斜边长是其竖直高度的2倍,均可视为质点,结果两球同时分别落在半圆轨道和斜面上,则小球的初速度大小为()(重力加速度为,不计空气阻力)A.B.C.D.第(5)题一定质量的理想气体在升温过程中A.分子平均势能减小B.每个分子速率都增大C.分子平均动能增大D.分子间作用力先增大后减小第(6)题龙年首发,“长征5号”遥七运载火箭搭载通信技术试验卫星十一号发射成功,卫星进入地球同步轨道后,主要用于开展多频段、高速率卫星通信技术验证。
下列说法正确的是( )A.同步卫星的加速度大于地球表面的重力加速度B.同步卫星的运行速度小于7.9km/sC.所有同步卫星都必须在赤道平面内运行D.卫星在同步轨道运行过程中受到的万有引力不变第(7)题小球以2m/s的初速度从离地高为3m的地方开始做竖直上抛运动,取g=10m/s2,则小球在空中运动的时间为()A.0.4s B.0.6s C.0.8s D.1.0s第(8)题一条小船位于200m宽的河正中A点处,从这里向下游处有一危险区,当时水流速度为4m/s,为了使小船避开危险区沿直线到达对岸,小船在静水中的速度至少是( )A.m/s B.m/s C.2m/s D.4m/s二、多项选择题(本题包含4小题,每小题4分,共16分。
云南省西双版纳傣族自治州2024高三冲刺(高考物理)部编版模拟(拓展卷)完整试卷一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题两颗人造卫星绕地球做匀速圆周运动,对轨道半径较大的卫星,下列说法正确的是( )A.线速度一定大B.角速度一定大C.周期一定大D.动能一定大第(2)题如图为常见的“汽车千斤顶”。
当汽车需要换轮胎时,司机将它放在车身底盘和地面之间,只需摇动手柄使螺旋杆转动,O、A之间的距离就会逐渐减小,O、C之间的距离就会增大,就能将汽车车身缓缓地顶起来。
在千斤顶将汽车顶起来的过程中,下列关于、之间的弹力的说法正确的是( )A.、之间的弹力不断变大B.、之间的弹力不断变小C.之间的弹力变大、之间的弹力变小D.之间的弹力变小、之间的弹力变大第(3)题下列说法中正确的是( )A.汤姆孙发现电子并提出原子的核式结构B.放射性的原子核发生衰变后产生的新核从高能级向低能级跃迁时,辐射出γ射线C.光电效应实验中,光照时间越长光电流越大D.太阳辐射能量的主要来源是太阳中发生的重核裂变第(4)题如图,长为L的粗糙长木板水平放置,在木板的A端放置一个质量为m的小物块.现缓慢抬高A端,使木板以左端为轴转动.当木板转到与水平面的夹角为α时,小物块开始滑动,此时停止转动木板,让小物块滑到底端.取重力加速度为g.下列说法正确的是()A.整个过程支持力对物块做功为零B.整个过程支持力对物块做功为mgLsinαC.整个过程木板对物块做功为零D.整个过程木板对物块做功大于物块机械能的增量第(5)题如图所示,容积为的汽缸固定在水平地面上,汽缸壁及活塞导热性能良好,活塞面积为S,厚度不计。
汽缸两侧的单向阀门(气体只进不出)均与打气筒相连,开始活塞两侧封闭空气的体积均为V,压强均为。
现用打气筒向活塞左侧打气15次,向活塞右侧打气10次。
已知打气筒每次能打入压强为﹑体积为的空气,外界温度恒定,空气视为理想气体,不计活塞与汽缸间的摩擦。
高能物理过程的精确
计算
中国科学技术大学张仁友
2006年10月31日桂林
1. 引言
⏹标准模型的检验
W,Z,top等粒子的物理特性的精确测量…
⏹Higgs粒子的寻找与测量
Higgs粒子是否存在
Higgs粒子的物理特性
是否是标准模型的Higgs粒子
⏹新物理的发现与精确测量
超对称,额外维,小Higgs模型…等新模型的发现;模型参数测量
高能对撞机
Tevatron (running)
•com:1.96TeV P Pbar
•lumi:2E32cm-2s-1
•CDF, D0
LHC (2007)
•com:14TeV P P
•lumi:2E33cm-2s-1 @low luminisity, then 2E34cm-2s-1•ATLAS,CMS,LHCb,Alice
LC (in the future)
•e+e-collision and gamma-gamma collision,or e-gamma collision •NLC, JLC,TESLA, CLIC
⏹大量费曼图的计算;
⏹标量积分函数的计算;
⏹张量积分函数推导为标量积分函数的计算;⏹
控制数值计算的精度。
多体末态!
高精度!
理论上高精度计算存在的四个主要问题:
2.量子场论计算的基础知识可观测量O的期望值:
其中为过程的矩阵元(动力学部分)
为相空间体积元
n M ),...,,,(121n n k k p p d
a) 费曼规则: 费曼图 数学表达式
⏹图形与幅度的转换过程是按照费曼图图形技术中所对应的
规则进行的;
⏹外线对应自由波函数,内线对应着传播函数,顶点对应相
互作用顶点。
例:费米子传播函数的规则和三胶子作用顶点的规则:
例:
矩阵元
其中
二阶张量圈图积分函数部分:
矩阵元中剩余部分:
标量积分函数:
b ) IR 和UV 发散的正规化
k ∙0, IR 发散! k ∙inf, UV 发散!
维数正规化方案(n=4-2
)UV 发散的l圈图积分函数则出现最高达阶极点项。
IR 发散的l圈图积分函数则可以出现直到阶的极点项。
()l ε/1()l 2/1ε
ε
c)N条外线过程的NLO计算
⏹含胶子、光子或轻夸克辐射的N+1条外线树图的对应幅度
产生;
⏹实(胶子、光子、轻夸克)辐射过程软、共线发散的分离;
⏹PDF抵消项贡献中红外发散(共线发散)的分离;
⏹N条外线单圈图(包括抵消项图)的对应幅度的产生;
⏹计算单圈图,分离出软、共线发散;
⏹将上述贡献相加,消除紫外及红外发散;
⏹有限贡献的幅度数值计算。
3. 单圈标量积分函数计算
n (=4-2 )维下费曼图对应的幅度可以表示为对张量积分函数与外部张量S 的乘积求和,即
其中
S
只与外线运动学相关.
I 的一般形式为:
对应于对称张量组合.例如:
标量系数可以通过Passarino-Veltman 方法求出.它们由标量积分函数表示出.
上述即为张量积分的约化过程。
()()
m n j s s s c ,...,,
1
(1)标量A,B,C,D 圈积分函数定义;
其中:
ε
24-==n D ⎰-=0
2)4(001)2()(D q d i m A D
D ππμ⎰-=1
02
)
4(10101
)2(),,(D D q d i m m p B D
D π
πμ⎰-=2102)4(2102101)2(),,,,(D D D q d i m m m p p C D
D ππμ⎰-=
3
2102
)
4(321032101
)2(),,,,,,(D D D D q d i m m m m p p p D D
D ππμε
i m q D +-=2
020ε
i m p q D +-+=21211)(ε
i m p q D +-+=2
2222)(ε
i m p q D +-+=23233)(
(2) 基本标量积分函数计算:
以
为例来说明标量函数的计算。
1)Feynman 或Schwiger 参数化.Feynman 参数化
Schwiger 参数化2)积分变量平移.
定义:
⎰---=)
)()((13
322212
/1k k k i k d I D D π
3)Wick旋转.
4)
D维欧氏空间的球坐标变换.
5)角向及径向积分.
作变换:
并对径向作积分:有:
)/(1233112212s x x s x x K t --=角向积分:
(3)A,B 标量积分函数的解析结果:
()()π
γμ4log 42
,41log 22
2
0+--=∆-+⎪⎪
⎭⎫ ⎝
⎛+-∆=E D
D O m m m A (
)
(
)
(
)
ε
μ
i p m
m
m p m m p x x x x x p m m p B +--+±-+=⎪⎪⎭⎫
⎝
⎛-+⎪⎪⎭⎫ ⎝⎛-+++∆=2
21
220
21
2
20
212
2
,1221122
102
02411log 11log log 2,,其中
G. 't Hooft and M. Veltman, NLB153,365(1979)
对标量五点积分函数:
(A. Denner and S. Dittmaier, hep-ph/0212259)
(4) 五点标量函数计算:
(5) 六点标量积分函数计算:
Guo 方法:
定义5点和6点标量积分函数:
并用表示消去传播子后得到的5点函数。
0()E i 0F i N
定选择系数,使得:
取:
得到:
其中,为Gram行列式。
Binoth的方法:
其中:
4.张量积分函数计算
(1) Passarino-Veltman
方法:
例如,对于3点2
阶张量积分:
N 点p 阶张量积分:
利用下面的性质降阶:
三、四、五点张量积分函数推导中出现的Gram矩阵分别为:
•将p阶的N点张量积分函数系数表示为低阶张量的N点和N-1,N-2,…的积分函数系数。
降阶过程中会出现Gram矩阵求逆。
•递归地采用PV方法,解线性方程组,最终将张量积分函数系数表示为标
量积分函数。
小结:
⏹该方法原则上适用于所有1,2,3,4,5点张量多点积分函数
的计算。
⏹这种方法会出现Gram 矩阵求逆,当Gram行列式值很小时
会产生积分函数数值计算的不稳定性。
⏹四点以下(含四点)积分函数数值计算中Gram行列式值很
小的区域仅仅出现在相空间的边缘附近(如前后向区,阈值附近)。
⏹5点积分函数数值计算中Gram行列式值很小的区域可能出现
在相空间中间。
(2) Denner-Dittmaier 方法:(hep-ph/0212259)
矢量积分:
2阶张量积分:
3阶张量积分:
该方法避免出现Gram矩阵求逆的计算。
5.六点张量积分的计算
(1)Guo 方法:
利用上式将6点张量积分化为5点同阶及低阶张量积分。
得到的5点张量积由Denner-Dittmaier方法化为5点及更低点标量积分的计算。
(2)Denner-Dittmaier 方法:(hep-ph/0509141)
6点张量积分:
张量积分的系数为:
6. IR发散的分离(Nucl.Phys. B675 (2003) 447)
定义变量:
一条无质量外线粒子连接两条无质量的内线传播子,
设外线动量为类光四矢量:
发散发生在
此时传播子n的动量与外线的动量在共线
位形上,因此这种发散称为共线发散。
两个在壳的粒子间交换一个无质量的粒子,
此时发散发生在,传播子n的动量,因
此这种发散称为软发散。
圈积分中的红外发散的分离:
为了得到维数正规化方案下的标量圈积分的表达式,将一个圈积分划分为有限部分和发散部分。
其中有限部分的计算是与正规化方案无关,我们可以用标准的程序包FF在质量正规化方案下计算。
而发散部分可以用相应的3点积分表示。
发散部分的计算:
其中对于共线发散:
对于软发散:
例: 五点图发散部分的计算
根据前面的公式计算出相应不为零的3 点函数的系数:
最后得到该五点函数的极点项表达式为:
三点标量圈积分的软发散部分:
例:三点标量圈积分的共线发散部分:其中:
三点标量圈积分的共线和软发散部分:
其中:
The End。