[经济学]第四章--根轨迹-maPPT课件

格式：ppt
大小：659.00 KB
文档页数：40

下载文档原格式

根轨迹法(自动控制原理)ppt课件精选全文完整版

1 K (s z1 )( s z2 )....( s zm ) 0 (s p1 )( s p2 )....( s pn )
课程：自动控制原理
第4章根轨迹法
➢ 以K为参变量的根轨迹上的每一点都必须满足以上方程，相应地，称之为‘典型根轨迹方程’。
也可以写成
m
n
(s zl ) K (s pi ) 0
可见，根轨迹可以清晰地描绘闭环极点与开环增益K之间的关系。
课程：自动控制原理
第4章根轨迹法
2.根轨迹的基本条件
❖ 考察图示系统，其闭环传递函数为:
Y(s) G(s) R(s) 1 G(s)H(s)
闭环特征方程为：
1 G(s)H(s) 0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根，所以根轨迹上的每一点都应满足：
l 1
i 1
对应的幅值条件为：
相角条件为：
n
( s pi ) K i1
m
(s zl )
l 1
m
n
(s zl ) (s pi ) (2k 1)180
k 1,2,
l 1
i 1
课程：自动控制原理
第4章根轨迹法
❖ 上述相角条件，即为绘制根轨迹图的依据。具体绘制方法是：在复平面上选足够多的试验点，对每一个试验点检查它是否满足相角条件，如果是则该点在根轨迹上，如果不是则该点不在根轨迹上，最后将在根轨迹上的试验点连接就得到根轨迹图。
显然，位于实轴上的两个相邻的开环极点之间一定有分离点，因为任何一条根轨迹不可能开始于一个开环极点终止于另一个开环极点。同理，位于实轴上的两个相邻的开环零点之间也一定有分离点。
课程：自动控制原理
第4章根轨迹法

第四章根轨迹.ppt

K1 时，s1 1 j，s2 1 j
3
§4- 2 绘制根轨迹依据
一绘制根轨迹的基本条件
系统特征方程
1+G(s)H(s)=0 G(s)H(s)=-1
幅值条件: |G(s)H(s)|=1 相角条件: ∠G(s)H(s)=±(2q+1)π, q=0,1,2,…
m
K1 (s z j )
12
§4-5 增加开环零极点对根轨迹的影响
一添加开环极点
添加位于左半平面的开环极点，将使根轨迹向右半平面移动，系统的稳定性能降低。
二添加开环零点
添加位于左半平面的开环零点，将使根轨迹向左半平面移动，系统的相对稳定性得到改善。
三增加开环偶极子对根轨迹的影响
1 偶极子指系统中相距很近的一对极点和零点。 2 偶极子不影响远处根轨迹的形状及根轨迹增益K，对
二通过输出反馈任意设定希望的闭环主导极点
15
i 1
j 1
n
s si 0
i 1
n
si a1
n
si an
i 1
i 1
可利用此性质判闭环极点的分布情况
n
n
n m 2时， si pi a1 常数
i 1
i 1
一些变化后,另一些会做相反变化.
8
三闭环极点的确定:
∵ G(s)H (s)
j 1 n
(s pi )
i 1
4
幅值条件:
m
K1 | s z j |
或
j 1
1
n
| s pi |
i 1
n
| s pi |
K1

第四章-根轨迹法PPT课件

i1 n
1
|spj |
j1
G(s)H(s) （s z1）（s z2）（szm）
（s p1）（s p2）（s pn）
m
n

(szi)(s pj)
i1
j1
(2l 1) 180 l360 l 0,1,2,
2021
4
1.根轨迹的分支数
m
k(szi)
特征方程式1G(s)H(s)1
i1 n
0
(spj)
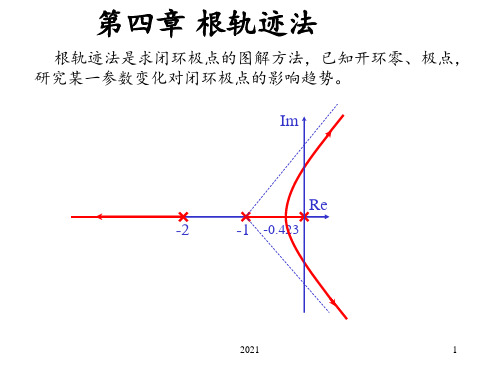
第四章根轨迹法
根轨迹法是求闭环极点的图解方法，已知开环零、极点，研究某一参数变化对闭环极点的影响趋势。
Im
Re
-2
-1 -0.423
2021
1
R(s)
K
Y(s) G(s) 2K k
s(0.5 s 1)
s(s2) s(s2)
两个开环极点p1 0, p2 2
( s ) Y R ( ( s s ) ) s 2 2 k s kD ( s ) s 2 2 s k 0s 1 ,2 1 1 k
满足上式的条件是什么？
1. s = zi 2. |s|→∞
规则3.根轨迹起始于开环极点，终止于开环零
点。若 n > m，还有n-m 条根轨迹终止于s
平面无穷远处。
2021
8
4.根轨迹的渐近线
若m < n ,当 k →∞时有 n-m 条根轨迹沿着 n-m 条渐近线
趋于s平面无穷远处。
n
m
pj zi
渐近线在实轴交于一点 j1 i1
幅值条件 | G ( s ) H ( s )| k |s z 1 ||s z 2 | |s z m | 1 讨论 nm,k 的情况 |, s p 1 ||s p 2 | |s p n | |sz1||sz2| |szm| 10 , k 时 |sp1||sp2| |spn| k

第四章根轨迹分析法1244页PPT

方程的根的变化。
例4-1 系统结构图如图所示，分析l 随开环放大系数K变化的趋势。
解. G(s) K Kg
s(0.5s1) s(s2)
K : 开环放大系数
Kg 2K: 根轨迹增益
(s)C(s) Kg R(s) s22sKg
D (s)s22sKg0
l1,2 1 1Kg
Kg l1 l2
2.根轨迹方程
j 1
则根轨迹的条件方程为幅值条件
m
(s zi )
K i1 gn
1
(s p j )
j 1
m
argK[g
(szi
i1
)
]180(2k1)
n
(spj )
j 1
方程
相角条件方程
m
n
ars g zi)( ars gpj( ) 1 8 (2 k 0 1 )
i 1
j 1
注意：
相角条件是确定根轨迹的充分而必要条件可从幅值条件方程求解得出Kg 。
解：
j 平面
-4
-1.5 -1 -0.5 0
取实轴上的点s
开环共轭极（零点）对相角条件无影响
j
[s]
p3
p1
z2 p5 s p2
z1 0
p4
实轴上的根轨迹仅由实轴上的开环零极点的分布所决定
6. 根轨迹的渐近线若 n>m，则 Kg 时，有n-m条根轨迹
k g= 0 .2 5 kg= 0
-1 -0 .5
k g= 0 .5
j
s1,2
1 2
1 2
s平面
1 4Kg
0 kg= 0
系统的开环传递函数中某一参数变化时，系统闭环特征方程的根在S平面上的变化轨迹即为根轨迹

第4章根轨迹PPT

轨迹
第四章根轨迹法
4.1 根轨迹的概念 4.2 绘制根轨迹的依据 4.3 绘制根轨迹的基本法则
4.4 参数根轨迹和多回路系统根轨迹
4.5 正反馈根轨迹 4.6 滞后系统的根轨迹 4.7 根轨迹的应用 4.8 计算机绘制根轨迹
小结
轨迹
§4—1 根轨迹的基本概念
一、根轨迹的定义如图所示一般闭环系统的闭环传递函数为
另外，必须指出，用上式求出的点不一定都是分离点或会合点，还必须满足特征方程或用相应的规则来检验。
轨迹
例4.1的分离点和汇合点
s( s 4)( s 2 2s 2) kg ( s 5)
dk g ds 0
得到-5.93,-3.38,-0.67+j0.46,-0.67-j0.46
轨迹
§4—4
一、参数根轨迹
参数根轨迹和多回路根轨迹
＊参数根轨迹：系统闭环极点随Kg以外的参数变化而变化的
轨迹。
＊绘制方法：把特征方程作等效处理，把要研究迹的绘制方法，进行绘制。
例4.2 单位反馈系统开环传递函数为
＊
绘制以a为变量的根轨迹。并分析a与系统性能的关系。
＊
软实验
轨迹
§4—5 正反馈系统的根轨迹
一、正反馈系统的特征方程传递函数
Y ( s) G1 ( s) G( s) X ( s) 1 G1 ( s) H ( s)
X(s)
G1(S) H(S)
Y(s)
特征方程
1 G1 (s) H (s) 1 G0 (s) 0
简写为
G0 ( s) 1
轨迹
§4—2 绘制根轨迹的依据和条件
根轨迹的绘制依据是特征方程，根据特征方程可以得出比

根轨迹法PPT课件

定闭环极点位置。另一方面分析设计系统时经常要研究一个或者多个参量在一定范围内变化时对闭环极点位置及系统性能的影响.
W.R.EVAOVS(依万斯)于1948年首先提出了求解特征方程式根的图解法─根轨迹法。
根轨迹简称根迹，它是开环系统某一参数从零变到无穷
时，闭环系统特征方程的根在 s 平面上变化的轨迹。
解： n 3，m 0
① p1 0，p2 1，p3 2 为根轨迹的起点；
开环无零点，故三个分支终点均趋向无穷远。
②
a
(2q 1)
nm
(2q 1)
3
60、180、300
(q 0,1,2)
n
m
a
i 1
pi z j
j 1
nm
3 0 1 3
③ 实轴上根轨迹：
（ ,2]，[1,0]
j
p3 2
第四章线性系统的根轨迹法
§4-1 根轨迹法的基本概念 §4-2 绘制根轨迹的基本条件和基本规则 §4-3 参数根轨迹 §4-4 正反馈回路和零度根轨迹 §4-5 利用根轨迹法分析系统的暂态响应
§4-1 根轨迹法的基本概念
一、根轨迹的概念
从上一章讨论知道，闭环系统的动态性能与闭环极点在
s 平面上的位置是密切相关的，分析系统性能时往往要求确
对于实轴上0至1线段的实数根而言，其对应的K*值在
b 点为极大值。
可以证明，当l 条根轨迹分支进入并立即离开分离点时，
分离角为 (2k 1) l .
k 0，1，，l -1
例4-3：求上例中 b 点的坐标。
[规则3] 根轨迹的渐进线
当开环有限极点数 n大于有限零点数时，有 (n m)
条根轨迹分支沿着与实轴交角为 a 、交点为 a的一组

根轨迹ppt课件.ppt

3.分析方法及思路 1）从数学模型的建立看开环传递函数的特点：物理元件→典型环节→开环结构→闭环结构→系统数学模型
（1）开环结构中的典型环节直接对应着开环传递函数的零极点，-------很容易获得；
（2）各个典型环节中的参数可以直接反映系统的物理参数，这一点对分析系统和改造系统非常有利；（3）可以直接求取稳态误差； (4）同各种传递函数（如闭环传递函数和误差传递函数）有简单的关系。 2)一个美好的愿望：开环零极点图+开环增益→闭环零极点全部可能的分布图→ 分析系统的三大类性能。
j 1 n i 1
)
(s z
j 1 n i 1
j
)
s ( s pi )
(s p )
i
则幅值条件和相角条件可以进一步写成如下实用形式：
幅值条件：
G1 ( s ) H1 ( s )
sz
j 1 n i 1
m
j
s p

1 K*
基本公式
i
幅值条件：
第四章根轨迹法
4.1 4.2 4.3 4.4 根轨迹法的基本概念根轨迹绘制的基本规则广义根轨迹线性系统性能的根轨迹分析法
一、本章内容提要: 1．介绍已知系统开环传递函数的极点、零点的条件下确定闭环系统的根轨迹法，并分析系统参量变化时对闭环极点位置的影响； 2．根据闭环特征方程得到相角条件和幅值条件由此推出绘制根轨迹的基本法则； 3．根轨迹绘制：常规根轨迹、参数根轨迹、根轨迹曲线族、零度根轨迹; 4．根轨迹法分析系统性能
三、本章重点、关键、难点 1．重点：根轨迹的绘制和利用根轨迹图分析控制系统 2．关键点：根轨迹方程，幅值条件，相角条件 3．难点：广义根轨迹的绘制

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3）闭环系统根轨迹增益=开环系统前向通道的根轨迹增益。
单位反馈系统
（1）闭环系统的根轨迹增益就等于开环系统的根轨迹增益；
（2）闭环系统的零点就是开环系统的零点。
K' KG'KH'
！根轨迹法：由开环系统的零点和极点，不通过解闭环特征方程找出闭环极点。
.
5
自动控制原理
第四章根轨迹分析法
幅角条件和幅值条件
自动控制原理
第四章根轨迹分析法
第四章根轨迹法
4.1 根轨迹法基本概念 4.2 绘制根轨迹图的基本规则
4.3 控制系统的根轨迹绘制 4.4 根轨迹法分析
.
1
自动控制原理
第四章根轨迹分析法
4.1根轨迹法基本概念
根轨迹法基本概念闭环零、极点与开环零、极点之间的关系幅角条件和幅值条件
.
2
自动控制原理
H(s) K H '
j1 h
(s p j )
j1
开环系统根轨迹增益 K' KG'KH'
.
m个零点(m=f + l ) n个极点(n= q + h)
f
l
(szi) (szj)
G(s)H(s) K' i1
j1
q
h
(spi) (spj)
i1
j1
m个零点(m=f + l )
z i 前向通道零点 z j 反馈通道零点 n个极点(n= q + h)
q
h
f
l
(spi) (spj)K ' (szi) (szj)
i1
j1
i1
j1
f
G(s)K sG (T (1s1s11))T ((2222ss2222T 22ss 11)) KG'
(szi)
i1 q
(spi)
i1
前向通道增益前向通道根轨迹增益
KG'
KG
122
T1T22
反馈通道根轨迹增益
l
(s z j )
特征方程的根为实根或共轭复数根。
！仅需先购画出S平面上半部和实轴上的根轨迹，下半部由镜象求得。
.
10
自动控制原理
第四章根轨迹分析法
实轴上的根轨迹
如果实轴上某一区段的右边的实数开环零点、极点个数之和为奇数，则该区段实轴必是根轨迹。
开环零点：z1 开环极点：p1、p2、p3、p4、p5
在实轴区段[p2，p3]上取试验点s1
p i前向通道极点 p j反馈通道极点
4
自动控制原理
第四章根轨迹分析法
f
h
KG' (szi) (spj)
(s)
i1
j1
q
h
f
l
(spi) (spj)K' (szi) (szj)
i1
j1
i1
j1
1）闭环系统的零点=前向通道的零点+反馈通道的极点；
2）闭环系统的极点与开环系统的极点、零点以及根轨迹增益均有关；
D (s) 1 G (s)H (s) 0
根轨迹方程 G(s)H(s)1
m
(s zi )
G(s)H(s) K' i1 n
1
(s pi )
i1
m个零点 n个极点
（nm）
m
幅值条件
s zi
K ' i1
1
n
s pi
i1
1）幅值条件不但与开环零、极点
有关，还与开环根轨迹增益有关；
2）必要条件：
幅角条件（k=0,1,2, …）
s pi
K '＝ i 1 m s zi i1
K' 0
s值必须趋近于
某个开环极点
根轨迹起始于开环极点
K'
s值必须趋近于
某个开环零点
根轨迹终止于开环零点
.
8
自动控制原理
根轨迹分支数
第四章根轨迹分析法
n阶系统，根轨迹有n个起始点，系统根轨迹有n个分支
1）系统特征方程的阶次为n次特征方程有n个根 K变化(0到∞ ),n个根随着变化n条根轨迹。
1
5
G (s1)H (s1) (szi) (spi)
i 1
i 1
？ G (s1 )H (s1 )＝ (2 k 1 )1 80
每对共轭复数极点所提供的幅角之和为360°；
s1右边所有位于实轴上的每一个极
点或零点所提供的幅角为180°；
s1左边所有位于实轴上的每一个极点或零点所提供的幅角为0°。
.
11
自动控制原理
根轨迹的渐近线
第四章根轨迹分析法
当系统n>m时，有（n－m）条根轨迹分支终止于无限远零点。
沿着渐近线趋于无限远处，
渐近线也对称于实轴（包括与实轴重合）。
渐近线与实轴的倾角（k=0，1，2，…）：
a
(2k1)180 nm
渐近线与实轴交点的坐标值：
n
m
pi zi
a＝ i1
i1
m
n
(szi) (spi)(2k1)
i 1
i 1
1）幅角条件只与开环零、极点
有关
2）充要条件：
！！用幅角条件来绘制根轨迹，用幅值条件来
确定已知根轨迹上某一点K’的值。
.
6
自动控制原理
第四章根轨迹分析法
4.2绘制根轨迹图的基本规则
➢根轨迹的起点和终点
➢根轨迹分支数
➢根轨迹的连续性和对称性！绘制注意点
nm
证明
.
12
自动控制原理
第四章根轨迹分析法
a
(2k1)180 nm
n
m
pi zi
a＝ i1
i1
nm
1）当k值取不同值时，a 有（n－m）个值，而a不变；
2）根轨迹在s∞时的渐近线为（n－m）条与实轴交点为a 、倾角a为的一组射线。
.
13
自动控制原理
2）实际物理系统，开环极点一般多于开环零点，
即 n > m。 m条终止于开环零点（有限值零点)；
（n－m）条根轨迹分支终止于（n－m）个无限
远零点。
.
9
自动控制原理
第四章根轨迹分析法
根轨迹的连续性和对称性
ቤተ መጻሕፍቲ ባይዱ
根轨迹是连续曲线，且对称于实轴。
闭环特征方程的根在开环零极点已定的情况下，
各根分别是K的连续函数；
1）实轴、虚轴相同的刻度
➢实轴上的根轨迹
2）“×”、 “〇”
➢根轨迹的渐近线
3）加粗线及箭头
➢根轨迹的分离点
4）关键点的标注
➢根轨迹的起始角和终止角
➢根轨迹与虚轴的交点 ➢闭环特征方程根之和与根之积
.
7
自动控制原理
第四章根轨迹分析法
根轨迹的起点和终点
根轨迹起始于开环极点，终止于开环零点
幅值条件
n
!系统特征根的图解方法
广义根轨迹:系统的任意一变化参数形成根轨迹。
狭义根轨迹（通常情况）：
变化参数为开环增益K，且其变化取值范围为0到∞。
.
3
自动控制原理
第四章根轨迹分析法
闭环零、极点与开环零、极点间的关系
f
h
(s) G (s)
K G' (szi) (spj)
i1
j1
1G (s)H (s)
第四章根轨迹分析法
根轨迹法基本概念
闭环极点（即闭环特征方程根）
闭环控制系统稳定性、瞬态响应特性
??希望按性能要求置于合适的位置。
??系统的某些参数（如开环增益）变化时，反复求解，不方便。
根轨迹：当系统某一参数在规定范围内变化时，相应的系
统闭环特征方程根在s平面上的位置也随之变化移动，一个
根形成一条轨迹。

[经济学]第四章--根轨迹-maPPT课件

合集下载