关于π的常见倍数

圆周率的倍数《圆周率的倍数》圆周率呀，那可是个神奇的数字。3.1415926……后面还跟着老长一串呢。咱们先来说说圆周率的一倍，那不就是它本身嘛，3.14多一点。这个数字在生活里可常见啦。就说做个圆形的蛋

糕，你要是想知道蛋糕的周长，那圆周率就派上用场了。直径乘以圆周率，得嘞，周长就出来了。

圆周率的两倍呢，那就是6.28左右啦。这时候我就想到那种两个圆连在一起的东西，像那种双环的小玩具。如果每个环的直径是1的话，那两个环连起来的外轮廓的周长差不多就是直径2乘以圆周率啦，也就是圆周率的两倍。

再看圆周率的三倍，9.42左右呢。我就琢磨着，要是有三个同样大小的圆，排成一排或者组合成一个什么有趣的形状，它们相关的长度计算可能就会涉及到这个圆周率的三倍啦。比如说，用三根等长的铁丝，每根弯成一个圆，然后把这三个圆连起来，这个整体的某个长度说不定就和圆周率的三倍有关。

圆周率的四倍，12.56左右咯。想象一下，四个圆拼成一个正方形的样子，每个圆都相切，这时候计算这个组合图形的一些长度或者面积啥的，圆周率的四倍可能就会冒出来啦。

随着圆周率倍数的增加，感觉就像打开了一个数字的魔法盒。每一个倍数都能在不同的几何图形或者实际的圆形物体的计算里找到它的意义。有时候觉得这些数字就像小精灵，在数学的世界里蹦跶着，给我们带来各种各样的惊喜。

圆周率的倍数，不管是在科学研究里，还是在咱们日常生活的小细节中，都有着不可忽视的作用。科学家们用它来计算天体的轨道，建筑工人用它来计算圆形柱子的用料，就连咱们做手工的时候，要是涉及到圆形的东西，说不定也得用到圆周率的倍数呢。

在我看来呀，圆周率的倍数就像是一把把神奇的钥匙，能打开不同的知识和应用的大门。它们充满了趣味，让我们看到数学和生活之间紧密又奇妙的联系。这圆周率的倍数啊，真的是又有趣又有用，就像生活中的小宝藏，等着我们去发现更多关于它们的奥秘呢。

小学五年级数学公式派的倍数π圆周率（Pi）是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的数学常数。

π也等于圆形之面积与半径平方之比。

是精确计算圆周长、圆面积、球体积等几何形状的关键值。

在分析学里，π可以严格地定义为满足siπx = 0的最小正实数x。

圆周率用希腊字母π（读作pài）表示，是一个常数（约等于3.141592654），是代表圆周长和直径的比值。

它是一个无理数，即无限不循环小数。

在日常生活中，通常都用3.14代表圆周率去进行近似计算。

而用十位小数3.141592654便足以应付一般计算。

即使是工程师或物理学家要进行较精密的计算，充其量也只需取值至小数点后几百个位。

π的几倍就写作：几π。

例如：5π就是π的五倍。

π的倍数如下：1π=3.142π=6.283π=9.424π=12.565π=15.76π=18.847π=21.988π=25.129π=28.2610π=31.4 11π= 34.54 12π= 37.68 13π= 40.82 14π=43.96 15π= 47.1 16π=50.24 17π=53.38 18π=56.52 19π= 59.66 20π=62.8 21π=65.94 22π=69.08 23π=72.22 24π=75.36 25π= 78.5 26π=81.64 27π=84.78 28π=87.92 29π=91.06 30π=94.2 31π=97.3432π=100.48 33π=103.92 34π=106.76 35π=109.9 36π=113.04 37π=116.18 38π=119.32 39π=122.46 40π=125.6 41π=128.74 42π=131.88 43π=135.02 44π=138.16 45π=141.3 46π=144.44 47π=147.58 48π=150.72 49x=153.86 50π=157 51π=160.14 52π=163.28 53π=166.4254π=169.56 55π=172.7 56π=175.84 57π=178.98 58π=1 82.12 59π=185.26 60π=188.4。

∏的倍数值规律π，即圆周率，是一个著名的无理数，它的值约为3.14159。

π的倍数值规律是指当π乘以某个整数时，所得的结果的小数部分的规律性变化。

在本文中，我将探讨π的倍数值规律，并解释其中的数学原理。

首先，让我们来计算一些π的倍数值，以观察它们的规律。

以下是一些π的倍数值的计算结果：1π ≈ 3.141592π ≈ 6.283183π ≈ 9.424774π ≈ 12.566365π ≈ 15.70795通过观察这些值，我们可以发现一些有趣的规律。

首先，无论π乘以多少倍数，结果的整数部分都是该倍数的整数部分。

例如，2π的整数部分是2，3π的整数部分是3，以此类推。

这是因为π的整数部分是一个常数，不会随着倍数的增加而改变。

然而，我们更关注的是π的倍数值的小数部分。

通过计算，我们可以发现π的倍数值的小数部分是周期性的。

也就是说，小数部分会在一定的位数后重复出现。

这是因为π是一个无理数，它的小数部分是无限不循环的。

但是，当我们将π乘以某个整数时，结果的小数部分会受到整数倍数的影响，从而呈现出周期性的规律。

让我们以2π为例来进一步观察这个规律。

2π的小数部分是0.28318，这个值可以写成0.28318 = 0.28318181818...，其中0.18是一个重复的部分。

这个重复的部分是由2π的倍数所决定的，因为2π的小数部分会在这个位置上重复出现。

同样的规律也适用于其他π的倍数值。

例如，3π的小数部分是0.42477，可以写成0.42477 = 0.4247742424...，其中0.424是一个重复的部分。

这个重复的部分也是由3π的倍数所决定的。

进一步观察可以发现，π的倍数值的小数部分的重复长度等于倍数的绝对值。

例如，2π的小数部分的重复长度是2，3π的小数部分的重复长度是3，以此类推。

这是一个有趣的数学现象，它与π的无理数属性密切相关。

通过研究π的倍数值的规律，数学家们可以推导出一些有关π的性质。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

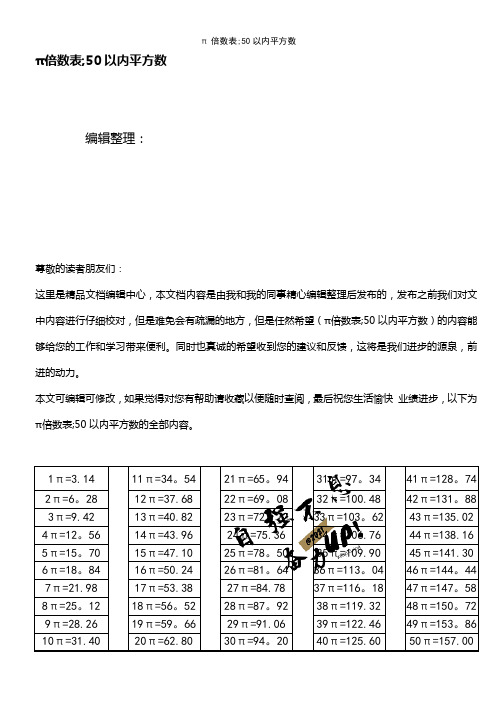
π倍数表;50以内平方数编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（π倍数表;50以内平方数）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为π倍数表;50以内平方数的全部内容。

1π=3.1411π=34。

5421π=65。

9431π=97。

3441π=128。

74 2π=6。

2812π=37.6822π=69。

0832π=100.4842π=131。

88 3π=9.4213π=40.8223π=72。

2233π=103。

6243π=135.02 4π=12。

5614π=43.9624π=75.3634π=106.7644π=138.16 5π=15。

7015π=47.1025π=78。

5035π=109.9045π=141.30 6π=18。

8416π=50.2426π=81。

6436π=113。

0446π=144。

44 7π=21.9817π=53.3827π=84.7837π=116。

1847π=147。

58 8π=25。

1218π=56。

5228π=87。

9238π=119.3248π=150。

72 9π=28.2619π=59。

6629π=91.0639π=122.4649π=153。

86 10π=31.4020π=62.8030π=94。

2040π=125.6050π=157.0050以内平方值π的倍数表(1-50倍)。

1 100圆周率倍数表1~100圆周率倍数表 1~100圆周率倍数表 1π=3.14 2π=6.28 3π=9.424π=12.56 1π=3.14 2π=6.28 3π=9.42 4π=12.56 5π=15.7 6π=18.847π=21.98 8π=25.12 5π=15.7 6π=18.84 7π=21.98 8π=25.12 9π=28.26 10π=31.4 11π=34.54 12π=37.68 9π=28.26 10π=31.4 11π=34.5412π=37.68 13π=40.82 14π=43.96 15π=47.1 16π=50.24 13π=40.8214π=43.96 15π=47.1 16π=50.24 17π=53.38 18π=56.52 19π=59.6620π=62.8 17π=53.38 18π=56.52 19π=59.66 20π=62.8 21π=65.9422π=69.08 23π=72.22 24π=75.36 21π=65.94 22π=69.08 23π=72.2224π=75.36 25π=78.5 26π=81.64 27π=84.78 28π=87.92 25π=78.526π=81.64 27π=84.78 28π=87.92 29π=91.06 30π=94.2 31π=97.3432π=100.48 29π=91.06 30π=94.2 31π=97.34 32π=100.48 33π=103.6234π=106.76 35π=109.9 36π=113.04 33π=103.62 34π=106.76 35π=109.9 36π=113.04 37π=116.18 38π=119.32 39π=122.46 40π=125.6 37π=116.18 38π=119.32 39π=122.46 40π=125.6 41π=128.74 42π=131.88 43π=135.02 44π=138.16 41π=128.74 42π=131.88 43π=135.02 44π=138.16 45π=141.3 46π=144.44 47π=147.58 48π=150.72 45π=141.3 46π=144.44 47π=147.58 48π=150.72 49π=153.86 50π=157 51π=160.14 52π=163.28 49π=153.86 50π=157 51π=160.14 52π=163.28 53π=166.42 54π=169.56 55π=172.756π=175.84 53π=166.42 54π=169.56 55π=172.7 56π=175.84 57π=178.98 58π=182.12 59π=185.26 60π=188.4 57π=178.98 58π=182.12 59π=185.26 60π=188.4 61π=191.54 62π=194.68 63π=197.82 64π=200.96 61π=191.54 62π=194.68 63π=197.82 64π=200.96 65π=204.1 66π=207.24 67π=210.3868π=213.52 65π=204.1 66π=207.24 67π=210.38 68π=213.52 69π=216.66 70π=219.8 71π=222.94 72π=226.08 69π=216.66 70π=219.8 71π=222.94 72π=226.08 73π=229.22 74π=232.36 75π=235.5 76π=238.64 73π=229.22 74π=232.36 75π=235.5 76π=238.64 77π=241.78 78π=244.92 79π=248.06 80π=251.2 77π=241.78 78π=244.92 79π=248.06 80π=251.2 81π=254.34 82π=257.48 83π=260.62 84π=263.76 81π=254.34 82π=257.48 83π=260.62 84π=263.76 85π=266.9 86π=270.04 87π=273.18 88π=276.32 85π=266.9 86π=270.04 87π=273.18 88π=276.32 89π=279.46 90π=282.6 91π=285.74 92π=288.88 89π=279.46 90π=282.6 91π=285.74 92π=288.88 93π=292.02 94π=295.16 95π=298.3 96π=301.44 93π=292.02 94π=295.16 95π=298.3 96π=301.44 97π=304.58 98π=307.72 99π=310.86 100π=314 97π=304.58 98π=307.72 99π=310.8 100π=314文案编辑词条B 添加义项 ? 文案英文:copywriter、copy、copywriting 文案，原指放书的桌子，后来指在桌子上写字的人。