011第11讲§1-3几何作图(椭圆的画法)
- 格式:doc
- 大小:550.50 KB
- 文档页数:2

数学中常⽤⼏何画板绘制椭圆圆锥曲线是⾼中数学的重点和难点,也是历来⾼考的必考内容,所以对于⾼中⽣来说,弄懂圆锥曲线这块难啃的⾻头,是很有必要的。
其中要熟练掌握的圆锥曲线之⼀就是椭圆,它是圆锥与平⾯的截线,其实要想画出椭圆,其⽅法不⽌⼀种,下⾯就⼀起来通过学学椭圆的五种画法。
⽅法⼀、利⽤椭圆第⼀定义构造椭圆椭圆第⼀定义:平⾯内到两个定点的距离之和等于定长2a(a>0)的点的轨迹就是椭圆,按照此定义可画出椭圆,具体步骤如下:1.单击“圆⼯具”,在画板的适当位置任意画⼀个圆,将圆⼼的标签改为F1。
单击“点⼯具”,在圆上任意画⼀点C,同时选中点F1和点C,执⾏“构造”-“线段”命令,构造出线段F1C。
单击“点⼯具”,在线段F1C任意画⼀点F2。
2.在圆上任意画⼀点E,并构造线段EF1和线段EF2。
选中线段EF2,执⾏“构造”-“中点”命令,构造线段EF2的中点F。
3.选中线段EF2和点F,执⾏“构造”-“垂线”命令,构造出线段EF2的垂直平分线j。
同时选中线段EF1和直线j,选择“构造”-“交点”命令,构造线段EF1和直线j的交点G。
4.选中点G和点E(把点E称做是点G的相关点,改变G点的位置,点E的位置也跟着改变),选择“构造”-“轨迹”命令,可画出椭圆。
拖动点B 和点F2可改变椭圆的形状。
⽅法⼆、利⽤椭圆第⼆定义画椭圆椭圆的第⼆定义:设动点M(x, y)与定点F(c, 0)的距离和它到定直线l: x=a2/c的距离的⽐是常数(a>c>0),则点M的轨迹是椭圆。
点F 是椭圆的⼀个焦点,直线l是椭圆中对应于焦点F的准线,常数e=c/a(0<e<1)。
具体的操作步骤如下:步骤⼀打开⼏何画板,使⽤“点⼯具”画任意⼀点F,使⽤“线⼯具”画直线L(点F不在L上)。
过点F作⼀条直线,在直线上取⼀点P;步骤⼆选中点F、P执⾏“度量”--“距离”命令,度量FP的长度;选中点F和度量的FP的长度,执⾏“构造”--“以圆⼼和半径绘圆”构造以点F为圆⼼,FP为半径的圆。



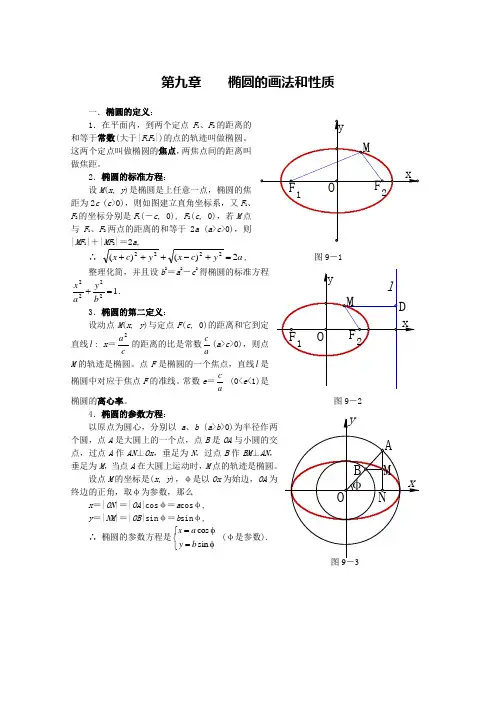
第九章 椭圆的画法和性质一.椭圆的定义:1.在平面内,到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2.椭圆的标准方程:设M (x , y )是椭圆是上任意一点,椭圆的焦距为2c (c >0),则如图建立直角坐标系,又F 1、F 2的坐标分别是F 1(-c , 0), F 2(c , 0),若M 点与F 1、F 2两点的距离的和等于2a (a >c >0),则 |MF 1|+|MF 2|=2a ,∴ a y c x y c x 2)()(2222=+-+++, 图9-1整理化简,并且设b 2=a 2-c 2得椭圆的标准方程12222=+b y a x . 3.椭圆的第二定义:设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x =c a 2的距离的比是常数ac (a >c >0),则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点,直线l 是椭圆中对应于焦点F 的准线。
常数e =ac(0<e <1)是椭圆的离心率。
图9-24.椭圆的参数方程:以原点为圆心,分别以a 、b (a >b >0)为半径作两个圆,点A 是大圆上的一个点,点B 是OA 与小圆的交点,过点A 作AN ⊥Ox ,垂足为N ,过点B 作BM ⊥AN ,垂足为M ,当点A 在大圆上运动时,M 点的轨迹是椭圆。
设点M 的坐标是(x , y ),φ是以Ox 为始边,OA 为终边的正角,取φ为参数,那么x =|ON |=|OA |cos φ=a cos φ, y =|NM |=|OB |sin φ=b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二.椭圆的画法: 画法1:图9-41.在x 轴上取两点F 1、F 2,使|OF 1|=|OF 2|,用它们作为两个焦点; 2.在图形外作一条线段CD ,使|CD |=2a ,(|CD |>|F 1F 2|); 3.以O 为中心,在x 轴上取两点A 1、A 2,使|A 1A 2|=|CD |;4.在CD 上分别取C '、D ',使|CC '|=|A 1F 1|=|DD '|;作线段C 'D ',并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ;5.分别以F 1、F 2为圆心,用|CM |、|MD |为半径作圆,两圆相交于P 1、P 2两点;同样方法分别以F 1、F 2为圆心,用|DM |、|CD |为半径作圆,两圆相交于P 3、P 4两点;并将这四个点定义为“追踪点”;6.依次选中点M 、点P 1 (或点M 、点P 2),用“作图”菜单中的“轨迹”功能,作出椭圆。

用几何画板画椭圆的六种方法椭圆是平面几何中常见的图形,具有许多特点和性质。
在绘制椭圆时,有多种方法可以使用。
下面将介绍六种常用的绘制椭圆的方法。
1. 绳和两个钉:这是最简单的方法之一。
取一根绳,将两个钉固定在纸上,钉的距离确定椭圆的长轴,绳长为椭圆的周长。
将绳套在两个钉上,再以笔紧绷绳子,沿纸面移动绳子的笔尖,即可得到一个完美的椭圆。
2. 立兰德椭圆仪:这是一种专门用于绘制椭圆的工具。
它由两个互相垂直的固定圆和一个移动圆组成。
通过调整移动圆的位置,使其切割固定圆的位置在不同角度,便可绘制出各种椭圆。
3. 画平行线法:在纸上画一条长直线,作为椭圆的长轴。
然后,在长轴上选择几个等分点,并与长轴垂直的方向上画平行线。
接下来,再在每个平行线上选择等分点,并连结相邻点,最终得到椭圆。
4. 两点距离法:选择椭圆上的两个任意点,并利用细线连接它们。
然后,取一根较长的尺,在椭圆外围固定两个点,使其到线的距离相同。
移动尺的另一段,让尺上的铅笔碰触到线,并沿着椭圆移动,最终形成一个椭圆。
5. 推拉法:选取一块矩形硬纸板或卡纸,将其弯曲成圆筒形。
两端的直径确定椭圆的长短轴。
然后,在圆筒上连接两个焦点,并用铅笔固定在纸上固定一个点,同时将纸沿着直径滑动,同时保持焦点的位置变化,最终形成一个椭圆。
6. 辅助圆法:在纸上确定椭圆的长轴和短轴的长度。
以长轴为直径,在一张纸上画一个大圆;再以短轴为直径,在同一张纸上画一个小圆。
以每个圆的切点为圆心,连结两个切点,最终形成一个完美的椭圆。
这几种方法都能够帮助我们绘制出精确的椭圆。
根据实际需求和使用条件的不同,我们可以选择适合自己的方法来画椭圆。
希望这些方法对您有所帮助!。
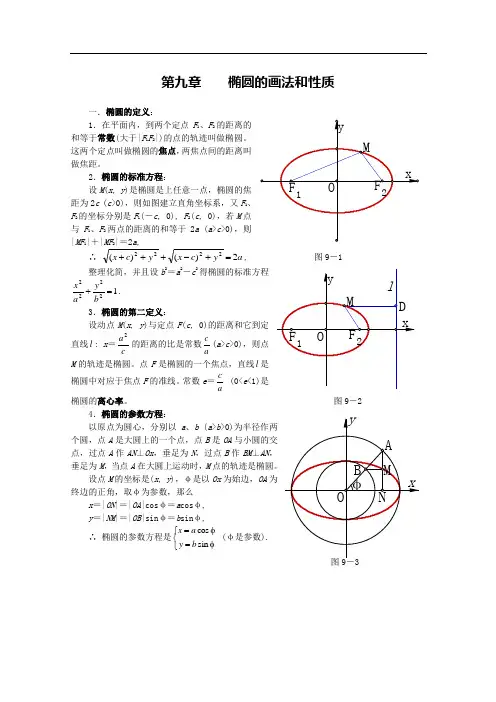
第九章 椭圆的画法和性质一.椭圆的定义:1.在平面内,到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2.椭圆的标准方程:设M (x , y )是椭圆是上任意一点,椭圆的焦距为2c (c >0),则如图建立直角坐标系,又F 1、F 2的坐标分别是F 1(-c , 0), F 2(c , 0),若M 点与F 1、F 2两点的距离的和等于2a (a >c >0),则 |MF 1|+|MF 2|=2a ,∴ a y c x y c x 2)()(2222=+-+++, 图9-1整理化简,并且设b 2=a 2-c 2得椭圆的标准方程12222=+b y a x . 3.椭圆的第二定义:设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x =c a 2的距离的比是常数ac (a >c >0),则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点,直线l 是椭圆中对应于焦点F 的准线。
常数e =ac(0<e <1)是椭圆的离心率。
图9-24.椭圆的参数方程:以原点为圆心,分别以a 、b (a >b >0)为半径作两个圆,点A 是大圆上的一个点,点B 是OA 与小圆的交点,过点A 作AN ⊥Ox ,垂足为N ,过点B 作BM ⊥AN ,垂足为M ,当点A 在大圆上运动时,M 点的轨迹是椭圆。
设点M 的坐标是(x , y ),φ是以Ox 为始边,OA 为终边的正角,取φ为参数,那么x =|ON |=|OA |cos φ=a cos φ, y =|NM |=|OB |sin φ=b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二.椭圆的画法:画法1:图9-41.在x 轴上取两点F 1、F 2,使|OF 1|=|OF 2|,用它们作为两个焦点; 2.在图形外作一条线段CD ,使|CD |=2a ,(|CD |>|F 1F 2|); 3.以O 为中心,在x 轴上取两点A 1、A 2,使|A 1A 2|=|CD |;4.在CD 上分别取C '、D ',使|CC '|=|A 1F 1|=|DD '|;作线段C 'D ',并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ;5.分别以F 1、F 2为圆心,用|CM |、|MD |为半径作圆,两圆相交于P 1、P 2两点;同样方法分别以F 1、F 2为圆心,用|DM |、|CD |为半径作圆,两圆相交于P 3、P 4两点;并将这四个点定义为“追踪点”;6.依次选中点M 、点P 1 (或点M 、点P 2),用“作图”菜单中的“轨迹”功能,作出椭圆。

椭圆的标准画法椭圆作为一种常见的几何图形,在绘画、设计以及数学等领域发挥着重要作用。
了解如何准确地绘制椭圆是每个有着创作冲动的人都应该掌握的基本技能。
在本文中,我们将介绍椭圆的标准画法,包括基本原理和几种常用的绘制方法。
椭圆的基本原理在开始具体介绍绘制椭圆的方法之前,我们有必要先了解一下椭圆的基本原理。
椭圆是一个和圆相关的形状,它是通过一个点(称为焦点)和一条线段(称为直线段)的集合定义的。
具体来说,椭圆是到焦点的距离之和恒定的点的轨迹。
这个距离之和等于椭圆的长轴和短轴之和。
标准画法方法一:使用椭圆板椭圆板是一种专门用于绘制椭圆的工具,它可以帮助我们画出精确的椭圆形状。
使用椭圆板绘制椭圆的步骤如下:1. 准备一个椭圆板和一支铅笔;2. 将椭圆板放置在绘画纸上,并确定椭圆的中心点;3. 调整椭圆板上的固定刻度,使其符合所需的长轴和短轴长度;4. 将铅笔顶端插入椭圆板上对应的刻度孔内,然后用手指固定住铅笔头部;5. 以椭圆板的中心点为固定点,旋转椭圆板,同时利用铅笔头在纸上画出完整的椭圆。
标准画法方法二:使用两个钉子和一根绳子除了椭圆板外,我们还可以使用常见的工具来绘制椭圆。
使用两个钉子和一根绳子绘制椭圆的步骤如下:1. 准备两个钉子、一根绳子和一支铅笔;2. 将两个钉子固定在绘画纸上,使其成为一个等边三角形的两个顶点;3. 将绳子的一端绑在一个钉子上,然后用手持另一端的铅笔;4. 以绳子为轴,将铅笔拖动沿着钉子之间的连线上方的路径移动,同时保持绳子始终保持紧绷的状态;5. 重复以上步骤,直到绘制出需要的椭圆形状。
标准画法方法三:使用分割线和纵横比例此外,我们还可以利用分割线和纵横比例来绘制椭圆。
绘制椭圆的步骤如下:1. 以纸张的中心点为标志,从上方和下方画一条水平线,将纸张平均分为上下两部分;2. 再从左边和右边画一条垂直线,将纸张平均分为左右两部分;3. 选择一个适当的纵横比例,然后在第一步中画出的水平线上标记出若干等距离的刻度点;4. 用直尺连接上方两个刻度点、下方两个刻度点和水平线的两个分割点;5. 重复以上步骤,在左边和右边的分割线上刻度并连接相应的点,直到绘制出完整的椭圆形状。
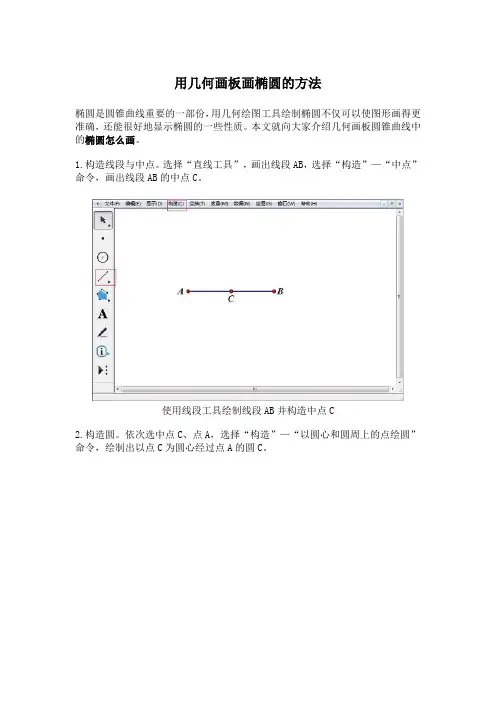
用几何画板画椭圆的方法
椭圆是圆锥曲线重要的一部份,用几何绘图工具绘制椭圆不仅可以使图形画得更准确,还能很好地显示椭圆的一些性质。
本文就向大家介绍几何画板圆锥曲线中的椭圆怎么画。
1.构造线段与中点。
选择“直线工具”,画出线段AB,选择“构造”—“中点”命令,画出线段AB的中点C。
使用线段工具绘制线段AB并构造中点C
2.构造圆。
依次选中点C、点A,选择“构造”—“以圆心和圆周上的点绘圆”命令,绘制出以点C为圆心经过点A的圆C。
选中点C、点A后构造以点C为圆心经过点A的圆C
3.构造垂线与交点。
选择“点工具”,在圆周上任意作一点D,选中点D和线段AB,选择“构造”—“垂线”命令,绘制出线段AB的垂线,与线段AB的交点为E。
绘制点D后构造线段AB的垂线并与之交于E点
4.隐藏圆和直线。
选中圆C和直线DE,选择“显示”—“隐藏路径对象”命令,隐藏圆C和直线DE。
选中圆C和直线DE后将之隐藏
5.构造线段和中点。
选择“线段工具”,绘制出线段DE。
选择“构造”—“中点”命令,绘制出线段DE的中点F。
用线段工具绘制出线段DE后构造其中点F
6.绘制椭圆。
依次选中点D、点F,选择“构造”—“轨迹”命令,绘制出椭圆。
如下图所示。
使用“构造”—“轨迹”命令绘制出椭圆
7.隐藏点与线段。
选中点D、点E、点F、线段DE,选择“显示”—“隐藏对象”命令,椭圆绘制完成。
隐藏点D、E、F和线段DF
以上向大家详细介绍了用几何画板画椭圆的方法,相信大家对此已经有所掌握。

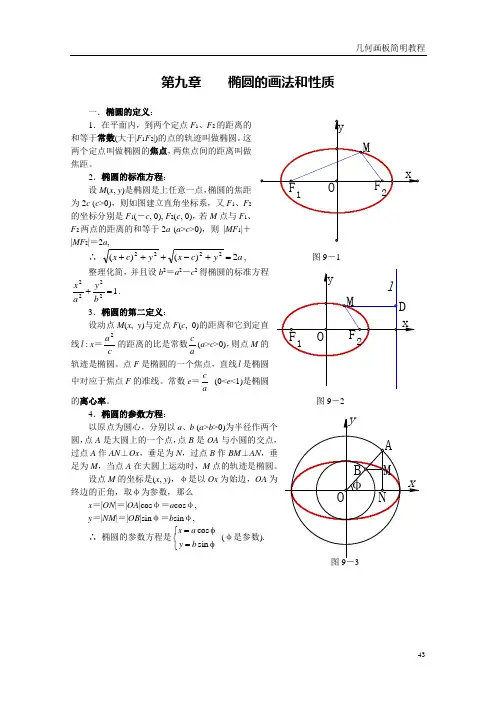
第九章 椭圆的画法和性质一.椭圆的定义:1.在平面内,到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2.椭圆的标准方程:设M (x , y )是椭圆是上任意一点,椭圆的焦距为2c (c >0),则如图建立直角坐标系,又F 1、F 2的坐标分别是F 1(-c , 0), F 2(c , 0),若M 点与F 1、F 2两点的距离的和等于2a (a >c >0),则 |MF 1|+|MF 2|=2a ,∴a y c x y c x 2)()(2222=+-+++, 图9-1整理化简,并且设b 2=a 2-c 2得椭圆的标准方程12222=+b y a x . 3.椭圆的第二定义:设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x =c a 2的距离的比是常数ac (a >c >0),则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点,直线l 是椭圆中对应于焦点F 的准线。
常数e =ac(0<e <1)是椭圆的离心率。
图9-24.椭圆的参数方程:以原点为圆心,分别以a 、b (a >b >0)为半径作两个圆,点A 是大圆上的一个点,点B 是OA 与小圆的交点,过点A 作AN ⊥Ox ,垂足为N ,过点B 作BM ⊥AN ,垂足为M ,当点A 在大圆上运动时,M 点的轨迹是椭圆。
设点M 的坐标是(x , y ),φ是以Ox 为始边,OA 为终边的正角,取φ为参数,那么x =|ON |=|OA |cos φ=a cos φ, y =|NM |=|OB |sin φ=b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二.椭圆的画法:画法1:图9-41.在x 轴上取两点F 1、F 2,使|OF 1|=|OF 2|,用它们作为两个焦点; 2.在图形外作一条线段CD ,使|CD |=2a ,(|CD |>|F 1F 2|); 3.以O 为中心,在x 轴上取两点A 1、A 2,使|A 1A 2|=|CD |;4.在CD 上分别取C '、D ',使|CC '|=|A 1F 1|=|DD '|;作线段C 'D ',并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ;5.分别以F 1、F 2为圆心,用|CM |、|MD |为半径作圆,两圆相交于P 1、P 2两点;同样方法分别以F 1、F 2为圆心,用|DM |、|CD |为半径作圆,两圆相交于P 3、P 4两点;并将这四个点定义为“追踪点”;6.依次选中点M 、点P 1 (或点M 、点P 2),用“作图”菜单中的“轨迹”功能,作出椭圆。
椭圆的画法和性质一.椭圆的定义: 1.在平面内,到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2.椭圆的标准方程:设M (x , y )是椭圆是上任意一点,椭圆的焦距为2c (c >0),则如图建立直角坐标系,又F 1、F 2的坐标分别是F 1(-c , 0), F 2(c , 0),若M 点与F 1、F 2两点的距离的和等于2a (a >c >0),则 |MF 1|+|MF 2|=2a ,∴a y c x y c x 2)()(2222=+-+++, 图9-1整理化简,并且设b 2=a 2-c 2得椭圆的标准方程12222=+b y a x . 3.椭圆的第二定义:设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x =ca2的距离的比是常数ac(a >c >0),则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点,直线l 是椭圆中对应于焦点F 的准线。
常数e =ac(0<e <1)是椭圆的离心率。
图9-24.椭圆的参数方程:以原点为圆心,分别以a 、b (a >b >0)为半径作两个圆,点A 是大圆上的一个点,点B 是OA 与小圆的交点,过点A 作AN ⊥Ox ,垂足为N ,过点B 作BM ⊥AN ,垂足为M ,当点A 在大圆上运动时,M 点的轨迹是椭圆。
设点M 的坐标是(x , y ),φ是以Ox 为始边,OA 为终边的正角,取φ为参数,那么x =|ON |=|OA |cos φ=a cos φ,y =|NM |=|OB |sin φ=b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二.椭圆的画法:画法1:1.在x 轴上取两点F 1、F 2,使|OF 1|=|OF 2|,用它们作为两个焦点; 2.在图形外作一条线段CD ,使|CD |=2a ,(|CD |>|F 1F 2|); 3.以O 为中心,在x 轴上取两点A 1、A 2,使|A 1A 2|=|CD |;4.在CD 上分别取C '、D ',使|CC '|=|A 1F 1|=|DD '|;作线段C 'D ',并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ;5.分别以F 1、F 2为圆心,用|CM |、|MD |为半径作圆,两圆相交于P 1、P 2两点;同样方法分别以F 1、F 2为圆心,用|DM |、|CD |为半径作圆,两圆相交于P 3、P 4两点;并将这四个点定义为“追踪点”;6.依次选中点M 、点P 1 (或点M 、点P 2),用“作图”菜单中的“轨迹”功能,作出椭圆。
附件:教学设计模板
如板书中含有特殊符号、图片等内容,为方便展示,可将板书以附件或图片形式上传。
1.椭圆的长轴和短轴:两条相互垂直而且对称的轴。
2.椭圆的几何性质:自椭圆上任意一点到两定点(焦点)的距离之和恒等于椭圆的长轴。
3.椭圆的理论画法(同心圆画法)
4. 椭圆的近似画法(四心画法)
5.老师总结
①理论画法跟近视画法都可以把椭圆画出来;
②理论画法适合精度要求非常高的场合;
③近似画法适合一般的绘图作业和测绘,而且可以借助绘图工具来完成,比较简单,易于控制,轨迹均匀,美观。
椭圆的标准画法标题:"椭圆的标准画法"椭圆作为几何图形中的一种,具有广泛的应用。
在绘制椭圆时,我们需要遵循一些标准的画法,以确保正确的形状和比例。
本文将介绍椭圆的标准画法,并提供一些技巧和注意事项。
第一,绘制椭圆的第一步是确定椭圆的中心点和两个轴线。
中心点是椭圆的几何中心,轴线是通过中心点的两条相互垂直的线。
这两条轴线被称为长轴和短轴,分别决定了椭圆的长度和宽度。
第二,根据确定的中心点和轴线,我们可以使用传统的绘图工具如铅笔或者画板上的直尺和圆规来绘制椭圆。
以中心点为起点,将圆规的一只脚放在长轴上,另一只脚放在短轴上。
然后,沿着这两个轴线来回移动圆规,直到覆盖整个椭圆。
第三,为了保证椭圆的形状和比例准确无误,我们可以使用更精确的工具如椭圆模板或计算机辅助设计软件。
椭圆模板是一个带有不同大小椭圆的图形工具,可以轻松地选择所需的椭圆尺寸。
而计算机辅助设计软件则提供了更多灵活性和精确性,使我们能够根据具体需求绘制椭圆。
第四,除了绘制标准的椭圆外,我们还可以通过椭圆的焦点和直径来绘制其他类型的椭圆。
椭圆的焦点是椭圆上所有点到两个焦点的距离之和相等的点。
直径是通过焦点的直线段,且经过椭圆的中心点。
这些绘制方法可以提供更多的创意和变化,使椭圆更具多样性。
在绘制椭圆时,我们需要注意以下几点。
首先,保持手的稳定性,确保绘制出的椭圆线条流畅。
其次,使用合适的绘图工具和辅助工具,以提高绘制的准确性。
最后,不断练习和尝试,只有通过不断的实践才能掌握椭圆的标准画法。
总结起来,椭圆的标准画法需要遵循一些基本原则和技巧。
通过正确的步骤和准确的工具,我们可以绘制出美观而准确的椭圆形状。
无论是在绘画、工程设计还是其他领域,椭圆都是重要的图形之一,掌握它的标准画法将会对我们的工作和学习有所帮助。
第11讲
椭圆的画法
【课题】§1-3几何作图(椭圆的画法)
【教学时数】2课时(其中:理论教学1课时、实训1课时)
【教学目的】掌握用四心法近似画椭圆
【教学重点】四心圆弧法画椭圆
【教学难点】同心圆法画椭圆
【教学方法】讲授法、演示法
【教具准备】圆规、三角板、彩色粉笔
【教学步骤】
[复习提问]
1、圆弧与直线连接
2、圆弧与圆弧内连接
3、圆弧与圆弧外连接
[引入新课]
在绘制回转体机械零件的投影图时,经常要画椭圆,椭圆常用画法有同心圆法和四心圆弧法两种
[讲授新课]
椭圆的画法
一、同心圆法画椭圆
如图1所示
1、以AB和CD为直径画同心圆,然后过圆心作一系列直径与两圆相交。
2、由各交点分别作与长轴、短轴平行的直线,即可相应找到椭圆上各点。
3、最后,光滑连接各点即可。
二、椭圆的近似画法(四心圆弧法)
如图1所示
已知条件:椭圆的长轴AB与短轴CD。
1、连AC,以O为圆心,OA为半径画圆弧,交CD延长线于E ;
2、以C为圆心,CE为半径画圆弧,截AC于E1;
3、作A E1的中垂线,交长轴于O1,交短轴于O2,并找出O1和O2的对称点O3和O4;
4、把O1与O2、O2与O3、O3与O4、O4与O1分别连直线;
5、以O1、O3为圆心,O1A为半径;O2、O4为圆心,O2C为半径,分别画圆弧到连心线,K、K1、N1、N为连接点即可。
【实训指导】
[案例]
已知长轴AB=60mm,短轴CD=40mm,用四心法近似画椭圆。
[温声提示]
1、画长短轴
2、找四心
[手把手教]
对称点的简单求法
[课堂小结]
1、同心圆法画椭圆
2、四心圆弧法画椭圆
[作业布置]
习题集P6§16\4
【板书设计】
1、据已知条件作出长短轴上的4点:A、B、C、D
2、连AC找F
四心法画椭圆 3、作AF的⊥平分线,找O1O2心
4、对称作出O3O4心
5、四心画弧(即得椭圆ABCD)
【板图设计】
1、同心圆法画椭圆示例图
2、四心圆弧法画椭圆示例图
【教后感】。