高斯小学奥数含答案三年级(上)第02讲枚举法中的字典排列

我们已经学过了枚举法，有时还需要先分类再按一定顺序进行枚举?接下来我们将要学习如果对某件事情的过程进行枚举，一般会使用另一种方法：树形图法?所谓树形图法就是用像树一样的、不断分叉的图来表示出所有情况的方法画出树形图与一棵树的生长过程类似，先从“树根”开始，然后不断长出新的“树枝每次长出新的“树枝”时都有可能产生分叉，最后长满了“果实这样一直下去把所有情况都画完，最后数一下“果实”的数目即可例题 1 乌龟、兔子、米老鼠站成一排，如果乌龟不站在第 1 个，兔子不站在第 2 个米老鼠不站在第 3 个，请问它们共有多少种不同的站法?分析：第 1 个位置可以站哪些小动物？第 2 个位置呢？以第一动物位置站的人作为“树根” 表用树形图示出所有的站法.甲、乙、丙4个人站队，站成一条直线?如果甲不站第1、2 个，乙不站第2、3个，丙不站第3、4 个丁不站第4、1 个，那么一共有多少种站队的方法?b厂第十四讲\r1树形图II. fi li (小高、墨莫和萱萱玩传球游戏，每次持球人都可以把球传给另外两人中的任 何一人 . 先由小高拿球，第 1 次传球可以传给其他两人中的任何一人，经过 次传球之后，球又回到了小高手里 . 请问一共有多少种不同的传球过程 ?分析：第 1 次有多少种传法？试着用树形图画出每次传球后给谁 里 上才是符合题意的传法 .不同，一共有多少个满足条件的四位数 ?分析：四位数的千位数字和个位数字分别有几种情况？应该选择哪个数位的数字作为: 练习 3）一个三位数 位上的数字都是 5、6、 7 中的某一个，并且相邻的两个数字不相同，一共有多少个满足条件的三位数 ?☆题2注意：只有第 4 次传球后回到小高手练习 2有 A 、B 、C 三片荷叶 ' 青蛙另一片荷叶上，结果它跳了呱呱”在荷叶 A 上，每次它都会从一片荷叶跳到3次之后，不在荷叶 A 上. 请问：它一共有多少种不同的跳法 ?例题 3一个四位数，每一位上的数字都是0、1、2 中的一个，并且相邻的两个数字树根”来画树形例题 4王老师有一个带密码锁的公文包，但是他忘记了密码 . 只记得密码是一个三位数. 这个三位数的个位数字比十位数字大，十位数字比百位数字大，并且没有比 5 大的数字 . 试问：王老师最多需要试多少次就肯定能打开这个公文包 画出树形图卜析：百位数字最小， 有几种情况？把这些情况分别作为“树根”一个三位数，百位比十位大，十位比个位大，个位不小于数一共有几个？例题5常昊与古力两人进行围棋赛，谁先胜三局就赢得比赛. 如果最后常昊获胜了，那么比赛的进程有多少种可能？分析：试着把每场比赛的结果用树形图表示出来?注意：不会有古常----- 古古- 常——（常）这样的过程出现，因为在这种情况下，赛完第 4 场后古力已经获胜，不符合题意.例题65 块六边形的地毯拼成了如下图的形状，每块地毯上都有一个编号，现在小高站在1 号地毯上，他想要走到5 号地毯上?如果小高每次都只能走到和他相邻的地毯上（两个六边形如果有公共边就成为相邻），并且只能向右边走，例如1f 2—3—5 就是一种可能的走法. 请问：小高一共有多少种不同的走法？分析：注意开始是从 1 号毯开始，结束在 5 号地毯才能符合题意汽车品牌家族树形图甲、乙、丙三个人传球，从甲开始传球，每次拿球的人都把球传给剩下两个人中的一人，传了次后球在丙的手上，那么一共有多少种可能的传球过程？2.且相邻的两个数字不一样，那么卡莉娅最多试多少次就一定能打开日记本？3. 粗心的卡莉娅忘记了日记本的三位密码，只记得密码是由1、2、7 三个数字中的某些数字构成的，4. 甲、乙比赛乒乓球，五局三胜. 已知甲胜了第 1 局，并最终获胜. 请问一共有多少种不同的比赛过程？5. 满足下面性质的数称为阶梯数：它的百位数字比十位数字小，十位数字比个位数字小，并且相邻两位数字的差不超过 2 . 例如：135 、234 为阶梯数，156 就不是阶梯数，那么共有多少个三位数是阶梯数？☆2种 121233龟兔鼠鼠龟兔212312344墨■墨小小萱萱小 墨萱小墨墨曰311222211212 2 2 1001 22141 第十四讲 树形图可以画成树形图，如下图，共详解 1 次可以给萱萱可以画成树形图，第8 种， 2 的也有 8 种，共 16树根有 1 的共有1、2 4 10 次2、3 三个数作为树可以画出三幅树形分别详例题 答案 例题答例题 答案 详解 例题 答案详解 种.1 2种2 6种3 16 种可以画成树形图，如下图，树根有 也可以给墨莫，如下图，共 6 种5. 例题 5答案：10 种6. 例题 6答案： 5 种详解：可以画成树形图，共有 5 种.4535245 145 3572种12341243甲甲甲乙丙丁 甲乙丁 丁8123 123 BBAACCCBBCAAC练习93答案简答 练习 答案 简答 6种 12 种 2 6种3 次后不在 A 荷叶上，如下图，共可以画成树形图，如下图，树根B 、 C 荷叶上 跳了 5、6、7 树根是 5的共有 4种，6 的也有 4种，7的也有 4 种，共 12可以画成树形图，第 1 次可跳在B丙 练习 1 答案： 2 种 简答：可以画成树 形图，如下图，共510 练习答案：简答：7610 种可以画成树形图，从个位开始枚举如下图，共百＞98581 作业 11答案：342;423简答：可以画成树形图3、4 2、2、3 12 作业 23答案：3简答：可以画成树形图710 种百＞513. 作业3简答：如下图. 首位是 2 或7 开头的密码也有 4 个，所以符合条件的有12 个，最多要试12 次.14. 作业 4答案：615. 作业 5答案：24 个简答：如下图，可分别画出百位是1、2、3、4、5、6、7的树形图，百位为1的有4种，百位为2的有4 种，百位为 3 的有 4 种，百位为 4 的有 4 种，百位为5 的有 4 种，百位为6 的有 3 种，百位为7 的有 1 种，共有24 个阶梯三位数.甲丙乙丙甲丙甲丙乙丙13. 作业 3答案：12简答：如下图．首位是2 或 7 开头的密码也有 4 个，所以符合条件的有 12 个，最多要试 12次．百十个127 117214. 作业 4答案： 6简答：可以画成树形图：1、 2 、 3、 4、 5 、 6、 7 的树形图，百位为 1 的有 4 种，百 位为 2 的有 4 种， 百位为 3 的有 4 种，百位为 4 的有 4 种，百位为 5 的有 4 种，百位为 6 的有 3 种，百位为 7 的有 1 种，共有 24 个阶梯三位数． 甲甲甲乙 乙甲甲乙 甲乙乙 甲15. 作业 5答案：24 个简答：如下图， 可分别画出百位是。

【专题简析】枚举是一种常见地分析问题、解决问题地方法.一般地，要根据问题要求，一一列举问题解答.运用枚举法解应用题时，必须注意无重复、无遗漏，因此必须有次序、有规律地进行枚举.个人收集整理勿做商业用途运用枚举法解题地关键是要正确分类，要注意以下两点：一是分类要全，不能造成遗漏；二是枚举要清，要将每一个符合条件地对象都列举出来.个人收集整理勿做商业用途【典型例题】【例】从小华家到学校有条路可以走，从学校到岐江公园有条路可以走，从小华家到岐江公园，有几种不同地走法？个人收集整理勿做商业用途【试一试】. 从甲地到乙地，有条公路直达，从乙地到丙地有条铁路可以直达，从甲地到丙地有多少种不同地走法？. 新华书店有种不同地英语书，种不同地数学读物销售，小明想买一种英语书和一种数学读物，共有多少种不同地买法？个人收集整理勿做商业用途【例】把个同样地苹果放在两个同样地盘子里，允许有地盘子空着不放，问共有多少种不同地分法？【试一试】．把个同样地苹果放在两个同样地盘子里，允许有地盘子空着不放，问共有多少种不同地分法？．把个同样地苹果放在三个同样地盘子里，不允许有地盘子空着不放，问共有多少种不同地分法？【例】从～这六个数字中，每次取个数字，这两个数字地和都必须大于，能有多少种取法？【试一试】．从～这九个数字中，每次取个数字，这两个数字地和都必须大于，能有多少种取法？．从～这十九个数字中，每次取个数字，这两个数字地和都必须大于，能有多少种取法？【例】一个长方形地周长是米，如果它地长和宽都是整米数，那么这个长方形地面积有多少种可能值？【试一试】．一个长方形地周长是厘米，如果它地长和宽都是整厘米数，那么这个长方形地面积有多少种可能值？．把个玻璃球分成数量不同地堆，共有多少种不同地分法？【例】有位小朋友，寒假中互相通一次电话，他们一共打了多少次电话？【试一试】．个小队进行排球比赛，每两队比赛一场，共要进行多少次比赛？．有位小朋友，要互通一次电话，他们一共打了多少次电话？【※例】一条铁路，共有个车站，如果每个起点站到终点站只用一种车票（中间至少相隔个车站），那么这样地车票共有多少种？个人收集整理勿做商业用途【※试一试】. 上海、北京、天津三个城市分别设有一个飞机场，它们之间通航一共需要多少种不同地机票？. 一条公路上，共有个站点，如果每个起点到终点只用一种车票（中间至少相隔个车站），那么共有多少种不同地车票？个人收集整理勿做商业用途【※例】在～中，任取两个和小于地数，共有多少种不同地取法？【※试一试】. 在两位整数中，十位数字小于个位数字地共有多少个？. 从～这九个数中，每次取个数，这两个数地和都必须大于，能有多少种取法？课外作业家长签名.小熊有件不同地上衣，条不同地裤子，最多可以搭配多少种不同地装束？．个自然数地乘积是，问由这样地个数所组成地数有多少个？如（，，）就是其中一个，而且数组中数字相同但顺序不同地算作同一数组，如（，，）和（，，）是同一数组.个人收集整理勿做商业用途．明明有件不同地上衣，条不同地裤子，双不同地鞋子，最多可以搭配多少种不同地装束？．个自然数地乘积是，问由这样地个数所组成地数有多少个？如（，，）就是其中一个，而且数组中数字相同但顺序不同地算作同一数组，如（，，）和（，，）是同一数组.个人收集整理勿做商业用途．小芳出席由人参加地联欢会，散会后，每两人都要握一次手，他们一共握了多少次手？※.在长江地某一航线上共有个码头，如果每个起点终点只许用一种船票（中间至少要相隔个码头），那么这样地船票共有多少种？个人收集整理勿做商业用途※.十把钥匙开十把锁，但钥匙放乱了，问最多要试多少次可以找到相应地锁？最多要试多少次才能开相应地锁？个人收集整理勿做商业用途。

16第四讲数字计数数有几个，就可以算出其它类的方法数这时就需要预先把所有情形分成若干小类，针对每一小类进行枚数一数，上图中一共有多少个正方形?枚举法是解决计数问题的基础，但是对于比较复杂的问题，如果直接枚举很容易出现重复或者在涉及数字的枚举时，需要注意0不能在首位.对于没有指定位数的问题，可以按位数分类枚举.类与类之间有时会有很多相似性.如果能够合理的利用这些相似性，就可以大大减少枚举的工作 利用数字0、1、2能拼出多少个无重复数字的自然数？（数字不必都用利用数字1、2、3能拼出多少个无重复数字的自然数？（数字不必都用量.比如例题1中，以1开头的三位数和以2开头的三位数是相类似的，只要枚举清楚以1开头的三已修习2在所有的两位数中，各位数字大于16的共有多少个?在分类时，一定注意类与类之间有没有重复的部分，或者有没有漏掉的情况.只有在分类已经做到“不重不漏”的前提下，才能够进行下一步的枚举.例题3用两个1, 一个2, 一个3,可以组成多少个不同的四位数？♦ + + + + + + + + +♦♦ + + + +♦♦ + + + +*♦ + + + +T'舂:练习3用三个2，一个4，一个5，可以组成多少个不同的五位奇数?如果题目中的数字是印在木板上的，如1、3、5：。

由于这是块木板，可以随意旋转，例如0、1、6、8、9这5个，而其他5个数字旋转之后什么都不是，没有意义，所以结果不变.如果把写着6的那块木板倒过来的话就会变成9,所以会多出来很多数，比如9、95、954等等，想一下.还有哪些数字可以倒过来看呢？老师拿来3块木板，上面分别写着数字0、3、6.你可以用这些木板拼出多少个不同的自然数?（木板可以颠倒，且数字不必都用上）老师拿来3块木板，上面分别写着数字4、5、6.你可以用这些木板拼出多少个不同的三位数？（木板可以颠倒）堡夕例题5如下图，四张卡片上写有数字2, 4, 7, 8.从中任取三张卡片，排成一行，就可以组成一个三位数.请问：一共可以组成多少个不同的三位数？其中有多少个不同的三位偶数？分类方式非常多样，有时可以像例1 一样按位数分类，有时可以像例2 一样按各个数位数字和分类，有时可以像例3一样按相同数字的位置分类，有时可以像例4一样，按用不同数字分类.无论是哪种分类方式，首先需要将有几类写清楚，然后再枚举出每类的情况数，最后再将每类的方法数相加，即分类相加.例题6在所有的四位数中，各位数字之和超过32的共有多少个?成语分类一、数字成语一唱一和两败俱伤三长两短三顾茅庐三令五申四海为家五体投地六根清净七零八落半斤八两九霄云外十拿九稳百无禁忌千变万化瞬息万变二、动物名称成语【鼠】鼠目寸光鼠肚鸡肠鼠窃狗盗投鼠忌器抱头鼠窜獐头鼠目【牛】牛鬼蛇神牛刀小试牛鼎烹鸡汗牛充栋对牛弹琴九牛一毛【虎】虎视眈眈虎口余生虎头虎脑虎背熊腰虎头蛇尾虎落平阳【兔】兔死狐悲兔死狗烹狡兔三窟鸟飞兔走守株待兔【龙】龙腾虎跃龙飞凤舞龙马精神龙凤呈祥画龙点睛来龙去脉【蛇】蛇蝎心肠画蛇添足惊蛇入草龙蛇混杂杯弓蛇影牛鬼蛇神三、带植物成语开花结果斩草除根顺藤摸瓜披荆斩棘奇花异果投桃报李粗枝大叶春兰秋菊火树银花四、带人体成语面无人色心旷神怡耳熟能详心花怒放蒙头转向满面春风屈指可数满目疮痍铁面无私五、带方位成语旁若无人前车之鉴旁敲侧击人间地狱节外生枝福如东海马放南山居高临下蒙在鼓里六、带色彩成语黄金时代白雪皑皑乌烟瘴气皓首穷经青面獠牙苍髯如戟金光灿烂红颜薄命白发苍苍七、叠字成语亭亭玉立姗姗来迟栩栩如生欣欣向荣惺惺作态洋洋得意绵绵不绝静静乐道虎视眈眈八、带“不”字成语不由自主不谋而合不寒而栗不同凡响不甘示弱不知深浅不露声色不择手段不足为奇九、带“人”字成语人心涣散人生如梦人情冷暖人地生疏人面兽心人困马乏人才济济人浮于事人才辈出十、“想”的成语想了又想（朝思暮想）苦苦地想（苦思冥想）静静地想（静思默想）十一、“多”的成语观众多（座无虚席）贵宾多（高朋满座）人很多（摩肩接踵）十二、带有“看”的近义词的成语见多识广望而生畏察言观色一视同仁一览无余高瞻远瞩坐井观天举世瞩目管中窥豹十三、含有一对近义词的成语惊心动魄争奇斗艳生龙活虎添油加醋降龙伏虎争权夺利高楼大厦狂风暴雨满山遍野十四、含有两对近义词的成语深思熟虑真凭实据灵丹妙药凶神恶煞心满意足街头巷议翻山越岭精雕细刻生拉硬扯1. 各位数字之和大于15的两位数有多少个?2. 由1、2、3、4各一个能组成多少个不同的四位奇数?3. 在三角形中，任意两条边之和都大于第三边.三条边的边长均为整数，且最长边的长度是8厘米，那么这样的三角形共有多少种?4. 现有数字1、2、2、3各一个能拼出多少个不同的三位数?5. 老师拿来3块木板，上面分别写着数字7、8、9.你可以用这些木板拼出多少个不同的自然数？（木板不必都用上，木板可以颠倒）☆尊介T第四讲数字计数1.例题i答案：ii.详解：一位数：0、1、2；两位数：10、12、20、21；三位数：102、120、201、210,共有11 个.2.例题2答案：20.详解：数字之和不超过4,意味着数字和有四种情形：1、2、3、4.我们就依此分类.数字和为1：100, 1 个.数字和为2：首位为1, 101、110；首位为2, 200；此类共3个.数字和为3：首位为1, 102、111、120；首位为2,201、210；首位为3, 300；此类共6个.数字和为4：首位为1, 103、112、121、130；首位为2, 202、211、220；首位为3, 301、310；首位为4, 400；此类共10个.所以，共有20个三位数.3.例题3答案：19.详解：先放两个1,它们的位置一共有6种可能，然后放2和3,每种可能下2、3的位置可以颠倒，则会有2 种，那么一共有12个不同的四位数.4.例题4答案：19.详解：6的木板还能反过来当9用.可以是一位数、两位数和三位数，一位数有0、3、6、9,共4个，两位数是30、36、39、60、63、90、93共有7个，三位数时：先考虑当6用的情况.首位不能为0.三位数有306、360、603、630,共4个.当9用也有4个.所以，共有4X2=8个三位数.则总共有4+7+8=19个不同的自然数.5.例题5答案：24；18.详解：（1）从2、4、7、8中先选3个数字，共有4种选法，每种选法下会有6个三位数，则一共有24个不同的三位数.（2）如果是偶数，则个位可以是2、4、8,共有3类，每类的方法下会有6种可能，则会有18 个不同的三位偶数.6.例题6答案：49个.详解：按各位数字和分类：数字和可能为33、34、35、36.这四类情形对应的四位数分别有：34个、10个、4个、1个.因此，共有49个四位数.7.练习1答案：15.简答：1打头的有1, 12, 13, 123, 132共5个.2、3打头的也有5个.一共15个.8.练习2答案：3.简答：数字之和是17,这样的两位数有89、98；数字之和是18,这样的两位数是99,共有3个.9.练习3答案：4.简答：个位一定是5,则只需把三个2和一个4放在千位、百位、十位即可，一共有4种可能：分别为22245、22425、24225、42225.10.练习4答案：12.简答：用数字4、5、6：有456、465、546、564、645、654, 6 个；用数字4、5、9：有459、495、549、594、945、954, 6 个；一共有12 个.11.作业1简答：数字之和为16的两位数有79、88、97,数字之和为17的两位数有89、98,数字之和为18的有99,则一共有6个这样的两位数.作业2答案：12.简答：个位为1的四位数有6个，个位为3的四位数有6个，则一共有12个.13.作业3答案：20.简答：三角形两边之和大于第三边，有(1, 8, 8) (2, 7, 8) (2, 8, 8) (3, 6, 8) (3, 7, 8) (3, 8, 8) (4, 5,8) (4, 6, 8) (4, 7, 8) (4, 8, 8) (5, 5, 8) (5, 6, 8) (5, 7, 8) (5, 8, 8) (6, 6, 8) (6, 7, 8) (6, 8,8) (7, 7, 8) (7, 8, 8) (8, 8, 8)二十种.14.作业4答案：12.简答：按数字组合来分类.用1、2、2可以拼出3个.用1、2、3可以拼出6个，用2、2、3可以拼出3个，共12个.15.作业5答案：26.简答：9也可以当成6用.一位数有4个，两位数有10个，三位数有12个，共26个.。

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -在学习基础的鸡兔同笼时，我们已经对假设法有了基本的了解．首先复习下“假设法”四步曲：第一步：假设：换句话说就是猜一个较为合理的答案．第二步：比较：比较假设和实际情况的差别，找出不同点，为调整找到方向．第三步：调整：逐步使得猜测的答案符合题目的已知条件．第四步：验算：看是否与题设条件相一致．“假设法”是一种循序渐进去解决问题的方法．就像饭要一口一口吃，路要一步一步走，假设法先去满足一部分条件，然后再通过恰当的调整去逐步满足所有的条件．这一讲我们继续学习鸡兔同笼问题，使大家对假设法有更深入的理解．接下来，我们看一道比较简单的鸡兔同笼问题．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题1 第十八讲 假设法进阶体育课上，三年一班的46名同学都在操场上玩球．每个篮球有6名同学玩，每个排球有8名同学玩，篮球和排球共有7个．问：玩排球的同学有多少人？分析：7个球里既有排球又有篮球，如果将这7个球都看成篮球，人数会有什么变化？练习1公园里的23条长凳上坐了50个人，每条长凳上可以坐2个大人或者3个小孩，那么这50个人中，有多少个小孩？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 有时题目中不会直接告诉“头和”，需要通过寻找不变量来求得“头和”．这也是解决鸡兔同笼很重要的方法之一．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题2集体劳动时，女生抬土，每2名女生用1根扁担抬1个筐；男生挑土，每1名男生用1根扁担挑2个筐．结果共用了27根扁担和44个筐，请问：女生和男生各有多少人？分析：扁担和筐之间有什么关系？一根扁担上可能挂着几个筐？练习2幼儿园里小朋友和老师共40人在一起喝汤，每个老师单独用1个碗喝，而2个小朋友合用1个碗喝，最后共用了27个碗，请问：有多少小朋友？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 有时题目中会隐藏着不变量，抓住不变量解决鸡兔问题也是很重要的方法之一．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题3天上一群九头鸟和地上一群九尾狐商量去吃唐僧，九头鸟有九头一尾，九尾狐有九尾一头．孙悟空将它们抓起来关进了笼子，猪八戒在笼子外得意地数出了134个头和166条尾巴．请同学们算一算：共有多少只九头鸟，多少只九尾狐？分析：不管是九头鸟还是九尾狐都有多少个头和尾巴？能不能把一共有多少只动物求出来？练习3男生手里拿2个红气球，5个蓝气球，女生手里拿3个红气球，4个蓝气球，一共有100个红气球和166个蓝气球，请问：男生多少人？女生多少人？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 前面3道例题比起上学期学的鸡兔同笼问题稍复杂些，涉及到的数量关系比较多，或是条件比较复杂，大家千万不要被题目“怪异”的外表吓到！只要对已知条件做适当的转化，把题目变为一个基本的鸡兔同笼问题，就可以轻松解决了．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题4某宿舍楼的大、小寝室一共有20间，已知大寝室每间住了6人，小寝室每间住了4人，并且大寝室的总人数比小寝室的总人数多30人．请问：大、小寝室各有多少间？分析：假设法是解决鸡兔同笼问题的重要方法，假设每个寝室都是大寝室的话，大寝室会比小寝室多住多少人？练习4春游时候同学们去划船，一共有船20条，每条大船可以坐12人，每条小船可以坐8人，结果大船上坐的人要比小船上的人多80个，那么一共有多少条大船？例题5新华书店一天内卖出了《哈利波特》和《魔戒》共40本，其中《哈利波特》每本30元，《魔戒》每本25元．经过统计，卖《哈利波特》的收入比《魔戒》多650元，这天卖出多少本《哈利波特》？分析：与例题4类似，本题应该怎么假设呢？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题4和例题5与前三道例题有很大不同，虽然也是用假设法来解决，但调整的时候每次变化的量与原先的鸡兔同笼问题有很大不同：原先把一只鸡换成一只兔子的时候，我们考虑的是鸡与兔的腿数和，于是变化了2；但现在考虑的是鸡与兔的腿数差，鸡腿数少了2，兔腿数反而增加了4，差距变化了6．请大家细心体会两者的差别．关于“腿数差”的鸡兔同笼问题：注意调整时“腿数差”的改变与之前“腿数和”的改变是不同的．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题6男生手里拿2个红气球，13个蓝气球，女生手里拿1个红气球，12个蓝气球，一共有62个红气球，且蓝气球的范围在495-510之间，请问男生多少人？女生多少人？分析：每人拿着的红气球和蓝气球之间有怎样不变的数量关系？课堂内外九头鸟的来历九头鸟的最基本特征就是有九个头．但是关于这九个头，也有多种不同的说法．有些人说它本来有十个头．如唐段成式《酉阳杂俎》卷十六《羽》：鬼车鸟，相传此鸟昔有十首，……一首为犬所噬．宋周密《齐东野语》卷十九：鬼车，俗称九头鸟，……世传此鸟昔有十首，为犬噬其一，至今血滴人家为灾咎．……身圆如箕，十脰环簇，其九有头，其一独无而鲜血点滴，如世所传．明杨慎《杨升庵全集》卷八一《鬼车》条：《小说》：周公居东周，恶闻此鸟，命庭氏射之，血其一首，馀九首．又有些人说它原本只有九个头，其中一个头受伤滴血永不愈合．如前引《三国典略》：齐后园有九头鸟见，……九头皆鸣．又唐刘恂《岭表录异》卷中云：鬼车，……或云九首，曾为犬啮其一，常滴血．以上传说中，以《齐东野语》所记的那个“十脰（脖子）九头”的模样最为吓人，试想九个鸟头之外，还有一个鸟脖子在那里流滴鲜血，那多么可怕？原名“鬼车”，长有十个脖子、九个头，据说它的第十个头是被周公旦命令猎师射掉的．那个没有头的脖子不断地滴出血，古人宣称如果九头鸟飞过，要吹灭灯火、放狗把它赶走．有些传说宣称九头鸟的每一个头拥有一对翅膀，结果18只翅膀互相挤兑、导致全都派不上用场．历史上，周、楚的确是死对头．周昭王率军亲征，竟死于汉水之中，成为异乡之鬼．周人对楚人之恨可想而知．我们知道：一个民族的神，在它的敌对民族那里必然会被说成妖．象埃及大神沙特（sat），在希伯来人《圣经》中就变成了撒旦（satan）．我国东夷部族之神蚩尤，在华夏族那里便成了能飞沙走石的妖怪，周人将楚人的九凤图腾说成妖怪，并编出天狗断其一首的故事，也符合这条比较神话学的基本规律，至于是周公本人确有此事，还是民间传说附会于周公身上，那倒是无关紧要的．作业1.大卡车一次能运7吨土，小卡车一次能运4吨土．现在有大、小卡车8辆，一次恰好能运土38吨．那么大卡车有多少辆？2.和尚们在庙里吃饭，3个小和尚公用1个大碗吃1碗米饭，1个大和尚独用1个大碗吃2碗米饭，结果一共用了32个碗，吃了54碗米饭，那么庙里有多少个小和尚？3.中国学生一顿饭能吃3个汉堡和2杯可乐，外国学生一顿饭能吃4个汉堡和1杯可乐，共吃了64个汉堡和26杯可乐，请问有多少个中国学生？4.鸡兔同笼共20只，兔子的腿数要比鸡的腿数多44条，请问一共有多少只鸡？5.男巫和女巫比赛魔法，男巫可以用1个魔法之尘变出3朵花，女巫可以用1个魔法之尘变出4朵花，最后他们一共用掉了14个魔法之尘，男巫变出的花比女巫变出的花多14朵，请问男巫用了多少个魔法之尘？第十八讲 假设法进阶1. 例题1答案：16人详解：假设7个球都是篮球，那么应该有同学：6742⨯=个，现在有46名同学，多了4个，每个排球比每个篮球玩的同学多862-=人，所以有排球：422÷=个，玩排球的的同学有：8216⨯=人． 2. 例题2答案：女生有20人；男生有17人详解：当女生用扁担时，1根扁担挑1筐，当男生用扁担时，1根扁担挑2筐，如果27根扁担都是女生用，那么只能挑27个筐，所以现在有()()44272117-÷-=根扁担男生在用，而剩下的10根扁担女生在用，所以共有男生17人，女生20人．3. 例题3答案：九头鸟有13只；九尾狐有17只详解：九头鸟和九尾狐的头脚加在一起全是10个，那么共有头尾134166300+=个，则共有3001030÷=只动物，假设30只动物全是九头的，则有309270⨯=个头，比较：270134136-=个头，将一个九头的变为一个单头的会少8个头，调整：()1369117÷-=次，每次调整出现1个单头的，那么有17只九尾狐，有301713-=只九头鸟．4. 例题4答案：大寝室有11间；小寝室有9间详解：如果20间都是大寝室，那么大寝室共住了206120⨯=人，小寝室住了0人，大寝室比小寝室多了120人，如果1间大寝室换成小寝室，那么大寝室住的人少了6人，小寝室住的人多了4人，人数差变小了6410+=人，所以会有：()12030109-÷=间小寝室，大寝室11间．5. 例题5答案：30本详解：如果卖的都是《哈利波特》，那么卖《哈》的收入比卖《魔》的收入多40301200⨯=元，每少卖1本《哈》、多卖1本《魔》，收入差会减少55元，所以卖了《魔》()12006505510-÷=本，卖了《哈》30本．6. 例题6答案：男生有32人；女生有18人详解：不管男生还是女生，每个人手中的蓝气球比红气球多11个，那么总的蓝气球比红气球多的必须是11的倍数，即62-W是11的倍数，且□的范围在495-510之间，则□=502才行，这样50262440-=才是11的倍数，那么总人数为4401140÷=人；假设这40人全是男生，那么会有红气球40280⨯=个，比较：806218-=个，将一个男生变为一个女生会少拿1个红气球，则有18118÷=个女生，那么男生有32人．7. 练习1答案：12个简答：假设23条长凳做的全是大人，则有23246⨯=个人，比较：50464-=人，将一条大人凳变为一条小孩凳会多1人，调整：()4324÷-=次，每次调整出现1条小孩凳，那么有4条小孩凳，有4312⨯=个小孩．8. 练习2简答：如果所有碗都是老师用的，那么会有27个人，则()()40272113-÷-=个小朋友碗，则小朋友有26人，大人有14人．9. 练习3答案：女生有24人；男生有14人简答：男生和女生手里的气球加在一起全是7个，且共有气球100166266+=个，则共有266738÷=人，假设38人全是男生，则有38276⨯=个红气球，比较：1007624-=个红气球，将一个男生的变为一个女生气球会多1个，调整：()243224÷-=次，每次调整出现1女生，那么有24个女生，有382414-=个男生．10. 练习4答案：12条简答：如果都是大船，那么大船比小船多坐240人，每把1条大船换成小船人数差会减少20，所以有小船：()24080208-÷=条，大船12条．11. 作业1答案：2辆简答：假设全是小卡车，可得大卡车有(3848)(74)2-⨯÷-=辆．12. 作业2答案：30个简答：每个大和尚吃的米饭比用的碗多一碗，共多了543222-=碗米饭，所以大和尚用了22个碗，小和尚用了322210-=个碗．可得小和尚有10330⨯=个．13. 作业3答案：8人简答：人一顿饭吃5样东西，共吃了266490+=样东西，说明共有90518÷=人，假设全是外国学生，则中国学生有()()18464438⨯-÷-=人．14. 作业4答案：6只简答：假设全是兔子，兔子腿比鸡腿多420080⨯-=条．每把一只兔子换成鸡，腿数之差减少426+=条，所以鸡有(8044)66-÷=只．15. 作业5答案：10个简答：假设魔法之尘全是男巫用的，那么男巫比女巫多变出143042⨯-=朵花，每个魔法之尘改由女巫使用，男巫与女巫变出花的数量差将减少347+=朵，所以女巫用的魔法之尘为(4214)74-÷=个，则男巫的为10个．。

（三年级奥数）枚举法教师姓名学科数学上课时间年月日---学生姓名年级三年级课题名称枚举法教学目标1、做到不重补漏，把复杂的问题简单化；2、按照一定的规律，特点去枚举；3、从思想上认识到枚举的重要性。

教学重点枚举法教学过程枚举法【课题引入】枚举法是一种常见的分析问题、解决问题的方法。

一般地，根据问题要求，一一枚举问题的解答，或者为了解决问题的方便，把问题分为不重复、不遗漏的有限种情况，一一枚举各种情况，并加以解决，最终达到解决整个问题的目的。

这种分析问题、解决问题的方法，称之为枚举法。

枚举法是一种常见的数学方法，当然枚举法也存在一些问题，那就是容易遗漏掉一些情况，所以应用枚举法的时候选择什么样的标准尤其重要。

运用枚举法解题的关键是要正确分类，要注意一下两点：一是分类要全，不能造成遗漏；二是枚举要清，要将每一个符合条件的对象都列举出来。

【例题学习】例1：用数字1、3、4可以组成多少个不同的三位数？【即时练习】1、用0、3、5可以组成多少个不同的三位数?2、用4、7、8这三个数字，可以组成多少个没有重复数字的三位数，它们有哪些？其中最大的数和最小的数各是多少？【例题学习】例2、用0，2，5，9可以组成多少个是5的倍数的三位数？【即时练习】1、从1、2、3、4、5、6这些数中，任取两个数，使其和不能被3整除，则有_______种取法。

2、从l～9这9个数码中取出3个，使它们的和是3的倍数，则不同取法有_______种。

3、小明的两个口袋中各有6张卡片，每张卡片上分别写着1，2，3，……，6。

从这两个口袋中各拿出一张卡片来计算上面所写两数的乘积，那么，其中能被6整除的不同乘积有_____个。

3、从1～8中每次取两个不同的数相加，和大于10的共有多少种取法？【例题学习】例5：甲、乙、丙三个工厂共订300份报纸，每个工厂至少订了99份，至多101份，问：一共有多少种不同的订法？【即时练习】1、四个学生每人做了一张贺年片，放在桌子上，然后每人去拿一张，但不能拿自己做的一张．问：一共有多少种不同的方法？2、一次，齐王与大将田忌赛马．每人有四匹马，分为四等．田忌知道齐王这次比赛马的出场顺序依次为一等，二等，三等，四等，而且还知道这八匹马跑的最快的是齐王的一等马，接着依次为自己的一等，齐王的二等，自己的二等，齐王的三等，自己的三等，齐王的四等，自己的四等．田忌有________种方法安排自己的马的出场顺序，保证自己至少能赢两场比赛．【例题学习】例6：用100元钱购买2元、4元或8元饭票若干张，没有剩钱，共有多少不同的买法?【即时练习】1、一个文具店橡皮每块5角、圆珠笔每支1元、钢笔每支2元5角．小明要在该店花5元5角购买两种文具，他有多少种不同的选择．2、用1元、5元、10元、50元、100元人民币各一张，20元人民币两张，在不找钱的情况下，最多可以支付种不同的款额。

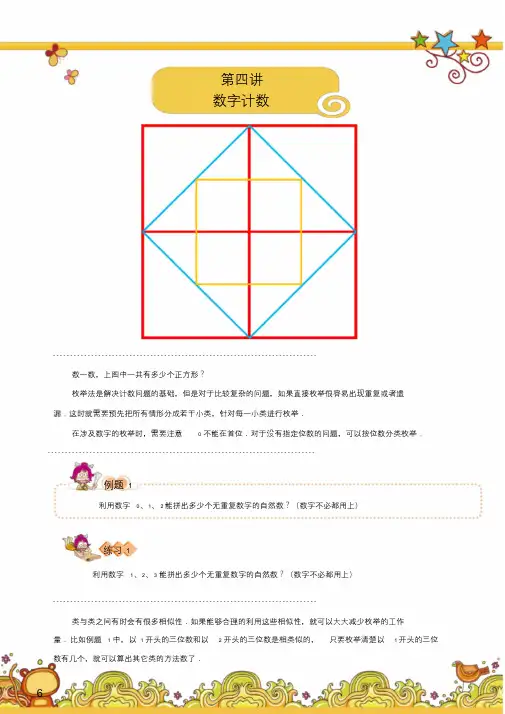
第四讲数字计数- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -数一数，上图中一共有多少个正方形？枚举法是解决计数问题的基础，但是对于比较复杂的问题，如果直接枚举很容易出现重复或者遗漏．这时就需要预先把所有情形分成若干小类，针对每一小类进行枚举．在涉及数字的枚举时，需要注意0 不能在首位．对于没有指定位数的问题，可以按位数分类枚举．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题1利用数字0、1、2 能拼出多少个无重复数字的自然数？（数字不必都用上）练习1利用数字1、2、3 能拼出多少个无重复数字的自然数？（数字不必都用上）- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -类与类之间有时会有很多相似性．如果能够合理的利用这些相似性，就可以大大减少枚举的工作量．比如例题 1 中，以1 开头的三位数和以 2 开头的三位数是相类似的，只要枚举清楚以 1 开头的三位数有几个，就可以算出其它类的方法数了．6- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题2在所有的三位数中，各位数字之和不超过 4 的共有多少个？练习2在所有的两位数中，各位数字大于16 的共有多少个？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -在分类时，一定注意类与类之间有没有重复的部分，或者有没有漏掉的情况．只有在分类已经做到“不重不漏”的前提下，才能够进行下一步的枚举．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3用两个1，一个2，一个3，可以组成多少个不同的四位数？练习3用三个2，一个4，一个5，可以组成多少个不同的五位奇数？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -如果题目中的数字是印在木板上的，如1、3、5：1 3 5由于这是块木板，可以随意旋转，例如0、1、6、8、9 这5 个，而其他 5 个数字旋转之后什么都不是，没有意义，所以结果不变．如果把写着 6 的那块木板倒过来的话就会变成9，所以会多出来很多数，比如9、95、954 等等，想一下．还有哪些数字可以倒过来看呢？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -7例题4老师拿来 3 块木板，上面分别写着数字0、3、6．你可以用这些木板拼出多少个不同的自然数？（木板可以颠倒，且数字不必都用上）练习4老师拿来 3 块木板，上面分别写着数字4、5、6．你可以用这些木板拼出多少个不同的三位数？（木板可以颠倒）例题5如下图，四张卡片上写有数字2，4，7，8．从中任取三张卡片，排成一行，就可以组成一个三位数．请问：一共可以组成多少个不同的三位数？其中有多少个不同的三位偶数？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -分类方式非常多样，有时可以像例 1 一样按位数分类，有时可以像例 2 一样按各个数位数字和分类，有时可以像例 3 一样按相同数字的位置分类，有时可以像例 4 一样，按用不同数字分类．无论是哪种分类方式，首先需要将有几类写清楚，然后再枚举出每类的情况数，最后再将每类的方法数相加，即分类相加．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题6在所有的四位数中，各位数字之和超过32 的共有多少个？8课堂内外成语分类一、数字成语一唱一和两败俱伤三长两短三顾茅庐三令五申四海为家五体投地六根清净七零八落半斤八两九霄云外十拿九稳百无禁忌千变万化瞬息万变二、动物名称成语【鼠】鼠目寸光鼠肚鸡肠鼠窃狗盗投鼠忌器抱头鼠窜獐头鼠目【牛】牛鬼蛇神牛刀小试牛鼎烹鸡汗牛充栋对牛弹琴九牛一毛【虎】虎视眈眈虎口余生虎头虎脑虎背熊腰虎头蛇尾虎落平阳【兔】兔死狐悲兔死狗烹狡兔三窟鸟飞兔走守株待兔【龙】龙腾虎跃龙飞凤舞龙马精神龙凤呈祥画龙点睛来龙去脉【蛇】蛇蝎心肠画蛇添足惊蛇入草龙蛇混杂杯弓蛇影牛鬼蛇神三、带植物成语开花结果斩草除根顺藤摸瓜披荆斩棘奇花异果投桃报李粗枝大叶春兰秋菊火树银花四、带人体成语面无人色心旷神怡耳熟能详心花怒放蒙头转向满面春风屈指可数满目疮痍铁面无私五、带方位成语旁若无人前车之鉴旁敲侧击人间地狱节外生枝福如东海马放南山居高临下蒙在鼓里六、带色彩成语黄金时代白雪皑皑乌烟瘴气皓首穷经青面獠牙苍髯如戟金光灿烂红颜薄命白发苍苍七、叠字成语亭亭玉立姗姗来迟栩栩如生欣欣向荣惺惺作态洋洋得意绵绵不绝静静乐道虎视眈眈八、带“不”字成语不由自主不谋而合不寒而栗不同凡响不甘示弱不知深浅不露声色不择手段不足为奇九、带“人”字成语人心涣散人生如梦人情冷暖人地生疏人面兽心人困马乏人才济济人浮于事人才辈出十、“想”的成语想了又想（朝思暮想）苦苦地想（苦思冥想）静静地想（静思默想）十一、“多”的成语观众多（座无虚席）贵宾多（高朋满座）人很多（摩肩接踵）十二、带有“看”的近义词的成语见多识广望而生畏察言观色一视同仁一览无余高瞻远瞩坐井观天举世瞩目管中窥豹十三、含有一对近义词的成语惊心动魄争奇斗艳生龙活虎添油加醋降龙伏虎争权夺利高楼大厦狂风暴雨满山遍野十四、含有两对近义词的成语深思熟虑真凭实据灵丹妙药凶神恶煞心满意足街头巷议翻山越岭精雕细刻生拉硬扯9作业1. 各位数字之和大于15 的两位数有多少个？2. 由1、2、3、4 各一个能组成多少个不同的四位奇数？3. 在三角形中，任意两条边之和都大于第三边．三条边的边长均为整数，且最长边的长度是8 厘米，那么这样的三角形共有多少种？4. 现有数字1、2、2、3 各一个能拼出多少个不同的三位数？5. 老师拿来 3 块木板，上面分别写着数字7、8、9．你可以用这些木板拼出多少个不同的自然数？（木板不必都用上，木板可以颠倒）10第四讲数字计数1. 例题1答案：11．详解：一位数：0、1、2；两位数：10、12、20、21；三位数：102、120、201、210，共有11 个．2. 例题2答案：20．详解：数字之和不超过4，意味着数字和有四种情形：1、2、3、4．我们就依此分类．数字和为1：100，1个．数字和为2：首位为1，101、110；首位为2，200；此类共 3 个．数字和为3：首位为1，102、111、120；首位为2，201、210；首位为3，300；此类共 6 个．数字和为4：首位为1，103、112、121、130；首位为2，202、211、220；首位为3，301、310；首位为4，400；此类共10 个．所以，共有20 个三位数．3. 例题3答案：19．详解：先放两个1，它们的位置一共有 6 种可能，然后放 2 和3，每种可能下2、3 的位置可以颠倒，则会有 2种，那么一共有12 个不同的四位数．4. 例题4答案：19．详解：6 的木板还能反过来当9 用．可以是一位数、两位数和三位数，一位数有0、3、6、9，共 4 个，两位数是30、36、39、60、63、90、93 共有7 个，三位数时：先考虑当 6 用的情况．首位不能为0．三位数有306、360、603、630，共4 个．当9 用也有 4 个．所以，共有4×2=8 个三位数．则总共有4+7+8=19 个不同的自然数．5. 例题5答案：24；18．详解：（1）从2、4、7、8 中先选 3 个数字，共有 4 种选法，每种选法下会有 6 个三位数，则一共有24 个不同的三位数．（2）如果是偶数，则个位可以是2、4、8，共有 3 类，每类的方法下会有 6 种可能，则会有18个不同的三位偶数．6. 例题6答案：49 个．详解：按各位数字和分类：数字和可能为33、34、35、36．这四类情形对应的四位数分别有：34 个、10 个、4 个、1 个．因此，共有49 个四位数．7. 练习1答案：15．简答：1 打头的有1，12，13，123，132 共5 个．2、3 打头的也有 5 个．一共15 个．8. 练习2答案：3．简答：数字之和是17，这样的两位数有89、98；数字之和是18，这样的两位数是99，共有 3 个．9. 练习3答案：4．简答：个位一定是5，则只需把三个 2 和一个 4 放在千位、百位、十位即可，一共有 4 种可能：分别为22245、22425、24225、42225．10. 练习4答案：12．简答：用数字4、5、6：有456、465、546、564、645、654，6 个；用数字4、5、9：有459、495、549、594、945、954，6 个；一共有12 个．11. 作业1答案：6．11简答：数字之和为16 的两位数有79、88、97，数字之和为17 的两位数有89、98，数字之和为18 的两位数有99，则一共有 6 个这样的两位数．12. 作业2答案：12．简答：个位为 1 的四位数有 6 个，个位为 3 的四位数有 6 个，则一共有12 个．13. 作业3答案：20．简答：三角形两边之和大于第三边，有（1，8，8）（2，7，8）（2，8，8）（3，6，8）（3，7，8）（3，8，8）（4，5，8）（4，6，8）（4，7，8）（4，8，8）（5，5，8）（5，6，8）（5，7，8）（5，8，8）（6，6，8）（6，7，8）（6，8，8）（7，7，8）（7，8，8）（8，8，8）二十种．14. 作业4答案：12．简答：按数字组合来分类．用1、2、2 可以拼出 3 个．用1、2、3 可以拼出 6 个，用2、2、3 可以拼出 3 个，共12 个．15. 作业5答案：26．简答：9 也可以当成 6 用．一位数有 4 个，两位数有10 个，三位数有12 个，共26 个．12。

J 第二讲 移多补少与等量代换 A i\ I } h 羊皮换稱咐 2帐羊皮换】头 我妲用1头赭换 你的5只鸡，启么样? 2 -Z 不行.我只想甫L 1 fcl " n ?只鸡换i 张羊罰别刁 我不更 •护 kJ J/ 中 做移多补少的题目，最好的办法就是借助于画线段图，画图能给人一种直观的感觉,ooooooooooo o oo(1)_______________________ 第一行比第二行多 .(2)_____________________ 第一行给第二行才能使第一行与第二行一样多.(3)_____________________ 第一行给第二行才能使第一行比第二行多2个.(4)_____________________ 第一行给第二行才能使第二行比第一行多2个.分析：动手试试，移动下，弄清开始时第一行比第二行多几个？练习1阿呆和阿瓜分糖果，开始时阿呆有14个，阿瓜有4个.后来阿呆给了阿瓜6个，这时谁的糖果多？多几个？例题2小高和墨莫分别有一些巧克力，小高比墨莫多10块.(1)小高给墨莫8个，这时谁的巧克力多？多几块？(2)小高给墨莫多少块才能使两人的巧克力一样多？(3)要让墨莫的巧克力比小高多4块，需要谁给谁巧克力？给几块？分析：可以画出增减示意图表示下给的过程？练习2一开始田鼠爸爸比田鼠妈妈多11块宝石，要让爸爸比妈妈多3块宝石，需要爸爸给妈妈多少块宝石？例题3开始时卡莉娅比萱萱多30张高思杀卡片.每次卡莉娅给萱萱3张.(1)给几次才能使两人的卡片一样多？(2)给几次才能使萱萱比卡莉娅多12张？分析：能不能先算清楚一共给多少张才能使两人的卡片一样多？或者萱萱比卡莉娅多12练习3刘老师有两盒糖果，红盒比蓝盒多 30粒糖，每次从红盒取5粒糖放到蓝盒，取几次后两 盒糖的粒数就同样多？之前例题中的移多补少基本上要借助于画图，画图是表示数量关系非常直观的方 法•除了画图之外，用简洁的语言来表示数量关系也十分重要•下面我们来看看等量代换 的相关题目，同学们要用简洁的语言来表示数量关系.等量代换的思想是解决应用题时的常用技巧之一，在使用等量代换时，一般从问题开 始分析.例题4体重大比拼：(1) 4只小狗=8只小猫，那么5只小狗等于多少只小猫的体重？(2) 2只小狗=4只小猫，1只小猫=2只鸭子，那么12只小狗等于多少只鸭 子的体重？(3) 3只小狗=4只小兔，5只小兔=7只小鸡，那么12只小狗加4只小兔等 于多少只小鸡的体重？分析：第(1)、(2)问中利用等量代换中的倍数关系，找清楚(3)问中能否将12只小狗加4只小兔变为全是小兔？例题51只兔子的重量加上1只猴子的重量等于8只鸡的重量，3只兔子的重量等于 9只鸡的重量，那么1只猴子的重量等于多少只鸡的重量？分析：1只兔子等于几只鸡的重量呢？再分析出猴子与鸡的重量关系？例题6已知所有大鸭子的重量均相同，所有小鸭子的重量均相同.3只大鸭子和2只小鸭子共重1只小狗等于几只小猫？第7头大象和10头长颈鹿重量相等，那么 40头长颈鹿和多少头大象重量相等? 练习①分析：能否将题目中的条件列出来？通过倍数关系将题目中都变为大鸭子或者小鸭子？求出大小鸭子各几千克？三藏西天去取经，一去十万八千程.每日常行七十五，问公几日得回程.这是明朝数学家程大位编写的趣题，收录在他的数学名著《算法统宗》里•诗中的三藏指的是唐朝高僧玄奘.因为他被人们认为是唐朝第一高僧，所以又被称为“唐僧”.他受唐太宗李世民派遣，到印度钻研佛教典籍，译出经、论七十五部，一千三百三十五卷，促进了中印文化的交流. 《西游记》里的唐僧便是以这位高僧为原型的.本题的意思是说：唐僧去西天取经，一共走了十万八千里.已知他每天走七十五里，问一共走了多少天？同学们，你们知道该怎么算吗？作业1. 阿呆有20个西瓜，阿瓜有48个西瓜，(1)阿瓜给阿呆多少个西瓜后，阿瓜和阿呆的西瓜数相等？(2)阿呆给阿瓜多少个西瓜后，阿瓜比阿呆多32个？2. 一开始阿呆比阿瓜多87个西瓜，要让阿呆比阿瓜多3个西瓜，需要阿呆给阿瓜多少个西瓜?3. 小高给萱萱28个苹果后,(1) 小高和萱萱一样多，问之前谁多？多几个?(2) 小高比萱萱多10个，问之前谁多？多几个?4.用3个鹅蛋可换9个鸡蛋，2个鸡蛋可换4个鸽子蛋，用5个鹅蛋能换多少个鸽子蛋?5师傅和两个徒弟一起组装零件，师傅组装3个与大徒弟组装2个所用的时间相同，而大徒弟组装个与小徒弟组装1个所用的时间相同•请问：小徒弟组装4个的时间三个人一共能装几个零件? o第二讲移多补少与等量代换1. 例题1答案：（1） 6 个；（2） 3 个；（3） 2 个；（4）4 个详解：（1）观察出来第一行比第二行多6个；（2）第一行比第二行多6个，给1差2,则给6 2 3个即可；（3）开始时第一行比第二行多6个，后来第一行比第二行多2个，则差4个，给1差2,则给4 2 2个即可；（4）开始时第一行比第二行多6个，后来第一行比第二行少2个，则差8个，给1差2,则给8 2 4个即可.2. 例题2答案：（1）墨莫，多6块；（2）5块；（3）小高给墨莫，7块详解：（1）墨莫多，多8 2 10 6块；（2） 5 块，10 2 5 块；（3）小高给墨莫，给10 4 2 7块.3. 例题3答案：（1）5次；（2）7次详解：（1 ）卡莉娅比萱萱多30张，卡莉娅给萱萱30 2 15张两人卡片才能一样多，而每次卡莉娅给萱萱3张，则需要15 3 5次；（2）卡莉娅比萱萱多30张，后来萱萱比卡莉娅多12张，则需要卡莉娅给萱萱30 12 2 21张，而每次卡莉娅给萱萱3张，则需要21 3 7次.4. 例题4答案：（1）10 只；（2）48 只；（3）28 只详解：（1）4狗=8猫，贝U 1狗=2猫，贝U 5狗=10猫；（2）2狗=4猫，贝U 12狗=24猫，因为1猫=2鸭，贝U 24猫=48鸭，贝U 12狗=48鸭；（3）因为3狗=4兔，贝U 12狗=16兔，那么变为20兔，5兔=7鸡，贝U 20兔=28鸡.5. 例题5答案：5只详解：1兔+1猴=8鸡，3兔=9鸡，则1兔=3鸡，那么3鸡+1猴=8鸡，所以1猴=5鸡.6. 例题6答案：20千克详解：①3大+2 小=32，②4大+3小=44，算式相减②-①得到：③1大+1小=12，现在①-③, 则2大+1小=20 .7. 练习1答案：阿瓜；多2个简答：开始阿呆比阿瓜多10个，后来阿呆给阿瓜6个，这时阿瓜比阿呆多，多6 2 10 2个.8. 练习2答案：4块简答：11 3 2 4块.9. 练习3答案：3次11简答124213小高多14 1528 2多56个；56 个.(2)1) 14 个；(2) 2 个3 2(2)现在阿瓜比阿呆多28个，要多32个，相当于多了4个，则必须阿呆给阿瓜：4 2 228头7象=10长，贝U 40长=28象个.作业2答案：42个简答：871鹅蛋=3鸡蛋，2鸡蛋换4鸽子蛋化简为1鸡蛋=2鸽子蛋，31鹅蛋=6鸽子蛋，则5鹅蛋=30鸽子蛋.则需要15 5 3次练习4答案：简答：作业1答案：(2)小高多，多66个28 2 10 66 个.1)阿瓜给阿呆：48 20 2 14作业3答案：(1)简答：(1) 作业4答案：30个简答：3鹅蛋=9鸡蛋，化简为鸡蛋=6鸽子蛋，代换掉鸡蛋，变为作业5答案：34个简答：小徒弟组装4个的时间，大徒弟能装12个，师傅能装18个•三人一共34个。

——一w咛厂第五讲< 植树问题这两讲我们将要学习一个新的问题一一间隔问题•植树问题是间隔问题中重要的一种, 像这样间隔数目和端点数目不同的情况我们在日常生活中会遇到很多，这一讲我们就主要来解决这类问题.对于植树问题而言，主要分为两类，第一类是直线上的植树问题，第二类是环线上的植树问题.下面先来讲讲直线上的植树问题.对于一条线段来说，两边的端点是特殊的地方，需要尤其注意.1(1)马路的一侧种树，且两端种树.若每隔5米种一棵树，马路长30问有几棵树？(2)马路的两侧种树，且两端种树.若每隔5米种一棵树，共有20棵树,• • • •问马路有多长？分析：审清楚题目，两端种树中的间隔数和棵树是什么关系呢？练习1道路的两侧插红旗，且两端.也要插上红旗•若每隔6米插一面，马路长24米，问有几面旗？例题2马路的一侧安路灯.• •(1)一端有路灯，另一端没有.若每隔4米安一盏灯，马路长40米，问有几盏灯？(2)两端都没有路灯.若每隔6米安一盏灯，共有12盏灯，问马路有多长？分析：审清楚题目，一端种树中的间隔数和棵树是什么关系呢？练习2马路的两侧种树，且两端不种.若每隔3米种一棵树，马路长30米，问有几棵树？种树，且每条马路的两端都种树.已知北路长40米，东路和西路分别长80米.每隔5米种一棵树，问共种几棵树？北路西路I 东路分析：试着一条路一条路的求出有几棵树？并且把树画一画?练习3在如图两条马路的一.侧安路灯，且每条马路的两.端都没有路灯.若每隔9米安一盏路灯, 一共安了20盏路灯.已知北路长81米，问西路长多少米？北路西路S环线上的植树问题除了一条直线上的间隔问题之外，环形的排列也会存在间隔，先来看一个示意图:例题4学校有一个圆形水池，(1)水池外的周长为40米.如果绕着水池每隔4米种一棵树，一共要种几棵树？(2)水池内的周长为30米.如果绕着水池内共有10个换水孔，且相邻两个换水孔的距离相等，问相邻的两个换水孔间的距离是多少米？分析：环形植树中，间隔数和棵树之间什么关系？练习4鸟巢外一周共有1000米，绕着鸟巢的一周有灯和树木，(1)如果每两盏灯之间的距离是5米，问鸟巢外一周有几盏灯？(2)如果鸟巢外共有250棵树，且相邻两棵树的距离相等，问相邻两棵树的距离是多少？例题510个男生沿着300米的跑道站成一圈，并且相邻两人之间的距离都相等.现在，每相邻两个男生之间又加入了两个女生，相邻两人之间的距离还是相等.请问：一共加入了多少个女生？加入女生后，相邻两人之间的距离又是多少米？分析：试着求出站好男生后有多少个间隔？每个间隔中加入2个女生后一共有多少人？例题6如下图所示，有一个长方形的“田”字道路，整个长方形的长为100米、宽为70米.现分析：试着求出每条线上种几棵数？交点处要额外注意， 加重了要去掉，少加了记得加上.“植树节”是一些国家以法律形式规定的以宣传森林效益， 并动员群众参加造林为活动内容的节日.按时间长短可分为植树日、植树周或植树月，总称植 树节.通过这种活动，激发人们爱林、造林的感情，提高人们对森林功用的认 识，促进国土绿化，达到爱林护林和扩大森林资源、改善生态环境的目的.是 为了动员全民植树而规定的节日.中国的植树节开始时是为纪念孙中山先生逝 世，1979年2月23 日,中国第五届全国人大常务委员会第六次会议决定， 以3月12日为中国的植树节，以鼓励全国各族人民植树造林，绿化祖国，改善环境， 造福子孙后代.）都要种上树，那么最少要种多少棵树?/中占丨占、作业一条长500米的路的两边都要种树，并且两头都要种，如果每隔5米种一棵树，请问一共要种多少棵树?2. 一条路的一边种树，并且两头都不种树，如果每隔12米种一棵树，(1) 共种了 6棵，请问马路长多少米？(2) 若马路长120米，则种了多少棵树？3. 有如图三条马路，长度都是 100米•现在要在马路的 一侧种树，且每条马路的 两端都种树•每隔54. 用蜡烛摆成一个周长 60厘米圆形的造型，(1) 若蜡烛每隔4厘米摆一个，一共需要多少根蜡烛？(2) 如果共有20根蜡烛，且相邻两个蜡烛间隔相同，问相邻的两根蜡烛间的距离是多少厘米？5. 同学12人围着长480米的操场玩游戏，每两名同学间距离相等•如果在每两名同学间插入3名老 师，使每两人间距离相等.请问：有多少名老师？每两人间距离是多少米？1.详解：(1)共有30 5 6个间隔，种7棵树.(2)每侧种10棵树，有10 1 9个间隔，马路长5 9 45米.2. 例题2答案：(1) 10盏；(2) 78米详解：(1)共有40 4 10个间隔，间隔和灯一样多，有10盏灯.(2)共有12 1 13个间隔，马路长13 6 78米.3. 例题3答案：41棵详解：北路有40 5 1 9棵树，东路和西路各有80 5 1 17棵树.交点处的树被重复计算了，要扣除，共9 17 17 2 41棵树.4. 例题4答案：(1) 10棵；(2) 3米详解：(1)有40 4 10个间隔，要种10棵树.(2)有10个间隔，每个间隔长30 10 3 米.5. 例题5答案：(1) 20个；(2) 10米详解：开始有10个间隔，加入了10 2 20个女生.后来总共30人，30个间隔，每个间隔长300 30 10 米.6. 例题6答案：99棵详解：每棵树的距离相等，间隔最长是5米，每条横线上种100 5 1 21棵，每条竖线上种70 5 1 15棵，扣除重复的9棵，共种21 3 15 3 9 99棵.7. 练习1答案：10面简答：共有24 6 4个间隔，每侧有5面旗，两侧共5 2 10面.8. 练习2答案：18棵简答：共有30 3 10个间隔，每侧有9棵树，两侧共9 2 18棵.9. 练习3答案：117米简答：北路有81 9 1 8盏灯，西路有20 8 12盏灯.马路两端没有灯，不会重复计算.西路长13 9 117米.10. 练习4答案：(1) 200盏；(2) 4米简答：(1)有1000 5 200个间隔，有200盏灯.(2)有250个间隔，每个间隔长1000 250 4 米.11. 作业1答案：202棵简答：把500米长的路分成每段5米，共要分成500 5 100段，单条线段端点数比段数多1, 所以共有100 1 101棵树.由于路的两边都种树，所以是202棵.简答：(1 )环形排列间隔数和端点数相同，所以每隔根；(2)共有20根蜡烛，则相邻蜡烛的距离为60 20 3厘米. 15.作业5答案：(1) 36名；(2) 10米简答：12名同学相当于将环形分为 12个间隔，每两名同学间插入 3名老师相当于每个间隔插入3名老师，所以共需插入老师 12 3 36名老师；插入老师后，环形上共有12 36 48人, 所以每两人之间的间隔是 480 48 10米.13. 14. 答案：(1) 84米；(2) 9棵简答：(1)因为两头不种，共种6棵树，所以共有7个间隔，每个间隔是12米，则长12 米；(2)共有120 12 10个间隔，两头不种，所以间隔比树多1，那么有10 1 9棵树. 作业3答案：60棵简答：三角形每条边种100 5 121棵，共种21 作业4答案：(1) 15根；(2) 3厘米 3 3 60棵•也可以看成环形问题来做.4厘米放一根蜡烛，共需蜡烛 60 4 15。

第2讲井井有序（字典排列法）D同学们，你们知道英文字典里的单词是怎么排列的么？翻开英汉字典，不难发现字典中单词排列的规律：整本字典按首字母从 a 到 z 排列，首字母相同的单词都在一起。

例如苹果apple，一个a、两个p、一个l、一个e。

先找首字母为a的单词，再找第2个字母为p的；然后是第 3 个字母为p的、第 4 个字母为l 的，第 5 个字母为e的，就找到了这个单词了。

那么为什么要按这种顺序排列呢？解决这个问题，就要谈到这讲我们要学的枚举法。

枚举法起源于原始的计数方法，即：数数。

枚举法的基本思想是：将问题所有可能的答案一一列举，然后根据条件判断此答案是否合适。

由于枚举法需要将所有可能的答案列举出来，因此，就不能毫无头绪的去尝试、瞎蒙瞎撞，否则很容易出现遗漏或重复。

所以枚举的八字箴言就是分类有序，不重不漏。

而 “字典排列法” 就是枚举最常用的方法之一，所谓 “字典排列法”，就是指：在枚举时，像字典里的单词顺序那样排列出所有答案。

同学们，你们能熟练地掌握字典排列法，并把它应用在生活中，帮助艾迪和薇儿解决他们在生活中所遇到的麻烦吗？1.逻辑梳理例1（两位数）数字组数例2（三位数）例3（自然数）简单应用例4（取数）例5、例6（生活应用）复杂应用例7、例8、例9（变型数）MISSION1掌握字典排列法的基本概念和使用方式，并用字典排列法对班上部分同学名字的拼音进行排序.请根据老师在黑板上写的名字为这些同学名字的拼音进行排序:①___________________________②___________________________③___________________________1完成下列各题：2完成下列各题3用数字4艾迪这道题的做法对么？如果不对，请你写一下正确的解法．5刘老师提着一个带密码锁的公文包赶火车，车票在包内但是他忘了密码，只记得密码是由都小于6艾迪与薇儿做游戏，在分别标有7艾迪去儿童餐厅买8在某地有四种不同面值的硬币，如图所示，假若你恰有这四种硬币各到了帮助刘老师的能力了，赶紧去帮助刘老师解决困扰吧！9“10博士给艾迪与薇儿上课，课上介绍了11加加与减减做游戏，两人轮流在一张白纸上写出一个数字，组成一个多位数的前12如果一个数的各位数字从左到右构成等差数串，我们就称这个数为13在组自然数的问题里，数字A、1B、a-1C、aD、a+1答案：D解析：每次将a设定为一个数后，b要从a+1开始尝试，一直到b>100停止，如果此时的a+b>100，那么将取法的数量加1。

第十三讲多个对象和差倍之前所学的都是两个量之间的和差倍问题，但有些问题往往不只有两个量，可能涉及到三个或者更多的量．在解决多个量之间的和差倍问题时，不要忘记解答此类问题的最基本方法——线段图法．例题1孙悟空、猪八戒、沙僧三人去天上比赛摘蟠桃，孙悟空摘的蟠桃数量是沙僧的2倍，猪八戒摘的是沙僧的3倍，他们一共摘了300个蟠桃．请问：他们三人各摘了多少个蟠桃？分析：如果把沙僧摘的蟠桃画成一段，那么孙悟空和猪八戒应该如何画线段图？练习1小高、墨莫和萱萱比赛跳绳．小高跳的个数是墨莫的4倍，萱萱跳的个数是墨莫的2倍，三人一共跳了280个．请问墨莫跳了多少个？6例题2孙悟空、猪八戒、沙僧三人在地面上比赛抓妖怪，猪八戒抓的妖怪个数是沙僧的3倍，孙悟空抓的是猪八戒的2倍，他们共抓了300个妖怪．请问：他们三人分别抓了多少个妖怪?分析：这三人抓的妖怪谁抓的最少？如果把这人画为一段的话，那么其他两人应该如何画线段图？三个火枪手共有子弹180发，其中小火枪手的子弹数目是中火枪手的2倍，中练习2火枪手的子弹数目是大火枪手的3倍．请问小火枪手比大火枪手多多少发子弹？例题3孙悟空、猪八戒、沙僧三人去海里比赛捕鱼，沙僧捕的数量比猪八戒的2倍多3条，猪八戒捕的是孙悟空的2倍，且三人一共捕了59条．请问：猪八戒捕了多少条鱼？分析：出现了“几倍多几”的情况，之前在和倍问题中是如何解决“几倍多几”的呢？小高、墨莫、卡莉娅一起去郊外钓鱼，已知小高钓的鱼比墨莫的3倍多1条，练习3墨莫钓的鱼是卡莉娅的3倍，一共钓了92条鱼，请问：小高钓了多少条鱼？例题4孙悟空、猪八戒、沙僧决定休息一会儿吃些包子，猪八戒吃的包子数是孙悟空的2倍，孙悟空吃的包子比沙僧的2倍多6个，他们一共吃了102个包子．请问：猪八戒吃了多少个包子？分析：出现了“几倍多几”的几倍的情况，那么线段图中的份数和数量应如何扩倍？71练习 4米老鼠、唐老鸭和小白兔三人比赛包饺子，10 分钟内他们一共包了 34 个饺子．米老鼠包的饺子个数是唐老鸭的 2 倍，唐老鸭比小白兔包的饺子多 6 个．请问：他们分别包了多少个饺子？例题 5孙悟空、猪八戒、沙僧三人决定进行最后一场“吹气球比赛”决胜负， 分钟 内吹破气球个数最多的人获胜．最后他们共吹破 110 个气球，其中孙悟空吹 破的气球比沙僧的 3 倍多 4 个，猪八戒吹破的气球比孙悟空的 2 倍少 2 个．请 问：最后获胜者吹破了多少个气球？分析：出现了“几倍多几”和“几倍少几”的情况，之前在和倍问题中是如何解决的呢？例题 6高思农场里一共养了 635 只鸡、鸭、鹅，鸡比鸭的 2 倍少 4 只，鸭比鹅的 2 倍多 3 只．请问农场里鸡、鸭、鹅分别有多少只？分析：出现了“几倍多几”和“几倍少几”的情况，之前在和倍问题中是如何解决的呢？8《《 《课堂内外西游记《西游记》是中国古典四大名著之一，作者吴承恩，又名《西游释厄传》 成书于 16 世纪明朝中叶，主要描写了唐僧、孙悟空、猪八戒、沙悟净师徒四人 去西天取经，历经九九八十一难的故事． 西游记》自问世以来在中国乃至世界 各地广为流传，被翻译成多种语言．书中孙悟空这个形象，以其鲜明的个性特 征，在中国文学史上立起了一座不朽的艺术丰碑． 西游记》不仅内容极其丰富， 故事情节完整严谨，而且人物塑造鲜活、丰满，想象多姿多彩，语言也朴实通 达．更为重要的是， 西游记》在思想境界和艺术境界上都达到了前所未有的高 度，可谓集大成者．《西游记》是中国古代第一部浪漫主义长篇神魔小说，也是一部群众创作 和吴承恩的创作相结合的作品．小说以整整七回的大闹天宫故事开始，把孙悟 空的形象提到全书首要的地位．第八至十二回写如来说法，观音访僧，魏征斩 龙，唐僧出世等故事，交待取经的缘起．从十三回到全书结束，讲述了孙悟空 被压于五行山下．五百年后，观音向孙悟空道出自救的方法：他须随唐三藏到 西方取经，作其徒弟，修成正果之日便得救．孙悟空遂紧随唐三藏上路，途中 屡遇妖魔鬼怪，二人与猪八戒、沙僧等合力对付，经过各种磨难，展开了一段 艰辛的取西经之旅．作品写于明朝中期，当时社会经济虽繁荣，但政治日渐败坏，百姓生活困 苦．作者对此不合理的现象，透过故事提出批评．共一百回，六十余万字．分 回标目，每一回目以整齐对偶展现．故事叙述唐三藏与徒弟孙悟空，猪八戒， 沙僧，白龙马，经过八十一次磨难，到西天取经的过程．内容分三大部分：第一部分（一到七回）介绍孙悟空的神通广大，大闹天 宫；第二部分（八到十二回）叙三藏取经的缘由；第三部分（十三到一百回） 是全书故事的主体，写悟空等降伏妖魔，最终到达西天取回真经．作业91.赤壁之战时，魏国军队的人数是蜀国军队的4倍，吴国军队的人数是蜀国军队的2倍，三个国家的军队一共有140万人．求魏国军队有多少万人？2.绿蝶数量是黄蝶的5倍，红蝶数量是黄蝶的2倍，绿蝶比红蝶多36只，问绿蝶有多少只？3.小高、墨莫和卡莉娅帮老师搬书，一共搬了352本，小高搬的书比墨莫的2倍多2本，而墨莫搬的书是卡莉娅的2倍，请问卡莉娅搬了多少本书？4.路边种着柳树、杨树和槐树，三种树一共有98棵．已知柳树比杨树的2倍多7棵，杨树比槐树的2倍多7棵，请问杨树有多少棵？5.三个物体平均重量是31千克，甲物体比乙、丙两个物体重量之和轻1千克，乙物体比丙物体重量的2倍还重2千克，三个物体各重多少千克？10第十三讲多个对象和差倍1.例题1答案：沙僧50个；孙悟空100个；猪八戒150个详解：首先还是根据倍数关系画出线段图：沙孙猪“1”“2”“3”300沙“1”：300÷(1+2+3)=50个孙：50⨯2=100个猪：50⨯3=150个2.例题2答案：沙僧30个；猪八戒90个；孙悟空180个详解：首先根据倍数关系画出线段图，此题的难点在于“3”的2倍该如何去画．沙“1”沙“1”：300÷(1+3+6)=30个猪孙“3”300“6”猪：30⨯3=90个孙：30⨯6=180个3.例题3答案：16条详解：首先根据倍数关系画出线段图：“1”孙猪沙“2”“4”59孙“1”：(59-3)÷(1+2+4)=8条猪：8⨯2=16条多34.例题4答案：60个详解：首先根据倍数关系画出线段图：“1”沙孙“2”102沙“1”：(102-6-12)÷(1+2+4)=12个多6猪：4⨯12+12=60个猪“4”多125.例题5答案：66个详解：首先根据倍数关系画出线段图：11沙“1”“3”孙110猪多4“6”多6沙“1”：(110-6-4)÷(1+3+6)=10个孙：3⨯10+4=34个猪：6⨯10+6=66个6.例题6答案：鹅90只；鸭183只；鸡362只详解：首先根据倍数关系画出线段图：“1”鹅鸭“2”鹅“1”：(635-3-2)÷(1+2+4)=90只635鸡多3“4”鸭：2⨯90+3=183只鸡：4⨯90+2=362只多27.练习1答案：40个简答：首先还是根据倍数关系画出线段图：“1”墨萱“3”“4”280墨“1”：280÷(1+2+4)=40个高8.练习2答案：90个简答：首先还是根据倍数关系画出线段图：“1”大“1”：180÷(1+3+6)=18个大中小“3”“6”180中：18⨯3=54个小：18⨯6=108个多：108-18=90个9.练习3答案：64条简答：首先还是根据倍数关系画出线段图：12卡“1”“3”92墨高“9”卡“1”：(92-1)÷(1+3+9)=7条高：9⨯7+1=64条10.练习4答案：兔4个；鸭10个；鼠20个简答：首先还是根据倍数关系画出线段图：多1兔鸭“1”“1”多6“2”34兔“1”：(34-6-12)÷(1+1+2)=4个鸭：4+6=10个鼠多12鼠：2⨯4+12=20个11.作业1答案：80万简答：蜀国军队140÷(1+2+4)=20万人，魏国军队20⨯4=80万．12.作业2答案：60只简答：黄蝶有36÷(5-2)=12只，绿蝶有12⨯5=60只．13.作业3答案：50本简答：卡莉娅有(352-2)÷(1+2+4)=50本．14.作业4答案：27棵简答：槐树有(98-7-21)÷(1+2+4)=10棵，杨树有10⨯2+7=27棵．15.作业5答案：甲46千克；乙32千克；丙15千克简答：甲、乙、丙共有31⨯3=93千克，则甲的重量为(93-1)÷2=46千克，乙、丙重量之和13(47-2)÷(2+1)=15千克，乙为32千克．为47千克，则丙14。

编者导语：奥数让学生不拘泥于书本，不依常规，积极提出自己的新见解、新发现，有自己的新思路、新设计，在思考和解决问题时，思路更畅通、方法更灵活、很有深度。

奥数对于发展学生的思维、培养学生的创新意识和实践能力是极为有效的。

查字典数学网为大家准备了小学三年级奥数题，希望小编整理的三年级奥数题及参考答案:枚举法问题，可以帮助到你们，助您快速通往高分之路!!【试题】现在1元、2元和5元的硬币各4枚，用其中的一些硬币支付23元钱，一共有多少种不同的支付方法?【答案解析】23=54+21+11， 23=54+13，23=53+24， 23=53+23+12， 23=53+22+14。

所以共有5不同的取法。

【小结】对于简单的计数问题，可以用枚举法，列出满足条件的所有情况。

但是对于种数比较多的计数问题常用到排列组合来解决，排列组合的知识我们将在四年级学习。

6 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 同学们看看漫画中的小蜗牛，它在第几天爬出井呢？ 其实蜗牛在最后一天的时候直接爬出了井口，并不会往下滑了，所以在考虑周期的时候要特别注意整个过程结束的时候是不是完整的周期． 当实际问题并不是一个完整的周期问题时，一定要先把周期之外的问题考虑好，再计算周期相关的问题． 比如一串数1、2、3、4、3、4、3、4……，在计算这个数列的相关问题时，一般要先排除掉前两个数的影响，即有头周期，要先“砍头”． 比如在蜗牛爬井问题中，爬出井口的那天不需要再下滑，所以要先去掉最后一天的影响，即有尾周期，要先“去尾”．注意最后的周期是否完整． - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题1

一只蜗牛在一口15米深的井底，如果它每个白天往上爬3米，但是在晚上又往下滑1米，请问：

第十六讲 复杂周期问题 7

这只蜗牛在第几天能爬出这口井？ 分析：经典的蜗牛爬井问题，想清楚每天会向上爬几米以及最后一次是怎么爬的？ 练习1

（1）工厂的仓库里有80吨货物，这些货物都由同一辆卡车负责运输．第一天卡车往仓库里运进50吨，第二天运出了60吨，第三天又运进50吨，第四天再运出60吨，…… 如此不停地循环下去．第几天的时候，仓库里的货物才会被运完？ （2）工厂的仓库里有80吨货物，同样是由一辆卡车负责货物的运输．第一天，卡车从仓库里运出60吨，第二天再运进50吨，第三天又运出60吨，第四天再运进50吨，…… 如此不停地循环下去．第几天的时候，仓库里的货物才会被运完？ 例题2 桌子上原本放着6块巧克力，第1天阿呆吃掉了2块，第2天妈妈又放了4块巧克力，第3天阿呆又吃掉2块，第4天妈妈又放上4块，…… 如此不停循环下去，请问第几天结束的时候桌子上有10块巧克力？（请写出所有的可能） 分析：这个题目的周期和例题1相似，每两天桌上多出2块巧克力，那么多少天以后桌上有10块巧克力？想想是否一定要两天两天的考虑？ 练习2

第十五讲多重周期问题- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -6在之前我们已经学过了两讲周期问题，实际生活中还存在一类更加复杂的周期规律．我们已经知道周期现象无处不在，那么自然的，这些周期现象就很可能组合起来，产生更复杂的规律．多重周期再怎么复杂也是由多个单一周期问题所组成的，这带给我们两种解决的思路．第一种思路，分别根据各自的周期计算结果，最后加以组合．如要计算某年的干支，可以先计算天干，再计算地支，最后合起来就行．下面我们来看一道由多个简单的单一周期问题组成的题目．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题1如图所示，表格中每行的文字都是循环出现的：第一行是“大灰狼”3个汉字不断重复，第二行是“坏人”2个汉字不断重复．那么，第200列从上到下依次是哪2个汉字？大灰狼大灰狼大灰狼…坏人坏人坏人坏人坏…分析：这两行各自的规律是什么？各自的周期又是什么？第200列的第一行是什么字？第二行呢？练习1如图所示，表格中每行的文字都是循环出现的：第一行是“小鸡炖蘑菇”5个汉字不断重复，第二行是“宫保鸡丁”4个汉字不断重复，第三行则是“回锅肉”3个汉字不断重复．那么第121列从上到下依次是哪3个汉字？小鸡炖蘑菇小鸡炖蘑…宫保鸡丁宫保鸡丁宫…回锅肉回锅肉回锅肉…例题2如图，用“疯、狂、原、始、人”5个字，在一张方格纸中自左上到右下的斜行里按顺序循环填入．求第92行92列交叉处填入的字是？7疯狂原始人…狂原始人…原始人…始人…分析：每行每列各自的规律是什么？各自的周期又是什么？第92行的第一个字是什么？92的周期规律又是什么？练习2如图，用“原、始、人”3个字，在一张方格纸中自左上到右下的斜行里按顺序循环填入．求第88行18列交叉处填入的字是？原始人…始人…人…- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -并归纳出公共周期内的具体情况，再进行计算．比如对于数列1、二、3、一、2、三、1、二、3、一、2、三，……，你会发现有两个周期规律，第一个是数字本身的数值，规律是1、2、3、1、2、3，……，周期为3，第二个是按数字汉字来分，规律是数字、汉字、数字、汉字，……，周期为2，于是你会发现从整体上看，公共周期是6．如何寻找公共周期呢？由于公共周期必须同时是两个规律甚至更多规律的周期，所以公共周期的长度必须是这些周期长度的公倍数，一般的，要找最小的那个，称之为最小公倍数．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题31201名士兵排成一横排，第一次从左到右1至3循环报数，第二次从左到右1至4循环报数．那么，两次都报1的士兵有多少名？分析：试着把每个士兵两次报的数都写出来，找找看有没有周期？练习32010名同学排成一队，先从排头向排尾1至2报数，再从排头向排尾1至5报数．两次分别报了1 89和4的同学有多少人？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -对于报数问题一般有两种，第一种是两次报数都是同向的，第二种是第一次报数是从左到右，第二次报数却是从右到左的，这时可以将反向的周期转化为同向的周期问题．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题4303名士兵排成一排，第一次从左到右1至3循环报数，第二次从右到左1至2循环报数．请问：有多少名士兵两次所报数相同？分析：试着把每个士兵两次报的数都写出来，找找看有没有周期？第二次是从右到左看能不能转化为从左到右？练习4100名士兵排成一排，第一次从左到右1至3循环报数，第二次从右到左1至4循环报数．请问：既报2又报3的士兵有多少名？例题5观察下图中图形的规律，（1）第200个图形应该是下面A ，B ，C ，D 四个图形中的哪一个？ （2）这200个图形中出现了多少个A 图形？分析：仔细观察，这些图形的形状有什么规律？这些图形的颜色又有什么规律？试着算出第200个图形分别是什么形状和颜色？例题6有六十多人站成一行，从左到右由1开始按1，2，3，4依次循环报数，然后从右到左由1开始按1，2，3依次循环报数，最后发现刚好有12个人既报了1又报了2．请问：这一行最少有多少人？最多有多少人？分析：试着把每个人两次报的数都写出来，找找看有没有周期？…AB CD课堂内外二十四节气中国人讲究二十四节气，即：立春、雨水、惊蛰、春分、清明、谷雨，立夏、小满、芒种、夏至、小暑、大暑，立秋、处暑、白露、秋分、寒露、霜降，立冬、小雪、大雪、冬至、小寒和大寒．远在春秋时期，中国古代先贤就定出仲春、仲夏、仲秋和仲冬等四个节气，以后不断地改进和完善，到秦汉年间，二十四节气已完全确立．农历二十四节气这一非物质文化遗产十分丰富，其中既包括相关的谚语、歌谣、传说等，又有传统生产工具、生活器具、工艺品、书画等艺术作品，还包括与节令关系密切的节日文化、生产仪式和民间风俗．二十四节气是中国古代农业文明的具体表现，具有很高的农业历史文化的研究价值．2011年6月入选第三批国家级非物质文化遗产名录．二十四节气反映了太阳的周年视运动，所以节气在现行的公历中日期基本固定，上半年在6日、21日，下半年在8日、23日，前后不差1～2天．但在农历中，节气的日期却不大好确定，再以立春为例，它最早可在上一年的农历12月15日，最晚可在正月15日．农历存在闰月，如按照正月初一至腊月除夕算作一年，则农历每一年的天数相差比很大（闰年13个月）．为了规范年的天数，农历纪年（天干地支）每年的第一天并不是正月初一，而是立春．即农历的一年是从当年的立春到次年立春的前一天．例如2008年是农历戊子年，戊子年的第一天不是公历2008年2月7日（农历正月初一），而是公历2008年2月4日．作业1.在下表中，第一行是“太阳系”3个汉字不断重复，第二行是“小行星系”4个汉字不断重复，那么第27列从上到下的两个字是什么？10112. 如图，用“高、思、学、校”4个字，在一张方格纸中自左上到右下的斜行里按顺序循环填入．求第21行40列交叉处填入的字是？3. 108名学生排成一横排，第一次从左到右1至2循环报数，第二次从左到右1至5循环报数．那么，第一次报1而第二次报5的学生有多少名？4. 在下面2行60列的方格表中，第一行从左至右依次填“A ”、“B ”、“A ”、“B ”…… 第二行从右至左依次填“1”、“2”、“3”、“1”、“2”、“3”……那么在方格表中，有多少列同时写有“A ”和“1”？5. 500名士兵排成一列横队，第一次从左到右1至5循环报数，第二次反过来从右到左1至3循环报数．那么，两次所报数的差（大减小）等于2的有多少名？ABAB…… … … … … … … … … … … ……321321高 思 学 校 … 思 学 校 … … 学 校 … … 校 … … … …太 阳 系 太 阳 系 太 阳 系 小 行 星 系 小 行 星 系 小12第十五讲 多重周期问题1. 例题1答案：灰人详解：直接求第200列是什么，可根据每行周期分别求出第200个字是什么．第1行：2003662÷=，第200个字是“灰”．第2行：2002100÷=，第200个字是“人”．所以第200列是“灰人”．2. 例题2答案：原详解：要找到第92行、92列的字是多少，首先可找一下每行、每列的规律，接下来要像电影院找座位一样先找到第92行的第1个字925182÷=，是“狂”．那这一行是“狂原始人疯狂原始人疯……”第92个字925182÷=，是“原”．既第92行第92列的数是“原”． 3. 例题3答案：101名详解：把士兵两次报数按从左到右的顺序写到有规律为止．第1行3个一周期，第2行4个一周期，公共周期为12，1201121001÷=，一个周期里只有1名两次均报1的士兵，余数里还有1名，共1001101+=名． 4. 例题4答案：102名详解：可以把士兵两次报数按从左到右的顺序写下来，找规律．将第2行从右到左报数转化为从左到右报数，30321511÷=，所以第2行从左到右第1个数是1，即1至2循环报数，第1行3个一周期，第2行2个一周期，这里需要按列来考虑周期，通过观察发现公共周期为6，3036503÷=，1个周期里有2名士兵两次所报数相同，注意余数里还有2名，共5022102⨯+=名． 5. 例题5答案：（1）A ；（2）81详解：（1），5个一周期．，是五角星．白，黑，黑，白，黑，黑，……，3个一周期．，2003662÷=⋅⋅⋅⋅⋅⋅ 200540÷= ...... 1 2 3 1 2 3 1 2 3 1 2 3 (1)21212121212…1 2 3 1 2 3 1 2 3 1 2 3 1 (1)234123412341…13是黑色．那么选A ．（2）可以把这串图形按照形状和颜色分别寻找周期，找规律．第1行5个一周期，第2行3个一周期，这里需要按列来考虑周期，通过观察发现公共周期为15，20015135÷=⋅⋅⋅⋅⋅⋅，1个周期里有6个A 图形，注意余数里还有3个，共136381⨯+=个A 图形． 6. 例题6答案：62；69详解：第一种情况如下表：人数除以3后不余，则第二次从右到左中第一个人报3；第二种情况如下表：人数除以3后余1，则第二次从右到左中第一个人报1；第三种情况如下表：人数除以3后余2，则第二次从右到左中第一个人报2．第三种情况中因为既报1又报2的靠前，所以是人数最少的情况，有5组多2人，则最少有512262⨯+=人．验证623202÷=⋅⋅⋅⋅⋅⋅，则的确第一个人报了2．第二种情况中因为既报1又报2的靠后，所以是人数最多的情况，有5组多10人，则最多有5121070⨯+=人．这是不成立的，题目中说到是六十多人！则最多的在第一种情况，是5组多6人，共有512666⨯+=人，当然还可以再多3人，69人，验证69323÷=，的确是第一个人报了3． 7. 练习1答案：小宫回简答：第1行：1215241÷=，第121个字是“小”．第2行：1214301÷=⋅⋅⋅⋅⋅⋅，第121个字是“宫”．第3行：1213401÷=，第121个字是“回”．所以第121列是“小宫回”． 8. 练习2答案：人简答：要找到第88行、18列的字是多少，首先可找一下每行、每列的规律，接下来要像电影院找座位一样先找到第88行的第1个字883291÷=，是“原”．那这一行是“原始人原始人……”第18个字1836÷=，是“人”．既第88行第18列的数是“人”．1 2 3 4 1 2 3 4 1 2 3 4 2132132132131 2 3 4 1 2 3 4 1 2 3 4 1321321321321 2 3 4 1 2 3 4 1 2 3 4 321321321321 四 五 五 四 五 四 五 五 四 五 四 五 … 白 黑 黑 白 黑 黑 白 黑 黑 白 黑 黑 …149. 练习3答案：201名简答：把同学两次报数按从左到右的顺序写到有规律为止．第1行2个一周期，第2行5个一周期，公共周期为10，201010201÷=，一个周期里只有1名两次分别报了1和4的同学，共201名． 10. 练习4答案：18名简答：可以把士兵两次报数按从左到右的顺序写下来，找规律．将第2行从右到左报数转化为从左到右报数，100425÷=，所以第2行从左到右第1个数是4，即4至1循环报数，第1行3个一周期，第2行4个一周期，这里需要按列来考虑周期，通过观察发现公共周期为12，1001284÷=，1个周期里有2名士兵既报2又报3，注意余数里还有2名，共82218⨯+=名．11. 作业1答案：系星简答：2739÷=，最后一个字是系，27463÷=，最后一个字是星，第27列从上到下是“系星”二字． 12. 作业2答案：校简答：第21行第1列的字是21451÷=⋅⋅⋅⋅⋅⋅，则第21行的第1个字是“高”，且第21行是按“高、思、学、校、高、思、学、校……”的顺序写的，40410÷=组，则第40个字为“校”． 13. 作业3答案：11名简答：每10名学生为一个周期，周期里第5个满足条件．10810108÷=⋅⋅⋅⋅⋅⋅，有10个完整周期还多8人．10个周期中有10个，多余8人中还有1个，共11个． 14. 作业4答案：10列简答：第一行从左至右依次填“A ”、“B ”、“A ”、“B ”，…… 因为60除以3余0，所以第二行从左至右依次填“3”、“2”、“1”、“3”、“2”、“1”…… 每6列为一个周期，每周期有一列同时写有“A ”和“1”，所以有10列同时写有“A ”和“1”． 15. 作业5答案：133名简答：第一行是1、2、3、4、5、1、2、3、4、5……，第二行是2、1、3、2、1、3……，发现是3515⨯=个一周期，50015335÷=⋅⋅⋅⋅⋅⋅，每组有4次所报数的差为2，那么有3341133⨯+=名．1 2 3 1 2 3 1 2 3 1 2 3 (4)32143214321…1 2 1 2 1 2 1 2 1 2 1 2 1 (1)234512345123…。

第三讲移多补少与等量代换做移多补少的题目，最好的办法就是借助于画线段图，画图能给人一种直观的感觉，6帮助我们理清数量关系．例题1（1）第一行比第二行多________个．（2）第一行给第二行________个才能使第一行与第二行一样多．（3）第一行给第二行________个才能使第一行比第二行多 2 个．（4）第一行给第二行________个才能使第二行比第一行多 2 个．分析：动手试试，移动下，弄清开始时第一行比第二行多几个？练习1阿呆和阿瓜分糖果，开始时阿呆有14 个，阿瓜有 4 个．后来阿呆给了阿瓜 6 个，这时谁的糖果多？多几个？例题2小高和墨莫分别有一些巧克力，小高比墨莫多10 块．（1）小高给墨莫8 个，这时谁的巧克力多？多几块？（2）小高给墨莫多少块才能使两人的巧克力一样多？（3）要让墨莫的巧克力比小高多 4 块，需要谁给谁巧克力？给几块？分析：可以画出增减示意图表示下给的过程？练习2一开始田鼠爸爸比田鼠妈妈多11块宝石，要让爸爸比妈妈多 3 块宝石，需要爸爸给妈妈多少块宝石？例题3开始时卡莉娅比萱萱多30 张高思杀卡片．每次卡莉娅给萱萱 3 张．（1）给几次才能使两人的卡片一样多？（2）给几次才能使萱萱比卡莉娅多12 张？分析：能不能先算清楚一共给多少张才能使两人的卡片一样多？或者萱萱比卡莉娅多12 张？7练习3刘老师有两盒糖果，红盒比蓝盒多30 粒糖，每次从红盒取 5 粒糖放到蓝盒，取几次后两盒糖的粒数就同样多？之前例题中的移多补少基本上要借助于画图，画图是表示数量关系非常直观的方法．除了画图之外，用简洁的语言来表示数量关系也十分重要．下面我们来看看等量代换的相关题目，同学们要用简洁的语言来表示数量关系．等量代换的思想是解决应用题时的常用技巧之一，在使用等量代换时，一般从问题开始分析．例题4体重大比拼：（1）4 只小狗=8 只小猫，那么 5 只小狗等于多少只小猫的体重？（2）2 只小狗=4 只小猫，1 只小猫=2 只鸭子，那么12 只小狗等于多少只鸭子的体重？（3）3 只小狗=4 只小兔，5 只小兔=7 只小鸡，那么12 只小狗加 4 只小兔等于多少只小鸡的体重？分析：第（1）、（2）问中利用等量代换中的倍数关系，找清楚 1 只小狗等于几只小猫？第（3）问中能否将12只小狗加 4 只小兔变为全是小兔？7 头大象和10 头长颈鹿重量相等，那么40头长颈鹿和多少头大象重量相等？练习4例题51 只兔子的重量加上 1 只猴子的重量等于8 只鸡的重量，3 只兔子的重量等于9 只鸡的重量，那么 1 只猴子的重量等于多少只鸡的重量？分析：1 只兔子等于几只鸡的重量呢？再分析出猴子与鸡的重量关系？例题6已知所有大鸭子的重量均相同，所有小鸭子的重量均相同． 3 只大鸭子和 2 只小鸭子共重32 千克，4 只大鸭子和 3 只小鸭子共重44 千克，请问 2 只大鸭子和 1 只小鸭子共重多少8千克？分析：能否将题目中的条件列出来？通过倍数关系将题目中都变为大鸭子或者小鸭子？求出大小鸭子各几千克？课堂内外三藏取经三藏西天去取经，一去十万八千程．每日常行七十五，问公几日得回程．这是明朝数学家程大位编写的趣题，收录在他的数学名著《算法统宗》里．诗中的三藏指的是唐朝高僧玄奘．因为他被人们认为是唐朝第一高僧，所以又被称为“唐僧”．他受唐太宗李世民派遣，到印度钻研佛教典籍，译出经、论七十五部，一千三百三十五卷，促进了中印文化的交流．《西游记》里的唐僧便是以这位高僧为原型的．本题的意思是说：唐僧去西天取经，一共走了十万八千里．已知他每天走七十五里，问一共走了多少天？同学们，你们知道该怎么算吗？作业1. 阿呆有20 个西瓜，阿瓜有48 个西瓜，（1）阿瓜给阿呆多少个西瓜后，阿瓜和阿呆的西瓜数相等？（2）阿呆给阿瓜多少个西瓜后，阿瓜比阿呆多32 个？2. 一开始阿呆比阿瓜多87 个西瓜，要让阿呆比阿瓜多 3 个西瓜，需要阿呆给阿瓜多少个西瓜？3. 小高给萱萱28 个苹果后，（1）小高和萱萱一样多，问之前谁多？多几个？（2）小高比萱萱多10 个，问之前谁多？多几个？4. 用3 个鹅蛋可换9 个鸡蛋，2 个鸡蛋可换 4 个鸽子蛋，用 5 个鹅蛋能换多少个鸽子蛋？5. 师傅和两个徒弟一起组装零件，师傅组装 3 个与大徒弟组装 2 个所用的时间相同，而大徒弟组装 39个与小徒弟组装 1 个所用的时间相同．请问：小徒弟组装 4 个的时间三个人一共能装几个零件？10第三讲移多补少与等量代换1. 例题1答案：（1）6 个；（2）3 个；（3）2 个；（4）4 个详解：（1）观察出来第一行比第二行多 6 个；（2）第一行比第二行多 6 个，给 1 差2，则给6 2 3个即可；（3）开始时第一行比第二行多 6 个，后来第一行比第二行多 2 个，则差 4 个，给 1 差2，则给 4 2 2个即可；（4）开始时第一行比第二行多 6 个，后来第一行比第二行少 2 个，则差8 个，给 1 差2，则给8 2 4个即可．2. 例题2答案：（1）墨莫，多 6 块；（2）5 块；（3）小高给墨莫，7 块详解：（1）墨莫多，多8 2 10 6块；（2）5 块，10 2 5 块；（3）小高给墨莫，给10 4 2 7 块．3. 例题3答案：（1）5 次；（2）7 次详解：（1）卡莉娅比萱萱多30 张，卡莉娅给萱萱30 2 15张两人卡片才能一样多，而每次卡莉娅给萱萱 3 张，则需要15 3 5次；（2）卡莉娅比萱萱多30 张，后来萱萱比卡莉娅多12 张，则需要卡莉娅给萱萱30 12 2 21张，而每次卡莉娅给萱萱 3 张，则需要21 3 7次．4. 例题4答案：（1）10 只；（2）48 只；（3）28 只详解：（1）4 狗=8 猫，则 1 狗=2 猫，则 5 狗=10 猫；（2）2 狗=4 猫，则12 狗=24 猫，因为 1 猫=2 鸭，则24 猫=48 鸭，则12 狗=48 鸭；（3）因为 3 狗=4 兔，则12 狗=16 兔，那么变为20 兔，5 兔=7 鸡，则20 兔=28 鸡．5. 例题5答案：5 只详解：1 兔+1 猴=8 鸡，3 兔=9 鸡，则 1 兔=3 鸡，那么 3 鸡+1 猴=8 鸡，所以 1 猴=5 鸡．6. 例题6答案：20 千克详解：① 3 大+2 小=32，②4 大+3 小=44，算式相减②-①得到：③ 1 大+1 小=12，现在①-③，则2 大+1 小=20．7. 练习1答案：阿瓜；多 2 个简答：开始阿呆比阿瓜多10 个，后来阿呆给阿瓜 6 个，这时阿瓜比阿呆多，多6 2 10 2个．8. 练习2答案：4 块简答：11 3 2 4 块．9. 练习3答案：3 次简答：红盒比蓝盒多30 粒，红盒给蓝盒30 2 15粒两者才一样多，而每次红盒给蓝盒 5 粒，11则需要15 5 3次．10. 练习4答案：28 头简答：7 象=10 长，则40 长=28 象．11. 作业1答案：（1）14 个；（2）2 个简答：（1）阿瓜给阿呆：48 20 2 14 ．（2）现在阿瓜比阿呆多28 个，要多32 个，相当于多了 4 个，则必须阿呆给阿瓜： 4 2 2 个．12. 作业2答案：42 个简答：87 3 2 42 ．13. 作业3答案：（1）小高多，多56 个；（2）小高多，多66 个简答：（1）28 2 56 个．（2）28 2 10 66 个．14. 作业4答案：30 个简答：3 鹅蛋=9 鸡蛋，化简为 1 鹅蛋=3 鸡蛋，2 鸡蛋换 4 鸽子蛋化简为 1 鸡蛋=2 鸽子蛋， 3鸡蛋=6 鸽子蛋，代换掉鸡蛋，变为 1 鹅蛋=6 鸽子蛋，则 5 鹅蛋=30 鸽子蛋．15. 作业5答案：34 个简答：小徒弟组装 4 个的时间，大徒弟能装12 个，师傅能装18 个．三人一共34 个．12。

第十九讲分组法进阶- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 通过上一讲的学习，同学们对于假设法有了更为深入的了解，这一讲我们就来深入学习解决鸡兔同笼问题的另一种重要方法——分组法．题目中的倍数关系往往是分组的依据，像例题1那样，条件说：“兔子数量是鸡的3．倍．”，于是就把3只兔子和1只鸡分为1组．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题1鸡兔同笼，兔子数量是鸡的3倍，且兔子腿数比鸡腿数多90条．求鸡和兔子各有几只？分析：兔子的数量是鸡的3倍，则一组中应为什么样子？注意一组中兔子腿比鸡腿多几条？6练习1鸡兔同笼，兔的数量是鸡的2倍，且兔腿数比鸡腿数多84条．求鸡和兔子各有几只？例题2独角兽数量比九角怪的3倍多5只，且九角怪比独角兽的角数多91个．求九角怪有几只？分析：一组中应为什么样子？注意将多余的5只独角兽对应的角减去，这时两种动物的角数差几个呢？练习2三脚猫数量比五脚蛇的3倍多2只，且三脚猫脚数比五脚蛇脚数多94只．求三脚猫有几只？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 前面几道例题都采用了分组的方法．要特别指出的是我们要从题目条件出发，选择适当的分组方式．如果知道的是两种动物的数量差，那么每组中就各有一个；如果知道两种动物的倍数关系，那么就按照倍数关系分组；如果两种动物的关系是几倍多几或者几倍少几，则可以通过“减多余”或“补不足”来凑成整倍数，然后求解．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3中秋节前夕，公司给员工发购物券．市场部每人得到2张月饼券和3张水果券，技术部每人得到2张月饼券和4张水果券．已知技术部得到的月饼券比市场部得到的多10张，且技术部得到的水果券比市场部得到的多64张，问：市场部和技术部各有多少人？分析：根据技术部得到的月饼券比市场部得到的多10张且市场部和技术部每人都有2张月饼券能否分析出两个部门之间的人数差？再根据这个人数差画出水果券的分组图？练习3儿童节前夕，老师给学生们发礼品．男生每人得到1支铅笔和3张电影券，女生每人得到1支铅笔和4张电影券．已知男生得到的铅笔数量与女生得到的铅笔数量一样，一共发了56张电影券，问：男生和女生各有多少人？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题3中涉及的关系比较多，一定要注意找出其中的不变量是什么？上节课在学习假设法进阶时提7到过有时的不变量是某个单一元素，有时是和不变，有时是差不变．本题的核心在于不管是市场部还是技术部每人所得的月饼券都是2张，这就是不变量，也是本题的突破口，从而可以弄清市场部和技术部人数上的差，从而得出“头差”，这就是解决隐藏“头差”的方法——寻找不变量，同时也是寻找隐藏“头和”的方法．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题4鸡兔同笼，鸡的腿数和兔的腿数一样多，而鸡比兔子多了15只，那么笼子里有多少只兔子？分析：几只鸡和1只兔子的腿数一样多？练习4鸡兔同笼，鸡的腿数和兔的腿数一样多，而鸡比兔子多了20只，那么一共有多少只鸡？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题4中没有明确给出倍数关系，但通过“腿数一样多”提示了2倍的关系．其实例题4也可以通过“鸡比兔子多了15只”来分组，因为这句话换个说法就是“鸡比兔子的1倍多15只”，因此也可以把1只鸡与1只兔子分为一组来解决．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题5高思地下停车库停了很多车，其中三轮车的轮子数是自行车轮子数的3倍，且三轮车比自行车多18辆，那么三轮车和自行车各有多少辆？（提示“三轮车有三个轮子，自行车有两个轮子”）分析：三轮车的轮子数是自行车轮子数的3倍，那么几辆三轮车几辆自行车在一组中？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 本堂的核心在于“头倍腿差”的题型以及“腿倍”的题型，其中“头倍腿和”与“头倍腿差”非常类似，都是要先“分组”，若是腿和则要找出每组所对应的“腿和”，若是腿差则要找出每组所对应的“腿差”．若遇到非整倍的题目，一定要注意“减多余，补不足”的原则．接下来是关于“腿倍”的题型，可以根据“腿倍”转化为“头倍”，再进行求解．其中会有一些稍难的题型，如涉及到不变量的题型，一定要注意寻找隐藏的不变量．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 8例题6鸡兔同笼，鸡和兔共有46条腿．如果将鸡与兔的数量互换，那么总腿数变为38条，请问原来鸡和兔各有几只？分析：如果开始和互换后总腿数相加代表什么？课堂内外自行车自行车，又称脚踏车或单车，通常是二轮的小型陆上车辆．人骑上车后，以脚踩踏板为动力，是绿色环保的交通工具．英文bicycle或bike的bi意指二，而cycle意指轮．在日本称为“自転（转）车”；在中国大陆、台湾、新加坡，通常称其为“自行车”或“脚踏车”；在港澳则通常称其为“单车”．有单人自行车，还有双人或多人自行车．自行车是传统产业，具有100多年的历史，由于环保以及交通的问题，自行车再度成为世界各国特别是发达国家居民喜爱的交通、健身工具．据《2013-2017年中国自行车制造行业产销需求与投资预测分析报告》数据显示，世界自行车行业的重心正从传统的代步型交通工具向运动型、山地型、休闲型转变，在美、欧、日等发达国家，自行车是一种较普遍的运动、健身、休闲和娱乐性产品．每年全世界自行车需求量巨大，日本CYCLEPRESS的数据统计显示，全世界自行车需求规模保持在1.05亿台的水平，自行车年交易额约为50亿美元．据前瞻网调查，由于产业特性和劳动力成本因素，近15年来全球自行车制造产业向以中国为主的有工业制造优势的国家和地区转移．到2013年，中国仍为世界最大的自行车生产基地，整车生产厂、零配件生产厂分别达到500多家、700多家，世界前五大厂商主要基地均在中国．而随着世界各国人民收入水平的提高，全球自行车需求量会进一步扩大，随着自行车进一步的结构升级，将给行业的参与者带来更大的利润空间，中国自行车行业的发展前景也将更加广阔．作业1.某班男生一顿可以吃10个包子，女生一顿可以吃7个包子．全班男生是女生的2倍，一顿一共可以吃297个包子，那么全班一共有多少名学生？2.鸡兔同笼，鸡是兔数量的5倍，且鸡腿比兔腿多96条，请问有多少只鸡？93.3个小孩坐一个红凳子，2个大人坐一个绿凳子，红凳子比绿凳子的2倍多14把，且小孩比大人多126人，请问有多少把红凳子？4.圣诞节前夕，圣诞老人发小礼品．男生每人得到3张玩具券和3张礼品券，女生每人得到3张玩具券和4张礼品券．已知男生得到的玩具券比女生得到的玩具券多15张，一共发了155张礼品券，问男生和女生各有多少人？5.兔的腿数是鸡的腿数的2倍，且鸡兔共有30只，请问有多少只鸡？1011第十九讲 分组法进阶1. 例题1答案：鸡有9只；兔有27只详解：把3只兔子1只鸡分成1组．现兔腿比鸡腿多90条，每组兔腿比鸡腿多43210⨯-=条，所以共有90109÷=组，那么有鸡919⨯=只，兔子9327⨯=只．2. 例题2答案：九角怪有16只；独角兽有53只详解：把3只独角兽1只九角怪分成1组．现在独角兽比九角怪的3倍多5只，所以如果去掉5只独角兽，那么正好能够分成若干组后独角兽和九角怪都没有多余．现九角怪比独角兽的角数多91个，去掉5只独角兽后九角怪比独角兽的角数多91+5=96个，每组九角怪比独角兽的角数多9136-⨯=个，所以共有96616÷=组，那么有九角怪16116⨯=只，独角兽163553⨯+=只． 3. 例题3答案：市场部有44人；技术部有49人详解：发现不管是技术部还是市场部每人都是2张月饼券，且技术部比市场部多10张，则技术部人多，且比市场部多1025÷=人，这时进行分组，相当于一个市场部和一个技术部为一组，会多出5个技术部的人，也就是多出5420⨯=张水果券，将这20张水果券去掉，就会变为技术部得到的水果券比市场部多642044-=张，每组技术部比市场部多1张水果券，则会有()443244÷-=组，则有44个市场部的人，49个技术部的人．4. 例题4答案：15只详解：鸡和兔子的腿数一样多，就按照腿数一样多分组，2只鸡和1只兔子的腿数一样多，所以每2只鸡和1只兔子分成一组，每组鸡比兔子多了：211-=只，所以共有15115÷=组，兔子15115⨯=只．5. 例题5答案：三轮车有36辆；自行车有18辆详解：三轮车是自行车轮子数的3倍，则说明一组中应该有2辆三轮车和1辆自行车，这样就可以保证一组的轮子数是三倍关系，且三轮车比自行车多18辆，变为一道差倍问题，则自行车：()182118÷-=辆，三轮车有36辆．6. 例题6答案：鸡有5只；兔有9只详解：把1只鸡和1只兔子分成一组，多出来的动物单方在一边．现在鸡、兔互换，在同一组内部鸡、兔互换没有任何变化，有变化的应该是多出来无法分组的动物．现在腿数变少了，应该是兔子变成了鸡，因此原来兔子比鸡多．1只兔子变成1只鸡会少2条腿，所以多出来()463824-÷=只兔子，即原来兔子比鸡多4只．由此进行进一步分析，马上就有原来鸡5只，兔子9只． 7. 练习1答案：鸡有14只；兔有28只简答：把2只兔子1只鸡分成1组．现兔腿比鸡腿多84条，每组兔腿比鸡腿多4226⨯-=条，所以共有84614÷=组，那么有鸡14114⨯=只，兔子14228⨯=只．8. 练习2答案：三脚猫有68只简答：把3只三脚猫1只五脚蛇分成1组．现在三脚猫比五脚蛇的3倍多2只，所以如果去掉2只三脚猫，那么正好能够分成若干组后三脚猫和五脚蛇都没有多余．现三脚猫比五脚蛇的脚数多12 94只，去掉2只三脚猫后三脚猫比五脚蛇的脚数多94688-=只，每组三脚猫比五脚蛇的脚数多33154⨯-⨯=只，所以共有88422÷=组，那么有五脚蛇22122⨯=只，三脚猫223268⨯+=只． 9.练习3 答案：男生有8人；女生有8人 简答：发现不管是男生还是女生每人都是1支铅笔，且男生得到的铅笔数量和女生的铅笔数量一样，则男生和女生人数相同，一共有56张电影券，则一男一女分为一组，一组中有347+=张电影券，则一共有5678÷=组，则男生有8人，女生有8人． 10.练习4 答案：40只 简答：鸡和兔子的腿数一样多，就按照腿数一样多分组，2只鸡和1只兔子的腿数一样多，所以每2只鸡和1只兔子分成一组，每组鸡比兔子多了：211-=只，所以共有20120÷=组，鸡20240⨯=只． 11.作业1 答案：33人 简答：2男1女为一组，有11组，学生共33人． 12.作业2 答案：80只 简答：5鸡1兔为一组，每组中鸡腿比兔腿多6条，共多96条，则共有16组，有80只鸡． 13.作业3 答案：56把 简答：去掉14把红凳子，则小孩会少31442⨯=人，则小孩比大人多1264284-=人，现在2红1绿为一组，那么相当于6小孩2大人为一组，则一组中小孩比大人多4人，这时共有84421÷=组，那么有21把绿凳子，有2121456⨯+=把红凳子． 14.作业4 答案：男生有25人；女生有20人 简答：对于男生和女生而言，发现都有3张玩具券，且男生的玩具券比女生的玩具券多15张，则男生比女生多1535÷=人，这时可以将一男一女放在一组，最后还多出5个男生，每组的礼品券共有347+=张，先将多出的5人刨掉，则会刨掉5315⨯=张礼品券，那么共有15515140-=张礼品券，则一共有140720÷=组，那么男生有20525+=人，女生有20人． 15. 作业5答案：15只简答：因为兔腿是鸡腿的2倍，则一组中1只兔子配上1只鸡，所以兔子和鸡的数量一样多，且鸡兔共有30只，则鸡有30215÷=只．。

第六讲复杂间隔问题看起来小高和卡莉娅每人都搬了三层楼，但仔细想一想是这样吗？其实小高从三层开始搬到6层的确是搬了3层楼，但卡莉娅要走的楼梯只有1到2一层和2到3一层，一共只有两层楼，所以小高会比卡莉娅累很多．其实我们在登楼的时候算的并不是具体的楼层，而是两层楼之间间隔的楼梯，我们可以把楼层看作是端点，把楼梯看作是点之间的线段，就可以画出这样的示意图：像这样间隔数目和端点数目不同的情况我们在日常生活中还会遇到很多，例如锯木头、排队、爬楼梯、铺砖等等，这一讲我们就主要来解决这类问题．例题1小马虎从1层开始爬楼梯，且速度保持不变．他爬到5层用了7分钟．又过了21分钟，他爬到几层？分析：从1层走到5层一共要走多少层？练习1小高从1层开始向上爬，且速度保持不变，他爬到3层用了3分钟．问小高从5层爬到11层要用几分钟？例题2萱萱和墨莫去王老师家玩，王老师住在15层．两人同时从一楼往上走，速度都保持不变，当萱萱走到第3层的时候，墨莫恰好到了第5层．那么当墨莫走到王老师家的时候，萱萱到了几层？分析：从1层走到3层一共要走多少层？到5层呢？阿呆和阿瓜比赛走楼梯，且各自速度保持不变，他们都从1层开始走，当阿呆走到4层的时候阿瓜刚走到3层，那么，当阿呆走到16层时候，阿瓜走到第几层？楼梯1 楼梯2 楼梯3 楼梯4 楼梯51楼2楼 3楼 4楼 5楼6楼间隔1 间隔2 间隔3 间隔4 间隔5端点 1端点 2 端点 3 端点 4 端点 5 端点 6练习2例题3王老师想自己做一套家具．他每锯断一次所花的时间相同．他先把4根木头每根锯成3段，共用了24分钟，如果要把另外8根木头每根锯成6段，共需要几分钟？分析：把一根木头锯成2段要锯几下？锯成3段要几下呢？锯成6段呢？吝啬鬼总喜欢把一条面包分成好多段吃，他把一条面包分成5段用了20秒，那练习3么若以同样的速度，他要把同一条面包分成4段要用多少秒？例题450个乌龟排成一列，乌龟“慢慢”是从前往后数第40个，而乌龟“吞吞”是从后往前数第32个，请问：这两只乌龟之间有多少个乌龟？分析：试着找到它俩的具体位置，再进行具体分析．练习4一群羊站成一排，喜羊羊是从前往后数第10只，也是从后往前数第10只，那么共有多少只羊？例题5班里一共有42名学生，做游戏站成一圈．从班长萱萱为起点开始数．（1）如果墨莫是顺时针数第26个，小高是顺时针数第17个，那么墨莫与小高间有多少名同学？（2）如果墨莫是顺时针数第13个，小高是逆时针数第27个，那么墨莫与小高间有多少名同学？例题6甲、乙、丙三人锯同样粗细的木棍，分别领取8米、10米、6米长的木棍，要求都按2米的规格锯开．劳动结束后，甲、乙、丙分别锯了24、25、27段，那么锯木头速度最快的比速度最慢的多锯多少次？分析：考虑8米、10米、6米长的木棍每根会锯成几段？再分析每人锯了几根？课堂内外作业1. 青蛙从9层跳到4层要跳25级台阶．如果各层楼之间的台阶数相同，那么青蛙从第3层跳到第7层一共需要上多少级台阶？2. 两只青蛙“蹦蹦”和“跳跳”正在比赛跳台阶上楼，当蹦蹦已经跳到3楼的时候，跳跳才刚到2楼，那么当蹦蹦跳到9楼的时候，跳跳能到几楼？3. 伐木场举行锯木头比赛，冠军把一根45米的木材锯成3米一段只要140秒，按这样的速度，他把同样一根木材锯成9段需要多少秒？4. 车站上共有30个人在排队等车，大李排在第15个，而小李排在倒数第23个，请问：大李和小李之间有多少人？5. 老师和同学们围成一圈做游戏，一共有40个人，从老师开始数，阿呆是顺时针数第33个人，阿瓜是逆时针数第11个人，请问：阿呆和阿瓜中间隔了几个人？语发音．战后国民党迁台，又传入多种中国各省食物，如馒头、烧饼、油条、包子、小笼包、馅饼等均属广义的面包．台湾自1990年代开始特有的早餐店文化逐渐风行，已经提供各式面包与吐司，类别十分独特，与一般西式三明治并不相同．第六讲 复杂间隔问题1. 例题1答案：17层详解：从1层到5层共上层，又过21分钟可以再上层，到达层． 2. 例题2答案：8层详解：萱萱爬2层的时间墨莫可以爬4层，墨莫的速度是萱萱的2倍，那么墨莫爬14层的时间萱萱爬了7层，到达第8层． 3. 例题3答案：120分钟详解：每根锯成3段需要2次，共需要8次，于是锯1次用时分钟．每根锯成6段需要锯5次，共需要40次，所以共需时间分钟． 4. 例题4答案：20个详解：倒数第32个是正数第19个，相隔了4019120--=个乌龟． 5. 例题5答案：（1）8名；（2）3名 详解：（1）相隔了261718--=名同学．（2）小高是顺时针数第4227217-+=名，他和墨莫隔着171313--=名同学． 6. 例题6答案：2次详解：甲每根锯成4段需要3次，24段共需要次．乙每根锯成5段需要4次，25段共需要次．丙每根锯成3段需要2次，27段共需要次．最快的比最慢的多2次． 7. 练习1答案：9分钟简答：从1层到3层用时3分钟共上层，从5层到11层需要爬层，需要分钟．8. 练习2答案：11层简答：阿呆爬3层的时间阿瓜可以爬2层，那么阿呆爬15层的时间阿瓜爬了10层，到达第11层． 9. 练习3答案：15秒6293÷=⨯ 1156-= 312-= 273182÷=⨯ 255204÷=⨯ 244183÷=⨯ 340120⨯= 2483÷= 51217+= 217124÷=⨯ 514-=简答：面包分成5段需要4次，于是分1次用时秒．分成4段需要3次，所以需秒．10. 练习4答案：19只简答：一共1010119+-=只羊． 11. 作业1答案：20级简答：青蛙从9层跳到4层共跳层，于是每次楼梯共有台阶级，从3层跳到7层共跳层，所以一共跳级台阶． 12. 作业2 答案：5楼简答：蹦蹦跳2层楼梯，跳跳只能跳1层楼梯，所以最后在()912115-÷⨯+=楼． 13. 作业3答案：80秒简答：锯成3米一段需要锯成15段，需要14次，于是锯1次用时间秒，锯成9段需要锯8次，所以共需时间秒．14. 作业4答案：6人简答：倒数第23个是正数第8个，相隔了15816--=人． 15. 作业5答案：1人简答：逆时针数第11人是顺时针数第31人，相隔了333111--=人． 81080⨯= 1401410÷= 4520⨯= 734-= 2555÷= 945-= 5315⨯= 2045÷=。