弹簧质量阻尼系统的建模与控制系统设计

《控制系统仿真与CAD》大作业二阶弹簧—阻尼系统的PID控制器设计及参数整定学校：上海海事大学学院：物流工程学院专业：电气工程及其自动化班级：电气173班学号：************姓名：李**老师：**时间：2020年6月13日1. 题目与要求考虑弹簧－阻尼系统如图1所示，其被控对象为二阶环节，传递函数()G s 如下，参数为M=1kg ，b=2N.s/m ，k=25N/m ，()1F s =。

设计要求：用.m 文件和simulink 模型完成。

图 1 弹簧--阻尼系统（1）控制器为P 控制器时，改变比例系数大小，分析其对系统性能的影响并绘制相应曲线。

（2）控制器为PI 控制器时，改变积分系数大小，分析其对系统性能的影响并绘制相应曲线。

(例如当Kp=50时，改变积分系数大小)（3）设计PID 控制器，选定合适的控制器参数，使闭环系统阶跃响应曲线的超调量σ%<20%，过渡过程时间Ts<2s, 并绘制相应曲线。

2. 分析：（1）根据受力分析可得系统合力与位移之间微分方程：F kx x b xM =++ （2）对上得微分方程进行拉普拉斯变换，转化后的系统开环传递函数：25211)()()(22++=++==s s k bs Ms s F s X s G（3）系统输入为力R(S)=F(S),系统输出C(S)为位移X(S),系统框图如下：图 2 闭环控制系统结构图3. 控制器为P 控制器时：控制器的传递函数p p K s G =)(，分别取p K 为1,10,20,30,40,50,60,70,80， （1）simulink 构建仿真模型如图3，文件名为：P_ctrl ；图 3 P控制器仿真模型（2）用m.文件编写仿真程序，用sim函数简单调用P_ctrl模型；cleara=[1 10 20 30 40 50 60 70 80];Mp=zeros(9,1);ess=zeros(9,1);B=' 11020304050607080';%图例显示字符串for i=1:9r=1;Kp=a(i);[t,x,y]=sim('P_ctrl');%调运仿真模型plot(t,y)hold onn=length(y);yss=y(n);Mp(i)=(max(y)-yss)/yss*100;%超调量ess(i)=1-yss;%稳态误差leg{i}=['Kp=',B(2*i-1),B(2*i)];endlegend(leg)xlabel('Time (sec)')ylabel('outputs')title('step-response')Mpess（3）不同Kp输出仿真波形图4:图 4 不同Kp阶跃响应曲线（4）仿真结果分析：随着Kp 值的增大，系统响应超调量加大，动作灵敏，系统的响应速度加快。

质量-弹簧系统的力控制考虑系统与环境接触，并假定环境具有刚度ke 。

m x k eff dist x k f e e =e distf m x k x f =++gg 1e e e distf mk f f f -=++gg 1e mk a -=e dist f f b =+力平衡方程f d e e f f =-f f a b¢=+e f f ¢=gg f d vf pf f f f k e k e ¢=++gg g 跟随控制律0f f vf pf f e k e k e ++=gg g控制律为：由于扰动力无法建模，因此该控制律难以实施。

如果在控制律中把扰动力的补偿项删除，则系统变为：质量-弹簧系统的力控制稳态误差为：1() ()f d vf pf ff e d vf pf f e dist f f k e k e mk f k e k e f f a b -=+++=++++gg ggg g 11()f e e e dist e d vf pf f e mk f f f mk f k e k e f --++=+++gg gg g()f dist f vf pf f f e k e k e a =++gg g dist f pf f e k a =一般情况下，环境是刚性的，不利于计算稳态误差。

如果在控制律中用f d 代替f e +f dist ，则控制律变为质量-弹簧系统的力控制相应地，稳态误差变为()f d vf pf f df f k e k e f a =+++gg g 1dist f pff e k a =+11()f e e e dist e d vf pf f d mk f f f mk f k e k e f --++=+++gggg g ()f dist f vf pf f ff e k e k e e a =+++gg g 稳态误差的计算得到了改善质量-弹簧系统的力控制在实际系统中，力“噪声”很大，对其微分不可行。

班级：研硕21班 姓名：丁德酉 学号：20130221071、弹簧质量阻尼器系统解：1) 数学建模由视察法，系统的振动微分方程具有如下形式，即[]{}[]{}[]{}{}()M x C x K x f t ++=(1.1)式中，{}[]{}[]{}[]121212,,,TTTx x x x x x x x x ===质量矩阵、阻尼矩阵和刚度矩阵分别为：[]1200m M m ⎡⎤=⎢⎥⎣⎦[]c c C c c -⎡⎤=⎢⎥-⎣⎦[]122223k k k K kk k +-⎡⎤=⎢⎥-+⎣⎦将121234,5,6,7,2,3m m c k k k ======代入式(1.1)，可得系统微分方程为：1112224066920056625()x x x x x x f t --⎧⎫⎧⎫⎧⎫⎡⎤⎡⎤⎡⎤⎧⎫++=⎨⎬⎨⎬⎨⎬⎨⎬⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎩⎭⎩⎭⎩⎭⎩⎭ (1.2)对式(1.2)拉氏变换，得：1224066920056625()X s s X F s ⎛--⎫⎧⎫⎡⎤⎡⎤⎡⎤⎧⎫++=⎨⎬⎨⎬ ⎪⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎩⎭⎩⎭⎝⎭ (1.3)解式(1.3)，可得系统传递函数：11432()2(31)()()2054656041X s s G s F s s s s s +==++++ 222432()469()()2054656041X s s s G s F s s s s s ++==++++Matlab语音描述如下：num1=[6 2];num2=[4 6 9];den=[20 54 65 60 41];sys1=tf(num1,den),sys2=tf(num2,den) step(sys1,'k',sys2,'k-.'),grid on legend('sys1','sys2')命令窗口输出如下：sys1 =6 s + 2------------------------------------ 20 s^4 + 54 s^3 + 65 s^2 + 60 s + 41Continuous-time transfer function.sys2 =4 s^2 + 6 s + 9------------------------------------ 20 s^4 + 54 s^3 + 65 s^2 + 60 s + 41Continuous-time transfer function.系统单位阶跃响应如图1.1所示。

标题： matlab中不同质量弹簧阻尼系数输出力分析1. 简介弹簧阻尼系统是一种常见的物理系统，它由弹簧和阻尼器组成，用于控制物体的振动和运动。

在实际工程中，弹簧阻尼系统的设计和分析对于系统的稳定性和性能至关重要。

本文将通过在matlab中对不同质量下弹簧阻尼系数对输出力的影响进行分析，探讨其对系统的影响。

2. 弹簧阻尼系统的基本原理弹簧阻尼系统是由弹簧和阻尼器组成，它们分别用于控制物体的弹簧振动和减震。

其中，弹簧的刚度系数和阻尼器的阻尼系数是两个关键参数。

在弹簧阻尼系统中，当外力作用在物体上时，系统将产生振动，而输出力将取决于系统的参数以及外力的大小和频率。

3. 不同质量下的弹簧阻尼系统建模在matlab中，我们可以通过建立弹簧阻尼系统的数学模型来模拟系统的运行。

为了分析不同质量下弹簧阻尼系数对输出力的影响，我们可以对弹簧阻尼系统进行建模，然后通过模拟不同质量下的系统运行来获取输出力的数据。

4. 弹簧阻尼系统模型的建立在matlab中，我们可以通过建立弹簧-质量-阻尼系统的数学模型来模拟系统的运行。

假设系统的质量为m，弹簧的刚度系数为k，阻尼器的阻尼系数为c，外力为f(t)，系统的振动方程可以表示为：\[m\ddot{x} + c\dot{x} + kx = f(t)\]其中，\(x\)为物体的位移，\(\dot{x}\)为物体的速度，\(\ddot{x}\)为物体的加速度。

这个方程描述了外力作用下系统的振动过程。

5. 不同质量下系统运行的模拟在matlab中，我们可以通过对系统振动方程进行数值求解来模拟系统的运行。

我们可以分别设定不同的质量，然后通过求解系统的振动方程来获取输出力随时间的变化。

我们还可以改变弹簧的刚度系数和阻尼器的阻尼系数，来分析它们对系统输出力的影响。

6. 数据分析与结果展示通过在matlab中对不同质量下的弹簧阻尼系数对输出力进行模拟，我们可以得到系统输出力随时间的变化曲线。

弹簧-质量-阻尼模型弹簧-质量-阻尼系统1 研究背景及意义弹簧-质量-阻尼系统是一种比较普遍的机械振动系统，研究这种系统对于我们的生活与科技也是具有意义的，生活中也随处可见这种系统，例如汽车缓冲器就是一种可以耗减运动能量的装置，是保证驾驶员行车安全的必备装置，再者在建筑抗震加固措施中引入阻尼器，改变结构的自振特性，增加结构阻尼，吸收地震能量，降低地震作用对建筑物的影响。

因此研究弹簧-质量-阻尼结构是很具有现实意义。

2 弹簧-质量-阻尼模型的建立数学模型是定量地描述系统的动态特性，揭示系统的结构、参数与动态特性之间关系的数学表达式。

其中，微分方程是基本的数学模型，不论是机械的、液压的、电气的或热力学的系统等都可以用微分方程来描述。

微分方程的解就是系统在输入作用下的输出响应。

所以，建立数学模型是研究系统、预测其动态响应的前提。

通常情况下，列写机械振动系统的微分方程都是应用力学中的牛顿定律、质量守恒定律等。

弹簧-质量-阻尼系统是最常见的机械振动系统。

机械系统如图2.1所示，图2.1 弹簧-质量-阻尼系统简图其中1m ，2m 表示小车的质量，ic 表示缓冲器的粘滞摩擦系数，ik 表示弹簧的弹性系数，i F （t ）表示小车所受的外力，是系统的输入即iU （t ）=iF （t ）,iX (t)表示小车的位移，是系统的输出，即iY （t ）=iX (t)，i=1,2。

设缓冲器的摩擦力与活塞的速度成正比，其中1m =1kg ，2m =2kg ，1k =3k =100N/cm ，2k =300N/cm ，1c =3c =3N ∙s/cm ，2c =6N ∙s/cm 。

由图 2.1，根据牛顿第二定律,，建立系统的动力学模型如下： 对1m 有：（2-1）对2m 有：（2-2）3 建立状态空间表达式令31421122,,,xx x x u F u F ====,则原式可化为：13123241212212423423232212()()()()()()m x l l x l x k k x k x u t m x l l x l x k k x k x u t ++-++-=++-++-= 化简得：1221211232431()()()u t k x k k x l l x l x x m +-++++=（2-3）2211223242342()()()u t k x k k x l l x l x x m +-+-++=（2-4）整理得：12112212211111324323222222221234001000000100()()10()()1010000100x x u k k k l l l x m m m m m x u x k k l l k l m m m m m x x y x x ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-++⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-++⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦（2-5）121321321,2,100,3003,6m m k k k l l l ========代入数据得：0100001400300961502003 4.5A ⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥--⎣⎦ 00001000.5B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦10000100C ⎡⎤=⎢⎥⎣⎦则系统的状态空间表达式为x y ux x ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=001000015.000100005.43200156930040010000100.4 化为对角标准型当系统矩阵A 有n 个不相等的特征根...)3,2,1(=i i λ时，相应的有n 个不相等的特征向量...)3,2,1(=i m i，所以有矩阵A 的特征矩阵[]m mm m M 4321...=根据矩阵论线性变换得：Mzx Tx z MT =⇒=⇒=-1可以使用matlab 进行对角标准型的运算，matlab 作为一种数学运算工具，很大程度的方便了了我们的计算，对于这个弹簧-质量-阻尼系统是一个四阶的状态空间表达式，所以可以用matlab 简化计算。

弹簧振子的阻尼弹簧振子是物理学中的一个重要模型，可以描述许多实际系统的振动行为。

在实际情况下，弹簧振子受到空气阻力等外界因素的影响，从而引入了阻尼效应。

本文将介绍弹簧振子的阻尼以及其对振动行为的影响。

一、弹簧振子的基本原理弹簧振子是由一根弹性系数为k的弹簧与一个质量为m的物体组成的系统。

当物体受到外力作用后，弹簧被拉伸或压缩，从而使系统恢复到平衡位置附近发生振动。

根据胡克定律，系统的振动满足简谐运动的特点。

二、阻尼的引入在实际情况下，弹簧振子受到空气阻力、摩擦力等外界因素的作用，这些因素会导致振动系统的能量耗散，从而引入阻尼。

阻尼可以分为三种类型：无阻尼、欠阻尼和过阻尼。

1. 无阻尼振动在理想情况下，即没有任何外界因素的干扰时，弹簧振子进行无阻尼振动。

在这种情况下，物体的振动是永久的，能量不会耗散，系统的振幅和频率保持不变。

2. 欠阻尼振动当引入一定程度的阻尼后，弹簧振子进行欠阻尼振动。

在这种情况下，振幅会逐渐减小，但是振动仍然是周期性的。

欠阻尼振动的周期比无阻尼振动稍微长一些。

3. 过阻尼振动当阻尼增加到一定程度时，弹簧振子进行过阻尼振动。

在这种情况下，振动逐渐衰减到平衡位置附近，且没有周期性。

过阻尼振动的振幅会更快地减小。

三、阻尼对振动行为的影响阻尼对弹簧振子的振动行为有着重要影响。

主要体现在以下两个方面：1. 振动幅度的减小阻尼的引入会使弹簧振子的振动幅度逐渐减小。

这是因为阻尼会耗散振动系统的能量，使振动逐渐衰减。

因此，可以通过调整阻尼的大小来控制弹簧振子的振幅。

2. 振动频率的变化阻尼的引入还会改变弹簧振子的振动频率。

在无阻尼情况下，振动频率只与弹簧的弹性系数和物体的质量有关。

但是在有阻尼情况下，振动频率会略微降低。

四、应用领域弹簧振子的阻尼效应在实际生活中有广泛的应用。

例如，在汽车的悬挂系统中，阻尼器起到了消除车辆振动的作用；在钟摆等机械装置中，阻尼器可以调节振幅和频率，使其保持稳定。

弹簧阻尼质量块系统你看啊，弹簧就像是这个小团队里最有弹性的小伙伴。

它能伸能缩，就像我们在生活中遇到困难的时候，要懂得灵活应对。

有时候它被压缩得很小很小，就像我们被压力压得喘不过气来，但只要压力一消失，它又能立马恢复原状，充满活力地蹦跶起来。

这弹簧啊，它的弹性可有着大作用呢。

在这个系统里，它就像是一种调和剂，不断地调整着整个系统的状态。

再说说阻尼吧。

阻尼这个东西啊，就像是一个小拖油瓶，但这个拖油瓶可是很重要的哦。

它总是在那里阻碍着一些东西的运动，就像我们生活中的那些小烦恼，虽然有点烦人，但也让我们的生活不会跑得太快，失去控制。

它让整个系统不会一下子就疯狂地摆动或者跳动，而是慢慢地、稳稳地朝着一个方向发展。

就好比我们在成长的道路上，不能太冒进，要有一些东西来拉住我们，让我们稳稳当当的。

还有质量块呢，这个质量块就像是团队里的老大哥。

它很沉稳，有自己的重量，不会轻易被外界影响。

它在那里就给整个系统一种踏实的感觉。

就像在一个家庭里，有一个很稳重的长辈，大家都会觉得很安心。

质量块的存在让整个弹簧阻尼质量块系统有了一个核心，围绕着它，弹簧和阻尼才能更好地发挥自己的作用。

这三个家伙组合在一起啊，就像我们身边的一群好朋友。

有时候它们会闹点小矛盾，就像系统可能会出现一些小故障或者不稳定的情况。

但是只要它们互相协调，互相包容，就又能很好地一起运转起来。

我们的生活也是这样的呀，每个人都有自己的性格和特点，就像弹簧、阻尼和质量块一样。

只有当我们找到彼此之间的平衡，才能像这个系统一样，稳定而又充满活力地前行。

这个系统虽然是个科学的东西，但你要是用心去感受，就会发现它和我们的生活有好多相似之处呢。

它就像一个小小的生活哲理，藏在那些科学的术语和原理背后，等待着我们去发现、去理解，然后让我们的生活也变得更加有趣、更加有秩序。

弹簧阻尼系统微分方程
弹簧阻尼系统是一种常见的物理系统，它包含一个弹簧和一个阻尼器。

这个系统可以用微分方程来描述。

假设弹簧的劲度系数为k，阻尼器的阻尼系数为b，物体的质量
为m，弹簧的长度为x。

根据牛顿第二定律，可以得到以下微分方程： m*x''(t) + b*x'(t) + k*x(t) = 0
其中，x''(t)表示物体在时间t的加速度，x'(t)表示物体在时
间t的速度。

这个微分方程描述了弹簧阻尼系统在给定时间内的运动。

这个微分方程可以通过数值方法或解析方法进行求解。

常见的解析方法包括使用特征方程来求解系统的特征根，从而得到系统的解析解。

数值方法则通过将微分方程转化为差分方程，然后用数值逼近的方式求解。

弹簧阻尼系统的微分方程可以用于描述很多实际系统，例如汽车避震器、机械振动器等。

通过分析和求解这个微分方程，可以帮助我们理解系统的运动规律，进而设计和优化系统的性能。

在实际应用中，弹簧阻尼系统的微分方程往往会进一步扩展，考虑更多的因素，例如外力的影响、非线性特性等。

这些扩展的微分方程可以更准确地描述系统的行为，并且可以应用于更复杂的工程问题中。

总而言之，弹簧阻尼系统的微分方程是描述该系统运动的重要工具，通过求解这个微分方程，我们可以深入了解系统的特性，从而实现系统的控制和优化。

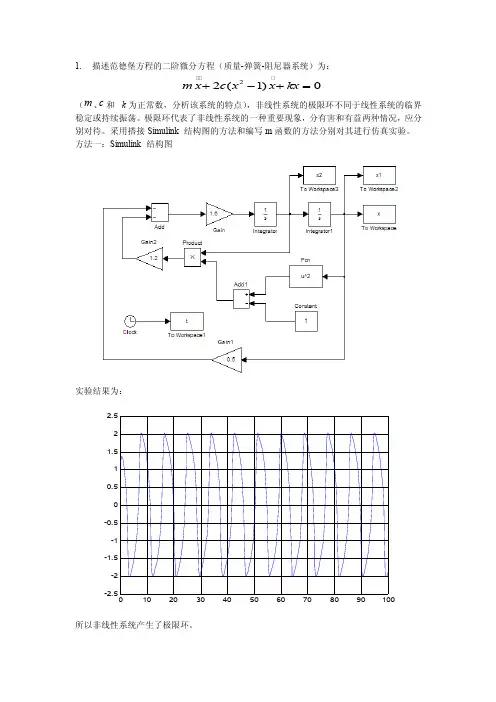
1.描述范德堡方程的二阶微分方程（质量-弹簧-阻尼器系统）为：（ 、 和 为正常数，分析该系统的特点），非线性系统的极限环不同于线性系统的临界稳定或持续振荡。

极限环代表了非线性系统的一种重要现象，分有害和有益两种情况，应分别对待。

采用搭接Simulink 结构图的方法和编写m 函数的方法分别对其进行仿真实验。

方法一：Simulink 结构图实验结果为：-2.5-2-1.5-1-0.500.511.522.5所以非线性系统产生了极限环。

22(1)0m x c x x kx +-+=m c k2. 为下面系统找一个平衡点，并确定稳定性，指出稳定性是否为渐近的以及是否为全局的？（1）34sin x x x =-+（2）()55x x =-解：（1）34(sin )0x x x =-+=，x=0; 平衡点（0，0），线性化结果为：0x =，不能由线性化说明系统稳定性性质。

（2）5(5)0x x =-=，x=5,平衡点（5，0），线性化结果为 0x =，不能由线性化说明系统稳定性性质。

3. 已知 2(1)m q q bq q u ++=，其中()q t 和()q t是可测量的状态， m=1.5 b=2，跟踪目标是()()d q t q t →，其中()()d e q t q t =- 可能的控制器设计方案之一：22(1)(1)()d u bq q m q q q kr am e =+++++a 和k 为控制器增益，r 为复合误差r e ae =+证明定理：控制器在以下函数下提供一个全局稳定的跟踪(0)(0)()(0)exp()[exp()exp()]/e ae ke t e at t at a k m m+=-+----解：取函数212V mr =求导得出：V mr r =⋅，因为r e ae =+所以，r e a e =+代入求出：()V mr e a e =⋅+又因为：()()d e q t q t =-；()()d e q t q t =-；()()d e q t q t =-所以 [()]d d V mr q q a q q =⋅-+-又因为 2(1)u b q qq m q -=+，代入上式求得：2[]1d u bq qV r mq am e q -=⋅-++因为：212V mr =22(1)(1)()d u bq q m q q q kr am e =+++++代入上式，求得2[()]d d V r m q m q kr am e am e kr =⋅--++=-所以 2V k V m=-又有 2V m r r k r=⋅=-所以 k r r m=-解得 ()(0)e x p ()k r t r t m=⋅-因为 r ea e =+；(0)(0)(0)r e ae =+求解方程，即得：(0)(0)()(0)exp()[exp()exp()]/e ae ke t e at t at a k m m+=-+----定理证毕。

弹簧质量阻尼所构成的机械系统摘要：一、弹簧质量阻尼机械系统的概述二、弹簧质量阻尼机械系统的工作原理三、弹簧质量阻尼机械系统的应用领域四、提高弹簧质量阻尼机械系统性能的方法五、我国在弹簧质量阻尼机械领域的发展现状与展望正文：弹簧质量阻尼所构成的机械系统在工程领域具有广泛的应用，如汽车、建筑、电子产品等。

了解其工作原理及性能提升方法对我国机械制造业的发展具有重要意义。

一、弹簧质量阻尼机械系统的概述弹簧质量阻尼机械系统是由弹簧、质量块和阻尼器组成的一种被动振动控制系统。

在这种系统中，弹簧起到承载和传递作用力、质量块负责平衡振动系统的重量，而阻尼器则负责消耗振动系统的能量，减小振动幅度和振动持续时间。

二、弹簧质量阻尼机械系统的工作原理弹簧质量阻尼机械系统在工作过程中，当外部作用力作用于质量块时，质量块产生振动。

振动通过弹簧传递，使弹簧发生变形。

随着振动的持续，阻尼器对振动的能量进行消耗，使振动幅度逐渐减小。

此外，弹簧的刚度和阻尼器的阻尼系数共同决定了系统的振动特性和稳定性。

三、弹簧质量阻尼机械系统的应用领域弹簧质量阻尼机械系统在多个领域具有广泛应用。

例如，在汽车工程中，减震器就是采用弹簧质量阻尼原理来减小车身振动，提高行驶舒适性；在建筑领域，隔震装置可以采用弹簧质量阻尼系统，有效降低地震对建筑物的影响；在电子产品中，如硬盘、摄像头等，采用弹簧质量阻尼系统可以降低振动对产品性能的影响，提高产品的可靠性和稳定性。

四、提高弹簧质量阻尼机械系统性能的方法1.合理设计弹簧的刚度和阻尼器的阻尼系数，以满足不同应用场景的需求。

2.优化阻尼器的材料和结构，提高能量消耗效率。

3.采用主动控制策略，如实时监测振动系统状态，调整阻尼器的阻尼参数，实现对振动的有效控制。

五、我国在弹簧质量阻尼机械领域的发展现状与展望近年来，我国在弹簧质量阻尼机械领域的研究取得了显著成果。

在材料、工艺、设计等方面不断取得突破，部分产品性能已达到国际先进水平。

质量弹簧阻尼二阶系统
质量弹簧阻尼二阶系统是一种由质量、弹簧和阻尼器组成的物理系统。

该系统是二阶的，因为它的运动方程是一个二阶微分方程。

在这个系统中，质量是系统中的核心部分，它具有一定的质量量值。

弹簧负责提供恢复力，通过拉伸或压缩来抵抗质量的位移。

阻尼器负
责阻碍质量的振动过程，通过消耗能量来减弱振动幅度和频率。

质量弹簧阻尼二阶系统的运动方程可以表示为：
m*d^2x/dt^2 + c*dx/dt + k*x = 0
其中，m是质量，c是阻尼系数，k是弹簧常数，x是质量的位移，t是时间。

这是一个关于位移x的二阶线性常微分方程。

解决这个方程可以得到系统的振动行为。

振动的频率和振幅取决于质量、弹簧和阻尼的参数取值。

不同的参数取值会导致不同的振动特性，如欠阻尼、临界阻尼和过阻尼等。

通过对质量弹簧阻尼二阶系统的分析，我们可以了解物体的振动行为，并应用于各种领域，如工程、物理学和机械学等。

弹簧阻尼系统运动方程弹簧阻尼系统是一种弹性系统，它可以实现用弹簧和阻尼器控制物体在动态环境中的运动。

它可以控制物体的动态变化，从而使它保持在某一稳定状态。

由于它受力能力强，可以抵抗大量外力，工程中被广泛应用，如机械设备的振动抑制、液压机械的传动系统、运输机械的支撑系统和结构动力学研究中的应用。

弹簧阻尼系统的运动方程反映了弹簧阻尼系统的运动规律，它是式中弹簧阻尼系统动力学模型的基础，对于理解和分析弹簧阻尼系统具有重要意义。

一般来讲，弹簧阻尼系统的运动方程可表示为：$$Mddot{X} + Cdot{X} + KX = F(t)$$其中，M为质量；C为惯性阻尼系数；K为弹簧系数；X为位移；F(t)为时间变化的外力。

弹簧阻尼系统的运动方程可以用以下三种形式之一来表示：1、振实形式：$$mddot{X} + c dot{X} + kX = F(t)$$2、传递函数形式：$$X(s) = frac{F(s)}{ms^2 + cs + k}$$3、状态变量形式：$$begin{bmatrix}dot{X_1}dot{X_2}end{bmatrix} =begin{bmatrix}0 & 1-frac{k}{m} & -frac{c}{m}end{bmatrix}begin{bmatrix}X_1X_2end{bmatrix} +begin{bmatrix}frac{1}{m}end{bmatrix}F(t)$$弹簧阻尼系统的运动特性可通过求解相应的运动方程推导出来，它可以反映物体在弹簧阻尼系统中的运动性能。

弹簧阻尼系统中的系统参数有M，K，C，其中K和C参数决定了系统的阻尼特性，影响着系统的稳定性，K和C参数的选择需要在系统稳定性和动态性之间充分考虑。

弹簧阻尼系统的运动方程是其动力学模型的基础，它可以表达系统的头尾运动规律。

它可以帮助我们了解弹簧阻尼系统的运动特性，从而有效控制系统的动态特性。

质量弹簧阻尼系统数学模型matlab辨识全文共四篇示例，供读者参考第一篇示例：质量弹簧阻尼系统是工程学中常见的一个系统模型，它描述了一个质量、被弹簧连接和被阻尼器连接的系统。

这种系统经常出现在机械、土木、航空等领域中，用于分析和优化系统的动态特性。

在工程实践中，我们常常需要通过实验数据来确定系统的性能，并建立数学模型来描述系统的运动规律。

在本文中，我们将讨论如何利用MATLAB进行质量弹簧阻尼系统的数学模型辨识。

我们将介绍质量弹簧阻尼系统的理论基础和运动方程。

然后，我们将讨论如何利用MATLAB进行数据处理和数学模型辨识。

我们将通过一个案例来展示如何使用MATLAB建立和验证质量弹簧阻尼系统的数学模型。

质量弹簧阻尼系统理论基础和运动方程质量弹簧阻尼系统是一个常见的动力学系统，它由一个质量、一个弹簧和一个阻尼器组成。

质量受到外力作用时，将受到弹簧和阻尼器的约束，从而产生运动。

系统的动力学方程可以表示为：m\ddot{x} + c\dot{x} + kx = f(t)m是质量，c是阻尼系数，k是弹簧刚度，x是位移，f(t)是外力。

这是一个二阶线性常微分方程，描述了系统在外力作用下的运动规律。

MATLAB数据处理和数学模型辨识在实际工程中，我们需要通过实验数据来确定系统的参数，以建立数学模型。

MATLAB是一个强大的数学计算软件，可以方便地处理数据和建立模型。

我们可以利用MATLAB进行数据导入、处理、拟合和模拟，从而辨识质量弹簧阻尼系统的数学模型。

我们需要采集实验数据，包括质量弹簧阻尼系统的位移、速度和加速度等信息。

然后，我们可以利用MATLAB进行数据处理，比如绘制位移-时间曲线、速度-时间曲线和加速度-时间曲线等。

接下来，我们可以利用MATLAB的曲线拟合工具来拟合实验数据，从而确定系统的参数。

第二篇示例：质量弹簧阻尼系统是工程领域中常见的一种动力学系统，其在机械、航空航天、汽车等领域中都有广泛的应用。

弹簧阻尼系统matlab仿真课程设计一、课程目标知识目标：1. 学生能理解弹簧阻尼系统的基本原理，掌握其数学模型构建方法。

2. 学生能掌握MATLAB软件的基本操作，运用其进行弹簧阻尼系统的仿真。

3. 学生能了解仿真结果分析的方法，对系统性能进行评估。

技能目标：1. 学生能运用所学的理论知识，建立弹簧阻尼系统的数学模型。

2. 学生能熟练运用MATLAB软件进行仿真实验，并掌握数据处理和分析技巧。

3. 学生能通过课程学习，培养解决实际工程问题的能力和团队协作能力。

情感态度价值观目标：1. 学生通过课程学习，培养对物理模型的兴趣，激发探究精神。

2. 学生在学习过程中，树立正确的价值观，认识到科学技术对社会发展的作用。

3. 学生通过团队协作，培养沟通、交流和合作的良好品质。

课程性质：本课程为理实一体化课程，结合理论教学与实践操作，旨在培养学生的动手能力和实际问题解决能力。

学生特点：学生具备一定的物理基础和数学建模能力，对MATLAB软件有一定了解，但实际操作能力有待提高。

教学要求：教师需结合学生特点，采用任务驱动、分组合作的教学方法，注重理论与实践相结合，提高学生的实际操作能力。

在教学过程中，关注学生的学习进度，及时调整教学策略，确保课程目标的实现。

通过本课程的学习，使学生具备弹簧阻尼系统仿真分析的能力，为后续相关课程打下坚实基础。

二、教学内容本课程教学内容主要包括以下三个方面：1. 弹簧阻尼系统理论基础- 深入讲解弹簧阻尼系统的基本原理，包括弹簧、阻尼器的力学特性。

- 学习弹簧阻尼系统的数学模型构建，涉及微分方程的建立和求解。

- 结合教材相关章节，复习动力学、控制理论等基础知识。

2. MATLAB仿真技术- 介绍MATLAB软件的基本操作，包括数据类型、矩阵运算和编程基础。

- 学习使用MATLAB进行弹簧阻尼系统的建模与仿真，掌握Simulink工具箱的应用。

- 结合教材，讲解仿真参数设置、模型搭建和结果分析等步骤。

MATLAB弹簧阻尼系统仿真书引言弹簧阻尼系统是工程中常见的一种物理系统，它由弹簧和阻尼器组成，用于控制和减缓振动和冲击。

在工程设计和分析中，仿真是一种重要的工具，可以帮助工程师更好地理解系统的行为和性能。

MATLAB是一款功能强大的数值计算软件，它提供了丰富的工具和函数，可以方便地进行弹簧阻尼系统的仿真。

MATLAB基础知识在开始进行弹簧阻尼系统的仿真之前，我们需要对MATLAB的基础知识有一定的了解。

MATLAB是一种解释型的编程语言，它的语法和操作与数学和工程领域的问题紧密相关。

我们需要了解MATLAB中的变量定义、矩阵运算、函数定义和调用等基本操作。

弹簧阻尼系统的数学模型在进行仿真前，我们需要先建立弹簧阻尼系统的数学模型。

弹簧阻尼系统可以用二阶微分方程来描述，其中包括质量、弹簧系数和阻尼系数等参数。

我们需要将这些参数转换为MATLAB中的变量，并定义系统的微分方程。

弹簧阻尼系统的仿真步骤步骤一：定义系统参数首先，我们需要定义弹簧阻尼系统的参数，包括质量、弹簧系数和阻尼系数等。

这些参数将用于建立系统的数学模型。

步骤二：建立系统的微分方程根据弹簧阻尼系统的数学模型，我们可以建立系统的微分方程。

在MATLAB中，我们可以使用函数定义的方式来表示微分方程。

通过定义一个函数，我们可以将微分方程转化为MATLAB中的可调用函数。

步骤三：选择数值求解方法在进行仿真时，我们需要选择合适的数值求解方法来求解系统的微分方程。

MATLAB 提供了多种求解方法，包括欧拉法、龙格-库塔法等。

我们需要根据系统的特点选择适合的数值求解方法。

步骤四：进行仿真计算在完成前面的准备工作后，我们可以进行仿真计算了。

通过调用MATLAB中的求解器函数，我们可以得到系统在不同时间点的状态和响应结果。

可以绘制系统的位移、速度和加速度等随时间的变化曲线。

弹簧阻尼系统的仿真案例为了更好地理解弹簧阻尼系统的仿真过程，我们将以一个具体的案例来进行说明。

弹簧质量阻尼系统的无量纲化
弹簧质量阻尼系统是工程力学与振动学中常见的一个系统模型，用于描述弹簧、质量和阻尼器之间的动态关系。

在进行弹簧质量阻尼系统的分析和研究时，常常需要对其进行无量纲化处理，以便更好地理解系统的特性和行为。

无量纲化是一种将物理问题转化为无量纲形式的方法，通过选取适当的基本量纲和参考量纲，将物理量表示成无量纲形式，从而简化问题的计算和分析。

对于弹簧质量阻尼系统来说，无量纲化可以帮助我们更好地理解系统的动态特性和响应。

在无量纲化的过程中，我们首先需要选择适当的基本量纲。

对于弹簧质量阻尼系统来说，通常选择力F、质量m和长度L作为基本量纲。

然后，我们需要选择适当的参考量纲，例如弹簧的刚度k、振动的频率ω和阻尼系数c。

通过将物理量表示为无量纲形式，可以得到无量纲化的动力学方程，从而更方便地进行分析和求解。

利用无量纲化的方法，我们可以得到弹簧质量阻尼系统的无量纲频率、阻尼比和无量纲振幅等重要无量纲参数，这些参数对系统的动态特性和稳定性具有重要的影响。

通过对这些无量纲参数的分析，可以更好地了解弹簧质量阻尼系统的振动特性和响应。

除了对系统的动态特性进行分析外，无量纲化还可以帮助我们进行系统的优化设计和参数选择。

通过对无量纲参数的研究和分析，可以找到系统的最佳工作状态和参数配置，从而提高系统的性能和稳定性。

总之，无量纲化是对弹簧质量阻尼系统进行分析和研究的重要方法，通过将系统的物理量表示为无量纲形式，可以更好地理解系统的动态特性和响应。

同时，无量纲化还可以帮助我们进行系统的优化设计和参数选择，从而提高系统的性能和稳定性。