下载文档原格式
spearman秩相关系数
Spearman秩相关系数是指研究者通过研究两组变量中任意两个变量之间的秩值差异而衡量它们之间的相关性，这种方法也叫做“Spearman相关系数”（Spearman Rank Correlation Coefficient），缩写为Src。
Spearman秩相关系数是一种可以衡量变量之间线性关系的测量方法。
它由美国统计学家威廉·斯皮尔曼（William Spearman）于1904年发表。
它用以反映两个变量之间的线性关系，其值范围在-1~1之间，其中-1表示完全负相关，0表示无相关，1表示完全正相关。
当Spearman秩相关系数值越大，表示两组变量之间的关系越紧密。
1、计算每个变量组的秩值。
秩值是每个变量在整个组中的排位，它的取值范围在1到样本量（如果样本量为10，则秩值最大为10），秩值越小表示变量在组中排位越高。
2、以秩值差值d=R1-R2计算秩差平方和。
3、将秩值平方和乘以6除以样本总量（N）减去N加1再除以N减去1。
最后计算的为Spearman秩相关系数的值。
该方法适用于不同的变量类型，如连续型变量、分类型变量和事件计数。
因此，Spearman秩相关系数是一种普遍适用的，精准度高的衡量变量之间的相关性的方法。
斯皮尔曼相关系数模型是查尔斯·爱德华·斯皮尔曼命名的，它是一种衡量两个变量的依赖性的非参数指标。
它利用单调方程评价两个统计变量的相关性。
斯皮尔曼相关系数的定义是：X和Y为两组数据，其斯皮尔曼（等级）相关系数定义为r s = 1 - 6 ∑ i = 1 n d i 2 n ( n 2 − 1 ) r_s=1-\frac{6\sum\limits_{i=1}^nd_i^2}{n(n^2-1)}rs
=1−n(n2−1)6i=1∑n di2 其中，d i d_idi为X i X_iXi和Y i Y_iYi之间的等级差。
斯皮尔曼相关系数为零表明当X增加时Y没有任何趋向性。
当数据中没有重复值，并且当两个变量完全单调相关时，斯皮尔曼相关系数则为+1或−1。
如果有需要，建议咨询专业人士获取更多详细信息。
斯皮尔曼相关系数结果怎么看斯皮尔曼相关系数(Spearman's Rank Correlation Coefficient，以下简称SRC)是根据数值变量两者之间关系的一种常用方法，广泛应用于社会科学、心理学及经济学中的统计分析，用来衡量两个变量之间的线性关系。
例如，我们可以测试某一事件的发生率是否与所处的气候环境有关系，此时需要用SRC来衡量这两者之间的关联程度。
斯皮尔曼相关系数介于-1.0到1.0之间，数值越大表明相关性越强，而0.0则表明两者之间没有相关性。
斯皮尔曼相关系数的测量结果是客观的，可以用于识别、评估收集的数据之间的相关性。
通常情况下，我们可以看到斯皮尔曼相关系数的数值在0.5到1.0之间，可以认为这两个变量之间的相关性非常强；反之，如果斯皮尔曼相关系数的值落在0.0-0.5之间，也可以认定它们之间的相关性相对较弱，但仍有一定的联系。
此外，任何斯皮尔曼相关系数小于0的结果都表明，这两个变量之间存在反向相关，即两个变量中的一个增加时，另一个会减少，反之亦然。
斯皮尔曼相关系数可以作为描述两个变量之间关系的定量分析方法。
当斯皮尔曼相关系数接近1或-1时，其结果表明两个变量之间有很强的相关性，如果斯皮尔曼相关系数值处于0.5到1.0之间，则可以认为它们之间存在强烈的正相关。
从另一方面讲，如果斯皮尔曼相关系数值约0.4到0.3之间，则可以认为它们之间存在一定的负相关关系。
最后，如果斯皮尔曼相关系数的值落在0.0-0.2之间，则表示两个变量之间没有直接的关系。
因此，当我们在评估两个变量之间的相关性时，使用斯皮尔曼相关系数是一个很好的方法。
它能够帮助我们准确地衡量两者之间的相关程度，指导后续分析、评估及其它推断活动。
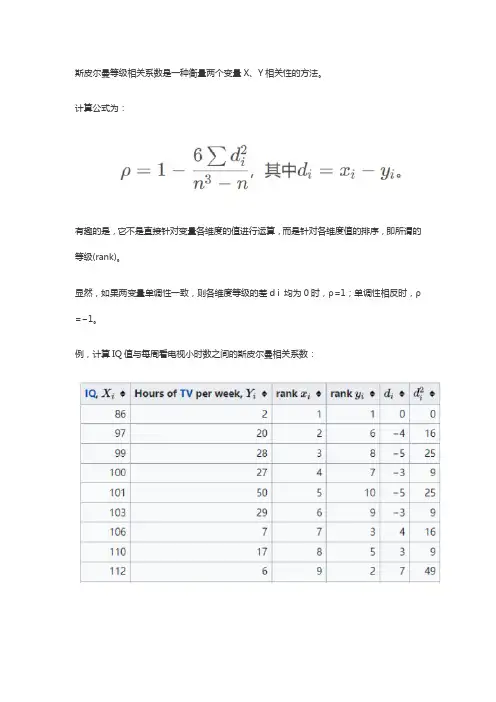
斯皮尔曼等级相关系数是一种衡量两个变量X、Y相关性的方法。
计算公式为：
有趣的是，它不是直接针对变量各维度的值进行运算，而是针对各维度值的排序，即所谓的等级(rank)。
显然，如果两变量单调性一致，则各维度等级的差d i 均为0时，ρ=1；单调性相反时，ρ=−1。
例，计算IQ值与每周看电视小时数之间的斯皮尔曼相关系数：
斯皮尔曼等级相关系数以Charles Spearman命名，并经常用希腊字母ρ（rho）表示其值。
斯皮尔曼等级相关系数用来估计两个变量X、Y之间的相关性，其中变量间的相关性可以使用单调函数来描述。
如果两个变量取值的两个集合中均不存在相同的两个元素，那么，当其中一个变量可以表示为另一个变量的很好的单调函数时（即两个变量的变化趋势相同），两个变量之间的ρ可以达到+1或-1。
三大相关系数统计学中的相关系数是研究两类变量之间关系的定量分析工具，它通常可以衡量两个变量之间的正负线性关系的程度。
这种关系可以指导我们对两个变量之间的关系和变化趋势有更深刻的认识。
相关系数分为三大类，它们分别是称为皮尔森相关系数、斯皮尔曼相关系数和泰勒斯相关系数。
皮尔森相关系数是最常用的相关系数，它可以用来检验两个变量之间的线性关系。
皮尔森相关系数的取值范围是-1（完全负相关）到1（完全正相关）。
如果相关系数的值靠近1或-1，那么可以说明两个变量之间存在显著的线性关系；如果相关系数的值是0，则可以说明两个变量之间不存在显著的线性关系。
另外，皮尔森相关系数可以用来测度定性变量两两之间的相关程度。
斯皮尔曼相关系数是用来衡量两个变量之间的秩相关性的相关系数，它的取值范围是-1（完全负相关）到1（完全正相关）。
与皮尔森相关系数不同，斯皮尔曼相关系数忽略了变量之间的变量尺度和原始数据的离散性，只关注变量的相对大小排列。
斯皮尔曼相关系数常用于判断连续变量之间的数量关系。
泰勒斯相关系数是用来衡量两个变量之间的非线性关系的相关系数，它的取值范围也是-1（完全负相关）到1（完全正相关）。
与皮尔森相关系数不同，泰勒斯相关系数关注变量之间的非线性关系，因此更容易捕捉到连续变量之间的非线性关系。
泰勒斯相关系数常用于判断连续变量之间的非线性关系，也可以检验定性变量之间的非线性关系。
虽然皮尔森相关系数、斯皮尔曼相关系数和泰勒斯相关系数都是研究两个变量之间关系的定量分析工具，但它们各自可以检验不同的关系，因此在分析时，要根据研究问题来选择最合适的相关系数。
一般而言，在连续变量之间检验线性关系时，应该优选皮尔森相关系数；在连续变量之间检验秩相关性时，应该优选斯皮尔曼相关系数；在连续变量或定性变量之间检验非线性关系时，应该优选泰勒斯相关系数。
总之，相关系数是用来检验两个变量之间关系的定量分析工具，它也是衡量两个变量之间的线性、秩、非线性关系的重要指标。
斯皮尔曼秩相关系数皮尔曼秩相关系数（Pearson Correlation Coefficient）是一种常用的测量两个变量之间相关性的统计学指标，也叫做皮尔森相关系数、变量相关系数或皮尔森-秩相关系数。
它是定量研究变量两个之间相关程度大小的一种经典统计分析工具，可以衡量两个变量的强弱程度，以及相关性的类型，并可以反映其他复杂关系的内在规律。
一、简介1.1 概念：皮尔曼秩相关系数（Pearson Correlation Coefficient）是测量两个定量变量之间相关性的重要指标，也可以用来衡量它们之间正弱性及相关性类型，该系数采用线性回归方程来描述变量之间的关系，它是一种量化评估两个变量相关系数的度量。
1.2 公式：一般来说，皮尔曼秩相关系数的计算公式为：r=xx'-sxsy/sxy，它由两个重要的参数xx' 和 sxsy 组成。
其中，xx' 是两个变量的协方差，sxsy 是两个变量的标准差的乘积。
xx' 即反映了两个变量的变化趋势是否相同，而sxsy 可以反映变量的变异程度。
所以，xx'和sxsy的乘积所得的sxy正好反映了两个变量之间的相关性强弱程度。
二、应用2.1 数理统计领域：在统计学领域，皮尔曼秩相关系数是最常用的测量变量之间相关性的统计指标。
它可以反映两种变量间相互作用的程度，帮助对实证数据作出合理的判断和解释。
2.2 经济学领域：在经济学领域，皮尔曼秩相关系数也有着重要的应用，比如用它测量某一国家的生活费用与装修费用的关系，或是考察某一投资组合的风险与收益的相关性，等等。
2.3 生物医学领域：在生物医学领域，皮尔曼秩相关系数也有许多重要的应用。
比如可以利用它来测量噪声与心率变异度或是睡眠期与国民健康状况的相互关联关系，并可以用它来研究不同病患的病因及治疗效果，以及提高诊断的准确性等等。
三、结论皮尔曼秩相关系数是一种有效的，经典的，重要的统计学指标。
数据分析中的相关性分析是一种统计方法，用于研究两个或多个变量之间的关系。
这种关系可以是正相关（一个变量增加时，另一个也增加）或负相关（一个变量增加时，另一个减少），也可以是零相关（两个变量之间没有明确的线性关系）。
以下是数据分析中常用的相关性分析方法，每种方法都会详细解释其原理、应用场景和优缺点。
1. 皮尔逊相关系数（Pearson Correlation Coefficient）原理：皮尔逊相关系数是衡量两个连续变量之间线性关系强度和方向的一种统计量。
其值域为-1到1，其中1表示完全正相关，-1表示完全负相关，0表示无相关。
应用场景：皮尔逊相关系数常用于衡量两个连续变量之间的线性关系，如身高与体重、温度与销售额等。
优缺点：优点是计算简单，易于解释；缺点是只能衡量线性关系，对于非线性关系和非连续变量可能不准确。
2. 斯皮尔曼秩次相关系数（Spearman's Rank Correlation Coefficient）原理：斯皮尔曼秩次相关系数是衡量两个变量之间排序关系的一种统计量。
它不要求数据连续或服从正态分布，因此适用范围更广。
应用场景：斯皮尔曼秩次相关系数适用于连续但不服从正态分布的变量，以及有序分类变量（如评级、排名等）。
优缺点：优点是对数据分布要求较低，适用范围广；缺点是计算相对复杂，对极端值较敏感。
3. 肯德尔秩次相关系数（Kendall's Tau）原理：肯德尔秩次相关系数是衡量两个有序分类变量之间排序一致性的一种统计量。
通过比较一对样本在各变量上的相对大小来计算排序关系。
应用场景：肯德尔秩次相关系数常用于分析有序分类变量，如调查问卷中的等级评价、体育比赛中的排名等。
优缺点：优点是对数据分布要求较低，适用于有序分类变量；缺点是计算复杂，对样本量有一定要求。
4. 距离相关系数（Distance Correlation Coefficient）原理：距离相关系数是衡量两个变量之间整体相关性的统计量。
皮尔逊和斯皮尔曼相关系数是统计学中常用的两种衡量变量之间相关性的方法。
它们可以帮助我们理解和量化变量之间的关系，并为我们提供数据分析和决策制定的依据。
本文将对这两种相关系数进行比较，并探讨它们结合使用的意义及方法。
一、皮尔逊相关系数皮尔逊相关系数是用来衡量两个连续变量之间线性关系强弱的统计量，通常用ρ表示。
其取值范围在-1到1之间，当ρ=1时，表示为完全正相关；ρ=-1时，表示为完全负相关；ρ=0时，表示没有线性相关。
二、斯皮尔曼相关系数斯皮尔曼相关系数是一种用来衡量两个变量之间单调关系程度的统计量，通常用rs表示。
它是通过将原始数据转化为等级数据，并计算等级数据的相关系数来得到的。
和皮尔逊相关系数不同，斯皮尔曼相关系数对数据的分布没有要求，更适合于非正态分布的数据。
三、两种相关系数的结合皮尔逊相关系数和斯皮尔曼相关系数各有其适用范围和局限性。
在实际应用中，我们经常会遇到数据不满足线性相关假设和正态分布假设的情况。
这时，结合使用这两种相关系数可以更全面地衡量变量之间的关系。
结合使用的方法有多种，一种常见的方法是先用皮尔逊相关系数来衡量变量之间的线性关系，再用斯皮尔曼相关系数来检验非线性相关的情况。
若两种相关系数得到的结果一致，则可以初步得出结论；若结果不一致，则需要深入分析数据的特点和背景，以得出更准确的结论。
另外，可以利用两种相关系数的特点，综合考虑变量之间的各种关系。
若两个变量在皮尔逊相关系数下呈现出线性关系，而在斯皮尔曼相关系数下呈现出非线性关系，则可以得出这两个变量之间存在复杂的关系，需要进行更深入的挖掘和分析。
四、结论皮尔逊相关系数和斯皮尔曼相关系数是两种常用的用来衡量变量之间相关性的统计方法。
它们各有适用的范围和局限性。
通过结合使用这两种相关系数，可以更全面地理解和量化变量之间的关系，为数据分析和决策制定提供更可靠的依据。
在实际应用中，我们应根据具体情况选择合适的方法，并结合数据的特点进行综合分析。
Pearson、Spearman秩相关系数、kendall等级相关系数（附python实现）⽬录：相关系数相关系数：考察两个事物（在数据⾥我们称之为变量）之间的相关程度。
如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：(1)、当相关系数为0时，X和Y两变量⽆关系。
(2)、当X的值增⼤（减⼩），Y值增⼤（减⼩），两个变量为正相关，相关系数在0.00与1.00之间。
(3)、当X的值增⼤（减⼩），Y值减⼩（增⼤），两个变量为负相关，相关系数在-1.00与0.00之间。
相关系数的绝对值越⼤，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。
通常情况下通过以下取值范围判断变量的相关强度：相关系数 0.8-1.0 极强相关0.6-0.8 强相关0.4-0.6 中等程度相关0.2-0.4 弱相关0.0-0.2 极弱相关或⽆相关Pearson（⽪尔逊）相关系数⽪尔逊相关也称为积差相关（或积矩相关）是英国统计学家⽪尔逊于20世纪提出的⼀种计算直线相关的⽅法。
假设有两个变量X、Y，那么两变量间的⽪尔逊相关系数可通过以下公式计算：以上列出的四个公式等价，其中E是数学期望，cov表⽰协⽅差，N表⽰变量取值的个数。
适⽤范围当两个变量的标准差都不为零时，相关系数才有定义，⽪尔逊相关系数适⽤于：(1)、两个变量之间是线性关系，都是连续数据。
(2)、两个变量的总体是正态分布，或接近正态的单峰分布。
(3)、两个变量的观测值是成对的，每对观测值之间相互独⽴。
pearson 描述的是线性相关关系，取值[-1, 1]。
负数表⽰负相关，正数表⽰正相关。
在显著性的前提下，绝对值越⼤，相关性越强。
绝对值为0，⽆线性关系；绝对值为1表⽰完全线性相关。
Python 实现DataFrame.corr(method='pearson', min_periods=1)参数说明：method：可选值为{‘pearson’, ‘kendall’, ‘spearman’}min_periods：样本最少的数据量返回值：各类型之间的相关系数DataFrame表格。
斯皮尔曼等级相关系数字母
斯皮尔曼等级相关系数，以查尔斯·爱德华·斯皮尔曼命名，是衡量两个变量的依赖性的非参数指标。
它利用单调方程评价两个统计变量的相关性。
经常用希腊字母ρ表示。
其基本思想是：分别对两个变量X、Y做等级变换(rank transformation)，用等级RX和RY表示；然后按Pearson相关性分析的方法计算RX和RY的相关性。
Spearman等级相关系数适用于定序变量与定序变量之间的相关系数。
计算公式为：其中，di=（xi-yi），xi和yi分别是两个变量按大小（或优劣）排序的秩，n是样本的容量。
与简单相关系数一样，Spearman等级相关系数的取值范围也为：[-1,1]，绝对值越大，相关性越强。
rs为正数时，则认为存在正的等级相关；rs为负数时，则认为存在负的等级相关。
同理，rs=1时，则表明两个变量的等级完全相同，存在完全的正相关。
反之亦然。
斯皮尔曼相关系数和皮尔森相关系数1、在统计学中, 以查尔斯·斯皮尔曼命名的斯皮尔曼等级相关系数，即斯皮尔曼相关系数。
2、它是衡量两个变量的依赖性的非参数指标。
3、经常用希腊字母ρ表示。
4、它利用单调方程评价两个统计变量的相关性。
5、如果数据中没有重复值，并且当两个变量完全单调相关时，斯皮尔曼相关系数则为+1或−1。
6、斯皮尔曼相关系数被定义成等级变量之间的皮尔逊相关系数。
7、对于样本容量为n的样本，n个原始数据被转换成等级数据，相关系数ρ为扩展资料斯皮尔曼相关系数表明X(独立变量)和Y(依赖变量)的相关方向。
8、如果当X增加时，Y趋向于增加，斯皮尔曼相关系数则为正。
9、如果当X增加时，Y趋向于减少，斯皮尔曼相关系数则为负。
10、斯皮尔曼相关系数为零表明当X增加时Y没有任何趋向性。
11、当X和Y越来越接近完全的单调相关时，斯皮尔曼相关系数会在绝对值上增加。
12、当X和Y完全单调相关时，斯皮尔曼相关系数的绝对值为1。
13、完全的单调递增关系意味着任意两对数据Xi，YiXj，Yj，有Xi−Xj 和Yi−Yj总是同号。
14、完全的单调递减关系意味着任意两对数据Xi，Yi和Xj，Yj，有Xi−Xj 和Yi−Yj总是异号。
15、斯皮尔曼相关系数经常被称作"非参数"的。
16、这里有两层含义：1.首先，当X和Y的关系是由任意单调函数描述的，则它们是完全皮尔逊相关的。
17、与此相应的，皮尔逊相关系数只能给出由线性方程描述的X和Y 的相关性。
18、2.其次，斯皮尔曼不需要先验知识(也就是说，知道其参数)便可以准确获取XandY的采样概率分布。
相关系数p值计算公式相关系数的p值是衡量两个变量之间关系强度的统计显著性值。
一般情况下，当p值小于0.05时，我们认为两个变量之间的关系是显著的。
相关系数的p值计算公式如下：1. 简单相关系数（Pearson相关系数）的p值计算公式：p = 2 * (1 - T.cdf(abs(r), n-2))其中，T是t分布，r是相关系数，n是样本的大小。
2. 斯皮尔曼相关系数（Spearman相关系数）的p值计算公式：p = 2 * (1 - T.cdf(abs(rs), n-2))其中，rs是斯皮尔曼相关系数，n是样本的大小。
在以上公式中，T.cdf(是累积分布函数，用于计算t分布中大于等于一些值的概率。
下面，我们将对这两个公式进行详细解释。
1. 简单相关系数（Pearson相关系数）的p值计算公式：假设我们有两个变量：X和Y，它们的简单相关系数为r。
我们想要计算这个相关系数的p值。
首先，我们需要计算t值。
t值的计算公式如下：t = r * sqrt((n-2) / (1 - r^2))其中，r是相关系数，n是样本的大小。
接下来，我们使用t值来计算p值。
p值的计算公式如下：p = 2 * (1 - T.cdf(abs(r), n-2))其中，T是t分布，T.cdf(是累积分布函数，用于计算t分布中大于等于一些值的概率。
2. 斯皮尔曼相关系数（Spearman相关系数）的p值计算公式：斯皮尔曼相关系数是一种通过将原始数据转换为秩次来计算的相关系数。
假设两个变量X和Y的斯皮尔曼相关系数为rs。
我们想要计算这个相关系数的p值。
首先，我们需要计算t值。
t值的计算公式如下：t = rs * sqrt((n-2) / (1 - rs^2))其中，rs是斯皮尔曼相关系数，n是样本的大小。
接下来，我们使用t值来计算p值。
p值的计算公式如下：p = 2 * (1 - T.cdf(abs(rs), n-2))其中，T是t分布，T.cdf(是累积分布函数，用于计算t分布中大于等于一些值的概率。
影像组学相关系数计算公式影像组学是一种利用医学影像数据进行分析和研究的新兴学科，它可以帮助医生更好地诊断疾病、制定治疗方案和预测疾病的发展趋势。
在影像组学中，相关系数是一种常用的统计方法，用于衡量两个变量之间的相关程度。
在医学影像中，相关系数可以帮助研究人员分析不同影像特征之间的关联，从而更好地理解疾病的发展规律和预测疾病的风险。
相关系数的计算公式是影像组学研究中的重要内容之一。
在影像组学中，常用的相关系数计算公式包括皮尔逊相关系数、斯皮尔曼相关系数和肯德尔相关系数。
下面我们将分别介绍这三种相关系数的计算公式及其应用。
1. 皮尔逊相关系数计算公式。
皮尔逊相关系数是一种衡量两个连续变量之间线性相关程度的方法，它的计算公式如下：r = Σ((X_i X_mean) (Y_i Y_mean)) / (sqrt(Σ(X_i X_mean)^2) sqrt(Σ(Y_iY_mean)^2))。
其中，r表示皮尔逊相关系数，X_i和Y_i分别表示两个变量的取值，X_mean和Y_mean分别表示两个变量的均值。
通过计算皮尔逊相关系数，可以得到两个变量之间的线性相关程度，其取值范围为-1到1，当r为1时表示完全正相关，当r为-1时表示完全负相关，当r为0时表示无相关。
在医学影像组学中，皮尔逊相关系数常用于分析不同影像特征之间的线性关联，从而帮助研究人员理解疾病的发展规律和预测疾病的风险。
例如，研究人员可以利用皮尔逊相关系数来分析肿瘤影像特征与患者临床表现之间的关联，从而帮助医生更好地制定治疗方案和预测患者的预后。
2. 斯皮尔曼相关系数计算公式。
斯皮尔曼相关系数是一种衡量两个变量之间非线性关联程度的方法，它的计算公式如下：ρ = 1 ((6 Σ(d_i^2)) / (n (n^2 1)))。
其中，ρ表示斯皮尔曼相关系数，d_i表示两个变量的秩次差，n表示样本量。
通过计算斯皮尔曼相关系数，可以得到两个变量之间的非线性关联程度，其取值范围为-1到1，当ρ为1时表示完全正相关，当ρ为-1时表示完全负相关，当ρ为0时表示无相关。
斯皮尔曼相关系数强弱斯皮尔曼相关系数是一种用来度量两个变量之间关联程度的统计指标。
它衡量的是两个变量的等级顺序之间的关系，可以用来描述变量之间的非线性关系。
斯皮尔曼相关系数的取值范围在-1到1之间，其中-1表示完全负相关，1表示完全正相关，0表示没有相关性。
相关系数的绝对值越接近1，表示两个变量之间的关联越强。
在实际应用中，斯皮尔曼相关系数有着广泛的应用。
下面将从几个不同的角度来解释斯皮尔曼相关系数的强弱。
当斯皮尔曼相关系数接近于1或-1时，表示两个变量之间的关联非常强。
例如，假设我们研究了一个班级的学生在数学和语文成绩之间的关系，斯皮尔曼相关系数为0.9，这意味着数学成绩高的学生通常也在语文方面表现出色，反之亦然。
这种关联性非常强，可以用来预测一个学生的数学成绩，只需知道他的语文成绩即可。
当斯皮尔曼相关系数接近于0时，表示两个变量之间几乎没有关联。
例如，假设我们研究了一个城市的降雨量和温度之间的关系，斯皮尔曼相关系数为0.1，这意味着降雨量和温度之间没有明显的关联性。
在这种情况下，我们不能使用一个变量的值来预测另一个变量的值。
当斯皮尔曼相关系数接近于0时，也可以表示两个变量之间存在非线性关系。
例如，假设我们研究了一个人的年龄和体重之间的关系，斯皮尔曼相关系数为0.3，这意味着年龄和体重之间存在一定的关联，但这种关联并不是线性的。
可能存在年轻时体重增加迅速，而年龄增长后体重增加趋于平缓的情况。
需要注意的是，斯皮尔曼相关系数只能用来描述两个变量之间的关系，不能用来说明因果关系。
即使两个变量之间的斯皮尔曼相关系数非常高，也不能得出一个变量的变化会导致另一个变量变化的结论。
相关性只能说明两个变量之间存在关联，而不能说明其中一个变量的变化是由于另一个变量的变化所导致的。
斯皮尔曼相关系数是一种衡量两个变量之间关联程度的统计指标。
它可以用来描述变量之间的非线性关系，对于研究变量之间的关联性有着重要的应用价值。
相关系数的区别
相关系数是用于衡量两个变量之间关联程度的统计指标。
常见的相关系数有皮尔逊相关系数和斯皮尔曼相关系数。
1. 皮尔逊相关系数（Pearson correlation coefficient）是用来衡量两个连续变量之间线性关系的强度和方向。
它的取值范围在-1到1之间，其中-1表示完全的负相关，1表示完全的正相关，0表示无相关。
当相关系数接近于-1或1时，表示两个变量之间存在较强的线性关系。
2. 斯皮尔曼相关系数（Spearman correlation coefficient）用于衡量两个变量之间的单调关系，不要求变量是连续的。
它通过将原始数据转换为排序数据，然后计算排序数据之间的皮尔逊相关系数来得到。
斯皮尔曼相关系数的取值范围也在-1到1之间，解释方式与皮尔逊相关系数类似。
总结来说，皮尔逊相关系数适用于衡量两个连续变量之间的线性关系，而斯皮尔曼相关系数适用于衡量两个变量之间的单调关系，无论变量是连续的还是离散的。
相关系数算法
相关系数是统计中最普遍使用的一种反映两变量之间关系强弱
的度量指标。
它的取值范围在[-1,1]之间，取值越大，表明两变量之间的相关性越大。
相关系数可以分为三种，即皮尔森相关系数，斯皮尔曼相关系数和秩相关系数。
皮尔森相关系数(Pearson Correlation Coefficient)，简称PCC，它是用来衡量两个变量之间的线性相关性的指标。
它的计算公式如下： PCC=∑(Xi-X)(Yi-Y)/(∑(Xi-X)2∑(Yi-Y)2)
其中Xi和Yi分别表示数据集中第i个样本点的X和Y变量的取值，X和Y分别表示所有Xi和Yi的均值。
斯皮尔曼相关系数（Spearman Correlation Coefficient），简
称SCC，它也称为秩相关系数，因为它的计算是基于变量的等级变化而不是它们的实际取值。
它的计算公式如下：
SCC=1-6∑(RXi-RYi)2/n(n2-1)
其中RXi和RYi分别表示Xi和Yi的等级(rank)，n表示样本数量。
秩相关系数(Rank Correlation Coefficient)，简称RCC，它是一种衡量两个变量的统计相关性的指标，它的计算过程是：先将变量的取值按照从小到大的顺序进行排序，然后求得变量的等级，最后计算两变量等级之差的平方和与样本数N的乘积的倒数即可。
其计算公式如下：
RCC=1-∑(RXi-RYi)2/N
其中RXi和RYi分别表示Xi和Yi的等级(rank)，n表示样本数量。
相关系数r 的两个公式(一)相关系数 r 的两个公式1. 皮尔逊相关系数公式•皮尔逊相关系数（Pearson correlation coefficient）是衡量两个变量之间线性相关程度的指标。
公式如下：r = cov(X, Y) / (σx * σy)其中： - r是皮尔逊相关系数 - cov(X, Y)是变量X和Y的协方差 - σx是变量X的标准差 - σy是变量Y的标准差2. 斯皮尔曼相关系数公式•斯皮尔曼相关系数（Spearman correlation coefficient）是一种非参数方法，用于衡量两个变量的单调关系程度。
公式如下：r = 1 - (6 * Σd^2) / (n^3 - n)其中： - r是斯皮尔曼相关系数 - Σd^2是变量X和Y的秩差之差的平方和 - n是样本数量示例假设我们要研究变量X（收入）和变量Y（消费金额）之间的相关性。
1.皮尔逊相关系数示例：–在一个样本中，假设收入变量X和消费金额变量Y的协方差为1000，标准差分别为50和20。
–根据皮尔逊相关系数公式，可以计算相关系数r为：r = 1000 / (50 * 20) = 1–由于r的值为1，说明收入和消费金额之间存在完全的正线性相关关系。
2.斯皮尔曼相关系数示例：–在一个样本中，假设收入变量X和消费金额变量Y的秩差之差的平方和为500，样本数量为100。
–根据斯皮尔曼相关系数公式，可以计算相关系数r为：r = 1 - (6 * 500) / (100^3 - 100) =–由于r的值为，说明收入和消费金额之间存在强烈的单调关系，但不一定是线性关系。
以上是相关系数r的两个公式以及示例解释。
相关系数是统计学中常用的指标，可以用来衡量两个变量之间的相关程度。
皮尔逊相关系数适用于衡量线性关系，而斯皮尔曼相关系数适用于衡量单调关系。
相关系数r 的两个公式(二)相关系数r 的两个公式1. 皮尔逊相关系数公式皮尔逊相关系数是一种用来衡量两个变量之间线性相关程度的统计量，常用符号表示为r。
其计算公式为：[ r = ]其中，x和y分别为两个变量的取值集合，({x})和({y})分别为x 和y的平均值。
2. 斯皮尔曼相关系数公式斯皮尔曼相关系数是一种用来衡量两个变量之间的相关程度的非参数统计量，常用符号表示为r。
其计算公式为：[ r = 1 - ]其中，d为变量的秩次差，n为样本个数。
示例解释假设有一组衡量学生学习时间和考试成绩的数据。
我们想要确定学习时间和考试成绩之间的相关程度。
•使用皮尔逊相关系数公式计算：假设学习时间的取值集合为x，考试成绩的取值集合为y。
首先计算x和y的平均值({x})和({y})。
然后根据公式，计算分子()，分母()和()。
将分子除以分母即可得到皮尔逊相关系数r。
•使用斯皮尔曼相关系数公式计算：首先将学习时间和考试成绩的取值分别转换为秩次。
然后根据公式，计算秩次差的平方和()。
最后将计算结果代入公式中计算斯皮尔曼相关系数r。
通过计算得到的相关系数r，我们可以判断学习时间和考试成绩之间的相关程度。
如果r接近于1或-1，则表示两个变量之间存在强相关关系；如果r接近于0，则表示两个变量之间不存在线性相关关系。
综上所述，皮尔逊相关系数公式和斯皮尔曼相关系数公式是衡量两个变量之间相关程度的常用方法。
它们能够帮助我们了解变量之间的关系，并在科学研究和数据分析中发挥重要作用。
皮尔逊积矩相关系数（Pearson product-moment correlation coefficient ）1 定义在统计学中，皮尔逊积矩相关系数（Pearson product-moment correlation coefficient ），有时也简称为PMCC ，通常用r 或是ρ表示，是用来度量两个变量X 和Y 之间的相互关系（线性相关）的，取值范围在[-1,+1]之间。
皮尔逊积矩相关系数在学术研究中被广泛应用来度量两个变量线性相关性的强弱，它是由Karl Pearson 在19世纪80年代从Francis Galton 介绍的想法基础发展起来的，但是发展后原想法相似但略有不同的，这种相关系数常被称为“Pearson 的r ”。
两个变量之间的皮尔逊积矩相关系数定义为这两个变量的协方差与二者标准差积的商，即()()cov(,)X Y XY X Y X YE X Y X Y -μ-μρ==σσσσ 上式定义了总体相关系数，一般用希腊字母ρ（rho ）表示。
若用样本计算的协方差和标准差代替总体的协方差和标准差，则为样本相关系数，一般用r 表示：1()()n i i i X X Y Y r =--=∑另外一个与上式等效的定义相关系数的公式是通过标准化以后变量均值的积定义的。
假设样本可以记为(,)i i X Y ，则样本Pearson 相关系数为111n i i i X Y X X Y Y r s s n =⎛⎫⎛⎫--= ⎪⎪-⎝⎭⎝⎭∑ 其中i XX X s -，X 和X s 分别为标准化变量，样本均值和样本标准差。
2 皮尔逊积矩相关系数的数学特性不论是样本的还是总体的Pearson 相关系数绝对值均小于等于1，相关系数等于1或-1时，所有数据的点都精确地落在一条直线上（为样本相关系数的情况），或是两变量的分布完全由一条直线支撑（为总体相关系数的情况）。
Pearson 相关系数具有对称性，即：corr corr(,)corr(,)X Y Y X =。
