黑龙江省哈师大附中2013-2014学年高二下学期期中考试 数学文(Word版含答案)

哈三中2013—2014学年度下学期高二学年第二模块数学(文科)试卷考试说明：（1）本试卷分第I卷（选择题）和第II卷（非选择题）两部分, 满分150分．考试时间为120分钟；（2）第I卷，第II卷试题答案均答在答题卡上，交卷时只交答题卡．第I卷（选择题, 共60分）一、选择题（本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的）1. 若复数，则的虚部为A. B . 3 C. D.2. 命题“”的否定A. B.C. D.3. 已知直线、，平面、，那么下列命题中正确的是A．若，，则B．若，，，则C．若，，则D．若，，则4. 在一次跳伞训练中，甲、乙两位学员各跳一次.设命题是“甲降落在指定范围”，是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为A. B. C. D.5. 若不等式的解集为，则实数等于A. -1B. -7C. 7D. -56. 在极坐标系中，圆的圆心的极坐标是A. B. C. D.7. 已知是函数的极小值点, 那么函数的极大值为A. 15B. 16C. 17D. 188. 阅读右侧程序框图，如果输出,那么在空白矩形框中应填入的语句为A.B.C.D.9. 已知三棱锥的所有顶点都在球的球A侧视图俯视图面上，为的中点，且，， ，则此棱锥的体积为 A ． B ．C ．D ．10. 一个棱锥的三视图如图，则该棱锥的表面积为A ．48+12B ．48+24C ．72+12D ．72+2411. 切线方程为 A ． B. C. D. 12. 若函数的图象与直线相切，则的值为A. B. C. D.第Ⅱ卷 （非选择题, 共90分）二、填空题(本大题共4小题，每小题5分，共20分．将答案填在答题卡相应的位置上) 13. 曲线（为参数）与曲线 （为参数）的交点个数 为__________个. 14. 执行右面的程序框图，若输入的的 值为，则输出的的值为____________.15. 目前四年一度的世界杯在巴西举行，为调查哈三中高二学生是否熬夜看世界杯用简单随机抽样的方法调查了110名高二学生，结果如下表：能否有99%以上的把握认为“熬夜看球与性别有关”？ _____________________。

哈师大附中高二下学期期中测试题历史试卷（时间90分钟总分100分）一、单项选择题（每题只有一个正确答案，共32题，每题1分，共32分）1.关于儒学的起源，《淮南子·要略》说：“孔子修成康之道，述周公之训，以教七十子，使服其衣冠，修其篇籍，故儒者之学生焉。

”认为儒学是由继承文武周公的王道政治传统而产生的。

周公的王道政治主要是指A．王位世袭制 B．井田制 C．宗法制与礼乐制 D．郡县制2.《禹鼎》记载：噩侯反叛伐周，厉王命禹出征，生获其君。

这反映了A．分封制趋向衰落，未能维护王权 B．宗法制度开始瓦解C．封国实力削弱，周王权力加强 D．周王铸鼎显示权威3.司马光《资治通鉴》：“初，（晋）智宣子将以瑶为后（继承人），智果曰：‘不如宵也。

瑶之贤于人者五，其不迭者一也。

美髯长大则贤，射御足力则贤，如是而甚不仁。

夫以其五贤陵人而以不仁行之，其谁能待之？若果立瑶也，智宗必灭。

’弗听。

”文中智果之言表明他A．反对立嫡以长 B．主张立君以仁 C．反对任人唯亲 D．提倡实行分封4.有学者认为：中国古代统治者为了维持皇权的“万世一系”和宗法等级社会的长治久安，特别重视以明人伦为核心的道德伦常教育，并使之与选官制度相结合。

下列最符合材料观点的是A．嫡长子继承制 B．察举制 C．九品中正制 D．科举制5.《宋会要辑稿·职官》载：“绍兴十四年（1144年）‘九月提举福建路市舶楼璹言……欲乞依广南市舶司体例每年于遣发船舶之际，宴设诸国蕃商，以示朝廷招徕远人之意。

从之。

”这段材料说明A.南宋政府对外贸易不计经济效益B.南宋政府加强了对外贸易的管理C.中国开始实行闭关锁国政策D.南宋政府重视蕃商来华贸易6.“孔子知言之不用，道之不行也，是非二百四十二年之中，以为天下仪表，…退诸侯，讨大夫，以达王事而已。

”材料反映这一时期的中国A．“礼崩乐坏”现象日趋严重 B．官学开始被私学取代C．专制主义中央集权制度初步建立 D．儒家学说成为统治思想7.某史学家认为:“后世官制,变化繁赜。

黑龙江省哈师大附中2013-2014学年高一下学期期中考试数学试卷（解析版）一、选择题1．已知数列,21,n -，则是它的( )A ．第22项B ．第23项C ．第24项D ．第28项 【答案】B 【解析】试题分析：由题意可知数列的通项公式n a 1-n 2，可得23n =． 考点：数列的通项公式．2．若1x <，则下列关系中正确的是( ) A ．11x> B ．21x < C ．31x < D ．||1x < 【答案】C 【解析】试题分析：对于A ，xx -11-x 1=，∵x<1,∴1-x<0，而分母x 与0的大小关系未定，∴无法判断差的符号，类似的对于B ，)1)(1(1-x 2-+=x x ，无法判断x+1的符号，从而无法判断差的符号，对于D ，取x=-2可验证D错误，对于C ，0]43)21)[(1()1)(1(1-x 223<++-=++-=x x x x x ，所以1x 3<．考点：作差法证明不等式．3．已知(2,=-a ，(7,0)=-b ，则a 与b 的夹角为( ) A ．o30B ．o60C ．o 120D ．o150【答案】C 【解析】 试题分析：a b ||||cos ,a b a b ⋅=⋅⋅<>，可得，2174)032()7(2,co s -=⋅⋅-+-⋅=>=<∴夹角为120°．考点：平面向量数量积．4．不等式||y x ≥表示的平面区域为( )【答案】A 【解析】试题分析：原不等式等价于⎩⎨⎧≥≥x y 0x 或⎩⎨⎧≥<-xy 0x ，左边的不等式组表示的是y=x 的上方与y轴右方所夹的区域，右边的不等式组表示的是y=-x 与y 轴左方所夹的区域，故选A ． 考点：二元一次不等式(组)表示平面区域．5．等差数列{}n a 的前n 项和为n S ，已知2110m m m a a a -++-=，2138m S -=，则m =( )A ．2B ．9C ．10D ．19 【答案】C 【解析】试题分析：由题意等差数列{n a }：2m 1m 1-m a 2a a =++，∴2m m 2a 0a =0m a -=⇒或2a m =，若0a m =，则0)12()12(2)(1211-m 2=-⋅=-⋅+=-m a m a a S m m ，无解，若2a m =，则1212m -1()(21)(21)4m-22m m a a S m a m -+=⋅-=⋅-==38，∴m=10． 考点：等差数列的性质，等差数列的前n 项和．6．等比数列{}n a 的各项均为正数，且187465=+a a a a ，则13l o g a +23log a + +103log a =( )A ．12B ．10C ．8D ．32log 5+ 【答案】B 【解析】试题分析：由题意等比数列{na }及187465=+a a a a ，∴9a a a a a a a a a a 65748392101=====，∴13lo ga +23log a ++103log a =)]a (a )a (a )a [(a log )a a a (a log 65921013103213⋯⋯⋅=⋯103log 9log 10353===．考点：等比数列的性质，对数的性质．7．设0a b <<，则下列不等式中正确的是( )A ．2a b a b +<<B ．2a ba b +<<<C．2a b a b +<<<D2a ba b +<<< 【答案】B【解析】试题分析：∵0a b <<，∴2a ab <，即ab <a2a b+<，而02b -a b -2b a <=+，∴b 2ba <+． 考点：作差法证明不等式，基本不等式．8．实数x y ，满足1,21y y x x y ⎧⎪-⎨⎪+⎩≥≤≤5.，求目标函数z x y =-+的最小值( )A ．1B ．0C ．3-D ．5 【答案】C 【解析】 试题分析：如图，画出题中所给的不等式组所表示的平面区域，易得A(2,3),B(1,1)，C(4,1)，求z 的最小值即求直线y=x+z 在y 轴上截距的最小值，而y=x+z 表示的是与y=x 平行的直线，从图中可以看出，当直线过C 点时，z 有最小值，3-14-z min =+=．考点：线性规划求目标函数的最值．9．已知等差数列{}n a 的前n 项和是n S ，若150S >，160S <，则n S 最大值是( ) A ．1S B ．7S C ．8S D ．15S 【答案】C 【解析】试题分析：∵等差数列{n a },15160,0S S ><,∴1115141615150,16022a d a d ⋅⋅+>+<，即11157002a d a d d +>>+⇒<，又∵819111570,802a a d a a d a d =+>=+<+<，∴前8项和最大．考点：等差数列的性质，前n 项和．10．已知点P 为ABC ∆所在平面上的一点，且13AP AB t AC =+，其中t 为实数，若点P 落在ABC ∆的内部（不含边界），则t 的取值范围是( ) A ．104t << B ．103t << C ．102t << D ．203t <<【答案】D 【解析】试题分析：如图，延长AP 交BC 于D ，设AD m AP =(m>1),(0)BD DC λλ=>,即1()()11AD AB AC AD AD AB AC λλλλ-=-⇒=+++,∴1111(1)(1)mAP AB AC AP AB AC m m λλλλλλ=+⇒=+++++，又∵13AP AB t AC =+，∴11(1)3113(1)m t m tm λλλ⎧=⎪+⎪⇒=-⎨⎪=⎪+⎩，又∵1110,,3(1)m m λλ>∴=<+∴1<m<3，∴203t <<．考点：平面向量的线性运算．11．已知数列{}n a 的通项公式是221sin()2n n a n π+=, 1232014a a a a ++++=则( )A ．201320132⨯ B ．20131007⨯C ．20141007⨯D ．20151007⨯【答案】D 【解析】试题分析：化简可得：2221sin()sin()22n n a n n n πππ+==+，当n=2k-1时，221(21)k a k -=--，当n=2k时，222(2)4k a k k ==，∴22212(21)441k k a a k k k -+=--+=-，所以1232014123220132014()()()(411)(421)+(410071)a a a a a a a a a a ++++=+++++=⋅-+⋅-+⋅-…1+1007=41007-1007=100720152⋅⋅⋅． 考点：数列求和． 12．定义12nnp +p ++p …为n 个正数n p p p ,,,21 的“均倒数”．若已知数列{}n a 的前n 项的“均倒数”为121n +，又14n n a b +=，则12231011111+b b b b b b ++…=( ) A ．111B ．910C ．1011D ．1112【答案】C【解析】试题分析：设数列{n a }的前n项和为n S ，则由题意可得2n n n 1==n(21)22n+1S n n n S +=+，， ∴2212[2(1)1]41(2)n n n a S S n n n n n n -=-=+--+-=-≥，1113,41,4n n n a a S a n b n +==∴=-==， ∴11111(1)1n n b b n n n n +==-++，∴1223111111+=1-+2231b b b b b ++……．考点：数列的通项公式，数列求和．二、填空题13． 已知{}n a 是等比数列，2=2a ，51=4a ，则公比=q ______________． 【答案】12【解析】试题分析：∵等比数列{n a },∴35211,82a q q a ===．考点：等比数列基本量的计算．14．已知等差数列{}n a 的前n 项和为n S ，若120OB a OA a OC =+，且A ，B ，C 三点共线（该直线不过点O ），则20S =_____________． 【答案】10 【解析】试题分析：∵A,B,C 三点共线，∴AB BC λ=，即()OB OA OC OB λ-=-,∴111OB OA OC λλλ=+++,∵120OB a OA a OC =+,∴1201211,,=+=1111+1+a a a a λλλλλλ==∴+++，∴1202020102a a S +=⋅=．考点：向量共线的充要条件，等差数列前n 项和．15． 在 ABC ∆ 中，角 A ，B ，C 的对边分别为 a ，b ，c ，且 c =o45B =，面积2S =，则=b _________．【答案】5 【解析】 试题分析：11sin ,245122S ac B a a =∴=⋅∴=。

哈尔滨市第六中学2013—2014学年度下学期期中考试高二（文科）数学试题考试时间：120分钟 满分：150分一、选择题：（每题5分共60分） 1．下列关于回归分析的说法中错误的是（ ）A. 回归直线一定过样本中心（y x ,）B. 残差图中残差点比较均匀地落在水平的带状区域中，说明选用的模型比较合适C. 两个模型中残差平方和越小的模型拟合的效果越好D ．甲、乙两个模型的2R 分别约为98.0和80.0，则模型乙的拟合效果更好 2．一个容量为20的样本，数据的分组及各组的频数如下：（10，20]，2；（20，30]，3；（30，40]，4；（40，50]，5；（50，60]，4；（60，70]，2. 则样本在区间（10，50]上的频率为（ ）A ．0.5B ．0.7C ．0.25D ．0.053．按ABO 血型系统学说，每个人的血型为A ，B ，O ，AB 型四种之一，依血型遗传学，当且仅当父母中至少有一人的血型是AB 型时，子女的血型一定不是O 型，若某人的血型的O 型，则父母血型的所有可能情况有（ ）A ．12种B ．6种C ．10种D ．9种4．有五条线段长度分别为1,3,5,7,9，从这5条线段中任取3条，则所取3条线段能构成一个锐角三角形的概率为（ ） A101 B 103 C 0 D 107 5．设x x x f ln )(=,若2)(0='x f ,则=0x( )A.2e B.e C.22ln D.2ln 6.从装有4粒大小、形状相同，颜色不同的玻璃球的瓶中，随意一次倒出若干粒玻璃球（至少一粒），则倒出奇数粒玻璃球的概率比倒出偶数粒玻璃球的概率 （ ）A.小B.大C.相等D.大小不能确定7．已知实数[]1,9x ∈，执行如右图所示的程序框图，则输出的x 不小于55的概率为 ( )A.58B.38C.23D.13 8.若右面的程序框图输出的S是126，则①应为（ ）A ．5n ≤？ B.6n ≤？C ．7n ≤？ D.8n ≤？（7题图） （8题图）9．设x x f ln )(=，若10<<<<a b c ，则a a f )(，bb f )(，c c f )(的大小关系为 （ ）A c c f b b f a a f )()()(>>B a a f b b f c c f )()()(>> C c c f a a f b b f )()()(>> D bb fc c f a a f )()()(>> 10．已知函数ax x x x f ++=2ln 2)(，若曲线)(x f y =存在与直线02=-y x 平行的切线，则实数a 的取值范围是（ ）A. (,2]-∞-B. (,2)-∞-C. (2,)-+∞D. [2,)-+∞ 11．在一次独立性检验中，有300人按性别和是否色弱分类如下表：由此表计算得统计量2=（ ） ．(参考公式：22()()()()(()ad bc a b c d K a b a c b d c d -+++=++++）)A. 2B. 3C. 2.4D. 3.612.已知)(x f y =在R 上开导，且2)1(=f ，若2)('>x f ，则不等式x x f 2)(>的解集为（ ）A. )1,(-∞B. ),1(+∞C. )0,(-∞D. ),0(+∞二、填空题（每题5分共20分）13．在区间（0，1）上任意取两个实数a ，b ，则b a +＜56的概率为 14.某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某3由表中数据能.(参考公式：x b y a xnxy x n yx bni ini ii -=--=∑∑==,1221)15．阅读下面的程序，当输入2000x =时，输出的y = ．16．已知极坐标系的极点与直角坐标系的原点重合，极轴与x 轴的正半轴重合，直线l 的倾斜角为，参数方程为（t 为参数，），圆C 的极坐标方程为，直线l 与圆C 交于A ，B 两点，则|OA|+|OB|= 。

2014-2015学年黑龙江省哈尔滨师大附中高二（下）期中数学试卷（文科）一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）对下列函数求导正确的是（）A．（x2）′=x B．（）′=﹣C．（）′=D．（ln2）′=2．（5分）复数z=在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3．（5分）函数y=x+的单调递增区间为（）A．（﹣2，0）∪（0，2）B．（﹣∞，﹣2）∪（2，+∞）C．（﹣2，0），（0，2）D．（﹣∞，﹣2），（2，+∞）4．（5分）下列函数中，在x=0处的导数不等于零的是（）A．y=x3+x2B．y=x+e﹣x C．y=（x﹣1）e2D．y=xsinx 5．（5分）已知函数f（x）=x3+2xf'（0），则f'（0）=（）A．﹣1B．0C．1D．26．（5分）f（x）=x3﹣3x2+2在区间[﹣1，1]上的最大值是（）A．﹣2B．0C．2D．47．（5分）做一个容积为4升的正方形底无盖水箱，要使得材料最省，则此水箱底面边长为（）A．分米B．1分米C．2分米D．4分米8．（5分）直线y=kx+1与曲线y=ax3+x+b相切于点（1，5），则a﹣b=（）A．﹣2B．0C．2D．69．（5分）函数f（x）=ax3﹣3x2+x+1恰有三个单调区间，则实数a的取值范围是（）A．（﹣∞，3）B．（﹣∞，3]C．（﹣∞，0）∪（0，3）D．（﹣∞，0）∪（0，3]10．（5分）已知f（x）=x2+sin，f′（x）为f（x）的导函数，则f′（x）的图象是（）A．B．C．D．11．（5分）已知函数f（x）=e x，g（x）=kx+k，若函数f（x）的图象恒在函数g （x）图象的上方，则实数k的取值范围是（）A．[0，+∞）B．[0，1）C．（0，1）D．（1，+∞）12．（5分）已知f（x）是可导的函数，且f′（x）＜f（x）对于x∈R恒成立，则（）A．f（1）＜ef（0），f（2015）＞e2015f（0）B．f（1）＞ef（0），f（2015）＞e2015f（0）C．f（1）＞ef（0），f（2015）＜e2015f（0）D．f（1）＜ef（0），f（2015）＜e2015f（0）二、填空题：本大题共4小题，每小题5分．13．（5分）函数f（x）=x﹣2lnx的单调递减区间是．14．（5分）函数f（x）=在x=0处取得极值，则a=．15．（5分）经过点（2，0）且与曲线y=相切的直线方程为．16．（5分）已知函数f（x）=x（lnx﹣ax）有两个极值点，则实数a的取值范围是．三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（10分）已知函数f（x）=（x﹣2）e x．（1）求f（x）的单调区间；（2）求f（x）在区间[0，2]上的最小值和最大值．18．（12分）已知在平面直角坐标系xOy中曲线C的参数方程为（θ为参数），直线l的参数方程为（t为参数），曲线C与直线l相交于点A，B，且定点P的坐标为（1，0）．（Ⅰ）求曲线C的普通方程；（Ⅱ）求|PA|•|PB|的值．19．（12分）已知函数f（x）=x3﹣ax2+x（x∈R）．（Ⅰ）若函数y=f（x）在（0，+∞）上为增函数，求a的取值范围；（Ⅱ）若a=1，当x＞1时，求证：f（x）＞x﹣1．20．（12分）已知函数f（x）=x2+mx﹣lnx．（Ⅰ）当m=0时，求曲线y=f（x）在（1，f（1））处的切线方程；（Ⅱ）令g（x）=f（x）﹣x2，当x∈（0，e]（e是自然常数）时，g（x）≥3，求实数m的取值范围．21．（12分）已知函数f（x）=ax3﹣（a+2）x2+6x﹣3（1）当a=﹣2时，求函数f（x）的极值；（2）当a＜2时，讨论函数f（x）零点的个数．22．（12分）在平面直角坐标系xOy中，已知椭圆C：+=1（a＞b＞0）的离心率为，且经过点（，1），过椭圆的左顶点A作直线l⊥x轴，点M 为直线l上的动点（点M与点A不重合），点B为椭圆右顶点，直线BM交椭圆C于点P．（Ⅰ）求椭圆C的方程；（Ⅱ）求证：AP⊥OM；（Ⅲ）试问•是否为定值？若是定值，请求出该定值；若不是，请说明理由．2014-2015学年黑龙江省哈尔滨师大附中高二（下）期中数学试卷（文科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）对下列函数求导正确的是（）A．（x2）′=x B．（）′=﹣C．（）′=D．（ln2）′=【解答】解：（x2）′=2x，（）′=﹣，（）′=，（ln2）′=0，故选：B．2．（5分）复数z=在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：∵复数z===1+i，∴复数z=在复平面内对应的点（1，1）位于第一象限．故选：A．3．（5分）函数y=x+的单调递增区间为（）A．（﹣2，0）∪（0，2）B．（﹣∞，﹣2）∪（2，+∞）C．（﹣2，0），（0，2）D．（﹣∞，﹣2），（2，+∞）【解答】解：对函数y=x+求导数，得：y′=1﹣；令y′＞0，得1﹣＞0，解得x＜﹣2或x＞2；所以函数y的增区间为（﹣∞，﹣2）和（2，+∞）．故选：D．4．（5分）下列函数中，在x=0处的导数不等于零的是（）A．y=x3+x2B．y=x+e﹣x C．y=（x﹣1）e2D．y=xsinx【解答】解：A选项，y=x3+x2的导函数y′=3x2+2x，令x=0得到y′=0；B选项，y=x+e﹣x的导函数y′=1﹣e x，令x=0得到y′=0；C选项，y=（x﹣1）e2的导函数y′=e2，令x=0得到y′=e2；D选项，y=xsinx的导函数y′=sinx+xcosx，令x=0得到y′=0；故选：C．5．（5分）已知函数f（x）=x3+2xf'（0），则f'（0）=（）A．﹣1B．0C．1D．2【解答】解：函数的导数f′（x）=3x2+2f′（0），令x=0，则f′（0）=2f′（0），解得f′（0）=0，故选：B．6．（5分）f（x）=x3﹣3x2+2在区间[﹣1，1]上的最大值是（）A．﹣2B．0C．2D．4【解答】解：f'（x）=3x2﹣6x=3x（x﹣2），令f'（x）=0可得x=0或2（2舍去），当﹣1＜x＜0时，f'（x）＞0，当0＜x＜1时，f'（x）＜0，∴当x=0时，f（x）取得最大值为f（0）=2．故选：C．7．（5分）做一个容积为4升的正方形底无盖水箱，要使得材料最省，则此水箱底面边长为（）A．分米B．1分米C．2分米D．4分米【解答】解：设长方体的底面边长为x分米，高为h分米，表面积为y，则由体积为4，得x2h=4，从而表面积y=x2+4x•h=x2+4x•=x2++≥3=12，当且仅当x2=，即x=2时，y min=12．即水箱用料最省时水箱底面边长为2分米．故选：C．8．（5分）直线y=kx+1与曲线y=ax3+x+b相切于点（1，5），则a﹣b=（）A．﹣2B．0C．2D．6【解答】解：∵y=ax3+x+b过点（1，5），∴a+b=4，∵直线y=kx+1过点（1，5），∴k+1=5，即k=4，又∵y′=3ax2+1，∴k=y′|x=1=3a+1=4，即a=1，∴b=4﹣a=4﹣1=3，∴a﹣b=1﹣3=﹣2．故选：A．9．（5分）函数f（x）=ax3﹣3x2+x+1恰有三个单调区间，则实数a的取值范围是（）A．（﹣∞，3）B．（﹣∞，3]C．（﹣∞，0）∪（0，3）D．（﹣∞，0）∪（0，3]【解答】解：∵函数f（x）=ax3﹣3x2+x+1，∴f′（x）=3ax2﹣6x+1，由函数f（x）恰好有三个单调区间，得f′（x）有两个不相等的零点，∴3ax2﹣6x+1=0满足：a≠0，且△=36﹣12a＞0，解得a＜3，∴a∈（﹣∞，0）∪（0，3）．故选：C．10．（5分）已知f（x）=x2+sin，f′（x）为f（x）的导函数，则f′（x）的图象是（）A．B．C．D．【解答】解：由f（x）=x2+sin=x2+cosx，∴f′（x）=x﹣sinx，它是一个奇函数，其图象关于原点对称，故排除B，D．又f″（x）=﹣cosx，当﹣＜x＜时，cosx＞，∴f″（x）＜0，故函数y=f′（x）在区间（﹣，）上单调递减，故排除C．故选：A．11．（5分）已知函数f（x）=e x，g（x）=kx+k，若函数f（x）的图象恒在函数g （x）图象的上方，则实数k的取值范围是（）A．[0，+∞）B．[0，1）C．（0，1）D．（1，+∞）【解答】解：如图示：，若函数f（x）图象恒在函数g（x）图象的上方，即f（x）﹣g（x）＞0恒成立，即e x﹣k（x+1）＞0，即e x＞k（x+1），若k=0，满足条件，若k＜0，则不满足条件．则当k＞0时，g（x）=k（x+1）过定点（﹣1，0），函数f（x）的导数为f′（x）=e x，设切点为（a，b），则对应的切线斜率k=f′（a）=e a，则对应的切线方程为y﹣e a=e a（x﹣a），∵直线过点（﹣1，0），∴﹣e a=e a（﹣1﹣a），解得a=0，此时切线斜率k=f′（0）=1，即此时k=1，则解得0＜k＜1，综上0≤k＜1，故选：B．12．（5分）已知f（x）是可导的函数，且f′（x）＜f（x）对于x∈R恒成立，则（）A．f（1）＜ef（0），f（2015）＞e2015f（0）B．f（1）＞ef（0），f（2015）＞e2015f（0）C．f（1）＞ef（0），f（2015）＜e2015f（0）D．f（1）＜ef（0），f（2015）＜e2015f（0）【解答】解：令，则，由于f'（x）＜f（x），e x＞0对于x∈R恒成立，所以h'（x）＜0在R上恒成立，所以为减函数，∴，即f（1）＜ef（0）；，即f（2015）＜e2015f（0）．故选：D．二、填空题：本大题共4小题，每小题5分．13．（5分）函数f（x）=x﹣2lnx的单调递减区间是（0，2）．【解答】解：函数y=x﹣lnx的导数为y=1﹣，令y′=1﹣＜0，得x＜2∴结合函数的定义域，得当x∈（0，2）时，函数为单调减函数．因此，函数y=x﹣lnx的单调递减区间是（0，2）故答案为：（0，2）．14．（5分）函数f（x）=在x=0处取得极值，则a=0．【解答】解：f′（x）=，若函数f（x）=在x=0处取得极值，则f′（0）=0，解得：a=0，故答案为：0．15．（5分）经过点（2，0）且与曲线y=相切的直线方程为4x+y﹣8=0．【解答】解：点P（2，0）不在曲线y=上．设经过点P（2，0）与曲线y=相切的直线方程为y=k（x﹣2），切点为Q（x0，y0），y′=，则k==，y0=，∴﹣4（x0﹣2）=×，解得x0=1，∴k=﹣=﹣4，∴切线方程为：y=﹣4（x﹣2），化为：4x+y﹣8=0．故答案为：4x+y﹣8=0．16．（5分）已知函数f（x）=x（lnx﹣ax）有两个极值点，则实数a的取值范围是．【解答】解：f（x）=xlnx﹣ax2（x＞0），f′（x）=lnx+1﹣2ax．令g（x）=lnx+1﹣2ax，∵函数f（x）=x（lnx﹣ax）有两个极值点，则g（x）=0在区间（0，+∞）上有两个实数根．g′（x）==，当a≤0时，g′（x）＞0，则函数g（x）在区间（0，+∞）单调递增，因此g（x）=0在区间（0，+∞）上不可能有两个实数根，应舍去．当a＞0时，令g′（x）=0，解得x=．令g′（x）＞0，解得，此时函数g（x）单调递增；令g′（x）＜0，解得，此时函数g（x）单调递减．∴当x=时，函数g（x）取得极大值．当x趋近于0与x趋近于+∞时，g（x）→﹣∞，要使g（x）=0在区间（0，+∞）上有两个实数根，则，解得．∴实数a的取值范围是．故答案为：．三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（10分）已知函数f（x）=（x﹣2）e x．（1）求f（x）的单调区间；（2）求f（x）在区间[0，2]上的最小值和最大值．【解答】解：（1）函数f（x）的导数为f′（x）=（x﹣1）e x，由f′（x）＞0，可得x＞1；由f′（x）＜0，可得x＜1．则f（x）的增区间为（1，+∞），减区间为（﹣∞，1）；（2）由（1）可得f（x）在[0，1]递减，在（1，2]递增，即有f（x）在x=1处取得极小值，且为最小值，且为f（1）=﹣e，由f（0）=﹣2，f（2）=0，可得f（x）的最大值为f（2）=0．则f（x）的最小值为﹣e，最大值为0．18．（12分）已知在平面直角坐标系xOy中曲线C的参数方程为（θ为参数），直线l的参数方程为（t为参数），曲线C与直线l相交于点A，B，且定点P的坐标为（1，0）．（Ⅰ）求曲线C的普通方程；（Ⅱ）求|PA|•|PB|的值．【解答】解：（Ⅰ）曲线C的普通方程为．（Ⅱ）把（t为参数）代入得，化简得：5t2+4t﹣12=0，设A，B对应的参数分别为t1，t2，则t1t2=﹣，∴|PA|•|PB|=|t1t2|=．19．（12分）已知函数f（x）=x3﹣ax2+x（x∈R）．（Ⅰ）若函数y=f（x）在（0，+∞）上为增函数，求a的取值范围；（Ⅱ）若a=1，当x＞1时，求证：f（x）＞x﹣1．【解答】解：（Ⅰ）由已知f'（x）=x2﹣ax+1≥0，即对x∈（0，+∞）恒成立，∵x＞0时，（当且仅当x=1取等号）∴a≤2…（5分）（Ⅱ）a=1时，，设，则g'（x）=x2﹣x=x（x﹣1）当x≥1时，g'（x）≥0，∴g（x）在[1，+∞）单调递减，∴当x＞1时，，即f（x）＞x﹣1．…（12分）20．（12分）已知函数f（x）=x2+mx﹣lnx．（Ⅰ）当m=0时，求曲线y=f（x）在（1，f（1））处的切线方程；（Ⅱ）令g（x）=f（x）﹣x2，当x∈（0，e]（e是自然常数）时，g（x）≥3，求实数m的取值范围．【解答】解：（Ⅰ）当m=0时，f（x）=x2﹣lnx，∴，∴k=f'（1）=1，又f（1）=1∴切线方程为y=x …（4分）（Ⅱ）（方法一）当x∈（0，e]时，g（x）=mx﹣lnx≥3，即对x∈（0，e]恒成立．设，则当时，h'（x）＞0；当时，h'（x）＜0∴h（x）的增区间为，减区间为∴∴m≥e2．…（12分）（方法二）g（x）=mx﹣lnx（0＜x≤e），则当x∈（0，e]时，①时，g'（x）≤0，∴g（x）在（0，e]单调递减∴g（x）min=g（e）=em﹣1≤0矛盾，（舍）②时，当时，g'（x）＜0；当时，g'（x）＞0∴g（x）在单调递减，单调递增∴，解得m≥e2综上，实数m的取值范围为[e2，+∞）．…（12分）21．（12分）已知函数f（x）=ax3﹣（a+2）x2+6x﹣3（1）当a=﹣2时，求函数f（x）的极值；（2）当a＜2时，讨论函数f（x）零点的个数．【解答】解：f'（x）=3ax2﹣3（a+2）x+6=3（ax﹣2）（x﹣1），（1）当a=﹣2时，f'（x）=﹣6（x+1）（x﹣1），令f'（x）=0得x1=1，x2=﹣1，f'（x）＜0时，x＜﹣1或x＞1；f'（x）＞0时，﹣1＜x＜1．∴f（x）的单调递减区间为（﹣∞，﹣1）和（1，+∞），单调递增区间为（﹣1，1），f（x）极小值=f（﹣1）=﹣7，f（x）极大值=f（1）=1．（2）①若a=0，则f（x）=﹣3（x﹣1）2∴f（x）只有一个零点．②若a＜0，f′（x）=0的两根为，则，∴当或x＞1时，f'（x）＜0，当时，f'（x）＞0∴f（x）的极大值为∵f（x）的极小值为∴f（x）有三个零点．③若0＜a＜2，则，∴当x＜1或时，f'（x）＞0，当时，f'（x）＜0，∴f（x）的极大值为∴f（x）有一个零点．综上，当a＜0时，f（x）有3个零点；当0≤a＜2时，f（x）有1个零点．22．（12分）在平面直角坐标系xOy中，已知椭圆C：+=1（a＞b＞0）的离心率为，且经过点（，1），过椭圆的左顶点A作直线l⊥x轴，点M 为直线l上的动点（点M与点A不重合），点B为椭圆右顶点，直线BM交椭圆C于点P．（Ⅰ）求椭圆C的方程；（Ⅱ）求证：AP⊥OM；（Ⅲ）试问•是否为定值？若是定值，请求出该定值；若不是，请说明理由．【解答】（Ⅰ）解：由已知，又，∴a2=b2+c2．联立解得：a2=4，b2=2．∴椭圆C的方程为．（Ⅱ）证明：由（Ⅰ）知，A（﹣2，0），B（2，0），直线BM斜率显然存在，设BM方程为y=k（x﹣2），则M（﹣2，﹣4k），由，得（2k2+1）x2﹣8k2+8k2﹣4=0，△＞0，则，∴，，即．又，，∴，即AP⊥OM．（Ⅲ）解：，∴为定值4．。

黑龙江省哈六中2013-2014学年高二下学期期末考试数学（文）试题考试说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合}12|{},31|{<<-=<<-=x x B x x M ，则=⋂B M ( ))1,2.(-A )1,1.(-B )3,1.(C )3,2.(-D2．命题“对任意的01,23≤+-∈x x R x ”的否定是 （ ）.A 不存在01,23≤+-∈x x R x .B 存在01,23≥+-∈x x R x .C 存在01,23>+-∈x x R x .D 对任意的01,23>+-∈x x R x3．已知某程序框图如图所示，则执行该程序后输出的结果是 （ ）.A 1- .B 21.C 2 .D 1 4.函数43)1ln(2+--+=x x x y 的定义域为 （ ）)1,4.(--A )1,4.(-B )1,1.(-C ]1,1.(-D5．已知函数)(x f y =在R 上是减函数，则)3(-=x f y 的单调减区间是 （ ）.A ),(+∞-∞ .B ),3[+∞ .C ),3[+∞- .D ]3,(-∞6.设函数)(),(x g x f 的定义域为R ，且)(x f 是奇函数，)(x g 是偶函数，则下列结论中正确的是 （ ）)()(.x g x f A 是偶函数 )(|)(|.x g x f B 是奇函数 |)(|)(.x g x f C 是奇函数 |)()(|.x g x f D 是奇函数7．为调查哈市高中三年级男生的身高情况，选取了5000人作为样本，右图是此次调查中的某一项流程图，若其输出的结果是3800，则身高在cm 170以下的频率为 （ ）.A 24.0 .B 38.0 .C 62.0 .D 76.08．下列各组函数中，表示同一函数的是 （ ）.A y y ==.B 112+-=x x y 与1-=x y.C ln ln x x y e y e ==与 .D 001y x y x==与9．已知2211)11(x x x x f +-=+-，则)(x f 的解析式是 （ ） .A 21x x + .B 212x x +- .C 212x x+.D 21xx +- 10. 已知函数)0,(1cos )(≠∈-=x R x xx x f ，则)1(f '值为 （ ）.A 1sin 1-- .B 1sin 1+ .C 1sin 1+- .D 1sin 1-11．已知命题1:≠x p 或2≠y ，命题3:≠+y x q ，则命题p 是q 的（ ）.A 充分不必要 .B 必要不充分 .C 充要条件 .D 既不充分也不必要12．定义在R 上的函数)(x f 满足1)1(=f ，且)(x f 的导数)(x f '在R 上恒有21)(<'x f ，则不等式212)(22+<x x f 的解集是（ ） .A ),1(+∞ .B )1,(--∞ .C )1,1(- .D ),1()1,(+∞⋃--∞第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分．13.甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服种选择1种，则他们选择相同颜色运动服的概率为______14.设函数⎪⎩⎪⎨⎧≥<=-1,1,)(311x x x e x f x ，则使得2)(≤x f 成立的x 的取值范围是15.已知)3,1(,)2()(2-∈-=x x x f ，函数)1(+x f 的单调减区间为16.函数1]3,0[142≠∈-+=x x x x y 且的值域为 三、解答题：解答应写出必要的文字说明，证明过程或演算步骤． 17．（本小题满分10分）已知命题p :方程012=++mx x 有两个不等的负根；命题q :方程244(2)10x m x +-+=无实根．若p 或q 为真，p 且q 为假，求m 的取值范围．18. （本小题满分12分）已知函数)(x f 是定义在R 上的偶函数，当0≥x 时，17)(2++-=x x xx f（1）求0<x 时，)(x f 的解析式； （2）求)(x f 的值域。

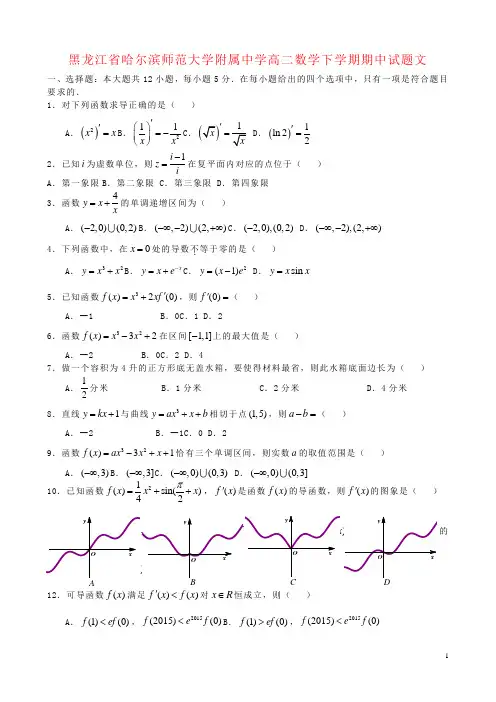
黑龙江省哈尔滨师范大学附属中学高二数学下学期期中试题文一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．对下列函数求导正确的是（ ）A ．()2x x '=B ．211x x '⎛⎫=- ⎪⎝⎭C．'=．()1ln 22'=2．已知i 为虚数单位，则1i z i-=在复平面内对应的点位于（ ） A ．第一象限B ．第二象限 C ．第三象限 D ．第四象限 3．函数4y x x=+的单调递增区间为（ ） A ．(2,0)(0,2)-B ．(,2)(2,)-∞-+∞C ．(2,0),(0,2)- D ．(,2),(2,)-∞-+∞4．下列函数中，在0x =处的导数不．等于零的是（ ） A ．32y x x =+B ．xy x e -=+C ．2(1)y x e =- D ．sin y x x = 5．已知函数3()2(0)f x x xf '=+，则(0)f '=（ ）A ．-1B ．0C ．1D ．26．函数32()32f x x x =-+在区间[1,1]-上的最大值是（ ）A ．-2B ．0C ．2D ．47．做一个容积为4升的正方形底无盖水箱，要使得材料最省，则此水箱底面边长为（ ）A ．12分米 B ．1分米 C ．2分米 D ．4分米 8．直线1y kx =+与曲线3y ax x b =++相切于点(1,5)，则a b -=（ ）A ．-2B ．-1C ．0D ．29．函数32()31f x ax x x =-++恰有三个单调区间，则实数a 的取值范围是（ ）A ．(,3)-∞B ．(,3]-∞C ．(,0)(0,3)-∞D ．(,0)(0,3]-∞10．已知函数21()sin()42f x x x π=++，()f x '是函数()f x 的导函数，则()f x '的图象是（ ）11．已知函数(),()x f x e g x kx k ==+，若函数()f x 的图象恒在函数()g x 图象的上方，则实数k 的取值范围是（ ） A ．[0,)+∞B ．[0,1)C ．(0,1) D ．(1,)+∞12．可导函数()f x 满足()()f x f x '<对x R ∈恒成立，则（ ）A ．(1)(0)f ef <，2015(2015)(0)f ef <B ．(1)(0)f ef >，2015(2015)(0)f e f <O yxOyxOyxOyxAB C DC ．(1)(0)f ef <，2015(2015)(0)f ef > D ．(1)(0)f ef >，2015(2015)(0)f e f >二、填空题：本大题共4小题，每小题5分．13．函数()2ln f x x x =-的单调递减区间为____________．14．函数2()1x af x x +=-在0x =处取得极值，则a =____________．15．经过点(2,0)且与曲线4y x=相切的直线方程为____________． 16．已知函数()(ln )f x x x ax =-有两个极值点，则实数a 的取值范围是____________． 三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（本题满分10分）已知函数()()2xf x x e =-．（Ⅰ）求()f x 的单调区间； （Ⅱ）求()f x 在[]2,0上的最值． 18．（本题满分12分）已知在平面直角坐标系xOy 中曲线C的参数方程为2cos ,x y θθ=⎧⎪⎨=⎪⎩（θ为参数），直线l 的参数方程为112x t y ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数），曲线C 与直线l 相交于点,,A B 且定点P 的坐标为(1,0)．（Ⅰ）求曲线C 的普通方程； （Ⅱ）求PA PB ⋅的值． 19．（本题满分12分）已知函数()()321132f x x ax x x R =-+∈． （Ⅰ）若函数()y f x =在()0,+∞上为增函数，求a 的取值范围； （Ⅱ）若1a =，当1x >时，求证：()1f x x >-． 20．（本题满分12分）已知函数()x mx x x f ln 2-+=．（Ⅰ）当0=m 时，求曲线=y )(x f 在()()1,1f 处的切线方程；（Ⅱ）令()()2x x f x g -=，当(]e x ,0∈（e 是自然常数）时，()3≥x g ，求实数m 的取值范围．21．（本题满分12分）已知函数36)2(23)(23-++-=x x a ax x f ． （Ⅰ）当2-=a 时，求函数)(x f 的极值； （Ⅱ）当2<a 时，讨论函数)(x f 零点的个数． 22．（本题满分12分）在平面直角坐标系xOy 中，已知椭圆C ：22221(0)x y a b a b +=>>的离心率为2，且经过点，过椭圆的左顶点A 作直线l ⊥x 轴，点M 为直线l 上的动点（点M 与点A不重合），点B为椭圆右顶点，直线BM 交椭圆C 于点P ．（Ⅰ）求椭圆C 的方程； （Ⅱ）求证：AP ⊥OM ；（Ⅲ）试问OP OM ⋅是否为定值？若是定值，请求出该定值；若不是，请说明理由． 三、解答题：本大题共6小题，共70分． 17．解：（Ⅰ）()()1xf x x e '=-．…………2分当1x <时，()0f x '<；当1x >时，()0f x '>．∴()f x 的单调减区间为(,1)-∞，增区间为(1,)+∞．…………6分 （Ⅱ）由（Ⅰ）知，()f x 在[0,1]上递减，在[1,2]上递增．又(0)2,(2)0f f =-=∴max ()(2)0f x f ==；min ()(1)f x f e ==-．…………10分18．解：（Ⅰ）曲线C 的普通方程为22143x y +=…………4分 （Ⅱ）将直线l 的参数方程代入曲线C 的普通方程得2213(1))1222t t ++=，即254120t t +-=，△>0设其两根为12,t t ，12125t t ∴⋅=-1212121255PA PB t t t t ∴⋅=⋅=⋅=-=．…………12分 19．解：（Ⅰ）由已知()210f x x ax '=-+≥，即21x a x+≤对()0,x ∈+∞恒成立．∵0x >时，2112x x x x+=+≥（当且仅当1x =取等号） ∴2a ≤…………5分 （Ⅱ）1a =时，()321132f x x x x =-+，设3211()132g x x x =-+，则2()(1)g x x x x x '=-=- 当1x ≥时，()0g x '≥，∴()g x 在[1,)+∞单调递减． ∴当1x >时，5()(1)06g x g >=>，即()1f x x >-．…………12分 20．解：（Ⅰ）当0=m 时，()2ln f x x x =-，∴()12f x x x'=-，∴(1)1k f '==，又(1)1f = ∴切线方程为y x =…………4分（Ⅱ）（方法一）当(]e x ,0∈时，()ln 3g x mx x =-≥，即3ln xm x+≥对(]e x ,0∈恒成立． 设3ln ()(0)x h x x e x+=<≤，则2ln ()xh x x --'=当210x e <<时，()0h x '>；当21x e e<<时，()0h x '<∴()h x 的增区间为21(0,)e ，减区间为21(,)e e∴2max 21()()h x h e e==∴2m e ≥．…………12分（方法二）()ln (0)g x mx x x e =-<≤，则()1g x m x'=-当(]e x ,0∈时，11x e≥①1m e≤时，()0g x '≤，∴()g x 在(]0,e 单调递减∴()min ()10g x g e em ==-≤矛盾，（舍）②1m e>时， 当10x m <<时，()0g x '<；当1x e m<<时，()0g x '>∴()g x 在1(0,)m 单调递减，1(,)e m 单调递增∴()min 1()1ln 3g x g m m==+≥，解得2m e ≥综上，实数m 的取值范围为2[,)e +∞．…………12分 21．解：())1)(2(36)2(332--=++-='x ax x a ax x f（Ⅰ）当2-=a 时，())1)(1(6-+-='x x x f 令()x f '=0得1,121-==x x∴极小值，极大值．…………4分 （Ⅱ）())1)(2(36)2(332--=++-='x ax x a ax x f …………5分①若0=a ，则2)13)(--=x x f （，由()0f x =，得1x = ∴)(x f 只有一个零点．…………6分 ②若0<a ，则12<a∴当a x 2<或x ＞1时，()x f '＜0；当12<<x a时，()x f '＞0 ∴)(x f 的单调递减区间为2(,)a -∞和),1(+∞，单调递增区间为2(,1)a∵=极大值)(x f 02)1(>-=af ，且=极小值)(x f 2246()30f a a a=-+-< ∴)(x f 有三个零点．…………9分 ③若20<<a ，则12>a∴当1<x 或a x 2>时，()x f '＞0；当12<<x a时，()x f '＜0 ∴)(x f 的单调递增区间为(,1)-∞和2(,)a +∞，单调递减区间为2(1,)a∴=极大值)(x f 02)1(<-=af∴)(x f 有一个零点．…………11分综上，02a ≤<时，)(x f 只有一个零点；0<a 时，)(x f 有三个零点．…………12分22．解：（Ⅰ）由已知c a =，则222a b =，又22211a b+=，∴224,2a b == ∴椭圆C 的方程为22142x y +=…………4分（Ⅱ）由（Ⅰ）知，(2,0),(2,0)A B -，直线BM 斜率显然存在，设BM 方程为(2)y k x =-，则(2,4)M k --由22(2)142y k x x y =-⎧⎪⎨+=⎪⎩，得2222(21)8840k x k k +-+-=，△>0则2284221P k x k -=+，∴224221P k x k -=+，24(2)21P P ky k x k -=-=+，即222424(,)2121k k P k k --++………7分 又22284(,)2121k kAP k k -=++，(2,4)OM k =-- ∴2222161602121k k AP OM k k -⋅=+=++，即AP ⊥OM ．…………10分 （Ⅲ）22222222424841684(,)(2,4)421212121k k k k k OP OM k k k k k ---+++⋅=⋅--===++++ ∴OP OM ⋅为定值4．…………12分。

2013-2014学年黑龙江省哈师大附中高二（下）期中化学试卷一．选择题（每小题只有一个选项符合题意，1-10题每小题2分，11-20题每小题2分，共50分）3．（2分）（2014春•哈尔滨校级期中）下列有关除杂质（括号中为杂质）的操作中，不正确4．（2分）（2012春•南充期末）有机物的天然提取和人工合成往往得到的是混合物，假设给你一种这样的有机混合物让你研究，一般要采取的几个步骤是（）5．（2分）（2012秋•朝阳区校级期末）下列有机物在适量的浓度时，不能用于杀菌、消毒的6．（2分）（2012秋•朝阳区校级期末）将转变为的方法为（）7．（2分）（2014春•哈尔滨校级期中）等质量的铜片，在酒精灯上加热后，分别插入下列溶9．（2分）（2015春•菏泽期中）某有机物的化学式为C5H10O，它能发生银镜反应和加成反10．（2分）（2013秋•巢湖期末）分子式为C N H2N O2的羧酸和某醇酯化生成分子式为11．（3分）（2014春•哈尔滨校级期中）分子式为C4H7Cl的氯代烯烃其同分异构体（含顺12．（3分）（2012春•吉林期末）分子式C4H8O2的有机物与硫酸溶液共热可得有机物A和B．将A氧化最终可得C，且B和C为同系物．若C可发生银镜反应，则原有机物的结构13．（3分）（2014春•东阿县校级期末）某一溴代烷水解后的产物在红热铜丝催化下，最多可被空气氧化生成4种不同的醛，该一溴代烷的分子式可能是（）COOH15．（3分）（2014春•花都区校级期末）某有机物的结构简式为，它可以发生反应的类型有（）①加成②消去③水解④酯化⑤氧化16．（3分）（2015春•九江校级期中）化合物丙由如下反应制得：C4H10OC4H8C4H8Br2（丙），丙的结构简式不可能是（）17．（3分）（2015春•大连校级期中）已知A物质的分子结构简式如图，1mol A与足量的NaOH溶液混合共热，充分反应后最多消耗NaOH的物质的量为（）18．（3分）（2014春•鞍山期末）甲醛、乙酸和丙醛组成的混合物中，氧元素的质量分数是19．（3分）（2013秋•芜湖期末）用18O标记的CH3CH218OH与乙酸反应制取乙酸乙酯，当20．（3分）（2014春•哈尔滨校级期中）在120℃、101KPa时，将1L丁烷和若干升O2混合，点燃使之充分反应．反应后，恢复到原温度和原压强，测得的气体体积为m L，若通过足量二．填空题（本题共4小题，共30分）21．（6分）（2014春•哈尔滨校级期中）用系统命名法写出下列有机物的名称：（1）．（2）．（3）．22．（4分）（2014春•哈尔滨校级期中）研究有机物的方法有很多，常用的有①核磁共振氢谱②蒸馏③重结晶④萃取⑤红外光谱⑥过滤，其中用于有机物分离或提纯的方法有，用于分子结构确定的有．（填序号）23．（8分）（2014春•哈尔滨校级期中）某酯A的化学式为C9H10O2，且A分子中只含有1个苯环，苯环上只有一个取代基．现测出A的1H﹣NMR谱图有5个峰，其面积之比为1：2：2：2：3．利用红外光谱仪可初步检测有机化合物中的某些基团，现测得A分子的红外光谱如图：试回答下列问题．（1）A的结构简式可为，请写出与其同类的另外两种有机物的结构简式：，．（2）A的芳香类同分异构体有多种，请写出其中不含甲基且属于芳香酸的B的结构简式．（3）已知C是A的同分异构体，分子中含有一个甲基，且遇FeCl3溶液显紫色，苯环上只有两个对位取代基的芳香醛，C的结构简式．24．（12分）（2014春•哈尔滨校级期中）已知醛在一定条件下可以发生如下转化：RCH2CHO+R′CH2CHO RCH2RCH2CH=物质B是一种可以作为药物的芳香族化合物，请根据如图（所有无机产物均已略去）中各有机物的转变关系回答问题：（1）B的结构简式为．A与新制的氢氧化铜悬浊液反应的方程式为．（2）G、D反应生成H的化学方程式是．（3）一定条件下，能够与1mol F发生反应的H2的最大用量是．（4）G有多种同分异构体，其中能与金属钠反应且苯环上只有一个取代基的同分异构体的结构简式为：、、、．三．实验题（本题共1小题，共12分）25．（12分）（2014春•哈尔滨校级期中）如图是实验室制乙酸乙酯的装置．（1）在大试管中配制一定比例的乙醇、乙酸和浓硫酸的混合溶液的操作方法．（2）从平衡移动原理角度解释浓硫酸在实验中的作用：．（3）饱和Na2CO3溶液的作用是．（4）实验生成的乙酸乙酯，其密度比水（填“大”或“小”），有气味．（5）实验中用3.6mL乙醇（过量）和2.4mL乙酸，若制得乙酸乙酯2.2g，则乙酸乙酯的产率为（乙酸的密度近似为1.0g/cm3）四．计算题（本题共1小题，共8分）26．（8分）（2014春•哈尔滨校级期中）某含氧有机化合物可以作为无铅汽油的抗爆震剂，它的相对分子质量在80～100之间，含C的质量分数为68.2%，含H的质量分数为13.6%，核磁共振氢谱显示该分子中有两种吸收峰，面积比为1：3．（1）写出其分子式（要求有计算过程）．（2）写出该物质的结构简式及所含的官能团的名称．2013-2014学年黑龙江省哈师大附中高二（下）期中化学试卷参考答案与试题解析一．选择题（每小题只有一个选项符合题意，1-10题每小题2分，11-20题每小题2分，共50分）3．（2分）（2014春•哈尔滨校级期中）下列有关除杂质（括号中为杂质）的操作中，不正确4．（2分）（2012春•南充期末）有机物的天然提取和人工合成往往得到的是混合物，假设给你一种这样的有机混合物让你研究，一般要采取的几个步骤是（）5．（2分）（2012秋•朝阳区校级期末）下列有机物在适量的浓度时，不能用于杀菌、消毒的6．（2分）（2012秋•朝阳区校级期末）将转变为的方法为（）转变为转变为，﹣水溶液中的水解生成生成7．（2分）（2014春•哈尔滨校级期中）等质量的铜片，在酒精灯上加热后，分别插入下列溶9．（2分）（2015春•菏泽期中）某有机物的化学式为C5H10O，它能发生银镜反应和加成反上，使之转化为：10．（2分）（2013秋•巢湖期末）分子式为C N H2N O2的羧酸和某醇酯化生成分子式为11．（3分）（2014春•哈尔滨校级期中）分子式为C4H7Cl的氯代烯烃其同分异构体（含顺反异构）的数目为（），12．（3分）（2012春•吉林期末）分子式C4H8O2的有机物与硫酸溶液共热可得有机物A和B．将A氧化最终可得C，且B和C为同系物．若C可发生银镜反应，则原有机物的结构13．（3分）（2014春•东阿县校级期末）某一溴代烷水解后的产物在红热铜丝催化下，最多可被空气氧化生成4种不同的醛，该一溴代烷的分子式可能是（）COOH15．（3分）（2014春•花都区校级期末）某有机物的结构简式为，它可以发生反应的类型有（）①加成②消去③水解④酯化⑤氧化专题：有机物的化学性质及推断．分析：，分子中含有的官能团为：酚羟基、醇羟基、羧基，还含有1个苯16．（3分）（2015春•九江校级期中）化合物丙由如下反应制得：C4H10OC4H8C4H8Br2（丙），丙的结构简式不可能是（）丙的反应为17．（3分）（2015春•大连校级期中）已知A物质的分子结构简式如图，1mol A与足量的NaOH溶液混合共热，充分反应后最多消耗NaOH的物质的量为（）18．（3分）（2014春•鞍山期末）甲醛、乙酸和丙醛组成的混合物中，氧元素的质量分数是×=54%19．（3分）（2013秋•芜湖期末）用18O标记的CH3CH218OH与乙酸反应制取乙酸乙酯，当OH20．（3分）（2014春•哈尔滨校级期中）在120℃、101KPa时，将1L丁烷和若干升O2混合，点燃使之充分反应．反应后，恢复到原温度和原压强，测得的气体体积为m L，若通过足量二．填空题（本题共4小题，共30分）21．（6分）（2014春•哈尔滨校级期中）用系统命名法写出下列有机物的名称：（1）2，6﹣二甲基﹣4﹣乙基辛烷．（2）2，5﹣二甲基﹣2，4己二烯．（3）1，2﹣二氯苯（邻二氯苯）．）含有）22．（4分）（2014春•哈尔滨校级期中）研究有机物的方法有很多，常用的有①核磁共振氢谱②蒸馏③重结晶④萃取⑤红外光谱⑥过滤，其中用于有机物分离或提纯的方法有②③④⑥，用于分子结构确定的有①⑤．（填序号）23．（8分）（2014春•哈尔滨校级期中）某酯A的化学式为C9H10O2，且A分子中只含有1个苯环，苯环上只有一个取代基．现测出A的1H﹣NMR谱图有5个峰，其面积之比为1：2：2：2：3．利用红外光谱仪可初步检测有机化合物中的某些基团，现测得A分子的红外光谱如图：试回答下列问题．（1）A的结构简式可为，请写出与其同类的另外两种有机物的结构简式：，．（2）A的芳香类同分异构体有多种，请写出其中不含甲基且属于芳香酸的B的结构简式．（3）已知C是A的同分异构体，分子中含有一个甲基，且遇FeCl3溶液显紫色，苯环上只有两个对位取代基的芳香醛，C的结构简式．）和同类的有机物即属于酯类的有机物，应该是官能团的，故答案为：，故答案为：24．（12分）（2014春•哈尔滨校级期中）已知醛在一定条件下可以发生如下转化：RCH2CHO+R′CH2CHO RCH2RCH2CH=物质B是一种可以作为药物的芳香族化合物，请根据如图（所有无机产物均已略去）中各有机物的转变关系回答问题：（1）B的结构简式为．A与新制的氢氧化铜悬浊液反应的方程式为．（2）G、D反应生成H的化学方程式是．（3）一定条件下，能够与1mol F发生反应的H2的最大用量是5mol．（4）G有多种同分异构体，其中能与金属钠反应且苯环上只有一个取代基的同分异构体的结构简式为：、、、．的不饱和度为：，故为，不饱和度为：为，据此解的不饱和度为：=6，故为，不饱和度为：为，为，故答案为：，，）有多种同分异构体，其中能与金属钠反应且苯环上只有一个取代基的同分异构体的结构简式为：、故答案为：、三．实验题（本题共1小题，共12分）25．（12分）（2014春•哈尔滨校级期中）如图是实验室制乙酸乙酯的装置．（1）在大试管中配制一定比例的乙醇、乙酸和浓硫酸的混合溶液的操作方法向一支试管中加入乙醇，然后边振荡试管边慢慢加入浓硫酸和乙酸．（2）从平衡移动原理角度解释浓硫酸在实验中的作用：浓硫酸吸收反应产生的水，降低了生成物浓度，有利于平衡正向移动．（3）饱和Na2CO3溶液的作用是吸收除去挥发出来的乙酸和乙醇、降低乙酸乙酯的溶解度．（4）实验生成的乙酸乙酯，其密度比水小（填“大”或“小”），有芳香气味．（5）实验中用3.6mL乙醇（过量）和2.4mL乙酸，若制得乙酸乙酯2.2g，则乙酸乙酯的产率为62.5%（乙酸的密度近似为1.0g/cm3）×=62.5%四．计算题（本题共1小题，共8分）26．（8分）（2014春•哈尔滨校级期中）某含氧有机化合物可以作为无铅汽油的抗爆震剂，它的相对分子质量在80～100之间，含C的质量分数为68.2%，含H的质量分数为13.6%，核磁共振氢谱显示该分子中有两种吸收峰，面积比为1：3．（1）写出其分子式（要求有计算过程）．（2）写出该物质的结构简式及所含的官能团的名称．：：=5；官能团的名称是醚键．。

高二2013-2014学年度（下）学期期中生物选修一考试题一．单选题（本题共有1～40小题，每题只有一个最佳答案，每题1.5分，共计60分）1.下图表示果酒和果醋制作过程中的物质变化过程，下列叙述正确的是（）A．过程①和②都只能发生在缺氧条件下B．过程①和③都发生在酵母菌细胞的线粒体中C．过程③和④都需要氧气的参与D．过程①－④所需的最适温度基本相同2. 在果酒制作实验结束时要检验是否有酒精产生，正确的操作步骤是（）A．先在试管中加入适量的发酵液，然后再加入硫酸和重铬酸钾的混合液B．先在试管中加入适量的发酵液，然后加入重铬酸钾，混匀后滴加硫酸C．先在试管中加入适量的发酵液，然后加入硫酸，混匀后滴加重铬酸钾D．先在试管中加入适量的发酵液，然后加入硫酸，混匀后滴加重铬酸钾，并加热3．在家庭中用鲜葡萄制作果酒时，正确的操作是（）A．让发酵装置接受光照 B．给发酵装置适时排气C．向发酵装置通入空气 D．将发酵装置放在45 ℃处4.下列哪种条件下，醋酸菌将乙醇变为乙醛，再将乙醛变为醋酸（）A．氧气、糖分充足 B．氧气充足，缺少糖源C．缺少氧气，糖分充足 D．氧气、糖源都缺少5.下列与果酒、果醋和腐乳制作相关的叙述，正确的是（）A．腐乳制作所需要的适宜温度最高B．果醋发酵包括无氧发酵和有氧发酵C．使用的菌种分别是酵母菌、醋酸菌、乳酸菌D．使用的菌种都具有细胞壁、核糖体、DNA和RNA6．在腐乳制作过程中，加盐和加酒所发挥的作用相同的是（）A．析出豆腐中的水分，使豆腐块变硬 B．抑制微生物的生长，避免豆腐块腐败变质C．使腐乳具有独特的香味 D．促进蛋白质水解成多肽和氨基酸7．腐乳味道鲜美，易于消化、吸收，是因为其内主要含有的营养成分是（）A．无机盐、水、维生素 B．NaCl、水、蛋白质C．多肽、氨基酸、甘油和脂肪酸 D．蛋白质、脂肪、NaCl、水8．亚硝酸盐在酸性条件下与对氨基苯磺酸重氮化后,再与N-1-奈基乙二胺盐酸盐反应生成的溶液呈( )A．紫红色Ｂ．玫瑰红色Ｃ．砖红色Ｄ．橘红色9.在果酒、果醋和泡菜制做过程中，所用原料的有机物总量及种类变化是（）A．减少、增加 B．减少、减少 C．增加、增加 D．增加、减少10．在制作泡菜的过程中，不正确的是（）A．按照清水与盐的质量4∶1的比例配制盐水B．按照清水与盐的质量5∶1的比例配制盐水C．盐水入坛前要煮沸冷却，以防污染D．在坛盖边沿的水槽中要注满水，以保证坛内的无氧环境11.下列关于亚硝酸盐的叙述中,正确的是( )A.亚硝酸盐为白色粉末,易溶于水,在食品生产中用作食品添加剂,可多加B.绿色食品不会含有亚硝酸盐C.亚硝酸盐在人体胃内易变成亚硝胺D.水煮的越久,亚硝酸盐的含量越少12.下列关于“测定亚硝酸盐含量”实验操作的叙述中,正确的是( )A.泡菜制作需要配制盐水,其中盐与水的质量比为4∶1B.在盐酸酸化条件下,亚硝酸盐与对氨基苯磺酸发生重氮化反应形成玫瑰红色染料C.制备样品处理液,加入氢氧化铝乳液的目的是除去色素等杂质,得到澄清溶液D.泡菜腌制时间长短会影响亚硝酸盐含量,但温度和食盐的用量不影响其含量13．关于制备牛肉膏蛋白胨固体培养基，叙述错误的是（）A．操作顺序为计算、称量、熔化、倒平板、灭菌B．将称好的牛肉膏连同称量纸一同放入烧杯C．待培养基冷却至50℃左右时进行倒平板D．待平板冷却凝固约5～10min后将平板倒过来放置14. 下列有关平板划线接种法的操作错误的是（）A．将接种环放在火焰上灼烧 B．将已冷却的接种环伸入菌液中蘸取一环液C．蘸取菌液和划线要在火焰旁进行 D．划线时要将最后一区的划线与第一区的划线相连15．可以作为硝化细菌碳源、氮源及能量来源的物质依次是（）A.含碳有机物、氨、光B.含碳无机物、氮、氮C.含碳有机物、氨、氨D.含碳无机物、氨、氨16.伊红—美蓝培养基常用来鉴别大肠杆菌，其原理是（）A．大肠杆菌在该培养基中形成特定的菌落B．大肠杆菌能使培养基改变颜色C．大肠杆菌菌的代谢产物与伊红—美蓝结合，使菌落呈深紫色，并有金属光泽D．大肠杆菌能在该培养基中很好生活，其余微生物不能很好生活17.能合成脲酶的微生物所需要的碳源和氮源分别是（）A．CO2和N2B．葡萄糖和NH3C．CO2和尿素 D．葡萄糖和尿素18．农田土壤的表层，自生固氮菌的含量比较多，将用表层土制成的稀泥浆，接种到特制的培养基上培养，可将自生固氮菌与其它细菌分开，对培养的要求是（）①加抗生素②不加抗生素③加氮素④不加氮素⑤加葡萄糖⑥不加葡萄糖⑦37℃恒温箱培养⑧28 ℃--30℃温度下培养A．①③⑤⑦ B．②④⑥⑧ C．②④⑤⑧ D．①④⑥⑦19.在以尿素为唯一氮源的培养基中加入酚红指示剂,培养细菌后,指示剂的颜色是 ( )A.蓝色B.红色C.黑色D.棕色20. 下列叙述错误的是 ( )A.因为土壤中各类微生物的数量不同，所以为获得不同类型的微生物 ,要按不同的稀释倍数进行分离B.测定土壤中细菌的总量和测定土壤中能分解尿素的细菌的数量，选用的稀释范围不同C.只有得到了3个或3个以上菌落数目在30~300的平板,才说明稀释操作比较成功,并能够进行菌落的计数D.牛肉膏蛋白胨培养基的菌落数明显大于选择培养基的数目,说明选择培养基已筛选出一些细菌菌落21.下列关于纤维素分解菌分离实验的说法不正确的是（）A．纤维素酶的发酵方法有液体发酵和固体发酵B．对分解纤维素的微生物进行了初步筛选后，无需再进行其他实验C．纤维素酶的测定方法，一般是对所产生的葡萄糖进行定量的测定D．纤维素酶是一种复合酶22.若将某种细菌置于适宜的培养基上，它会繁殖并形成细胞群（如下图）。

2012-2013学年度哈师大附中第二学期高二期中考试数学试题（文）参考答案一、选择题1．A 、2．C 、3．D 、4．C 、5．A 、6．B 、7．B 、8．C 、9．A 、10．C 、11．C 、12．C 二、填空题 13．58 14．[)1,2 15．131616．①②③ 三、解答题17．（本小题满分10分）（1）2(2)()(1)x e x f x x -'=-，所以(0)2k f '==- (0)1f =- 所以切点为(0,1)-，切线：21y x =--．5分（2）()0f x '>时2x >，()0f x '<时2x <且1x ≠()f x 的减区间为(,1)-∞、(1,2)，增区间为(2,)+∞．10分18．（本小题满分12分） （1）98362⨯=（种） （或8765432136+++++++=种）6分（2）设抽取的两道题编号之和小于17但不小于11为事件A ，事件包括以下15个基本事件：(9,7)、(9,6)、(9,5)、(9,4)、(9,3)、(9,2)、(8,7)、(8,6)、(8,5)、(8,4)、(8,3)、(7,6)、(7,5)、(7,4)、(6,5)，所以155()366P A == 12分19．（本小题满分12分） （1）()3(2)f x x ax '=-由已知是函数)(x f 的一个极值点，(1)3(2)0,2f a a '∴=-=∴=，故()6(1)f x x x '=-，得函数()f x 在区间(0,1)递减，(1,)+∞递增，是函数的值小点，2a ∴=．6分（2）函数)(x f 在区间)0,1(-上是增函数，()0f x '∴≥在)0,1(-恒成立， 即3(2)0x ax -≤在(1,0)-恒成立， 2a x∴≥在(1,0)-恒成立，8分(1,0)x ∈-时，2(,2)x∈-∞-，所以2a ≥-12分20．（本小题满分12分） （1）1a =时，()x bf x x-'=()f x 在区间(3,)+∞递增，所以3x >时()0f x '≥恒成立，2分 需3x >时b x ≤恒成立，所以3b ≤，即1,2,3b =4分设第二次抛掷骰子时，使函数()y f x =在区间(3,)+∞递增为事件A ，31()62p A == 5分（2）()ax bf x x -'=()0f x '>时，b x a >，()0f x '<时，0bx a <<；函数()f x 在区间(0,)b a 递减，在区间(,)ba +∞递增，min ()()(1ln )b bf x f b a a ∴==-，8分0,0b x ∴>∴>且0x →时ln ax b x -→+∞，所以若函数()f x 存在零点，需min ()0f x ∴≤，需1ln0b a -≤，所以be a≥， 1a =时，3,4,5,6b =；2a =时，6b =10分设函数()y f x =存在零点为事件B ，55()6636P B ==⨯。

高二下学期期末考试数学（文）试题考试时间：7: 40~9:40 满分：150分一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的选项中,只有一个选项是符合题目要求的.）1.设集合N }的真子集．．．的个数是（）A．3 B．7 C．8 D．152.复数（i是虚数单位），则z的共轭复数是（）A. B. C. D.3.在右图的正方体中，M、N分别为棱BC和棱CC1的中点，则异面直线AC和MN所成的角为（）A．30° B．45° C．60° D． 90°4.以下有关命题的说法错误的是（）A．命题“若则x=1”的逆否命题为“若”B．“”是“”的充分不必要条件C．若为假命题，则p、q均为假命题D．对于命题5. 设平面与平面相交于直线，直线在平面内，直线在平面内，且，则是的（）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.设函数，则（）A.x=1为的极大值点B. x=-1为的极大值点C.x=1为的极小值点D. x=-1为的极小值点7.在样本的频率分布直方图中，共有11个小长方形，若中间一个小长方形的面积等于其他10个小长方形面积和的，且样本容量为160，则中间一组的频数为（）A.28B.32C.64D.1288. 下面框图所给的程序运行结果为S＝28，那么判断框中应填入的关于k的条件是( )A．? B．k≤7?C．k<7? D．k>7?9. 一只昆虫在边长分别为6,8,10的三角形区域内随机爬行，则其到三角形顶点的距离小于2的地方的概率为（）A. B. C. D.10.已知两条不同直线、，两个不同平面、，给出下列命题：①若∥，则平行于内的所有直线；②若，且⊥，则⊥；③若，，则⊥；④若，且∥，则∥；其中正确命题的个数为（）A.1个B.2个C.3个D.4个11.某四面体的三视图如图所示，该四面体四个面的面积中最大的是()A．8 B．6 2 C．10 D．8 212.定义在R上的函数满足，且对任意都有，则不等式的解集为（）A.(1，2)B.(0，1)C.D.(-1，1)二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上.）13.在平面直角坐标系xoy中，若直线（t为参数）过椭圆C:（为参数）的右顶点，则常数a的值为______.14. 已知边长分别为a、b、c的三角形ABC面积为S，内切圆O半径为r，连接OA、OB、OC，则三角形OAB、OBC、OAC的面积分别为、、，由得，类比得四面体的体积为V，四个面的面积分别为,则内切球的半径R=_________________15.已知函数的图象在点（-1,2）处的切线恰好与直线3x+y=0平行，若在区间上单调递减，则实数t的取值范围是_____________16.已知球的直径SC=4，A.,B是该球球面上的两点，AB=2，∠ASC=∠BSC=45°，则棱锥S-ABC的体积为_________三、解答题(本大题共6小题，共70分.解答应写出必要的文字说明、证明过程及演算步骤)17. （本题满分10分）.已知圆的极坐标方程为：.（Ⅰ）将极坐标方程化为普通方程；（Ⅱ）若点在该圆上，求的最大值和最小值.18. （本小题满分12分）如图1，在直角梯形中，，，且．现以为一边向形外作正方形，然后沿边将正方形翻折，使平面与平面垂直，为的中点，如图2．（1）求证：∥平面；（2）求证：平面；（3）求点到平面的距离.19. （本小题满分12分）某学校准备参加市运动会，对本校甲、乙两个田径队中30名跳高运动员进行了测试，并用茎叶图表示出本次测试30人的跳高成绩（单位cm），跳高成绩在175cm以上（包括175cm）定义为“合格”，成绩在175以下（不包括175cm）定义为“不合格”（1）求甲队队员跳高成绩的中位数（2）如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取5人，则5人中“合格”与“不合格”的人数各为多少？（3）从甲队178cm以上（包括178cm）选取2人，至少有一人在186cm以上（包括186cm）的概率为多少？20. （本小题12分）如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2，以BD的中点O为球心、BD为直径的球面交PD于点M.(1)求证：平面ABM平面PCD;(2)求三棱锥M-ABD的体积.21. （本小题满分12分）某大学生在开学季准备销售一种文具套盒进行试创业，在一个开学季内，每售出1盒该产品获利润50元，未售出的产品，每盒亏损30元．根据历史资料，得到开学季市场需求量的频率分布直方图，如下图所示．该同学为这个开学季购进了160盒该产品，以X（单位：盒，100≤X≤200）表示这个开学季内的市场需求量，Y（单位：元）表示这个开学季内经销该产品的利润．（I）根据直方图估计这个开学季内市场需求量X的平均数和众数；（II）将Y表示为X的函数；（III）根据直方图估计利润不少于4800元的概率．22.（本小题满分12分）已知函数(Ⅰ)试判断函数的单调性；(Ⅱ)设，求在上的最大值；(Ⅲ)试证明：对，不等式.哈四中2015届高二下学期期末考试数学（文）答案一、选择题：二、填空题：18.（1）证明：取中点，连结．在△中，分别为的中点，所以∥，且．由已知∥，，所以∥，且．…………………………3分所以四边形为平行四边形．所以∥．…………………………4分又因为平面，且平面，所以∥平面．………………………4分（3）由（2）知，所以又因为平面又= …………………………10分所以，D到面BEC的距离为…………………………12分19. (1)177 …………………………2分(2)由茎叶图可知，甲、乙两队合格人数共有12人，不合格人数为18人，所以，抽取五人，合格人数为人不合格人数为人…………………………6分（3）…………………………12分20.（1）又由题意得,又…………………………6分（2)设平面ABM与PC交于N∵PD⊥平面ABM∴MN是PN在平面ABM上的射影∴∠PNM是PC与平面ABM所成的角，…………………………8分且∠PNM=∠PCD …………………………9分tan∠PNM=tan∠PCD=PD/DC=2√2 …………………………12分（Ⅲ）∵利润不少于4800元，∴80x-4800≥4800，解得x≥120，∴由（Ⅰ）知利润不少于4800元的概率p=1-0.1=0.9．……………………12分22．解：（I）函数的定义域是：由已知………………………………1分令得，，当时，，当时，函数在上单调递增，在上单调递减…………………3分（III）由（I）知，当时，………………10分在上恒有，即且当时“=”成立对恒有即对，不等式恒成立；………………………………12分。

2014-2015年度高二下学期期中考试数学试卷(理科)考试时间：120分钟 试卷满分：150分一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1.用分析法证明问题时是从要证明的结论出发，逐步寻求使它成立的（ ）A ．充要条件B ．充分条件C ．必要条件D ．既不充分也不必要条件 2.“三角函数是周期函数，tan ,(,)22y x x ππ=∈-是三角函数，所以tan ,(,)22y x x ππ=∈-是周期函数．”在以上演绎推理中，下列说法正确的是（ ）A ．推理完全正确B ．大前提不正确C ．小前提不正确D ．推理形式不正确 3.已知随机变量2(0,)X N σ:,且(2)0.4P X >=,则(20)P X -≤≤=（ ）A ．0.1B ．0.2C ．0.4D ．0.8 4.已知i 为虚数单位，则1i z i-=在复平面内对应的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限5.已知在平面直角坐标系xOy 中圆C 的参数方程为3cos ,13sin .x y θθ⎧=⎪⎨=+⎪⎩（θ为参数），以原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为cos()06πρθ+=，则圆C 截直线l 所得弦长为（ ）A ．6B ．C ．D ．6.若1()nx x-展开式的二项式系数之和为64，则展开式的常数项为（ ）A ．10B ．20C ．20-D ．1207.某校高二年级共有六个班，现从外地转入4名学生，要安排到该年级的两个班级且每班安排2名，则不同的安排方案种数为（ ）A ．2264A CB ．262A C ．2264A A D ．226412A C 8.用反证法证明命题：若整系数一元二次方程20ax bx c ++=(0)a ≠有有理数根，那么,,a b c 中至少有一个是偶数时，下列假设中正确的是（ ）A ．假设,,a b c 都是偶数B ．假设,,a b c 都不是偶数C ．假设,,a b c 至多有一个偶数D ．假设,,a b c 至多有两个偶数9.某班有五十名学生，其中有五名班干部，现选派三名同学完成某项任务，在班干部甲被选中的条件下班干部乙被选中的概率为（ ）A ．149 B ．249 C ．449 D ．64910.某班学生参加植树节活动，苗圃中有甲、乙、丙3种不同的树苗，每种树苗足够多，从中取出5棵分别种植在排成一排的5个树坑内，同种树苗不能相邻，且第一个树坑和第5个树坑只能种甲种树苗的种法共有（ ）A ．15种B ．12种C ．9种D ．6种11.某农科院在3×3的9块试验田中选出3块种植某品种水稻进行试验，则每行每列都有一块试验田种植水稻的概率为 （ ） A ．114 B ．17 C ．314 D ．15612.由正方体1111ABCD A B C D -的8个顶点构成的所有三角形中，任取其中的两个，则它们不共面的概率为（ ） A.18385 B. 192385 C. 367385 D. 376385二、填空题(本大题共4小题，每小题5分，共20分) 13.已知z 是纯虚数,21z i+-是实数,那么z = .14.将全体正整数排成一个三角形数阵 12 3 4 5 6 7 8 9 10 11 12 13 14 15……根据以上排列规律，数阵中第100行的从左至右的第3个数是 .15.2x ()6211x x x x ⎛⎫++- ⎪⎝⎭的展开式中2x 项的系数为 .16.在送医下乡活动中，某医院安排甲、乙、丙、丁、戊五名医生到三所乡医院工作，每所医院至少安排一名医生，且甲、乙两名医生不安排在同一医院工作，丙、丁两名医生也不安排在同一医院工作，则不同的分配方法总数为 .三、解答题（本大题共6小题，17题满分10分，18、19、20、21、22题每题12分，共70分）17.已知在平面直角坐标系xOy 中曲线C的参数方程为2cos ,.x y θθ=⎧⎪⎨=⎪⎩（θ为参数），直线l 的参数方程为11,2.2x t y t ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数），曲线C 与直线l 相交于点,,A B 且定点P 的坐标为(1,0).（Ⅰ）求曲线C 的普通方程；（Ⅱ）求PA PB ⋅的值.18.某商场经销某商品，根据以往资料统计，顾客采用的付款期数ξ的分布列为商场经销一件该商品，采用1期付款，其利润为200元；分2期或3期付款，其利润为250元；分4期或5期付款，其利润为300元．η表示经销一件该商品的利润． （Ⅰ）求事件A ：“购买该商品的3位顾客中，至少有1位采用1期付款”的概率()P A ； （Ⅱ）求η的分布列及数学期望E η．19.某地要举行一次大型国际博览会，为使志愿者较好地服务于大会，主办方决定对40名志愿者进行一次考核．考核分为两个科目：“地域文化”和“志愿者知识”，其中“地域文化”的考核成绩分为10分、8分、6分、4分共四个档次，“志愿者知识”的考核分为A 、B 、C 、D 共四个等级．这40名志愿者的考核结果如下表：（Ⅰ）从“志愿者知识”等级A 中挑选2人，求这2人的“地域文化”考核得分均不小于8分的概率；（Ⅱ）从“地域文化”考核成绩为10分的志愿者中挑选3人，记这3人中“志愿者知识”考核结果为A 等级的人数为X ，求随机变量X 的分布列及数学期望.20.某城市号召中学生在今年春节期间至少参加一次社会公益活动（以下简称活动）．该城市某学校学生会共有12名学生，他们参加活动的次数统计如图所示．（Ⅰ）从学生会中任意选两名学生组成一个小组，若这两人参加活动次数恰好相等，则称该小组为“和谐小组”，求任选该校两名学生会成员组成的小组是“和谐小组”的概率； （Ⅱ）用样本估计总体，从该城市的中学生中任选4个小组（每小组两人），求这4个小组中“和谐小组”的组数X 的分布列及数学期望．21.一次数学考试共有12道选择题，每道选择题都有4个选项，其中有且只有一个是正确的，评分标准规定：“每题只有一个正确选项，答对得5分，不答或答错不得分”．某考生已确定有8道题的答案是正确的，其余题中：有两道题都可判断两个选项是错误的，另两道题都可判断有一个选项是错误的，求该考生 （Ⅰ）得60分的概率；（Ⅱ）所得分数ξ的分布列及其数学期望．24 6参加人数22.如图，分别过椭圆L 的左顶点(3,0)A -和下顶点B 且斜率为k （0k >）的两条直线1l 和2l 分别交椭圆L 于点,C D ，且1l 交y 轴于点M ，2l 交x 轴于点N ，且线段CD 与线段MN 相交于点P .当3k =时，ABM ∆是直角三角形. （Ⅰ）求椭圆L 的标准方程；（Ⅱ）（ⅰ）求证：存在实数λ，使得AM OP λ=uuu r uu u r；（ⅱ）求OP 的最小值.y2014-2015年度高二下学期期中考试数学试卷(理科答案)一、选择题1～6 BCAACC 7～12 DBBDAC 二、填空题13、2i - 14、 4953 15、5- 16、84 三、解答题17、（Ⅰ）曲线C 的普通方程为22143x y += （Ⅱ）将直线l 的参数方程代入曲线C的普通方程得2213(1))122t ++=， 即254120t t +-=设其两根为12,t t ，12125t t ∴⋅=-1212121255PA PB t t t t ∴⋅=⋅=⋅=-= 18、（Ⅰ）由A 表示事件“购买该商品的3位顾客中至少有1位采用1期付款”． 知A 表示事件“购买该商品的3位顾客中无人采用1期付款”3()(10.4)0.216P A =-=，()1()10.2160.784P A P A =-=-=．（Ⅱ）η的可能取值为200元，250元，300元．(200)(1)0.4P P ηξ====，(250)(2)(3)0.20.20.4P P P ηξξ===+==+=，(300)1(200)(250)10.40.40.2P P P ηηη==-=-==--=．η的分布列为2000.42500.43000.2E η=⨯+⨯+⨯240=．19、解（Ⅰ）设“这2人的“地域文化”考核得分均不小于8分”为事件A ,()P A ∴=26213526C C =（Ⅱ）X 的可能取值为0,1,2,3X 服从超几何分布，355310()(0,1,2,3)k kC C P X k k C -⋅=== X ∴的分布列为150123*********EX =⨯+⨯+⨯+⨯=． 20、解（Ⅰ）设“该校两名学生会成员组成的小组是“和谐小组””为事件A ，()P A ∴=22226421213C C C C ++= （Ⅱ）1(4,)3X B Q :4412()(0,1,2,3,4)33kkk P X k C k -⎛⎫⎛⎫∴==⋅⋅= ⎪ ⎪⎝⎭⎝⎭X ∴的分布列为14433EX =⨯=．21、解（Ⅰ）设“得60分”为事件A()P A ∴=11111223336⨯⨯⨯= （Ⅱ）ξ的可能取值为40，45，50，55，6011221(40)22339P ξ==⨯⨯⨯= ，1122112211121(45)223322333P C C ξ==⨯⨯⨯+⨯⨯= ， 112211221112111113(50)22332233223336P C C ξ==⨯⨯⨯+⨯⨯+⨯⨯⨯= ， 1122111211111(55)223322336P C C ξ==⨯⨯⨯+⨯⨯⨯=11111(60)223336P ξ==⨯⨯⨯=. ∴ξ的分布列11404550556093366363E ξ=⨯+⨯+⨯+⨯+⨯=．22、解（Ⅰ）Q 当3k =时，ABM ∆是直角三角形.AM BM ∴⊥，13AB k ∴=-，设(0,)B b -，133AB b k ∴=-=-，1b ∴=∴椭圆L 的标准方程为2219x y +=.（Ⅱ）（ⅰ）直线1:(3)l y k x =+(0,3)M k ∴22(3)99y k x x y =+⎧⎨+=⎩2222(19)548190k x k x k ∴+++-= 2254,319A C A k x x x k -∴+==-+22225432731919C k k x k k --∴=+=++26(3)19C C ky k x k ∴=+=+直线2:1l y kx =-1(,0)N k ∴22199y kx x y =-⎧⎨+=⎩22(19)180k x kx ∴+-= 218,019B D B k x x x k ∴+==+21819D k x k ∴=+2291119D D k y kx k-∴=-=+ 12//l l Q ，设MP PN μ=uuu r uuu r 则CP PD μ=u u r u u u r ，P C P M N P D Px x x xx x x x μ--∴==--2222221813270319191813273101919M D N C P M D N Ck k x x x x k k k x k k x x x x k k k k -⨯-⨯⋅-⋅++∴===-+--++--++ 直线2:33MN y k x k =-+，331P k y k ∴=+33(3,3),(,)3131k AM k OP k k ==++uuu r uu u r ∴存在实数31k λ=+，使得AM uuu r OP λ=uu u r（ⅱ）解法（1）OP =13(1)k t t +=>则OP ==∴当1110t =时，即3k =时min 10OP =. 解法（2）消去参数k 得点P 的轨迹方程是330(03)x y x +-=<<∴OP的最小值是原点O到直线330+-=的距离d==x y。

哈师大附中2012—2013学年度下学期期中考试高二数学理试题第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.从1、2、3、4、5五个数字中任选两个组成个位和十位数字不同的两位数，这个数字是偶数的概率为（ ）A.25 B.35 C.14 D.342. 函数214y x x=+的单调递增区间为（ ）A.(0,)+∞B.(,1)-∞C.1(,)2+∞ D.(1,)+∞3.若甲以10发6中，乙以10发5中的命中率打靶，两人各射击一次，则他们都中靶的概率是( )A.35 B.12 C.310 D.154. 若a ＝⎠⎛02x 2d x ，b ＝⎠⎛02x 3d x ，c ＝⎠⎛02sin x d x ，则a 、b 、c 的大小关系是( )A.a<c<bB.a<b<cC.c<b<aD.c<a<b5. 函数f (x )的定义域为开区间(a ，b )，导函数f ′(x )在(a ，b )内的图象如图所示，则函数f (x )在开区间(a ，b )内有极小值点( )A.1个B.2个C.3个D.4个6. 有3个相识的人某天各自乘火车外出，假设火车有10节车厢，那么至少有2人在同一车厢内相遇的概率为( ) A.29200 B.725 C.29144 D.7187. 如图所示，曲线是函数32()f x x bx cx d =+++的大致图象，则2212x x +等于（ ） A.89B.109C.169D.548. 直线y kx b =+与曲线31y x ax =++相切于点（2,3），则b 的值为（ ） A.-3 B.9 C.-15 D.-79. 已知函数2()=f x x cos x -，则(0.6),(0),(-0.5)f f f 的大小关系是（ ） A.(0)<(0.6)<(-0.5)f f f B.(0)<(-0.5)<(0.6)f f f C.(0.6)<(-0.5)<(0)f f fD.(-0.5)<(0)<(0.6)f f f10. 甲乙两人一起去游“2010上海世博会”，他们约定，各自独立地从1到6号景点中任选4个进行游览，每个景点参观1小时，则最后一小时他们同在一个景点的概率是( ) A.136 B.19 C.536 D.1611.已知实数a ，b 满足1-≤a ≤1，1-≤b ≤1，则函数y ＝13x 3－ax 2＋bx ＋5有极值的概率为( )A.14B.12C.23D.3412. 定义在R 上的可导函数f(x),且f(x)图像连续,当x≠0时, 1'()()0f x x f x -+>,则函数1()()g x f x x -=+的零点的个数为（ ） A.1B.2C.0D.0或2第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分.13. 某厂生产的灯泡能用3000小时的概率为0.8，能用4500小时的概率为0.2，则已用3000小时的灯泡能用到4500小时的概率为 . 14.⎰--2224dx x =________.15.小波通过做游戏的方式来确定周末活动，他随机地往单位圆内掷一点，若此点到圆心的距离大于12，则周末去看电影；若此点到圆心的距离小于14，则去打篮球；否则，在家看书。

哈师大附中2013-2014年度高一下学期期中考试数学试卷考试时间：120分钟 满 分：150分 出 题 人：王健 张治宇审题人：韩长城第Ⅰ卷 （选择题 60分）一．选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知数列,21,n -，则是它的( )A ．第22项B ．第23项C ．第24项D ．第28项2. 若1x <，则下列关系中正确的是 ( )A ． 11x >B ．21x <C ．31x <D ．||1x <3. 已知(2,=-a ，(7,0)=-b ，则a 与b 的夹角为( )A ． o30B ．o60C ．o120D ．o1504. 不等式||y x ≥表示的平面区域为( )5. 等差数列{}n a 的前n 项和为n S ，已知2110m m m a a a -++-=，2138m S -=，则m =( )A ． 2B ． 9C ．10D ． 196. 等比数列{}n a 的各项均为正数，且187465=+a a a a ，则13l o g a +23log a +…+103log a =( )A ． 12B ． 10C ．8D ．32log 5+7. 设0a b <<，则下列不等式中正确的是( )A ． 2a ba b +<<<B ．2a ba b +<<<C ． 2a ba b +<<<D 2a ba b +<<<8. 实数x y ，满足1,21y y x x y ⎧⎪-⎨⎪+⎩≥≤≤5.，求目标函数z x y =-+的最小值( )A ． 1B ． 0C ．3-D ． 5 9. 已知等差数列{}n a 的前n 项和是n S ，若150S >，160S <，则n S 最大值是( )A ． 1SB ． 7SC ． 8SD ． 15S10. 已知点P 为ABC ∆所在平面上的一点，且13AP AB t AC =+，其中t 为实数，若点P 落在ABC ∆的内部（不含边界），则t 的取值范围是( ) A ．104t <<B ．103t <<C ．102t <<D ．203t <<11.已知数列{}n a 的通项公式是221sin()2n n a n π+=, 1232014a a a a ++++=则( )A ．201320132⨯ B ．20131007⨯ C ．20141007⨯D ． 20151007⨯12. 定义np p p n+++ 21为n 个正数n p p p ,,,21 的“均倒数”．若已知数列}{n a 的前n 项的“均倒数”为121+n ，又41+=n n a b ，则11103221111b b b b b b +++ =( ) A ．111 B ．109 C ．1110D ．1211第Ⅱ卷 （非选择题 90分）二．填空题（本大题共4小题，每小题5分，共20分） 13. 已知{}n a 是等比数列，2=2a ，51=4a ，则公比=q ______________． 14. 已知等差数列{}n a 的前n 项和为n S ，若120OB a OA a OC =+，且A ，B ，C 三点共线（该直线不过点O ），则20S =_____________．15. 在 ABC ∆ 中，角 A ，B ，C 的对边分别为 a ，b ，c ，且c =o45B =，面积 2S =，则=b ______________．16. 设12，e e 为两个不共线向量，若12x y =+a e e ，其中,x y 为实数，则记[,]x y =a .已知两个非零向量,m n 满足1122[,],[,]x y x y ==m n ，则下述四个论断中正确的序号为______________．（所有正确序号都填上）① 1212[,]x x y y +=++m n ； ②11[,]x y λλλ=m ，其中R λ∈； ③ m ∥1221x y x y ⇔=n ；④m ⊥12120x x y y ⇔+=n ．三．解答题（本大题共6小题，共70分，解答题应写出文字说明、证明过程或演算步骤） 17．（本小题满分10分）等差数列{}n a 的前n 项和为n S ，已知2=1a ，1045S =．（Ⅰ）求数列{}n a 的通项公式； （Ⅱ）若数列{}n b 满足na nb -=2，求数列{}n b 的前n 项和n T ．18.（本小题满分12分）在锐角ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，且4s i n ()5B C +=，a =5b =．（Ⅰ）求角B 与边c 的值；（Ⅱ）求向量BA 在BC 方向上的投影．19.（本小题满分12分）设数列{}n a 是等差数列，数列{}n b 是各项都为正数的等比数列，且 111a b ==，3521a b +=，5313a b +=.（Ⅰ）求数列{}n a ，数列{}n b 的通项公式； （Ⅱ）求数列{}n n a b ⋅的前n 项和n S ．20.（本小题满分12分）已知向量1(sin ,)2A =m ，(3,sin )A A =n ，且m ∥n ，其中A 是ABC ∆的内角.（Ⅰ）求角A 的大小；（Ⅱ）若2BC =，求ABC ∆面积S 的最大值．21.（本小题满分12分）已知数列{}n a 满足41=a ，)(441*+∈=-N n a a n n n ，数列{}n b 满足4nn na b =． （Ⅰ）求证：数列{}n b 是等差数列； （Ⅱ）设3654321+++++=n a a a a S n n ，求满足不等式5125712<<n n S S 的所有正整数n 的值.22.（本小题满分12分）数列{}n a 的前n 项和为n S ，11a =，121n n a S +=+，等差数列{}n b 满足33b =，59b =． （Ⅰ）求数列{}n a ，数列{}n b 的通项公式；（Ⅱ）若对任意的*n N ∈，不等式1()2n n S k b +⋅≥恒成立，求实数k 的取值范围．2013-2014年度高一下学期期中考试数学参考答案一、选择题：BCCAC BBCCDDC二、填空题：13．12；14．10；15．5；16．①②③ 三、解答题：17．解：设等差数列{}n a 公差为d ，首项为1a………………（1分）则1012110(101)104521S a d a a d -⎧=+=⎪⎨⎪=+=⎩，解得101a d =⎧⎨=⎩，1(1)1n a a n d n =+-=-.……………（6分）（Ⅱ）由（Ⅰ）知，则(1)112()2n n n b ---==………………（8分）()11212211211111--=-⎪⎭⎫ ⎝⎛-⋅=--=n n nn qq b T .………………（10分）18．解：（Ⅰ）由4sin()sin 5B C A +==，………………（2分）由正弦定理，有sin sin a b A B =，所以sin B＝sin b A a =………………（4分） 由题知2B π0<<，故π4B =.………………（5分） 又3cos 5A =，根据余弦定理，22235255c c =+-⋅⋅，解得()71=-=c c 或舍．……（8分）(Ⅱ) 由（Ⅰ）知，cos 2B =，向量BA 在BC 方向上的投影为|BA |cos B ＝227.…（12分） 19．设{}n a 的公差为d ，{}n b 的公比为q ，则依题意有0q >且4212211413d q d q ⎧++=⎪⎨++=⎪⎩，，……………（3分） 解得2d =，2q =．所以1(1)n a n d n =+-=-，112n n n b q --==． ………………（6分）（Ⅱ）由（Ⅰ）得1(21)2n n n a b n -⋅=-⋅，01221123252(23)2(21)2n n n S n n --=⋅+⋅+⋅++-+-，①①左右两端同乘以2得：12312123252(23)2(21)2n nn S n n -=⋅+⋅+⋅++-+-，② ……（9分） ①－②得()121112222(21)22(2n nnnn S n n -+-=+⨯+++--=---，(23)23n n S n =-+…（12分）20．解：由两向量共线知，22sin sin 3A A A +=………………（2分）即32sin 32cos 1=+-A A ，可化为22cos 2sin 3=-A A………………（4分）故2)62sin(2=-πA ，1)62sin(=-πA ，0A π<<，112666A πππ-<-<解得3π=A .………（6分）（Ⅱ）由222222cos 2cos43a b c bc A b c bc π=+-⋅=+-⋅=，………………（8分）又bc c b 222≥+，可知4≤bc ，其中当2b c ==时，等号成立………………（10分）因为111sin sin 42232ABC S bc A bc π∆==≤⋅=.………………（12分）21．证明：由n n n a b 4=，得1114+++=n n n a b ，∴4144111=-=-+++n n n n nn a a b b…………（4分）所以数列{}n b 是等差数列，首项11b =，公差为41.…………（6分） （Ⅱ）43)1(411+=-+=n n b n ，则14)3(4-+==n n n n n b a…………（8分）从而有143-=+n nn a ，故3654321+++++=n a a a a S n n 124441-++++=n 3144141-=--=n n （10分） 则141141422+=--=nn n n n S S ，由5125712<<n n S S ，得511412571<+<n ，即25644<<n ，得41<<n . 故满足不等式5125712<<n n S S 的所有正整数n 的值为3,2.…………（12分）22．设等差数列{}n b 公差为d ，则5329b b d =+=，解得3d =，3(3)36n b b n d n =+-=-，…（2分）当2n ≥时，121n n a S -=+，则13n na a +=()2≥n ，21213a a =+=13a =∴13n n a a +=()1≥n011≠=a ∴{}n a 是以1为首项3为公比的等比数列，则11-=n n q a a 13-=n . …………（6分）（Ⅱ）由（Ⅰ）知，1(1)13311132n n nn a q S q ---===--，原不等式可化为6(2)3nn k -≥…………（8分） 若对任意的*n N ∈恒成立，max6(2)[]3n n k -≥，问题转化为求数列6(2){}3nn -的最大项 令6(2)3n nn c -=，则11n n n n c c c c +-⎧⎨⎩≥≥，解得5722n ≤≤，所以3n =，………………（10分） 即{}n c 的最大项为第3项，3627c =，所以实数k 的取值范围29k ≥.………………（12分）说明：标准答案仅供参考，解答题出现其它方法，只要答案正确可酌情给分.。

哈师大附中— 度下学期期中考试高二数学理试题一．(此题总分值60分,每题5分.在所给的四个选项中有且只有一个是正确的．) 1．x ，y37那么y 与x 的回归方程必经过点 Ａ．〔2，2〕 Ｂ．〔1，3〕Ｃ．〔1.5，4〕 Ｄ．(2，5)2．设1F 、2F 分别是双曲线2219y x -=P 在双曲线上，且120PF PF ⋅=，那么12PF PF += A. 2 2 B. 10 C. 4 2 D. 2103．设函数()y f x =在定义域内可导，()y f x =的图象如图1所示，那么导函数()y f x '=可能为4．A. 24种 B . 36种 C. 72 种 D. 144种5．设函数3()34f x x x =-〔[0,1]x ∈〕，那么()f x 的最小值是A.1B. 1.524x y =上一点到直线54-=x y 的距离最短，那么该点的坐标是A ．)2,1(B ．)0,0(C ．)1,21( D ．)4,1(7. 假设函数()f x 满足321()(1),3f x x f x x '=-⋅-那么(1)f '的值为 A.0 B. 2 C8. 椭圆22221(0)x y a b a b+=>>的两顶点为(,0),(0,)A a B b ，且左焦点为F ，FAB ∆是以点B为直角顶点的直角三角形，那么椭圆的离心率e 为A ．12 B ．12- C ．14+ D ．14+ 9. 某农科院在3×3的9块试验田中选出3块种植某品种水稻进行试验，那么每行每列都有一块试验田种植水稻的概率为A BC DA ．114 B ．17 C ．314 D ． 15610. 函数32()1f x x x mx =+++是R 上的单调函数，那么实数m 的取值范围是 A. 1(,)3+∞ B. 1[,)3+∞ C. 1(,)3-∞ D. 1(,]3-∞11. 抛掷甲、乙两颗骰子，假设事件A ：“甲骰子的点数大于4”； 事件B ：“甲、乙两骰子的点数之和等于7”，那么(|)P B A 的值等于Ａ．13Ｂ．118 Ｃ．19Ｄ．1612.在1,2,3,4,5,6,7的任一排列1234567,,,,,,a a a a a a a 中,使相邻两数都互质的排列方式种数共有Ａ．576 Ｂ．720 Ｃ．864 Ｄ．1440 二. (此题总分值20分.每题5分.)13.三门大炮各自独立击中目标的概率都为0.9，那么三门大炮同时攻击目标，恰有两门大炮击中目标的概率等于 ． 14.假设52345012345(23)x a a x a x a x a x a x -=+++++,那么123452345a a a a a ++++= ．15. 某名考生的高考数学成绩近似服从正态分布N 〔120，100〕，那么此校数学成绩在140 分以上的考生人数约为 ．〔注：正态总体2(,)N μσ在区间(2,2)μσμσ-+内取值的概率约为0.954〕 16.()ln 0f x ax x =->对一切0x >恒成立,那么实数a 的取值范是 ． 三．〔本大题总分值70分〕 17．〔此题总分值10分〕某小组有5名女生和4名男生,现从中任选3人去参加一项公益活动． (1)求所选3人中恰有一名男生的概率:(2)设所选3人中男生人数为ξ,求ξ的分布列与期望．18．(此题总分值12分) 函数2()(713)xf x x x e =-+．(1)求曲线()y f x =在其上一点(0,(0))P f 处的切线的方程; (2)求函数()y f x =的极值．19．(此题总分值12分)某的课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某假设单科成绩在85分以上(含85分)，那么该科成绩为优秀．〔2〕根据〔1〕中表格的数据计算，是否有99%的把握，认为学生的数学成绩与物理成绩之间有关系？〔3〕假设从这20个人中抽出1人来了解有关情况，求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率．参考公式:22()()()()()n ad bc K a b c d a c b d -=++++20．(此题总分值12分) 设函数()ln (0,)af x x x a R x=+>∈． 〔1〕求()f x 的单调区间；〔2〕设[]1,2x ∈，求()f x 的最小值．21. (此题总分值12分)设函数()2(1)ln(1)(0,)f x ax x x x a R =++-≥∈． (1)当0a =时,求证:()f x x ≤；(2)假设0a <,证明:()0f x ≥对一切0x ≥不恒成立；(3)假设12a ≥,证明:()0f x ≥对一切0x ≥恒成立．22. (此题总分值12分)椭圆22221(0)y x a b a b +=>>的离心率为2．斜率为(0)k k ≠的直线过椭圆的上焦点且与椭圆相交于P ，Q 两点，线段PQ 的垂直平分线与y 轴相交于点(0,)M m ，且当1k =时，下焦点到直线 〔1〕求椭圆的方程； 〔2〕求m 的取值范围；〔3〕试用m 表示MPQ ∆的面积，并求面积的最大值．参考答案一．二、17．解：〔1〕设所选3人中恰有一名男生的事件为A ，那么21543910()21C C P A C == 〔2〕ξ所有可能取值为：0，1，2，335395(0)42C P C ξ===，21543910(1)21C C P C ξ===， 1254395(2)14C C P C ξ===，0354391(2)21C C P C ξ=== ， ξ的分布列为： 5105140123422114213E ξ∴=⨯+⨯+⨯+⨯= 18．解：2()(56)(2)(3)x x f x x x e x x e '=-+=-- 〔1〕(0)13,(0)6f f '==曲线()y f x =在其上一点(0,(0))P f 处的切线的方程为：613y x =+〔2〕()02f x x '=⇔=或3x =当x 变化时，()f x '、()f x 变化如下表：23(2)3,(3)y f e y f e ∴====极大值极小值19〔1〕〔2〕根据列联表可以求得：2220(51212)8.802 6.635614713k ⨯⨯-⨯=≈>⨯⨯⨯， 所以，我们有99%的把握认为：学生的数学成绩与物理成绩之间有关系 〔3〕设数学成绩与物理成绩至少有一门不优秀的事件为A ，那么A 表示数学成绩与物理成绩都优秀的事件，那么53()1()1204P A P A =-=-=． 20．解：221()a x a f x x x x-'=-= 〔1〕①当0a ≤时，()0,()f x f x '≥∴的递增区间为(0,)+∞；②当0a >时，()0f x x a '=⇔=，当0x a <<时，()0f x '<，当x a >时，()0f x '>，()f x ∴的递增区间为(,)a +∞，()f x 的递减区间为(0,)a ． 〔2〕①当1a ≤时，()0,()f x f x '≥∴在[]1,2上单调递增，min (1)y f a ∴==；②当2a ≥时，()0,()f x f x '≤∴在[]1,2上单调递减，min (2)ln 22a y f ∴==+； ③当12a <<时，由〔1〕知：()f x 在(,)a -∞上单调递减，()f x 在(,)a +∞单调递增，∴当x a =时，min ()ln 1y f a a ==+．21．解：〔1〕当0a =时，()ln(1)0f x x x x ≤⇔+-≤； 令()ln(1)(0)g x x x x =+-≥，1()1011xg x x x -'=-=≤++，()g x ∴在[0,)+∞上递减， ()(0)0g x g ∴≤=， ()f x x ∴≤；〔2〕当0a <时，取1x a>-，那么0x >，10,ln(1)0,0ax x x +<+>-<，()2(1)ln(1)0f x ax x x ∴=++-<，故此时，()0f x ≥对一切0x ≥不恒成立； 〔3〕当12a ≥时， 〔法一〕由〔1〕可知，11ln()11x x >++ 22()2ln(1)112ln(1)1111ln()011ax f x a x x x x x x x +'=++-++≥++-+=->++()f x ∴在[)0,+∞上单调递增，()(0)0f x f ∴≥=． 〔法二〕22()2ln(1)11ax f x a x x +'=++-+，令22()2ln(1)11ax g x a x x +=++-+，10,,(21)02x a ax a ≥≥∴+-≥，2212[(21)]()2[]01(1)(1)a a ax a g x x x x -+-'∴=+=≥+++， ()g x ∴在[)0,+∞上单调递增，()(0)0g x g ∴≥>，即()0f x '>， ()f x ∴在[)0,+∞上单调递增，()(0)0f x f ∴≥=．22． 〔1〕依题意可得，22=a c ，1c =，可得1,b a =．所以椭圆方程为2212y x +=． 〔2〕设直线l 的方程为1y kx =+，由221,1,2y kx y x =+⎧⎪⎨+=⎪⎩可得22(2)210k x kx ++-=． 设1122(,),(,)P x y Q x y ，那么12222k x x k -+=+，12212x x k =-+． 可得121224()22y y k x x k +=++=+． 设线段PQ 中点为N ，那么点N 的坐标为222(,)22k k k -++， 由题意有1-=⋅k k MN ，可得222212m k k k k -+⋅=-+．可得212m k =+， 又0k ≠，所以102m <<． 〔3〕设椭圆上焦点为F ，那么1212MPQ S FM x x ∆=⋅⋅-. 12x x -== 由212m k =+，可得212k m+=．所以12x x -== 又1FM m =-，所以MPQ S ∆=所以△MPQ 的面积为3)1(2m m -〔210<<m 〕． 设3)1()(m m m f -=，那么)41()1()('2m m m f --=．可知)(m f 在区间)41,0(单调递增，在区间)21,41(单调递减． 所以，当41=m 时，)(m f 有最大值127()4256f =． 所以，当41=m 时，△MPQ．。